GW231123: a Binary Black Hole Merger with Total Mass 190-265
Abstract
On 2023 November 23 the two LIGO observatories both detected GW231123, a gravitational-wave signal consistent with the merger of two black holes with masses and (90% credible intervals), at luminosity distance 0.7–4.1 Gpc and redshift of , and a network signal-to-noise ratio of 22.5. Both black holes exhibit high spins, and respectively. A massive black hole remnant is supported by an independent ringdown analysis. Some properties of GW231123 are subject to large systematic uncertainties, as indicated by differences in inferred parameters between signal models. The primary black hole lies within or above the theorized mass gap where black holes between 60–130 should be rare due to pair instability mechanisms, while the secondary spans the gap. The observation of GW231123 therefore suggests the formation of black holes from channels beyond standard stellar collapse, and that intermediate-mass black holes of mass 200 form through gravitational-wave driven mergers.
]Compiled: September 21, 2025
04.80.Nn, 04.25.dg, 95.85.Sz, 97.80.-d 04.30.Db, 04.30.Tv
1 Introduction
From 2015 to 2020 the LIGO-Virgo-KAGRA Collaboration identified 69 gravitational-wave signals from binary black hole mergers with false alarm rates below one per year (Aasi et al., 2015; Acernese et al., 2015; Abbott et al., 2020c; Akutsu et al., 2020; Abbott et al., 2023a). Of these, the most massive was the source of GW190521, with a merger remnant of 140 (Abbott et al., 2020d, e). The small number of observable cycles of GW190521 limits our ability to accurately infer the source’s properties, and subsequent studies have proposed a wide range of alternative interpretations, including highly eccentric orbits, dynamical capture scenarios, exotic object mergers, and cosmic string collapse (Gayathri et al., 2022; Romero-Shaw et al., 2020a; Gamba et al., 2023; Calderón Bustillo et al., 2021b; Aurrekoetxea et al., 2024). Here we present a yet more challenging signal: GW231123_135430 (hereafter referred to as GW231123), confidently observed through a coincident detection in both the LIGO Hanford and Livingston detectors during the first part of their fourth observing run, O4a (2023 May 24 to 2024 January 16). The combination of data from the two observatories was essential in making a confident detection.
GW231123 consists of 5 cycles over a frequency range of 30–80 Hz. We interpret GW231123 as a binary-black-hole merger and infer a total mass between 190 and 265 and high component black-hole spins (0.9 and 0.8). While a few gravitational-wave candidates have been observed with similarly high total masses (Abbott et al., 2023a; Wadekar et al., 2023), none have false alarm rates less than 1 per year; in addition, GW231123 has both a large signal-to-noise ratio and high statistical significance. Such high masses and spins pose a challenge to our most accurate waveform models, leading to larger uncertainties in the black-hole masses, and the binary orientation and distance, than any previous signal of comparable strength.
Pair instability supernovae and pulsational pair instability supernovae are expected to preclude stellar collapse to black holes with masses –130 (Farmer et al., 2019, 2020; Woosley & Heger, 2021; Hendriks et al., 2023), and the majority of the astrophysical population of black holes inferred from gravitational-wave catalogs lies below this gap (Abbott et al., 2023b). The large measurement uncertainties in the source of GW231123 mean that the primary black hole may be within or beyond the mass gap, while the range of possible values for the secondary mass spans the entire gap. It is also possible that the two black-hole masses lie on either side of the gap. The scenarios with the highest probability require a formation channel that populates the mass gap, such as prior stellar (e.g., Di Carlo et al., 2020; Renzo et al., 2020a; Kremer et al., 2020) or black-hole (Gerosa & Fishbach, 2021) mergers. The high inferred spins do not exclude these interpretations, although their values may be higher than the inferred spins of the remnant black holes produced in the binary-black-hole mergers observed so far.
In this paper we present the LIGO-Virgo-KAGRA analysis of GW231123. In Section 2, we establish GW231123 as a confident gravitational wave (GW) detection. In Section 3, we discuss the data quality at the time of the observation. In Section 4, we first discuss our treatment of waveform uncertainties, then present the source properties and additional waveform consistency checks. In Section 5, we analyse the ringdown portion to test the consistency of a black hole (BH) remnant interpretation. In Section 6 we present a range of potential astrophysical implications. Although the binary black hole (BBH) merger scenario presented throughout this paper is the most plausible astrophysical explanation for the source of GW231123, alternative scenarios cannot be ruled out and we discuss a selection of these in Section 7. We conclude in Section 8, and provide additional material in support of our results in a series of appendices.
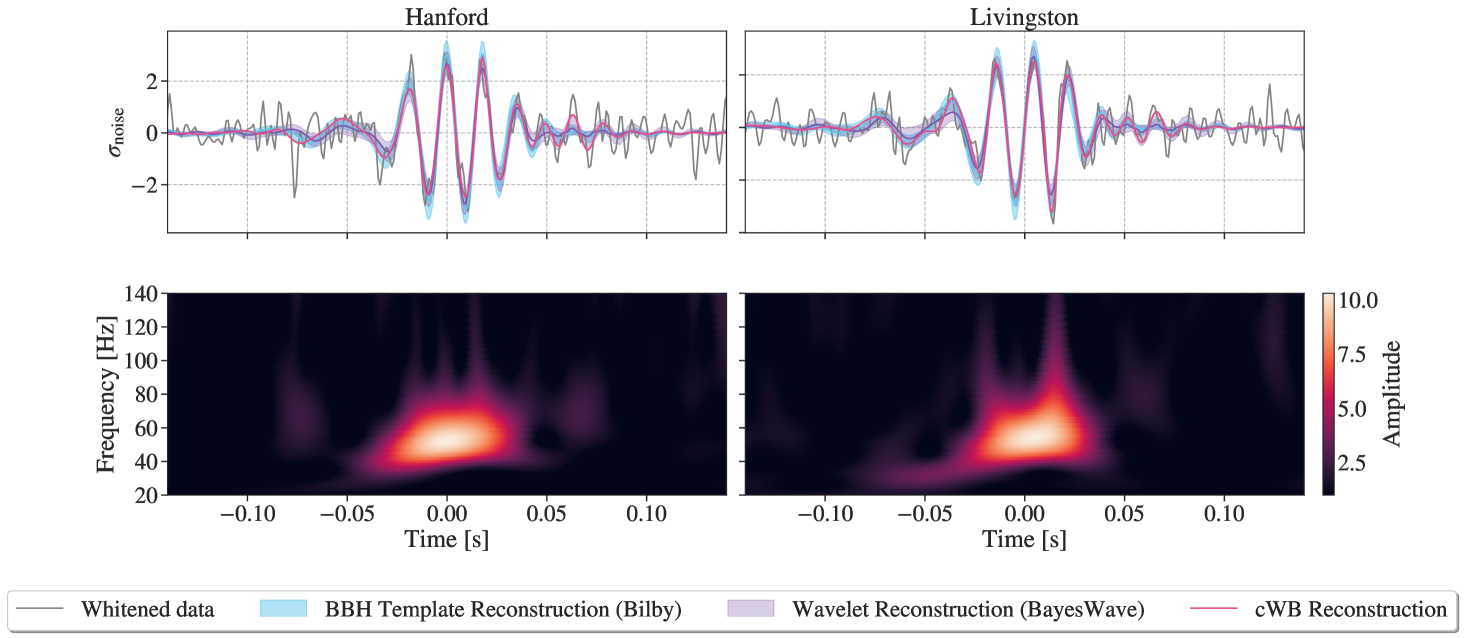
2 Detection Significance
On 2023 November 23, at 13:54:30 UTC, the Advanced LIGO Hanford and Livingston detectors observed the GW transient GW231123. Despite its short duration (0.1 s) and limited bandwidth (Figure 1), the signal was identified in low-latency analyses with high statistical significance, reported in terms of inverse false-alarm rate (IFAR); see Table. 1. It was first detected by PyCBC Live, a matched-filter search for compact binaries (Allen, 2005; Usman et al., 2016; Nitz et al., 2017; Dal Canton et al., 2021). It was also reported by coherent WaveBurst (cWB)-BBH, a minimally modelled coherent excess power search (Mishra et al., 2025). The cWB-BBH search uses the WaveScan time–frequency (TF) transformation (Klimenko, 2022) and ranks identified triggers using a machine-learning classifier trained specifically on BBH signals (Mishra et al., 2021, 2022, 2025). In addition, the event was also detected by two model-independent low-latency cWB searches, or burst searches, designed to identify generic GW transients: cWB-2G and cWB-XP. The former is based on the Wilson–Debauchies–Meyer TF transformation (Klimenko et al., 2008, 2016a; Drago et al., 2020), while the latter uses the WaveScan TF transformation. Both apply a machine-learning classifier (XGBoost), trained on generic white-noise-bursts to rank identified triggers (Szczepańczyk et al., 2023). For further details on model-independent searches, see Abac et al. (2025a).
Subsequent offline or archival reanalyses using improved background estimation and data quality information further increased the event’s statistical significance in both the PyCBC and cWB pipelines (Table 1). Furthermore, two additional matched-filter searches, GstLAL (Messick et al., 2017; Sachdev et al., 2019; Hanna et al., 2020; Cannon et al., 2021; Sakon et al., 2024; Ewing et al., 2024; Tsukada et al., 2023; Joshi et al., 2025) and MBTA (Adams et al., 2016; Aubin et al., 2021; Alléné et al., 2025), which did not detect this event with significant confidence in low-latency (IFAR higher than 1 year), recovered it in their offline analyses. These searches differ from PyCBC (Davies et al., 2020; Chandra et al., 2021b; Davis et al., 2022; Kumar & Dent, 2024) in their implementation and use of signal–noise discriminators. GstLAL’s enhanced significance (the higher IFAR in Table. 1) is primarily driven by a higher mass extension of the search with specific settings to compute the background for such higher mass mergers accurately. More details are provided in Abac et al. (2025b). These changes improved the signal and noise models in this part of the parameter space in general, leading to a better recovery of this high mass signal. Additionally, cWB-GMM, an entirely offline model-independent search, uses Gaussian Mixture Models (Gayathri et al., 2020; Lopez et al., 2022; Smith et al., 2024) to rerank the triggers identified by cWB-2G.
| CBC pipelines | Offline | Online | Offline |
| SNR | IFAR (yr) | IFAR (yr) | |
| PyCBC | 19.9 | 160 | |
| GstLAL | 20.1 | ||
| MBTA | 19.0 | – | 60 |
| cWB-BBH | 21.8 | 9700 | |
| Burst pipelines | |||
| cWB-2G | 21.4 | ||
| cWB-XP | 21.1 | ||
| cWB-GMM | 21.4 | – | 100 |
The differences in the IFARs reported by the offline search pipelines—despite broadly consistent signal-to-noise ratios—primarily reflect differences in their ability to separate GW231123-like signals from background noise in a comparable parameter range. Similar discrepancies have been observed previously, particularly between matched-filter and minimally-modelled searches, when searching for non-eccentric intermediate-mass black hole (IMBH) binaries (Calderón Bustillo et al., 2018; Chandra et al., 2020; Abbott et al., 2020d; Chandra et al., 2021a; Szczepańczyk et al., 2021). These differences arise not only from how effectively each search separates signals from glitches, but also from the differing approaches used to estimate the noise background.
To assess whether the observed variation in statistical significance across pipelines is consistent with expectations, we conducted a dedicated injection campaign. Using the NRSur7dq4 (NRSur) waveform model (Varma et al., 2019), we simulated 8000 non-eccentric BBH signals with intrinsic parameters consistent with those inferred for GW231123 (Section 4). We sampled the sky positions and binary orientations isotropically and drew redshifts uniformly in comoving volume up to , assuming a flat CDM cosmology (Ade et al., 2016). We added these simulated signals uniformly over several days around the event and re-ran our offline search pipelines using the same configuration as applied to the real data.
We found that for simulated signals observed in both Advanced LIGO detectors, the CBC searches recovered the following fractions with a IFAR above 100 years, cWB-BBH 32%, PyCBC 27%, GstLAL 41%, and MBTA 16%. For the Burst searches, cWB-2G and cWB-XP each recovered 22%, while cWB-GMM recovered 10%. Since Burst searches identify coherent power across the detector network without relying on BBH waveform models, their efficiencies are not directly comparable to CBC searches. However, within each search category, detection pipelines reporting a higher IFAR for GW231123 consistently demonstrated higher recovery fractions for simulated signals with masses and spins representative of those inferred for GW231123.
Given the reported IFAR for GW231123 across the different searches and the results of the injection study, we consider GW231123 to be a confident detection with strong support for an astrophysical origin.
3 Data quality
The event GW231123 was detected during the first part of the fourth observing run (O4a), a time when the LIGO Hanford and LIGO Livingston detectors were observing with a typical binary neutron star inspiral range of 152 Mpc and 160 Mpc (Capote et al., 2025). The detectors’ data were calibrated in near real-time to produce the online dataset used for low-latency searches (Abbott et al., 2020b; Klimenko et al., 2016b; Tsukada et al., 2023; Ewing et al., 2024; Dal Canton et al., 2021; Chu et al., 2022; Aubin et al., 2021) and parameter estimation (Singer & Price, 2016; Ashton et al., 2019; Pankow et al., 2015). The calibration process subtracts linear spectral features from known instrumental sources, identified through auxiliary witness sensors, and intentionally injected calibration lines used to measure the instruments’ response at various frequencies (Viets et al., 2018a; Sun et al., 2020, 2021).
Following the data-quality procedures established for O4a (Soni et al., 2025), including broadband noise subtraction (Vajente et al., 2020) and data-quality report analysis routines (Davis et al., 2021), detector data surrounding the event were evaluated for signs of non-Gaussian excess power (glitches) within the target time-frequency analysis window using a spectrogram-based glitch-identification tool (Vazsonyi & Davis, 2023). It was determined that glitches were present in each detector around, but not coincident with the event.
From spectrograms, we determined that a glitch was present in the LIGO Hanford data 1.7–1.1 s before the event, in a frequency range between 15–30 Hz. The glitch is possibly related to the LIGO Hanford differential arm control loop (Aasi et al., 2015). This control loop leads to nonstationary noise from the high root-mean-square drive applied to the electrostatic drive actuator. This issue has been fixed in the second part of the fourth observing run (Vajente, 2024). This glitch was close to the event and within the time–frequency window used to infer the source properties, so BayesWave (Cornish & Littenberg, 2015; Cornish et al., 2021; Chatziioannou et al., 2021) was used to model simultaneously the compact binary signal and the glitch (Soni et al., 2025). We removed this non-Gaussianity from the data by subtracting a phenomenological, wavelet-based model of the excess power noise (Hourihane et al., 2022; Ghonge et al., 2024). The glitch-subtracted data successfully passed the validation process, which compares the residual noise to Gaussian noise (Soni et al., 2025; Vazsonyi & Davis, 2023). Additional broadband non-stationary noise was present in the Hanford detector in the hours of data surrounding GW231123, but we found no evidence that this impacted the analysis of GW231123.
In LIGO Livingston data, a glitch was identified 3.0–2.0 s before the event, in a frequency range between 10–20 Hz. Given that LIGO Livingston had recurring low-frequency scattered light glitches (Soni et al., 2025), this glitch was likely caused by scattered light. We determined the time–frequency profile of the glitch to have no measurable effect on the GW231123 analysis, so the analyses from here on use the LIGO Livingston original data and the LIGO Hanford glitch-subtracted data.
4 Source properties
In the following, we describe the methods used to estimate the source properties (Section 4.1), and how we deal with the systematic differences in results from multiple signal models (Section 4.2). Having discussed our methods and sources of error, we present and discuss our estimates of the source properties in Section 4.3, and finally our waveform consistency checks (Section 4.4).
4.1 Methods
We report the properties of GW231123 assuming a non-eccentric BBH merger. We perform a coherent Bayesian analysis (Abbott et al., 2016a) of the LIGO Hanford and LIGO Livingston data around the time of GW231123. We calculate the likelihood using 8 s of data (6 s before and 2 s after the reported merger time of GW231123), and consider frequencies within the range 20–448 Hz. All analyses employ standard priors used in previous analyses (Abbott et al., 2021a, 2024a, 2023a), and we use a Planck 2015 cosmology (Ade et al., 2016). The NRSur analysis employs a reduced prior mass range due to model constraints, mass ratios below 6:1. The other models employ a wider mass prior, mass ratios below 10:1, and no posterior support is found beyond the NRSur analysis. We characterize the detector noise via the median on-source power spectral density (PSD) produced from BayesWave (Cornish & Littenberg, 2015; Littenberg & Cornish, 2015). To sample the posterior distribution, we interface with dynesty (Speagle, 2020) via the bilby library (Ashton et al., 2019; Romero-Shaw et al., 2020b). We use live points and the bilby-implemented acceptance-walk sampling algorithm. We verify that the results remain consistent when the number of live points is increased, as well as when we lower the frequency range to include data between 16–20 Hz.
4.2 Waveform Systematics
The source properties of GW231123 lie in a challenging region of parameter space for current waveform models, to such an extent that measurements using different models show significant disagreement, with multiple parameters failing to agree within 90% credible intervals. (See Appendix A for examples.) In general, our models are well within our observations’ accuracy requirements, and the level of model disagreement for GW231123 has not been seen in any previous LVK GW observation with moderate SNRs (12). All models show strong support for spins 0.8, and since no theoretical signal model is calibrated to numerical-relativity (NR) waveforms from precessing binaries with spins above 0.8, waveform uncertainties are one possible cause of the measurement differences. Hence, before presenting the source properties, we describe how we quantify waveform-model uncertainties. We do not study in detail the impact of Gaussian noise fluctuations or low-SNR glitches that are difficult to identify and mitigate using the methods presented in Section 3.
We consider five state-of-the-art signal models, NRSur7dq4 (NRSur; Varma et al., 2019), SEOBNRv5PHM (v5PHM; Ramos-Buades et al., 2023a), IMRPhenomTPHM (TPHM; Estellés et al., 2022a), IMRPhenomXPHM (XPHM; Colleoni et al., 2025) and IMRPhenomXO4a (XO4a; Thompson et al., 2024). (More details are given in Appendix A.) The model papers referenced here include studies to assess the accuracy of these models across the BBH parameter space, but here we focus on the likely region of parameter space for this observation; high total mass, , and moderate to high spins.
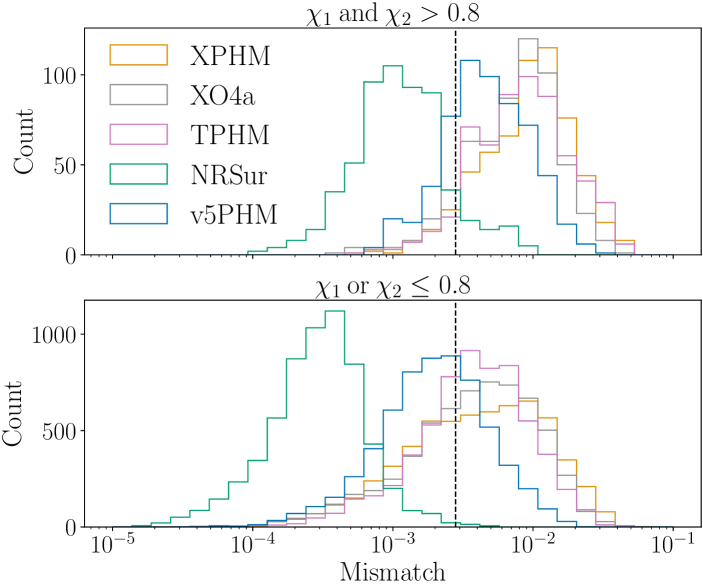
We quantify the models’ accuracy against NR results, including a set of simulations that extend up to spins of 0.95 (Boyle et al., 2019; Hamilton et al., 2024; Scheel et al., 2025). A standard waveform accuracy measure is the mismatch between two waveforms (Cutler & Flanagan, 1994), where waveform uncertainties will not bias a parameter measurement if the model’s mismatch uncertainty is less than (McWilliams et al., 2010; Baird et al., 2013), where is the SNR and is the chi-square value for degrees of freedom at probability . For single-parameter measurements provides a lower bound (Thompson et al., 2025), so the mismatch criterion for the 90% credible interval at is . Figure 2 reports the distribution of mismatches of each model against 1123 NR waveforms with , all scaled to the redshifted (detector-frame) total mass , at six equally spaced inclinations in from to inclusive. The mismatches are calculated for precessing systems (Schmidt et al., 2015; Harry et al., 2016) following the procedure described in Hamilton et al. (2021), maximising over time shifts, a global phase and template polarisation and optimising over in-plane spin rotations. A subset of the simulations come from the third release of the SXS catalog (Scheel et al., 2025) and contain GW memory, which introduces a constant late-time offset that we handle with a highpass filtering technique (Xu et al., 2024; Valencia et al., 2024; Chen et al., 2024) to mitigate possible artifacts in the Fourier domain. We employ the same PSD for the LIGO Livingston detector as utilised in the coherent Bayesian analysis. NRSur performs better than the other models (by roughly an order of magnitude for low-spin cases), and all other models have comparable accuracy. However, NRSur does not meet the conservative accuracy criterion for all cases, and for spins greater than 0.8 the mismatches are higher in 10% of 98 cases. Even if we apply a less conservative mismatch criterion from the literature (e.g., with for non-eccentric binaries and (Chatziioannou et al., 2017; Scheel et al., 2025) we have 0.0072) there are configurations where NRSur exceeds the criterion (2%). The relative accuracy of models is also not uniform across all cases, e.g., we find cases in which other models show comparable or improved performance relative to NRSur.
To test whether these waveform uncertainties will incur biases, we performed our standard Bayesian parameter estimation analysis on a series of NR injections, as detailed in Appendix A. We observe that, while the five models considered here perform well for most signals, there are configurations where all models may incur biases for massive high-spin signals. We also find that the relative performance of each model can change in the presence of Gaussian noise, although this requires more detailed study in future work. To properly correct for this, we would ideally marginalise over waveform uncertainties or incorporate model accuracy into Bayesian analyses (Read, 2023; Khan, 2024; Hoy et al., 2024; Pompili et al., 2024; Kumar et al., 2025; Mezzasoma et al., 2025). Without access to a model of the waveform-model uncertainties, we follow what has been done previously (Abbott et al., 2016a) and combine the results from multiple models to marginalise over the model uncertainties. In choosing models in addition to NRSur, we note that all other models exhibit a comparable range of mismatches, and no model is clearly preferred in our injection studies, and so we include all five state-of-the-art models. We combine posterior results inferred from NRSur, v5PHM, TPHM, XPHM, XO4a with equal weight and report the combined samples throughout this paper. To illustrate the variation between the combined results and single models, in some figures we also show the NRSur results. In some analyses we expect the choice of model to have little impact, e.g., the detection significance study in Section 2, and in these cases, we use only the NRSur samples.
4.3 Inference
Our Bayesian analysis indicates that GW231123 was produced from a high-mass compact binary merger with highly spinning components. We infer individual source component masses and with spin magnitudes and . We present a summary of the key source properties of GW231123 in Table 2. Unless otherwise stated, we report all mass measurements in the source frame.
| Primary mass | |
| Secondary mass | |
| Mass ratio | |
| Total mass | |
| Final mass | |
| Primary spin magnitude | |
| Secondary spin magnitude | |
| Effective inspiral spin | |
| Effective precessing spin | |
| Final spin | |
| Luminosity distance | |
| Inclination angle | |
| Source redshift | |
| Network matched filter SNR |
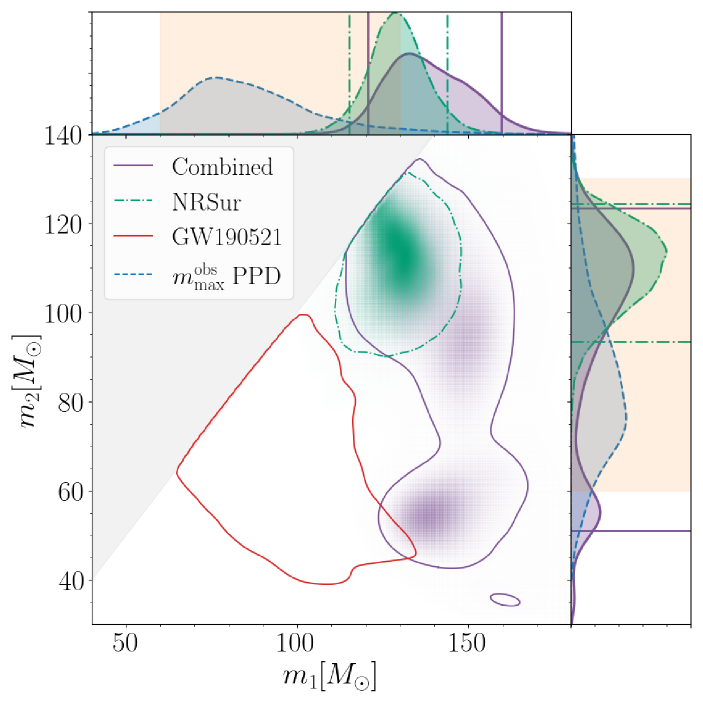
Although we observe differences depending on the model, the primary and secondary component masses nevertheless have a significant probability of lying within the mass gap from (pulsational) pair-instability supernova (PISN) processes, as shown in Figure 3, where we assume a nominal gap ranging from 60–130 (see Section 6 for a detailed discussion). The binary’s total mass is constrained to be within \IfEqCaseGW231123cg_combinedGW231123cg_combined189GW231123cg_nrsur214GW231123cg_xphm217GW231123cg_xo4a181GW231123cg_tphm225GW231123cg_seob222–\IfEqCaseGW231123cg_combinedGW231123cg_combined266GW231123cg_nrsur261GW231123cg_xphm268GW231123cg_xo4a226GW231123cg_tphm270GW231123cg_seob273 . This measurement exceeds the 95th percentile of the inferred total mass from GW190521 (Abbott et al., 2023a). Assuming a FAR threshold of one per year, similar to Abbott et al. (2023b), the source of GW231123 is the highest mass BBH observed by the LVK to date; other lower significance high-mass observations have been discussed in Abbott et al. (2024a); Wadekar et al. (2023); Williams (2025); Ruiz-Rocha et al. (2025).
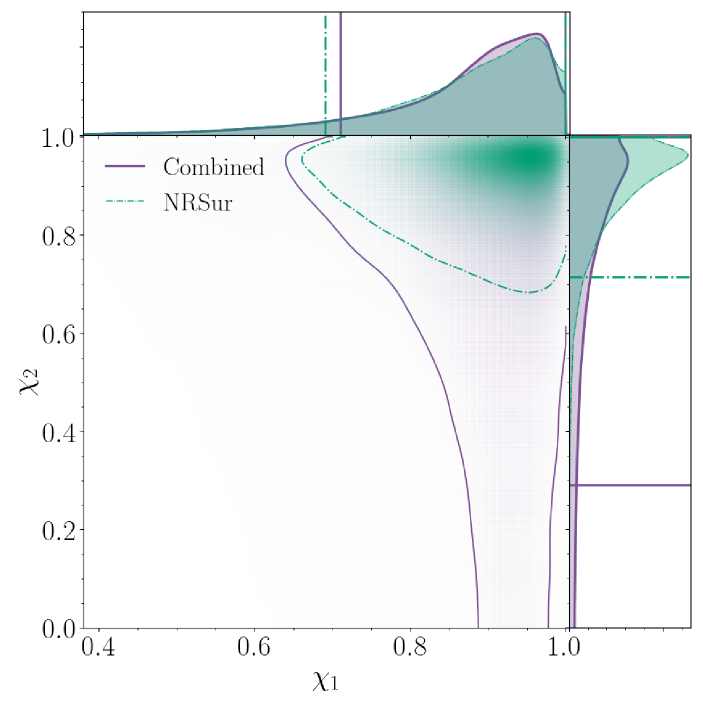
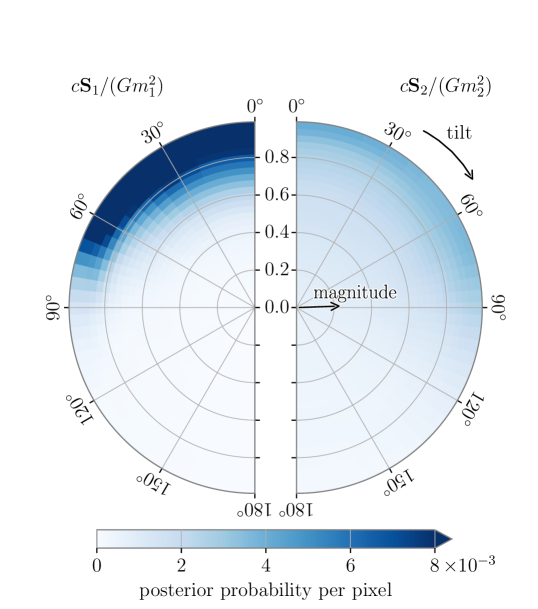
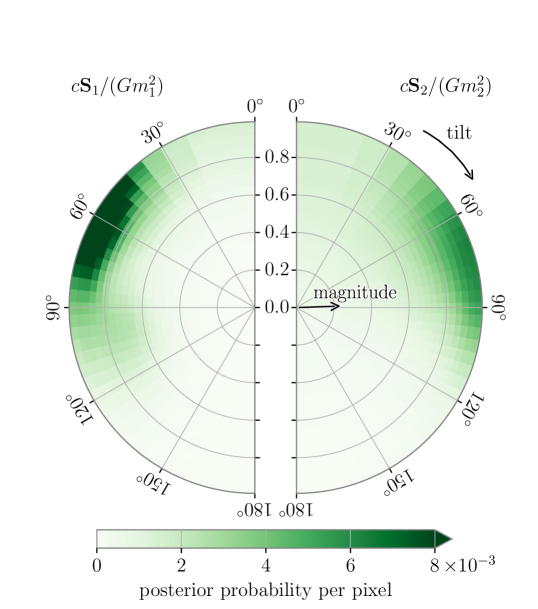
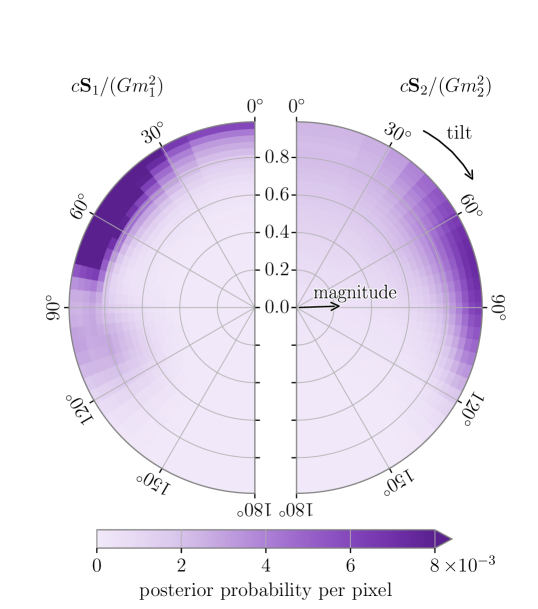
We consistently infer that both BH are highly spinning independent of the model we use. As shown in Figure 4, we infer that the primary spin magnitude at probability and the secondary spin magnitude at probability. The primary component of GW231123 has one of the highest confidently measured BH spins observed through GWs (evidence for highly spinning BH has also been presented in Hannam et al., 2022; Nitz et al., 2020; Abbott et al., 2024a, 2023a; Wadekar et al., 2023; Williams, 2025).
We are unable to reliably infer the spin orientation of the binary; we infer polar angles between each spin vector and the orbital angular momentum that vary not only between models, but also when independently analysing data obtained by LIGO Livingston compared to LIGO Hanford, see Appendix B. To understand these differences, we carried out a series of analyses with different frequency ranges. We found that all models consistently infer greater support for spin components aligned with the orbital angular momentum when independently analysing LIGO Hanford data, and when excluding data from LIGO Livingston below . When spin misalignment is inferred, we are unable to conclusively constrain the spin orientation away from aligned.
The uncertainty in the spin misalignment affects the inferred effective inspiral spin , which parameterizes the spin aligned with the orbital angular momentum (Santamaria et al., 2010; Ajith et al., 2011). Negative would imply that at least one spin is misaligned with the orbital angular momentum by more than ninety degrees. We cannot rule out , but there is an probability that is positive. The inferred effective precessing spin (Schmidt et al., 2015) is consistently measured between models and deviates from the prior, . Although we infer variation between models, we consistently obtain large Bayes factors (5–10) in favour of precession. Since the distribution of Bayes factors from noise alone is unknown, we additionally quantify the evidence for precession in GW231123 by computing the precession SNR, (Fairhurst et al., 2020a, b). In the absence of any precession in the signal, we expect in 90% of cases. We infer an SNR of . Although the high SNR tail is consistent with the large Bayes factors (Green et al., 2021; Pratten et al., 2020b), we infer non-negligible support below . We are therefore unable to confidently claim precession in GW231123. GW190521 was also found to exhibit mild evidence for spin-precession (Abbott et al., 2020d, e).
We observe significant differences in the inferred luminosity distance and inclination angle of GW231123’s source, depending on the model, although most models infer comparable probabilities for face-on vs face-off ( and ) configurations. We also infer substantial variation in the detector-frame quantities, despite seeing agreement between several models in the source-frame parameters. See Appendix A for a detailed discussion. Owing to disagreements in the inferred inclination angle of the binary, we similarly observe differences in the inferred higher-order multipole SNRs from each model. Following the methodology in Abbott et al. (2020f, g), where for each multipole the IMRPhenomXHM signal model (Garc´ıa-Quirós et al., 2020) is used to remove any contribution parallel to the dominant multipole and to calculate the orthogonal optimal SNR (Mills & Fairhurst, 2021), we nevertheless find that all models provide support for the multipole in GW231123. We infer an average orthogonal optimal SNR of when combining the results from all models with equal weight.
The properties of the remnant BH are estimated in different ways depending on the model. We apply the NRSur7dq4Remnant model (Varma et al., 2019) to the samples obtained by NRSur, and we average several fits calibrated to numerical relativity simulations (Hofmann et al., 2016; Healy & Lousto, 2017; Jiménez-Forteza et al., 2017) for samples obtained by v5PHM, TPHM, XPHM, XO4a. When combining the results with equal weight, we infer the final mass and spin of the remnant BH to be and respectively. For certain binary configurations, the remnant BH may receive a recoil velocity that is enough to eject the remnant from its host galaxy (Merritt et al., 2004). We infer a measurement of the remnant BH’s recoil velocity that differs from the effective prior distribution: . This measurement is based on the NRSur analysis and the NRSur7dq4Remnant remnant model, the only fit providing recoil velocities estimates (Varma et al., 2019, 2020).
4.4 Waveform Consistency Checks
To further assess whether a CBC signal with the inferred parameters in Section 4.3 adequately represents the data, we perform several consistency checks using a signal-agnostic approach that reconstructs coherent transient power, and through a model incorporating a modified wave dispersion relationship. First, we compare the waveform of the maximum-likelihood sample from parameter estimation in Section 4.1 to one obtained through minimally modelled analyses that make no assumptions about the source or morphology of the signal (Szczepańczyk et al., 2021; Salemi et al., 2019; Ghonge et al., 2020). Second, we conduct a residuals analysis, subtracting the best-fit waveform from the detector data and searching for coherent residual power (Abbott et al., 2021b). Discrepancies between the modelled and minimally modelled waveforms, or the presence of significant excess residual power, could indicate physical effects in addition to or alternative to those in our BBH signal models or unaccounted-for noise features (Johnson-McDaniel et al., 2022).
For the waveform reconstruction comparisons, we use BayesWave, cWB-2G, and cWB-BBH for the minimally modelled analysis. To evaluate the agreement between the signal as found by the modelled analysis and minimally modelled approach, we calculate the overlap between the maximum-likelihood sample from parameter estimation using the NRSur model and the median BayesWave or cWB maximum-likelihood waveform. An overlap of 1 indicates perfect agreement, while an overlap of 0 indicates no similarity between waveforms. To assess whether the overlaps are consistent with signals of comparable parameters and noise realizations, we perform a dedicated set of injections wherein we inject waveforms generated by draws from the posterior distribution of the source parameters into detector data surrounding the event. The BayesWave analysis performed 400 injections into approximately 8 hours of data surrounding the event, and the cWB analysis injected about 2800 draws from the posterior distribution in an interval of two weeks around the event. We find good agreement between the minimally modelled and CBC waveform reconstructions. The overlaps between the CBC maximum-likelihood waveform and BayesWave, cWB-2G, and cWB-BBH are 0.97, 0.96, and 0.98, respectively. Compared to the distributions of overlaps from the injections, the -values (defined as the fraction of injections with overlaps below that of the real event) are 0.74, 0.57, and 0.92 for BayesWave, cWB-2G, and cWB-BBH, respectively. Under the null hypothesis, the -values should be distributed uniformly from 0 to 1, so these results indicate that the overlaps are consistent with expectations from systems similar to GW231123.
For the residuals test, we produce residual data by subtracting from the original data the maximum-likelihood waveform from the NRSur parameter estimation samples. If the signal has been modelled sufficiently, the residual data should be consistent with Gaussian noise. We analyze the residual data with BayesWave, and calculate the 90% credible upper limit on the recovered network SNR (). To compare to expected values of , we also analyze segments of data (with no injected signal) selected randomly from 16384 s of data surrounding the event, and calculate the probability of obtaining an higher than that of residual data. Details of this procedure can be found in (Abbott et al., 2021b). We find no significant excess SNR in the residual data beyond what is expected from only Gaussian noise. Compared to the distribution of from the noise-only runs, the -value is 0.35. This further confirms that minimally modelled tests do not flag any features in the data missed by the analyses described in Section 4.1.
We additionally search for post-ringdown echo signals (Tsang et al., 2018, 2020) with a BayesWave-based search, finding negative evidence for their presence (as quantified by the Bayes factor ), consistent with the above findings. As a final consistency check, an analysis incorporating a modified wave dispersion relation due to non-zero graviton mass (Abbott et al., 2021b) yields agreement with massless wave propagation when based on the NRSur or TPHM models. Instead, when assuming the XPHM or XO4a templates, a statistically significant violation is found, suggesting missing signal components not captured by these models, which is consistent with the discussion of systematics in Section 4.2.
5 Black-hole ringdown
Massive systems dominated by merger-ringdown, such as GW231123, are ideal to test the BH signal interpretation by applying BH spectroscopy techniques (Dreyer et al., 2004; Berti et al., 2009, 2025), yielding remnant properties under minimal assumptions on the remnant formation process. We fit superpositions of damped sinusoids, aiming to associate them with characteristic quasi-normal modes (QNMs) of a BH, which drive its relaxation to equilibrium. The resulting parameter estimates make it possible to robustly validate inspiral–merger–ringdown (IMR) measurements, since a QNM description is generic to any BH remnant (e.g., a BH formed from an eccentric binary).
We truncate portions of data in the time domain at different analysis start times , and fit two sets of models. The first (DS-) is a superposition of damped-sinusoids , with constants as free parameters, assuming (circularly polarized wave). In the second (Kerr), complex frequencies are identified with QNMs of a Kerr BH, and , with detector frame (redshifted) mass , spin , and the QNM angular () and overtone () indices. In addition to the longest-lived , we consider , the linear QNMs with the largest predicted amplitudes for binary mergers (Kamaretsos et al., 2012; London et al., 2014; Cheung et al., 2024; Zhu et al., 2025; Nobili et al., 2025; Carullo, 2024). Here, we include both contributions, accommodating generic signal polarizations, and enters the expression as mode amplitudes are degenerate with the source distance.
We use the pyRing pipeline (Carullo et al., 2019) with standard analysis settings (Isi & Farr, 2021; Abbott et al., 2021b; Gennari et al., 2024). We pre-condition the data by subtracting the Hz power line, which reduces the required analysis duration to s (Siegel et al., 2025). We sample the posterior distribution using the CPNest nested sampling algorithm (Veitch et al., 2020). Times are relative to the median of the polarizations peak time in the LIGO Hanford data, computed from the NRSur reconstructed waveform. The sky location is fixed to the NRSur maximum likelihood value, fixing the analysis start time in LIGO Livingston, as required by the truncated time-domain formulation of the analysis (Isi & Farr, 2021). We have verified that repeating the analysis at different sky location values drawn from the NRSur posterior does not affect our conclusions.
Damped sinusoids are expected to be valid in the stationary regime of BH relaxation, typically (namely ms assuming ) past the signal peak; fitting earlier may provide spurious support for additional modes (Berti et al., 2025). However, a time-domain waveform reconstruction of GW231123 indicates a highly complex morphology, displaying a monotonic decay only after ms, significantly later than the nominal ; see Appendix C. Given this uncertainty, we explore a wide range of times ms in steps of ms.
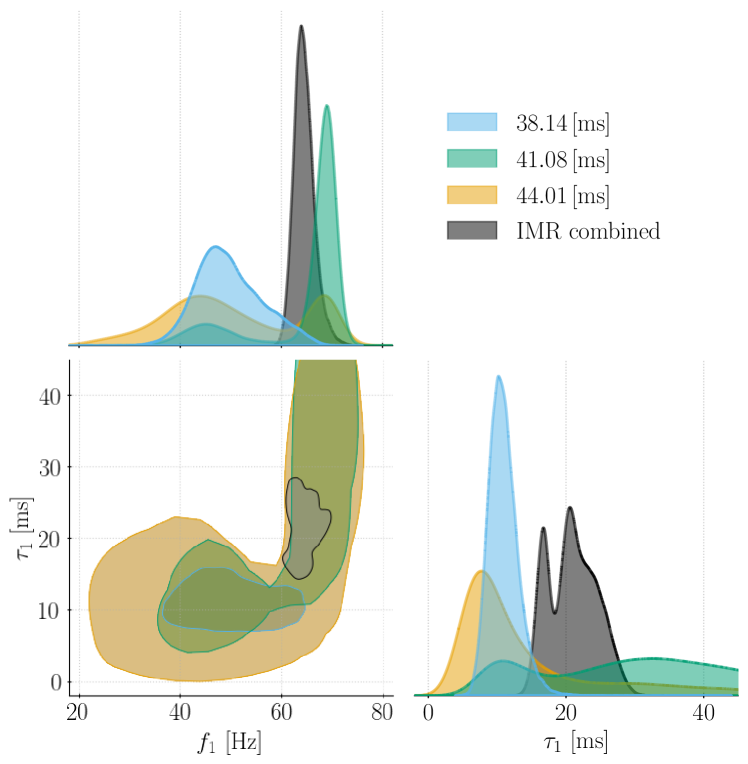
Fits that start at late times ms, when we are confident on the validity of an exponential decay description, find preference for a single mode with both models (as quantified by Bayes factors ). A single damped sinusoid (DS-1) fit yields a multi-modal distribution, shown in Figure 5, unlike what is observed in previous events at such late times. One peak with Hz and overlaps with the dominant Kerr frequency as predicted by IMR models, supporting the BH hypothesis. The damping time spans a broad range, overlapping with . A second peak is centred around Hz, correlating with a larger amplitude value . Among linear Kerr QNMs predicted by the IMR models, this frequency peak shows the largest overlap with . The damping time is also bimodal: the peak associated to Hz is centred around ms, a smaller value compared to ms, but overlapping the latter distribution. Under a Kerr fit, the two-dimensional – distribution is also multi-modal: one peak overlaps with the IMR predictions, while a second prefers lower remnant spins.
Fitting at earlier times, Bayes factors indicate overwhelming preference () for two modes over one until ms in both the DS- and Kerr models, but in this range we may be fitting a complex merger signal, and a QNM superposition may not be valid. At these early times, a DS-2 fit yields two frequencies consistent with the two peaks observed at later times. Amplitudes and damping times are comparable in magnitude between the two damped sinusoids, and both damping times are larger than the ms peak observed at later times. In addition to the mode, in the time range explored we find the Kerr modes to be on average the most favoured by Bayes factors, while is preferred around ms. The Kerr two-modes combinations robustly yield a massive remnant, , also at these earlier times.
These multi-mode combinations are in tension with IMR analyses. The most favoured Kerr mode in addition to the according to Bayes factors, the , implies a – distribution that does not overlap with IMR estimates. Adding only results in partial overlap, while the overlaps to a larger degree. However, the short-lived mode alone is not expected to give rise to the features observed in the signal until late times. The mode addition results in the most significant overlap, with a amplitude comparable to the , consistently with later times results. While QNMs can be strongly excited in highly precessing systems with large mass asymmetry (O’Shaughnessy et al., 2013; Zhu et al., 2025; Nobili et al., 2025), the IMR analyses of GW231123 predict minimal power in the mode, as discussed in Appendix D. Highly eccentric configurations can excite modes (Sperhake et al., 2008), but we lack sufficiently complete merger–ringdown models for eccentric-binary signals to reliably assess this possibility; see Section 7 for further discussion. DS- analyses with did not prefer more than two modes, but future investigations will be required to determine whether the observed features can be induced by a superposition of many overlapping modes.
In summary, the Kerr fits recover the remnant spin with large uncertainty, and they robustly predict at all times, supporting the interpretation of a massive BH remnant. Further investigations will be required to characterize the nature of the bi-modal features persistently observed in the signal and consistently interpret the multi-mode fits at earlier times. Given these large uncertainties, we do not consider tests of the no-hair properties of BHs in general relativity that would be enabled by a confident two-mode identification (Dreyer et al., 2004; Berti et al., 2009; Gossan et al., 2012; Brito et al., 2018; Carullo et al., 2018; Bhagwat et al., 2020; Isi & Farr, 2021).
6 Astrophysical implications
Here, we discuss the astrophysical implications of the large masses and spins of GW231123’s source and its possible origin given current understanding of (pulsational) PISNe and formation channels of merging BBHs.
6.1 Single-event rate estimate
First, we quantify the merger rate of GW231123-like events following (Kim et al., 2003; Abbott et al., 2016b). The sensitive volume–time of the detectors to such signals is estimated using the cWB-BBH results for the injection campaign discussed in Section 2. Assuming a constant merger rate over comoving volume and source-frame time with prior and a Poisson likelihood for the number of triggers, we find . This is consistent with the rate of mergers like GW190521 and upper limits of IMBH mergers (Abbott et al., 2020d, e, 2022), but much lower than the overall rate 16–61 Gpc-3 yr-1 of BBHs with component masses inferred through GWTC-3 (Abbott et al., 2023b).
6.2 Relation to the previous inferred population
To further assess GW231123 in the context of the 69 BBH mergers with through GWTC-3 (Abbott et al., 2023a) and test if its masses and spins are surprising, we perform posterior predictive checks based on the fiducial BBH population fit from (Abbott et al., 2023b, Section III C; we extend the prior on the maximum BH mass up to as there is support from GW190521 above the limit of 100 imposed in the original GWTC-3 analysis). From the inferred population, we construct mock catalogs containing 69 detected events and plot the distribution of their largest BH mass in Figure 3. Using the Combined parameter estimates, the primary mass of GW231123 falls at the level of this distribution, indeed indicating that this event is an unlikely draw. However, due to large uncertainties in its masses, it is not conclusively an outlier as it may be less massive than the most massive mock events (equivalent comparisons for secondary and total mass are less significant). Similarly, the largest BH spin in these catalogs is , against which the primary and secondary spins of GW231123 can fall at any percentile and thus are not outliers. Compared to its masses, the spins of GW231123’s source are more consistent with the known population as it does not rule out large values.
6.3 Possible formation channels
From theoretical predictions for the late-stage evolution of massive stars (Fowler & Hoyle, 1964; Barkat et al., 1967; Rakavy & Shaviv, 1967; Fraley, 1968; Bond et al., 1984; Woosley et al., 2002; Woosley, 2017), contraction of the core leads to electron–positron pair production that reduces internal pressure support, causing further contraction that powers explosive nuclear burning and a rebounding shock. For helium-core masses –, multiple pulsational episodes can eject sufficient material to reduce the mass below the pair-instability regime, ending with a BH remnant. A single pulse can entirely disrupt stars with larger helium cores, leaving behind no remnant in a PISN. At even larger helium-core masses , this is avoided as the high core temperature results in photodisintegration that accelerates gravitational collapse to a massive BH. This leads to the robust prediction from single-star evolution of the existence of a gap in the BH mass distribution. Though this gap is broadly consistent with the range –, there are several theoretical uncertainties that affect both the lower edge and total extent of the gap (Belczynski et al., 2016; Stevenson et al., 2019; Farmer et al., 2019; Mapelli et al., 2020; Renzo et al., 2020b; Marchant & Moriya, 2020; Woosley & Heger, 2021; Hendriks et al., 2023). Uncertainties in nuclear reaction rates alone can shift the lower edge of the pair-instability mass gap from to (Farmer et al., 2020).
Some stellar and binary evolution processes are predicted to be able to populate the pair-instability mass gap. Weaker stellar winds (Mapelli et al., 2020) or core dredge-up episodes (Costa et al., 2021) may allow a star to retain a hydrogen envelope and collapse to a BH with mass inside the gap (Spera et al., 2019). Stellar mergers in dense clusters or multiple systems could similarly produce stars that collapse to more massive BHs, with the large masses inferred from GW231123 perhaps requiring multiple such mergers (Mapelli, 2016; Di Carlo et al., 2020; Renzo et al., 2020a; Kremer et al., 2020; González et al., 2021; Rizzuto et al., 2022; Costa et al., 2022; Arca Sedda et al., 2023a). Short-period stellar binaries might avoid merging and produce binary BHs with large, equal masses from rapidly rotating metal-poor stars due to chemically homogeneous evolution (de Mink & Mandel, 2016; Mandel & de Mink, 2016; Marchant et al., 2016). However, most models of isolated-binary formation predict small natal spins and at most one of the BHs spinning, due to tidal synchronization or accretion-induced spin up, and so binaries with masses and spins like those inferred from GW231123 are difficult to form (Belczynski et al., 2020; Qin et al., 2018; Fuller & Ma, 2019; Bavera et al., 2020; Belczynski et al., 2020; van Son et al., 2020). In fact, the components BHs and especially the primary are so massive that they may have formed through core collapse above the pair-instability mass gap (Ezquiaga & Holz, 2021; Franciolini et al., 2024).
Alternatively, in hierarchical mergers, one or both of the binary components is the product of a previous BBH merger, with characteristically large masses and spins (Gerosa & Fishbach, 2021). Previous analyses have suggested evidence for hierarchical mergers in GW catalogs (Kimball et al., 2021; Mould et al., 2022; Wang et al., 2022; Li et al., 2024; Pierra et al., 2024; Hussain et al., 2024; Antonini et al., 2025), but the population of BH remnants receive gravitational recoils as high as – (Doctor et al., 2021; Mahapatra et al., 2021), requiring environments with high escape speeds (Antonini & Rasio, 2016) such as dense stellar clusters (Miller & Hamilton, 2002; Antonini et al., 2019; Rodriguez et al., 2019; Fragione & Silk, 2020; Mapelli et al., 2021; Arca Sedda et al., 2021; Kritos et al., 2023; Mahapatra et al., 2025) or the disks of active galactic nuclei (Bartos et al., 2017; Stone et al., 2017; Mckernan et al., 2018; Yang et al., 2019; Tagawa et al., 2020; McKernan et al., 2020; Vaccaro et al., 2024; Arca Sedda et al., 2023b) to be retained. This is in contrast to high-mass stellar mergers, which receive smaller recoils from asymmetric mass loss (Gaburov et al., 2010; Glebbeek et al., 2013) and therefore may be more efficient at producing BHs with large masses in dynamical environments. As seen in Figure 4, the spins inferred from GW231123 may be even larger than typically predicted from hierarchical BH mergers (Gerosa & Berti, 2017; Fishbach et al., 2017), although the expected distribution for sources retained in their host environments may accommodate a wider range of spins (Borchers et al., 2025).
A different possibility is that of primordial BH being the binary components, which may exist across a range of mass scales, including within the pair-instability mass gap (Bird et al., 2016, 2023; Clesse & Garc´ıa-Bellido, 2017, 2022). However, there are remaining theoretical uncertainties, e.g., on whether primordial BH could accrete sufficiently to spin up as rapidly as the BH inferred from GW231123 (Green & Kavanagh, 2021).
Altogether, these theoretical predictions and their uncertainties make it difficult to determine whether or not the BH in the source of GW231123 have an astrophysical origin directly from stellar collapse, or due to close encounters in dense clusters (Jaraba & Garc´ıa-Bellido, 2021). We quantify this in more detail below.
6.4 Stellar collapse
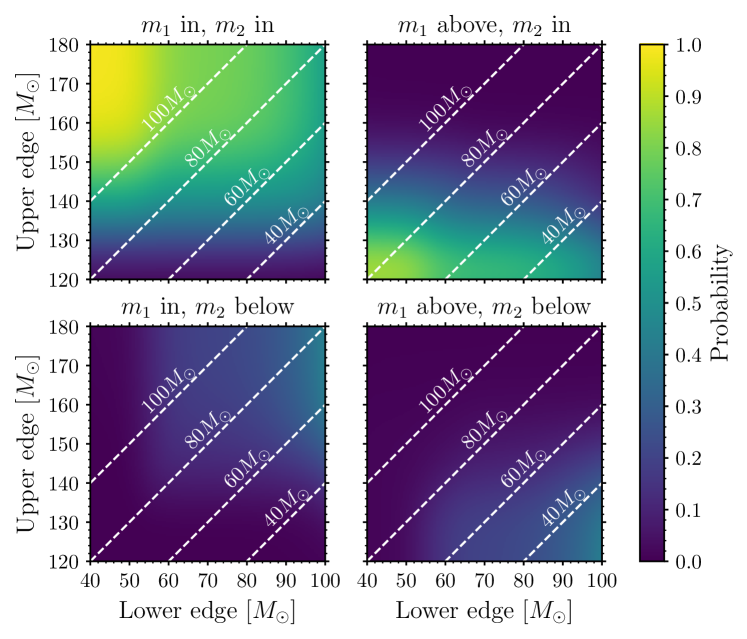
To account for a range of possible locations for the pair-instability mass gap, in Figure 6 we compute the probability that one or both component masses fall within the gap as a function of its lower edge from 40–100 and upper edge from 120–180 , using the Combined parameter estimates. In the following, we quote these probabilities specifically for the putative gap 60–130 . The probabilities that the secondary (primary) BH lies in, above, and below this gap are 83 % (26 %), 1 % (74 %), and 16 % (0 %), respectively. Considering scenarios in which at least one of the components falls in this gap, the joint probability that: both BH are in the gap (upper left panel of Figure 6) is 25 %; the primary is above while the secondary is within (upper right) is 58 %; and that the primary is within while the secondary is below (lower left) is 1 %. Alternatively, a scenario with neither BH in the gap is possible in the case of a straddling binary (Fishbach & Holz, 2020), with a primary BH above the upper edge and secondary below the lower edge (lower right) having a probability of 14 %.
Overall, this implies that within the uncertainties on the Combined parameter estimates (assuming our default prior) and the location of the pair-instability mass gap, scenarios with both BH outside the gap have lower probability than those with at least one BH in the gap.
6.5 Hierarchical mergers
Given the high probability of at least one of the BH lying inside the pair-instability mass gap, we consider the possibility that this is due to repeated BBH mergers. Assuming hierarchical origins, several works have inferred the source properties of potential BBHs whose merger products are observed with GWs in a subsequent merger (Baibhav et al., 2021; Barrera & Bartos, 2022; Álvarez et al., 2024; Mahapatra et al., 2024). We follow (Álvarez et al., 2024) and use the NRSur7dq4Remnant surrogate model (Varma et al., 2019) to find the distribution of BBH source properties such that the corresponding distribution of BH remnant properties reproduces the Combined posterior over mass and spin for the primary and secondary BH inferred from GW231123. As the primary-spin posterior favors large values , this constrains the parent binary of the primary BH to have unequal masses and ; for more equal masses, both BH spins can reduce the total angular momentum if misaligned, whereas unequal-mass binaries are dominated by the single heavier BH. The parent binary of the primary BH may have had a large effective inspiral spin, with , but is not ruled out. A similar picture holds for the secondary BH, with parent masses and , but more uncertain effective inspiral spin due to the larger uncertainty on the secondary spin in the source of GW231123. These mergers would have imparted kicks of and in the case of the primary and secondary, respectively, resulting in ejection from young star clusters or globular clusters (Antonini & Rasio, 2016).
The heavier of the two BH in both parent binaries may also lie within the pair-instability mass gap, with probabilities 91 % and 74 % for the heavier parent of the primary and secondary, respectively, when taking a gap from 60–130 , as above. Therefore, if either of the component BH of GW231123’s source is interpreted as the product of a previous BH merger, it may be the result of multiple previous mergers. Alternatively, the parent BH could themselves have formed with large masses by the other astrophysical processes discussed above, such as stellar mergers.
7 Alternative interpretations
All GW observations to date have been inferred to be from compact binaries consisting of BH and/or neutron stars (Abbott et al., 2016c, 2021a, 2024a, 2023a; Venumadhav et al., 2020; Olsen et al., 2022; Mehta et al., 2025; Nitz et al., 2023; Wadekar et al., 2023), and we consider a BBH the most astrophysically plausible interpretation of GW231123, finding that a non-eccentric BBH model fits the signal with no significant residual. Nonetheless, the low number of observable GW cycles invites alternative interpretations. We discuss several here.
7.1 Eccentricity
Binaries formed in dense environments may retain residual eccentricity in the sensitive band of current GW detectors (Samsing, 2018; Rodriguez et al., 2018; Zevin et al., 2019; Chattopadhyay et al., 2023; Dall’Amico et al., 2024) or merge following a dynamical capture (Gold & Brügmann, 2013; East et al., 2013; Gamba et al., 2023; Andrade et al., 2024; Albanesi et al., 2025b), but for high masses their GW signals can be confused with those of non-eccentric mergers (Romero-Shaw et al., 2020a; Calderón Bustillo et al., 2021a; Romero-Shaw et al., 2023). Our signal models assume a non-eccentric inspiral, while state-of-the-art IMR models that include eccentricity (Liu et al., 2022; Gamboa et al., 2024; Paul et al., 2025; Albanesi et al., 2025a; Planas et al., 2025a) assume circularization in the merger–ringdown stages and would thus be unsuitable to infer the parameters of GW231123’s source if it was eccentric when observed (Ramos-Buades et al., 2023b; Iglesias et al., 2024; Gupte et al., 2024; Planas et al., 2025b). Extensions of QNM amplitude models beyond eccentric non-spinning configurations (Carullo, 2024) will be required to investigate the possible ringdown mode excitation hinted at in Section 5. Relaxing the non-eccentric assumption is not expected to significantly change our results unless the eccentricity is larger than close to merger (Hinder et al., 2008; Huerta et al., 2019; Healy & Lousto, 2022; Carullo et al., 2024; Nee et al., 2025), which would be rare in the dynamical-capture scenarios above. Therefore, although we consider large eccentricity at merger astrophysically unlikely, we cannot rule it out for the source of GW231123.
7.2 Gravitational lensing
GW signals may be strongly lensed by galaxies or galaxy clusters, producing multiple copies of the original signal (Hannuksela et al., 2019; Abbott et al., 2021c, 2024b). However, no closely matching super-threshold counterpart candidates for GW231123 have been found from standard CBC searches. GWs can also undergo wave-optics lensing (Takahashi & Nakamura, 2003) when they encounter smaller objects (– for signals in the LVK band). GW231123 shows the strongest support for distorted lensed signals seen so far for both a point-mass model (Wright & Hendry, 2022) and phenomenological analyses (Liu et al., 2023), although preliminary background analyses suggest that some GW231123-like signals may be mis-identified as lensed. More in-depth investigations are needed to assess the significance of the lensing hypothesis, and these will be presented in future work.
7.3 Other scenarios
Several possible burst-like sources (Powell & Lasky, 2025) of astrophysical and cosmological origin may produce signals of similar duration to GW231123, such as core-collapse supernovae, cosmic strings, and exotic compact objects. For most supernova waveforms, the peak signal is expected at frequencies higher than observed in GW231123 (Abdikamalov et al., 2020; Mezzacappa & Zanolin, 2024). The ringdown-dominated signals of high-mass BBH mergers can be mimicked by waveforms from the collapse of cosmic strings (Abbott et al., 2020e; Aurrekoetxea et al., 2024) and collisions of exotic compact objects (e.g. boson stars) (Calderón Bustillo et al., 2021b; Siemonsen & East, 2023; Evstafyeva et al., 2024). Though we do not explicitly rule out these scenarios, the detection of GW231123 is consistent with the rates and properties of the currently understood population under the interpretation of a high-mass BBH merger, which has higher astrophysical probability.
8 Summary
GW231123 is a short-duration GW signal consisting of 5 observable cycles, most likely produced by a binary-black-hole merger. On that basis, we infer a total mass between 190 and 265 , which is larger than any previously observed with high confidence in GWs, and strong support for large spins on both black holes. We report source property measurements with larger uncertainties than we would expect for a binary of this mass and a signal with SNR 22, most likely due to uncertainties in current signal models at high spins. A ringdown analysis also supports a massive remnant under minimal assumptions, consistent with full-signal estimates. The measured masses of GW231123’s source lie at the edge of the currently understood population of binary black holes. The scenario with the highest probability is that at least one of the black hole sits in the pair-instability mass gap. If either is interpreted as the product of a previous black-hole merger, at least one of the black holes in its parent binary probably also lies in the mass gap. Such a sequence of black-hole mergers would require an environment with high escape speed, unless the black-hole masses are grown by other astrophysical processes, such as stellar mergers.
Given the small number of observable GW cycles, the large uncertainties in our measurements, and the limitations of current signal models, we expect that there is much still to learn about GW231123 and its source. The feasibility of a wide range of other alternatives to black-hole mergers remains to be investigated. Even within the binary-black-hole merger interpretation, we expect to learn more from detailed studies of high-spin binaries, high-eccentricity mergers, hyperbolic encounters, and lensed signals. Forthcoming analyses of the combined catalog of GW events, alongside continued studies of pair-instability processes and the formation of intermediate-mass black holes, may help to reveal the origins of GW231123. All studies will have to contend with the limited information that can be extracted from short signals, but a clearer picture may emerge if a population of such signals is observed in future observing runs.
Strain data from the LIGO detectors associated with GW231123 are available from the Gravitational Wave Open Science Center 111https://doi.org/10.7935/anj7-6q40. Samples from posterior distributions of the source parameters, additional materials, and notebooks for reproducing the figures are available on Zenodo (LIGO Scientific, Virgo, and KAGRA Collaboration, 2025). The software packages used in our analyses are open-source.
This material is based upon work supported by NSF’s LIGO Laboratory, which is a major facility fully funded by the National Science Foundation. The authors also gratefully acknowledge the support of the Science and Technology Facilities Council (STFC) of the United Kingdom, the Max-Planck-Society (MPS), and the State of Niedersachsen/Germany for support of the construction of Advanced LIGO and construction and operation of the GEO 600 detector. Additional support for Advanced LIGO was provided by the Australian Research Council. The authors gratefully acknowledge the Italian Istituto Nazionale di Fisica Nucleare (INFN), the French Centre National de la Recherche Scientifique (CNRS) and the Netherlands Organization for Scientific Research (NWO) for the construction and operation of the Virgo detector and the creation and support of the EGO consortium. The authors also gratefully acknowledge research support from these agencies as well as by the Council of Scientific and Industrial Research of India, the Department of Science and Technology, India, the Science & Engineering Research Board (SERB), India, the Ministry of Human Resource Development, India, the Spanish Agencia Estatal de Investigación (AEI), the Spanish Ministerio de Ciencia, Innovación y Universidades, the European Union NextGenerationEU/PRTR (PRTR-C17.I1), the ICSC - CentroNazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by the European Union NextGenerationEU, the Comunitat Autonòma de les Illes Balears through the Conselleria d’Educació i Universitats, the Conselleria d’Innovació, Universitats, Ciència i Societat Digital de la Generalitat Valenciana and the CERCA Programme Generalitat de Catalunya, Spain, the Polish National Agency for Academic Exchange, the National Science Centre of Poland and the European Union - European Regional Development Fund; the Foundation for Polish Science (FNP), the Polish Ministry of Science and Higher Education, the Swiss National Science Foundation (SNSF), the Russian Science Foundation, the European Commission, the European Social Funds (ESF), the European Regional Development Funds (ERDF), the Royal Society, the Scottish Funding Council, the Scottish Universities Physics Alliance, the Hungarian Scientific Research Fund (OTKA), the French Lyon Institute of Origins (LIO), the Belgian Fonds de la Recherche Scientifique (FRS-FNRS), Actions de Recherche Concertées (ARC) and Fonds Wetenschappelijk Onderzoek - Vlaanderen (FWO), Belgium, the Paris Île-de-France Region, the National Research, Development and Innovation Office of Hungary (NKFIH), the National Research Foundation of Korea, the Natural Sciences and Engineering Research Council of Canada (NSERC), the Canadian Foundation for Innovation (CFI), the Brazilian Ministry of Science, Technology, and Innovations, the International Center for Theoretical Physics South American Institute for Fundamental Research (ICTP-SAIFR), the Research Grants Council of Hong Kong, the National Natural Science Foundation of China (NSFC), the Israel Science Foundation (ISF), the US-Israel Binational Science Fund (BSF), the Leverhulme Trust, the Research Corporation, the National Science and Technology Council (NSTC), Taiwan, the United States Department of Energy, and the Kavli Foundation. The authors gratefully acknowledge the support of the NSF, STFC, INFN and CNRS for provision of computational resources.
This work was supported by MEXT, the JSPS Leading-edge Research Infrastructure Program, JSPS Grant-in-Aid for Specially Promoted Research 26000005, JSPS Grant-in-Aid for Scientific Research on Innovative Areas 2402: 24103006, 24103005, and 2905: JP17H06358, JP17H06361 and JP17H06364, JSPS Core-to-Core Program A. Advanced Research Networks, JSPS Grants-in-Aid for Scientific Research (S) 17H06133 and 20H05639, JSPS Grant-in-Aid for Transformative Research Areas (A) 20A203: JP20H05854, the joint research program of the Institute for Cosmic Ray Research, University of Tokyo, the National Research Foundation (NRF), the Computing Infrastructure Project of the Global Science experimental Data hub Center (GSDC) at KISTI, the Korea Astronomy and Space Science Institute (KASI), the Ministry of Science and ICT (MSIT) in Korea, Academia Sinica (AS), the AS Grid Center (ASGC) and the National Science and Technology Council (NSTC) in Taiwan under grants including the Science Vanguard Research Program, the Advanced Technology Center (ATC) of NAOJ, and the Mechanical Engineering Center of KEK.
Additional acknowledgements for support of individual authors may be found in the following document:
https://dcc.ligo.org/LIGO-M2300033/public.
For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY)
license to any Author Accepted Manuscript version arising.
We request that citations to this article use ’A. G. Abac et al. (LIGO-Virgo-KAGRA Collaboration), …’ or similar phrasing, depending on journal convention.
Appendix A Systematics studies
For this analysis we consider the models NRSur, v5PHM, TPHM, XPHM and XO4a. These models all describe precessing quasi-circular binaries and include higher multipole content. The three model families NRSur, SEOB and Phenom use different approaches to model the waveforms (Chatziioannou et al., 2024). In short, NRSur interpolates between NR data (Field et al., 2014; Blackman et al., 2015), making it typically the most accurate of the models for high-mass signals, such as GW231123. The SEOB and Phenom families instead use a combination of analytical and numerical information to create a complete inspiral-merger-ringdown model applicable to systems at any total mass (Buonanno & Damour, 1999, 2000; Buonanno et al., 2007; Ajith et al., 2011). The models NRSur, v5PHM, and TPHM calculate the signal in the time domain, while XPHM and XO4a model directly in the frequency domain. These models comprise the five state-of-the-art models currently available for LVK analyses of observations in O4a.
NRSur is fully calibrated to numerical waveforms over the binary parameter space up to dimensionless spin magnitudes and mass ratios , and can be extrapolated up to dimensionless spin magnitudes and mass ratios . By construction, NRSur automatically includes all multipoles up to and characteristics of precession such as mode asymmetry (Varma et al., 2019). By contrast, v5PHM, TPHM, and XPHM are calibrated to NR only in the aligned-spin sector (Pompili et al., 2023; Estellés et al., 2022b; Pratten et al., 2020a; Garc´ıa-Quirós et al., 2020) and instead model precession either by extending post-Newtonian and effective-one-body results or by employing BH perturbation theory results through merger and ringdown. During the inspiral, v5PHM, TPHM, and XPHM implement precession dynamics by numerically evolving the spins (Khalil et al., 2023; Estellés et al., 2021; Colleoni et al., 2025). XO4a uses closed-form, orbit-averaged expressions during the inspiral Chatziioannou et al. (2017); Pratten et al. (2021) and phenomenological expressions calibrated to single-spin precessing simulations with through merger and ringdown (Hamilton et al., 2021). Further, XO4a includes mode asymmetry of the dominant multipole (Ghosh et al., 2024). By employing multiple models with these key differences in their construction, we expect that our signal analysis will be more robust in more challenging regions of parameter space.
The different modeling approaches and treatments of the precession dynamics make these models relatively independent. In the presence of features in the data beyond the physical effects incorporated in the models (e.g., mismodelling in the high-spin regime, eccentricity, GW memory, or noise artefacts) one might therefore expect the models to interact with these features differently and display model systematics, as are seen in the posteriors for this event. The accuracy of these models for typical signals has been comprehensively assessed through comparison to NR, both in the modelling papers themselves and elsewhere (e.g., Mac Uilliam et al. (2024)). For GW231123 we have performed the accuracy analysis in Section 4.2, and a series of targeted NR injections, which we now describe. We hope that more can be learned in the future from improved models in the high-spin regime, and a detailed study of the behaviour of our models in Gaussian noise.
In order to investigate the likelihood of the presence of waveform systematics in the high total mass, comparable-mass (), highly precessing region of parameter space, we perform a simulation study where we simulate a set of signals consisting of highly precessing NR waveforms from the SXS catalog (Boyle et al., 2019; Scheel et al., 2025) and recover with the five waveform models under consideration. From several tens of simulations, we discuss here the results from two that span the range of observed results, from unbiased parameter estimation displaying no systematics to large systematic differences between models and clear biases in parameter recovery.
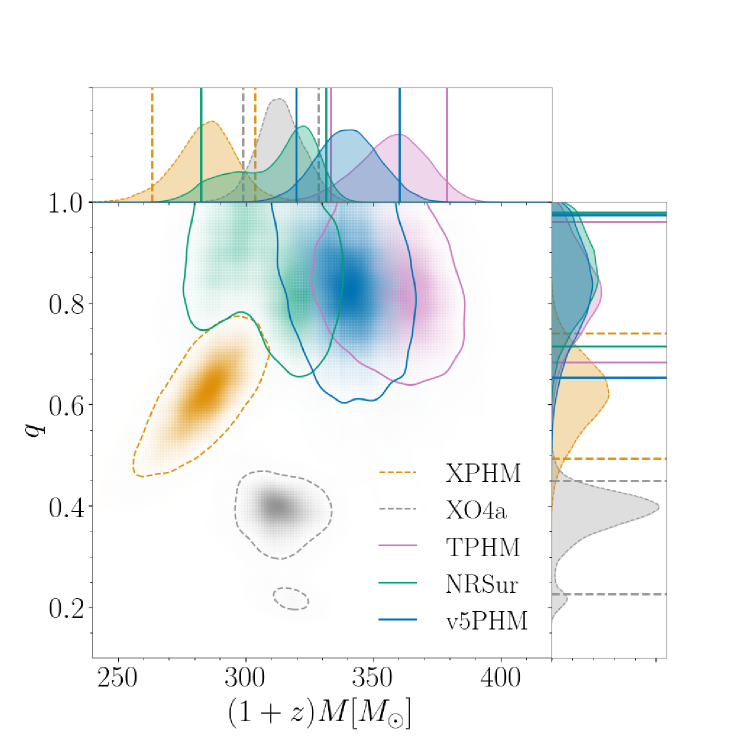
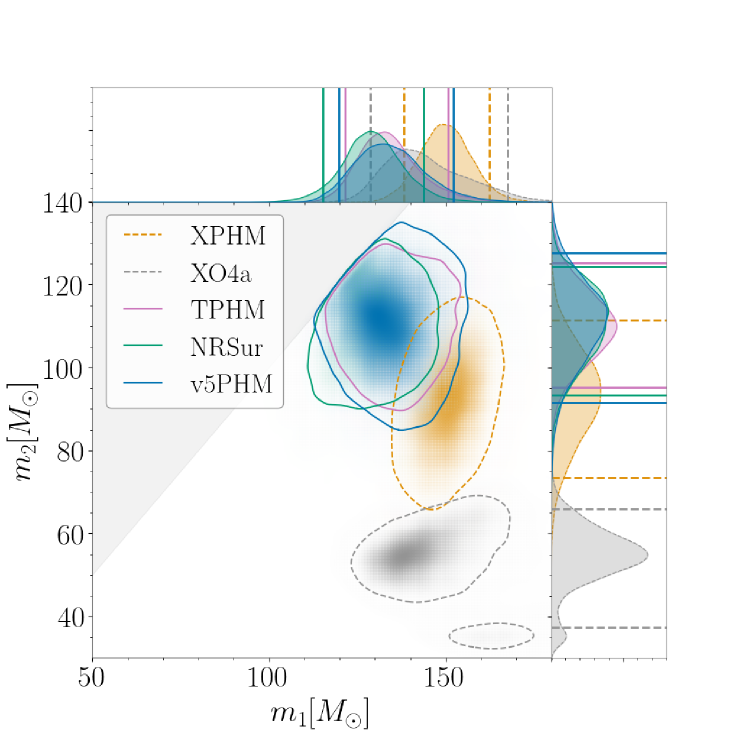
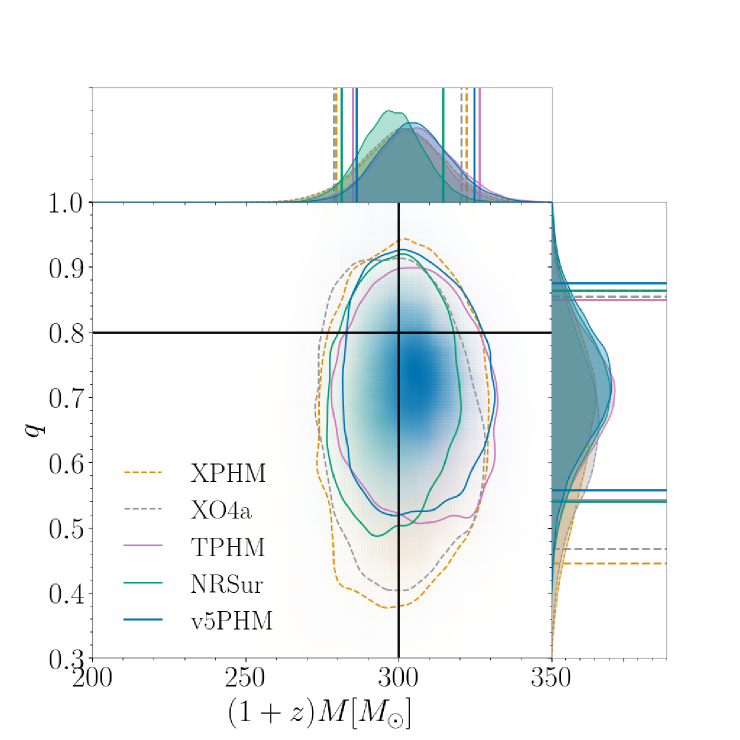
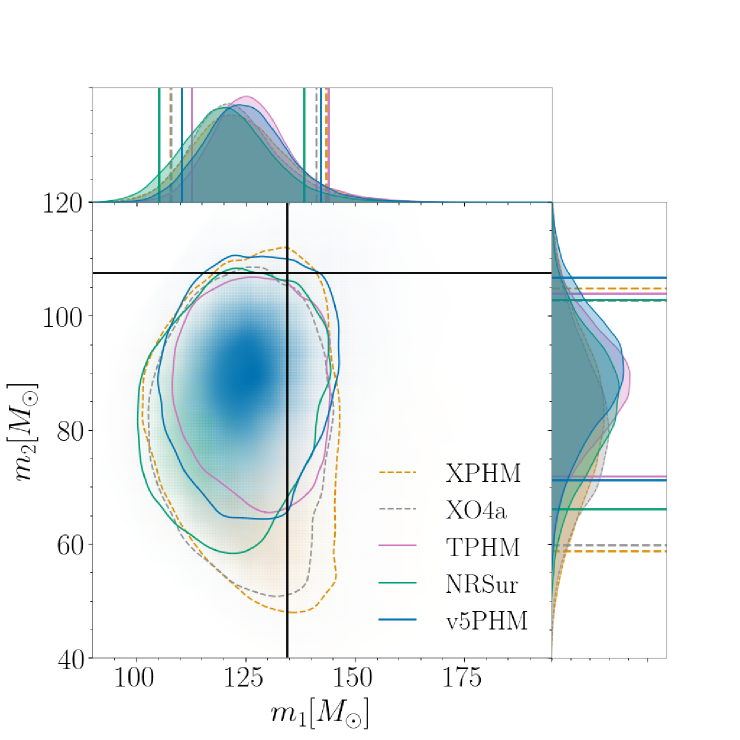
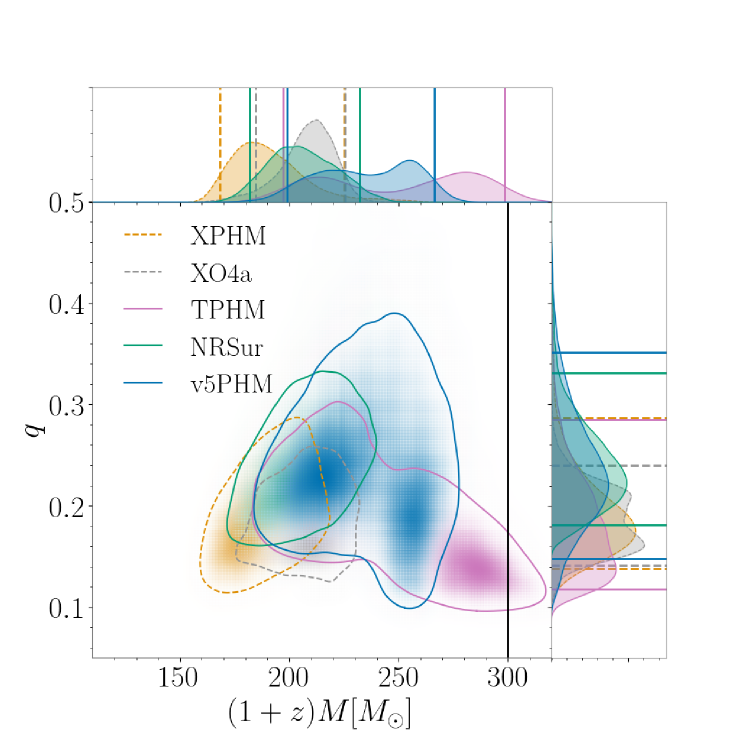
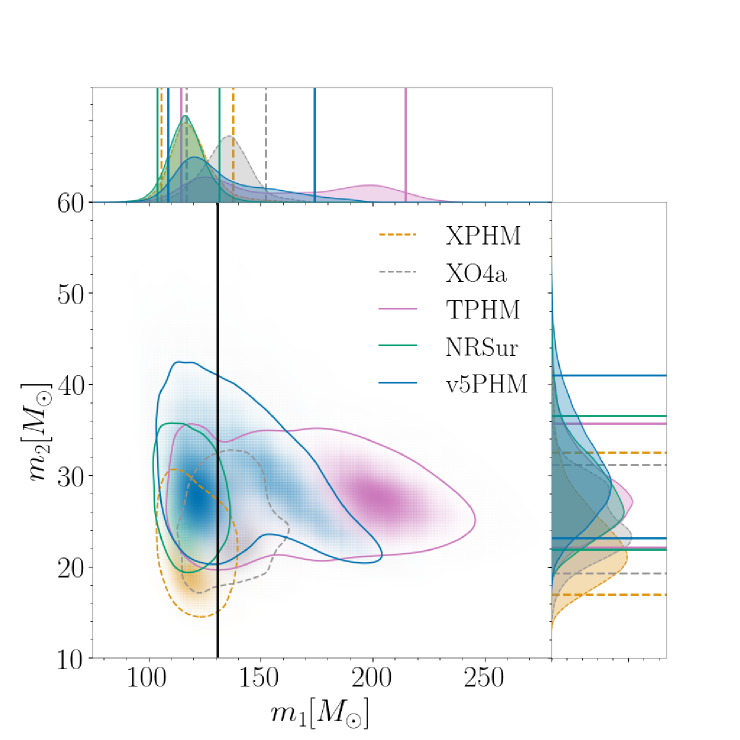
For both configurations, we show the total mass and mass ratio as measured in the data (the detector frame). For high-mass binaries, we expect the total mass to be one of the most reliably measured quantities. The detector-frame masses are not the true source masses, but the redshifted masses, and to calculate the true masses, we must also measure the redshift. The relative accuracy of the detector-frame and source-frame masses may therefore differ, depending on the accuracy of the redshift. For this reason, we also show the individual masses and after correcting for the redshift.
The results for GW231123 are shown in Figure 7. In the left panel, we see clear evidence of systematics in the measurement of both the total mass and the mass ratio, with no overlap of the 90% credible intervals for some models in both parameters. When we correct for the redshift, some of the differences appear to “cancel out”, and we see agreement between several models in the source masses. This is likely coincidental; we expect any model biases in the detector-frame masses and redshift to be independent. This expectation is borne out in the examples below.
In the majority of cases simulated, we were unable to reproduce this degree of systematics. In both examples discussed here, we choose a large inclination angle as the mismatch performance is worst, and thus the associated expectations of evidence of systematics are greater, for systems with the greatest contribution from higher multipoles. It should be noted, however, that since the orbital plane precesses, the inclination is not constant over the binary’s evolution. An example of a typical recovery is shown in the top row of Figure 8, where we consider the SXS:BBH:0483 precessing NR simulation with total mass , mass ratio , and spin magnitudes on both BHs. The simulation is added to zero-noise using the fiducial inclination angle at 10 Hz. For this configuration, the mismatch for NRSur was unambiguously below the conservative distinguishability criterion, with a value of , while for the other models we see values . In this case, the large differences in mismatch do not translate into noticeable differences in the accuracy of parameter recovery. The posteriors from all models overlap and we can be confident in our recovered source properties. Note, however, that the source-frame is too low. This is a known bias for edge-on configurations: signals from face-on and face-off binaries are louder, meaning that larger distances (redshifts) are consistent with a fixed GW amplitude. This leads to a significantly larger prior volume, and thus a prior preference for smaller inclination angles (Usman et al., 2019), larger distances, and thus lower (redshifted) source masses.
Clear evidence of systematics was nevertheless seen in a limited number of simulations, as is demonstrated in the bottom row of Figure 8. We consider the SXS:BBH:4030 precessing NR simulation with total mass , equal mass components (), and spin magnitudes on both BHs. The simulation is added to zero-noise using the fiducial inclination angle at 15 Hz. This injection was chosen from the set of cases with very high spins, with a mismatch between (NRSur) and (TPHM), mostly above the conservative indistinguishability criterion. This numerical relativity (NR) waveform also includes GW memory, which can require additional data processing for injection (Xu et al., 2024; Valencia et al., 2024; Chen et al., 2024), but we find that our results are unchanged if we first subtract the memory features before injection. We see unequivocal evidence of waveform systematics and biases in all models. Only the posterior of TPHM includes the true value of the detector-frame total mass, and all models exclude it at 90% credibility. No model recovers the true mass ratio (). In the source-frame, the true value of lies in the 90% credible region for all models, but is significantly biased from its true value of 100 .
Appendix B Source properties
| XPHM | XO4a | TPHM | NRSur | v5PHM | |
| Primary mass | |||||
| Secondary mass | |||||
| Mass ratio | |||||
| Total mass | |||||
| Final mass | |||||
| Primary spin magnitude | |||||
| Secondary spin magnitude | |||||
| Effective inspiral spin | |||||
| Effective precessing spin | |||||
| Final spin | |||||
| Luminosity distance | |||||
| Inclination angle | |||||
| Source redshift | |||||
| Network matched filter SNR |
In Table 3, we present the individual source properties of GW231123 for each of the five models considered in the analysis of this event for those interested in a more detailed picture of the systematics. As demonstrated in Appendix A, the source properties of this event lie in a challenging region of parameter space for all waveform models employed. From the analysis performed here, we cannot guarantee that the results from any given model will be free from bias in this region of parameter space. We also find that different models fit the data better than others. All models except XPHM obtain a larger Bayesian evidence than the NRSur analysis, as reflected in the differing SNRs in Table 3. For example, for some parameters XO4a yields significantly different results to many of the other models, yet it obtains a Bayes factor of at least 200:1 over NRSur. However, such differences are not necessarily indicative of one model being more accurate than another (Hoy, 2022; Hoy et al., 2024). Consequently, we combine the posteriors from multiple models to achieve a conservative error estimate, which is reported throughout the main body of the paper.
We also illustrate in Figure 9 the differences in inferred spin orientation when considering the data from LIGO Hanford (left), LIGO Livingston (middle), and the full detector network (right). LIGO Hanford shows support for aligned-spin binaries, while LIGO Livingston has a clear preference for misalignment. The stronger signal in LIGO Livingston dominates the network results. The differences between the results in the two detectors could potentially be explained by lower signal power in LIGO Hanford (such that precession is not measurable), but we have not been able to reproduce this discrepancy between detectors with injections in zero-noise, for example, of the NRSur waveform at its maximum-likelihood parameters.
Appendix C Signal peak time
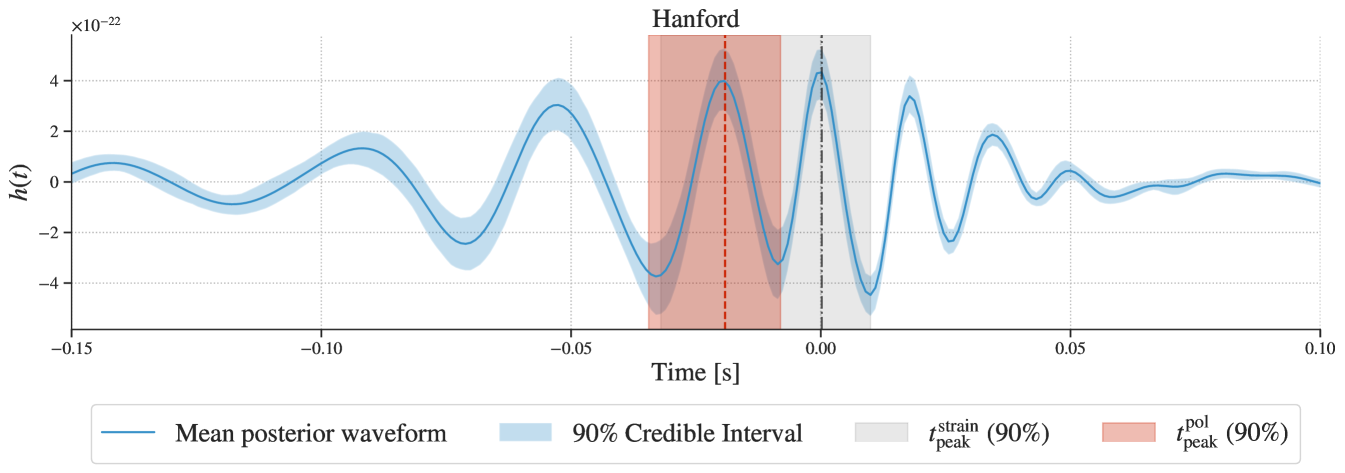
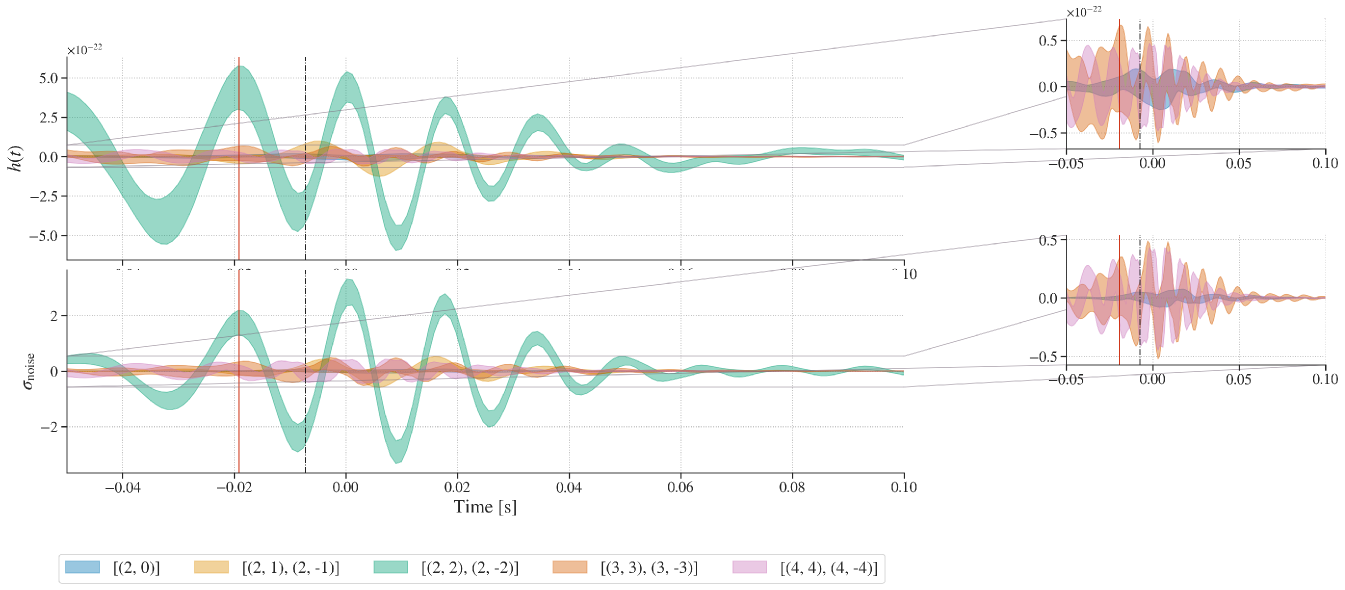
We require the time of peak GW emission to determine a valid starting time for ringdown analyses. The peak GW power is emitted at time , where are the multipoles in a spin-weighted spherical-harmonic decomposition of the signal. Alternatively, we can estimate the peak time using the peak of the polarisation . This quantity depends on the binary’s relative orientation to the detector and will be uncertain to within roughly one GW period, but it can be compared to an estimate computed through an unmodelled waveform reconstruction, allowing for a more agnostic analysis. One can also conservatively estimate the onset of ringdown directly from the maximum value of the strain , after which the signal displays a clear decay. Figure 10 shows these times for GW231123, on top of the unwhitened NRSur strain reconstruction from which they were computed. From this reconstruction, we find is s and s in the LIGO Hanford and Livingston detectors respectively. Instead, in the LIGO Hanford detector (chosen as reference for the ringdown analysis), we find .
The differences among these estimates, together with the time-domain reconstruction shown in Figure 10, attest to the highly complex signal morphology and invite care when selecting a peak time definition to be used as reference in a ringdown analysis. Hence, in the main text we repeat the analysis over a wide range of times, and plot results around a conservative (assuming ), when we are confident on the validity of a QNM description.
Appendix D Higher-order radiation multipoles
Given the support for large binary inclination from most IMR models, subdominant multipole moments (referred to as “modes” below) beyond the dominant spherical-harmonic multipole moment are expected to contribute appreciably to the observed signal (Blanchet, 2014). Here, we investigate in detail their contribution throughout the signal. Using NRSur posterior samples, we estimate optimal SNR values of for the mode, for the mode, for the mode and for the mode. Unlike the and modes, the inferred distribution for the modes are consistent with expectations from random Gaussian noise fluctuations, implying a lack of statistically significant support for their presence in the data. Relevant to the ringdown analysis, the strain contribution from the mode remains significantly subdominant compared to the more prominent and modes throughout the signal duration, as illustrated in Figure 10 (showing LIGO Hanford, with similar conclusions obtained for LIGO Livingston). As seen in the bottom panel, the whitening process suppresses the lower-frequency content of the signal, causing the peak amplitude to appear quieter relative to the higher-frequency ringdown. This filtering effect also reduces the visibility of subdominant modes such as and , which fall largely outside the detector’s sensitive band. In contrast, the and modes remain visible post-merger due to their higher frequency content, making them detectable. This result is consistent with the SNR estimates above. The IMR modes are defined with respect to the binary’s total angular momentum at a given reference time during the inspiral, while the ringdown modes are defined with respect to the remnant spin at asymptotically late times. The direction between these two vectors may be offset by a few degrees (Hamilton et al., 2021), but we do not expect that would be sufficient to increase the power in or to a level measurable in Gaussian noise, i.e., above an SNR of 2.1.
In summary, we conclude that a significant excitation of the or ringdown modes, suggested by the overlap of damped sinusoids fitting parameters with the remnant properties inferred by NRSur, is in tension with NRSur multipole moments content.
References
- Aasi et al. (2015) Aasi, J., et al. 2015, Class. Quant. Grav., 32, 074001
- Abac et al. (2025a) Abac, A. G., et al. 2025a, in preparation
- Abac et al. (2025b) —. 2025b, in preparation
- Abbott et al. (2016a) Abbott, B. P., et al. 2016a, Phys. Rev. Lett., 116, 241102
- Abbott et al. (2016b) —. 2016b, Astrophys. J. Lett., 833, L1
- Abbott et al. (2016c) —. 2016c, Phys. Rev. X, 6, 041015, [Erratum: Phys.Rev.X 8, 039903 (2018)]
- Abbott et al. (2020a) —. 2020a, Class. Quant. Grav., 37, 055002
- Abbott et al. (2020b) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2020b, Classical and Quantum Gravity, 37, 055002
- Abbott et al. (2020c) Abbott, R., Abbott, T., Ackley, K., et al. 2020c, Living reviews in relativity, 23, 1
- Abbott et al. (2020d) Abbott, R., et al. 2020d, Phys. Rev. Lett., 125, 101102
- Abbott et al. (2020e) —. 2020e, Astrophys. J. Lett., 900, L13
- Abbott et al. (2020f) —. 2020f, Phys. Rev. D, 102, 043015
- Abbott et al. (2020g) —. 2020g, Astrophys. J. Lett., 896, L44
- Abbott et al. (2021a) —. 2021a, Phys. Rev. X, 11, 021053
- Abbott et al. (2021b) —. 2021b, arXiv:2112.06861
- Abbott et al. (2021c) —. 2021c, Astrophys. J., 923, 14
- Abbott et al. (2022) —. 2022, Astron. Astrophys., 659, A84
- Abbott et al. (2023a) —. 2023a, Phys. Rev. X, 13, 041039
- Abbott et al. (2023b) —. 2023b, Phys. Rev. X, 13, 011048
- Abbott et al. (2024a) —. 2024a, Phys. Rev. D, 109, 022001
- Abbott et al. (2024b) —. 2024b, Astrophys. J., 970, 191
- Abdikamalov et al. (2020) Abdikamalov, E., Pagliaroli, G., & Radice, D. 2020, arXiv:2010.04356
- Acernese et al. (2015) Acernese, F., et al. 2015, Class. Quant. Grav., 32, 024001
- Adams et al. (2016) Adams, T., Buskulic, D., Germain, V., et al. 2016, Class. Quant. Grav., 33, 175012
- Ade et al. (2016) Ade, P. A. R., et al. 2016, Astron. Astrophys., 594, A13
- Ajith et al. (2011) Ajith, P., et al. 2011, Phys. Rev. Lett., 106, 241101
- Akutsu et al. (2020) Akutsu, T., Ando, M., Arai, K., et al. 2020, Progress of Theoretical and Experimental Physics, 2021, 05A101. https://doi.org/10.1093/ptep/ptaa125
- Albanesi et al. (2025a) Albanesi, S., Gamba, R., Bernuzzi, S., et al. 2025a, arXiv:2503.14580
- Albanesi et al. (2025b) Albanesi, S., Rashti, A., Zappa, F., et al. 2025b, Phys. Rev. D, 111, 024069
- Allen (2005) Allen, B. 2005, Phys. Rev. D, 71, 062001
- Alléné et al. (2025) Alléné, C., et al. 2025, Class. Quant. Grav., 42, 105009
- Álvarez et al. (2024) Álvarez, C. A., Wong, H. W. Y., Liu, A., & Calderón Bustillo, J. 2024, Astrophys. J., 977, 220
- Andrade et al. (2024) Andrade, T., et al. 2024, Phys. Rev. D, 109, 084025
- Antonini et al. (2019) Antonini, F., Gieles, M., & Gualandris, A. 2019, Mon. Not. Roy. Astron. Soc., 486, 5008
- Antonini & Rasio (2016) Antonini, F., & Rasio, F. A. 2016, Astrophys. J., 831, 187
- Antonini et al. (2025) Antonini, F., Romero-Shaw, I. M., & Callister, T. 2025, Phys. Rev. Lett., 134, 011401
- Arca Sedda et al. (2023a) Arca Sedda, M., Kamlah, A. W. H., Spurzem, R., et al. 2023a, Mon. Not. Roy. Astron. Soc., 526, 429
- Arca Sedda et al. (2023b) Arca Sedda, M., Naoz, S., & Kocsis, B. 2023b, Universe, 9, 138
- Arca Sedda et al. (2021) Arca Sedda, M., Rizzuto, F. P., Naab, T., et al. 2021, Astrophys. J., 920, 128
- Ashton et al. (2019) Ashton, G., et al. 2019, Astrophys. J. Suppl., 241, 27
- Aubin et al. (2021) Aubin, F., et al. 2021, Class. Quant. Grav., 38, 095004
- Aurrekoetxea et al. (2024) Aurrekoetxea, J. C., Hoy, C., & Hannam, M. 2024, Phys. Rev. Lett., 132, 181401
- Baibhav et al. (2021) Baibhav, V., Berti, E., Gerosa, D., Mould, M., & Wong, K. W. K. 2021, Phys. Rev. D, 104, 084002
- Baird et al. (2013) Baird, E., Fairhurst, S., Hannam, M., & Murphy, P. 2013, Phys. Rev. D, 87, 024035
- Barkat et al. (1967) Barkat, Z., Rakavy, G., & Sack, N. 1967, Phys. Rev. Lett., 18, 379
- Barrera & Bartos (2022) Barrera, O., & Bartos, I. 2022, Astrophys. J. Lett., 929, L1
- Bartos et al. (2017) Bartos, I., Kocsis, B., Haiman, Z., & Márka, S. 2017, Astrophys. J., 835, 165
- Bavera et al. (2020) Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, Astron. Astrophys., 635, A97
- Belczynski et al. (2016) Belczynski, K., et al. 2016, Astron. Astrophys., 594, A97
- Belczynski et al. (2020) —. 2020, Astron. Astrophys., 636, A104
- Berti et al. (2009) Berti, E., Cardoso, V., & Starinets, A. O. 2009, Class. Quant. Grav., 26, 163001
- Berti et al. (2025) Berti, E., et al. 2025, arXiv:2505.23895
- Bhagwat et al. (2020) Bhagwat, S., Cabero, M., Capano, C. D., Krishnan, B., & Brown, D. A. 2020, Phys. Rev. D, 102, 024023
- Bird et al. (2016) Bird, S., Cholis, I., Muñoz, J. B., et al. 2016, Phys. Rev. Lett., 116, 201301
- Bird et al. (2023) Bird, S., et al. 2023, Phys. Dark Univ., 41, 101231
- Blackman et al. (2015) Blackman, J., Field, S. E., Galley, C. R., et al. 2015, Phys. Rev. Lett., 115, 121102
- Blanchet (2014) Blanchet, L. 2014, Living Rev. Rel., 17, 2
- Bond et al. (1984) Bond, J. R., Arnett, W. D., & Carr, B. J. 1984, Astrophys. J., 280, 825
- Borchers et al. (2025) Borchers, A., Ye, C. S., & Fishbach, M. 2025, arXiv:2503.21278
- Boyle et al. (2019) Boyle, M., et al. 2019, Class. Quant. Grav., 36, 195006
- Brito et al. (2018) Brito, R., Buonanno, A., & Raymond, V. 2018, Phys. Rev. D, 98, 084038
- Buonanno & Damour (1999) Buonanno, A., & Damour, T. 1999, Phys. Rev. D, 59, 084006
- Buonanno & Damour (2000) —. 2000, Phys. Rev. D, 62, 064015
- Buonanno et al. (2007) Buonanno, A., Pan, Y., Baker, J. G., et al. 2007, Phys. Rev. D, 76, 104049
- Calderón Bustillo et al. (2018) Calderón Bustillo, J., Salemi, F., Dal Canton, T., & Jani, K. P. 2018, Phys. Rev. D, 97, 024016
- Calderón Bustillo et al. (2021a) Calderón Bustillo, J., Sanchis-Gual, N., Torres-Forné, A., & Font, J. A. 2021a, Phys. Rev. Lett., 126, 201101
- Calderón Bustillo et al. (2021b) Calderón Bustillo, J., Sanchis-Gual, N., Torres-Forné, A., et al. 2021b, Phys. Rev. Lett., 126, 081101
- Cannon et al. (2021) Cannon, K., Caudill, S., Chan, C., et al. 2021, SoftwareX, 14, 100680
- Capote et al. (2025) Capote, E., et al. 2025, Phys. Rev. D, 111, 062002
- Carullo (2024) Carullo, G. 2024, JCAP, 10, 061
- Carullo et al. (2024) Carullo, G., Albanesi, S., Nagar, A., et al. 2024, Phys. Rev. Lett., 132, 101401
- Carullo et al. (2019) Carullo, G., Del Pozzo, W., & Veitch, J. 2019, Phys. Rev. D, 99, 123029, [Erratum: Phys.Rev.D 100, 089903 (2019)]
- Carullo et al. (2025) —. 2025, pyRing, v2.7.0, Zenodo, doi:10.5281/zenodo.8165507. https://doi.org/10.5281/zenodo.8165507
- Carullo et al. (2018) Carullo, G., et al. 2018, Phys. Rev. D, 98, 104020
- Chandra et al. (2020) Chandra, K., Gayathri, V., Bustillo, J. C., & Pai, A. 2020, Phys. Rev. D, 102, 044035
- Chandra et al. (2021a) Chandra, K., Pai, A., Villa-Ortega, V., et al. 2021a, in 16th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories
- Chandra et al. (2021b) Chandra, K., Villa-Ortega, V., Dent, T., et al. 2021b, Phys. Rev. D, 104, 042004
- Chattopadhyay et al. (2023) Chattopadhyay, D., Stegmann, J., Antonini, F., Barber, J., & Romero-Shaw, I. M. 2023, Mon. Not. Roy. Astron. Soc., 526, 4908
- Chatziioannou et al. (2021) Chatziioannou, K., Cornish, N., Wijngaarden, M., & Littenberg, T. B. 2021, Phys. Rev. D, 103, 044013
- Chatziioannou et al. (2024) Chatziioannou, K., Dent, T., Fishbach, M., et al. 2024, arXiv:2409.02037
- Chatziioannou et al. (2017) Chatziioannou, K., Klein, A., Yunes, N., & Cornish, N. 2017, Phys. Rev. D, 95, 104004
- Chen et al. (2024) Chen, Y., et al. 2024, Phys. Rev. D, 110, 064049
- Cheung et al. (2024) Cheung, M. H.-Y., Berti, E., Baibhav, V., & Cotesta, R. 2024, Phys. Rev. D, 109, 044069, [Erratum: Phys.Rev.D 110, 049902 (2024)]
- Chu et al. (2022) Chu, Q., et al. 2022, Phys. Rev. D, 105, 024023
- Clesse & Garc´ıa-Bellido (2017) Clesse, S., & García-Bellido, J. 2017, Phys. Dark Univ., 15, 142
- Clesse & Garc´ıa-Bellido (2022) —. 2022, Phys. Dark Univ., 38, 101111
- Colleoni et al. (2025) Colleoni, M., Vidal, F. A. R., García-Quirós, C., Akçay, S., & Bera, S. 2025, Phys. Rev. D, 111, 104019
- Cornish & Littenberg (2015) Cornish, N. J., & Littenberg, T. B. 2015, Class. Quant. Grav., 32, 135012
- Cornish et al. (2021) Cornish, N. J., Littenberg, T. B., Bécsy, B., et al. 2021, Phys. Rev. D, 103, 044006
- Costa et al. (2022) Costa, G., Ballone, A., Mapelli, M., & Bressan, A. 2022, Mon. Not. Roy. Astron. Soc., 516, 1072
- Costa et al. (2021) Costa, G., Bressan, A., Mapelli, M., et al. 2021, Mon. Not. Roy. Astron. Soc., 501, 4514
- Cutler & Flanagan (1994) Cutler, C., & Flanagan, E. E. 1994, Phys. Rev. D, 49, 2658
- Dal Canton et al. (2021) Dal Canton, T., Nitz, A. H., Gadre, B., et al. 2021, Astrophys. J., 923, 254
- Dall’Amico et al. (2024) Dall’Amico, M., Mapelli, M., Torniamenti, S., & Arca Sedda, M. 2024, Astron. Astrophys., 683, A186
- Davies et al. (2020) Davies, G. S., Dent, T., Tápai, M., et al. 2020, Phys. Rev. D, 102, 022004
- Davis et al. (2022) Davis, D., Trevor, M., Mozzon, S., & Nuttall, L. K. 2022, Phys. Rev. D, 106, 102006
- Davis et al. (2021) Davis, D., et al. 2021, Class. Quant. Grav., 38, 135014
- de Mink & Mandel (2016) de Mink, S. E., & Mandel, I. 2016, Mon. Not. Roy. Astron. Soc., 460, 3545
- Di Carlo et al. (2020) Di Carlo, U. N., Mapelli, M., Bouffanais, Y., et al. 2020, Mon. Not. Roy. Astron. Soc., 497, 1043
- Doctor et al. (2021) Doctor, Z., Farr, B., & Holz, D. E. 2021, Astrophys. J. Lett., 914, L18
- Drago et al. (2020) Drago, M., et al. 2020, arXiv:2006.12604
- Dreyer et al. (2004) Dreyer, O., Kelly, B. J., Krishnan, B., et al. 2004, Class. Quant. Grav., 21, 787
- East et al. (2013) East, W. E., McWilliams, S. T., Levin, J., & Pretorius, F. 2013, Phys. Rev. D, 87, 043004
- Essick et al. (2020) Essick, R., Godwin, P., Hanna, C., Blackburn, L., & Katsavounidis, E. 2020, Mach. Learn. Sci. Technol., 2, 015004
- Estellés et al. (2022a) Estellés, H., Colleoni, M., García-Quirós, C., et al. 2022a, Phys. Rev. D, 105, 084040
- Estellés et al. (2022b) Estellés, H., Husa, S., Colleoni, M., et al. 2022b, Phys. Rev. D, 105, 084039
- Estellés et al. (2021) Estellés, H., Ramos-Buades, A., Husa, S., et al. 2021, Phys. Rev. D, 103, 124060
- Evstafyeva et al. (2024) Evstafyeva, T., Sperhake, U., Romero-Shaw, I. M., & Agathos, M. 2024, Phys. Rev. Lett., 133, 131401
- Ewing et al. (2024) Ewing, B., Huxford, R., Singh, D., et al. 2024, Phys. Rev. D, 109, 042008
- Ewing et al. (2024) Ewing, B., et al. 2024, Phys. Rev. D, 109, 042008
- Ezquiaga & Holz (2021) Ezquiaga, J. M., & Holz, D. E. 2021, Astrophys. J. Lett., 909, L23
- Fairhurst et al. (2020a) Fairhurst, S., Green, R., Hannam, M., & Hoy, C. 2020a, Phys. Rev. D, 102, 041302
- Fairhurst et al. (2020b) Fairhurst, S., Green, R., Hoy, C., Hannam, M., & Muir, A. 2020b, Phys. Rev. D, 102, 024055
- Farmer et al. (2020) Farmer, R., Renzo, M., de Mink, S., Fishbach, M., & Justham, S. 2020, Astrophys. J. Lett., 902, L36
- Farmer et al. (2019) Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53
- Field et al. (2014) Field, S. E., Galley, C. R., Hesthaven, J. S., Kaye, J., & Tiglio, M. 2014, Phys. Rev. X, 4, 031006
- Fishbach & Holz (2020) Fishbach, M., & Holz, D. E. 2020, Astrophys. J. Lett., 904, L26
- Fishbach et al. (2017) Fishbach, M., Holz, D. E., & Farr, B. 2017, Astrophys. J. Lett., 840, L24
- Fisher et al. (2021) Fisher, R. P., Hemming, G., Bizouard, M.-A., et al. 2021, SoftwareX, 14, 100677
- Fowler & Hoyle (1964) Fowler, W. A., & Hoyle, F. 1964, Astrophys. J. Suppl., 9, 201
- Fragione & Silk (2020) Fragione, G., & Silk, J. 2020, Mon. Not. Roy. Astron. Soc., 498, 4591
- Fraley (1968) Fraley, G. S. 1968, Ap&SS, 2, 96
- Franciolini et al. (2024) Franciolini, G., Kritos, K., Reali, L., Broekgaarden, F., & Berti, E. 2024, Phys. Rev. D, 110, 023036
- Fuller & Ma (2019) Fuller, J., & Ma, L. 2019, Astrophys. J. Lett., 881, L1
- Gaburov et al. (2010) Gaburov, E., Lombardi, J., & Portegies Zwart, S. 2010, Mon. Not. Roy. Astron. Soc., 402, 105
- Gamba et al. (2023) Gamba, R., Breschi, M., Carullo, G., et al. 2023, Nature Astron., 7, 11
- Gamboa et al. (2024) Gamboa, A., et al. 2024, arXiv:2412.12823
- Garc´ıa-Quirós et al. (2020) García-Quirós, C., Colleoni, M., Husa, S., et al. 2020, Phys. Rev. D, 102, 064002
- Gayathri et al. (2020) Gayathri, V., Lopez, D., Pranjal, R. S., et al. 2020, Phys. Rev. D, 102, 104023
- Gayathri et al. (2022) Gayathri, V., Healy, J., Lange, J., et al. 2022, Nature Astron., 6, 344
- Gennari et al. (2024) Gennari, V., Carullo, G., & Del Pozzo, W. 2024, Eur. Phys. J. C, 84, 233
- Gerosa & Berti (2017) Gerosa, D., & Berti, E. 2017, Phys. Rev. D, 95, 124046
- Gerosa & Fishbach (2021) Gerosa, D., & Fishbach, M. 2021, Nature Astron., 5, 749
- Ghonge et al. (2020) Ghonge, S., Chatziioannou, K., Clark, J. A., et al. 2020, Phys. Rev. D, 102, 064056
- Ghonge et al. (2024) Ghonge, S., Brandt, J., Sullivan, J. M., et al. 2024, Phys. Rev. D, 110, 122002
- Ghosh et al. (2024) Ghosh, S., Kolitsidou, P., & Hannam, M. 2024, Phys. Rev. D, 109, 024061
- Glebbeek et al. (2013) Glebbeek, E., Gaburov, E., Portegies Zwart, S., & Pols, O. R. 2013, Mon. Not. Roy. Astron. Soc., 434, 3497
- Gold & Brügmann (2013) Gold, R., & Brügmann, B. 2013, Phys. Rev. D, 88, 064051
- González et al. (2021) González, E., Kremer, K., Chatterjee, S., et al. 2021, Astrophys. J. Lett., 908, L29
- Gossan et al. (2012) Gossan, S., Veitch, J., & Sathyaprakash, B. S. 2012, Phys. Rev. D, 85, 124056
- Green & Kavanagh (2021) Green, A. M., & Kavanagh, B. J. 2021, J. Phys. G, 48, 043001
- Green et al. (2021) Green, R., Hoy, C., Fairhurst, S., et al. 2021, Phys. Rev. D, 103, 124023
- Gupte et al. (2024) Gupte, N., et al. 2024, arXiv:2404.14286
- Hamilton et al. (2021) Hamilton, E., London, L., Thompson, J. E., et al. 2021, Phys. Rev. D, 104, 124027
- Hamilton et al. (2024) Hamilton, E., et al. 2024, Phys. Rev. D, 109, 044032
- Hanna et al. (2020) Hanna, C., et al. 2020, Phys. Rev. D, 101, 022003
- Hannam et al. (2022) Hannam, M., et al. 2022, Nature, 610, 652
- Hannuksela et al. (2019) Hannuksela, O. A., Haris, K., Ng, K. K. Y., et al. 2019, Astrophys. J. Lett., 874, L2
- Harris et al. (2020) Harris, C. R., et al. 2020, Nature (London), 585, 357. https://doi.org/10.1038/s41586-020-2649-2
- Harry et al. (2016) Harry, I., Privitera, S., Bohé, A., & Buonanno, A. 2016, Phys. Rev. D, 94, 024012
- Healy & Lousto (2017) Healy, J., & Lousto, C. O. 2017, Phys. Rev. D, 95, 024037
- Healy & Lousto (2022) —. 2022, Phys. Rev. D, 105, 124010
- Hendriks et al. (2023) Hendriks, D. D., van Son, L. A. C., Renzo, M., Izzard, R. G., & Farmer, R. 2023, Mon. Not. Roy. Astron. Soc., 526, 4130
- Hinder et al. (2008) Hinder, I., Vaishnav, B., Herrmann, F., Shoemaker, D., & Laguna, P. 2008, Phys. Rev. D, 77, 081502
- Hofmann et al. (2016) Hofmann, F., Barausse, E., & Rezzolla, L. 2016, Astrophys. J. Lett., 825, L19
- Hourihane et al. (2022) Hourihane, S., Chatziioannou, K., Wijngaarden, M., et al. 2022, Phys. Rev. D, 106, 042006
- Hoy (2022) Hoy, C. 2022, Phys. Rev. D, 106, 083003
- Hoy et al. (2024) Hoy, C., Akcay, S., Mac Uilliam, J., & Thompson, J. E. 2024, arXiv:2409.19404
- Hoy & Raymond (2021) Hoy, C., & Raymond, V. 2021, SoftwareX, 15, 100765
- Huerta et al. (2019) Huerta, E. A., et al. 2019, Phys. Rev. D, 100, 064003
- Hunter (2007) Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90
- Hussain et al. (2024) Hussain, A., Isi, M., & Zimmerman, A. 2024, arXiv:2411.02252
- Iglesias et al. (2024) Iglesias, H. L., et al. 2024, Astrophys. J., 972, 65
- Isi & Farr (2021) Isi, M., & Farr, W. M. 2021, arXiv:2107.05609
- Jaraba & Garc´ıa-Bellido (2021) Jaraba, S., & García-Bellido, J. 2021, Phys. Dark Univ., 34, 100882
- Jiménez-Forteza et al. (2017) Jiménez-Forteza, X., Keitel, D., Husa, S., et al. 2017, Phys. Rev. D, 95, 064024
- Johnson-McDaniel et al. (2022) Johnson-McDaniel, N. K., Ghosh, A., Ghonge, S., et al. 2022, Phys. Rev. D, 105, 044020
- Joshi et al. (2025) Joshi, P., et al. 2025, arXiv:2506.06497
- Kamaretsos et al. (2012) Kamaretsos, I., Hannam, M., & Sathyaprakash, B. 2012, Phys. Rev. Lett., 109, 141102
- Khalil et al. (2023) Khalil, M., Buonanno, A., Estelles, H., et al. 2023, Phys. Rev. D, 108, 124036
- Khan (2024) Khan, S. 2024, Phys. Rev. D, 109, 104045
- Kim et al. (2003) Kim, C., Kalogera, V., & Lorimer, D. R. 2003, Astrophys. J., 584, 985
- Kimball et al. (2021) Kimball, C., et al. 2021, Astrophys. J. Lett., 915, L35
- Klimenko (2022) Klimenko, S. 2022, arXiv:2201.01096
- Klimenko et al. (2008) Klimenko, S., Yakushin, I., Mercer, A., & Mitselmakher, G. 2008, Class. Quant. Grav., 25, 114029
- Klimenko et al. (2016a) Klimenko, S., et al. 2016a, Phys. Rev. D, 93, 042004
- Klimenko et al. (2016b) Klimenko, S., Vedovato, G., Drago, M., et al. 2016b, Phys. Rev. D, 93, 042004
- Kremer et al. (2020) Kremer, K., Spera, M., Becker, D., et al. 2020, Astrophys. J., 903, 45
- Kritos et al. (2023) Kritos, K., Berti, E., & Silk, J. 2023, Phys. Rev. D, 108, 083012
- Kumar & Dent (2024) Kumar, P., & Dent, T. 2024, Phys. Rev. D, 110, 043036
- Kumar et al. (2025) Kumar, S., Melching, M., & Ohme, F. 2025, arXiv:2502.17400
- Li et al. (2024) Li, Y.-J., Wang, Y.-Z., Tang, S.-P., & Fan, Y.-Z. 2024, Phys. Rev. Lett., 133, 051401
- LIGO Scientific Collaboration and Virgo Collaboration (2018) LIGO Scientific Collaboration and Virgo Collaboration. 2018, Data quality report user documentation, docs.ligo.org/detchar/data-quality-report/, ,
- LIGO Scientific, Virgo, and KAGRA Collaboration (2018) LIGO Scientific, Virgo, and KAGRA Collaboration. 2018, LVK Algorithm Library - LALSuite, Free software (GPL), , , doi:10.7935/GT1W-FZ16
- LIGO Scientific, Virgo, and KAGRA Collaboration (2025) —. 2025, GW231123: a Binary Black Hole Merger with Total Mass 190-265 — Data Release, Zenodo, doi:10.5281/zenodo.15832843. https://doi.org/10.5281/zenodo.15832843
- Littenberg & Cornish (2015) Littenberg, T. B., & Cornish, N. J. 2015, Phys. Rev. D, 91, 084034
- Liu et al. (2023) Liu, A., Wong, I. C. F., Leong, S. H. W., et al. 2023, Mon. Not. Roy. Astron. Soc., 525, 4149
- Liu et al. (2022) Liu, X., Cao, Z., & Zhu, Z.-H. 2022, Class. Quant. Grav., 39, 035009
- London et al. (2014) London, L., Shoemaker, D., & Healy, J. 2014, Phys. Rev. D, 90, 124032, [Erratum: Phys.Rev.D 94, 069902 (2016)]
- Lopez et al. (2022) Lopez, D., Gayathri, V., Pai, A., et al. 2022, Phys. Rev. D, 105, 063024
- Mac Uilliam et al. (2024) Mac Uilliam, J., Akcay, S., & Thompson, J. E. 2024, Phys. Rev. D, 109, 084077
- Mahapatra et al. (2024) Mahapatra, P., Chattopadhyay, D., Gupta, A., et al. 2024, Astrophys. J., 975, 117
- Mahapatra et al. (2025) —. 2025, Phys. Rev. D, 111, 023013
- Mahapatra et al. (2021) Mahapatra, P., Gupta, A., Favata, M., Arun, K. G., & Sathyaprakash, B. S. 2021, Astrophys. J. Lett., 918, L31
- Mandel & de Mink (2016) Mandel, I., & de Mink, S. E. 2016, Mon. Not. Roy. Astron. Soc., 458, 2634
- Mapelli (2016) Mapelli, M. 2016, Mon. Not. Roy. Astron. Soc., 459, 3432
- Mapelli et al. (2021) Mapelli, M., Santoliquido, F., Bouffanais, Y., et al. 2021, Symmetry, 13, 1678
- Mapelli et al. (2020) Mapelli, M., Spera, M., Montanari, E., et al. 2020, Astrophys. J., 888, 76
- Marchant et al. (2016) Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, Astron. Astrophys., 588, A50
- Marchant & Moriya (2020) Marchant, P., & Moriya, T. 2020, Astron. Astrophys., 640, L18
- McKernan et al. (2020) McKernan, B., Ford, K. E. S., O’Shaughnessy, R., & Wysocki, D. 2020, Mon. Not. Roy. Astron. Soc., 494, 1203
- Mckernan et al. (2018) Mckernan, B., et al. 2018, Astrophys. J., 866, 66
- McWilliams et al. (2010) McWilliams, S. T., Kelly, B. J., & Baker, J. G. 2010, Phys. Rev. D, 82, 024014
- Mehta et al. (2025) Mehta, A. K., Olsen, S., Wadekar, D., et al. 2025, Phys. Rev. D, 111, 024049
- Merritt et al. (2004) Merritt, D., Milosavljevic, M., Favata, M., Hughes, S. A., & Holz, D. E. 2004, Astrophys. J. Lett., 607, L9
- Messick et al. (2017) Messick, C., et al. 2017, Phys. Rev. D, 95, 042001
- Mezzacappa & Zanolin (2024) Mezzacappa, A., & Zanolin, M. 2024, arXiv:2401.11635
- Mezzasoma et al. (2025) Mezzasoma, S., Haster, C.-J., Owen, C. B., Cornish, N. J., & Yunes, N. 2025, arXiv:2503.23304
- Mihaylov et al. (2025) Mihaylov, D. P., Ossokine, S., Buonanno, A., et al. 2025, SoftwareX, 30, 102080
- Miller & Hamilton (2002) Miller, M. C., & Hamilton, D. P. 2002, Mon. Not. Roy. Astron. Soc., 330, 232
- Mills & Fairhurst (2021) Mills, C., & Fairhurst, S. 2021, Phys. Rev. D, 103, 024042
- Mishra et al. (2025) Mishra, T., Bhaumik, S., Gayathri, V., et al. 2025, Phys. Rev. D, 111, 023054
- Mishra et al. (2021) Mishra, T., O’Brien, B., Gayathri, V., et al. 2021, Phys. Rev. D, 104, 023014
- Mishra et al. (2022) Mishra, T., et al. 2022, Phys. Rev. D, 105, 083018
- Mould et al. (2022) Mould, M., Gerosa, D., & Taylor, S. R. 2022, Phys. Rev. D, 106, 103013
- Nee et al. (2025) Nee, P. J., et al. 2025, arXiv:2503.05422
- Nitz et al. (2017) Nitz, A. H., Dent, T., Dal Canton, T., Fairhurst, S., & Brown, D. A. 2017, Astrophys. J., 849, 118
- Nitz et al. (2023) Nitz, A. H., Kumar, S., Wang, Y.-F., et al. 2023, Astrophys. J., 946, 59
- Nitz et al. (2020) Nitz, A. H., Dent, T., Davies, G. S., et al. 2020, Astrophys. J., 891, 123
- Nobili et al. (2025) Nobili, F., Bhagwat, S., Pacilio, C., & Gerosa, D. 2025, arXiv:2504.17021
- Olsen et al. (2022) Olsen, S., Venumadhav, T., Mushkin, J., et al. 2022, Phys. Rev. D, 106, 043009
- O’Shaughnessy et al. (2013) O’Shaughnessy, R., London, L., Healy, J., & Shoemaker, D. 2013, Phys. Rev. D, 87, 044038
- Pankow et al. (2015) Pankow, C., Brady, P., Ochsner, E., & O’Shaughnessy, R. 2015, Phys. Rev. D, 92, 023002
- Paul et al. (2025) Paul, K., Maurya, A., Henry, Q., et al. 2025, Phys. Rev. D, 111, 084074
- Pierra et al. (2024) Pierra, G., Mastrogiovanni, S., & Perriès, S. 2024, Astron. Astrophys., 692, A80
- Planas et al. (2025a) Planas, M. d. L., Ramos-Buades, A., García-Quirós, C., et al. 2025a, arXiv:2503.13062
- Planas et al. (2025b) —. 2025b, arXiv:2504.15833
- Pompili et al. (2024) Pompili, L., Buonanno, A., & Pürrer, M. 2024, arXiv:2410.16859
- Pompili et al. (2023) Pompili, L., et al. 2023, Phys. Rev. D, 108, 124035
- Powell & Lasky (2025) Powell, J., & Lasky, P. D. 2025, Publ. Astron. Soc. Austral., 42, e030
- Pratten et al. (2020a) Pratten, G., Husa, S., Garcia-Quiros, C., et al. 2020a, Phys. Rev. D, 102, 064001
- Pratten et al. (2020b) Pratten, G., Schmidt, P., Buscicchio, R., & Thomas, L. M. 2020b, Phys. Rev. Res., 2, 043096
- Pratten et al. (2021) Pratten, G., et al. 2021, Phys. Rev. D, 103, 104056
- Qin et al. (2018) Qin, Y., Fragos, T., Meynet, G., et al. 2018, Astron. Astrophys., 616, A28
- Rakavy & Shaviv (1967) Rakavy, G., & Shaviv, G. 1967, ApJ, 148, 803
- Ramos-Buades et al. (2023a) Ramos-Buades, A., Buonanno, A., Estellés, H., et al. 2023a, Phys. Rev. D, 108, 124037
- Ramos-Buades et al. (2023b) Ramos-Buades, A., Buonanno, A., & Gair, J. 2023b, Phys. Rev. D, 108, 124063
- Read (2023) Read, J. S. 2023, Class. Quant. Grav., 40, 135002
- Renzo et al. (2020a) Renzo, M., Cantiello, M., Metzger, B. D., & Jiang, Y. F. 2020a, Astrophys. J. Lett., 904, L13
- Renzo et al. (2020b) Renzo, M., Farmer, R. J., Justham, S., et al. 2020b, Mon. Not. Roy. Astron. Soc., 493, 4333
- Rizzuto et al. (2022) Rizzuto, F. P., Naab, T., Spurzem, R., et al. 2022, Mon. Not. Roy. Astron. Soc., 512, 884
- Robinet et al. (2020) Robinet, F., Arnaud, N., Leroy, N., et al. 2020, SoftwareX, 12, 100620
- Rodriguez et al. (2018) Rodriguez, C. L., Amaro-Seoane, P., Chatterjee, S., & Rasio, F. A. 2018, Phys. Rev. Lett., 120, 151101
- Rodriguez et al. (2019) Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027
- Romero-Shaw et al. (2023) Romero-Shaw, I. M., Gerosa, D., & Loutrel, N. 2023, Mon. Not. Roy. Astron. Soc., 519, 5352
- Romero-Shaw et al. (2020a) Romero-Shaw, I. M., Lasky, P. D., Thrane, E., & Bustillo, J. C. 2020a, Astrophys. J. Lett., 903, L5
- Romero-Shaw et al. (2020b) Romero-Shaw, I. M., et al. 2020b, Mon. Not. Roy. Astron. Soc., 499, 3295
- Ruiz-Rocha et al. (2025) Ruiz-Rocha, K., Yelikar, A. B., Lange, J., et al. 2025, Astrophys. J. Lett., 985, L37
- Sachdev et al. (2019) Sachdev, S., et al. 2019, arXiv e-prints, arXiv:1901.08580
- Sakon et al. (2024) Sakon, S., et al. 2024, Phys. Rev. D, 109, 044066
- Salemi et al. (2019) Salemi, F., Milotti, E., Prodi, G. A., et al. 2019, Phys. Rev. D, 100, 042003
- Samsing (2018) Samsing, J. 2018, Phys. Rev. D, 97, 103014
- Santamaria et al. (2010) Santamaria, L., et al. 2010, Phys. Rev. D, 82, 064016
- Scheel et al. (2025) Scheel, M. A., et al. 2025, arXiv:2505.13378
- Schmidt et al. (2015) Schmidt, P., Ohme, F., & Hannam, M. 2015, Phys. Rev. D, 91, 024043
- Siegel et al. (2025) Siegel, H., Isi, M., & Farr, W. M. 2025, Phys. Rev. D, 111, 044070
- Siemonsen & East (2023) Siemonsen, N., & East, W. E. 2023, Phys. Rev. D, 107, 124018
- Singer & Price (2016) Singer, L. P., & Price, L. R. 2016, Phys. Rev. D, 93, 024013
- Smith et al. (2011) Smith, J. R., Abbott, T., Hirose, E., et al. 2011, Class. Quant. Grav., 28, 235005
- Smith et al. (2024) Smith, L., Ghosh, S., Sun, J., et al. 2024, Phys. Rev. D, 110, 083032
- Smith et al. (2020) Smith, R. J. E., Ashton, G., Vajpeyi, A., & Talbot, C. 2020, Mon. Not. R. Astron. Soc., 498, 4492
- Soni et al. (2025) Soni, S., et al. 2025, Class. Quant. Grav., 42, 085016
- Speagle (2020) Speagle, J. S. 2020, Mon. Not. Roy. Astron. Soc., 493, 3132
- Spera et al. (2019) Spera, M., Mapelli, M., Giacobbo, N., et al. 2019, Mon. Not. Roy. Astron. Soc., 485, 889
- Sperhake et al. (2008) Sperhake, U., Berti, E., Cardoso, V., et al. 2008, Phys. Rev. D, 78, 064069
- Stevenson et al. (2019) Stevenson, S., Sampson, M., Powell, J., et al. 2019, ApJ, 882, 121
- Stone et al. (2017) Stone, N. C., Metzger, B. D., & Haiman, Z. 2017, Mon. Not. Roy. Astron. Soc., 464, 946
- Sun et al. (2020) Sun, L., et al. 2020, Class. Quant. Grav., 37, 225008
- Sun et al. (2021) —. 2021, arXiv:2107.00129
- Szczepańczyk et al. (2021) Szczepańczyk, M., et al. 2021, Phys. Rev. D, 103, 082002
- Szczepańczyk et al. (2023) Szczepańczyk, M. J., et al. 2023, Phys. Rev. D, 107, 062002
- Tagawa et al. (2020) Tagawa, H., Haiman, Z., & Kocsis, B. 2020, Astrophys. J., 898, 25
- Takahashi & Nakamura (2003) Takahashi, R., & Nakamura, T. 2003, Astrophys. J., 595, 1039
- Thompson et al. (2025) Thompson, J., Hoy, C., Fauchon-Jones, E., & Hannam, M. 2025, arXiv:2506.10530
- Thompson et al. (2024) Thompson, J. E., Hamilton, E., London, L., et al. 2024, Phys. Rev. D, 109, 063012
- Tsang et al. (2020) Tsang, K. W., Ghosh, A., Samajdar, A., et al. 2020, Phys. Rev. D, 101, 064012
- Tsang et al. (2018) Tsang, K. W., Rollier, M., Ghosh, A., et al. 2018, Phys. Rev. D, 98, 024023
- Tsukada et al. (2023) Tsukada, L., et al. 2023, Phys. Rev. D, 108, 043004
- Urban et al. (2021) Urban, A. L., et al. 2021, gwdetchar/gwdetchar, Zenodo, doi:10.5281/zenodo.597016
- Usman et al. (2019) Usman, S. A., Mills, J. C., & Fairhurst, S. 2019, Astrophys. J., 877, 82
- Usman et al. (2016) Usman, S. A., et al. 2016, Class. Quant. Grav., 33, 215004
- Vaccaro et al. (2024) Vaccaro, M. P., Mapelli, M., Périgois, C., et al. 2024, Astron. Astrophys., 685, A51
- Vajente (2024) Vajente, G. 2024, aLIGO LHO Logbook, 76459, ,
- Vajente et al. (2020) Vajente, G., Huang, Y., Isi, M., et al. 2020, Phys. Rev. D, 101, 042003
- Valencia et al. (2024) Valencia, J., Tenorio, R., Rosselló-Sastre, M., & Husa, S. 2024, Phys. Rev. D, 110, 124026
- van Son et al. (2020) van Son, L. A. C., de Mink, S. E., Broekgaarden, F. S., et al. 2020, Astrophys. J., 897, 100
- Varma et al. (2019) Varma, V., Field, S. E., Scheel, M. A., et al. 2019, Phys. Rev. Research., 1, 033015
- Varma et al. (2020) Varma, V., Isi, M., & Biscoveanu, S. 2020, Phys. Rev. Lett., 124, 101104
- Vazsonyi & Davis (2023) Vazsonyi, L., & Davis, D. 2023, Class. Quant. Grav., 40, 035008
- Veitch et al. (2020) Veitch, J., Pozzo, W. D., Williams, M., et al. 2020, johnveitch/cpnest: v0.9.9, vv0.9.9, Zenodo, doi:10.5281/zenodo.4109271. https://doi.org/10.5281/zenodo.4109271
- Venumadhav et al. (2020) Venumadhav, T., Zackay, B., Roulet, J., Dai, L., & Zaldarriaga, M. 2020, Phys. Rev. D, 101, 083030
- Viets et al. (2018a) Viets, A., Wade, M., Urban, A., et al. 2018a, Classical and Quantum Gravity, 35, 095015
- Viets et al. (2018b) Viets, A., et al. 2018b, Class. Quant. Grav., 35, 095015
- Virgo Collaboration (2021) Virgo Collaboration. 2021, PythonVirgoTools, git.ligo.org/virgo/virgoapp/PythonVirgoTools, vv5.1.1, ,
- Virtanen & others (2020) Virtanen, P., et al. 2020, Nature Methods, 17, 261. https://doi.org/10.1038/s41592-019-0686-2
- Wadekar et al. (2023) Wadekar, D., Roulet, J., Venumadhav, T., et al. 2023, arXiv e-prints, arXiv:2312.06631
- Wang et al. (2022) Wang, Y.-Z., Li, Y.-J., Vink, J. S., et al. 2022, Astrophys. J. Lett., 941, L39
- Waskom et al. (2021) Waskom, M., et al. 2021, mwaskom/seaborn: v0.11.2 (August 2021), vv0.11.2, Zenodo, doi:10.5281/zenodo.592845. https://doi.org/10.5281/zenodo.592845
- Wette (2020) Wette, K. 2020, SoftwareX, 12, 100634
- Williams (2025) Williams, D. 2025, Class. Quant. Grav., 42, 105012
- Williams et al. (2023) Williams, D., Veitch, J., Chiofalo, M. L., et al. 2023, J. Open Source Softw., 8, 4170
- Woosley (2017) Woosley, S. E. 2017, Astrophys. J., 836, 244
- Woosley & Heger (2021) Woosley, S. E., & Heger, A. 2021, Astrophys. J. Lett., 912, L31
- Woosley et al. (2002) Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015
- Wright & Hendry (2022) Wright, M., & Hendry, M. 2022, The Astrophysical Journal, 935, 68. https://doi.org/10.3847/1538-4357/ac7ec2
- Xu et al. (2024) Xu, Y., Rosselló-Sastre, M., Tiwari, S., et al. 2024, Phys. Rev. D, 109, 123034
- Yang et al. (2019) Yang, Y., et al. 2019, Phys. Rev. Lett., 123, 181101
- Zevin et al. (2019) Zevin, M., Samsing, J., Rodriguez, C., Haster, C.-J., & Ramirez-Ruiz, E. 2019, Astrophys. J., 871, 91
- Zhu et al. (2025) Zhu, H., et al. 2025, Phys. Rev. D, 111, 064052
- Zweizig, J. (2006) Zweizig, J. 2006, The Data Monitor Tool Project, labcit.ligo.caltech.edu/˜jzweizig/DMT-Project.html, ,