H2CO ortho-to-para ratio in the protoplanetary disk HD 163296
Abstract
Ortho-to-para (o/p) ratios of species like water, ammonia and formaldehyde () are believed to encode information about the formation history of the molecule. Measurements of o/p ratios in protoplanetary disks could thus be used to constrain their physical and chemical histories. We present the first measurement of the o/p ratio in a protoplanetary disk, using three ortho and two para lines observed with the Sub-millimeter Array (SMA) combined with one highly resolved measurement of a single line with ALMA toward the disk around Herbig Ae star HD 163296. We find a disk-averaged o/p ratio of 1.8-2.8 (depending on the assumed disk structure), corresponding to a spin temperature of K. We also derive a rotational temperature of 24 K from the flux ratio of the three ortho lines. The observed spatial distribution, as seen by ALMA, as well as the rotational temperature and the o/p ratio, at the large scales the SMA is most sensitive to, are consistent with a low-temperature formation pathway, most likely grain surface chemistry, of in this disk.
Subject headings:
astrochemistry – ISM: clouds – ISM: molecules – radiative transfer – radio lines: ISM1. Introduction
| Line | Freq. | Chan width | Beam | PA | Chan. rms | Mom 0 rmsa |
|---|---|---|---|---|---|---|
| GHz | ” | ∘ | mJy beam-1 | mJy beam-1 | ||
| SMA observations | ||||||
| 218.222 | 0.6 | 32.36 | 50.93 | 99.85 | ||
| 225.698 | 0.6 | 56.04 | 53.26 | 105.67 | ||
| 281.527 | 0.6 | 12.76 | 80.74 | 145.35 | ||
| 290.623 | 0.6 | 45.29 | 112.05 | 280.79 | ||
| 300.837 | 0.6 | 45.17 | 118.25 | 271.34 | ||
| ALMA observations | ||||||
| 290.623 | 0.6 | -72.80 | 7.22 | 15.90 | ||
aThe cubes are integrated from 2 to 10.
Formaldehyde () is a simple organic molecule that is easily detected in the interstellar medium (ISM). Being a slightly asymmetric rotor, it is an excellent tracer of the gas density and temperature. In addition, could potentially be used to trace snowlines in protoplanetary disks, an important parameter for gas giant planet formation (Qi et al., 2013). However, to correctly interpret the observations it is necessary to understand the dominant formation pathway of . Understanding its formation in disks is of especial importance because disks provide the material for new planetary systems. can form both in the gas-phase and on the surface of dust grains (e.g., Fuchs et al., 2009), but the relative importance of these two mechanisms is poorly constrained in many interstellar environments, including disks. A possible way to discriminate between the two is to measure the ortho-to-para (o/p) ratio.
Molecules that contain two or more hydrogen atoms, such as H2, H2O, and NH3, exist in two isomeric forms: ortho (hydrogen nuclei spin are parallel) and para (hydrogen nuclei spin are anti-parallel). In thermal equilibrium, the relative population between the two isomers is given by:
| (1) |
where and are the level degeneracies and energies, respectively, is the Boltzmann constant and is the spin temperature.
If the formation temperature is high compared to the energy difference between the two species, the molecule will form with an o/p ratio equal to the statistical value, which corresponds to the statistical weight () ratio between the ground states of the ortho and para species. At thermal equilibrium, low-temperature formation pathways should deviate from the statistical value, and result in a lower . In the case of (and ), when it forms in the warm gas-phase, an o/p ratio of 3 is expected. In contrast, a lower o/p ratio could result if forms on the surface of dust grains (Kahane et al., 1984; Dickens & Irvine, 1999).
A broad range of o/p ratios have been measured in comets and in the ISM, for (e.g., Kahane et al., 1984; Maret et al., 2004; Jørgensen et al., 2005; Guzmán et al., 2011) and other species, like H2Cl+ (Le Gal et al., 2017) and NH3 (Persson et al., 2012). Observations of o/p ratios for water and ammonia have been commonly used to deduce a cold origin of the cometary volatiles in the Solar Nebula (Mumma & Charnley, 2011). However, the interpretation of o/p ratios is now disputed, as recent laboratory experiments of ices are not able to reproduce the low o/p ratios that are observed in comets and in the ISM (Hama et al., 2016).
Measurements of o/p ratios in Solar nebula analogs, i.e. protoplanetary disks, could help to elucidate the meaning of o/p ratios in solar system bodies. So far, only the water o/p ratio has been measured in TW Hya using Herschel observations, where a large range of possible values was found (0.2-3.0; Hogerheijde et al., 2011; Salinas et al., 2016) depending on the disk model. is particularly well suited for such studies because its lines are bright in disks at millimeter wavelengths, and several lines of both its ortho and para states can now be easily detected with interferometers. Indeed, has been detected in several disks (Aikawa et al., 2002; Öberg et al., 2010, 2011; Qi et al., 2013; Loomis et al., 2015; Öberg et al., 2017; Carney et al., 2017), but so far too few lines have been observed to put any constraints on the o/p ratio. In this paper, we provide the first measurement of the disk-averaged o/p ratio in a protoplanetary disk.
Our target, the HD 163296 disk, is inclined by (as measured by CO and dust continuum emission), and the position angle (defined from North to West) is 132∘ (Isella et al., 2007). The central star has a mass of 2.3 , a disk mass of , and it is located pc away (Gaia Collaboration et al., 2018). For consistency with previous analysis, we use the old distance of 122 pc (van den Ancker et al., 1998) throughout the paper. The size of the dust disk at milimeter wavelengths is au and the CO emission extends to au (Isella et al., 2016). The location of the CO snowline has been measured with ALMA observations of N2H+ (Qi et al., 2015), providing an additional constraint on the possible origin in this particular disk. HD 163296 is thus particularly well suited as a test case for this work.
The observations and data reduction are presented in section 2. In section 3 we describe the spatial distribution seen by the ALMA observations, and derive a rotational temperature from the SMA observations. In section 4 we describe the model used to reproduce the line emission, and extract the disk-averaged o/p ratio. A discussion is presented in section 5, and a we summarize the results in section 6.
2. Observations and data reduction
We obtained Atacama Large Millimeter/submillimeter Array (ALMA) observations of the para line, and Submillimeter-Array (SMA) observations of the and lines of both ortho and para towards the disk around the Herbig Ae star HD 163296. A description of the observations and data reduction is given next.
2.1. ALMA
We observed the line at 290.623 GHz with ALMA in May 2014 during Cycle 1 (project ADS/JAO.ALMA#2012.1.00681; PI: C. Qi.) with 32 antennas. The Band 7 observations have baselines lengths spanning between 27 and 650 m, and a total on-source time of 45.5 min. The correlator was configured with four spectral windows, covering the N2H+ , DCO+ and the lines, as well as a window dedicated to continuum. A detailed description of the observations and the results of the N2H+ and DCO+ lines are given in Qi et al. (2015). The line was covered with a spectral window of 58 MHz bandwidth and 15 kHz channel width. To calibrate the amplitude and phase temporal variations, the quasar J1733-1304 was observed.
We used the standard calibration performed by the ALMA staff, and further self-calibrated the data in phase and amplitude to improve the signal-to-noise ratio. The continuum subtracted visibilities were cleaned in CASA 4.7, using the CLEAN algorithm with Briggs weighting of 2. The data were regridded to a spectral resolution of 0.6. We applied a Gaussian taper of to improve the signal-to-noise. In addition, we created a mask to help the cleaning process, by selecting regions in each channel with line emission that is consistent with the expected Keplerian rotation of the disk. The resulting noise properties and beam information are summarized in Table 1.
2.2. SMA
We observed five lines with the SMA. The lines at 218 GHz and 290 GHz, and the line at 300 GHz were observed in March 2014 with 7 antennas in the sub-compact (SUB) array configuration. The 218 GHz line was observed in one spectral setting, with a spectral window of 104 MHz and 406 kHz channel width. The 290 and 300 GHz lines were covered in another setting, with two spectral windows of 104 MHz and 406 kHz channel width each. The quasars NRAO 530 and were observed to calibrate amplitude and phase variations, and the frequency bandpass was calibrated using observations of 3C279. Titan and Mars were used as flux calibrators. We also include observations of the and lines at 281.527 and 225.698 GHz, respectively, which have been presented in Qi et al. (2013). A detailed description of the observations can be found in Qi et al. (2013). For consistency with the other lines, we present an independent imaging in this paper.
The SMA data were first calibrated with the MIR software package using standard procedures111https://www.cfa.harvard.edu/~cqi/mircook.html. The calibrated data were then exported to CASA and cleaned in the same way as the ALMA line. The data were regridded to a common spectral resolution of 0.6. A robust parameter of 2 was used to optimize the sensitivity. To help the cleaning process, we created circular masks for each line, that was the same for each channel. The radius of the mask was chosen to cover the line emission in all channels, and varied for the different lines. The resulting rms noise levels and observational parameters are summarized in Table 1.
3. Observational results
3.1. spatial distribution
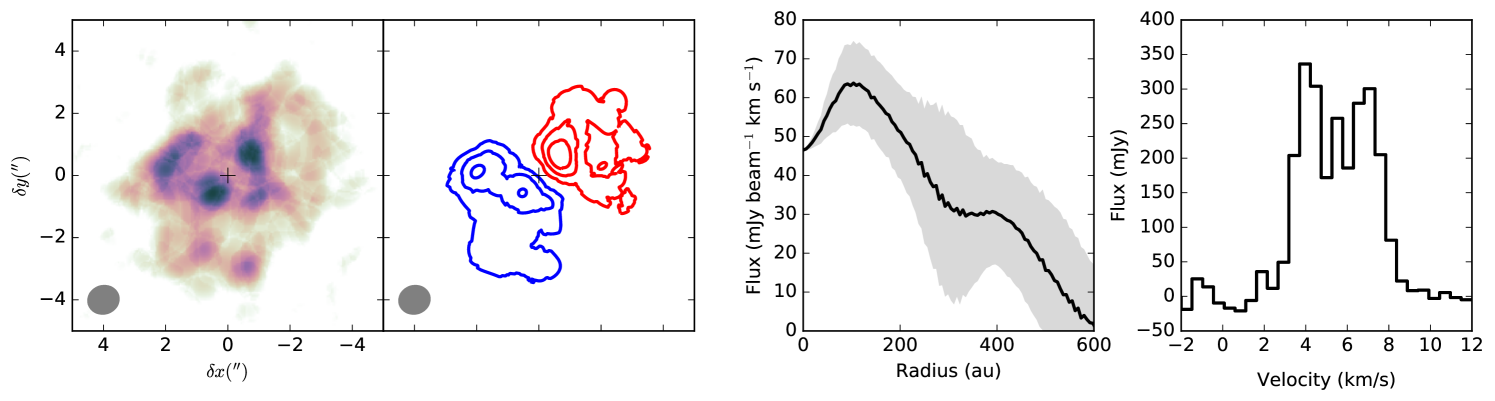
Fig. 1 shows the ALMA observations of the line. The two left panels show the velocity integrated map, integrated over the full velocity range (left) and over the blue- and red-shifted part of the line (right). The third panel in Fig. 1 shows the azimuthally-averaged deprojected profile of the line emission. It was obtained by extracting elliptical anulii in the unclipped moment-zero map, taking into account the inclination and position angle of the disk. The right-most panel shows the disk-integrated spectra, which was obtained using an elliptical mask. The integrated spectra shows a double-peaked profile, typical of Keplerian rotation of an inclined disk. The emission presents a ring-like spatial distribution, with a depletion of emission at the disk center, a peak of emission at intermediate radii ( au), and either a second but weaker peak or a plateau in the outer disk near au. This second bump is located farther out in the disk than the milimeter dust edge near au (Isella et al., 2016). Carney et al. (2017) presented higher-angular resolution observations (0.5”) of the lower energy ( K) line, which has a similar radial profile.
The observed distribution is not unique to the HD 163296 disk. Spatially resolved observations of the low-energy ( K) line in TW Hya also show a depression of the emission at the disk center and a bump in the outer disk (Öberg et al., 2017). In contrast, observations of the higher-energy ( K) line in DM Tau and TW Hya present centrally peaked emission profiles (Loomis et al., 2015; Öberg et al., 2017). Such different morphologies of the and lines are well explained by the presence of hot close to the star followed by a lack of until cold formation becomes possible in the outer disk. In summary, the observed morphology toward HD 163296 is consistent with previous disk observations, suggesting that it is a good object for a case study on chemistry in disks.
3.2. excitation temperature
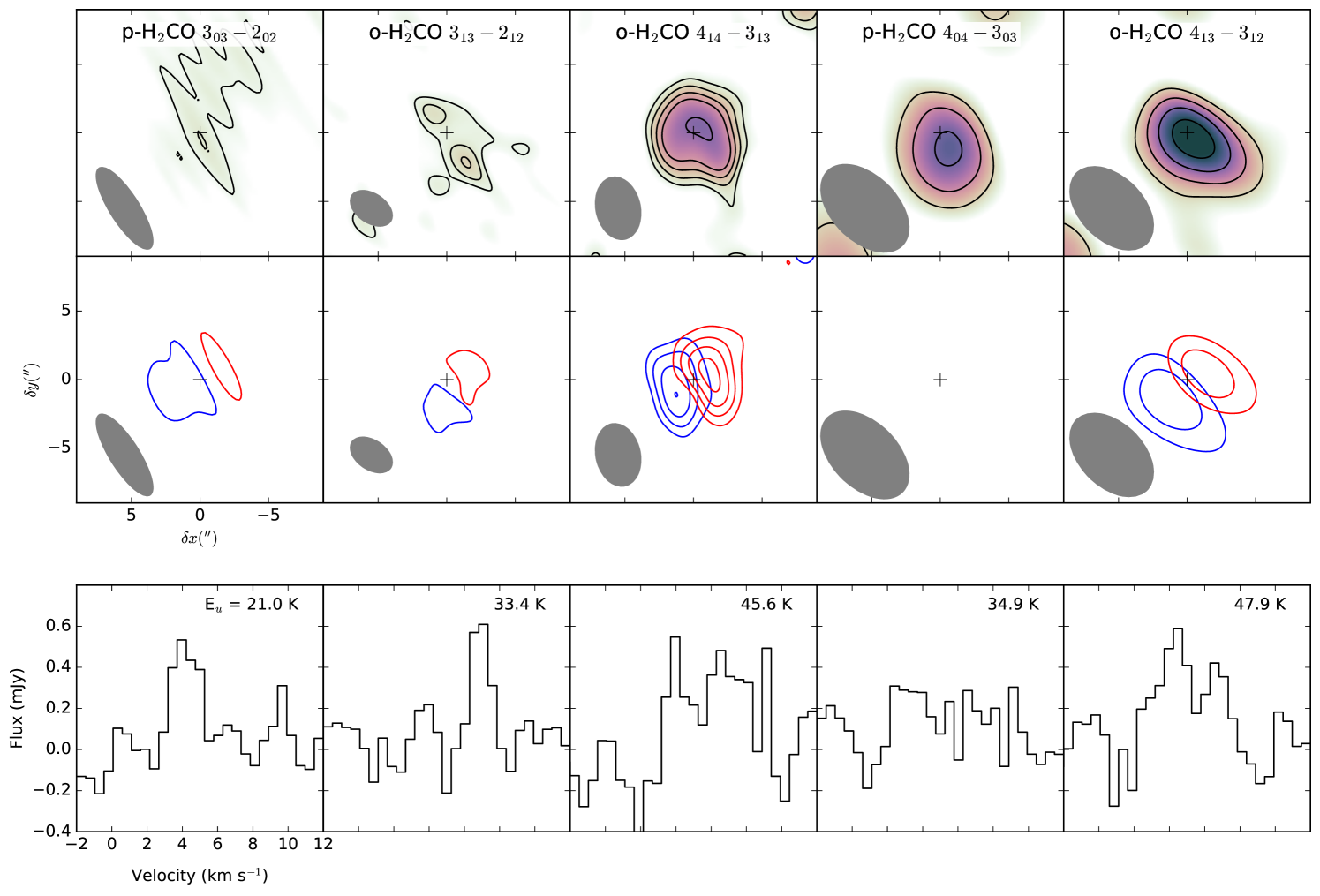
The SMA observations are shown in Fig. 2. The top row shows the velocity integrated maps of the five lines, while the red- and blue-shifted parts of the emission are shown in the second row. The bottom row shows the disk-integrated spectra, obtained using a circular mask with a radius of 6”. Although the emission looks washed-out in the moment-zero maps for some of the lines, visual inspection of the individual channels show line emission consistent with the expected Keplerian rotation of the disk. The two higher energy lines ( K) are centrally peaked. The peak emission of the remaining lines with K are not centered, suggesting ring-like emission patterns or a drop of the emission in the inner disk consistent with the higher-angular resolution ALMA observations.
We extracted disk-integrated fluxes using a circular mask with a radius of 6”. The fluxes are reported in Table 2. The uncertainty in the flux was estimated by taking the standard deviation of 500 simulated flux measurements from regions free of signal, using the same circular mask but centered at random positions in the map. The fluxes of the 290 GHz line observed with ALMA and SMA are consistent within the uncertainties. We use the disk-integrated fluxes to estimate an excitation temperature for .
The critical densities of the observed lines, defined as the density at which the spontaneous radiative de-excitation rate () is equal to the collisional de-excitation rate (), are given in Table 2 for a temperature of 20 K. For a higher temperature of 60 K, the critical densities increase by less than 20%. When the gas density is comparable or larger than the critical density, the emission is thermalized and the excitation temperature is equal to the gas kinetic temperature. When the gas density is lower, then the emission becomes sub-thermally excited and . Given the high () gas densities in protoplanetary disks, in particular closer to the midplane (see Fig. 4), we expect the bulk of the emission to be thermalized.
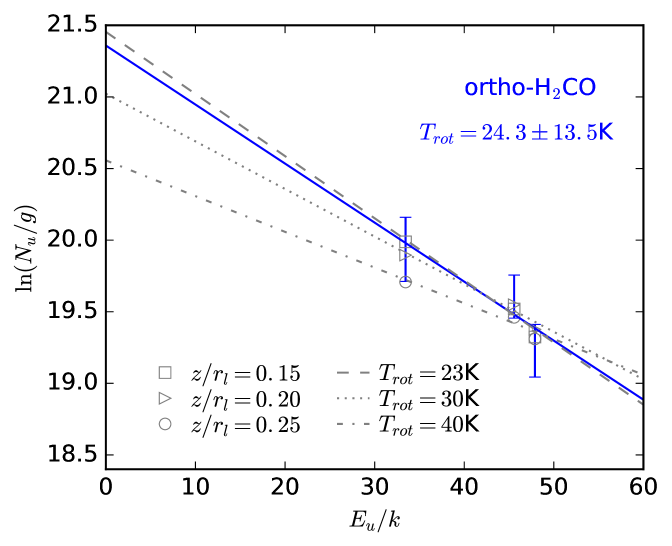
Using the three ortho lines we constructed a rotational diagram (Fig. 3). We obtain a rotational temperature of K. This temperature is consistent with the temperature of 24 K derived by Carney et al. (2017), from the , and lines, using a match-filter technique to extract the fluxes of the two weaker lines. The derived rotational temperature also matches the CO freeze-out temperature found by Qi et al. (2015) for this disk, using N2H+ and C18O observations. This suggest that the emission at the large scales, to which the SMA is sensitive, arises predominantly from the cold layers close to the midplane, where CO starts to freeze-out onto dust grains and can be hydrogenated to form . In the next section, we use this measured rotational temperature to inform our model on the distribution of in the disk.
| Line | Flux density | ||
|---|---|---|---|
| K | Jy | ||
| SMA observations | |||
| 21.0 | |||
| 33.4 | |||
| 45.6 | |||
| 34.9 | |||
| 47.9 | |||
| ALMA observations | |||
| 34.9 | |||
| Fixed | Best fit parameters | ||||
|---|---|---|---|---|---|
| parameters | |||||
| ALMA data | |||||
| 1 au | |||||
| 80 au | |||||
| 600 au | |||||
| 0.5 | 1.0716999 | 1.0717228 | 1.0717574 | ||
| SMA data | |||||
| 1.0479973 | 1.0479993 | 1.0480178 | |||
4. Line modeling
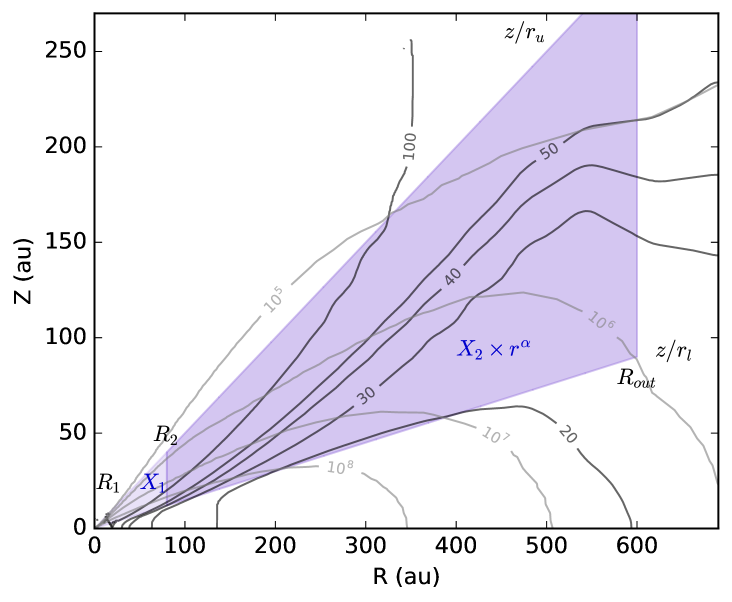
In this section we aim at measuring the disk averaged o/p ratio in the HD 163296 disk. For this, we use the disk physical structure of Qi et al. (2011), that was constrained by fitting the spectral energy distribution, the millimeter dust continuum, and multiple CO and CO isotopologue lines. The adopted gas density and temperature structure is shown in Fig. 4 with gray and black contours, respectively. We first model the abundance structure of using the high angular resolution observations of the line. Keeping the spatial distribution of constant, we then fit the five lines observed with the SMA to find the best-fit o/p ratio.
4.1. abundance structure
Based on chemical model predictions of disks, the distribution of can be separated in two main components: 1) A warm component towards the center of the disk, that is mainly produced by gas-phase chemistry (e.g., Loomis et al., 2015), and 2) a colder component located in the layers above the midplane in the outer disk, where the formation is dominated by grain surface chemistry (e.g., Öberg et al., 2017). In the midplane, remains frozen on the surfaces of dust grains. Following this, we parameterize the abundance structure of assuming the two components displayed in Fig. 4. The first component is located in the inner disk, between and , with constant abundance . The second component is located between and , and has an abundance described by a power-law, . Both components have lower and upper boundaries, and .
Given the uncertainties when modeling only one transition, we fixed some of the parameters. The fixed parameters are and ; and only and are left free in the line fitting. The adopted values in the model are given in the left column of Table 3. The values for and are chosen based on predictions from chemical models of this disk (Cleeves et al., private communication). is fixed to 600 au, corresponding to the extent of the emission. We note that due to the low-angular resolution of the SMA observations, the inferred disk-averaged o/p ratio (see section 4.2) is not very sensitive to variations in the position of the inner component (i.e., and ). We consider three different values (0.15, 0.20 and 0.25) for the lower boundary, , to investigate the impact of the adopted height of the disk emission layer on the derived o/p ratio. The upper boundary, , is fixed to 0.5; we tried different values, and found that the results were not sensitive to this paramter.
We use a Bayesian approach to find the best fit of the model to the ALMA visibilities. For this, we first create a synthetic observation of the line emission using the RADMC-3D package (Dullemond et al., 2012) to compute the level populations, assuming the gas is under local thermal equilibrium (LTE). We then compute the Fourier Transform of the modeled line emission, using the vis-sample Python package222https://pypi.python.org/pypi/vissample that re-projects the modeled visibilities on the observed points. We then compute the weighted difference between model and observations, for the real and imaginary parts of the complex visibility, which gives the likelihood of the model. This process is repeated by sampling the posterior distribution with the MCMC method implemented in the emcee package by Foreman-Mackey et al. (2013).
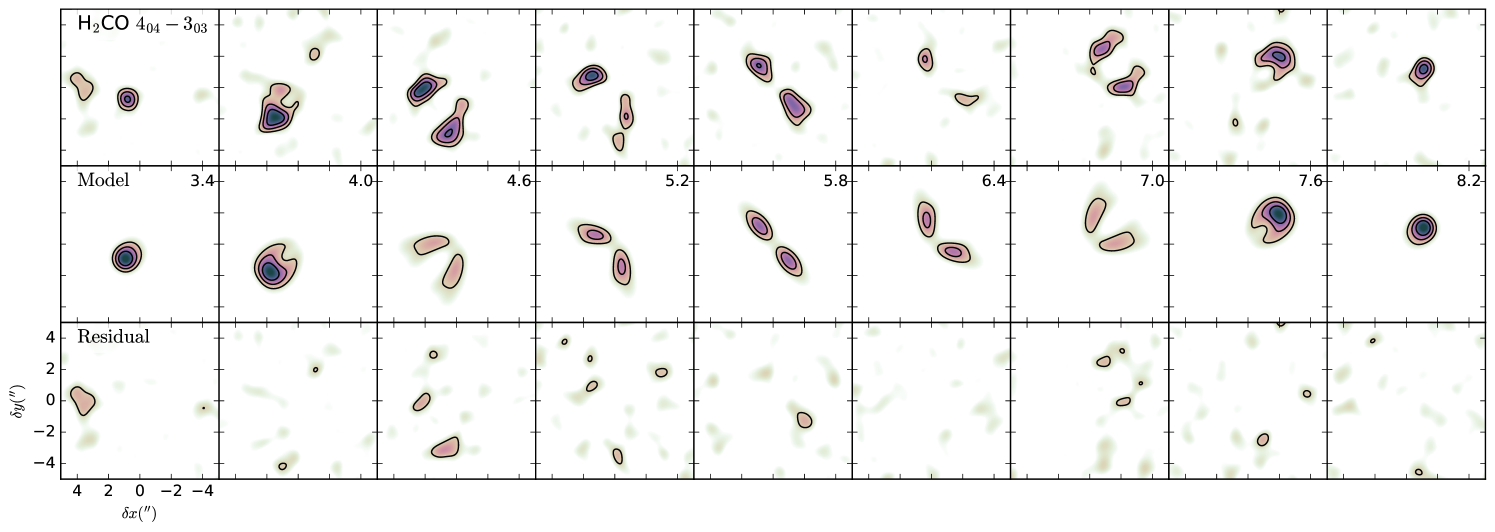
The best fit values of the model parameters are listed in the right columns in Table 3, for the three different lower boundaries we consider. Because we only model one line, the abundance we derive corresponds to that of . The abundances listed in Table 3, however, correspond to the total abundance, including both ortho and para, and are computed assuming a uniform o/p ratio of 3. We allow this parameter to vary in the next section. The best-fit is found for the model with . Fig. 5 shows channel maps of the line observed with ALMA (top row), together with the best fit model (middle row), and the residuals (bottom row). The inferred abundances in the inner au change considerably (by more than one order of magnitude) depending on the adopted value for the lower boundary. The abundance in the outer disk, given by the second component, change by a factor of (at au) within the three sets of models.
Motivated by the bump observed in the radial profile of the ALMA line (see Fig. 1), we also explored the presence of a third component in the outer disk that is closer to the midplane. For this, we ran another set of models including a third component of constant abundance between 350 and 600 au, and upper boundary equal to the lower boundary of the second component (i.e., ). The best-fit abundance of this third component remained low compared to the two other components no matter the adopted value, suggesting that the contribution of such a third cold component to the overall emission is small. We note that these models improved slightly the fit of the ALMA line but resulted in similar results for the SMA observations.
4.2. Disk-average o/p ratio
We model the line emission of the two para and three ortho lines of in the same way we did for the ALMA observations. Given the lower angular resolution of the SMA observations, we keep the abundance structure fixed, and vary only the o/p ratio. We assume a uniform o/p ratio across the disk. In order to take into account for differences in the absolute fluxes between the ALMA and SMA data due to absolute flux calibration uncertainites of 10-20%, we introduce a scale factor for the total abundance in the disk. That is, the total abundance derived in the previous section is multiplied by this scale factor, which is a free parameter in the SMA line fitting.
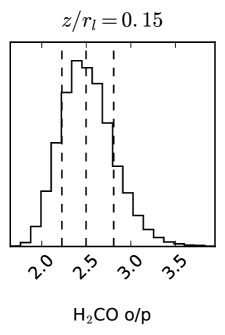
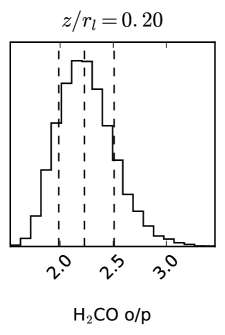
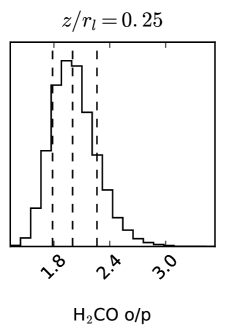
The resulting best-fit parameters are shown in the bottom rows of Table 3. Fig. 6 shows the posterior probability distribution for the disk-averaged o/p ratio. The scale factor is (depending on ), and increases somewhat with increasing lower boundary. These values are of the expected magnitude when considering the differences in measured fluxes with ALMA and SMA (see section 3.2).
The inferred o/p ratio changes depending on the assumed lower boundary but remains consistently lower than 3, the high-temperature value. The highest o/p value (2.5) is obtained when is located closer to the midplane, and lower values (2.2 and 2.0) are obtained when is closer to the disk surface. The possible values for the o/p ratio are (within 1), corresponding to spin temperatures of K. Fig. 3 shows the rotational diagram of , and compares the observed and best-fit model integrated fluxes for the three choices. The best-fit is obtained for , which gives an o/p ratio of , corresponding to K. This is the only model resulting in consistent spin and rotational temperatures. However, we cannot rule out any of the vertical distribution choices based on the SMA data.
We note that this corresponds to a disk-averaged o/p ratio. Most likely, this value changes across the disk, both radially and vertically. Our inferred o/p value thus suggest that a considerable amount of the gas in the HD 63296 disk has an o/p ratio that is lower than 3. Higher-angular resolution observations are needed to disentangle regions in the disk with low o/p ratios from regions presenting a high-temperature statistical value.
5. Discussion
It is believed that o/p measurements provide information on the formation conditions of the molecule. In this section we aim at comparing the observed o/p ratio in the HD 163296 protoplanetary disk with values observed in the ISM and solar system bodies (for different species) to better understand how and if o/p ratios can be used to elucidate the formation pathway of . We also discuss the meaning of the o/p value in light of the new observations and what additional observations can resolve existing o/p puzzles.
5.1. Observed o/p ratios in the ISM and comets
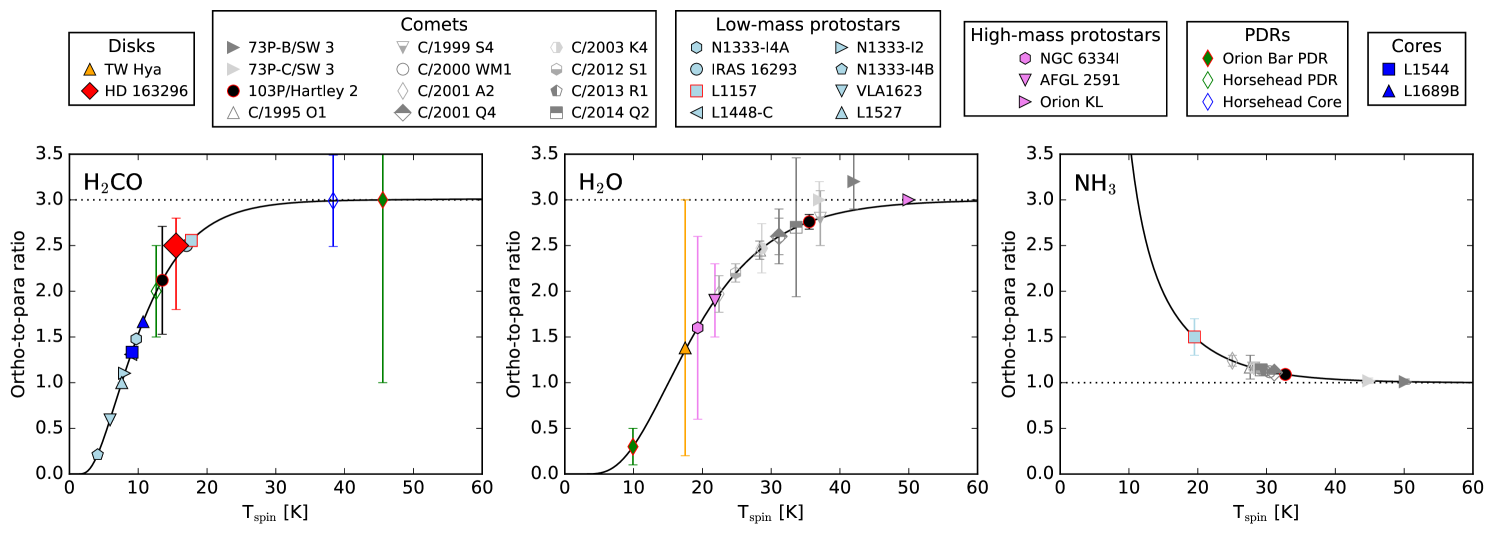
The o/p ratio has been measured in a variety of interstellar environments and one comet. Fig. 7 presents a compilation from the literature of measured o/p ratios. In the subsequent panels we present the same data on and . We highlight with red edges those sources where the o/p ratio has been measured for and another species. The solid curves in Fig. 7 correspond to the predicted o/p curves given by the Boltzmann distribution of the ortho and para energy levels. The observations are also listed in Table 4.
A range of o/p ratios is found in the ISM. Low-temperature ( K) values have been observed in different environments, such as the envelopes around low-mass stars (Jørgensen et al., 2005), outflows (Dickens & Irvine, 1999), and the Horsehead PDR (Guzmán et al., 2011). o/p ratio consistent with the high-temperature value of 3 have been observed towards quiescent cores, such as the cold ( K) UV-shielded core located just behind the Horsehead PDR (Guzmán et al., 2011), and the Orion-Bar PDR (Cuadrado et al., 2017). Because the Orion-Bar ( K) is a much stronger UV-illuminated PDR, dust grains at the cloud edge are free from ice mantles, in contrast to the Horsehead PDR where icy mantles can exist ( K). Cuadrado et al. (2017) have thus suggested that forms predominantly in the gas-phase in the Orion-Bar, while it forms on ices and is later non-thermally desorbed into the gas-phase in the Horsehad PDR. However, recent results from laboratory experiments cast doubt on this interpretation (see section 5.2 for a discussion).
The o/p ratio has been measured in one comet, 103P/Hartley 2, where a value of was found, corresponding to K (Gicquel et al., 2014). This o/p value is consistent with our disk measurement of , but the spin temperature is lower compared to what has been deduced from a sample of and o/p ratio comet measurements; Shinnaka et al. (2016) measured the o/p ratio in 26 comets, and found values of , corresponding to a spin temperature of 30 K. The o/p ratio has been measured towards about half of them. The similar and suggests that they share a common chemical history and/or they follow a similar thermalization mechanism, while either forms or thermalizes differently. Observations of o/p ratios in more comets are needed to confirm this is a general behavior.
Towards disks, only the water o/p ratio has been measured so far and only in one source, TW Hya, but the range of estimated ratios is too wide to provide any constraints. Hogerheijde et al. (2011) first reported an o/p ratio of , but later Salinas et al. (2016) explored different disk models and found values between 0.2 and 3. The disk-averaged o/p ratio measured in the HD 163296 disk is consistent with the o/p ratio measured in TW Hya.
| Source | o/p | o/p | Refs. | |
| Comets | ||||
| 73P-B | 1.010.03 | 3.200.30 | - | 1 |
| 73P-C | 1.020.03 | 3.000.20 | - | 1 |
| 103P | 1.090.03 | 2.760.08 | 2.120.59 | 1,2,3 |
| C1995O1 | 1.170.13 | 2.450.10 | - | 1 |
| C1999S4 | 1.160.05 | 2.800.30 | - | 1 |
| C2000WM1 | 1.120.02 | 2.600.20 | - | 1 |
| C2001A2 | 1.240.06 | 1.970.20 | - | 1 |
| C2001Q4 | 1.110.02 | 2.600.30 | - | 1 |
| C2003K4 | 1.160.04 | 2.470.27 | - | 1 |
| C2012S1 | 1.140.02 | 2.200.10 | - | 1 |
| C2013R1 | 1.130.02 | 3.010.49 | - | 1 |
| C2014Q2 | 1.140.04 | 2.700.76 | - | 1 |
| Protoplanetary disks | ||||
| TW Hya | - | - | 4 | |
| HD 163296 | - | - | 1.8-2.8 | This work |
| Low-mass protostars | ||||
| N1333I4A | - | - | 1.48 | 5 |
| IRAS16293 | - | - | 2.50 | 5 |
| L1157 | 1.50.2 | - | 2.56 | 5,6 |
| L1448C | - | - | 1.31 | 5 |
| N1333I2 | - | - | 1.10 | 5 |
| N1333I4B | - | - | 0.21 | 5 |
| VLA1623 | - | - | 0.59 | 5 |
| L1527 | - | - | 1.00 | 5 |
| High-mass star forming regions | ||||
| NGC 6334 I env | - | 1.61.0 | - | 7 |
| AFGL 2591 env | - | 1.90.4 | - | 8 |
| Orion-KL outf | - | 3.0 | - | 9 |
| Photo-dissociation regions | ||||
| Orion-Bar | - | 0.30.2 | 3.2 | 10,11 |
| Horsehead PDR | - | - | 2.0.5 | 12 |
| Horsehead Core | - | - | 3.0.5 | 12 |
| Pre-stellar clouds | ||||
| L1689B | - | - | 1.7 | 5 |
| L1544 | - | - | 1.3 | 5 |
1) Shinnaka et al. (2016), 2) Bonev et al. (2013), 3) Gicquel et al. (2014), 4) Salinas et al. (2016), 5) Jørgensen et al. (2005), 6) Umemoto et al. (1999), 7) Emprechtinger et al. (2010), 8) Choi et al. (2015), 9) Melnick et al. (2010), 10) Choi et al. (2014), 11) Cuadrado et al. (2017), 12) Guzmán et al. (2011).
5.2. The meaning of o/p ratios and future directions
It has long been thought that the o/p ratio upon formation is preserved and should reflect the formation temperature. This is because the ortho-para inter-conversion by spontaneous radiative transitions and non reactive collisions are extremely slow (e.g. Pachucki & Komasa, 2008; Tudorie et al., 2006), so the o/p ratio upon formation should be preserved.
In general, the o/p ratio upon formation of any molecule will depend on its formation mechanism, the spin selection rules, and the o/p of the reactants. Then, the ortho and para symmetry species can relax to the lowest energy rotational levels through spontaneous emission. Ortho-para conversion can occur via reactive collisions, for example with hydrogen atoms, in which a proton is exchanged. This process, known as equilibration, will compete with the destruction of the molecule. Whether equilibration or destruction dominates will depend on the specific rates, and will determine the resulting o/p ratio of the molecule. A good description of the different interstellar processes that determine the o/p ratio is given by Herbst (2015), for the example of the water cation.
In the specific case of , the dominant gas-phase formation pathway are reactions of atomic oxygen with CH3. The destruction of will depend on the conditions of the gas. In the presence of strong UV fields (i.e., in the disk surface layers and inner disk), will mainly be photo-dissociated, while in UV-shielded regions (i.e., in the disk midplane and outer disk) it will mainly be destroyed by reactions with ions (Guzmán et al., 2011). The original o/p ratio will thus depend on the o/p ratio of CH3. CH3 forms from the dissociative recombination of CH with electrons, where CH in turn forms from a series of reactions involving H2, starting from C+. The fraction of ortho and para formed in each of these reactions (the branching ratios) will depend on the details of the formation mechanism, which are not fully understood. When a di-hydrogenated molecule like forms in the gas-phase through full proton scrambling mechanisms, the resulting o/p ratio should reflect the o/p ratio of its parent molecule. Gas-phase formation in cold gas that is enriched in p- should thus result in o/p ratio , while formation in the warmer gas should result in the high-temperature limit. However, if full proton scrambling mechanisms are not possible/allowed and only restrictive mechanisms pertain (such as H-abstraction), then even a cold gas-phase formation pathway could result in a statistical ratio of 3 resulting in a complete loss of chemical history information. The exact calculations require an accurate treatment of the selection rules (see for example Gerlich et al. (2006) for the case of H, and Le Gal et al. (2017) for the case of H2Cl+). These do not yet exist, and theoretical studies focused on are needed to determine which of these processes dominate, and thus whether the thermal history of the gas can be traced with o/p ratio measurements.
The resulting o/p ratio from grain surface formation is even less clear, although it is often suggested that the will reflect the temperature of the ice (e.g., Kahane et al., 1984). Only recently have the nuclear-spin conversion on ices, by thermal and non-thermal desorption processes, been investigated. Laboratory experiments have shown that after formation on water ices (at K), has the statistical o/p ratio of 3. But the o/p ratio was found to decrease substantially if is re-trapped in the ice (Watanabe et al., 2010). The resulting o/p ratio thus seems to depend on how long the molecule resides in the ice. More recently, Hama et al. (2016) investigated the o/p conversion of water on ices, and found that the statistical value of 3 is preserved after the water ices are thermally desorbed into the gas-phase (when heating the ices to K), no matter if the ice is formed by vapor-deposition or it is formed in-situ at 10 K. One could argue that the water o/p ratio will equilibrate to the (high) temperature during thermal desorption, while it can remain low in the case of photo-desorption. However, Hama et al. (2016) also investigated the case of photo-desorption, and found that the desorbed water also has an o/p ratio of 3. This unexpected result raised the question of what is the real meaning of the low o/p ratios measured in comets, star and planet forming regions.
Assuming that behaves similarly to water, it is possible that the o/p ratio is not indicative of the ice formation temperature, but could instead provide information on the desorption mechanism and/or the physical conditions of the gas at the time of desorption. Indeed, the spin temperature inferred from in HD 163296 agrees well with the expected gas temperature in the regions where the bulk of is expected to form. More laboratory experiments and theoretical predictions are needed to better understand the different formation and desorption processes and how they affect the resulting o/p ratio of .
Finally, the current SMA observations are sensitive to the colder outer disk, where is formed predominantly by grain surface chemistry. Future observations at higher-angular resolution will allow us to measure variations of the o/p ratio in the disk. A direct comparison of the o/p ratio with the gas temperature structure of the disk at different radii will help us test different formation scenarios and elucidate what information can be extracted from o/p measurements.
6. Conclusions
We have presented SMA observations (at angular resolution) of 3 ortho and 2 para lines in the HD 163296 protoplanetary disk and constrained the disk-averaged o/p ratio. We complemented these observations with one line of at 290 GHz at higher angular resolution () to determine the abundance distribution. We consider a range of distributions, locating at different heights in the disk, and modeled the observed visibilities to constrain the best-fit o/p ratio to the SMA observations. We derive an o/p value of , depending on the adopted spatial distribution, corresponding to a spin temperature of 11-22 K. We also derive a rotational temperature of 24 K from the flux ratio of the three ortho lines. These results suggests that the bulk of forms by CO hydrogenation on the surface of dust grains, in agreement with the chemical model predictions, and is later released into the gas-phase through some desorption mechanism.
Observations of o/p ratios could be powerful diagnostics of the physical and chemical conditions of the gas. Moreover, future resolved observations of disks, where regions with low o/p ratios can be disentangled from regions presenting the statistical value of 3, have great potential to constrain the formation pathway of (gas-phase vs. grain surface chemistry) in disks.
References
-
Aikawa et al. (2002)
Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622
-
Bonev et al. (2013)
Bonev, B. P., Villanueva, G. L., Paganini, L., et al. 2013, Icarus, 222, 740
-
Carney et al. (2017)
Carney, M. T., Hogerheijde, M. R., Loomis, R. A., et al. 2017, arXiv:1705.10188
-
Choi et al. (2014)
Choi, Y., van der Tak, F. F. S., Bergin, E. A., & Plume, R. 2014, A&A, 572, L10
-
Choi et al. (2015)
Choi, Y., van der Tak, F. F. S., van Dishoeck, E. F., Herpin, F., & Wyrowski, F. 2015, A&A, 576, A85
-
Cleeves (2016)
Cleeves, L. I. 2016, ApJ, 816, L21
-
Cuadrado et al. (2017)
Cuadrado, S., Goicoechea, J. R., Cernicharo, J., et al. 2017, A&A, 603, A124
-
Dickens & Irvine (1999)
Dickens, J. E., & Irvine, W. M. 1999, ApJ, 518, 733
-
Dullemond et al. (2012)
Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library, ascl:1202.015
-
Emprechtinger et al. (2010)
Emprechtinger, M., Lis, D. C., Bell, T., et al. 2010, A&A, 521, L28
-
Foreman-Mackey et al. (2013)
Foreman-Mackey, D., Conley, A., Meierjurgen Farr, W., et al. 2013, Astrophysics Source Code Library, ascl:1303.002
-
Gaia Collaboration et al. (2018)
Gaia Collaboration, Brown, A. G. A., Vallenari, A., et al. 2018, arXiv:1804.09365
-
Gicquel et al. (2014)
Gicquel, A., Milam, S. N., Villanueva, G. L., et al. 2014, ApJ, 794, 1
-
Gerlich et al. (2006)
Gerlich, D., Windisch, F., Hlavenka, P., & et al. 2006, Philosophical Transactions of the Royal Society of London Series A, 364, 3007
-
Guzmán et al. (2011)
Guzmán, V., Pety, J., Goicoechea, J. R., Gerin, M., & Roueff, E. 2011, A&A, 534, A49
-
Fuchs et al. (2009)
Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629
-
Hama et al. (2016)
Hama, T., Kouchi, A., & Watanabe, N. 2016, Science, 351, 65
-
Herbst (2015)
Herbst, E. 2015, European Physical Journal Web of Conferences, 84, 06002
-
Hogerheijde et al. (2011)
Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2011, Science, 334, 338
-
Isella et al. (2007)
Isella, A., Testi, L., Natta, A., et al. 2007, A&A, 469, 213
-
Isella et al. (2016)
Isella, A., Guidi, G., Testi, L., et al. 2016, Physical Review Letters, 117, 251101
-
Jørgensen et al. (2005)
Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2005, A&A, 437, 501
-
Kahane et al. (1984)
Kahane, C., Lucas, R., Frerking, M. A., Langer, W. D., & Encrenaz, P. 1984, A&A, 137, 211
-
Le Gal et al. (2017)
Le Gal, R., Xie, C., Herbst, E., et al. 2017, arXiv:1708.08980
-
Lis et al. (2010)
Lis, D. C., Phillips, T. G., Goldsmith, P. F., et al. 2010, A&A, 521, L26
-
Loomis et al. (2015)
Loomis, R. A., Cleeves, L. I., Öberg, K. I., Guzman, V. V., & Andrews, S. M. 2015, ApJ, 809, L25
-
Maret et al. (2004)
Maret, S., Ceccarelli, C., Caux, E., et al. 2004, A&A, 416, 577
-
Melnick et al. (2010)
Melnick, G. J., Tolls, V., Neufeld, D. A., et al. 2010, A&A, 521, L27
-
Mumma & Charnley (2011)
Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471
-
Nagayama et al. (2009)
Nagayama, T., Omodaka, T., Handa, T., et al. 2009, PASJ, 61, 1023
-
Nishitani et al. (2012)
Nishitani, H., Sorai, K., Habe, A., et al. 2012, PASJ, 64, 30
-
Öberg et al. (2010)
Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480
-
Öberg et al. (2011)
Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2011, ApJ, 734, 98
-
Öberg et al. (2017)
Öberg, K. I., Guzmán, V. V., Merchantz, C. J., et al. 2017, ApJ, 839, 43
-
Pachucki & Komasa (2008)
Pachucki, K., & Komasa, J. 2008, Phys. Rev. A, 77, 030501
-
Persson et al. (2012)
Persson, C. M., De Luca, M., Mookerjea, B., et al. 2012, A&A, 543, A145
-
Qi et al. (2011)
Qi, C., D’Alessio, P., Öberg, K. I., et al. 2011, ApJ, 740, 84
-
Qi et al. (2013)
Qi, C., Öberg, K. I., & Wilner, D. J. 2013, ApJ, 765, 34
-
Qi et al. (2015)
Qi, C., Öberg, K. I., Andrews, S. M., et al. 2015, ApJ, 813, 128
-
Salinas et al. (2016)
Salinas, V. N., Hogerheijde, M. R., Bergin, E. A., et al. 2016, A&A, 591, A122
-
Schöier et al. (2002)
Schöier, F. L., Jørgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2002, A&A, 390, 1001
-
Shinnaka et al. (2016)
Shinnaka, Y., Kawakita, H., Jehin, E., et al. 2016, MNRAS, 462, S124
-
Takano et al. (2002)
Takano, S., Nakai, N., & Kawaguchi, K. 2002, PASJ, 54, 195
-
Tudorie et al. (2006)
Tudorie, M., Cacciani, P., Cosléou, J., et al. 2006, A&A, 453, 755
-
Umemoto et al. (1999)
Umemoto, T., Mikami, H., Yamamoto, S., & Hirano, N. 1999, ApJ, 525, L105
-
van den Ancker et al. (1998)
van den Ancker, M. E., de Winter, D., & Tjin A Djie, H. R. E. 1998, A&A, 330, 145
-
Vastel et al. (2010)
Vastel, C., Ceccarelli, C., Caux, E., et al. 2010, A&A, 521, L31
- Watanabe et al. (2010) Watanabe, N., Kimura, Y., Kouchi, A., et al. 2010, ApJ, 714, L233