HAT-P-7b: An Extremely Hot Massive Planet Transiting a Bright Star in the Kepler Field

Following the HATNet photometric detection, HAT-P-7 (then a transit candidate) was observed spectroscopically with the CfA Digital Speedometer (DS, see Latham, 1992) at the FLWO 1.5 m Tillinghast reflector, in order to rule out a number of blend scenarios that mimic planetary transits (e.g. Brown, 2003; O’Donovan et al., 2007), as well as to characterize the stellar parameters, such as surface gravity, effective temperature, and rotation. Four spectra were obtained over an interval of 29 days. These observations cover $45$ Å in a single echelle order centered at $5187$  Å, and have a resolving power of $\lambda/\Delta\lambda\approx 35,\!000$. Radial velocities were derived by cross-correlation, and have a typical precision of $1$ $\rm km\,s^{-1}$. Using these measurements, we have ruled out an unblended companion of stellar mass (e.g. an M dwarf orbiting an F dwarf), since the radial velocities did not show any variation within the uncertainties. The mean heliocentric radial velocity of HAT-P-7 was measured to be $-11$  $\rm km\,s^{-1}$. Based on an analysis similar to that described in Torres et al. (2002), the DS spectra indicated that the host star is a slightly evolved dwarf with $\log{g}=3.5$ (cgs), $T_{\rm eff}=6250$ K and $v\sin{i}\approx 6\,\rm km\,s^{-1}$.

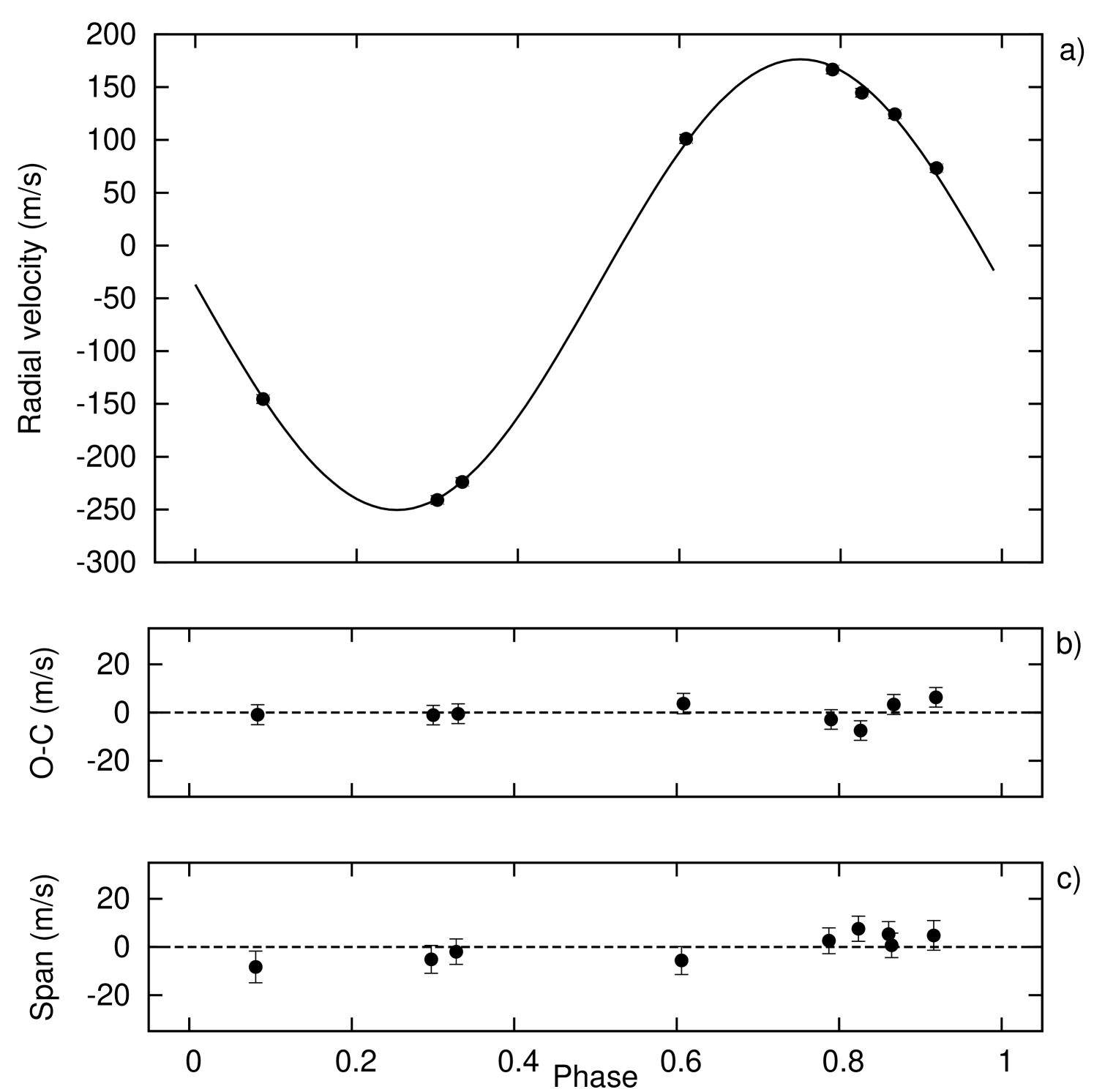
For the characterization of the radial velocity variations and for the more precise determination of the stellar parameters, we obtained 8 exposures with an iodine cell, plus one iodine-free template, using the HIRES instrument (Vogt et al., 1994) on the Keck I telescope, Hawaii, between 2007 August 24 and 2007 September 1. The width of the spectrometer slit was $0\farcs 86$ resulting a resolving power of $\lambda/\Delta\lambda\approx 55,\!000$, while the wavelength coverage was $\sim 3800-8000$ Å. The iodine gas absorption cell was used to superimpose a dense forest of $\mathrm{I}_{2}$ lines on the stellar spectrum and establish an accurate wavelength fiducial (see Marcy & Butler, 1992). Relative radial velocities in the Solar System barycentric frame were derived as described by Butler et al. (1996), incorporating full modeling of the spatial and temporal variations of the instrumental profile. The final radial velocity data and their errors are listed in Table 1. The folded data, with our best fit (see § 4.2) superimposed, are plotted in Fig. 2a.

Partial photometric coverage of a transit event of HAT-P-7 was carried out in the Sloan $z$-band with the KeplerCam CCD on the 1.2 m telescope at FLWO, on 2007 November 2. The total number of frames taken from HAT-P-7 was 514 with cadence of 28 seconds. During the reduction of the KeplerCam data, we used the following method. After bias and flat calibration of the images, an astrometric transformation (in the form of first order polynomials) between the $\sim 450$ brightest stars and the 2MASS catalog was derived, as described in Pál & Bakos (2006), yielding a residual of $\sim 1/4$ pixel. Aperture photometry was then performed using a series of apertures of with the radius of 4, 6 and 8 pixels in fixed positions calculated from this solution and the actual 2MASS positions. The instrumental magnitude transformation was obtained using $\sim 350$ stars on a frame taken near culmination of the field. The transformation fit was initially weighted by the estimated photon- and background-noise error of each star, then the procedure was repeated weighting by the inverse variance of the light curves. From the set of apertures we have chosen the aperture for which the out-of-transit (OOT) rms of HAT-P-7 was the smallest; the radius of this aperture is 6 pixels. This light curve was then de-correlated against trends using the OOT sections, which yielded a light curve with an overall rms of 1.9mmag at a cadence of one frame per 28 seconds. This is a bit larger than the expected rms of 1.5mmag, derived from the photon noise (1.2mmag) and scintillation noise – which has an expected amplitude of 0.8mmag, based on the observational conditions and the calculations of Young (1967) – possibly due to unresolved trends and other noise sources. The resulting light curve is shown in Fig. 1d.

For the independent fit procedure, we first analyzed the HATNet light curves, as observed by the HAT-6, HAT-7, HAT-8 and HAT-9 telescopes. Using the initial period and transit length from the BLS analysis, we fitted a model to the 214 cycles of observations spanned by all the HATNet data. Although at this stage we were interested only in the epoch and period, we have used the transit light curve model with the assumption quadratic limb darkening, where the flux decrease was calculated using the models provided by Mandel & Agol (2002). In principle, fitting the epoch and period as two independent variables is equivalent to fitting the time instant of the centers of the first and last observed individual transits, $T_{\mathrm{c,first}}$ and $T_{\mathrm{c,last}}$, with a constraint that all intermediate transits are regularly spaced with period $P$. Note that this fit takes into account all transits that occurred during the HATNet observations, even though it is described only by $T_{\mathrm{c,first}}$ and $T_{\mathrm{c,last}}$. The fit yielded $T_{\mathrm{c,first}}=2453153.0924\pm 0.0021$ (BJD) and $T_{\mathrm{c,last}}=2453624.9044\pm 0.0023$ (BJD). The period derived from the $T_{\mathrm{c,first}}$ and $T_{\mathrm{c,last}}$ epochs was $P^{(1)}=2.20480\pm 0.00049$ days. Using these values, we found that there were 326 cycles between $T_{\mathrm{c,last}}$ and the end of the RV campaign. The epoch extrapolated to the approximate time of RV measurements was $T_{\mathrm{c,RV}}=2454343.646\pm 0.008$ (BJD). Note that the error in $T_{\mathrm{c,RV}}$ is much smaller than the period itself ($\sim 2.2$ days), so there is no ambiguity in the number of elapsed cycles when folding the periodic signal.

We then analyzed the radial velocity data in the following way. We defined the $N_{\rm tr}\equiv 0$ transit as that being closest to the end of the radial velocity measurements. This means that the first transit observed by HATNet (at $T_{\mathrm{c,first}}$) was the $N_{\rm tr,first}=-540$ event. Given the short period, we assumed that the orbit has been circularized (Hut, 1981) (later verified; see below). The orbital fit is linear if we choose the radial velocity zero-point $\gamma$ and the amplitudes $A$ and $B$ as adjusted values, namely:

where $t_{0}$ is an arbitrary time instant (chosen to be $t_{0}=2454342.6$ BJD), $K\equiv\sqrt{A^{2}+B^{2}}$ is the semi-amplitude of the RV variations, and $P$ is the initial period $P^{(1)}$ taken from the previous independent HATNet fit. The actual epoch can be derived from the above equation since for circular orbits transit center occurs when the RV curve has the most negative slope. Using the equations above, we derived the initial epoch of the $N_{\rm tr}=0$ transit center to be $T_{c}=2454343.6462\pm 0.0042\equiv T^{(1)}_{\mathrm{c},0}$ (BJD). We also performed a more general (non-linear) fit to the RV in which we let the eccentricity float. This fit yielded an eccentricity consistent with zero, namely $e\cos\omega=-0.003\pm 0.007$ and $e\sin\omega=0.000\pm 0.010$. Therefore, we adopt a circular orbit in the further analysis.

Combining the RV epoch $T^{(1)}_{\mathrm{c},0}$ with the first epoch observed by HATNet ($T_{\mathrm{c,first}}$), we obtained a somewhat refined period, $P^{(2)}=2.204732\pm 0.000016$ days. This was fed back into phasing the RV data, and we performed the RV fit again to the parameters $\gamma$, $A$ and $B$. The fit yielded $\gamma=-37.0\pm 1.5$ $\rm m\,s^{-1}$, $K\equiv\sqrt{A^{2}+B^{2}}=213.4\pm 2.0$ $\rm m\,s^{-1}$and $T^{(2)}_{\mathrm{c},0}=2454343.6470\pm 0.0042$ (BJD). This epoch was used to further refine the period to get $P^{(3)}=2.204731\pm 0.000016$ d, where the error calculation assumes that $T_{\mathrm{c},0}$ and $T_{\mathrm{c},-540}$ are uncorrelated. At this point we stopped the above iterative procedure of refining the epoch and period; instead a final refinement of epoch and period was obtained through performing a joint fit, (as described later in § 4.2). We note that in order to get a reduced chi-square value near unity for the radial velocity fit, it was necessary to quadratically increase the noise component with an amplitude of $3.8$ $\rm m\,s^{-1}$, which is well within the range of stellar jitter observed for late F stars; see Butler et al. (2006).

Using the improved period $P^{(3)}$ and the epoch $T_{\mathrm{c},0}$, we extrapolated to the center of KeplerCam follow-up transit ($N_{\rm tr}=29$). Since the follow-up observation only recorded a partial event (see Fig. 1d), this extrapolation was necessary to improve the light curve modeling. For this, we have used a quadratic limb-darkening approximation, based on the formalism of Mandel & Agol (2002). The limb-darkening coefficients were based on the results of the SME analysis (notably, $T_{\rm eff}$; see § 4.3 for further details), which yielded $\gamma_{1}^{(z)}=0.1329$ and $\gamma_{2}^{(z)}=0.3738$. Using these values and the extrapolated time of the transit center, we adjusted the light curve parameters: the relative radius of the planet $p=R_{p}/R_{\star}$, the square of the impact parameter $b^{2}$ and the quantity $\zeta/R_{\star}=(a/R_{\star})(2\pi/P)(1-b^{2})^{-1/2}$ as independent parameters (see Bakos et al., 2007, for the choice of parameters). The result of the fit was $p=0.0762\pm 0.0012$, $b^{2}=0.205\pm 0.144$ and $\zeta/R_{\star}=13.60\pm 0.83$ day^-1, where the uncertainty of the transit center time due to the relatively high error in the transit epoch $T_{\mathrm{c},0}$ was also taken into account in the error estimates.

The results of the individual fits described above provide the starting values for a joint fit, i.e. a simultaneous fit to all of the available HATNet, radial velocity and the partial follow-up light curve data. The adjusted parameters were $T_{\mathrm{c},-540}$, the time of first transit center in the HATNet campaign, $m$, the out-of-transit magnitude of the HATNet light curve in $I$-band and the previously defined parameters of $\gamma$, $A$, $B$, $p$, $b^{2}$ and $\zeta/R_{\star}$. We note that in this joint fit all of the transits in the HATNet light curve have been adjusted simultaneously, tied together by the constraint of assuming a strictly periodic signal; the shape of all these transits were characterized by $p$, $b^{2}$ and $\zeta/R_{\star}$ (and the limb-darkening coefficients) while the distinct transit center time instants were interpolated using $T_{\mathrm{c},-540}=T_{\mathrm{c,first}}$ and $A$, $B$ via the RV fit. For initial values we used the results of the independent fits (§ 4.1). The error estimation based on method refitting to synthetic data sets gives the distribution of the adjusted values, and moreover, this distribution can be used directly as an input for a Monte-Carlo parameter determination for stellar evolution modeling, as described later (§ 4.3).

Final results of the joint fit were: $T_{\mathrm{c},-540}=2453153.0924\pm 0.0015$ (BJD), $m=9.85053\pm 0.00015$ mag, $\gamma=-37.0\pm 1.5$ $\rm m\,s^{-1}$, $A=33.8\pm 0.9$ $\rm m\,s^{-1}$, $B=210.7\pm 1.9$ $\rm m\,s^{-1}$, $p=0.0763\pm 0.0010$, $b^{2}=0.135_{-0.116}^{+0.149}$ and $\zeta/R_{\star}=13.34\pm 0.23$ $\mathrm{day^{-1}}$. Using the distribution of these parameters, it is straightforward to obtain the values and the errors of the additional parameters derived from the joint derived fit, namely $T_{\mathrm{c},0}$, $a/R_{\star}$, $K$ and $P$. All final fit parameters are listed in Table 3.

The results of the joint fit enable us to refine the parameters of the star. First, the iodine-free template spectrum from Keck was used for an initial determination of the atmospheric parameters. Spectral synthesis modeling was carried out using the SME software (Valenti & Piskunov, 1996), with wavelength ranges and atomic line data as described by Valenti & Fischer (2005). We obtained the following initial values: effective temperature $6350\pm 80$ K, surface gravity $\log g_{\star}=4.06\pm 0.10$ (cgs), iron abundance $\mathrm{[Fe/H]}=+0.26\pm 0.08$, and projected rotational velocity $v\sin i=3.8\pm 0.5$ $\rm km\,s^{-1}$. The rotational velocity is slightly smaller than the value given by the DS measurements. The temperature and surface gravity correspond to a slightly evolved F6 star. The uncertainties quoted here and in the remaining of this discussion are twice the statistical uncertainties for the values given by the SME analysis. This reflects our attempt, based on prior experience, to incorporate systematic errors (e.g. Noyes et al. (2008); see also Valenti & Fischer (2005)). Note that the previously discussed limb darkening coefficients, $\gamma_{1}^{(z)}$, $\gamma_{2}^{(z)}$, $\gamma_{1}^{(I)}$ and $\gamma_{2}^{(I)}$ have been taken from the tables of Claret (2004) by interpolation to the above-mentioned SME values for $T_{\rm eff}$, $\log g_{\star}$, and $\mathrm{[Fe/H]}$.

As described by Sozzetti et al. (2007), $a/R_{\star}$ is a better luminosity indicator than the spectroscopic value of $\log g_{\star}$ since the variation of stellar surface gravity has a subtle effect on the line profiles. Therefore, we used the values of $T_{\rm eff}$ and $\mathrm{[Fe/H]}$ from the initial SME analysis, together with the distribution of $a/R_{\star}$ to estimate the stellar properties from comparison with the Yonsei-Yale (Y²) stellar evolution models by Yi et al. (2001). Since a Monte-Carlo set for $a/R_{\star}$ values has been derived during the joint fit, we performed the stellar parameter determination as follows. For a selected value of $a/R_{\star}$, two Gaussian random values were drawn for $T_{\rm eff}$ and $\mathrm{[Fe/H]}$ with the mean and standard deviation as given by SME (with formal SME uncertainties doubled as indicated above).Using these three values, we searched the nearest isochrone and the corresponding mass by using the interpolator provided by Demarque et al. (2004). Repeating this procedure for values of $a/R_{\star}$, $T_{\rm eff}$, $\mathrm{[Fe/H]}$, the set of the a posteriori distribution of the stellar parameters was obtained, including the mass, radius, age, luminosity and color (in multiple bands). The age determined in this way is $2.2$ Gy with a statistical uncertainty of $\pm 0.3$ Gy; however, the uncertainty in the theoretical isochrone ages is about 1.0 Gy. Since the corresponding value for the surface gravity of the star, $\log g_{\star}=4.07^{+0.04}_{-0.08}$ (cgs),is well within 1-$\sigma$ of the value determined by the SME analysis, we accept the values from the joint fit as the final stellar parameters. These parameters are summarized in Table 2.

We note that the Yonsei-Yale isochrones contain the absolute magnitudes and colors for different photometric bands from $U$ up to $M$, providing an easy comparison of the estimated and the observed colors. Using these data, we determined the $V-I$ and $J-K$ colors of the best fitted stellar model: $(V-I)_{\rm YY}=0.54\pm 0.02$ and $(J-K)_{\rm YY}=0.27\pm 0.02$. Since the colors for the infrared bands provided by Yi et al. (2001) and Demarque et al. (2004) are given in the ESO photometric standard system, for the comparison with catalog data, we converted the infrared color $(J-K)_{\rm YY}$ to the 2MASS system $(J-K_{S})$ using the transformations given by Carpenter (2001). The color of the best fit stellar model was $(J-K_{S})_{\rm YY}=0.25\pm 0.03$, which is in fairly good agreement with the actual 2MASS color of HAT-P-7: $(J-K_{S})=0.22\pm 0.04$. We have also compared the $(V-I)_{\rm YY}$ color of the best fit model to the catalog data, and found that although HAT-P-7 has a low galactic latitude, $b_{\rm II}=13\fdg 8$, the model color agrees well with the observed TASS color of $(V-I)_{\rm TASS}=0.60\pm 0.07$ (see Droege et al., 2006). Hence, the star is not affected by the interstellar reddening within the errors, since $E(V-I)\equiv(V-I)_{\rm TASS}-(V-I)_{\rm YY}=0.06\pm 0.07$. For estimating the distance of HAT-P-7, we used the absolute magnitude $M_{V}=3.00\pm 0.22$ (resulting from the isochrone analysis, see also Table 2) and the $V_{\rm TASS}=10.51\pm 0.06$ observed magnitude. These two yield a distance modulus of $V_{\rm TASS}-M_{V}=7.51\pm 0.28$, i.e. distance of $d=320^{+50}_{-40}$ pc.

The determination of the stellar properties was followed by the characterization of the planet itself. Since Monte-Carlo distributions were derived for both the light curve and the stellar parameters, the final planetary and orbital data were also obtained by the statistical analysis of the a posteriori distribution of the appropriate combination of these two Monte-Carlo data sets. We found that the mass of the planet is $M_{p}=1.776^{+0.077}_{-0.049}$ $M_{\rm J}$, the radius is $R_{p}=1.363^{+0.195}_{-0.087}$ $R_{\rm J}$ and its density is $\rho_{p}=0.876^{+0.17}_{-0.24}$ $\rm g\,cm^{-3}$. We note that in the case of binary systems with large mass and radius ratios (such as the one here) there is a strong correlation between $M_{p}$ and $R_{p}$ (see e.g. Beatty et al., 2007). This correlation is also exhibited here with $C(M_{p},R_{p})=0.89$. The final planetary parameters are also summarized at the bottom of Table 3.

Due to the way we derived the period, i.e. $P=(T_{\mathrm{c},0}-T_{\mathrm{c},-540})/540$, one can expect a large correlation between the epochs $T_{\mathrm{c},0}$, $T_{\mathrm{c},-540}$ and the period itself. Indeed, $C(T_{\mathrm{c},-540},P)=-0.783$ and $C(T_{\mathrm{c},0},P)=0.704$, while the correlation between the two epochs is negligible; $C(T_{\mathrm{c},-540},T_{\mathrm{c},0})=-0.111$. It is easy to show that if the signs of the correlations between two epochs $T_{\rm A}$ and $T_{\rm B}$ (in our case $T_{\mathrm{c},0}$ and $T_{\mathrm{c},-540}$) and the period are different, respectively, then there exists an optimal epoch $E$, which has the smallest error among all of the interpolated epochs. We note that $E$ will be such that it also exhibits the smallest correlation with the period. If $\sigma(T_{\rm A})$ and $\sigma(T_{\rm B})$ are the respective uncorrelated errors of the two epochs, then

where square brackets denote the time of the transit event nearest to the time instance $t$. In the case of HAT-P-7b, $T_{\rm A}\equiv T_{\mathrm{c},-540}$ and $T_{\rm B}\equiv T_{\mathrm{c},0}$, the corresponding epoch is the event $N_{\rm tr}=-251$ at $E\equiv T_{\mathrm{c},-251}=2,453,790.2593\pm 0.0010$ (BJD). The final ephemeris and planetary parameters are summarized in Table 3.

Following Torres et al. (2007), we explored the possibility that the measured radial velocities are not real, but instead caused by distortions in the spectral line profiles due to contamination from a nearby unresolved eclipsing binary. In that case the “bisector span” of the average spectral line should vary periodically with amplitude and phase similar to the measured velocities themselves (Queloz et al., 2001; Mandushev et al., 2005). We cross-correlated each Keck spectrum against a synthetic template matching the properties of the star (i.e. based on the SME results, see § 4.3), and averaged the correlation functions over all orders blueward of the region affected by the iodine lines. From this representation of the average spectral line profile we computed the mean bisectors, and as a measure of the line asymmetry we computed the “bisector spans” as the velocity difference between points selected near the top and bottom of the mean bisectors (Torres et al., 2005). If the velocities were the result of a blend with an eclipsing binary, we would expect the line bisectors to vary in phase with the photometric period with an amplitude similar to that of the velocities. Instead, we detect no variation in excess of the measurement uncertainties (see Fig. 2c). We have also tested the significance of the correlation between the radial velocity and the bisector variations. Therefore, we conclude that the velocity variations are real and that the star is orbited by a Jovian planet. We note here that the mean bisector span ratio relative to the radial velocity amplitude is the smallest ($\sim 0.026$) among all the HATNet planets, indicating an exceptionally high confidence that the RV signal is not due to a blend with an eclipsing binary companion.