Hawking temperature and the bound on greybody factors in $D=4$ double field theory

In original work in 1974 [1], Hawking showed that black holes can emit particles spontaneously at a temperature which is inversely proportional to their mass. Since then, black holes have been becoming increasingly popular in classical and quantum gravity theories [2]. Meanwhile, a series of works devoted to calculating the Hawking radiation spectrum and temperature to explore a possible theory of quantum gravity [3-5]. Here we only list some main developments in this area. For example, Page tried to calculate the particle emit rates from a nonrotating and rotating black hole in refs.[3] and [4], respectively. In 1999, in their famous paper Wilczek and Parikh [5] showed such a possibility, i.e., Hawking radiation can be considered a tunnelling process, in which particles pass through the contracting horizon of the black hole [5]. In the following years, these above results have been generalized by other researchers to other cases, such as Einstein-Gauss-Bonnet de Sitter black holes [6], charged black holes [2,7] etc.
In this article, we intend to consider the properties of Hawking radiation in $D=4$ double field theory. Double field theory (DFT) is an exciting research area in string theory in recent years. The primary goal of DFT [8–11] was to reformulate supergravity with doubled coordinates, namely, $x_{A}=(\tilde{x}_{\mu},x^{\nu})$, in a way that realizes T-duality as a manifest symmetry of the action and unifies diffeomorphisms and B-field gauge symmetry into ‘doubled diffeomorphisms’ [12–14]. In ref.[8], the authors have derived the most general, spherically symmetric, asymptotically flat, static vacuum solution to $D=4$ double field theory. Furthermore, in ref.[15], Stephen Angus, Kyoungho Cho and Jeong-Hyuck Park studied more general properties of Einstein double field equations. In this artilce, we intend to study some basic properties of the Hawking radiation for the solution in ref.[8]. In section 2, we review the double field theory and sperical solutions in $D=4$ double field theory briefly. In section 3, we obtain the general expression of Hawking temperature for the spherical solutions in $D=4$ double field theory. Moreover, we discuss the results of several various limits listed in ref.[8]. In section 4, we obtain the bounding of greybody factors for spherical solutions in $D=4$ double field theory, especially the case of F-JNW solution. In section 5, the results of the article have been discussed.

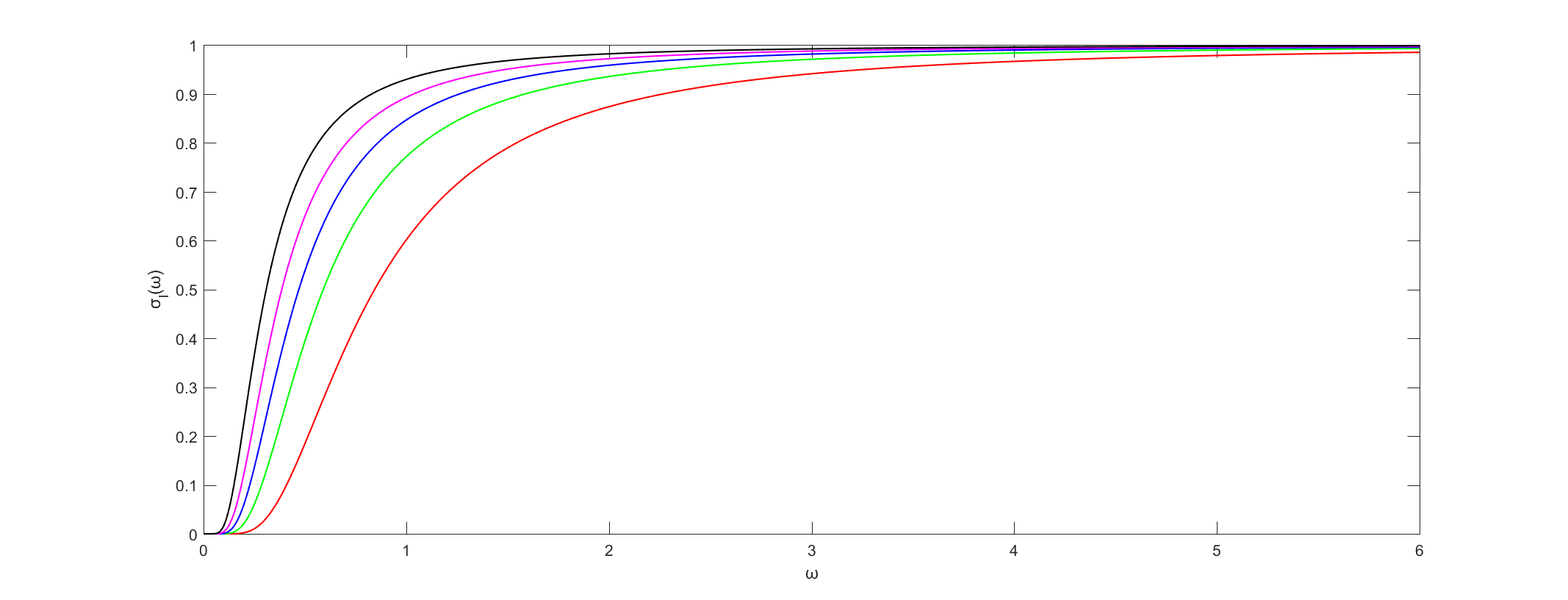
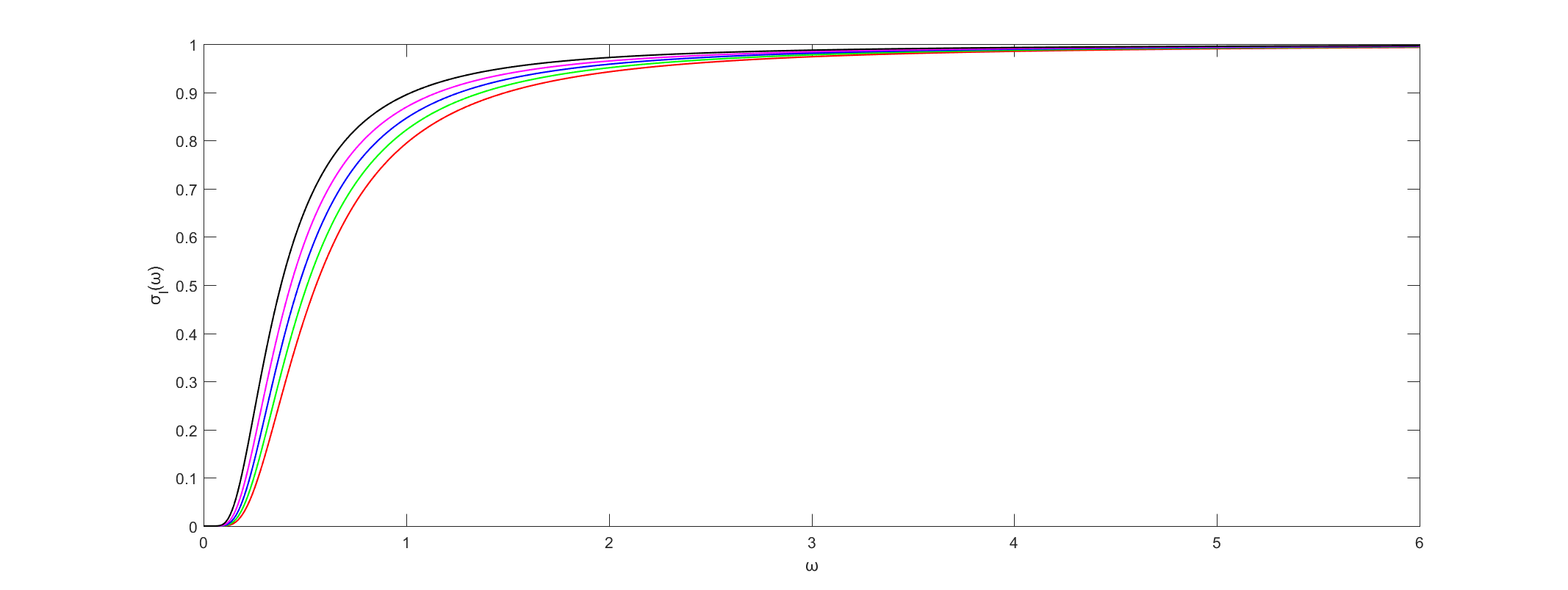
In line with the analysis of refs.[5,21], we study the semiclassical tunnelling of particles through the horizon of black holes in this section. Further discussion can be seen in refs.[22-25]. On the one hand, the rate of emission $\Gamma$ will have exponential part given by [21]

$$\Gamma\sim\exp(-2ImS),$$

(33)

where $S$ is the tunnelling action of particles and $ImS$ is the imaginary part of the tunnelling action $S$. On the other hand, according to the Planck radiation law, the emitted rate $\Gamma$ of particles with frequency $\omega$ can be written as [21]

$$\Gamma\sim\exp(-\omega/T_{BH}).$$

(34)

Therefore, combining eqs.$(3.1)$ and $(3.2)$, the temperature at which the black hole radiates can be read off [21]:

$$T_{BH}=\frac{\omega}{2ImS}.$$

(35)

In section 3, we will study Hawking radiation process in Painlevé-Gullstrand coordinates. Firstly, we will rewrite the metric $(2.21)$ in Painlevé-Gullstrand coordinates. We define

$$t_{r}=t-a(r),$$

(36)

where $a(r)$ is a function of radial coordinate $r$. Then

$$dt^{2}=dt^{2}_{r}+a^{\prime 2}(r)dr^{2}+2a^{\prime}dt_{r}dr,$$

(37)

where $a^{\prime}=da(r)/dr$. The time coordinate $t_{r}$, in fact, corresponds to the time measured by a stationary observer at infinity [21]. Inserting $(3.5)$ into the general static and spherical metric

$$ds^{2}=-f(r)dt^{2}+g(r)dr^{2}+r^{2}d\Omega^{2},$$

(38)

where $d\Omega^{2}=d\theta^{2}+\sin^{2}\theta d\phi^{2}$, then metric $(3.6)$ can be rewritten as

$$ds^{2}=-f(r)dt^{2}_{r}-2f(r)a^{\prime}dt_{r}dr+\left(g(r)-f(r)a^{{}^{\prime}2}\right)dr^{2}+r^{2}d\Omega^{2}.$$

(39)

We require

$$g(r)-f(r)a^{\prime 2}=1,$$

(40)

and choose $a^{\prime}=-\sqrt{\frac{g(r)-1}{f(r)}}$. Then

$$-2f(r)a^{\prime}=2\sqrt{f(r)\left(g(r)-1\right)}.$$

(41)

Considering metric $(2.5)$, then $f(r)=e^{2\phi(r)}A(r)$ and $g(r)=e^{2\phi(r)}A^{-1}(r)$, then we have

$$-2f(r)a^{\prime}=2e^{2\phi(r)}\sqrt{1-A(r)},$$

(42)

where

$$A(r)=\left(\frac{r-c_{+}}{r-c_{-}}\right)^{\frac{a}{c_{+}-c_{-}}}=\left(\frac{r-c-\frac{1}{2}\sqrt{a^{2}+b^{2}}}{r-c+\frac{1}{2}\sqrt{a^{2}+b^{2}}}\right)^{\frac{a}{\sqrt{a^{2}+b^{2}}}}.$$

(43)

Then the metric can be rewritten in Painlevé-Gullstrand coordinates as follows:

$$ds^{2}=-e^{2\phi(r)}A(r)dt^{2}_{r}+2e^{2\phi(r)}\sqrt{1-A(r)}dt_{r}dr+dr^{2}+e^{2\phi(r)}A^{-1}(r)C(r)d\Omega^{2}.$$

(44)

In the following part of section 3, we will take $dt^{2}=dt^{2}_{r}$ for convenience, i.e.,

$$ds^{2}=-e^{2\phi(r)}A(r)dt^{2}+2e^{2\phi(r)}\sqrt{1-A(r)}dtdr+dr^{2}+e^{2\phi(r)}A^{-1}(r)C(r)d\Omega^{2}.$$

(45)

The action for a particle moving freely in a curved background can be written as:

$$S=\int p_{\mu}dx^{\mu},$$

(46)

with

$$p_{\mu}=mg_{\mu\nu}\frac{dx^{\nu}}{d\sigma},$$

(47)

where $\sigma$ is an affine parameter along the worldline of the particle, chosen so that $p^{\mu}$ coincides with the physical 4-momentum of the particle. For a massive particle, this requires that $d\sigma=d\tau/m$, with $\tau$ the proper time [21]. For simplicity, in this paper we only consider the case of massless scalar field $\Phi$ and ignore the angular directions. Following the spirit of ref.[21], we will obtain the formula of Hawking temrature for for spherical solutions in $D=4$ double field theory.
The radial dynamics of massless particles in $4d$ spacetime are determined by the equations:

$$e^{2\phi(r)}A(r)\dot{t}^{2}-2e^{2\phi(r)}\sqrt{1-A(r)}\dot{t}\dot{r}-\dot{r}^{2}=0,$$

(48)

$$e^{2\phi(r)}A(r)\dot{t}-e^{2\phi(r)}\sqrt{1-A(r)}\dot{r}=\omega.$$

(49)

The second equation is the geodesic equation corresponding to the time-independence of the metric; in terms of the momentum defined in eq. $(3.15)$, it can be written $p_{t}=-\omega$, and so $\omega$ has the interpretation of the energy of the particle as measured at infinity [21].
Now we consider the the trajectory of an outgoing particle. For classical Schwarzschild solution, outgoing trajectory which crosses the horizon is forbidden [21]. The analytic continuation of an outgoing trajectory with $r>2M$ backwards across the horizon [21], however, will give rise to an imaginary term in our action, and this term actually represents the tunnelling amplitude [5]. For an outgoing particle, eq. $(3.16)$ can be factorised to yield, the equation

$$\frac{dr}{dt}=-e^{2\phi(r)}\sqrt{1-A(r)}+e^{\phi(r)}\sqrt{e^{2\phi(r)}(1-A(r))+A(r)}.$$

(50)

In fact, for outgoing particles, the null $\frac{dr}{dt}=0$ implies $A(r)=0$ which is consistent with the metric $(2.5)$, i.e., at $A(r)=0$ there exists a horizon.
From eq.$(3.17)$, we have

$$\frac{dr}{dt}=\frac{\dot{r}}{\dot{t}}=\frac{e^{2\phi(r)}A(r)-\frac{\omega}{\dot{t}}}{e^{2\phi(r)}\sqrt{1-A(r)}}.$$

(51)

Combining eqs.$(3.18)$ and $(3.19)$, we obtain

$$\dot{t}=\frac{\omega}{e^{2\phi(r)}A(r)+e^{4\phi(r)}(1-A(r))-e^{3\phi(r)}\sqrt{e^{2\phi(r)}(1-A(r))^{2}+A(r)(1-A(r))}},$$

(52)

and

$$\dot{r}=\frac{e^{2\phi(r)}A(r)\dot{t}-\omega}{e^{2\phi(r)}\sqrt{1-A(r)}}.$$

(53)

For the case we are considering,

$$p_{r}=g_{rt}\dot{t}+g_{rr}\dot{r}=e^{2\phi(r)}\sqrt{1-A(r)}\dot{t}+\dot{r}.$$

(54)

Inserting eqs.$(3.20)$ and $(3.21)$ into $(3.22)$, we have

$$p_{r}=\frac{\omega\sqrt{e^{2\phi(r)}(1-A(r))+A(r)}}{e^{\phi(r)}A(r)+e^{3\phi(r)}(1-A(r))-e^{2\phi(r)}\sqrt{e^{2\phi(r)}(1-A(r))^{2}+A(r)(1-A(r))}},$$

(55)

then

$$ImS=Im\int p_{r}dr.$$

(56)

Then Hawking temperature is given by eq.$(3.3)$,

$$T_{BH}=\frac{\omega}{2ImS}=\frac{1}{2Im\int\frac{\sqrt{e^{2\phi(r)}(1-A(r))+A(r)}}{e^{\phi(r)}A(r)+e^{3\phi(r)}(1-A(r))-e^{2\phi(r)}\sqrt{e^{2\phi(r)}(1-A(r))^{2}+A(r)(1-A(r))}}dr}.$$

(57)

Now we will consider the various limits we have listed in section 2.2.
$\bullet$ If $b=h=0$, $a=2M_{\infty}G>0$ and $\phi(r)=0$, then we have

$$p_{r}=\frac{\omega}{1-\sqrt{\frac{2M_{\infty}G}{r}}},$$

(58)

then

$$T_{BH}=\frac{\omega}{2ImS}=\frac{\omega}{2Im\int\frac{\omega}{1-\sqrt{\frac{2M_{\infty}G}{r}}dr}}=\frac{1}{8\pi GM_{\infty}},$$

(59)

which is consistent with the result of Schwarzschild black hole [21].
If $b=h=0$, $a=2M_{\infty}G<0$, after the radial coordinate redefinition, $r\rightarrow R-2M_{\infty}G$, then the metric reduces to Schwarzschild metric with negative mass. Therefore, there does not exist event horizon, namely, in the usual sense the Hawking radiation does not exist for this limit.
$\bullet$ If $a=h=0$, regardless of the sign of $b$, from metric $(2.26)$ we have $A(r)=1$. Therefore, for this limit, the Hawking radiation does not exist.
$\bullet$ If $h=0$, then F-JNW solution can be recovered [8]. The location of event horizon can be obtained by setting $A(r)=0$. From metric $(2.27)$, we have that the event horizon is located at $r_{h}=\sqrt{a^{2}+b^{2}}$. Combining eqs.$(2.27)$, $(2.28)$ and $(3.25)$, we can obtain the Hawking temperature for F-JNW solution in principle although the integration is complicated.
$\bullet$ If $h=0$ and $a=b$, with the proper radius, $R=\sqrt{r^{2}-\alpha^{2}}$, and a positive number, $\alpha\equiv\frac{1}{\sqrt{2}}|a|>0$. According to metric $(2.25)$, we can obtain the location of event horizon at $R=0$, namely, $r=\alpha\equiv\frac{1}{\sqrt{2}}|a|$. Then metric $(2.29)$ becomes $ds^{2}=dr^{2}$. Therefore, for this limit, the Hawking radiation does not exist.
$\bullet$ If $a=0$ with $b^{2}\geq h^{2}$, then from metric $(2.30)$, we obtain $A(r)=0$. In other words, no Hawking radiation exists.
In particular, if $a=0$ with $b^{2}=h^{2}$, it is no longer necessary to impose the constraint $R\geq\frac{1}{2}|h|$. However, the gravity becomes repulsive and the orbital velocity becomes imaginary which has no physical sense [8].

In section 3, we have obtained the formula of Hawking temperature for spherical solutions in $D=4$ double field theory. It is natural to discuss Hawking radiation spectrum in section 4. The Hawking radiation power $P(\omega)$ is given by [7]:

$$P(\omega)=\sum_{l}\int_{0}^{\infty}P_{l}(\omega)d\omega,$$

(60)

where

$$P_{l}(\omega)=\frac{A}{8\pi^{2}}\sigma_{l}(\omega)\frac{\omega^{3}}{\exp(\omega/T_{BH})-1},$$

(61)

is the power emitted per unit frequency in the $l$th mode, $A$ is a a multiple of the horizon area, $l$ is the angular momentum quantum number and $\sigma_{l}(\omega)$ is the frequency dependent greybody factor [7].
Various methods have been applied to calculate greybody factors $\sigma_{l}(\omega)$, however, only very few cases can obtain exact analytical expressions [7]. Moreover, considering the complexity of $(3.25)$, it is difficult to obtain the general formula for Hawking radiation power $P(\omega)$. Therefore, in this section, we only briefly consider the bound on greybody factors for spherical solutions in $D=4$ double field theory following ref.[8]. Petarpa Boonserm and Matt Visser proposed that the general bounds on the greybody factor is given by [26,2,7]:

$$\sigma_{l}(\omega)\geq sech^{2}\left(\int^{\infty}_{-\infty}\Theta dr_{\ast}\right),$$

(62)

where

$$\Theta=\frac{\sqrt{[h^{\prime}(r)^{2}]+[\omega^{2}-V_{eff}-h(r)^{2}]^{2}}}{2h(r)}.$$

(63)

The arbitrary function $h(r)$ has to be positive definite everywhere and satisfy the boundary condition, $h(\infty)=h(-\infty)=\omega$ for the bound eq.$(4.3)$ to hold [7] and $V_{eff}$ is the effective potential [26,2,7] which will be given later.
The equation of motion for a massless scalar field $\Phi$ is given by

$$\Box\Phi=0.$$

(64)

Since metric $(2.5)$ has spherical symmetry, according to ref.[27], the angular variables can be seperated from the other coordinates, i.e.,

$$\Phi(t,r,\theta,\phi)=\Phi(t,r)S(\theta,\phi),$$

(65)

where $S(\theta,\phi)$ can be decomposed in the usual spherical harmonics satisfying [27]

$$\left(\partial^{2}_{\theta}+\frac{\cos\theta}{\sin\theta}\partial_{\theta}+\frac{1}{\sin^{2}\theta}\partial^{2}_{\phi}\right)Y(\theta,\phi)=-l(l+1)Y(\theta,\phi).$$

(66)

In addtion, we can seperate time $t$ from from the radial coordinate, namely,

$$\Phi(t,r)=\Psi(t)\Phi(r),$$

(67)

where $\Psi(t)\sim e^{i\omega t}$ and satisfies $\ddot{\Psi}(t)=-\omega^{2}\Psi(t)$ [27].
For the general static and spherical metric $(3.6)$, we can rewrite it as [27]

$$ds^{2}=-f(r)(dt^{2}+dr_{\ast}^{2})+r^{2}d\Omega^{2},$$

(68)

by introducing the tortoise coordinate [27]:

$$r_{\ast}=\int^{r}\sqrt{\frac{g(r^{\prime})}{f(r^{\prime})}}dr^{\prime}.$$

(69)

For the metric $(2.5)$, we have

$$dr_{\ast}=\frac{1}{A(r)}dr.$$

(70)

Then the radial equation can be writen as [2,7,26,27]:

$$\left(\frac{d^{2}}{dr_{\ast}^{2}}+\omega^{2}-V_{eff}\right)u(r)=0,$$

(71)

where

$$V_{eff}=f(r)\frac{l(l+1)}{r^{2}}=e^{2\phi(r)}A(r)\frac{l(l+1)}{r^{2}}.$$

(72)

Considering $(4.3)$, we obtain the bound on the greybody factor:

$$\sigma_{l}(\omega)\geq sech^{2}\left(\int^{\infty}_{r_{h}}\frac{V_{eff}}{2\omega A(r)}dr\right),$$

(73)

where $r_{h}$ is the location of event horizon.
For the various limits we considered in section 3, we found that except for Schwarzschild solution, the only solution which exists Hawking radiation is the F-JNW solution. The bound on greybody factor for Schwarzschild solution has been obtained in ref.[26]. We focus on the bound for the case of F-JNW solution.
Combining $(2.27)$ and $(4.14)$, we have

$$\sigma_{l}(\omega)\geq sech^{2}\left(\frac{l(l+1)}{2\omega}\int^{\infty}_{\sqrt{a^{2}+b^{2}}}\frac{(1-\frac{\sqrt{a^{2}+b^{2}}}{r})^{\frac{b}{\sqrt{a^{2}+b^{2}}}}}{r^{2}}dr\right).$$

(74)

Completing the integration, we obtain

$$\sigma_{l}(\omega)\geq sech^{2}\left(\frac{l(l+1)}{2\omega}\frac{1}{b+\sqrt{a^{2}+b^{2}}}\right).$$

(75)

Figure 1 and 2 depict the lower bound of greybody factor $\sigma_{l}(\omega)$. From figure 1, we know that $\sigma_{l}(\omega)$ monotonically increases with the increase of $b$ for fixed $a$. Similarly, $\sigma_{l}(\omega)$ monotonically increases with the increase of $a$ for fixed $b$.

In principle, if we combine eqs.$(2.23)$, $(2.24)$, $(3.25)$ and $(4.2)$, we can obtain the lower bound on Hawking radiation spectrum $P_{l}(\omega)$, but we will not do it in this article.

On the one hand, since Hawking’s original work in 1974 [1], black holes, as a fascinating and elegant object, have been increasingly popular in classical and quantum gravity theories [2]. In the following years, a series of works devoted to studying Hawking radiation, such as [3,4,5]. On the other hand, in recent years, double field theory (DFT) is an exciting research area in string theory. Sung Moon Ko, Jeong-Hyuck Park and Minwoo Suh [8] obtained the the most general, spherically symmetric, asymptotically flat, static vacuum solution to $D=4$ double field theory.
In this article, we studied the basic properties of Hawking radiation in $D=4$ double field theory. Firstly, we give the formula of Hawking temperature for the sphrecial solution in $D=4$ double field theory given in ref.[8]. For all limits we considered only Schwarzschild solution and F-JNW solution can generate Hawking radiation. Furthermore, we discussed the lower bound of greybody factors $\sigma_{l}(\omega)$ for the spherical solution in $D=4$ double field theory. Since the bound of Schwarzshild solution has been obtained in ref.[26], we mainly focus on the F-NJW solution. For F-JNW solution, we found that $\sigma_{l}(\omega)$ monotonically increases with the increase of $a(b)$ for fixed $b(a)$.
Future work can be directed along at least three lines of further research. Firstly, the solutions of other metric in double field theory should be obtained. Secondly, in refs.[27,28] the authors have obtained quantum corrected black hole metric using effective field theory. It is natural to investigate the relationship between the two metrics in double field theory and effective field theory. Thirdly, Hawking radiation rates and information paradox in double field theory should be considered. There is therefore great potential for development of this work in the future.