Heat kernel estimates for Dirichlet forms degenerate at the boundary

In this paper, we study both conservative and non-conservative purely discontinuous (self-similar) Markov processes in the upper half-space of ${\mathbb{R}}^{d}$ with jump kernels of the form $J(x,y)=|x-y|^{-d-\alpha}{\cal B}(x,y)$, $\alpha\in(0,2)$. The function ${\cal B}(x,y)$ may tend to 0 when $x$ or $y$ tends to boundary of the half-space, and so the jump kernel may be degenerate. The main focus of the paper is to show the existence and continuity of the transition densities of the processes (or the heat kernels of the corresponding non-local operators), and to establish their sharp two-sided estimates. Heat kernel estimates for non-local operators have been the subject of many papers in the last twenty years, see [2, 4, 5, 10, 12, 13, 15, 16, 17, 19, 24, 26] and the references therein. In all of the papers mentioned above, the function ${\cal B}$ is assumed to be bounded between two positive constants, which can be viewed as a uniform ellipticity condition for non-local operators. To the best of our knowledge, the current paper is the first one to study sharp two-sided heat kernel estimates when the jump kernel is degenerate. Boundary Harnack principle and sharp two-sided Green function estimates for purely discontinuous Markov processes with degenerate jump kernels, which can be viewed as the elliptic counterpart of results of the current paper, have been recently obtained in [30, 31, 32].

The first type of processes we look at are conservative jump processes on $\overline{{\mathbb{R}}}^{d}_{+}:=\{x=(\widetilde{x},x_{d}):\widetilde{x}\in{\mathbb{R}}^{d-1},x_{d}\geq 0\}$ with jump kernel $J(x,y)=|x-y|^{-d-\alpha}{\cal B}(x,y)$, where the function ${\cal B}(x,y)$ is symmetric, homogeneous, horizontally translation invariant, and is allowed to approach 0 at the boundary at arbitrary fixed polynomial rate in terms of some non-negative parameters $\beta_{1},\beta_{2},\beta_{3},\beta_{4}$. The generator of such a process is the non-local operator

When ${\cal B}(x,y)$ is bounded between two positive constants, the heat kernel estimates for such processes are of the form $\min\{t^{-d/\alpha},tJ(x,y)\}$. This was first established in the pioneering work [15], even for the case of metric measure spaces. This form of the estimates reflects the fact that the main contribution to the heat kernel comes from one (big) jump from $x$ to $y$. This feature has been observed in all subsequent studies, see [2, 16, 10, 17, 19, 24] and the references therein. In our setting of jump kernel degenerate at the boundary, there are two novel features in the heat kernel estimates. The first one appears in the case when the involved parameters satisfy $\beta_{2}<\alpha+\beta_{1}$, in which case the heat kernel is comparable to $\min\{t^{-d/\alpha},tJ(x+t^{1/\alpha}\mathbf{e}_{d},y+t^{1/\alpha}\mathbf{e}_{d})\}$, where $\mathbf{e}_{d}=(\widetilde{0},1)$. In words, the form of the heat kernel estimates shows that the main contribution to the heat kernel at time $t$ comes from one jump from the point $t^{1/\alpha}$ units above $x$ to the point $t^{1/\alpha}$ units above $y$. Due to the fact the jump kernel vanishes at the boundary, it is very unlikely that the process will make one (big) jump from (or to) a point very close to the boundary. The second feature is more striking and indicates a sort of a phase-transition at the level $\beta_{2}=\alpha+\beta_{1}$: When the parameters satisfy $\beta_{2}\geq\alpha+\beta_{1}$, in addition to the already mentioned part $\min\{t^{-d/\alpha},tJ(x+t^{1/\alpha}\mathbf{e}_{d},y+t^{1/\alpha}\mathbf{e}_{d})\}$, the sharp heat kernel estimates include a part which reflects a significant contribution to the heat kernel coming from two jumps connecting $x$ and $y$. The precise description is given in Theorem 1.1.

The second type of processes we look at are the ones described in the previous paragraph but killed either by a critical potential $\kappa x_{d}^{-\alpha}$ or upon hitting the boundary of ${\mathbb{R}}^{d}_{+}:=\{x=(\widetilde{x},x_{d}):\widetilde{x}\in{\mathbb{R}}^{d-1},x_{d}>0\}$ (the latter happens only when $\alpha\in(1,2)$). The generator of such a process is the non-local operator $L^{{\cal B}}f(x)=L^{{\cal B}}_{\alpha}f(x)-\kappa x_{d}^{-\alpha}f(x)$. We study the effect of such killings on the heat kernel. When ${\cal B}(x,y)$ is bounded between two positive constants, the effect of killing on the heat kernel of the process is, after intensive research during the last fifteen years, fairly well understood. In most cases, the heat kernel of the killed process has the so called approximate factorization property: It is comparable to the product of the heat kernel of non-killed (original) process and the survival probabilities starting from points $x$ and $y$. In case of smooth open sets, the survival probability can be expressed in terms of the distance between the point and the boundary, see [4, 5, 8, 12, 13, 21, 27] and the references therein. In our setting of jump kernel degenerate at the boundary, we establish the same property: The heat kernel of the killed process enjoys the approximate factorization property with survival probabilities decaying as the $q$-th power of the distance to the boundary, where $q$ is in one-to-one correspondence with the constant $\kappa\geq 0$, see Theorem 1.2. When $\kappa=0$, this theorem generalizes [14] (for half spaces) where the factorization property for censored stable process is established. Due to the quite complicated form of the heat kernel estimates in Theorem 1.1, obtaining the factorization property in Theorem 1.2 is a formidable task.

We now introduce the precise setup and state the main results of this paper. This setup was first introduced in [30] and was motivated by the results of [28, 29] on subordinate killed Lévy processes. In fact, subordinate killed Lévy processes, whose analytical counterparts are fractional powers of Dirichlet fractional Laplacians, are the main natural examples of Markov processes with jump kernels satisfying the assumptions below.

Let $d\geq 1$ and $0<\alpha<2$. Recall that ${\mathbb{R}}^{d}_{+}=\{(\widetilde{x},x_{d})\in{\mathbb{R}}^{d}:x_{d}>0\}$ and $\overline{\mathbb{R}}^{d}_{+}=\{(\widetilde{x},x_{d})\in{\mathbb{R}}^{d}:x_{d}\geq 0\}$. Here and below, $a\wedge b:=\min\{a,b\}$, $a\vee b:=\max\{a,b\}$, and $a\asymp b$ means that $c\leq b/a\leq c^{-1}$ for some $c\in(0,1)$. For $b_{1},b_{2},b_{3},b_{4}\geq 0$, let

Let $J(x,y)=|x-y|^{-d-\alpha}{\cal B}(x,y)$, where the function ${\cal B}:\overline{{\mathbb{R}}}^{d}_{+}\times\overline{{\mathbb{R}}}^{d}_{+}\to[0,\infty)$ will be assumed to satisfy some or all of the following hypotheses:

(II) There exists $C_{3}>0$ such that

where $\beta_{1},\beta_{2},\beta_{3},\beta_{4}$ are the same constants as in (I).

These four hypotheses were introduced in [30], and with the same notation as above repeated in [31, 32]. Condition (A2) is not needed in Theorems 1.1 and 1.3, while in Theorems 1.2 and 1.4 it is used through several results from [30, 31, 32].

Throughout this paper, we always assume that ${\cal B}(x,y)$ satisfies (A1), (A3)(I) and (A4).

Consider the following symmetric form

Since ${\cal B}(x,y)$ is bounded, $C_{c}^{\infty}({\overline{\mathbb{R}}}^{d}_{+})$ is closable in $L^{2}({\overline{\mathbb{R}}}^{d}_{+},dx)=L^{2}({\mathbb{R}}^{d}_{+},dx)$ by Fatou’s lemma. Let ${\overline{\cal F}}$ be the closure of $C_{c}^{\infty}({\overline{\mathbb{R}}}^{d}_{+})$ in $L^{2}({\mathbb{R}}^{d}_{+},dx)$ under the norm ${\cal E}^{0}_{1}:={\cal E}^{0}+(\cdot,\cdot)_{L^{2}({\mathbb{R}}^{d}_{+},dx)}$. Then $({\cal E}^{0},{\overline{\cal F}})$ is a regular Dirichlet form on $L^{2}({\mathbb{R}}^{d}_{+},dx)$. Let $\overline{Y}=(\overline{Y}_{t},t\geq 0;{\mathbb{P}}_{x},x\in\overline{\mathbb{R}}^{d}_{+}\setminus{\cal N}^{\prime})$ be the Hunt process associated with $({\cal E}^{0},{\overline{\cal F}})$, where ${\cal N}^{\prime}$ is an exceptional set.

Here is our first main result. The heat kernel estimates are expressed in different but equivalent forms, each providing a different viewpoint. Recall that ${\mathbf{e}}_{d}=(\widetilde{0},1)\in{\mathbb{R}}^{d}$.

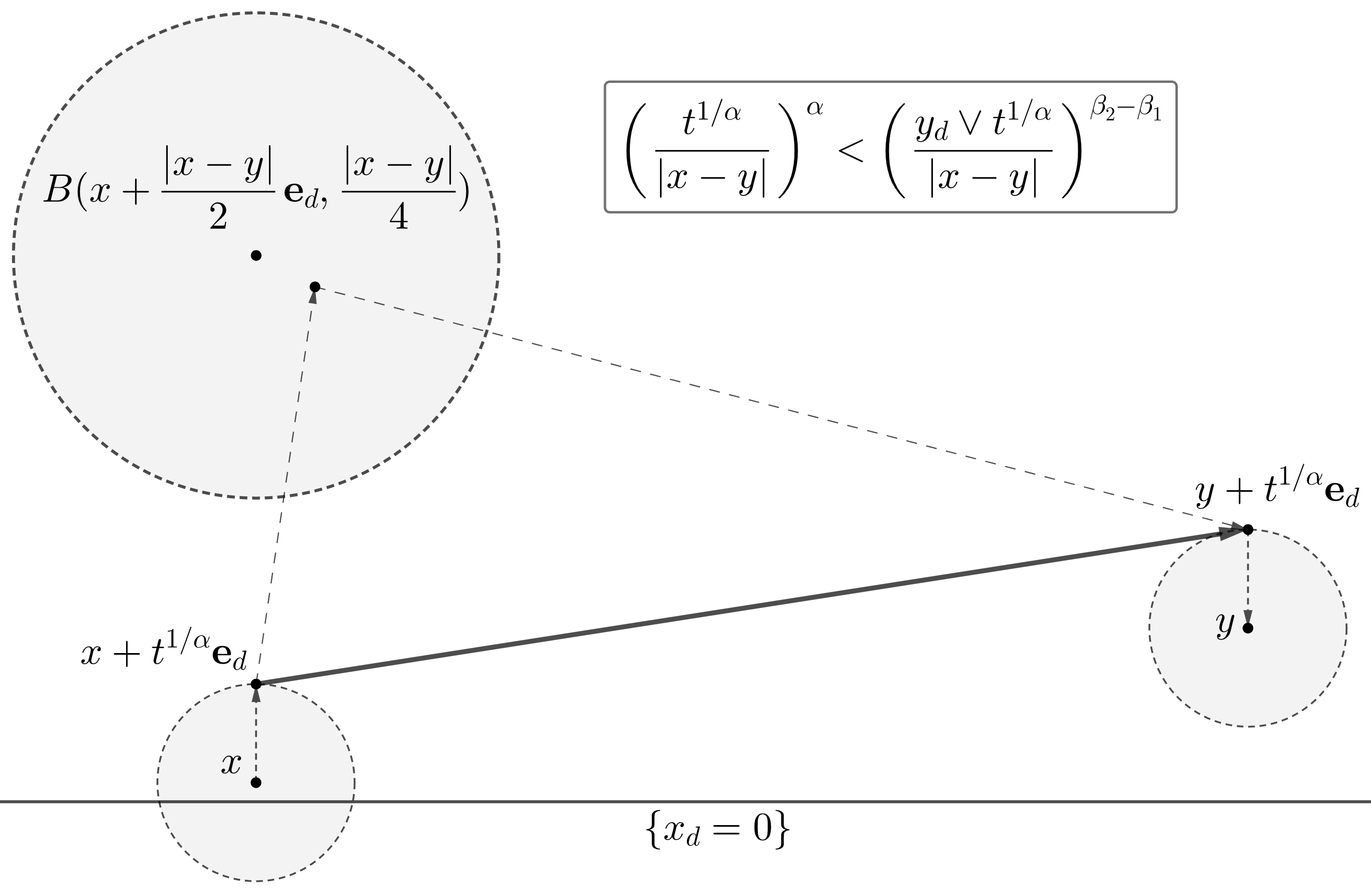
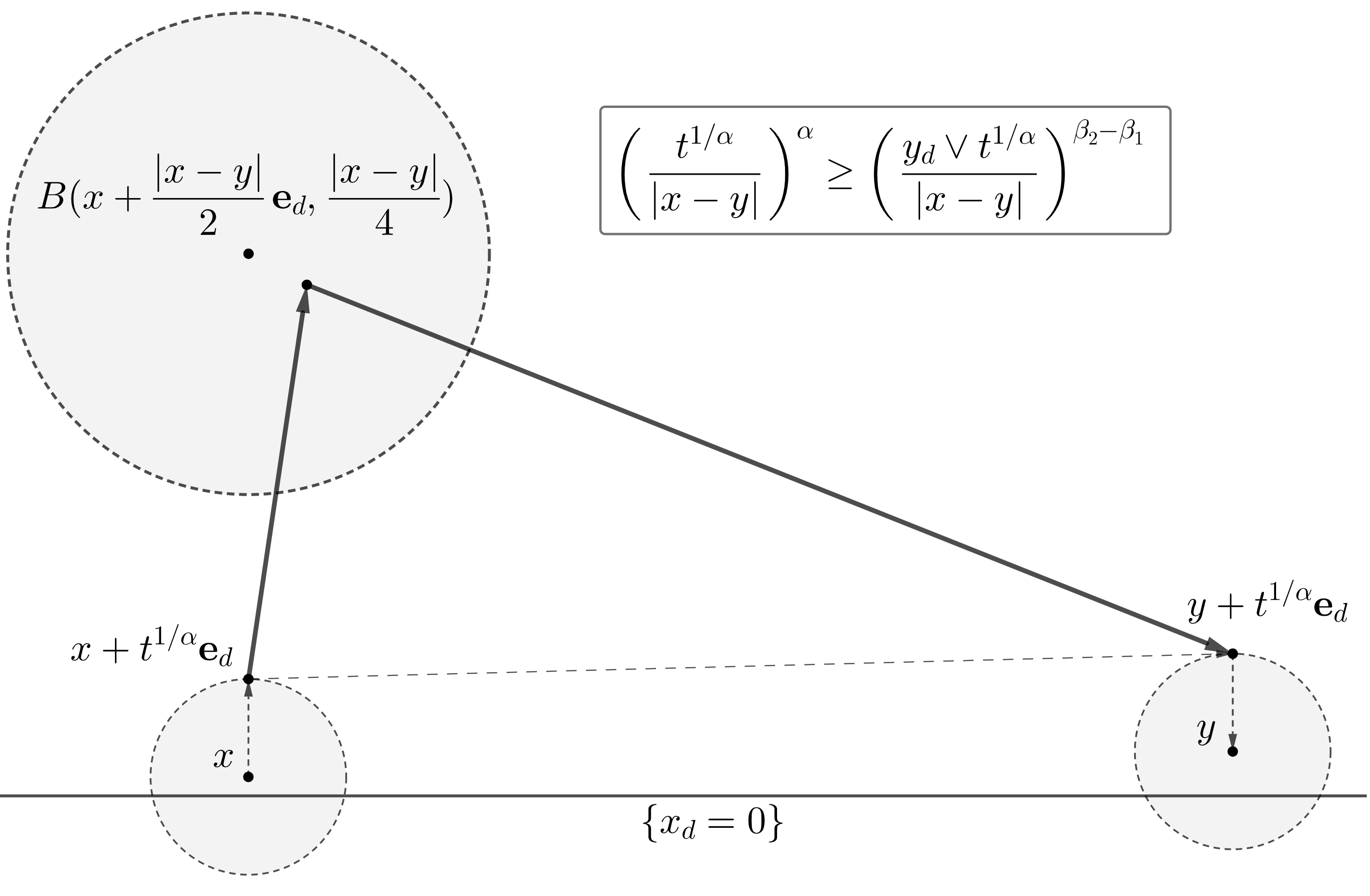
Note that if $x$ or $y$ is close to the boundary, then $J(x+t^{1/\alpha}{\mathbf{e}}_{d},y+t^{1/\alpha}{\mathbf{e}}_{d})$ is not comparable to $J(x,y)$ in our setting. Thus, even in case $\beta_{2}<\alpha+\beta_{1}$, the form of the heat kernel is different from the usual form. The appearance of the two terms in the brackets on the right-hand sides of (1.4)–(1.1) reflects the fact that the dominant contribution to the heat kernel may come from either one jump or two jumps. Moreover, it is easy to see that neither of these two terms dominates the other one for all $(t,x,y)$. Below we illustrate this feature when $\beta_{2}>\alpha+\beta_{1}$.

Let $\beta_{2}>\alpha+\beta_{1}$. When $|x-y|>6t^{1/\alpha}$, the second term in the brackets in (1.4), i.e.,

is comparable to

see Remark 6.5 below. In the special case when $\beta_{3}=\beta_{4}=0$ (and $\beta_{2}>\alpha+\beta_{1}$), Figure 1(b), where the comparability of (1.6) and (1.7) is used, illustrates the regions where one jump and two jumps dominate.

The different forms of the heat kernel estimates in Theorem 1.1 are consequences of the relationship among $\beta_{1}$, $\beta_{2}$ and $\alpha$ only, the values of $\beta_{3}$ and $\beta_{4}$ do not play any role in this. To reduce technicalities, the reader, on a first reading, may assume $\beta_{3}=\beta_{4}=0$, without loosing the essential features of this paper. Note that, even in this special case, a logarithmic term appears in the estimates when $\beta_{2}=\alpha+\beta_{1}$. We need the logarithmic terms in the assumptions to cover the important examples in [21, 29].

Let ${\cal F}^{0}$ be the closure of $C_{c}^{\infty}({\mathbb{R}}^{d}_{+})$ in $L^{2}({\mathbb{R}}^{d}_{+},dx)$ under the norm ${\cal E}^{0}_{1}$. Then $({\cal E}^{0},{\cal F}^{0})$ is also a regular Dirichlet form on $L^{2}({\mathbb{R}}^{d}_{+},dx)$ and it is the part form of $({\cal E}^{0},{\overline{\cal F}})$ on ${\mathbb{R}}^{d}_{+}$. Let $Y^{0}=(Y^{0}_{t},t\geq 0;{\mathbb{P}}_{x},x\in{\mathbb{R}}^{d}_{+}\setminus{\cal N}_{0})$ be the Hunt process associated with $({\cal E}^{0},{\cal F}^{0})$ where ${\cal N}_{0}$ is an exceptional set. $Y^{0}$ can be regarded as the part process of $\overline{Y}$ killed upon exiting ${\mathbb{R}}^{d}_{+}$.

For $\kappa\in(0,\infty)$, define

where $\widetilde{\cal F}^{0}$ is the family of all ${\cal E}^{0}_{1}$-quasi-continuous functions in ${\cal F}^{0}$. Then $({\cal E}^{\kappa},{\cal F}^{\kappa})$ is a regular Dirichlet form on $L^{2}({\mathbb{R}}^{d}_{+},dx)$ with $C_{c}^{\infty}({\mathbb{R}}^{d}_{+})$ as a special standard core, see [23, Theorems 6.1.1 and 6.1.2]. Let $Y^{\kappa}=(Y^{\kappa}_{t},t\geq 0;{\mathbb{P}}_{x},x\in{\mathbb{R}}^{d}_{+}\setminus{\cal N}_{\kappa})$ be the Hunt process associated with $({\cal E}^{\kappa},{\cal F}^{\kappa})$ where ${\cal N}_{\kappa}$ is an exceptional set. For $\kappa\in[0,\infty)$, we denote by $\zeta^{\kappa}$ the lifetime of $Y^{\kappa}$. Define $Y^{\kappa}_{t}=\partial$ for $t\geq\zeta^{\kappa}$, where $\partial$ is a cemetery point added to the state space ${\mathbb{R}}^{d}_{+}$.

We now associate with the constant $\kappa$ a positive parameter $q$ which plays an important role in the paper. For $q\in(-1,\alpha+\beta_{1})$, set

If we additionally assume that (A3)(II) holds, then the constant $C(\alpha,q,{\cal B})$ is well defined and finite for every $q\in(-1,\alpha+\beta_{1})$, $C(\alpha,q,{\cal B})=0$ if and only if $q\in\{0,\alpha-1\}$, and $\lim_{q\to-1}C(\alpha,q,{\cal B})=\lim_{q\to\alpha+\beta_{1}}C(\alpha,q,{\cal B})=\infty$ (see [30, Lemma 5.4 and Remark 5.5]). Note that for every $s\in(0,1)$, $q\mapsto(s^{q}-1)(1-s^{\alpha-q-1})$ is strictly decreasing on $(-1,(\alpha-1)/2)$ and strictly increasing on $((\alpha-1)/2,\alpha+\beta_{1})$. Thus, the shape of the map $q\mapsto C(\alpha,q,{\cal B})$ is given as follows.

Consequently, for every $\kappa\geq 0$, there exists a unique $q_{\kappa}\in[(\alpha-1)_{+},\alpha+\beta_{1})$ such that

As a consequence of Lemma 2.3 below, we will see that, when $\alpha\leq 1$, the process $\overline{Y}$ started from ${\mathbb{R}}^{d}_{+}$ will never hit $\partial{\mathbb{R}}^{d}_{+}$ and is equal to $Y^{0}$. Thus for $x,y\in{\mathbb{R}}^{d}_{+}$ we have that $p^{0}(t,x,y)=\overline{p}(t,x,y)$, implying that the non-trivial content of Theorem 1.2 is for $\kappa>0$ when $\alpha\leq 1$.

Let

When $\overline{G}(\cdot,\cdot)$ is not identically infinite, it is called the Green function of $\overline{Y}$, and when $G^{\kappa}(\cdot,\cdot)$ is not identically infinite, it is called the Green function of $Y^{\kappa}$.

As a consequence of the heat kernel estimates, we get the Green function estimates. The following theorem says that the Green function of $\overline{Y}$ is comparable to that of the isotropic $\alpha$-stable process in ${\mathbb{R}}^{d}$ even though the jump kernel of $\overline{Y}$ may be degenerate.

When $d>(\alpha+\beta_{1}+\beta_{2})\wedge 2$, sharp two-sided estimates on $G^{\kappa}(x,y)$ were obtained in [31, 32]. In the following theorem, we extend those results by removing the restriction on $d$ and give another proof using the heat kernel estimates. The advantage of the new proof is that it explains the reason for the phase transition in the Green function estimates for $d\geq 2$.

Let

Note that when $d\geq 2$, at the threshold $q_{\kappa}=\alpha+\frac{1}{2}(\beta_{1}+\beta_{2})$, there is a transition from the usual behavior of the Green function estimates to anomalous behavior.

We describe now the strategy for proving our main results and the organization of the paper.

It is well known that an appropriate Nash-type inequality implies the existence of the heat kernel (outside an exceptional set) and its $\alpha$-stable-type upper bound. So we start in Section 2 with establishing a Nash-type inequality, see Proposition 2.6. To this end, we consider a certain Feller process in ${\mathbb{R}}^{d}_{+}$ with continuous paths, subordinate it by an independent $\alpha/2$-stable subordinator, and show a Nash-type inequality for the Dirichlet form of the subordinate process. In case $\alpha<1$, one can estimate the Dirichlet form of the subordinate process from above by ${\cal E}^{0}$ and thus prove a Nash-type inequality for ${\cal E}^{0}$. In case $\alpha\geq 1$, we use the scaling property of the process and a truncation of the jump kernel together with the already obtained inequality for $\alpha<1$.

In Section 3, we prove parabolic Hölder regularity for both $\overline{Y}$ and $Y^{\kappa}$ and use this to remove the exceptional sets and extend $\overline{p}(t,x,y)$ and $p^{\kappa}(t,x,y)$ continuously to $(0,\infty)\times\overline{{\mathbb{R}}}^{d}_{+}\times\overline{{\mathbb{R}}}^{d}_{+}$, respectively $(0,\infty)\times{\mathbb{R}}^{d}_{+}\times{\mathbb{R}}^{d}_{+}$. To prove the parabolic Hölder regularity, we need an interior lower bound on the heat kernels. The proof of this lower bound is based on an argument that has already appeared in [30, Section 3] and is given here in Proposition 3.1. Next, we prove several lower bounds on the heat kernels, mean exit times and exit distributions of the underlying process and its killed version that allow us to apply the standard arguments for establishing the parabolic Hölder regularity. We end Section 3 with the elementary Lemma 3.15 which will be used repeatedly in deriving the heat kernel upper bounds.

Following the arguments from [9, 21], in Section 4 we establish the parabolic Harnack inequality, see Theorem 4.3, and use it to establish the important preliminary off-diagonal lower bound $p^{\kappa}(t,x,y)\geq ctJ(x,y)$ for $t$ small compared to $|x-y|$, $x_{d}$ and $y_{d}$, see Proposition 4.5.

In Section 5 we prove the following preliminary upper bound:

for all $q_{\kappa}\in[(\alpha-1)_{+},\alpha+\beta_{1})$, see Proposition 5.1. Proposition 5.1 is proved in two steps: Using Lemma 3.15 and several results from [30, 31, 32] (see Lemmas 5.10-5.11) we first prove Proposition 5.1 in case $q_{\kappa}<\alpha$. The real challenge is to extend it to the full range of $q_{\kappa}$ by covering the case $q_{\kappa}\geq\alpha$. For this we use the upper bound on Green potentials of powers of the distance to the boundary. In case $d\geq 2$, such bound was proved in [31, 32], and here we prove the corresponding result for $d=1$. The restriction $q_{\kappa}<\alpha$ is removed in Lemma 5.13 by using a bootstrap (induction) argument.

Section 6 is devoted to proving sharp heat kernel lower bounds. The estimates are given in terms of a function $A_{b_{1},b_{2},b_{3},b_{4}}(t,x,y)$, a space-time version of the function $B_{b_{1},b_{2},b_{3},b_{4}}(x,y)$. We first prove a preliminary lower bound, Proposition 6.2, by using the semigroup property and some interior lower bound on the heat kernel. This bound turns out to be sufficient in case $\beta_{2}<\alpha+\beta_{1}$. For the case $\beta_{2}\geq\alpha+\beta_{1}$ we need a sharper lower bound obtained in the key Lemma 6.4. There we apply the semigroup property (and the preliminary lower bound) on a carefully chosen interior set on which we have good control of the terms appearing in the preliminary lower bound. By combining Proposition 6.2 and Lemma 6.4, we obtain in Proposition 6.6 the sharp lower bound in cases $\beta_{2}\neq\alpha+\beta_{1}$. The remaining case $\beta_{2}=\alpha+\beta_{1}$ is more delicate and is covered in Proposition 6.9.

Sharp heat kernel upper bound is more difficult to establish and Section 7 is devoted to this task. The first step is to establish in Lemma 7.2 an upper bound which includes the function $A_{\beta_{1},0,\beta_{3},0}$. The proof uses Lemma 3.15 and an induction argument which consecutively increases the first parameter of the function $A$ until reaching $\beta_{1}$, thus making the decay successively sharper. The sharp upper bound in case $\beta_{2}<\alpha+\beta_{1}$, respectively $\beta_{2}\geq\alpha+\beta_{1}$, is given in Theorem 7.5 and Corollary 7.9, respectively Theorem 7.10. The proofs are based on Lemma 3.15, Lemma 7.2, and a number of delicate technical lemmas involving multiple space-time integrals of the preliminary heat kernel estimates.

In Section 8, we combine the upper bounds obtained in Section 7 with the lower bounds from Section 6 and give the proofs of Theorems 1.1–1.2.

It is well known that the Green function is the integral over time of the heat kernel. In Section 9 we first use this observation together with the estimates of $\overline{p}(t,x,y)$ obtained in Proposition 2.7 and Lemma 3.7 (see also Remark 3.12) to prove Theorem 1.3. By using the same method of integrating the heat kernel estimates of $p^{\kappa}(t,x,y)$ over time we establish Theorem 1.4, thus reproving and extending the main result of [31]. This new proof sheds more light on the anomalous behavior of these Green function estimates. Lemma 9.1 clearly shows that they are consequences of the different forms of the small time heat kernel estimates.

The paper ends with an appendix which contains a number of technical results not depending on the preliminary estimates of the heat kernel.

Throughout this paper, the constants $\beta_{1}$, $\beta_{2}$, $\beta_{3}$, $\beta_{4}$ will remain the same, and $\kappa$ always stands for a non-negative number. The notation $C=C(a,b,\ldots)$ indicates that the constant $C$ depends on $a,b,\ldots$. The dependence on $\kappa,d$ and $\alpha$ may not be mentioned explicitly. Lower case letters $c_{i},i=1,2,\dots$ are used to denote the constants in the proofs and the labeling of these constants starts anew in each proof. We denote by $m_{d}$ the Lebesgue measure on ${\mathbb{R}}^{d}$. For Borel subset $D\subset{\mathbb{R}}^{d}$, $\delta_{D}(x)$ denotes the distance between $x$ and the boundary $\partial D$.

The goal of this section is (i) to prove a Nash type inequality (Proposition 2.6); (ii) to deduce the existence of the heat kernels of $\overline{Y}$ and $Y^{\kappa}$; and (iii) to establish their preliminary upper bounds (Proposition 2.7).

We begin the section by introducing the notation for the relevant semigroups and establishing their scale invariance and horizontal translation invariance.

For $\kappa\geq 0$, we denote by $(\overline{P}_{t})_{t\geq 0}$ and $(P_{t}^{\kappa})_{t\geq 0}$ the semigroups corresponding to $({\cal E}^{0},\overline{\cal F})$ and $({\cal E}^{\kappa},{\cal F}^{\kappa})$ respectively. $(\overline{P}_{t})_{t\geq 0}$ and $(P_{t}^{\kappa})_{t\geq 0}$ define contraction semigroups on $L^{p}({\overline{\mathbb{R}}}^{d}_{+},dx)=L^{p}({\mathbb{R}}^{d}_{+},dx)$ for every $p\in[1,\infty]$, and when $p\in[1,\infty)$, these semigroups are strongly continuous. For $t>0$ and $p,q\in[1,\infty]$, define

For $f:{\mathbb{R}}^{d}\to{\mathbb{R}}$ and $r>0$, define $f^{(r)}(x)=f(rx)$. The following scaling property of $(P_{t}^{\kappa})_{t\geq 0}$ comes from [30, Lemma 5.1] and [32, Lemma 2.1]. By the same proof, $(\overline{P}_{t})_{t\geq 0}$ also has the same scaling property. We give the proof for the reader’s convenience.