M&D Data Science Center, Tokyo Medical and Dental University (TMDU), Japanhdbn.dsc@tmd.ac.jphttps://orcid.org/0000-0002-6856-5185JSPS KAKENHI Grant Numbers JP20H04141, JP24K02899. NTT Communication Science Laboratories, Japanmitsuru.funakoshi@ntt.comhttps://orcid.org/0000-0002-2547-1509 M&D Data Science Center, Tokyo Medical and Dental University (TMDU), Japandiptarama.hendrian@tmd.ac.jphttps://orcid.org/0000-0002-8168-7312 Graduate School of Medical and Dental Sciences, Tokyo Medical and Dental University (TMDU), Japanma190093@tmd.ac.jp Department of Computer Science, University of Helsinki, Helsinki, Finlandpuglisi@cs.helsinki.fihttps://orcid.org/0000-0001-7668-7636Academy of Finland grants 339070 and 351150. \CopyrightHideo Bannai, Mitsuru Funakoshi, Diptarama Hendrian, Myuji Matsuda, Simon J. Puglisi \ccsdesc[500]Theory of computation Data compression \supplementSoftware available at https://github.com/dscalgo/lzhb/.
Acknowledgements.
Computing resources were provided by Human Genome Center (the Univ. of Tokyo), through the usage service provided by M&D Data Science Center, Tokyo Medical and Dental University.Height-bounded Lempel-Ziv encodings
Abstract
We introduce height-bounded LZ encodings (LZHB), a new family of compressed representations that are variants of Lempel-Ziv parsings with a focus on bounding the worst-case access time to arbitrary positions in the text directly via the compressed representation. An LZ-like encoding is a partitioning of the string into phrases of length which can be encoded literally, or phrases of length at least which have a previous occurrence in the string and can be encoded by its position and length. An LZ-like encoding induces an implicit referencing forest on the set of positions of the string. An LZHB encoding is an LZ-like encoding where the height of the implicit referencing forest is bounded. An LZHB encoding with height constraint allows access to an arbitrary position of the underlying text using predecessor queries.
While computing the optimal (i.e., smallest) LZHB encoding efficiently seems to be difficult [Cicalese & Ugazio 2024, arxiv], we give the first linear time algorithm for strings over a constant size alphabet that computes the greedy LZHB encoding, i.e., the string is processed from beginning to end, and the longest prefix of the remaining string that can satisfy the height constraint is taken as the next phrase. Our algorithms significantly improve both theoretically and practically, the very recently and independently proposed algorithms by Lipták et al. (arxiv, to appear at CPM 2024).
We also analyze the size of height bounded LZ encodings in the context of repetitiveness measures, and show that there exists a constant such that the size of the optimal LZHB encoding whose height is bounded by for any string of length is , where is the size of the smallest run-length grammar. Furthermore, we show that there exists a family of strings such that , thus making one of the smallest known repetitiveness measures for which time access is possible using linear () space.
keywords:
Lempel-Ziv parsing, data compressioncategory:
\relatedversion1 Introduction
Dictionary compressors are a family of algorithms that produce compressed representations of input strings essentially as sequences of copy and paste operations. These representations are widely used in general compression tools such as gzip and LZ4, and have also received much recent attention since they are especially effective for highly repetitive data sets, such as versioned documents and pangenomes [23].
A desirable operation to support on compressed data is that of random access to arbitrary positions in the original data. Access should be supported without decompressing the data in its entirety, and ideally by decompressing little else than the sought positions. Recent years have seen intense research on the access problem in the context of dictionary compression, most notably for grammar compressors (SLPs) and Lempel-Ziv (LZ)-like schemes. The general approach is to impose structure on the output of the compressor and in doing so add small amounts of information to support fast queries. While LZ77 [34] is known to be theoretically and practically one of the smallest compressed representations that can be computed efficiently, a long-standing question is whether time access can be achieved with a data structure using space [23], where is the size of the LZ77 parsing.
In an LZ-like compression scheme, the input string of length is parsed into phrases (substrings of ), where each phrase is of length , or, is a phrase of length at least which has a previous occurrence. Each phrase can be encoded by a pair , where is the length of the phrase, and is the symbol representing the phrase if , or otherwise, a position of a previous occurrence (source) of the phrase. A greedy left-to-right algorithm that takes the longest prefix of the remaining string that can be a phrase leads to the aforementioned LZ77 parsing. An LZ-like encoding of a string induces a referencing forest, where each position of the string is a node, phrases of length 1 are roots of a tree in the forest, and the parent of all other positions are induced by the previous occurrence of the phrase it is contained in. The principle hurdle to support fast access to an arbitrary symbol from an LZ-like parsing is to trace the symbol to a root in the referencing forest. For LZ77, the height of the referencing forest can be .
Contributions.
In this paper, we explore LZ-like parsings specifically designed to bound the height of the referencing forest, i.e., LZ-like parsers in which the parsing rules prevent the introduction of phrases that would exceed a specified maximum height of the referencing forest. Our contributions are summarized as follows:
-
1.
We propose the first linear time111Assuming a constant-size alphabet. algorithm LZHB for computing the greedy height-bounded LZ-like encoding, i.e., the string is processed from beginning to end, and each phrase is greedily taken as the longest prefix of the remaining string that can satisfy the height constraint. This problem was first considered by Kreft and Navarro [16], where an algorithm called LZ-COST, with no efficient implementation, is mentioned. Very recently, contemporaneously and independently of our work, this problem was also revisited by Lipták et al. [18], who presented an algorithm called greedy-BATLZ running in time. Lipták et al. also proposed greedier-BATLZ that runs in time, where is the size of the parsing, further adding the requirement that the previous occurrence of the phrase is chosen so as to minimize the maximum height. We show that our algorithms can be modified to support this heuristic in time, where is the total number of previous occurrences of all phrases.
-
2.
We show that our algorithms allow for simple, lightweight implementations based on suffix arrays and segment trees, and that our implementations are an order of magnitude (or two) faster than the recent implementations of related schemes by Lipták et al.
-
3.
We propose a new LZ-like encoding, which may be of independent theoretical interest, which can be considered as a run-length variant of standard LZ-like encodings which can potentially reduce the referencing height further.
-
4.
We analyze the size of height bounded LZ-like encodings in the context of repetitiveness measures [23]. We show that for some constant , there exits data structures of size that allow access in time, where is the size of the smallest LZ-like encoding whose height is bounded by . Furthermore is always , and further can be for some family of strings, where denotes the size of the smallest run-length grammar (RLSLP) [27] representing the string. This makes one of the smallest known measures that can achieve time access using linear space. The other two are the size of the LZ-End parse [16, 17, 14], and the size of the smallest iterated SLPs (ISLPs) [26]. Note that while there exist string families such that , we do not yet know if it can be that .
2 Preliminaries
2.1 Strings
Let be a set of symbols called the alphabet, and the set of strings over . For any non-negative integer , is the set of strings of length . For any string , denotes the length of . The empty string (the string of length ) is denoted by . For any integer , is the th symbol of , and for any integers , if , and otherwise. We will write to denote . For string , is a period of if for all . For any string , is an occurrence of in if . For any position , the length of the longest previously occurring factor of position is , and let . For any with , the leftmost occurrence of the length- substring starting at is , which can be undefined when is the leftmost occurrence of . We will omit the subscript when the underlying string considered is clear.
A string that is both a prefix and suffix of a string is called a border of that string. The border array of a string is an array of integers, where the is the length of the longest proper border of . The border array is computable in time and space [15], in an on-line fashion, i.e., at each step , the border array of is obtained in amortized constant ( total) time. Notice that the minimum period of is . Thus, the minimum periods of all prefixes of a (possibly growing) string can be computed in time linear in the length of the string.
Lemma 2.1 ([15]).
The minimum period of a semi-dynamic string that allows symbols to be appended is non-decreasing and computable in amortized constant time per symbol.
The following is another useful lemma, rediscovered many times in the literature.
Lemma 2.2 (e.g. Lemma 8 of [28]).
The set of occurrences of a word inside a word which is exactly twice longer than forms a single arithmetic progression.
Our parsing algorithms make use of the suffix tree data structure [32]. We assume some familiarity with suffix trees, and give only the basic properties essential to our methods below. We refer the reader to the many textbook treatments of suffix trees for further details [13, 22].
-
1.
The suffix tree of a string , denoted (or just when the context is clear) is a compacted trie containing all the suffixes of . Each leaf of the suffix tree corresponds to a suffix of the string and is labelled with the starting position of that suffix.
- 2.
-
3.
Suffix trees can support prefix queries that return a pair , where is the length of the longest prefix of the query string that occurs in the indexed string, and is the leftmost position of an occurrence of that prefix. Prefix queries can be conducted simply by traversing the suffix tree from the root with the query string and take time. The query string can be processed left-to-right, where each symbol is processed in time, which is the cost of finding the correct out-going child edge from the current suffix tree node. Prefix queries can be answered in the same time complexity even if the underlying string is extended in an online fashion as mentioned in Property 2.
-
4.
The suffix tree of can be preprocessed in linear time to answer, given , the leftmost occurrence in of the substring , i.e., in constant time [2].
2.2 LZ encodings and random access
An LZ-like parsing of a string is a decomposition of the string into phrases of length (literal phrases), or a phrase of length at least which has a previous occurrence in the string. An LZ-like encoding is a representation of the LZ-like parsing, where literal phrases are encoded as the pair , where is the phrase itself, and phrases of length at least are encoded as the pair , where is the length of the phrase and is a previous occurrence (or the source) of the phrase. Although LZ parsing and encoding are sometimes used as synonyms, we differentiate them in that a parsing only specifies the length of each phrase, while an encoding specifies the previous occurrence of each phrase as well. The size of an LZ-like encoding is the number of phrases. For example, for the string , we can have an encoding of size . A common variant of LZ-like encodings adds an extra symbol explicitly to the phrase, and each phrase is encoded by a triplet. For simplicity, our description will not consider this extra symbol; the required modifications for the algorithms to include this are straightforward. We note that our experiments in Section 6 will include the extra character, in order to compare with implementations of previous work.

An LZ-like encoding of a string induces an implicit referencing forest, where: each position of the string is a node, literal phrases are roots of a tree in the forest, and the parent of all other positions are induced by the source of the phrase it is contained in. For example, for the encoding of the string as above, the referencing forest is shown in Figure 1. Let be an LZ-like encoding of string . Given an arbitrary position , suppose we would like to retrieve the symbol . This can be done by traversing the implicit referencing forest using predecessor queries. We first find the phrase with starting position 222We note that it is possible to encode each phrase as , since then, . that the position is contained in, i.e., s.t. . Then, we can deduce that the parent position of is . This is repeated until a literal phrase is reached, in which case . The number of times a parent must be traversed (i.e., the number of predecessor queries) is bounded by the height of the referencing forest. This notion of height for LZ-like encodings was introduced by Kreft and Navarro [17].
3 Height bounded LZ-like encodings
We first consider modifying the definition of the height of the referencing forest under some conditions, by implicitly rerouting edges. Consider the case of a unary string and LZ-like encoding . The straightforward definition above gives a height of for position . This is a result of the second phrase being self-referencing, i.e., the phrase overlaps with its referenced occurrence, and each position references its preceding position. An important observation is that self-referencing phrases are periodic; in particular a self-referencing phrase starting at position with source has period . Due to this periodicity, any position in the phrase can refer to an appropriate position in .
More formally, let be an LZ-like encoding of . For any position , let be the starting position of the phrase such that . Then, if , and otherwise.
We define the height of position by an encoding as
| (1) |
The subscript will be omitted if the underlying encoding considered is clear. Since can be computed using a predecessor query on the set of phrase starting positions, can be computed using time using a data structure of size , where is the time required for predecessor queries on elements in using space. is using a simple binary search, and faster using more sophisticated methods [21].
For example, for the encoding of string , the heights are: . Notice that the phrase that starts at position , representing is self-referencing, and the height of the last position in the phrase (position 6) is , since it is defined to reference position . We note that even with this modified definition, the height of the optimal LZ-like encoding (LZ77) can be . See Appendix A in Appendix A.
In order to bound the worstcase query time complexity for access operations, we consider LZ-like encodings with bounded height. An -bounded LZ-like encoding is an LZ-like encoding where .
There are many ways one could enforce such a height restriction. Unfortunately, finding the smallest such encoding was very recently shown to be NP-hard by Cicalese and Ugazio [8]. Therefore, we propose several greedy heuristics to compute -bounded LZ-like encodings. Given an encoding for (which defines for any ), the next phrase starting at position is defined as follows.
- LZHB1
-
is the largest value such that satisfies the height constraint, where , i.e., the leftmost occurrence of the longest previously occurring factor at position .
- LZHB2
-
is the largest value such that for all , the leftmost occurrence of satisfies the height constraint. is the leftmost occurrence of .
- LZHB3
-
is the largest value such that for all , there exists some previous occurrence of that satisfies the height constraint. is the leftmost occurrence of that satisfies the height constraint.
Note that for all variations, if there is no occurrence of that satisfies the corresponding conditions described above, in which case, .
We note that LZHB1 corresponds to the baseline algorithm BATLZ2 in [18]. LZHB3 essentially corresponds to greedy-BATLZ in [18] as well, but greedy-BATLZ does not require that the occurrence is leftmost. The difference between LZHB2 and LZHB3 lies in the priority of the choice of the leftmost occurrence and when to check the height constraint. LZHB2 greedily extends the prefix, checking each time whether its leftmost occurrence satisfies the height constraint. LZHB3 finds the leftmost occurrence out of the longest prefix that can satisfy the height constraint. Note that when the height is unbounded, the size of all three variants will be equivalent to the regular LZ77 parsing.
We show that LZHB1 and LZHB2 can be computed in time and space for linearly-sortable alphabets, and LZHB3 can be computed online in time and space for general ordered alphabets.
We also propose a new encoding of LZ-like parsings that re-routes edges of the implicit referencing forest in an attempt to further reduce the heights, again using periodicity. In the case of self-referencing phrases, our definition of height in Equation (1) utilized the fact that self-referencing phrases implies a period in the phrase. Using this period, we could re-route the parents of all positions inside the phrase to the first period in the previous occurrence of the phrase, which is outside the phrase. Here, we make two further observations: 1) since the referenced substring is the first period of the phrase, we could extended the phrase for free while the period continues, possibly making the phrase longer, and 2) the referenced substring could have a previous occurrence further to the left, which should tend to have shorter heights. Therefore, if we were to store the period of the phrase explicitly, this could be applied to and benefit all periodic phrases, self-referencing or not.
Specifically then, under this scheme, a phrase with period can be encoded as the triple , where is a symbol, and a phrase with period can be encoded as the triple , where is the length of the phrase with period , and is a previous occurrence of the length- prefix of the phrase. We will call such an encoding, a modified LZ-like encoding. For example, would be a modified LZ-like encoding for the string .
The implicit referencing forest and heights of the modified LZ-like encoding can be defined analogously: a position in the th phrase that begins at position , i.e., , will reference position , where the second is to deal with the case where the occurrence of the prefix period is self-referencing. For the above example, the heights are: .
A greedy left-to-right algorithm computes the th phrase starting at as:
- LZHB4
-
is the largest value such that has period , or, for all , there exists some previous occurrence of that satisfies the height constraint, where is the minimum period of . is the leftmost occurrence of that satisfies the height constraint, and is the minimum period of .
4 Efficient parsing algorithms for height-bounded encodings
4.1 A linear time algorithm for LZHB1
Theorem 4.1.
For any integer , an -bounded encoding based on LZHB1 for a string over a linearly-sortable alphabet can be computed in linear time and space.
Proof 4.2.
The algorithm maintains an array of integers, initially set to 0. Phrases are produced left to right. The algorithm maintains the invariant that when the encoding is computed up to position , gives the height in the referencing forest of position . Using Property 2 in Section 2.1, we build the suffix tree of in linear time, and preprocess it, again in linear time, for Property 4. We also precompute and store all the lengths of the longest previously occurring factor at each position, i.e., for all , in linear time [10].
Suppose we have computed the -bounded encoding for and would like to compute the th phrase starting at position . We can compute , i.e., the leftmost occurrence of the longest previously occurring factor starting at position , in constant time (Property 4). The encoding of the phrase starting at is then , where is the largest value such that every value in is less than . This can be computed in time by simply scanning the above values in . Notice that we do not need to check the height beyond position , since this would imply that the phrase is self-referencing, and the remaining heights will be copies of the first period of the phrase which were already checked to satisfy the height constraint. After pair is determined, values in are determined according to Equation (1), in time.
The total time is thus proportional to the sum of the phrase lengths, which is .
4.2 A linear time algorithm for LZHB2
The difference between LZHB1 and LZHB2 is that while LZHB1 fixes the source to the leftmost occurrence of the longest previously occurring factor starting at , LZHB2 considers the leftmost position of the candidate substring. Since shorter lengths allow the source to be further to the left where heights tend to be shorter, it may allow longer phrases.
We show below that we can still achieve a linear time parsing algorithm.
Theorem 4.3.
For any integer , an -bounded encoding based on LZHB2 for a string over a linearly-sortable alphabet can be computed in linear time and space.
Proof 4.4.
The same steps as in the first paragraph in the description of LZHB1 in Theorem 4.1 are taken (except for the precomputing of which is not needed here).
Suppose we have computed the -bounded encoding for and would like to compute the th phrase starting at position . We start with , and increase incrementally until there is no previous occurrence of , or the leftmost occurrence of violates the height constraint, and will use the last valid value of for .
For a given , using Property 4, we can obtain the leftmost occurrence of , i.e., , in constant time. We need to check whether all values in are less than . Since may change for different values of , we potentially need to check all values in .
To do this efficiently, we maintain another array , where stores the position in , such that is the smallest position in that is greater than or equal to , such that , if it exists, or otherwise, i.e., . Then, if and only if . Thus, checking the height constraint can be done in constant time for a given .
After are determined, values in are determined according to Equation (1), in time. The array can be maintained in linear total time: all values in are initially set to , and whenever we store the value in for some , we set for all such that , i.e., we update all values in that were . Clearly each element of is set at most once. Thus, the total time is .
4.3 An time algorithm for LZHB3
Theorem 4.5.
For any integer , an -bounded encoding based on LZHB3 for a string can be computed in time and space.
Proof 4.6.
Our algorithm is a slight modification of a folklore algorithm to compute LZ77 in time based on Ukkonen’s online algorithm for computing suffix trees [30] described, e.g., by Gusfield [13]. We first describe a simple version which does not allow self-references.
At a high level, when computing the th phrase that starts at position , we use the suffix tree of so that we can find the longest previous occurrence of . We can find this by simply traversing the suffix tree from the root with as long as possible (Property 3 in Section 2.1). Once we know the length of the phrase, we simply append the phrase to the suffix tree to obtain the suffix tree for , and continue. An occurrence (particularly, the leftmost occurrence) can be obtained easily by storing this information on each edge when it is constructed.
For our height-bounded case, the precise height of a position in a phrase can only be determined after is determined, and if , the leftmost occurrence of that satisfies the height constraint must be determined. Since a reference adds 1 to the height, we know that the height constraint is satisfied if and only if we reference positions that have height less than . Therefore, when adding the symbols of the phrase to the suffix tree after determining their heights, we change symbols corresponding to positions with height to a special symbol which does not match any other symbols. In other words, for and their heights , we use and maintain a suffix tree for , where if and otherwise. This simple modification allows us to reference only and all substrings with heights less than , so that we can find the longest prefix of that occurs in and also satisfies the height constraint, by simply traversing the suffix tree of (Property 3).
Next, in order to allow self-references, we utilize a combinatorial observation made previously, that self-references lead to periodicity. Let be the longest prefix of such that there is a non-self-referencing occurrence in . We can find a longer self-referencing prefix of , if it exists, as follows: Any such occurrence must be prefixed by , and in order for the phrase to be self-referencing, this must occur as a substring in . Since the heights after the first period of the phrase are essentially defined as copies of the heights of the first period of the phrase (see Equation (1)), any occurrence of (and any of its extensions) at or after the leftmost position in such that , would satisfy the height constraint.
If there is no occurrence of in , then a longer self-referencing phrase satisfying the height constraint cannot exist, so . If there is only one such occurrence of , we can use this occurrence and extend the phrase by naive symbol comparisons to obtain . If there are more than one such occurrence, it follows that there are at least three occurrences of in , a string of length (at most) . From Lemma 2.2, this implies that the occurrences of form an arithmetic progression, whose common difference is the minimum period of . Thus, extending the phrase as above from any occurrence of in will lead to the same maximal length due to the periodicity, i.e., is the maximum value such that has the same minimum period as . We can find all such occurrences (which obviously includes the leftmost) in time using any linear time pattern matching algorithm, e.g., KMP [15].
The time to compute phrase is , so we spend time in total.
Pseudo-code for the algorithm is shown in Algorithm 1 in Appendix B.
4.4 An time algorithm for LZHB4
Theorem 4.7.
For any integer , an -bounded encoding for a string based on LZHB4 can be computed in time and space.
Proof 4.8.
The algorithm is similar to LZHB3, in that it computes the suffix tree of in an online manner, and after determining the new phrase and their heights , symbols of the new phrase are added to the suffix tree except when its position has height , in which case is added.
In order to determine the LZHB4 phrase, we first compute the LZHB3 phrase, i.e., the longest prefix of that has a previous occurrence satisfying the height constraint. Let its length be . This implies that any prefix period of that can be referenced (and satisfies the height constraint) is at most . Since prefix periods are non-decreasing (Lemma 2.1), we have that the LZHB4 phrase is the longest prefix of with period . This can be computed in time (again Lemma 2.1). The leftmost occurrence of to be referenced can be found simply by traversing the suffix tree if is at most the length of the longest non-self-referencing prefix of the LZHB3 phrase, and otherwise, will coincide with (the starting position of) the self-referencing occurrence of the LZHB3 phrase. Since must hold as well, each LZHB4 phrase is computed in time, and thus, LZHB4 can be computed in total time and space.
4.5 Algorithms for the greedier heuristic
Lipták et al. [18] also propose a greedier heuristic for height bounded LZ-like encodings, in which, for any phrase, the previous occurrence that minimimzes the maximum height is chosen. While a naïve algorithm runs in time, Lipták et al. propose an algorithm for which they show an upper bound of time. We show here that LZHB3 and LZHB4 can be modified to support the greedier heuristic in total time, where is the total number of previous occurrences of all phrases.
Suppose we are able to obtain all previous occurrences of the phrases. The array is not static, but only append operations are performed on it, and so a range maximum query data structure for can be maintained in amortized time per update and query [12, 29]. Using this, the maximum height of a given occurrence can be checked in amortized time, and the occurrence giving the smallest maximum height can be found in additional time.
All previous occrrences of a phrase can be obtained in additional total time using standard techniques on the suffix tree. Recall that when computing the th phrase, our algorithm traverses the suffix tree for finding a longest non-self-referencing occurrence. The leaves below the reached position contain the occurrences of the phrase, and since any non-leaf node of a suffix tree has at least two children, these leaves can be found in time linear in their number, thus in additional total time. All self-referencing occurrences can be found in time as described in Section 4.3. A minor detail we have skipped is that since we only have the implicit suffix tree being built via Ukkonen’s online construction algorithm, the suffix tree does not have leaves corresponding to suffixes that have a previous occurrence. This can be dealt with as follows. Since Ukkonen’s algorithm maintains the longest repeating suffix of the current text as the active point in the suffix tree, we can also maintain some previous occurrence of it. Since any previous occurrence of the phrase contained in the longest repeating suffix can be mapped to an occurrence in , we can, given all the occurrences of the phrase in for which there is a corresponding leaf in the suffix tree, find all occurrences in the longest repeating suffix in total time.
4.6 Implementation using suffix arrays
The suffix array [19] of a string of length , is an array of integers such that is the th lexicographically smallest suffix of .
Suffix arrays are well known as a lightweight alternative to suffix trees. While it is not difficult to use suffix arrays in place of suffix trees for static strings [1] by mapping nodes of the suffix tree to ranges in the suffix array, it is not straightforward to do this for LZHB3 and LZHB4, since the algorithms work in an online manner: the string for which the suffix tree is maintained is determined during the computation, and is not known in advance. Here, we show how to simulate the algorithm on the suffix tree for by using the suffix array of , in amortized time per suffix tree operation, thus obtaining an time algorithm for LZHB3 and LZHB4. The running times of the greedier versions can be similarly bounded by .
In a suffix tree of , the effect of replacing a symbol at position with can be viewed as an operation that truncates the paths of suffixes starting at position for which does not contain , to length , i.e., to . We will maintain an array of integers, where holds the valid length of the suffix starting at position and is the lexicographic rank of the suffix , i.e., . All values are initially set to , indicating that the suffix has not yet been inserted into the suffix tree. During the online construction of the suffix tree of , when the suffix is added to the suffix tree, we set . When a symbol is appended, we modify the values in of relevant suffixes. Since the value of each position in is modified at most twice (from to and then to the length up to the next ), the total number of updates on is at most .
The traversal on the suffix tree can then be simulated by a standard search for finding the lexicographic range in the suffix array of suffixes that are prefixed by the considered substring. This range can be computed in time per symbol by a simple binary search. In order to make sure we do not traverse truncated suffixes, we allow the traversal if and only if there exists at least one suffix in the lexicographic range whose valid length is at least the length of the substring being traversed. This can be checked in time by using a segment tree [3, 7] for representing , which allows updates and range maximum queries on in time. All occurrences, i.e., suffixes in the range for which the value in is at least the length of the substring, can be enumerated in time per occurrence, by a common technique [20] that calls range maximum queries recursively on sub-ranges excluding the maximum value, until all ranges only contain values less than the desired length.
A minor difference with the suffix tree version is that because we are able to insert the whole suffix starting at a given position rather than just a single symbol at the position, the algorithm will naturally handle self-referencing occurrences, and they no longer require special care. Also, while retrieving an occurrence is easy, we note that we can no longer retrieve the leftmost occurrence for the greedy versions in the same time bound - the chosen occurrence will be a prefix of the suffix with longest valid length.
5 Height bounded LZ-like encodings as repetitiveness measures
Here, we consider the strength of height bounded encodings as repetitiveness measures [23]. Denote by , the optimal (smallest) LZHB encoding whose height is at most . It easily follows that is monotonically non-increasing in , i.e., for any , it holds that . We will also denote by , the optimal modified LZ-like encoding whose height is at most .
A first, and obvious, observation is that if the height is allowed to grow to , then the size of the height-bounded encoding and the LZ parsing are equivalent. {observation} .
It is also interesting to note height-bounded and run-length encodings can be related: {observation} is equivalent to the run-length encoding.
The following relation between and the smallest size of RLSLPs (SLPs with run-length rules) and of ISLPs [26] can be shown.
Theorem 5.1.
There exists a constant such that holds.
Theorem 5.2.
There exist a family of strings such that for some constant , and .
When there is no height constraint, LZHB3 is equivalent to LZ77 and thus gives an optimal LZ-like parsing. For modified LZ-like encodings with no height contraints, LZHB4 can be worse than optimal. For example, for the string , greedy gives while is a slightly smaller parsing. However, we can show that the greedy algorithm has an approximation ratio of at most .
Theorem 5.3.
Let denote the size of the modified LZ-like encoding generated by LZHB4 with no height constraints. We also denote . Then, .
6 Computational Experiments
We have developed prototype implementations of our algorithms described above, in C++. Since Lipták et al. [18] have already demonstrated the effectiveness and superiority of greedy-BATLZ and greedier-BATLZ (which correspond to LZHB3 and the greedier LZHB3) compared to the baselines and that the height can be reduced without increasing the size of the parse too much, our experiments here focus on the performance of our algorithms LZHB3 and LZHB4 in comparison with greedy-BATLZ and greedier-BATLZ. For the BAT-LZ variants, we use the code provided by Lipt’ak et al.333Available at: https://github.com/fmasillo/BAT-LZ. with slight modifications to fit our test environment. Our implementations for LZHB3 and LZHB4 are available at https://github.com/dscalgo/lzhb/.
Experiments were conducted on a system with dual AMD EPYC 9654 2.4GHz processors and 768GB RAM running RedHat Linux 8. We use the Real subset of the repetitive corpus444https://pizzachili.dcc.uchile.cl/repcorpus.html.
Figure 2 shows the running times for various height constraints of the BAT-LZ variants as well as LZHB3, LZHB3SA, LZHB4, and LZHB4SA, and their greedier versions, where the suffix SA denotes the suffix array implementation. Although greedy-BATLZ is fast when there is no height constraint, its performance seems to diminish rapidly when a height constraint is set. Interestingly, greedier-BATLZ seemed to run faster than greedy-BATLZ. We observe that all versions of our LZHB3 and LZHB4 implementation outperform greedy-BATLZ and greedier-BATLZ by a large margin. For the greedier variants, the running times increase as the height constraint decreases. This is because stricter height constraints generally lead to shorter phrase lengths and therefore increases and . This becomes more apparent in the suffix array versions, perhaps because the in the factor for finding the suffix array range is actually the size of the range considered, which becomes larger for shorter pharses.
Figure 3 shows the memory usage of the above mentioned implementations. The memory usage for LZHB3 and LZHB4 (the suffix tree versions) are smallest for small heights, because smaller height constraints imply that many paths in the suffix tree become truncated. On the other hand, the memory usage is the highest for larger heights. Memory usage for the other versions is unaffected by the height constraint. LZHB3SA and LZHB4SA are always superior to greedy-BATLZ, and the same can be said for the greedier versions and their counterparts.
In summary, our suffix array implementations are always faster and use less memory than their BATLZ counterparts, with the exception of greedy-BATLZ with no height constraints.
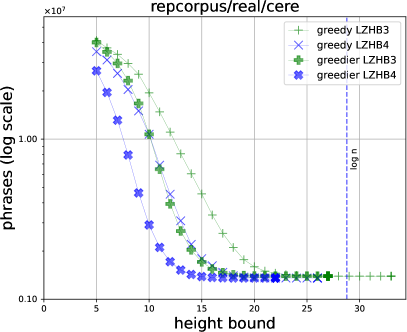
Figure 4 shows the sizes of the phrases of LZHB3, LZHB4 and their greedier versions555We also ran experiments for LZ End parsing, but do not include results in the figures because they distort the plots. We include statistics for LZ End in Table 1 in the Appendix.. Although a phrase of the modified LZ-like encoding is slightly larger than the traditional LZ-like encoding since it includes the period, we can see that a much smaller encoding with the same height, which can more than compensate for this increase, can be obtained in some cases. This seemed to be prominent for cere, para, and Escherichia_Coli, which are all DNA.


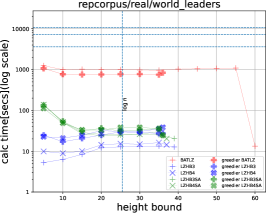






7 Discussion
We have introduced new variants of LZ-like encodings that directly focus on supporting random access to the underlying data. We also proposed a modified LZ-like encoding, which naturally connects the run-length encoding (), and LZ77 (). We described linear time algorithms for several greedy variants of such encodings, as well as how to adapt them to support the greedier heuristic. We showed that our algorithms are faster both theoretically and practically, compared to contemporaneously proposed algorithms by Lipták et al. [18]. We also showed some relations between height-bounded encodings and existing repetitiveness measures. In particular, we have shown that the optimal LZ-like encoding with a height constraint of , is one of the asymptotically smallest repetitiveness measures achieving fast (i.e., -time) access.
There are numerous avenues future work could take. An obvious next step is to engineer actual random-access data structures from height-bounded encodings, which our experiments presented here indicate should be competitive with current state-of-the-art methods. Also, other heuristics for reducing the height while retaining the small size should be explored.
From a theoretical perspective, a natural open problem is whether we can remove the factor from the running times of LZHB3 and LZHB4. The biggest open problem we leave is whether better bounds on the size of height-bounded encodings can be established. Cicalese and Ugazio show that [8] cannot be achieved for costant . We note that since there exist linear sized data structures that can answer predecessor queries for a set of values in the range in time [33], even better lower bounds on the height for which can be shown by using access time lower bound results of Verbin and Yu [31]. However, these do not rule out height. Can we balance the height (achieve height) of an LZ-like encoding or a modified LZ-like encoding, by only increasing the size by a constant factor?
References
- [1] Mohamed Ibrahim Abouelhoda, Stefan Kurtz, and Enno Ohlebusch. Replacing suffix trees with enhanced suffix arrays. J. Discrete Algorithms, 2(1):53–86, 2004. doi:10.1016/S1570-8667(03)00065-0.
- [2] Djamal Belazzougui, Dmitry Kosolobov, Simon J. Puglisi, and Rajeev Raman. Weighted ancestors in suffix trees revisited. In Pawel Gawrychowski and Tatiana Starikovskaya, editors, 32nd Annual Symposium on Combinatorial Pattern Matching, CPM 2021, July 5-7, 2021, Wrocław, Poland, volume 191 of LIPIcs, pages 8:1–8:15. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2021. URL: https://doi.org/10.4230/LIPIcs.CPM.2021.8, doi:10.4230/LIPICS.CPM.2021.8.
- [3] Jon Louis Bentley and Derick Wood. An optimal worst case algorithm for reporting intersections of rectangles. IEEE Trans. Computers, 29(7):571–577, 1980. doi:10.1109/TC.1980.1675628.
- [4] Jean Berstel and Alessandra Savelli. Crochemore factorization of sturmian and other infinite words. In Rastislav Kralovic and Pawel Urzyczyn, editors, Mathematical Foundations of Computer Science 2006, 31st International Symposium, MFCS 2006, Stará Lesná, Slovakia, August 28-September 1, 2006, Proceedings, volume 4162 of Lecture Notes in Computer Science, pages 157–166. Springer, 2006. doi:10.1007/11821069\_14.
- [5] Philip Bille, Travis Gagie, Inge Li Gørtz, and Nicola Prezza. A separation between RLSLPs and LZ77. J. Discrete Algorithms, 50:36–39, 2018. URL: https://doi.org/10.1016/j.jda.2018.09.002, doi:10.1016/J.JDA.2018.09.002.
- [6] Moses Charikar, Eric Lehman, Ding Liu, Rina Panigrahy, Manoj Prabhakaran, Amit Sahai, and Abhi Shelat. The smallest grammar problem. IEEE Trans. Inf. Theory, 51(7):2554–2576, 2005. doi:10.1109/TIT.2005.850116.
- [7] Bernard Chazelle. A functional approach to data structures and its use in multidimensional searching. SIAM J. Comput., 17(3):427–462, 1988. doi:10.1137/0217026.
- [8] Ferdinando Cicalese and Francesca Ugazio. On the complexity and approximability of bounded access Lempel Ziv coding. CoRR, abs/2403.15871, 2024. URL: https://doi.org/10.48550/arXiv.2403.15871, arXiv:2403.15871, doi:10.48550/ARXIV.2403.15871.
- [9] Sorin Constantinescu and Lucian Ilie. The Lempel–Ziv complexity of fixed points of morphisms. SIAM J. Discret. Math., 21(2):466–481, 2007. doi:10.1137/050646846.
- [10] Maxime Crochemore, Lucian Ilie, Costas S. Iliopoulos, Marcin Kubica, Wojciech Rytter, and Tomasz Walen. Computing the longest previous factor. Eur. J. Comb., 34(1):15–26, 2013. URL: https://doi.org/10.1016/j.ejc.2012.07.011, doi:10.1016/J.EJC.2012.07.011.
- [11] Martin Farach. Optimal suffix tree construction with large alphabets. In 38th Annual Symposium on Foundations of Computer Science, FOCS ’97, Miami Beach, Florida, USA, October 19-22, 1997, pages 137–143. IEEE Computer Society, 1997. doi:10.1109/SFCS.1997.646102.
- [12] Johannes Fischer. Inducing the lcp-array. In Frank Dehne, John Iacono, and Jörg-Rüdiger Sack, editors, Algorithms and Data Structures - 12th International Symposium, WADS 2011, New York, NY, USA, August 15-17, 2011. Proceedings, volume 6844 of Lecture Notes in Computer Science, pages 374–385. Springer, 2011. doi:10.1007/978-3-642-22300-6\_32.
- [13] Dan Gusfield. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology. Cambridge University Press, 1997. doi:10.1017/CBO9780511574931.
- [14] Dominik Kempa and Barna Saha. An upper bound and linear-space queries on the LZ-end parsing. In Joseph (Seffi) Naor and Niv Buchbinder, editors, Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, January 9 - 12, 2022, pages 2847–2866. SIAM, 2022. doi:10.1137/1.9781611977073.111.
- [15] Donald E. Knuth, James H. Morris Jr., and Vaughan R. Pratt. Fast pattern matching in strings. SIAM J. Comput., 6(2):323–350, 1977. doi:10.1137/0206024.
- [16] Sebastian Kreft and Gonzalo Navarro. LZ77-like compression with fast random access. In James A. Storer and Michael W. Marcellin, editors, 2010 Data Compression Conference (DCC 2010), 24-26 March 2010, Snowbird, UT, USA, pages 239–248. IEEE Computer Society, 2010. doi:10.1109/DCC.2010.29.
- [17] Sebastian Kreft and Gonzalo Navarro. On compressing and indexing repetitive sequences. Theor. Comput. Sci., 483:115–133, 2013. URL: https://doi.org/10.1016/j.tcs.2012.02.006, doi:10.1016/J.TCS.2012.02.006.
- [18] Zsuzsanna Lipták, Francesco Masillo, and Gonzalo Navarro. BAT-LZ out of hell. CoRR, abs/2403.09893, 2024. To appear at CPM ’24. URL: https://doi.org/10.48550/arXiv.2403.09893, arXiv:2403.09893, doi:10.48550/ARXIV.2403.09893.
- [19] Udi Manber and Gene Myers. Suffix arrays: A new method for on-line string searches. In David S. Johnson, editor, Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms, 22-24 January 1990, San Francisco, California, USA, pages 319–327. SIAM, 1990. URL: http://dl.acm.org/citation.cfm?id=320176.320218.
- [20] S. Muthukrishnan. Efficient algorithms for document retrieval problems. In David Eppstein, editor, Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms, January 6-8, 2002, San Francisco, CA, USA, pages 657–666. ACM/SIAM, 2002. URL: http://dl.acm.org/citation.cfm?id=545381.545469.
- [21] G. Navarro and J. Rojas-Ledesma. Predecessor search. ACM Computing Surveys, 53(5):article 105, 2020.
- [22] Gonzalo Navarro. Compact Data Structures - A Practical Approach. Cambridge University Press, 2016.
- [23] Gonzalo Navarro. Indexing highly repetitive string collections, part I: repetitiveness measures. ACM Comput. Surv., 54(2):29:1–29:31, 2022. doi:10.1145/3434399.
- [24] Gonzalo Navarro, Carlos Ochoa, and Nicola Prezza. On the approximation ratio of ordered parsings. IEEE Trans. Inf. Theory, 67(2):1008–1026, 2021. doi:10.1109/TIT.2020.3042746.
- [25] Gonzalo Navarro, Francisco Olivares, and Cristian Urbina. Balancing run-length straight-line programs. In Diego Arroyuelo and Barbara Poblete, editors, String Processing and Information Retrieval - 29th International Symposium, SPIRE 2022, Concepción, Chile, November 8-10, 2022, Proceedings, volume 13617 of Lecture Notes in Computer Science, pages 117–131. Springer, 2022. doi:10.1007/978-3-031-20643-6\_9.
- [26] Gonzalo Navarro and Cristian Urbina. Iterated straight-line programs. In Proc. LATIN 2024, Lecture Notes in Computer Science, 2024.
- [27] Takaaki Nishimoto, Tomohiro I, Shunsuke Inenaga, Hideo Bannai, and Masayuki Takeda. Fully dynamic data structure for LCE queries in compressed space. In 41st International Symposium on Mathematical Foundations of Computer Science, MFCS 2016, August 22-26, 2016 - Kraków, Poland, volume 58 of LIPIcs, pages 72:1–72:15. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2016.
- [28] Wojciech Plandowski and Wojciech Rytter. Application of Lempel-Ziv encodings to the solution of words equations. In Kim Guldstrand Larsen, Sven Skyum, and Glynn Winskel, editors, Automata, Languages and Programming, 25th International Colloquium, ICALP’98, Aalborg, Denmark, July 13-17, 1998, Proceedings, volume 1443 of Lecture Notes in Computer Science, pages 731–742. Springer, 1998.
- [29] Yohei Ueki, Diptarama, Masatoshi Kurihara, Yoshiaki Matsuoka, Kazuyuki Narisawa, Ryo Yoshinaka, Hideo Bannai, Shunsuke Inenaga, and Ayumi Shinohara. Longest common subsequence in at least k length order-isomorphic substrings. In Bernhard Steffen, Christel Baier, Mark van den Brand, Johann Eder, Mike Hinchey, and Tiziana Margaria, editors, SOFSEM 2017: Theory and Practice of Computer Science - 43rd International Conference on Current Trends in Theory and Practice of Computer Science, Limerick, Ireland, January 16-20, 2017, Proceedings, volume 10139 of Lecture Notes in Computer Science, pages 363–374. Springer, 2017. doi:10.1007/978-3-319-51963-0\_28.
- [30] Esko Ukkonen. On-line construction of suffix trees. Algorithmica, 14(3):249–260, 1995. doi:10.1007/BF01206331.
- [31] Elad Verbin and Wei Yu. Data structure lower bounds on random access to grammar-compressed strings. In Johannes Fischer and Peter Sanders, editors, Combinatorial Pattern Matching, 24th Annual Symposium, CPM 2013, Bad Herrenalb, Germany, June 17-19, 2013. Proceedings, volume 7922 of Lecture Notes in Computer Science, pages 247–258. Springer, 2013. doi:10.1007/978-3-642-38905-4\_24.
- [32] Peter Weiner. Linear pattern matching algorithms. In 14th Annual Symposium on Switching and Automata Theory, Iowa City, Iowa, USA, October 15-17, 1973, pages 1–11. IEEE Computer Society, 1973.
- [33] Dan E. Willard. Log-logarithmic worst-case range queries are possible in space theta(n). Inf. Process. Lett., 17(2):81–84, 1983. doi:10.1016/0020-0190(83)90075-3.
- [34] Jacob Ziv and Abraham Lempel. A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory, 23(3):337–343, 1977. doi:10.1109/TIT.1977.1055714.
Appendix A Ommitted Proofs
The height of the optimal LZ-like encoding (LZ77) can be .
Proof A.1.
Consider the height of in the string:
It is not difficult to see each will reference the closest previously occurring .
See 5.1
Proof A.2.
It is known that a given RLSLP can be balanced, i.e., transformed into another RLSLP whose parse tree height is , without changing the asymptotic size of the RLSLP [25].
Theorem A.3 (Theorem 1 in [25]).
Given an RLSLP generating a string , it is possible to construct an equivalent balanced RLSLP of size , in linear time, with only rules of the form ,, and , where is a terminal, and are variables, and .
Given an RLSLP with parse tree height , a partial parse tree of the RLSLP, as defined in Theorem 5 of [24], can be obtained. Based on this partial parse tree, it is possible to obtain an LZ-like encoding of size at most that of the run-length grammar. The height of the LZ-like encoding corresponds to the height of the parse tree, and thus is -bounded. Since, from Theorem A.3, we can obtain a grammar of size with height , we have that the size of an optimal -bounded LZ-like encoding will have size at most , where is a constant incurred by the height of the balanced RLSLP obtained from balancing the optimal run-length grammar.
See 5.2
Proof A.4.
The proof follows similar arguments to those of Bille et al. [5]. In their proof, they consider a string (originally used by Charikar et al. [6])
where denotes the length- prefix of the Thue-Morse word, are distinct symbols, and is an integer sequence where is the largest of the , , and show that the integers can be chosen so that the smallest RLSLP for has size . They further observe that the size of an LZ77 parsing of the length- prefix of the Thue-Morse word is [4, 9]. Since is the largest of the ’s, the size of the LZ77 parsing of is for this class of strings.
Now, observe that the height, as defined in Equation (1), of an LZ-like encoding with size is , since any position in a phrase references a position in a previous phrase. Therefore, we have that for some , as well, thus showing that .
Since Thue-Morse words are cube-free, the extra rules in the iterated SLPs do not improve the asymptotic size compared to RLSLPs, and thus, as shown in Lemma 3 of [26], for this family of strings. Therefore, we have .
See 5.3
Proof A.5.
It is obvious that . We first claim . This can be seen from the fact that a phrase that starts at position in (the greedy) LZHB4 is at least as long as , and so any LZHB phrase must extend at least to the end of the LZ77 phrase it starts in. Thus, for each LZHB phrase, we can assign a distinct LZ77 phrase (the LZ77 phrase it starts in), and therefore the number of LZHB4 phrases cannot be more than the number of LZ77 phrases.
Next, we claim for any modified LZ-like encoding with no height constraints, whose size is denoted by . This can be seen from the fact that a given phrase in a modified LZ-like encoding can contain at most two LZ77 phrases that start in it. Let be a phrase in the modified LZ-like encoding starting at position , whose minimum period is and is a prefix of . Since there is a previous occurrence of , the first LZ77 phrase that starts in the LZHB phrase must extend to at least the end of the first . Since there is a previous occurrence of any suffix of , the next LZ77 phrase will extend at least to the end of the LZHB phrase. The theorem follows from the above arguments, using for .
Appendix B Pseudo codes
Appendix C More results of computational experiments


























| Dataset | Max. Height | # Factors |
|---|---|---|
| Escherichia_Coli | 27 | 2212539 |
| cere | 256 | 1863246 |
| coreutils | 174 | 1555394 |
| einstein.de.txt | 60 | 39587 |
| einstein.en.txt | 117 | 104087 |
| influenza | 79 | 919565 |
| kernel | 45 | 868362 |
| para | 258 | 2539381 |
| world_leaders | 102 | 207269 |