as a Probe of the Magnetic Dipole Moment
Abstract
Low energy observables involving the Standard Model fermions which are chirality-violating, such as anomalous electromagnetic moments, necessarily involve an insertion of the Higgs in order to maintain gauge invariance. As the result, the properties of the Higgs boson measured at the LHC impact our understanding of the associated low-energy quantities. We illustrate this feature with a discussion of the electromagnetic moments of the -lepton, as probed by the rare decay . We assess the feasibility of measuring this decay at the LHC, and show that the current bounds from lower energy measurements imply that running is very likely to improve our understanding of new physics contributing to the anomalous magnetic moment of the tau.
I Introduction
The discovery of the Higgs boson by the LHC Aad:2012tfa ; Chatrchyan:2012xdj in the and datasets represents a key milestone in the ongoing study of the Standard Model (SM). The fact that the observed boson has features which, at least in the broad brush, match with the SM expectations confirms that it is the principle agent of electroweak symmetry breaking. A major focus of the LHC run II is to establish its properties to high precision to either confirm the SM vision for electroweak breaking or to find the influence of new physics Morrissey:2009tf ; Chang:2008cw ; Curtin:2013fra ; Belusca-Maito:2016axk .
As the agent of the electroweak breaking, the observed Higgs boson is connected to any process for which the chirality of a SM fermion must flip. To maintain gauge invariance, such processes must contain an insertion of an electro-weak breaking vacuum expectation value (VEV), and the Higgs boson, as the fluctuations around the electroweak vacuum, has interactions connected with all such terms. A particularly interesting class of such observables are the electroweak dipole moments of the SM fermions, dimension five operators which can be sensitive probes of physics beyond the Standard Model. In fact, a long-standing mystery surrounds the magnetic dipole moment of the muon, whose experimental determination defies the best available theoretical predictions of the SM at more than two sigma Bennett:2006fi .
The anomalous magnetic dipole moment of a fermion is usually written in terms of the mass and the electromagnetic coupling as:
| (1) |
where is the electromagnetic field strength tensor and the real quantity parameterizes the size of the anomalous magnetic moment. The chiral structure of demands that one of or be left-chiral (and thus part of an doublet), and the other right-chiral (and thus an singlet). In the UV theory, it descends from a pair of dimension six operators combining with an additional Higgs doublet (and field strengths for the and gauge bosons). This obscured dependence on electroweak symmetry breaking is the origin of the well known fact that, in a theory where the SM Yukawa interactions account for all of the chiral symmetry breaking, the anomalous magnetic moment is proportional to itself. It also implies that maps uniquely (in a theory with a single source of electroweak breaking) to an interaction between the Higgs boson, , and a photon.
In this article, we focus on the magnetic dipole moment of the lepton. As the heaviest of the SM leptons111Quark dipole moments are more subtle, manifesting as properties of the hadrons into which they are bound., the is a natural place to search for new physics, and the fact that neutrino masses imply some kind of physics beyond the Standard Model may be a further indication that the lepton sector is a good place to look for its influence. Indeed, if the anomalous magnetic moment of the muon is indeed a manifestation of such physics, one could hope that even larger relative deviations could be present in the sector. At the same time, measurements of the dipole moment are currently relatively mildly constrained, leaving room for large deviations.
Higgs decays thus furnish an opportunity to study the magnetic dipole, through the rare decay,
| (2) |
which we find is potentially observable during high luminosity running of the LHC. As explained above, this process is related through gauge invariance to the more traditional probes of the ’s electroweak interactions via precision measurements of its production and/or decay Silverman:1982ft ; Almeida:1991hq ; delAguila:1991rm ; Samuel:1992fm ; Aeppli:1992tp ; Escribano:1993pq ; Escribano:1996wp ; GonzalezSprinberg:2000mk ; Bernabeu:2007rr ; Bernabeu:2008ii ; Atag:2010ja ; Peressutti:2012zz ; Hayreter:2013vna ; Fael:2013ij ; Hayreter:2015cia ; Eidelman:2016aih , and we will see that Higgs decays provide both an opportunity to discover physics beyond the Standard model, or to provide some of the best constraints on an anomalous contribution to the magnetic moment.
This work is structured as follows. In Section II we discuss the operators which parameterize new physics contributions to the magnetic moment, and review the existing constraints. In Section III, we outline the search strategy and discuss backgrounds, and in Section IV we discuss the potential for discovery or limits in the case no excess of signal events is found. We conclude in Section V.
II Dipole Operators of the Lepton: Current Constraints
Anomalous contributions to the electroweak dipole moments of the tau (at low-energy scales) originate from dimension six operators:
| (3) |
where is the third family left-handed doublet, is the Higgs doublet, and are the field strengths for the hypercharge and gauge bosons, and and are complex numbers with units of . After electroweak symmetry-breaking, linear combinations of these operators lead to anomalous magnetic and electric dipole interactions, and analogous terms involving the boson.
Currently, the most stringent constraints on the dipole operators are from LEP2, where the DELPHI collaboration searched for events, at various collision energies between and with a dataset corresponding to an integrated luminosity of Abdallah:2003xd . The results were found to be consistent with the SM expectations, leading to the constraint
| (4) |
Similarly, the ALEPH collaboration searched for events on the -pole with a dataset corresponding to an integrated luminosity of Heister:2002ik , and obtained the limit
| (5) |
Since the magnetic dipole interaction is much more severely constrained, we choose to focus on from here on.
The combination related to the magnetic moment is described by,
| (6) |
where is the Higgs boson and is a real parameter with dimensions of . The anomalous magnetic moment is related to and the Higgs VEV via:
| (7) |
In terms of , the LEP bound (4) implies
| (8) |
The second term of Eq. (6) leads to the rare Higgs decay . Measurements of this decay therefore translate into measurements of the dipole moment. In fact, the SM contribution to this decay mode has the same chirality structure as the dipole operator, allowing for constructive interference, and resulting in a relative enhancement of the new physics contribution compared to the direct search by LEP.
It is worth mentioning that the imaginary parts of and would also lead to a CP-violating electric dipole moment (and its analogue) for the . While interesting in their own right Zhang:2002zw ; Bower:2002zx ; Desch:2003mw ; Harnik:2013aja ; Berge:2008wi ; Berge:2008dr ; Berge:2011ij ; Berge:2013jra ; Hagiwara:2016zqz , CP symmetry prevents these new physics amplitudes from interfering with the SM contribution to , thus leading to greatly decreased LHC sensitivity (see also Chen:2014ona ). For this reason, we choose here to focus on the magnetic dipole moment for which Higgs decays are a more sensitive probe.
III at the LHC
In this section we estimate the LHC sensitivity reach to the magnetic dipole moment through the decay . This is a challenging signal to reconstruct at a hadron collider for a number of reasons. First, leptons decay promptly, producing missing momentum along with either a charged lepton or a handful of hadrons. Events containing more than one of them can at best be incompletely reconstructed. Decays involving neutral pions also contain energetic photons, which can potentially fake the additional which distinguishes our rare decay mode from background associated with . Photons themselves receive non-perturbative contributions to their production from QCD, which are not very well understood. Minimizing these uncontrolled contributions to photon production typically requires tight isolation cuts, which can be inefficient for events with dense angular population of energy in the detector. In addition, jets can fake both taus and photons at a rate which is intimately tied to the detector response, which is beyond our ability to reliably estimate. To work around these difficulties, we base our on the existing CMS search for Chatrchyan:2014nva , allowing us to draw from its detailed background study. We augment this search by requiring an additional energetic final state photon that along with the system reconstructs the Higgs.
III.1 Signal Selection
The CMS search analyzes multiple signal categories, based on the -pair decay modes, the decay products transverse momentum () spectrum, and , the number of high jets in the event. It is inclusive with regard to photons. The background estimates in each category are useful in deducing the dominant background components when an additional photon is required. Moreover, the results for the categories can be used in estimating the backgrounds from jets faking photons by scaling the yields with the appropriate fake factor.
We focus on categories which have one hadronic tau (), and one leptonic tau decaying either to an or a ( and , respectively). This is motivated by the fact that the efficiency of the -pair reconstruction method is larger for the modes than for purely leptonic modes which have more neutrinos, as well as for purely hadronic modes which suffer from uncertainties related to -tagged jets Chatrchyan:2014nva .
We select the “low-” categories, for which the selection criteria for the candidates are close to the trigger threshold. This category is particularly sensitive to the decay because: the additional photon in the Higgs decay implies that the pairs are on average less energetic than in the two-body decay; we expect our additional selection requirements to substantially reduce backgrounds, and low-threshold signal categories are likely to result in a larger signal sample to start with. We further select the categories because a Higgs produced recoiling against additional jets has its acceptance reduced because its boosted decay products become more collimated, and tend to fail the isolation criteria more often.
CMS also employs a transverse mass cut, , which substantially reduces -boson related backgrounds. The final selection cuts for the two search categories ( and ) are shown in Table 1. For completeness, we also include the additional cuts of our analysis which are discussed in subsequent sections.
| Decay Mode | CMS Cuts | Additional Cuts |
|---|---|---|
| , | ||
| , | ||
It is worth mentioning that one could also consider different production topologies for the Higgs in searching for , such as the vector boson + (VH) Aad:2015zrx or vector boson fusion (VBF) Chatrchyan:2014nva production modes, which show good sensitivity to . These modes yield a richer final state, and thus are somewhat more fragile with respect to tight photon and tau isolation criteria. While it would be worthwhile to pursue them as part of a multi-channel analysis of , we leave their detailed investigation for future work.
III.2 Backgrounds
A detailed study of the backgrounds contributing to the search for is presented in the CMS study, Ref. Chatrchyan:2014nva . In this section, we use these results to infer the most important backgrounds for in the , topology. The dominant background for arises from production of a boson which subsequently decays into . There are also much smaller contributions from electroweak and QCD processes. We further require an additional energetic isolated photon to be present, which can either correspond to real electromagnetic radiation or a jet which is misidentified as a photon.
The contributions to the real photon backgrounds can be roughly estimated from the backgrounds studied in Chatrchyan:2014nva scaled222Note that the required stringent isolation cuts control large collinear logarithms. by . This scaling suggests that of the backgrounds considered, only the is large enough to be relevant. Thus, the real photon background can be approximated as coming entirely from diboson production.
The size of the background from jets misidentified as a photon can be estimated based on the analysis of Chatrchyan:2014nva scaled by the fake rate of CMS:2015loa . To make a fair comparison, we apply a cut of and on signal photons in order to match the jet cut in the categories. Once again, the only relevant background after applying the fake rate is jet production, where the decays into taus and the jet fakes a photon.
The backgrounds can be reduced by applying further cuts on top of the CMS analysis. First, we require (see also CMS:2015mca ), which reduces contributions from (and ) boson decays, while having negligible effects on the signal yield. Second, we impose a cut on the invariant mass, in order to reduce the -background which is narrowly centered around . In a realistic setting, the distribution is smeared out by the imperfect reconstruction; nonetheless we will see below that an upper cut removes most of the background, while still preserving a large part of the signal.
III.3 Monte Carlo Simulation
To assess future LHC sensitivity to the dipole operator from searches for the decay mode, we perform a Monte Carlo simulation of the signal and and jet backgrounds described above. All three processes are simulated in MadGraph5_aMC@NLO (MG5) MG5 , with showering and hadronization by Pythia6 PYTHIA6 ; pythia-pgs , and jet matching under the CKKW prescription Catani:2001cc ; Krauss:2002up ; Alwall:2007fs . Tau decays are handled at the generator level Hagiwara:2012vz (as opposed to by Pythia), as discussed below. The hard matrix elements are derived from FeynRules implementations Degrande:2011ua ; Alloul:2013bka , supplemented by higgs effective vertices with gluons and photons and the tau dipole operators Alloul:2013naa . For the jet background, we include a K-factor of representing the enhancement of the cross-section from higher order QCD corrections Ridder:2015dxa .
The detector reconstruction is simulated by the Delphes 3.3.0 Delphes detector emulator with parameters from its default CMS card. At the detector level, anti- jets AntiKt are reconstructed with FastJet Cacciari:2011ma . Electrons, muons, and photons are required to be isolated within a cone of size , where an object is considered to be isolated if the ratio of the sum of depositions within the cone around it to its own is smaller than . Photon isolation, is applied in MG5 using the built-in Frixione prescription Frixione:1998jh with parameters and . We decay the taus at the generator level in order to include the pions from their decay in this isolation cut.
The tau pair kinematics are reconstructed using the public stand-alone version of the package, SVFitStandAlone Bianchini:2014vza , employing a likelihood based method Elagin:2010aw ; Chatrchyan:2014nva ; SVFitStandAlone which improves on the collinear approximation Ellis:1987xu . We calibrate this package with the Delphes-level covariance matrix of the transverse missing-energy two-vector using a Monte Carlo sample of jet in the CMS fiducial region. By comparing the “truth”-level missing energy information ( neutrinos ) with the reconstructed , we deduce the covariance matrix parameters. We find that SVFitStandAlone reconstructs masses for the and that are systematically somewhat higher than their pole masses. As a result, the Higgs peak is smeared into the range . We thus define as the signal region of our analysis.
We note that Ref. Chatrchyan:2014nva also imposes a cut on the energy deposited near the hadronically decaying tau. This cut is not possible to implement via our work-flow, and thus is neglected. However, because of the strong isolation cuts already imposed on the other hard final state objects in the event, we expect this omission has little effect on our final conclusions.
IV Results and Projected Limits
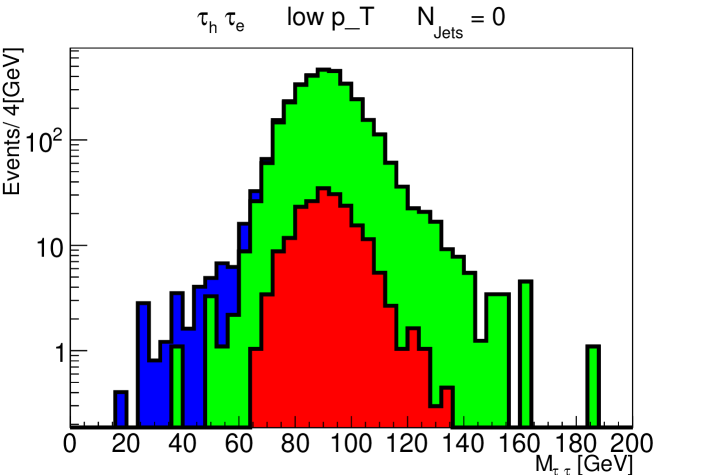
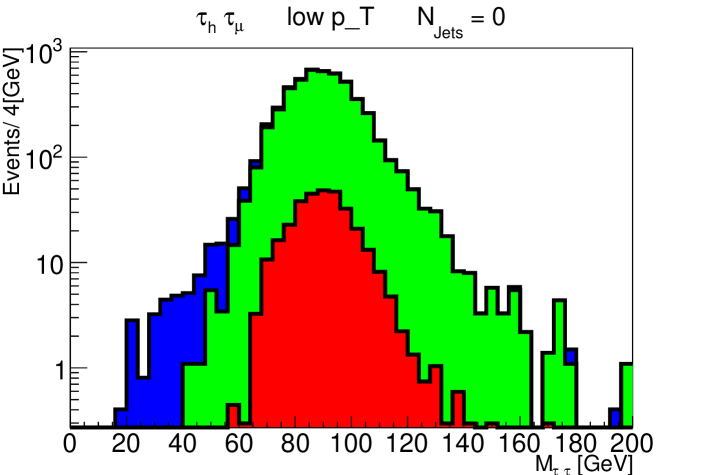
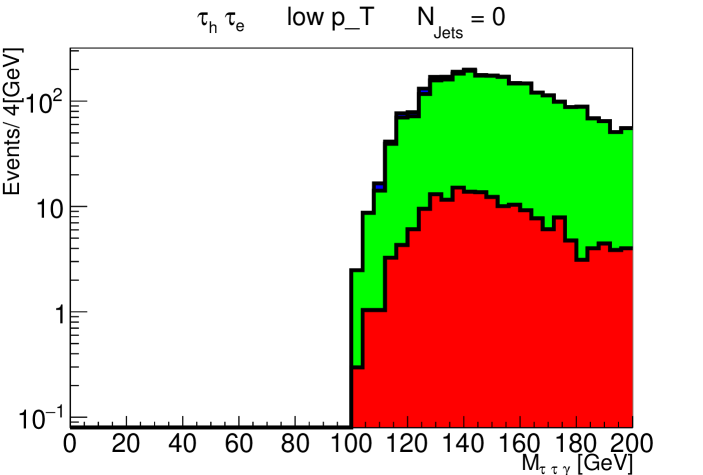
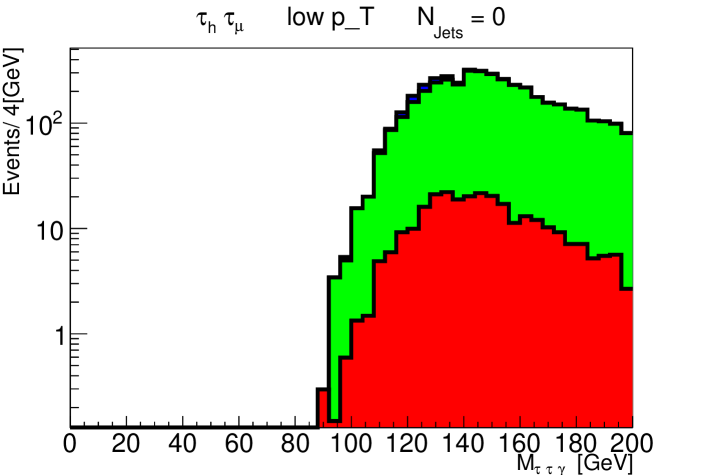
We analyze the reach of the LHC running at , with the reconstruction strategy outlined above. In Fig. 1 we show the expected and distributions for the signal (with , ) and and background processes, in the and topologies, for an integrated luminosity of . All analysis cuts with the exception of the cut are applied. Evident from the upper plots is the motivation for the cut to separate the signal from the backgrounds. The distributions after this cut are presented in Fig. 2, and demonstrate its dramatic efficacy, with only a handful of background events left in the signal region.
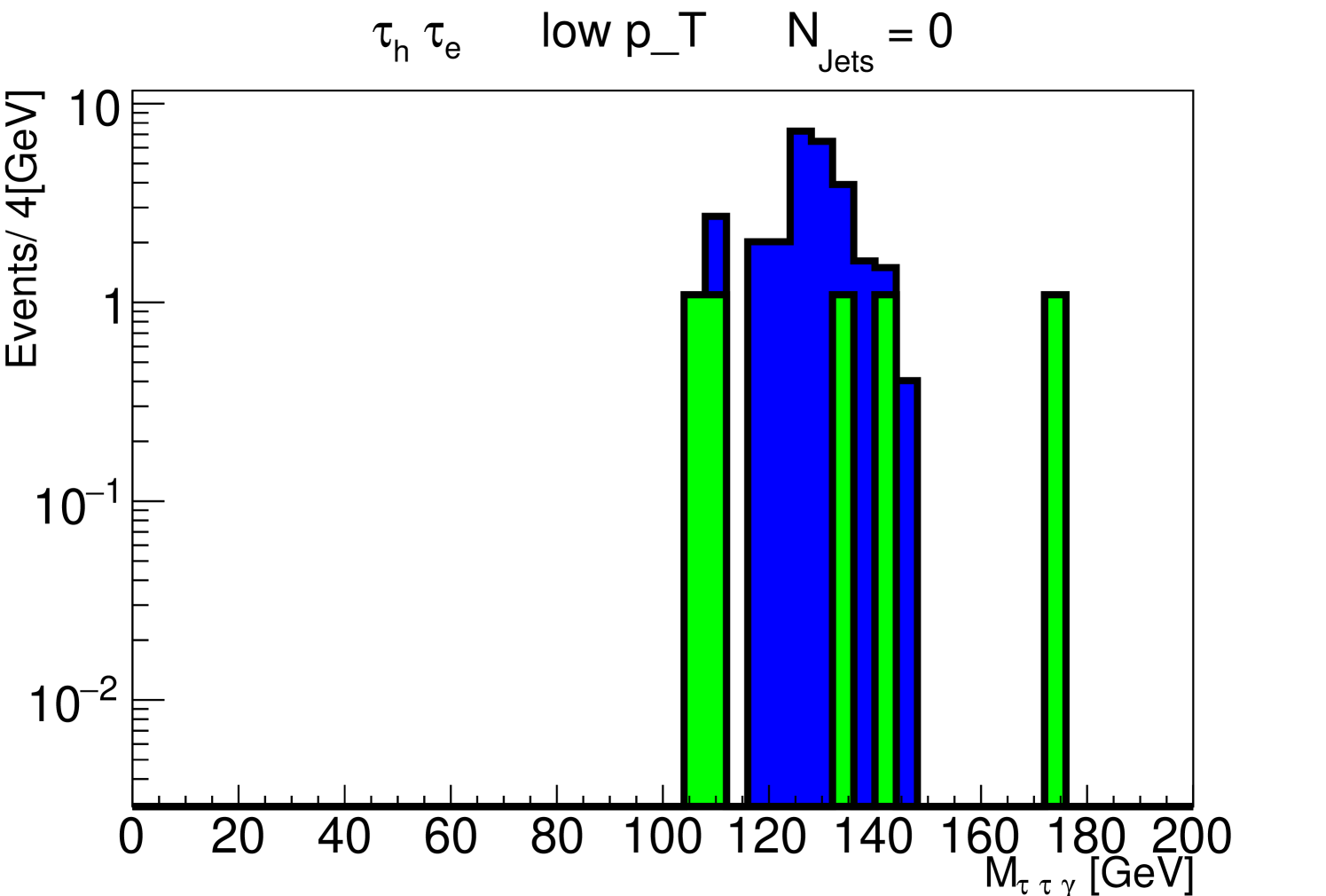
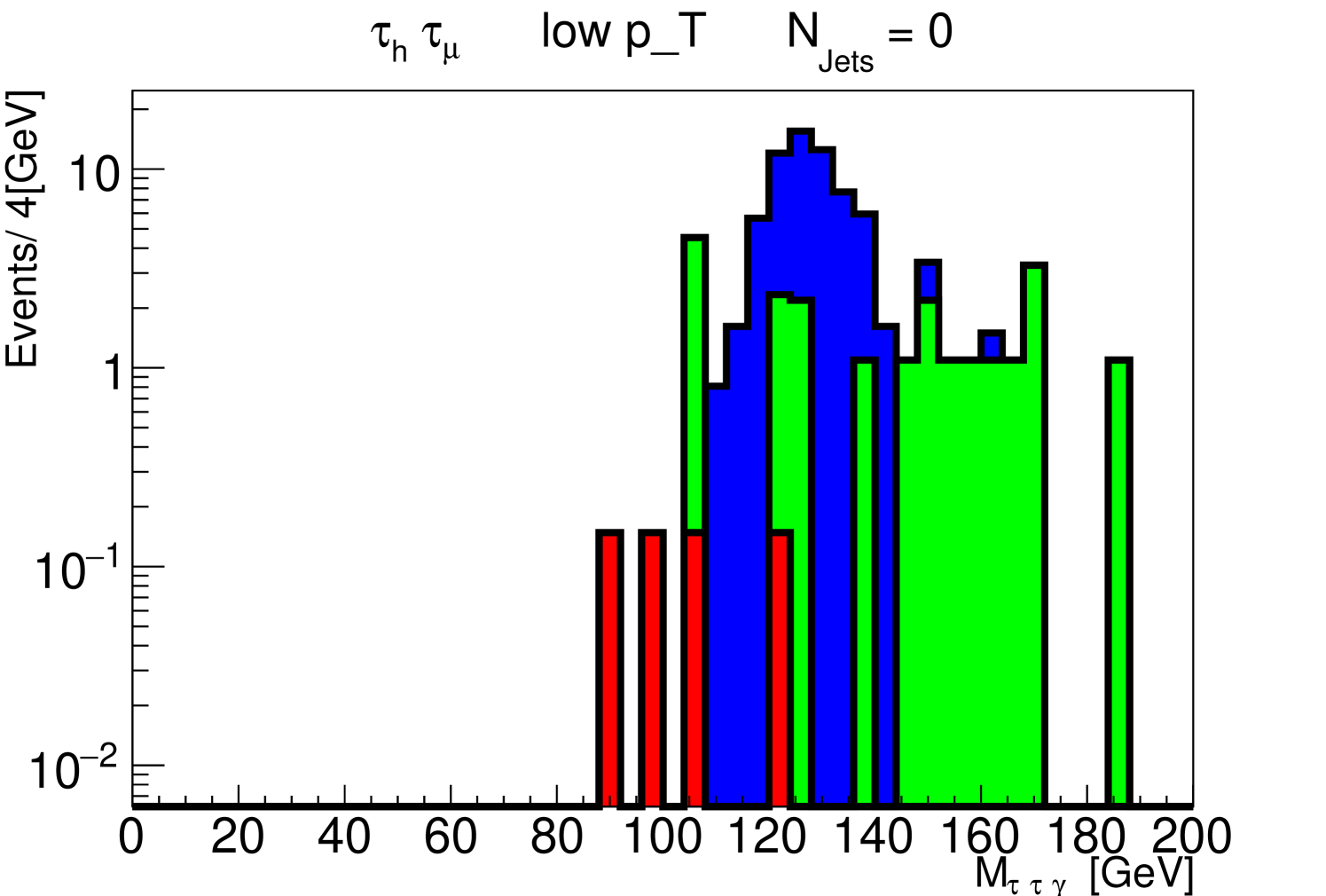
To estimate the eventual sensitivity of the high luminosity LHC to new physics in the tau magnetic dipole, we write the amplitude for the signal process as
| (9) |
with the dependence explicitly factored out. The yield of signal events (for ) after cuts is:
| (10) |
The sizes of these three coefficients, after all analysis cuts, are shown in Table 2. We present as a function of for both signs of in Fig. 3, including the and channels, and also the combined number of events in both signal categories, .
| Signal Region | |||
|---|---|---|---|
| GeV2 | GeV4 | ||
| GeV2 | GeV4 |
Under the Assumption that no signal is observed, and the mean number of background events, 6.7, is obtained, one may place a lower limit on the new physics scale . The CL bound on in that case would be given by:
| (11) |
which translates into a projected limit on the anomalous moment of
| (12) |
approximately a factor of two improvement on for or for .
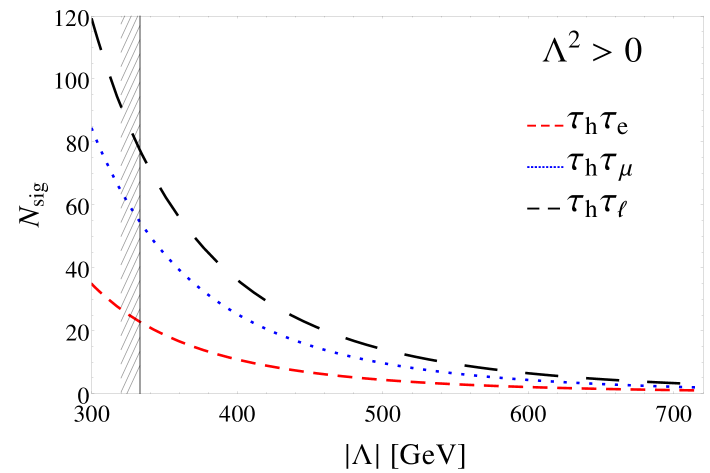
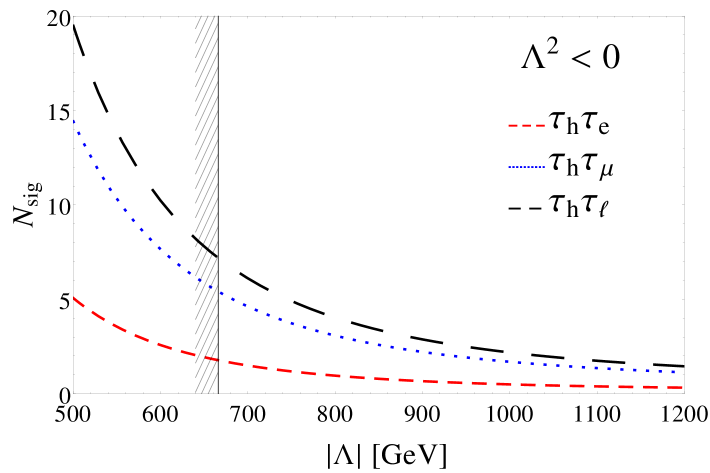
V Conclusions and Outlook
As measurements of the Higgs boson become more sophisticated, we move into a regime where it becomes a tool in its own right to search for new physics. In particular, low energy observables involving a chiral flip of the SM fermions necessarily invoke electroweak symmetry-breaking, and thus imply a modification of the properties of the Higgs. In this work, we have examined the possibility that one can place bounds on the electromagnetic moments of the by searching for the rare decay of the Higgs into . Given the longstanding discrepancy between measurements of the muon’s magnetic moment and SM predictions, one could hope that might also be a likely target for which to search for manifestations of new physics.
We find the promising result that the LHC with a large data set should be sensitive to modifications of the magnetic dipole moment beyond the current bounds extracted from LEP – by about a factor of two on the new physics scale if . Given these promising results, it would be worthwhile to follow up with a study based on more realistic detector simulations and including effects beyond our ability to reliably simulate, such as pile-up. We hope that our study will motivate the experimental collaborations to carry out this effort.
Another interesting direction for the future would be to study the prospects at a future collider such as the ILC or a future circular collider Ozguven:2016rst . While the rate for production at such colliders is considerably smaller than the inclusive Higgs production at the LHC, new physics saturating the LEP bound nonetheless allows for a handful of events, and the prospects depend sensitively on the ability to efficiently reconstruct the signal events and reject backgrounds.
The discovery of the Higgs is a triumph of run I of the LHC. We look forward to run II and beyond to follow up with precision measurements that reveal the deep secrets that reflect its character.
Acknowledgments
The authors are supported in part by National Science Foundation grants PHY-1316792 and PHY-1620638. We thank Enrique Kajomovitz, Olivier Mattelaer, Andrew Nelson, Yoram Rozen, Yael Shadmi, Yotam Soreq, Philip Tanedo and Scott Thomas for useful discussions; Christian Veelken for his assistance with setting up the tau reconstruction platform and for useful discussions; and David Cohen for assistance in grid-based computing. IG and TMPT are grateful to the Mainz Institute for Theoretical Physics for its hospitality and its partial support during the completion of this work.
References
- (1) ATLAS Collaboration, G. Aad et al., “Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC,” Phys. Lett. B716 (2012) 1–29, arXiv:1207.7214 [hep-ex].
- (2) CMS Collaboration, S. Chatrchyan et al., “Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC,” Phys. Lett. B716 (2012) 30–61, arXiv:1207.7235 [hep-ex].
- (3) D. E. Morrissey, T. Plehn, and T. M. P. Tait, “Physics searches at the LHC,” Phys. Rept. 515 (2012) 1–113, arXiv:0912.3259 [hep-ph].
- (4) S. Chang, R. Dermisek, J. F. Gunion, and N. Weiner, “Nonstandard Higgs Boson Decays,” Ann. Rev. Nucl. Part. Sci. 58 (2008) 75–98, arXiv:0801.4554 [hep-ph].
- (5) D. Curtin et al., “Exotic decays of the 125 GeV Higgs boson,” Phys. Rev. D90 (2014) no. 7, 075004, arXiv:1312.4992 [hep-ph].
- (6) H. Bélusca-Maïto and A. Falkowski, “On the exotic Higgs decays in effective field theory,” arXiv:1602.02645 [hep-ph].
- (7) Muon g-2 Collaboration, G. W. Bennett et al., “Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL,” Phys. Rev. D73 (2006) 072003, arXiv:hep-ex/0602035 [hep-ex].
- (8) D. J. Silverman and G. L. Shaw, “Limits on the Composite Structure of the Tau Lepton and Quarks From Anomalous Magnetic Moment Measurements in Annihilation,” Phys. Rev. D27 (1983) 1196.
- (9) L. D. Almeida, A. A. Natale, S. F. Novaes, and O. J. P. Eboli, “Nonstandard gamma gamma lepton+ lepton- processes in relativistic heavy ion collisions,” Phys. Rev. D44 (1991) 118–126.
- (10) F. del Aguila, F. Cornet, and J. I. Illana, “The Possibility of using a large heavy ion collider for measuring the electromagnetic properties of the tau-lepton,” Phys. Lett. B271 (1991) 256–260.
- (11) M. A. Samuel and G. Li, “Measuring the magnetic moment of the tau lepton at the Fermilab tevatron, the, SSC and the LHC,” Int. J. Theor. Phys. 33 (1994) 1471–1478.
- (12) A. Aeppli and A. Soni, “Analysis of the tau dipole moment via e+ e- and gamma gamma reactions,” Phys. Rev. D46 (1992) 315–321.
- (13) R. Escribano and E. Masso, “New bounds on the magnetic and electric moments of the tau lepton,” Phys. Lett. B301 (1993) 419–422.
- (14) R. Escribano and E. Masso, “Improved bounds on the electromagnetic dipole moments of the lepton,” Phys. Lett. B395 (1997) 369–372, arXiv:hep-ph/9609423 [hep-ph].
- (15) G. A. Gonzalez-Sprinberg, A. Santamaria, and J. Vidal, “Model independent bounds on the tau lepton electromagnetic and weak magnetic moments,” Nucl. Phys. B582 (2000) 3–18, arXiv:hep-ph/0002203 [hep-ph].
- (16) J. Bernabeu, G. A. Gonzalez-Sprinberg, J. Papavassiliou, and J. Vidal, “Tau anomalous magnetic moment form-factor at super B/flavor factories,” Nucl. Phys. B790 (2008) 160–174, arXiv:0707.2496 [hep-ph].
- (17) J. Bernabeu, G. A. Gonzalez-Sprinberg, and J. Vidal, “Tau spin correlations and the anomalous magnetic moment,” JHEP 01 (2009) 062, arXiv:0807.2366 [hep-ph].
- (18) S. Atag and A. A. Billur, “Possibility of Determining Lepton Electromagnetic Moments in Process at the CERN-LHC,” JHEP 11 (2010) 060, arXiv:1005.2841 [hep-ph].
- (19) J. Peressutti and O. A. Sampayo, “ anomalous magnetic moment in colliders,” Phys. Rev. D86 (2012) 035016.
- (20) A. Hayreter and G. Valencia, “Constraining -lepton dipole moments and gluon couplings at the LHC,” Phys. Rev. D88 (2013) no. 1, 013015, arXiv:1305.6833 [hep-ph]. [Erratum: Phys. Rev.D91,no.9,099902(2015)].
- (21) M. Fael, L. Mercolli, and M. Passera, “Towards a determination of the tau lepton dipole moments,” Nucl. Phys. Proc. Suppl. 253-255 (2014) 103–106, arXiv:1301.5302 [hep-ph].
- (22) A. Hayreter and G. Valencia, “Spin correlations and new physics in τ-lepton decays at the LHC,” JHEP 07 (2015) 174, arXiv:1505.02176 [hep-ph].
- (23) S. Eidelman, D. Epifanov, M. Fael, L. Mercolli, and M. Passera, “ dipole moments via radiative leptonic decays,” JHEP 03 (2016) 140, arXiv:1601.07987 [hep-ph].
- (24) DELPHI Collaboration, J. Abdallah et al., “Study of tau-pair production in photon-photon collisions at LEP and limits on the anomalous electromagnetic moments of the tau lepton,” Eur. Phys. J. C35 (2004) 159–170, arXiv:hep-ex/0406010 [hep-ex].
- (25) ALEPH Collaboration, A. Heister et al., “Search for anomalous weak dipole moments of the tau lepton,” Eur. Phys. J. C30 (2003) 291–304, arXiv:hep-ex/0209066 [hep-ex].
- (26) J.-Q. Zhang, X.-C. Song, W.-J. Huo, and T.-F. Feng, “Anomalous magnetic and electric moments of tau and lepton flavor mixing matrix in effective Lagrangian approach,” Submitted to: Commun. Theor. Phys. (2002) , arXiv:hep-ph/0205309 [hep-ph].
- (27) G. R. Bower, T. Pierzchala, Z. Was, and M. Worek, “Measuring the Higgs boson’s parity using tau rho nu,” Phys. Lett. B543 (2002) 227–234, arXiv:hep-ph/0204292 [hep-ph].
- (28) K. Desch, Z. Was, and M. Worek, “Measuring the Higgs boson parity at a linear collider using the tau impact parameter and tau rho nu decay,” Eur. Phys. J. C29 (2003) 491–496, arXiv:hep-ph/0302046 [hep-ph].
- (29) R. Harnik, A. Martin, T. Okui, R. Primulando, and F. Yu, “Measuring CP violation in at colliders,” Phys. Rev. D88 (2013) no. 7, 076009, arXiv:1308.1094 [hep-ph].
- (30) S. Berge, W. Bernreuther, and J. Ziethe, “Determining the CP parity of Higgs bosons at the LHC in their tau decay channels,” Phys. Rev. Lett. 100 (2008) 171605, arXiv:0801.2297 [hep-ph].
- (31) S. Berge and W. Bernreuther, “Determining the CP parity of Higgs bosons at the LHC in the tau to 1-prong decay channels,” Phys. Lett. B671 (2009) 470–476, arXiv:0812.1910 [hep-ph].
- (32) S. Berge, W. Bernreuther, B. Niepelt, and H. Spiesberger, “How to pin down the CP quantum numbers of a Higgs boson in its tau decays at the LHC,” Phys. Rev. D84 (2011) 116003, arXiv:1108.0670 [hep-ph].
- (33) S. Berge, W. Bernreuther, and H. Spiesberger, “Higgs CP properties using the decay modes at the ILC,” Phys. Lett. B727 (2013) 488–495, arXiv:1308.2674 [hep-ph].
- (34) K. Hagiwara, K. Ma, and S. Mori, “Probing CP violation in at the LHC,” arXiv:1609.00943 [hep-ph].
- (35) Y. Chen, A. Falkowski, I. Low, and R. Vega-Morales, “New Observables for CP Violation in Higgs Decays,” Phys. Rev. D90 (2014) no. 11, 113006, arXiv:1405.6723 [hep-ph].
- (36) CMS Collaboration, S. Chatrchyan et al., “Evidence for the 125 GeV Higgs boson decaying to a pair of leptons,” JHEP 05 (2014) 104, arXiv:1401.5041 [hep-ex].
- (37) ATLAS Collaboration, G. Aad et al., “Search for the Standard Model Higgs Boson Produced in Association with a Vector Boson and Decaying into a Tau Pair in Collisions at TeV with the ATLAS Detector,” arXiv:1511.08352 [hep-ex].
- (38) CMS Collaboration, V. Khachatryan et al., “Search for supersymmetry in events with a photon, a lepton, and missing transverse momentum in pp collisions at 8 TeV,” Phys. Lett. B757 (2016) 6–31, arXiv:1508.01218 [hep-ex].
- (39) CMS Collaboration, C. Collaboration, “Search for additional neutral Higgs bosons decaying to a pair of tau leptons in collisions at = 7 and 8 TeV,”.
- (40) J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, et al., “The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations,” JHEP 1407 (2014) 079, arXiv:1405.0301 [hep-ph].
- (41) T. Sjostrand, S. Mrenna, and P. Z. Skands, “PYTHIA 6.4 Physics and Manual,” JHEP 0605 (2006) 026, arXiv:hep-ph/0603175 [hep-ph].
- (42) J. Alwall, “Pythia-Pgs Package,” https://cp3.irmp.ucl.ac.be/projects/madgraph/wiki/PythiaInterface .
- (43) S. Catani, F. Krauss, R. Kuhn, and B. R. Webber, “QCD matrix elements + parton showers,” JHEP 11 (2001) 063, arXiv:hep-ph/0109231 [hep-ph].
- (44) F. Krauss, “Matrix elements and parton showers in hadronic interactions,” JHEP 08 (2002) 015, arXiv:hep-ph/0205283 [hep-ph].
- (45) J. Alwall et al., “Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions,” Eur. Phys. J. C53 (2008) 473–500, arXiv:0706.2569 [hep-ph].
- (46) K. Hagiwara, T. Li, K. Mawatari, and J. Nakamura, “TauDecay: a library to simulate polarized tau decays via FeynRules and MadGraph5,” Eur. Phys. J. C73 (2013) 2489, arXiv:1212.6247 [hep-ph].
- (47) C. Degrande, C. Duhr, B. Fuks, D. Grellscheid, O. Mattelaer, and T. Reiter, “UFO - The Universal FeynRules Output,” Comput. Phys. Commun. 183 (2012) 1201–1214, arXiv:1108.2040 [hep-ph].
- (48) A. Alloul, N. D. Christensen, C. Degrande, C. Duhr, and B. Fuks, “FeynRules 2.0 - A complete toolbox for tree-level phenomenology,” Comput. Phys. Commun. 185 (2014) 2250–2300, arXiv:1310.1921 [hep-ph].
- (49) A. Alloul, B. Fuks, and V. Sanz, “Phenomenology of the Higgs Effective Lagrangian via FEYNRULES,” JHEP 04 (2014) 110, arXiv:1310.5150 [hep-ph].
- (50) A. Gehrmann-De Ridder, T. Gehrmann, E. W. N. Glover, A. Huss, and T. A. Morgan, “Precise QCD predictions for the production of a Z boson in association with a hadronic jet,” Phys. Rev. Lett. 117 (2016) no. 2, 022001, arXiv:1507.02850 [hep-ph].
- (51) DELPHES 3 Collaboration, J. de Favereau et al., “DELPHES 3, A modular framework for fast simulation of a generic collider experiment,” JHEP 1402 (2014) 057, arXiv:1307.6346 [hep-ex].
- (52) M. Cacciari, G. P. Salam, and G. Soyez, “The Anti-k(t) jet clustering algorithm,” JHEP 0804 (2008) 063, arXiv:0802.1189 [hep-ph].
- (53) M. Cacciari, G. P. Salam, and G. Soyez, “FastJet User Manual,” Eur. Phys. J. C72 (2012) 1896, arXiv:1111.6097 [hep-ph].
- (54) S. Frixione, “Isolated photons in perturbative QCD,” Phys. Lett. B429 (1998) 369–374, arXiv:hep-ph/9801442 [hep-ph].
- (55) L. Bianchini, J. Conway, E. K. Friis, and C. Veelken, “Reconstruction of the Higgs mass in Events by Dynamical Likelihood techniques,” J. Phys. Conf. Ser. 513 (2014) 022035.
- (56) A. Elagin, P. Murat, A. Pranko, and A. Safonov, “A New Mass Reconstruction Technique for Resonances Decaying to di-tau,” Nucl. Instrum. Meth. A654 (2011) 481–489, arXiv:1012.4686 [hep-ex].
- (57) C. Veelken, “SVFitStandAlone,” https://github.com/veelken/SVfit_standalone .
- (58) R. K. Ellis, I. Hinchliffe, M. Soldate, and J. J. van der Bij, “Higgs Decay to tau+ tau-: A Possible Signature of Intermediate Mass Higgs Bosons at the SSC,” Nucl. Phys. B297 (1988) 221–243.
- (59) Y. Ozguven, S. C. İnan, A. A. Billur, M. Köksal, and M. K. Bahar, “Search for the anomalous electromagnetic moments of the tau lepton through electron-photon scattering at the CLIC,” arXiv:1609.08348 [hep-ph].