Hierarchical Spherical CNNs with Lifting-based Adaptive Wavelets for Pooling and Unpooling
Abstract
Pooling and unpooling are two essential operations in constructing hierarchical spherical convolutional neural networks (HS-CNNs) for comprehensive feature learning in the spherical domain. Most existing models employ downsampling-based pooling, which will inevitably incur information loss and cannot adapt to different spherical signals (with different spectra) and tasks (dependent on different frequency components). Besides, the preserved information after pooling cannot be well restored by the subsequent unpooling to characterize the desirable features for a task. In this paper, we propose a novel framework of HS-CNNs with a lifting structure to learn adaptive spherical wavelets for pooling and unpooling, dubbed LiftHS-CNN, which ensures a more efficient hierarchical feature learning for both image- and pixel-level tasks. Specifically, adaptive spherical wavelets are learned with a lifting structure that consists of trainable lifting operators (i.e., update and predict operators). With this learnable lifting structure, we can adaptively partition a signal into two sub-bands containing low- and high-frequency components, respectively, and thus generate a better down-scaled representation for pooling by preserving more information in the low-frequency sub-band. The update and predict operators are parameterized with graph-based attention to jointly consider the signal’s characteristics and the underlying geometries. We further show that particular properties (i.e., spatial locality and vanishing moments) are promised by the learned wavelets, ensuring the spatial-frequency localization for better exploiting the signal’s correlation in both spatial and frequency domains. We then propose an unpooling operation that is invertible to the lifting-based pooling, where an inverse wavelet transform is performed by using the learned lifting operators to restore an up-scaled representation. Extensive empirical evaluations on various spherical domain tasks (e.g., spherical image reconstruction, classification, and semantic segmentation) validate the superiority of the proposed LiftHS-CNN.
1 Introduction
Recently, there is an ever-increasing interest in developing spherical CNNs boomsma2017spherical ; cobb2020efficient ; cohen2019gauge ; cohen2018spherical ; coors2018spherenet ; defferrard2020deepsphere ; esteves2018learning ; esteves2020spin ; jiang2019spherical ; kondor2018clebsch ; mcewen2021scattering ; perraudin2019deepsphere , which generalize classical CNNs to processing ubiquitous spherical data. Examples include omnidirectional images and videos in virtual reality coors2018spherenet , planetary data in climate science racah2017extremeweather , observations of the universe and LIDAR scans geiger2013vision ; perraudin2019deepsphere , molecular structures in chemistry boomsma2017spherical . Spherical CNNs can extract features with convolutions defined in a spherical harmonic space cobb2020efficient ; cohen2018spherical ; esteves2018learning ; esteves2020spin ; kondor2018clebsch or discrete space boomsma2017spherical ; cohen2019gauge ; defferrard2020deepsphere ; perraudin2019deepsphere , achieving striking performance in many tasks such as classification and semantic segmentation for spherical images. Nevertheless, most of the effort to date has been devoted to designing spherical convolutions that extract features at a single scale, while learning of hierarchical features in the spherical domain is not well explored yet. To address this, hierarchical spherical CNNs (HS-CNNs) are thus demanded for comprehensive feature learning.
In classical CNNs, pooling and unpooling operations are indispensable for an efficient learning of the hierarchical features, which unfortunately are mostly overlooked in HS-CNNs. Mimicking classical CNNs, and with the aid of the naturally hierarchical structures of some sphere discretization schemes (e.g., icosahedral baumgardner1985icosahedral , equiangular driscoll1994computing , and healpix gorski2005healpix samplings), pooling in HS-CNNs defferrard2020deepsphere ; jiang2019spherical ; perraudin2019deepsphere ; shen2021pdo is typically performed through a downsampling (or mean, max) operation within a local region. However, inspired by the notions of signal processing such as sampling theorem and filtering, simply downsampling (or taking the average or maximum of) a representation will inevitably result in information loss saeedan2018detail ; williams2018wavelet , since these operations are rigid without considering the spatial-frequency characteristics of original signals. For example, the sampling theorem suggests that the information can be well preserved after downsampling only if the signals are sufficiently smooth within a limited band. When this is not the case, important information may be lost, which will greatly hamper the information flow across a deep model. Furthermore, the notion of important information is also varying with signals (with different spectra) or tasks (dependent on different frequency components). Therefore, a desirable pooling should have the capacity to adaptively produce a down-scaled representation that maintains the important information with respect to the data and tasks at hand. On the opposite, existing HS-CNNs widely adopt the padding-based unpooling by trivially inserting zeros for an up-scaled representation defferrard2020deepsphere ; jiang2019spherical ; perraudin2019deepsphere ; shen2021pdo . This, however, cannot well restore the information preserved after pooling, which will inevitably introduce annoying artifacts and discontinuities, and thus degrade the overall performance of HS-CNNs.
To alleviate the information loss between representations of different scales, we resort to the lifting structure, a widely-adopted technique for multi-resolution analysis in signal processing, to learn adaptive spherical wavelets for constructing advanced pooling and unpooling operations. The spatial-frequency localization of the wavelets enables a better exploitation of the signal’s characteristics in both spatial and frequency domains. In particular, the spatial locality is brought by the local compact support, while the smoothness and vanishing moments together contribute to its frequency locality. It is worth mentioning that constructing wavelets on the sphere is a nontrivial task, since the sphere in essence is a non-Euclidean domain schroder1995spherical , let alone the adaptive ones. The lifting structure sweldens1996lifting ; sweldens1998lifting provides us with an efficient way to construct wavelets adaptive to arbitrary domains, while its spatial implementation ensures an easy control of some desirable properties of the resulting wavelets, such as the spatial locality and vanishing moments. Moreover, an inverse wavelet transform can be easily performed with the backward lifting, where invertibility of the resulting wavelets is theoretically guaranteed. Besides, adaptivity can also be incorporated to adapt wavelets to various data and tasks.
We are thus motivated to propose a novel framework of HS-CNNs, dubbed LiftHS-CNN, with a lifting structure to learn adaptive spherical wavelets for pooling and unpooling with reduced information loss, which is thus able to ensure a more efficient learning of hierarchical features for both image- and pixel-level tasks in the spherical domain. Specifically, adaptive spherical wavelets are learned with a lifting structure that consists of trainable lifting operators (i.e., update and predict operators) to adaptively partition a signal into two sub-bands containing low- and high-frequency components. The low-frequency sub-band is encouraged to preserve more information by minimizing the energy of the high-frequency sub-band, which is kept after pooling and helps generate a better down-scaled representation. The update and predict operators are parameterized with graph-based attention to jointly consider the signal’s characteristics and the underlying geometries. We further show that particular properties (i.e., spatial locality and primary/dual first-order vanishing moment in our case) are promised by the learned wavelets, which ensure the spatial-frequency localization for better exploiting the signal’s characteristics. We then propose an unpooling operation that is invertible to the lifting-based pooling, by leveraging an inverse wavelet transform with the learned lifting operators to recover an up-scaled representation. The proposed lifting-based pooling and unpooling are compatible with most existing spherical convolutions to form an HS-CNN, which can be optimized in an end-to-end manner. To evaluate the superiority of the proposed model, we perform extensive experiments on a wide range of spherical datasets (i.e., SCIFAR10, SMNIST, SModelNet40, and Standford 2D3DS) for spherical image reconstruction, classification, and semantic segmentation. Experimental results validate the effectiveness and efficiency of the proposed LiftHS-CNN. Our contributions can be summarized as follows:
-
•
We leverage lifting structure to learn adaptive spherical wavelets for constructing advanced pooling and unpooling operations. Based on them, we further introduce a novel framework of LiftHS-CNNs for a more efficient learning of hierarchical features in the spherical domain.
-
•
We implement the lifting operators (i.e., update and predict operators) with graph-based attention, to jointly consider the characteristics of local signals and the underlying geometries.
-
•
We show that desirable properties (i.e., spatial locality, and vanishing moments) are promised by the learned spherical wavelets, which ensure the spatial-frequency localization.
2 Related Work
Spherical CNNs. Existing models can be categorized into two groups, based on the spaces (harmonic or discrete grid spaces) in which the spherical convolution is defined. cohen2018spherical ; esteves2018learning ; esteves2020spin ; kondor2018clebsch define spherical convolutions via spherical harmonic transforms. Though preserving excellent rotational equivariance, these models are typically costly and flat, without the capacity to learn hierarchical features. In contrast, cohen2019gauge ; defferrard2020deepsphere ; jiang2019spherical ; khasanova2017graph ; perraudin2019deepsphere ; shen2021pdo ; yang2020rotation ; zhang2019orientation define convolutions on a discrete grid space (e.g., Healpix and icosahedral grids), striking a trade-off between efficiency and rotational equivariance. For example, jiang2019spherical ; shen2021pdo adopt parameterized differential operators for feature extraction, while defferrard2020deepsphere ; khasanova2017graph ; perraudin2019deepsphere ; yang2020rotation represent the sphere with a weighted graph and process it with graph CNNs. The natural hierarchy of discrete grids enables hierarchical feature learning, requiring more efficient pooling and unpooling.
Hierarchical CNNs. Pooling and unpooling are ubiquitous in classical CNNs for hierarchical feature learning. Unpooling is typically performed by padding zeros into an up-scaled representation, while various pooling operations are studied. Mean lecun1989handwritten and max pooling jarrett2009best are the most widely-used techniques, which, however, ignore the signal’s spatial-frequency characteristics, causing information loss and lack of adaptivity. Mixed pooling lee2016generalizing ; yu2014mixed and pooling estrach2014signal ; gulcehre2014learned are then proposed to improve them. To preserve more structured details, detail-preserved pooling saeedan2018detail is then introduced. For a more compact representation with less artifacts, wavelet-based pooling operations williams2018wavelet ; wolter2021adaptive are proposed. However, the capacity of pooling williams2018wavelet based on fixed Haar wavelets is limited, while the parameterized wavelets wolter2021adaptive are hard to optimize without a theoretical guarantee of some desirable properties, such as spatial locality, vanishing moments and invertibility. The most relevant work to ours is LiftPool zhao2021liftpool , which leverages the invertibility of lifting scheme to improve pooling and unpooling in the 2D Euclidean domain. However, the proposed nonlinear neural network-based lifting operators with the changed down-scaled input inevitably break the invertibility, while some desirable properties of the learned transforms are unfortunately not guaranteed and studied. Furthermore, its 2D separable lifting scheme cannot be easily applied to the spherical domain, as directions are not well defined on the sphere. In contrast, we leverage the lifting structure to learn adaptive spherical wavelets whose desirable properties are theoretically guaranteed. The learned operators can also be directly reused for inverse wavelet transform in the unpooling process, thus maintaining the invertibility.
Lifting scheme. The lifting scheme sweldens1996lifting ; sweldens1998lifting is a general signal processing technique for constructing wavelets for both regular and irregular domains. For instance, it is widely used in generating adaptive wavelets for perfect-reconstruction filter banks piella2002adaptive , image coding claypoole2003nonlinear , and denosing wu2004adaptive . Besides, it is also prevalent in constructing wavelets in irregular domains, such as spheres schroder1995spherical , trees shen2008optimized , and graphs narang2009lifting . Recently, there is a surge of interest in integrating the lifting scheme with deep learning li2021reversible ; rodriguez2020deep ; rustamov2013wavelets ; xu2022graph to improve its interpretability and model capacity. To the best of our knowledge, constructing adaptive wavelets on the sphere with lifting has nevertheless not been explored yet, which is non-trivial since both the signal’s characteristics and the non-Euclidean geometry should be considered. We resort to graph-based lifting to learn adaptive spherical wavelets, where lifting operators are implemented with graph-based attention to jointly consider both of them.
3 Lifting-based Hierarchical Spherical CNNs
In HS-CNNs, hierarchical features are typically extracted by alternating the convolution and pooling operations, while unpooling is further needed for the pixel-level tasks, such as reconstruction. To promote the information flow, it is critical for pooling to produce a down-scaled representation that maintains the most important information, and for unpooling to restore the preserved information to an up-scaled representation that characterizes the desirable features for a task. This goal is arguably difficult to achieve with the standard pooling (e.g., downsampling, mean or max) and unpooling (e.g., padding). In this section, we first describe the classic lifting structure with handcrafted spherical wavelets, and then introduce the proposed graph attention-based lifting for adaptive spherical wavelets. We finally construct the lifting-based pooling and unpooling, as well as the proposed LiftHS-CNN.
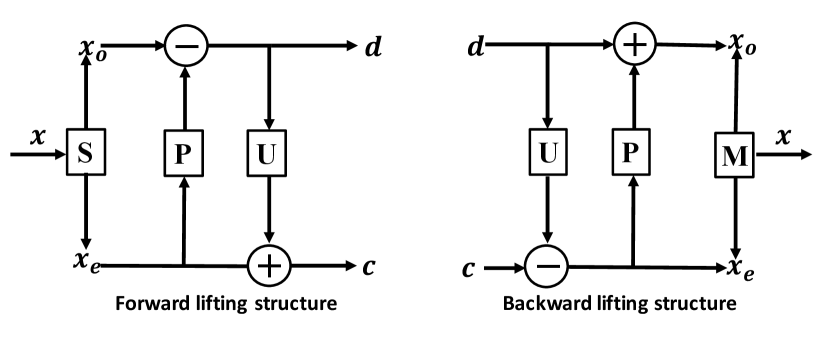
3.1 Lifting Scheme for Handcrafted Spherical Wavelets
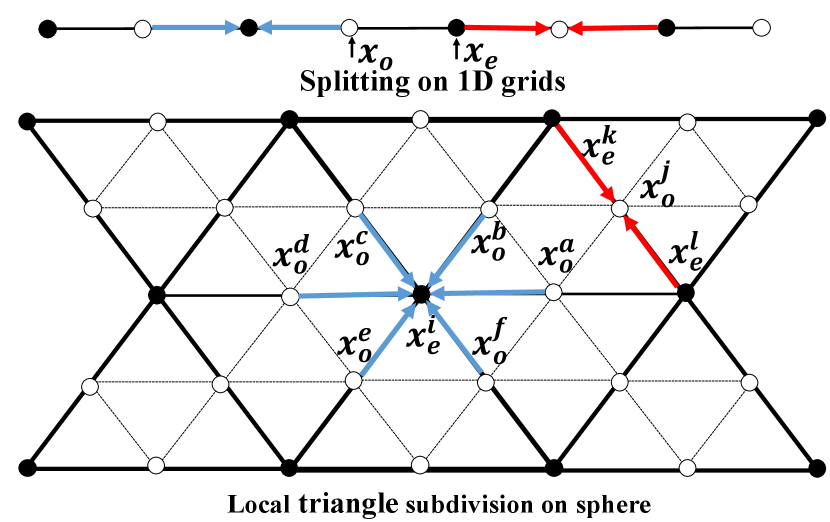
In the lifting scheme as shown in Fig. 1(a), the forward lifting structure consists of three elementary operations, i.e., splitting, prediction and update. Given a single-channel 1D signal with an even number , as shown in Fig. 1(b), it is first split into two complementary partitions, i.e., the odd and the even . For each odd component indexed by , we perform the prediction operation based on its neighboring two even components, which subtracts with the estimation to generate the residual , where is the predict weight. A down-scaled approximation of is then obtained as , by updating each even component with the residual , where is the update weight. A critically-sampled wavelet transform is implicitly and efficiently performed with this structure, where in frequency domain the signal’s sub-band splitting and downsampling are simultaneously realized, i.e., and carry the high- and low-frequency components, respectively. The resulting wavelet and its properties (e.g., spatial locality, vanishing moments) are entirely controlled by the predict and update operators. The inverse wavelet transform can be performed with the backward lifting structure as shown in Fig. 1(a). It is worth noting that, ideally, the splitting should bipartite to make the odd and even partitions highly correlated. By doing so, the correlation between neighboring odd and even components can be further leveraged by the predict and update operators to attenuate while producing a more informative .
The lifting scheme has also been applied on the sphere for handcrafted spherical wavelets, based on the geodesic construction of spheres with triangle subdivision schroder1995spherical . To ease the presentation, we take a local triangle subdivision of the sphere in Fig. 1(b) as an example. The splitting is naturally done according to the hierarchical subdivision structure (though not ideally bipartite), to partition signals lying on the coarser-level grids as even and those on the remaining grids as odd. The prediction and update operations can then be extended to the sphere. For example, the even components and are used to predict , while the residuals of the six odd elements are adopted to update , as , . Consequently, spherical wavelets with desirable properties can be analytically constructed. For instance, wavelets with the first-order vanishing moment can be constructed by setting . This setting has properly considered the fact that the geodesic distance between and is equal, such that for constant input signals, the detail (wavelet) coefficients (i.e., ) will always be zeros. To obtain stable wavelets, a dual first-order vanishing moment is preferred rustamov2013wavelets , which requires the update operation to maintain the first-order moment (i.e., mean) of the input signal in its approximation . We denote the coarsest-level subdivision of the sphere as and the -th level subdivision as . If further defining the integral on as , the dual first-order vanishing moment then requires .
3.2 Graph Attention-based Lifting for Adaptive Spherical Wavelets
The above spherical wavelet transform is fixed with a handcrafted design of the predict weights, resulting in a rigid frequency sub-band splitting. Though considering geometry of the sphere (i.e., almost invariant everywhere with the triangle subdivision), it cannot adapt to the signal’s spatial-frequency characteristics and the frequency preference of a particular task. Thus, we propose in this subsection to learn adaptive spherical wavelets with graph-based attention, which can flexibly split a signal into two sub-bands by jointly considering both the characteristics of signals and tasks. The lifting operators are parameterized with graph attention, and can be optimized in an end-to-end manner. Moreover, specific designs are introduced to theoretically guarantee the spatial locality and the first-order vanishing moment of the resulting wavelets. These designs together ensure the spatial-frequency localization of the learned spherical wavelets for better exploiting the signal’s characteristics in both spatial and frequency domains. Note that, to better restore up-scaled representations, the update-first lifting scheme is usually adopted (e.g., in classical image coding claypoole2003nonlinear ; li2021reversible ; rustamov2013wavelets ), which is slightly different from Fig. 1(a) in that the order of prediction and update operations is switched. Namely, in the forward lifting, update is performed first and then the prediction, while in the backward lifting, prediction implements first and then the update. With this update-first lifting, more neighbors can be incorporated for the prediction (i.e., determining the wavelets), such that both the predict and update operators can be utilized in the backward lifting even without transmitting the detail coefficients, i.e., by setting .
Graph construction with subdivisions of sphere. We adopt the icosahedron-based subdivision of sphere for lifting, as shown in Fig. 2, since it is the most uniform and accurate discretization of a sphere baumgardner1985icosahedral ; jiang2019spherical , which preserves geometry of the sphere. Besides, the geodesic distance between any two discretized nodes is almost invariant everywhere, which eases learning of the lifting operators and enables weight sharing. Starting with the unit icosahedron, each face is recursively divided into four smaller triangles by putting three additional points at the mid-point of each edge. The newly generated points are then projected onto the unit sphere. By repeating this process, we obtain a sequence of subdivisions of the sphere, where the number of nodes of a level- subdivision is . This subdivision process provides a natural splitting scheme of even and odd partitions for lifting. Specifically, for , the nodes that belong to its precedent subdivision constitute the even partition, while the remaining nodes form the odd partition. At each level , a graph can be accordingly constructed to represent the geometric structure of sphere, and specify connectivity between nodes from the even and odd partitions. In Fig. 2, we adopt the inherent graph of each triangle subdivision due to its simplicity, which has an approximate bi-partition with the aforementioned splitting. This graph construction incorporates a limited number of neighbors in the predict and update operators, which provides good spatial locality, but limits the possible orders of vanishing moments of the learned wavelets. More advanced graph construction and splitting scheme will be left for future study.
Graph attention-based lifting. To further incorporate the signal’s characteristics, graph attention velivckovic2017graph is adopted to learn the predict and update operators for constructing adaptive spherical wavelets. These learned lifting operators can be directly used in the backward lifting structure to perform the inverse wavelet transform. As will be discussed in detail, by restricting the attention on local sub-graphs, the spatial locality of resulting wavelets is guaranteed, while the primary first-order vanishing moment is further ensured by constraining the learned lifting operators.
We denote as the adjacency matrices of the graphs constructed for , each of which consists of ones and zeros describing connectivity of the graph. For example, the nonzero elements in the -th row of indicate which nodes are connected with the -th node in a level- graph . We further denote the features (or representations) on as . After splitting, features of the even partition can be grouped as , while features of the remaining odd partition collected as . Here, denotes the number of nodes, is the feature dimensionality, and for simplicity. Hence, can be reorganized as
| (1) |
where and indicate the sub-graphs that connect nodes within the even and odd partitions, respectively, and and represent the sub-graphs connecting nodes between the even and odd partitions, respectively. Here, since is symmetric. The update-first lifting on can be written in matrix form as , and , where and are the approximation and detail coefficient matrices that carry the information of low- and high-frequency sub-bands, respectively, and matrices and are the learnable update and predict operators.
For two nodes and on a level- graph , we denote their features as . With graph attention, the attention weight that attends node to node is calculated as
| (2) |
where denotes concatenation, is a trainable weight matrix projecting input features to a hidden space for correlation exploitation, contains weights of a neural network that calculates attention scores with concatenated , and is an activation function. In practice, graph attention is performed efficiently with sparse matrix operations. Attention on the whole graph can be rewritten in a more compact matrix form, by masking the global attention matrix with 0-1 matrices and in Eq. (1). The predict and update operators are thus given by
| (3) |
where are learnable projection matrices, are learnable vectors, is the modified Kronecker product that replaces multiplication of two elements with summation, is the element-wise product between two matrices to perform local attention (spatial locality). Note that the learnable weights for predict and update operators can be further shared to reduce parameters. Post-processing is further performed on the learned predict and update operators, to guarantee that at least the first-order vanishing moment holds by the learned wavelets xu2022graph
| (4) |
where is performed row-wise. We detail other desired properties of wavelets in Section 4.

3.3 Lifting-based Hierarchical Spherical CNNs
With the learned and , pooling can be performed by implicitly performing wavelet transforms with the graph lifting, and by preserving the approximation coefficients that carry the information of low-frequency sub-band. To obtain , e.g., the entire process of pooling is
| (5) |
where is preserved as the down-scaled representation while is dropped. The energy of is thus penalized as a regularization term in the final loss function to maximize the information preserved in ((i.e., by pushing )). Besides, to make the learned wavelets have dual first-order vanishing moment with improved stability, the first-order moment (i.e., mean) of is forced to be retained with another regularization term (i.e., ).
For dense prediction tasks with the encoder-decoder architecture in Fig. 3, unpooling is required to restore up-scaled representations, i.e., . Here, we leverage the inverse wavelet transform for up-scaling, maintaining the perfect information recovery with respect to the preserved low-frequency sub-band after pooling (we detail this property in Section 4). Specifically, the learned predict and update operators and are reused in the backward lifting structure to perform the inverse wavelet transform for restoring from , leading to the unpooling
| (6) |
where and are merged to form the up-scaled representation for further processing. To train the model, the final loss function is: , where the is the task-related loss (e.g., cross entropy loss for classification, and mean square error loss for reconstruction), and and are the hyper-parameters for the two regularization terms.
4 Properties and Complexity
We discuss here some desirable properties of the adaptive spherical wavelets, the information recovery capability and computation complexity of the proposed lifting-based pooling and unpooling.
Spatial locality. The spatial locality of resulting wavelets is a direct result of our design, where update and prediction operations are performed with one-hop neighbors on the graph. Therefore, the wavelets realized with the lifting structure (i.e., Eq. (5)) consisting of a single update and prediction operations are localized within two-hops on the graph xu2022graph . More lifting steps (i.e., prediction and update) in a single forward lifting structure can be iterated down to progressively enlarge the spatial locality and possibly improve vanishing moments for more advanced spherical wavelets.
Primary/dual first-order vanishing moments. The primary first-order vanishing moment requires that for constant input signals, information can be perfectly preserved in the approximation coefficients, i.e., the detail coefficients are all zeros. With the proposed lifting scheme in Eq. (5), the resulting wavelets guarantee the primary first-order vanishing moment. Please see Appendix B.1 for the proof. The dual first-order vanishing moment is enforced by the last regularization term in the loss function, which constrains the first-order moment of input signals after the wavelet transforms.
Perfect recovery of preserved information after pooling. To better understand the information flow across the entire forward and backward lifting scheme, we interpret the lifting process in frequency domain, with low- and high-pass filtering, and downsampling and upsampling operations mallat1999wavelet as shown in the right half of Fig. 3. The forward lifting process realizes a critically-sampled wavelet transform by performing filtering and downsampling simultaneously, which can be disentangled into two processes. i) The input signal on level-2 graph is firstly filtered by low- and high-pass filters, and partitioned into a low-frequency sub-band and a high-frequency sub-band with the same resolution of . ii) Downsampling is then performed for both sub-band signals to obtain the down-scaled approximation and detail . Similarly, the backward lifting process that realizes an inverse wavelet transform can be disentangled as upsampling and sub-band signal merging processes. It can be proved that the information of is perfectly restored in through the proposed lifting-based unpooling with the inverse wavelet transform in backward lifting, except for being processed by the spherical convolutional layers in between (i.e., SConvBlock). In contrast, such information cannot be restored with the downsampling-based pooling and padding-based unpooling due to frequency aliasing and artifacts. Please see Appendix B.2 for the introduction of frequency domain interpretation of the entire lifting process, and the proof for the perfect recovery property.
Computation/parameter complexity. The lifting-based pooling may slightly bring additional computation and parameter complexity. To get from with pooling, graph attention in Eqs. (3) and (4) is performed along the edges of to obtain and . We denote the number of nonzero elements in as , where due to sparsity of the constructed graphs. The total computation complexity of the lifting structure with a single update and prediction operation in Eq. (5) is then , where is the dimensionality of hidden space in Eq. (2). This computation complexity is linearly with the number of nodes and edges in the graph, and thus scalable to high-resolution spherical signals. The additional parameter complexity is , so the proposed learnable lifting structure is also lightweight.
5 Experiments
We evaluate the proposed LiftHS-CNNs on various tasks on benchmark spherical datasets. Specifically, spherical image reconstruction on SCIFAR10 aims to directly verify the information preservation ability of LiftHS-CNN with lifting-based adaptive wavelet for pooling and unpooling, which can be directly reflected by reconstruction error. We then evaluate the model in spherical image classification on SMNIST and SModelNet40 datasets, to show that more task-related information can be preserved by the proposed lifting-based pooling for better discriminality. We further apply the model to spherical image segmentation on Standford 2D3DS dataset, to demonstrate the superiority in dense pixel-level prediction tasks. We end up with the ablation study to better explore the model. We briefly describe here for each experimental setting. Please see Appendix A for detailed description.
| Training | Test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Models | DownSamp | Mean | Max | LiftHS-CNN∗ | LiftHS-CNNH | LiftHS-CNN | DownSamp | Mean | Max | LiftHS-CNN∗ | LiftHS-CNNH | LiftHS-CNN |
| MSE | 0.0031 | 0.0038 | 0.0038 | 0.0028 | 0.0023 | 0.0019 | 0.0030 | 0.0036 | 0.0039 | 0.0025 | 0.0021 | 0.0017 |

5.1 Reconstruction of Spherical Images
Experimental setting. Following the common practice cohen2018spherical ; jiang2019spherical , we construct SCIFAR10 by projecting images in CIFAR10 krizhevsky2009learning onto a unit sphere. SCIFAR10 consists of 50000 training and 10000 test color images, which are more realistic than those in MNIST and thus more challenging to reconstruct. Input signals are sampled with level-4 icosahedron-based subdivision grids, and with 3 channels (i.e., RGB) each of which is normalized into . The encoder-decoder architecture with 4 pooling and unpooling operations is adopted (similar to the architecture in Fig. 3, but with the maximum level of graph being 4). For feature extraction at each level (i.e, SConvBlock in Fig. 3), we employ the same feature extractor built upon MeshConv as jiang2019spherical , due to its effectiveness and high efficiency. Hereafter, this feature extractor is adopted for feature extraction without further specification. To validate the superior information preservation ability of the proposed pooling and unpooling, we adopt the same backbone with different pooling (i.e., downsampling, mean, and max) and unpooling (i.e., padding). LiftHS-CNN is the proposed model, LiftHS-CNNH denotes the same model with handcrafted spherical wavelets, and LiftHS-CNN∗ denotes the model with the proposed pooling and padding-based unpooling. Mean square error (MSE) is used to measure reconstruction performance.
Results. The MSE loss on training and test datasets are reported in Table 1. Compared to standard pooling, the converged training MSE loss is reduced when incorporating the proposed lifting-based pooling (i.e., liftHS-CNN∗). Furthermore, the performance is largely improved with pooling and unpooling based on both handcrafted and the proposed adaptive wavelets (i.e., LiftHS-CNNH and LiftHS-CNN). These results imply that model capacity for information preservation is consistently improved by the proposed pooling and unpooling with adaptive spherical wavelets. The generalization ability is further shown by the reduced MSE loss on test dataset, which is consistent with the results on training set, showing that the proposed lifting structures can learn meaningful spherical wavelets that can be generalized to unseen images by preserving more information. We further show visualization results of different models in Fig. 4, and more visualization results are given in Appendix D.
5.2 Classification of Spherical Images
Experimental setting. Two datasets, SMNIST and SModelNet40, are employed to evaluate the proposed model. SMNIST is constructed from MNIST lecun1989handwritten in the same way as SCIFAR10. MNIST consists of 60000 training and 10000 test images presenting handwritten digits. Since SMNIST is relatively easy, we further construct SModelNet40 dataset by transforming geometries of the 3D CAD models in ModelNet40 wu20153d to spherical signals. The architecture shown in the upper-left of Fig. 3 is adopted for spherical signal classification. Specifically, for SMNIST, the model with 2 pooling operations from the maximum level of 4 to minimum level of 2 is adopted, while the model with 3 pooling operations from the maximum level of 5 to minimum level of 2 is leveraged for SModelNet40 as it is more challenging. We compare with prevalent spherical CNNs, including S2CNN cohen2018spherical , SphCNN esteves2018learning , FFS2CNN kondor2018clebsch , GaugeCNN cohen2019gauge , SWSCNN esteves2020spin , EGSCNN cobb2020efficient , eCNN shen2021pdo , Deepsphere defferrard2020deepsphere , and UGSCNN jiang2019spherical . Note that eCNN, Deepsphere, and UGSCNN are hierarchical models, and we adopt the same architecture as UGSCNN except for a lifting-based pooling.
| Models | S2CNN cohen2018spherical | FFS2CNN kondor2018clebsch | GaugeCNN cohen2019gauge | SWSCNN esteves2020spin | EGSCNN cobb2020efficient | eCNN shen2021pdo | Deepsphere defferrard2020deepsphere | UGSCNN jiang2019spherical | LiftHS-CNN |
|---|---|---|---|---|---|---|---|---|---|
| Acc (%) | 95.59 | 96.4 | 99.43 | 99.37 | 99.35 | 99.44 | 98.4 | 99.23 | 99.60 |
| Params | 58k | 286k | 182k | 58k | 58k | 73k | 75k | 62k | 66k |
| Models | SphCNN esteves2018learning | SWSCNN esteves2020spin | Deepsphere defferrard2020deepsphere | UGSCNN jiang2019spherical | LiftHS-CNN |
|---|---|---|---|---|---|
| Acc (%) | 89.3 | 90.1 | 89.47 | 90.5 | 91.37 |
| Models | Unet ronneberger2015u | GaugeCNN cohen2019gauge | HexRUNet zhang2019orientation | SWSCNN esteves2020spin ] | eCNN shen2021pdo | UGSCNN jiang2019spherical | LiftHS-CNN |
|---|---|---|---|---|---|---|---|
| mIou | 0.3587 | 0.3940 | 0.433 | 0.419 | 0.446 | 0.3829 | 0.4534 |
| mAcc (%) | 50.8 | 55.9 | 58.4 | 55.6 | 60.4 | 54.65 | 61.87 |
Results. Different from reconstruction tasks, image classification requires models to preserve information with a higher discriminality. Classification results on the two datasets are shown in Tables 3 and 3. We achieve state-of-the-art performance on both datasets, compared to other baselines. Notably, we outperform UGSCNN by 0.37% on SMNIST and 0.87% on SModelNet40. These results verify the superiority of the proposed pooling in adaptively preserving important information.
5.3 Semantic Segmentation of Spherical Images
Experimental setting. We adopt the challenging Stardford 2D3DS dataset armeni2017joint containing 1413 RGB-D equirectangular images with 13 semantic classes that are collected in 6 different areas. It is officially split into 3 folds for cross validation. We compare with prevalent models, including Unet ronneberger2015u , GaugeCNN cohen2019gauge , HexRUNet zhang2019orientation , SWSCNN esteves2020spin ], eCNN shen2021pdo , UGSCNN jiang2019spherical .
Results. The performance are shown in Table 4. We outperform all the models, and achieve state-of-the-art performance on this challenging dataset. Notably, compared with UGSCNN that employs a similar architecture but with downsampling-based pooling and padding-based unpooling, we achieve significant improvement on both metrics (e.g., 0.0705 and 7.22% on mIou and mAcc, respectively), indicating the effectiveness of adaptively preserving important information and restoring finer-level features by leveraging the correlation structures encoded with learned spherical wavelets.
5.4 Ablation Study
We further perform ablation study to verify the superiority of proposed LiftPool and LiftUnPool, compared with prevalent pooling (i.e., downsampling, mean and max) and unpooling (i.e., padding) operations, and handcrafted spherical wavelets constructed by fixed predict and update operators (i.e., LiftHS-CNNH). We adopt for each task the same backbone as UGSCNN, except for different pooling and unpooling operations. The superiority of LiftPool can be validated by results shown in Table 5, where we outperform all the standard pooling and the one with handcrafted spherical wavelets. Mean and max poolings are better than downsampling for classification tasks, probably because more information loss and aliasing are induced by downsampling. This implies the necessity of advanced pooling for HS-CNNs. The effectiveness of our framework with LiftPool and LiftUnPool is also clearly shown by results in Table 6, where we outperform all the other models by significant margins, demonstrating the advantage of our model in dense pixel-level prediction tasks. Notably, the model with handcrafted spherical wavelets outperforms other standard models, suggesting the importance of information recovery in pooling and unpooling. Please see Appendix C for more ablation study.
| SMNIST | SModelNet40 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Models | DownSamp | Mean | Max | LiftHS-CNNH | LiftHS-CNN | DownSamp | Mean | Max | LiftHS-CNNH | LiftHS-CNN |
| Acc (%) | 99.28 | 99.55 | 99.54 | 99.50 | 99.60 | 89.26 | 90.76 | 91.05 | 90.96 | 91.37 |
| Models | DownSamp | Mean | Max | LiftHS-CNNH | LiftHS-CNN |
|---|---|---|---|---|---|
| mIou | 0.3789 | 0.4110 | 0.4042 | 0.4217 | 0.4534 |
| mAcc (%) | 53.85 | 56.82 | 56.05 | 58.84 | 61.87 |
6 Conclusion
We proposed LiftHS-CNN to improve hierarchical feature learning in spherical domains. Lifting-based adaptive spherical wavelets were learned for pooling and unpooling to alleviate the information loss problem of existing models, where we adopted graph attention to learn the lifting operators. The spatial locality and vanishing moments of resulting wavelets were also studied. Experiments on various tasks validated the superiority of LiftHS-CNN. Our future study will include the optimal graph construction, and the applications to tasks such as spherical image denoising and super-resolution.
References
- [1] Iro Armeni, Sasha Sax, Amir R Zamir, and Silvio Savarese. Joint 2d-3d-semantic data for indoor scene understanding. arXiv preprint arXiv:1702.01105, 2017.
- [2] John R Baumgardner and Paul O Frederickson. Icosahedral discretization of the two-sphere. SIAM Journal on Numerical Analysis, 22(6):1107–1115, 1985.
- [3] Wouter Boomsma and Jes Frellsen. Spherical convolutions and their application in molecular modelling. Advances in neural information processing systems, 30, 2017.
- [4] Roger L Claypoole, Geoffrey M Davis, Wim Sweldens, and Richard G Baraniuk. Nonlinear wavelet transforms for image coding via lifting. IEEE Transactions on Image Processing, 12(12):1449–1459, 2003.
- [5] Oliver J Cobb, Christopher GR Wallis, Augustine N Mavor-Parker, Augustin Marignier, Matthew A Price, Mayeul d’Avezac, and Jason D McEwen. Efficient generalized spherical cnns. arXiv preprint arXiv:2010.11661, 2020.
- [6] Taco Cohen, Maurice Weiler, Berkay Kicanaoglu, and Max Welling. Gauge equivariant convolutional networks and the icosahedral cnn. In International conference on Machine learning, pages 1321–1330. PMLR, 2019.
- [7] Taco S Cohen, Mario Geiger, Jonas Köhler, and Max Welling. Spherical cnns. arXiv preprint arXiv:1801.10130, 2018.
- [8] Benjamin Coors, Alexandru Paul Condurache, and Andreas Geiger. Spherenet: Learning spherical representations for detection and classification in omnidirectional images. In Proceedings of the European conference on computer vision (ECCV), pages 518–533, 2018.
- [9] Michaël Defferrard, Martino Milani, Frédérick Gusset, and Nathanaël Perraudin. Deepsphere: a graph-based spherical cnn. arXiv preprint arXiv:2012.15000, 2020.
- [10] James R Driscoll and Dennis M Healy. Computing fourier transforms and convolutions on the 2-sphere. Advances in applied mathematics, 15(2):202–250, 1994.
- [11] Carlos Esteves, Christine Allen-Blanchette, Ameesh Makadia, and Kostas Daniilidis. Learning so (3) equivariant representations with spherical cnns. In Proceedings of the European Conference on Computer Vision (ECCV), pages 52–68, 2018.
- [12] Carlos Esteves, Ameesh Makadia, and Kostas Daniilidis. Spin-weighted spherical cnns. Advances in Neural Information Processing Systems, 33:8614–8625, 2020.
- [13] Joan Bruna Estrach, Arthur Szlam, and Yann LeCun. Signal recovery from pooling representations. In International conference on machine learning, pages 307–315. PMLR, 2014.
- [14] Andreas Geiger, Philip Lenz, Christoph Stiller, and Raquel Urtasun. Vision meets robotics: The kitti dataset. The International Journal of Robotics Research, 32(11):1231–1237, 2013.
- [15] Krzysztof M Gorski, Eric Hivon, Anthony J Banday, Benjamin D Wandelt, Frode K Hansen, Mstvos Reinecke, and Matthia Bartelmann. Healpix: A framework for high-resolution discretization and fast analysis of data distributed on the sphere. The Astrophysical Journal, 622(2):759, 2005.
- [16] Caglar Gulcehre, Kyunghyun Cho, Razvan Pascanu, and Yoshua Bengio. Learned-norm pooling for deep feedforward and recurrent neural networks. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pages 530–546. Springer, 2014.
- [17] Kevin Jarrett, Koray Kavukcuoglu, Marc’Aurelio Ranzato, and Yann LeCun. What is the best multi-stage architecture for object recognition? In 2009 IEEE 12th international conference on computer vision, pages 2146–2153. IEEE, 2009.
- [18] Chiyu Jiang, Jingwei Huang, Karthik Kashinath, Philip Marcus, Matthias Niessner, et al. Spherical cnns on unstructured grids. arXiv preprint arXiv:1901.02039, 2019.
- [19] Renata Khasanova and Pascal Frossard. Graph-based classification of omnidirectional images. In Proceedings of the IEEE International Conference on Computer Vision Workshops, pages 869–878, 2017.
- [20] Risi Kondor, Zhen Lin, and Shubhendu Trivedi. Clebsch–gordan nets: a fully fourier space spherical convolutional neural network. Advances in Neural Information Processing Systems, 31, 2018.
- [21] Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
- [22] Yann LeCun, Bernhard Boser, John Denker, Donnie Henderson, Richard Howard, Wayne Hubbard, and Lawrence Jackel. Handwritten digit recognition with a back-propagation network. Advances in neural information processing systems, 2, 1989.
- [23] Chen-Yu Lee, Patrick W Gallagher, and Zhuowen Tu. Generalizing pooling functions in convolutional neural networks: Mixed, gated, and tree. In Artificial intelligence and statistics, pages 464–472. PMLR, 2016.
- [24] Shaohui Li, Wenrui Dai, Ziyang Zheng, Chenglin Li, Junni Zou, and Hongkai Xiong. Reversible autoencoder: A cnn-based nonlinear lifting scheme for image reconstruction. IEEE Transactions on Signal Processing, 69:3117–3131, 2021.
- [25] Stéphane Mallat. A wavelet tour of signal processing. Elsevier, 1999.
- [26] Jason D McEwen, Christopher GR Wallis, and Augustine N Mavor-Parker. Scattering networks on the sphere for scalable and rotationally equivariant spherical cnns. arXiv preprint arXiv:2102.02828, 2021.
- [27] Sunil K Narang and Antonio Ortega. Lifting based wavelet transforms on graphs. In Proceedings: APSIPA ASC 2009: Asia-Pacific Signal and Information Processing Association, 2009 Annual Summit and Conference, pages 441–444. Asia-Pacific Signal and Information Processing Association, 2009 Annual …, 2009.
- [28] Nathanaël Perraudin, Michaël Defferrard, Tomasz Kacprzak, and Raphael Sgier. Deepsphere: Efficient spherical convolutional neural network with healpix sampling for cosmological applications. Astronomy and Computing, 27:130–146, 2019.
- [29] Gemma Piella and Henk JAM Heijmans. Adaptive lifting schemes with perfect reconstruction. IEEE Transactions on Signal Processing, 50(7):1620–1630, 2002.
- [30] Evan Racah, Christopher Beckham, Tegan Maharaj, Samira Ebrahimi Kahou, Mr Prabhat, and Chris Pal. Extremeweather: A large-scale climate dataset for semi-supervised detection, localization, and understanding of extreme weather events. Advances in neural information processing systems, 30, 2017.
- [31] Maria Ximena Bastidas Rodriguez, Adrien Gruson, Luisa Polania, Shin Fujieda, Flavio Prieto, Kohei Takayama, and Toshiya Hachisuka. Deep adaptive wavelet network. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pages 3111–3119, 2020.
- [32] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pages 234–241. Springer, 2015.
- [33] Raif Rustamov and Leonidas J Guibas. Wavelets on graphs via deep learning. Advances in neural information processing systems, 26, 2013.
- [34] Faraz Saeedan, Nicolas Weber, Michael Goesele, and Stefan Roth. Detail-preserving pooling in deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 9108–9116, 2018.
- [35] Peter Schröder and Wim Sweldens. Spherical wavelets: Efficiently representing functions on the sphere. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques, pages 161–172, 1995.
- [36] Godwin Shen and Antonio Ortega. Optimized distributed 2d transforms for irregularly sampled sensor network grids using wavelet lifting. In 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, pages 2513–2516. IEEE, 2008.
- [37] Zhengyang Shen, Tiancheng Shen, Zhouchen Lin, and Jinwen Ma. Pdo-es 2 cnns: Partial differential operator based equivariant spherical cnns. 2021.
- [38] Wim Sweldens. The lifting scheme: A custom-design construction of biorthogonal wavelets. Applied and computational harmonic analysis, 3(2):186–200, 1996.
- [39] Wim Sweldens. The lifting scheme: A construction of second generation wavelets. SIAM journal on mathematical analysis, 29(2):511–546, 1998.
- [40] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. arXiv preprint arXiv:1710.10903, 2017.
- [41] Travis Williams and Robert Li. Wavelet pooling for convolutional neural networks. In International Conference on Learning Representations, 2018.
- [42] Moritz Wolter and Jochen Garcke. Adaptive wavelet pooling for convolutional neural networks. In International Conference on Artificial Intelligence and Statistics, pages 1936–1944. PMLR, 2021.
- [43] Yonghong Wu, Quan Pan, Hongcai Zhang, and Shaowu Zhang. Adaptive denoising based on lifting scheme. In Proceedings 7th International Conference on Signal Processing, 2004. Proceedings. ICSP’04. 2004., volume 1, pages 352–355. IEEE, 2004.
- [44] Zhirong Wu, Shuran Song, Aditya Khosla, Fisher Yu, Linguang Zhang, Xiaoou Tang, and Jianxiong Xiao. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1912–1920, 2015.
- [45] Mingxing Xu, Wenrui Dai, Chenglin Li, Junni Zou, Hongkai Xiong, and Pascal Frossard. Graph neural networks with lifting-based adaptive graph wavelets. IEEE Transactions on Signal and Information Processing over Networks, 2022.
- [46] Qin Yang, Chenglin Li, Wenrui Dai, Junni Zou, Guo-Jun Qi, and Hongkai Xiong. Rotation equivariant graph convolutional network for spherical image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 4303–4312, 2020.
- [47] Dingjun Yu, Hanli Wang, Peiqiu Chen, and Zhihua Wei. Mixed pooling for convolutional neural networks. In International conference on rough sets and knowledge technology, pages 364–375. Springer, 2014.
- [48] Chao Zhang, Stephan Liwicki, William Smith, and Roberto Cipolla. Orientation-aware semantic segmentation on icosahedron spheres. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 3533–3541, 2019.
- [49] Jiaojiao Zhao and Cees GM Snoek. Liftpool: Bidirectional convnet pooling. arXiv preprint arXiv:2104.00996, 2021.