Chopina 12/18, 87-100 Toruń, Poland 22institutetext: Faculty of Mathematics and Computer Science, Nicolaus Copernicus University,
Chopina 12/18, 87-100 Toruń, Poland - retired 33institutetext: Institute of Computer Science, Polish Academy of Sciences,
Jana Kazimierza 5, 01-248 Warszawa, Poland - retired
Hierarchy of persistence
with respect to the length of action’s disability
Abstract
The notion of persistence, based on the rule "no action can disable another one" is one of the classical notions in concurrency theory. It is also one of the issues discussed in the Petri net theory. We recall two ways of generalization of this notion: the first is "no action can kill another one" (called l/l-persistence) and the second "no action can kill another enabled one" (called the delayed persistence, or shortly e/l-persistence). Afterwards we introduce a more precise notion, called e/l-k-persistence, in which one action disables another one for no longer than a specified number k of single sequential steps. Then we consider an infinite hierarchy of such e/l-k persistencies. We prove that if an action is disabled, and not killed, by another one, it can not be postponed indefinitely. Afterwards, we investigate the set of markings in which two actions are enabled simultaneously, and also the set of reachable markings with that feature. We show that the minimum of the latter is finite and effectively computable. Finally we deal with decision problems about e/l-k persistencies. We show that all the kinds of e/l-k persistencies are decidable with respect to steps, markings and nets.
etri nets, concurrency, persistence, decision problems
Keywords:
P1 Introduction
Petri nets constitute a very useful and suitable tool for concurrent systems modeling. Thanks to them, we can not only model real systems, but also analyze their properties and design systems which fulfill given criteria. For many years, concurrent systems have been examined in the context of their compliance with certain desirable properties, which fits in with the trend of the so-called ethics of concurrent computations. One of the commonly found undesirable properties of concurrent systems is the presence of conflicts, and thus, one of the most desirable properties of them is conflict-freeness. The notion of persistence, proposed by Karp/Miller [11] is one of the the most important notions in concurrency theory. It is based on the behaviourally oriented rule "no action can disable another one", and generalizes the structurally defined notion of conflict-freeness.
The notion of persistence is one of the issues frequently discussed in the Petri net theory - [4, 9, 10, 14, 15, 13] and many others. It is being studied not only in terms of theoretical properties, and also as a useful tool for designing and analyzing software environments [3]. In engineering, persistence is a highly desirable property, especially in a case of designing systems to be implemented in hardware. Many systems can not work properly without satisfying this property.
We say that an action of a processing system is persistent if, whenever it becomes enabled, it remains enabled until executed. A system is said to be persistent if all its actions are persistent. This classical notion has been introduced by Karp/Miller [11]. In section 2.6, we show two generalizations of the classical notion (defined in [2]): l/l-persistence and e/l-persistence which form the following hierarchy: . An action is said to be l/l-persistent if it remains live until executed, and is e/l-persistent if, whenever it is enabled, it cannot be killed by another action. For uniformity, we name the traditional persistence notion e/e-persistence. Next, we recall that those kinds of persistence are decidable in place/transition nets.
In section 3.1, we extend the hierarchy mentioned above with an infinite hierarchy of e/l-persistent steps. A step is said to be e/l-k-persistent for some k if the execution of an action pushes the execution of any other enabled action away for at most k steps (more precise: if the execution of an action stops the enabledness of any other action, then the enabledness is restored not later than after k steps).
In section 3.2 we study decision problems related to the notion of e/l-k-persistence. These problems include EL-k Step Persistence Problem and EL-k Marking Persistence Problem. We show that both problems are decidable (Theorem 3.1 and Theorem 3.2).
The next problem we want to focus on is EL-k Net Persistence Problem. In order to check the decidability of the problem we need to take advantage of additional tools and facts.
That is why we investigate the set of markings in which two actions are enabled simultaneously, and also the set of reachable markings with that feature. We show that the minimum of the latter is finite and effectively computable. We also prove that if some action pushes the enabledness of another one away for more than k steps, then it also needs to happen in some minimal reachable marking enabling these two actions. In our proofs we use the decidability of the Set Reachability Problem (from [2]) and also we make use of the theory of residual sets of Valk/Jantzen [18]. Finally, we show that e/l-k-persistence is decidable with respect to nets (Theorem 3.7).
We also prove (section 3.3) that if an action of an arbitrary p/t-net is disabled (but not killed) by another one, it can not be postponed indefinitely. We show that if a p/t-net is e/l-persistent, then it is e/l-k-persistent for some k (Theorem 3.8), and such a number k can be effectively found (Theorem 3.10). We also point, that the above-cited result does not hold for nets which do not have the monotonicity property (i.e. it is not true that the action enabled in some marking is also enabled in any marking greater than ), for example for inhibitor nets.
The concluding section contains some questions and plans for further investigations.
A preliminary version of the paper was presented on the International Workshop on Petri Nets and Software Engineering (Hamburg, Germany, June 25-26, 2012) with electronical proceedings available online at CEUR-WS.org as Volume 851. The present paper is an improved and extended version of it.
2 Basic Notions
2.1 Denotations
The set of non-negative integers is denoted by . Given a set , the cardinality (number of elements) of is denoted by , the powerset (set of all subsets) by , the cardinality of the powerset is . Multisets over are members of , i.e. functions from into .
2.2 Petri Nets and Their Computations
The definitions concerning Petri nets are mostly based on [5].
Definition 1 (Nets)
Net is a triple , where:
-
•
and are finite disjoint sets, of places and transitions, respectively;
-
•
is a relation, called the flow relation.
For all we denote:
- the set of entries to
- the set of exits from .
Petri nets admit a natural graphical representation. Nodes represent places and transitions, arcs represent the flow relation. Places are indicated by circles, and transitions by boxes.
The set of all finite strings of transitions is denoted by , the length of is denoted by , number of occurrences of a transition in a string is denoted by , two strings such that are said to be Parikh equivalent, which is denoted by .
Definition 2 (Place/Transition Nets)
Place/transition net (shortly, p/t-net) is a quadruple , where:
-
•
is a net, as defined above;
-
•
is a multiset of places, named the initial marking; it is marked by tokens inside the circles, capacity of places is unlimited.
Multisets of places are named markings. In the context of p/t-nets, they are mostly represented by nonnegative integer vectors of dimension , assuming that is strictly ordered. The natural generalizations, for vectors, of arithmetic operations and , as well as the partial oder , all defined componentwise, are well known and their formal definitions are omitted here.
In this context, by we understand a vector of dimension which has 1 in every coordinate corresponding to a place that is an entry to (an exit from, respectively) and 0 in other coordinates.
A transition is enabled in a marking whenever (all its entries are marked). If is enabled in , then it can be executed, but the execution is not forced. The execution of a transition changes the current marking to the new marking (tokens are removed from entries, then put to exits). The execution of an action in a marking we call a (sequential) step. We shall denote for the predicate "a is enabled in " and for the predicate " is enabled in and is the resulting marking".
This notions and predicates we extend, in a natural way, to strings of transitions: for any marking , and () iff and .
Remark: Wherever this will not lead to confusion, we will use a notation to denote the fact that the action is enabled in a marking and a marking is the result of the execution of action in a marking .
If , for some , then is said to be reachable from ; the set of all markings reachable from is denoted by . Given a p/t-net , the set of markings reachable from the initial marking is called the reachability set of S, and markings in are said to be reachable in S.
A transition is said to be live in a marking if there is a string such that is enabled in . A transition that is not live in a marking is said to be dead in a marking . Let be a marking such that for some , then if a transition is enabled (live) in and not enabled (not live) in , we say that (the execution of) disables (kills) in a marking . We also say that an action disables (kills) (in a net ) if disables (kills) in some reachable marking .
Definition 3 (Inhibitor nets )
Inhibitor net is a quintuple , where:
-
•
is a p/t-net, as defined above;
-
•
is the set of inhibitor arcs (depicted by edges ended with a small empty circle). Sets of entries and exits are denoted by and , as in p/t-nets; the set of inhibitor entries to is denoted by .
A transition (of an inhibitor net) is enabled in a marking whenever (all its entries are marked) and - all inhibitor entries to are empty. The execution of leads to the resulting marking .
The following well-known fact follows easily from Definitions 1 and 2.
Fact 1 (Diamond and big diamond properties)
Any place/transition net possesses the following property:
Big Diamond Property:
If (Parikh equivalence), then .
Its special case with is called the Diamond Property:
If , then .
Definition 4
We say that a Petri net has the monotonicity property if and only if .
Fact 2
P/t-nets have the monotonicity property.
Proof
Obvious, since in p/t-nets the tokens of can be regarded as frozen (disactive) tokens.
Fact 3
Inhibitor nets do not have the monotonicity property.
Proof
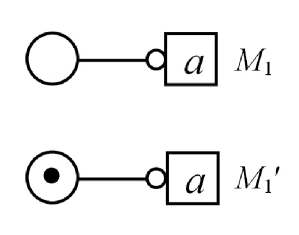
Let us look at the example of Fig. 1. It can be easily seen that . holds but doesn’t hold.
2.3 Monoid
Definition 5 (Monoid , rational operations, rational subsets)
The monoid is the set of -dimensional non-negative integer vectors with the componentwise addition .
If then and the star operation is defined as , where and . The partial order is understood componentwise, and means and . Rational subsets of are subsets built from finite subsets with finitely many operations of union , addition and star ∗.
Theorem 2.1 (Ginsburg/Spanier[8])
Rational subsets of form an effective boolean algebra (i.e. are closed under union, intersection and difference).
Definition 6 (-extension)
Let , where is a new symbol (denoting infinity). We extend, in a natural way, arithmetic operations:
, , and the order: .
The set of k-dimensional vectors over we shall denote by , and its elements we shall call -vectors. Operations and the order in are componentwise.
For , we denote by Min() the set of all minimal (wrt ) members of , and by Max() the set of all maximal (wrt ) members of . Let be -vectors such that , then we say that covers ( is covered by ) .
Let us recall the well known important fact known as the Dickson’s Lemma.
Lemma 1 ([6])
Any subset of incomparable elements of is finite.
Definition 7 (Closures, convex sets)
-
•
Let and . We denote: ,
, , , and call the sets and of , respectively; -
•
A set such that () is said to be -(-) ;
-
•
A set such that is said to be .
We also recall a fact proved in [2]:
Proposition 1
Any convex subset of is rational.
2.4 Reachability graph/tree and coverability graph
Let us recall the notions of a reachability graph/tree and a coverability graph. Their definitions can be also found in any monograph or survey about Petri nets (see [5, 17] or arbitrary else). Reachability graphs/trees are used for studying complete behaviors of nets, but they are usually infinite, whichmakes an accurate analysis of them difficult. That is why we study coverability graphs, which represent the behaviours of nets only partially, but are always finite.
The reachability graph of a p/t-net is a couple where .
The reachability graph represents graphically the behaviour of the net . Vertices of the graph are reachable markings from the set , while edges are ordered pairs of reachable states, labeled by actions. More precisely: the edge iff is a state reachable from the initial marking , an action (the label of the edge ) is enabled in a state and . The existence of an edge in the reachability graph of the net indicates that the marking is reachable in , the action is enabled in and after the execution ot the action in the marking , the net reaches the state .
Sometimes it is more convenient to use a special graph structure for listing all reachable markings of a given p/t-net, namely a tree structure. Such a tree is called a reachability tree.
For a given net we construct its reachability tree proceeding as follows:
-
•
We start with the initial marking which is the root vertex of the reachability tree.
-
•
For each action enabled in the initial marking of the net, we create a new vertex , such that , and an edge leading from to labelled by .
-
•
We repeat the procedure for all the newly created vertices (markings).
Remark: The construction of a reachability tree is a process potentially endless, as the structure is infinite in many cases.
Definition 8
Let be a reachability tree of a net . The k-component of the reachability tree is the initial part of the tree of the depth k (all vertices at depth lower than or equal to k).
In the case of a coverability tree it is convenient to present a constructional definition. That is why we introduce:
Algorithm of the construction of a coverability graph
We create a coverability graph for a p/t-net
-
•
Step 0. An initial vertex
We set blue for a start.
GOTO Step 1. -
•
Step 1. Generating of new working vertices
If there is no blue vertices then STOP.
We take an arbitrary blue vertex and draw from it all the arcs of the form for all enabled in , where . If the vertex already exists (in any colour), then the newly created arc leads to the existing vertex (we do not create a new one). New vertices are set yellow. After drawing all such arcs we set the vertex grey (a final node).
GOTO Step 2. -
•
Step 2. Coverability checking
If there is no yellow vertices GOTO Step 1.
We take an arbitrary yellow vertex and check for any of the paths from to whether a vertex such that lies on the path. If such a vertex exists then every coordinate of the marking greater than the corresponding coordinate of the marking changes to . Finally we set the vertex blue.
GOTO Step 2.
Example 1
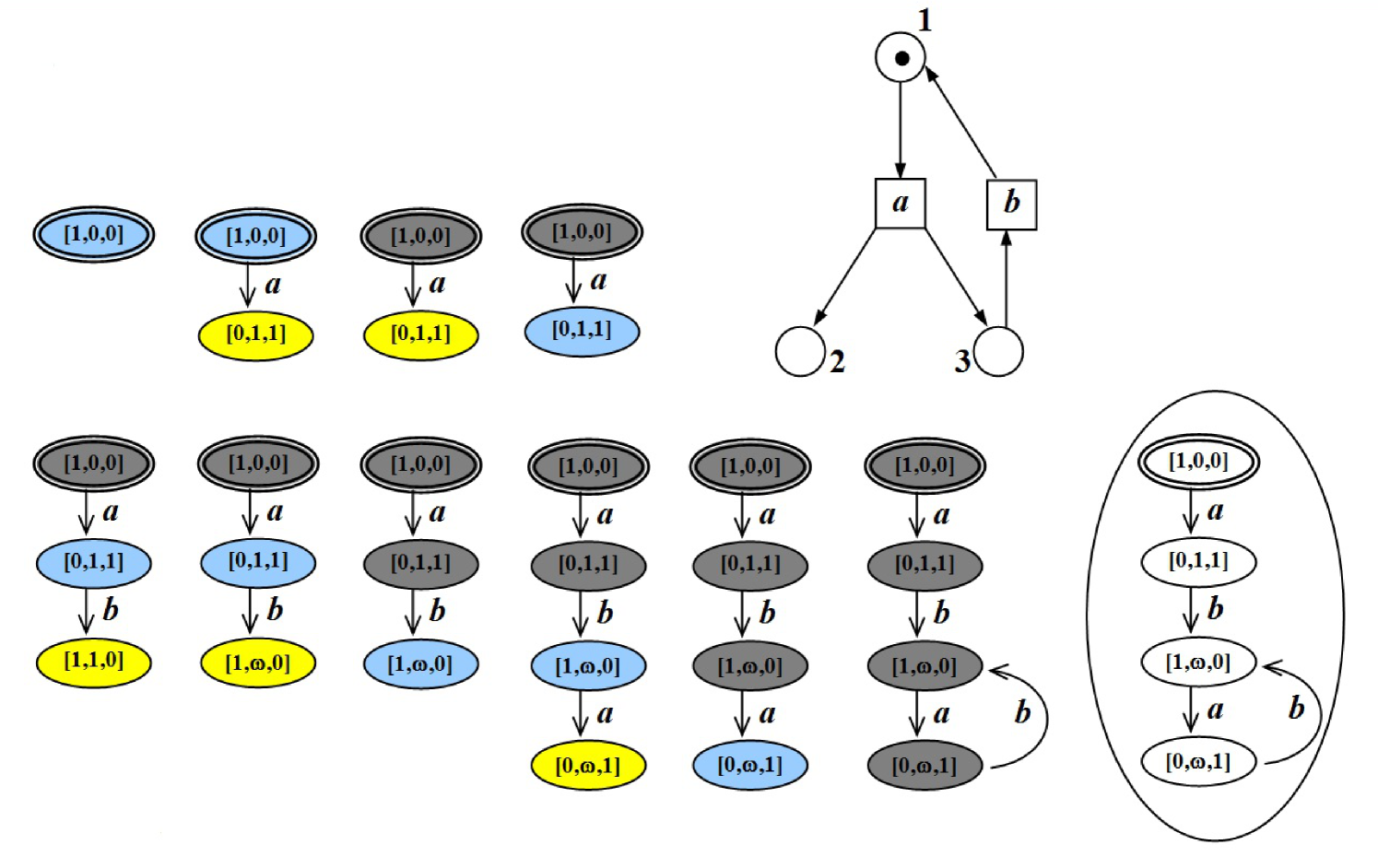
Let us look at the Example of Figure 2. A p/t-net and stages of the construction of its coverabilty graph are presented there.
2.5 Reachability and Coverability Problems
Let us now recall very famous decision problems concerning Petri nets, namely the Reachability Problem and the Coverability Problem.
Reachability Problem
Instance: P/t-net , and a marking .
Question: Is reachable in S?
Coverability Problem
Instance: P/t-net , and a marking .
Question: Is coverable in S?
Remark: It is well known that the above problems are decidable (coverability: Karp/Miller [11], Hack [10]; reachability: Mayr [15], Kosaraju [12]).
2.6 Three Kinds of Persistence
The notion of persistence is one of the classical notions in concurrency theory. The notion is recalled in [2] (named in the sequel e/e-persistence). Some of its generalizations: l/l-persistence and e/l-persistence are also introduced there.
Note on terminology
The notion of persistence in its classical meaning is a property of nets. The definition of [14] involves the entire concurrent system.
If we choose to define the concept of persistence starting from actions by markings, ending with whole nets, the classic definition can be interpreted in two ways. Namely, one can consider concepts of persistence and nonviolence. An extensive discussion on the links between persistence and nonviolence can be found in [13]. In the context of [1] and [13] it seems that it would be more appropriate to use the notion of nonviolence instead of using the concept of persistence. However, because our paper is an extension of [2], we decided to stick to the concept of persistence.
Let us sketch the notions of e/e-persistence, l/l-persistence and e/l-persistence informally. The classical e/e-persistence means "no action can disable another one", the l/l-persistence means "no action can kill another one" and the e/l-persistence means "no action can kill another enabled one". Let us go on to formal definitions.
Definition 9 (Three kinds of persistence)
Let be a place/transition net.
If
-
•
, then is said to be e/e-persistent;
-
•
, then is said to be l/l-persistent;
-
•
, then is said to be e/l-persistent.
The classes of e/e-persistent (l/l-persistent, e/l-persistent) p/t-nets will be denoted by , and , respectively.
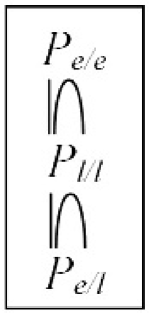
In [2] one can find a proof of the following theorem:
Theorem 2.2
The three classes of persistent place/transition nets
form an increasing hierarchy: .
Example 2
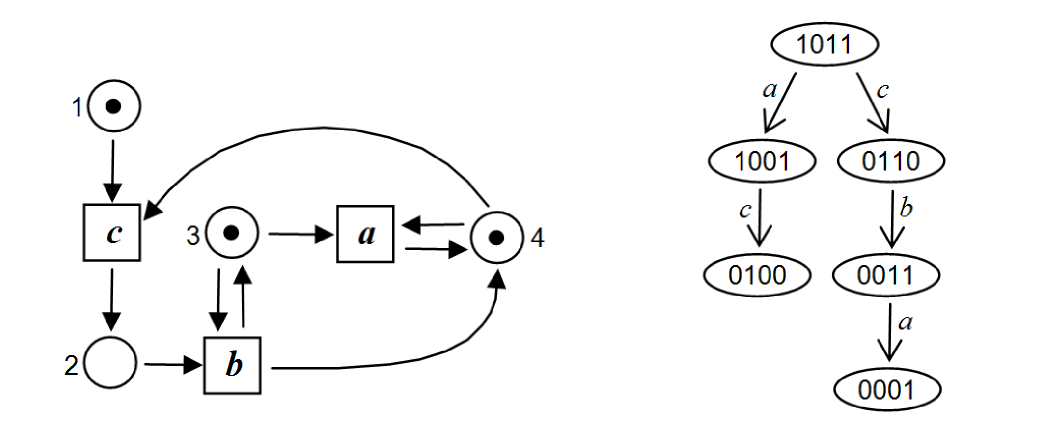
It is also shown in [2] that the following decision problems are decidable:
Instance: A p/t-net
Questions:
EE Net Persistence Problem: Is the net S e/e-persistent?
LL Net Persistence Problem: Is the net S l/l-persistent?
EL Net Persistence Problem: Is the net S e/l-persistent?
The proofs of decidability of the above problems need to put into work a very efficient result of Valk/Jantzen [18] and benefit from the decidability of reachability problem (more specifically - decidability of the Set Reachability Problem for rational convex sets).
The alternative proof of Theorem 3.7 uses exactly the same proving technique as the proofs of decidability of the persistence problems mentioned above.
3 Properties of e/l-persistence
3.1 Hierarchy of e/l-persistence
In the previous section we defined three kinds of persistence. Now, we extend the hierarchy mentioned above with an infinite hierarchy of e/l-persistent steps.
Definition 10 (E/l-persistent steps - an infinite hierarchy)
Let be a p/t-net, let be a marking. We call a step :
-
•
e/l-0-persistent iff it is e/e-persistent (the execution of an action a does not disable any other action);
-
•
e/l-1-persistent iff (the execution of an action a pushes the execution of any other enabled action away for at most 1 step);
-
•
e/l-2-persistent iff (the execution of an action a pushes the execution of any other enabled action away for at most 2 steps);
… -
•
e/l-k-persistent for some iff (the execution of an action a pushes the execution of any other enabled action away for at most steps);
… -
•
e/l--persistent iff (the execution of an action a pushes the execution of any other enabled action away).
Remark: Note that e/l--persistent steps are exactly e/l-persistent steps.
Directly from Definition 10 we get the
Fact 4
Let be a p/t-net, let be a marking. If the step is e/l--persistent for some , then it is also e/l--persistent for every .
Definition 11
Let be a p/t-net, be a marking and . Marking is e/l-k-persistent iff for every action that is enabled in the step is e/l-k-persistent. P/t-net is e/l-k-persistent iff every marking reachable in S is e/l-k-persistent. We denote the class of e/l--persistent p/t-nets by .
Example 3
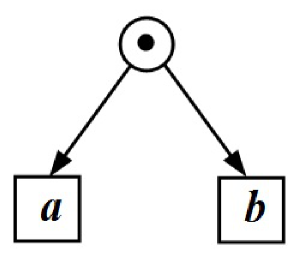
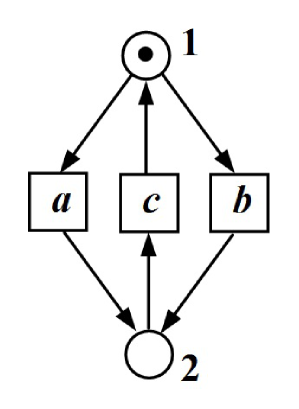
Let us look at the example of Fig. 6. Both actions and are enabled in the initial marking. After the execution of the action , the action is never enabled again, and after the execution of the action , the action is never enabled again. So the net can not be e/l-k-persistent for any natural number k.
Example 4
Let us look at the example of Fig. 4. The net is not e/l-0-persistent but it is e/l-1-persistent.
Example 5
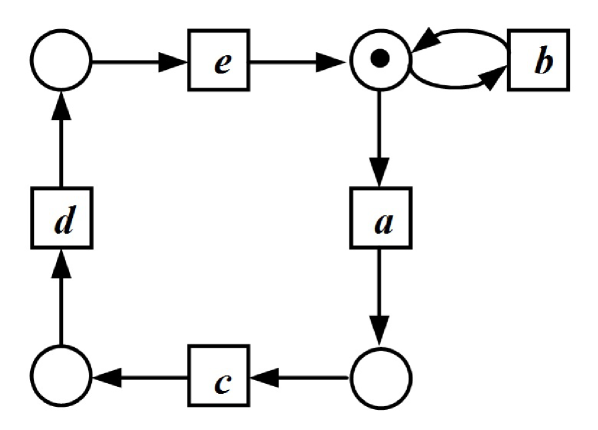
Let us look at the example of Fig. 7. The only possible situation for temporary disabling an action by another one is the execution of that disables . And then could be enabled again after the execution of the sequence , so after 3 steps. Hence, the net is e/l-3-persistent, and obviously not e/l-2-persistent.
Fact 5
Let be a p/t-net, be a marking, and . If the marking is e/l--persistent, then it is also e/l--persistent for every . If the net S is e/l--persistent, then it is also e/l--persistent for every .
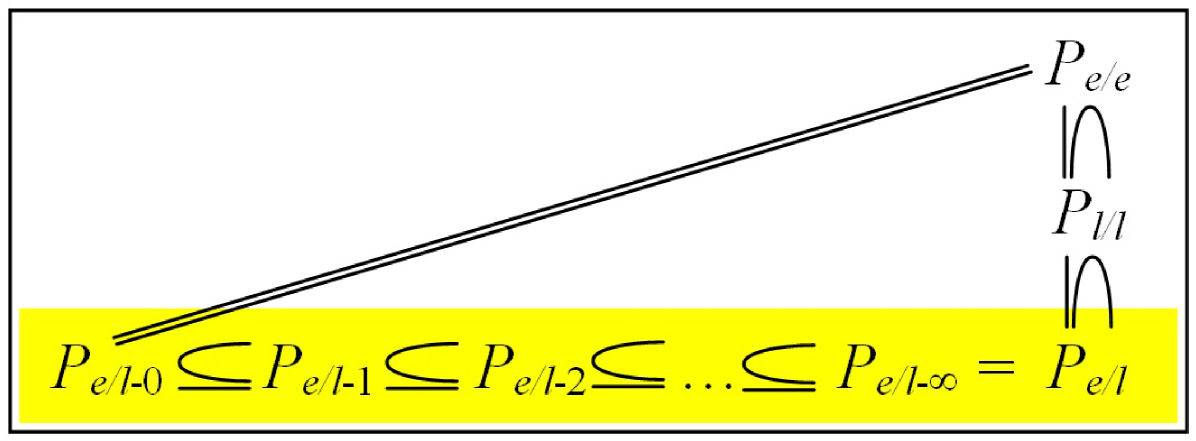
Remark: Based on this Fact 5 we can extend the existing hierarchy of persistent nets as shown in Figure 8.
3.2 Related decision problems
3.2.1 • EL-k Step Persistence Problem
and EL-k Marking Persistence Problem
Let be a fixed natural number. Now we can formulate basic problems regarding the concept of e/l-k-persistence.
The first problem is as follows:
EL-k Step Persistence Problem
Instance: P/t-net S, marking , action enabled in .
Question:Is the step e/l-k-persistent?
Theorem 3.1
The EL-k Step Persistence Problem is decidable (for any ).
Proof
An algorithm to check if a step is e/l-k-persistent (for some ) for a given net :
Let us build the part of the depth of k+1 (we call it the (k+1)-component) of the reachability tree of , where is a marking obtained from by execution of . The step is e/l-k-persistent if for every action , such that and is enabled in , there is a path in the (k+1)-component of the reachability tree of containing an arc labeled by .
Let us introduce another problem:
EL-k Marking Persistence Problem
Instance:P/t-net , marking .
Question:Is the marking e/l-k-persistent?
Theorem 3.2
The EL-k Marking Persistence Problem is decidable
(for any .
Proof
For every action that is enabled in a marking , we check if a step is e/l-k-persistent (for some ) for a given net , using the algorithm of Theorem 3.1.
3.2.2 • EL-k Net Persistence Problem
Let us consider the following problem:
EL-k Net Persistence Problem
Instance:P/t-net .
Question:Is the net S e/l-k-persistent?
To solve this problem we must prove a set of auxiliary facts.
From this moment, let be an arbitrary p/t-net.
Let us define the following set of markings:
- the set of markings enabling actions and simultaneously.
Let us define , the minimum marking enabling actions and simultaneously: if then else (for .
Note that .
3.2.3 • Mutual Enabledness Reachability Problem
Let us formulate an auxiliary problem:
Mutual Enabledness Reachability Problem
Instance:P/t-net , actions .
Question:Is there a marking such that and ?
(Is there a reachable marking such that
actions and are both enabled in ?)
Theorem 3.3
The Mutual Enabledness Reachability Problem is decidable.
Proof
Let . We build a coverability graph for the p/t-net S. We check whether in the graph exists a vertex corresponding to an -marking such that covers . If so, then actions and are simultaneously enabled in some reachable marking of the net S. Otherwise, those transitions are never enabled at the same time.
Let be the set of minimal (wrt ) reachable markings of the net S. As members of are incomparable, the set is finite, by Lemma 1.
Le us denote by the set of all reachable markings of the net S enabling actions and simultaneously: .
Let be a set of all minimal reachable markings of the net S enabling action and simultaneously.
3.2.4 • Results of Valk and Jantzen
In order to construct the set , we put into work the theory of residue sets of Valk/Jantzen [18].
Definition 12 (Valk/Jantzen [18])
A subset has property if and only if the problem "Does intersect ?" is decidable for any -vector .
Theorem 3.4 (Valk/Jantzen [18])
Let be a right-closed set. Then the set is effectively computable if and only if has property .
3.2.5 • Set Reachability Problem
We also use the fact of decidability of the Set Reachability Problem for rational convex sets (Def. 5,7), proved in [2].
Set Reachability Problem
Instance:P/t-net and a set .
Question:Is there a marking , reachable in S?
Theorem 3.5
The Set Reachability Problem is decidable for rational convex sets in p/t-nets.
The Set Reachability Problem is a generalization of the classical Marking Reachability Problem. The proof uses decidability of the Reachability Problem.
3.2.6 • Minimal reachable markings enabling two actions simultaneously
Now we are ready to prove:
Proposition 2
The set can be effectively constructed for a given net .
Proof
Let us take the right closure of the set .
Note that . To show that the set of minimal elements of the set is effectively computable, it is enough to demonstrate that the set has the property RES (i.e. for any -vector the problem "?" is decidable) and apply Theorem 3.4.
Let , where . Let us notice, that is a convex set, hence rational (Proposition 1). The set is also a rational convex set. As an intersection of convex rational sets, the set is convex and rational (Theorem 2.1) as well.
Hence, putting into work decidability of the Set Reachability Problem for rational convex sets (Theorem 3.5) we decide whether any marking from the set is reachable in S. Therefore, we can decide whether the set is nonempty. (It is the case when at least one marking from the set is reachable in S.) Let us notice that the set is nonempty if and only if the set is nonempty. That is why the set has the property RES, and consequently the set is effectively computable by Theorem 3.4.
Example 6
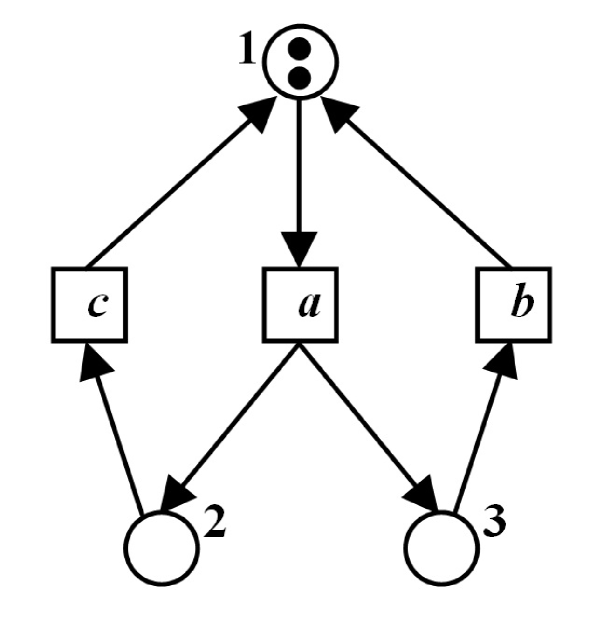
The set of all minimal reachable markings of the net depicted in Figure 9 enabling action and simultaneously, is .
Proposition 3
If there exists a marking such that the execution of an action in pushes the execution of an action away for more than steps (for some ), then there exists some minimal marking such that the execution of an action in pushes the execution of an action away for more than steps, too.
Proof
Let be a marking, such that the execution of an action in pushes the execution of an action away for more than k steps (for some ). Let such that . Such a marking has to exist. Suppose that there is a string , such that . Then obviously also (from the monotonicity property - Fact 2). We obtain a contradiction. Hence, the execution of an action in postpones the execution of for more than k steps.
3.2.7 • EL-k Transition Persistence Problem and EL-k Net Persistence Problem
Now, we are ready to introduce the following problem:
EL-k Transition Persistence Problem
Instance:P/t-net , ordered pair , .
Question:Is there a reachable marking such that
?
(Does postpone for more than k steps?)
Theorem 3.6
The EL-k Transition Persistence Problem is decidable.
Proof
We introduce an algorithm of deciding if an action pushes the execution of an action away for more than k steps in some reachable marking .
-
1.
We check whether both actions and are enabled in some reachable marking (using decidability of Mutual Enabledness Reachability Problem).
-
(a)
If not, we answer NO.
-
(b)
Otherwise:
-
i.
We build the set . This set can be effectively computed by Proposition 2 using Valk/Jantzen algorithm.
-
ii.
For all markings :
.
We build an initial part of the depth of k+1 (the (k+1)-component) of the reachability tree of . If the piece has an edge labeled by , we answer NO. Otherwise we answer YES.
-
i.
-
(a)
And now the proof of decidability of the EL-k Net Persistence Problem is ready.
Theorem 3.7
The EL-k Net Persistence Problem is decidable (for any ).
Proof
S is e/l-k-persistent iff the algorithm solving EL-k Transition Persistence Problem answers NO for all ordered pairs , .
Example 7
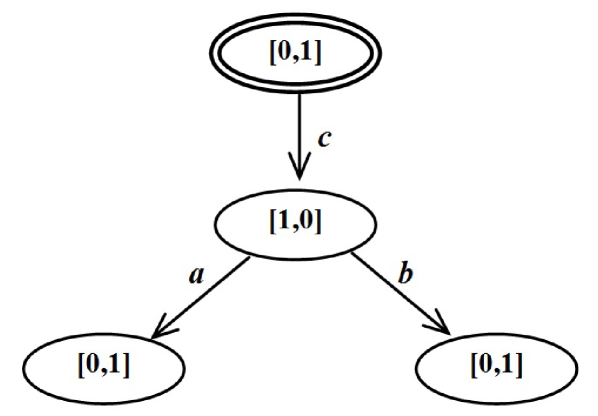
Let us check whether the action of the net S of Figure 4 postpones the action for more than 1 step.
Actions and are both enabled in the initial marking.
The set consists of a single marking .
We take . We build a 2-component of the reachability tree of the net . The tree is depicted in Figure 10. The tree has an edge labeled by so the action does not postpone the action for more than 1 step.
3.2.8 • EL-k Transition Persistence Problem - an alternative approach
In order to show decidability of the EL-k Net Persistence Problem we can use the technique used for proving decidability of LL Net Persistence Problem and EL Net Persistence Problem, presented in [2].
Again, we deal with the EL-k Transition Persistence Problem, crucial for the proof. We show an alternative proof of decidability of that problem.
EL-k Transition Persistence Problem
Instance:P/t-net , ordered pair , .
Question:Is there a reachable marking such that
?
Let us define, in order to reformulate the problem above, the following sets of markings:
- markings enabling
- markings enabling
- markings enabling a such that after the execution of a the action b is potentially enabled after at most k steps.
Now we can reformulate the question of the problem above:
Question:Is the set
reachable in ?
Let us look again at
Theorem 3.7.
The EL-k Net Persistence Problem is decidable (for any ).
Proof
First note that, by the monotonicity property (Fact 2), the set
is convex, thus rational (by Proposition 1). The rational expressions for and are and . Clearly, the set is right-closed, by the monotonicity property. We shall prove that it has the property RES. Namely, ()intersects if and only if (i.e. is enabled in ) and there is a path in the reachability tree, limited to (k+1) first levels, of the net , where is an -marking obtained from by the execution of , containing an arc labelled by . It is obviously decidable. Hence, the set has the property RES, thus (by Theorem 3.4) the set is effectively computable. As is right-closed, we get the rational expression for it: . Finally, using Theorem 2.1 of Ginsburg/Spanier [8], we compute rational expression for and Theorem 3.4 yields decidability of the problem.
3.3 Collapsing of the hierarchy of e/l-persistence
3.3.1 • k-enabledness
Let us recall the well-known fact, that follows from the Dickson’s Lemma (Lemma 1).
Fact 6
Every infinite sequence of markings contains an infinite increasing (not necessarily strictly) subsequence of markings.
Recall also that p/t-nets have the monotonicity property - Fact 2.
Let us define the notion of k-enabledness.
Definition 13 (k-enabledness)
Let be a p/t-net, let be a marking. For we say that the action is k-enabled in the marking if and only if , such that .
Now, we can show:
Lemma 2
Let be a p/t-net. For an arbitrary there exists a natural number , such that in every marking the transition is -enabled or it is dead.
Proof
Suppose that the lemma does not hold for some action . It means that for each there is a marking such that is not k-enabled but not dead. This means that is -enabled for some . Thus, there exists an infinite sets of markings and integers , such that the action is live in each marking and it is not -enabled in for all . Let us choose (by Fact 6) an infinite increasing sequence of markings . Since the action is live in , it is k-enabled in , for some . As the strictly increasing sequence is infinite, for some j. By the monotonicity property (Fact 2), the action is k-enabled, hence -enabled in the marking . Contradiction.
Remark: Note that the proof of Lemma 2 is purely existential, it does not present any algorithm for finding k.
Now, we are ready to formulate the main theorem of the section:
Theorem 3.8
If a p/t-net is e/l-persistent, then it is e/l--persistent for some .
In words: Whenever an action is disabled by another one, it is pushed away for not more than -steps.
Proof
If the net is e/l-persistent, then no action kills another enabled one. From the Lemma 2 we know, that if an action is not dead then it is -enabled. Let us take , for the numbers from the Lemma 2. One can see that every action in the net that is not dead, is K-enabled. Thus, the execution of any action may postpone the execution of an action for at most K steps. So we have the implication: if a p/t-net is e/l-persistent, then it is e/l-K-persistent, for K defined above.
Remark: As the proof of Lemma 2 explicitly uses the monotonicity property of p/t-nets, the Theorem 3.8 holds only for nets satisfying this property. The following example shows that Theorem 3.8 does not hold for nets without the monotonicity property (for instance, inhibitor nets).
Example 8
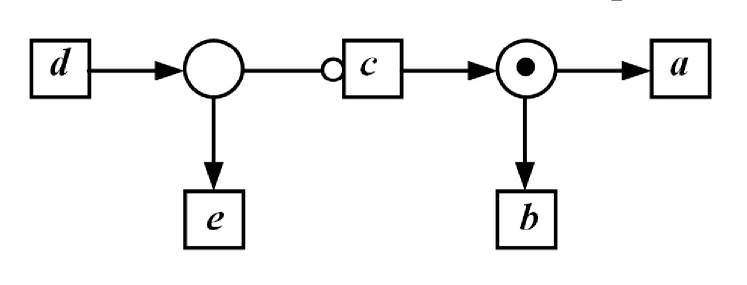
Let us look at the example of Fig. 11. We can see an inhibitor net and its computation such that for every one can push an action away for a distance greater than k steps.
This net is live, hence it is e/l-persistent, but it is not e/l-k-persistent for any .
In the infinite computation the first pushes away for 1 step, the second - for 2 steps and every k-th - for k steps.
3.3.2 • Collapsing of the hierarchy - an effective proof
Finally, let us recall other decision results of [2]:
Transitions Persistence Problems
Instance:P/t-net , and transitions .
Questions (informally):
EE-Persistence Problem: Does disable an enabled ?
LL-Persistence Problem: Does kill a live ?
EL-Persistence Problem: Does kill an enabled ?
From [2] we know that the problems are decidable.
Theorem 3.9
For a given p/t-net and a pair of transitions one can calculate a minimum number such that postpones an enabled for at most steps (if such a number exists).
Proof
-
•
We check whether both actions and are enabled in some reachable marking (using decidability of Mutual Enabledness Reachability Problem). If not, does not exist (actions and are never enabled at the same time). Otherwise:
-
–
We ask whether kills an enabled (EL-Persistence Problem).
If YES then does not exist ( kills )
else:-
*
We compute the set .This set can be effectively computed by Proposition 2 using Valk/Jantzen algorithm.
-
*
We build the initial part of reachability tree of the net as long as from every we get a marking with the property that a path leads to a vertex (it can be an empty path) such that . Clearly, such part of the tree is finite, as we get the whole and for any a finite path leading from to a vertex such that . The maximum length of such paths is the desired number .
-
*
-
–
Theorem 3.10
If a p/t-net is e/l-persistent, then it is e/l--persistent for some and such a can be effectively computed.
Proof
For every pair of transitions we find defined above. The number we are looking for is .
We established that an action can not postpone another action (without killing it) indefinitely (Theorem 3.8). We proved, that if a p/t-net is e/l-persistent, then it is e/l-k-persistent for some . We showed that such a k exists and we present any algorithm for finding this k.
4 Conclusions
It is shown in [1] that if we change the firing rule in the following way: only e/e-persistent computations are permitted, then we get a new class of nets (we call them nonviolence nets) which are computationally equivalent to Turing machines.
We plan to investigate net classes, with firing rules changed (only e/l-k-persistent computations are allowed) and answer the question:
Question 1:
What is the computational power of nets created this way?
In this paper, we have investigated the hierarchy of persistence in p/t-nets. We would like to study the hierarchy of e/l-k-persistence in some extensions of p/t-nets, for instance nets with read arcs and reset nets.
All results of the paper hold for nets with read arcs ([16]), as they can be simulated by classical Petri nets with self-loops with the same reachability set (but with distinct step semantics).
On the contrary, only Lemma 2 and Theorem 3.8 hold (with the same proof) for other extended Petri nets posessing the monotonicity property (e.g. reset, double, transfer nets), but the results supported with the fact of decidability of the Reachability Problem (Proposition 2, Theorem 3.7, Theorem 3.9) cannot be applied to those nets, because of undecidability of the Reachability Problem in them (see [7]).
References
- [1] Kamila Barylska, Lukasz Mikulski, and Edward Ochmanski. On persistent reachability in Petri nets. Inf. Comput., 223:67–77, 2013.
- [2] Kamila Barylska and Edward Ochmanski. Levels of persistency in place/transition nets. Fundam. Inform, 93(1-3):33–43, 2009.
- [3] E. Best and J. Esparza. Model checking of persistent Petri nets. Lecture Notes in Computer Science, 626:35–52, 1992.
- [4] Eike Best and Philippe Darondeau. Decomposition theorems for bounded persistent petri nets. In Kees M. van Hee and Rüdiger Valk, editors, Petri Nets, volume 5062 of Lecture Notes in Computer Science, pages 33–51. Springer, 2008.
- [5] Jorg Desel and Wolfgang Reisig. Place or transition petri nets. In Wolfgang Reisig and Grzegorz Rozenberg, editors, Lectures on Petri Nets, Vol. I: Basic Models, Advances in Petri Nets, volume 1491 (Volume I) of Lecture Notes in Computer Science (LNCS), pages 122–173. Springer-Verlag (New York), Dagstuhl, Germany, September 1996, revised paper 1998.
- [6] Leonard E. Dickson. Finiteness of the odd perfect and primitive abundant numbers with distinct prime factors. Amer. J. Math., 35:413–422, 1913.
- [7] Catherine Dufourd, Alain Finkel, and Ph. Schnoebelen. Reset nets between decidability and undecidability. In Kim Guldstrand Larsen, Sven Skyum, and Glynn Winskel, editors, ICALP, volume 1443 of Lecture Notes in Computer Science, pages 103–115. Springer, 1998.
- [8] Seymour Ginsburg and Edwin Spanier. Bounded algol-like languages, 1964.
- [9] Jan Grabowski. The decidability of persistence for vector addition systems. Information Processing Letters, 11(1):20–23, 29 August 1980.
- [10] M. Hack. Decidability questions for petri nets. Technical Report TR-161, MIT Lab. for Comp. Sci., June 1976.
- [11] R. Karp and R. Miller. Parallel program schemata. Journal of Computer and System Sciences, 3:147–195, 1969.
- [12] S. Rao Kosaraju. Decidability of reachability in vector addition systems (preliminary version). In Harry R. Lewis, Barbara B. Simons, Walter A. Burkhard, and Lawrence H. Landweber, editors, STOC, pages 267–281. ACM, 1982.
- [13] Maciej Koutny, Lukasz Mikulski, and Marta Pietkiewicz-Koutny. A taxonomy of persistent and nonviolent steps. In José Manuel Colom and Jörg Desel, editors, Petri Nets, volume 7927 of Lecture Notes in Computer Science, pages 210–229. Springer, 2013.
- [14] Landweber and Robertson. Properties of conflict-free and persistent petri nets. JACM: Journal of the ACM, 25, 1978.
- [15] Ernst W. Mayr. Persistence of vector replacement systems is decidable. Acta Informatica, 15:309–318, 1981.
- [16] Ugo Montanari and Francesca Rossi. Contextual nets. Acta Inf., 32(6):545–596, 1995.
- [17] P. Starke. Petri-Netze (in German). VEB Deutscher Verlag der Wissenschaften, East Berlin, GDR, 1980.
- [18] Valk and Jantzen. The residue of vector sets with applications to decidability problems in petri nets. ACTAINF: Acta Informatica, 21, 1985.