High-Dimensional Differentially-Private EM Algorithm: Methods and Near-Optimal Statistical Guarantees
Abstract
In this paper, we develop a general framework to design differentially private expectation-maximization (EM) algorithms in high-dimensional latent variable models, based on the noisy iterative hard-thresholding. We derive the statistical guarantees of the proposed framework and apply it to three specific models: Gaussian mixture, mixture of regression, and regression with missing covariates. In each model, we establish the near-optimal rate of convergence with differential privacy constraints, and show the proposed algorithm is minimax rate optimal up to logarithm factors. The technical tools developed for the high-dimensional setting are then extended to the classic low-dimensional latent variable models, and we propose a near rate-optimal EM algorithm with differential privacy guarantees in this setting. Simulation studies and real data analysis are conducted to support our results.
Keywords: Differential privacy; High-dimensional data; EM algorithm; Optimal rate of convergence.
1 Introduction
In the era of big data, there is an unprecedented number of large data sets becoming available for researchers/industries to retrieve important information. In the meantime, these large data sets often include some sensitive personal information, urgently generating demands for privacy-preserving algorithms that can protect the individual information during the data analysis. One widely adopted criterion for privacy-preserving algorithms is differential privacy (DP) (Dwork et al., 2006b, a). This notion has been widely developed and used nowadays in Microsoft (Erlingsson et al., 2014), Google (Ding et al., 2017), Facebook (Kifer et al., 2020) and the U.S. Census Bureau (Abowd, 2016) to help protect individual privacy including user habits, browsing history, social connections, and health records. The basic idea behind differential privacy is that the information of a single individual in the training data should appear as hidden so that given the outcome, it is almost impossible to distinguish if a certain individual is in the dataset.
The attractiveness of differential privacy could possibly be attributed to the ease of building privacy-preserving algorithms. Many traditional algorithms and statistical methods have been extended to their private counterparts, including top- selection (Bafna and Ullman, 2017; Steinke and Ullman, 2017), multiple testing (Dwork et al., 2018), decision trees (Jagannathan et al., 2009), and random forests (Rana et al., 2015). However, many existing works only focus on designing privacy-preserving algorithms while lacking the sharp analysis of accuracy in terms of minimax optimality. At the high-level, these privatized algorithms are designed by injecting random noise into the traditional algorithms. Such noise-injection procedures typically sacrifice statistical accuracy, and therefore, it is essential to understand what is the best accuracy an algorithm would output while maintaining a certain level of differential privacy requirement. This motivates us to study the trade-off between the privacy and the statistical accuracy.
This paper is devoted to studying this trade-off in latent variable models by proposing a DP version of the expectation-maximization (EM) algorithm. The EM algorithm is a commonly used approach when dealing with latent variables and missing values Ranjan et al. (2016); Quost and Denoeux (2016); Kadir et al. (2014); Ding and Song (2016). The statistical properties, such as the local convergence and minimax optimality of standard EM algorithm has been recently studied in Balakrishnan et al. (2017); Wang et al. (2015); Yi and Caramanis (2015); Cai et al. (2019a); Zhao et al. (2020), while the development of DP EM algorithm, especially the theories of the optimal trade-off between privacy and accuracy, is still largely unexplored. In this paper, we propose novel DP EM algorithms in both the classic low-dimensional setting and the contemporary high-dimensional setting, where the parameter we are interested in is sparse and its dimension is greatly larger than the sample size. We demonstrate the superiority of the proposed algorithm by applying it to specific statistical models. Under these specific statistical models, the convergence rates of the proposed algorithm are found to be minimax optimal with privacy constraints. The main contributions of this paper are summarized in the following.
-
•
We design a novel DP EM algorithm in the high-dimensional setting based on a noisy iterative hard-thresholding algorithm in the M-step. Such a step effectively enforces the sparsity of the attained estimator while maintaining differential privacy, and allows us to establish sharp rate of convergence of the algorithm. To the best of our knowledge, this algorithm is the first DP EM algorithm in high-dimensions with statistical guarantees.
-
•
We then apply the proposed DP EM algorithm to three common models in the high-dimensional setting: Gaussian mixture model, mixture of regression model, and regression with missing covariates. Under mild regularity conditions, we show that our algorithm obtains the minimax optimal rate of convergence with privacy constraints.
-
•
In the classical low-dimensional setting, a DP EM algorithm based on the Gaussian mechanism is designed. The technical tools developed for the high-dimensional setting are then used to establish the optimality in this general low-dimensional setting. We show that both theoretically and numerically, the proposed algorithm outperforms several existing private EM algorithms in this classical setting.
Related Work. The expectation-maximization (EM) algorithm, proposed in (Dempster et al., 1977), is a common approach in handling latent variable models. There has been a long history on the study of the EM algorithm (Wu, 1983; McLachlan and Krishnan, 2007). Recently, a seminal work (Balakrishnan et al., 2017) obtains a general framework to study the statistical guarantees of EM algorithms in the classic low-dimensional setting. In subsequent works, the convergence rates of EM algorithm under various hidden variable models are studied, including the Gaussian mixture (Xu et al., 2016; Daskalakis et al., 2017; Yan et al., 2017; Kwon and Caramanis, 2020) and mixture of linear regression (Yi et al., 2014; Kwon et al., 2019, 2020). Another important direction is to design variants of EM algorithms in the high-dimensional regime. Such a goal is fulfilled through regularization (Cai et al., 2019a; Yi and Caramanis, 2015; Zhang et al., 2020) and truncation (Wang et al., 2015) in the M-step. Due to the increasing attention on data privacy nowadays, the design of private EM algorithms is in great demand but still largely lacking.
The differential privacy is arguably the most popular notion of privacy nowadays. After its invention, the basic properties has been studied in (Dwork et al., 2010; Dwork and Roth, 2014; Dwork et al., 2017; Dwork and Feldman, 2018; Mirshani et al., 2019). The trade-off between statistical accuracy and privacy is one of the fundamental topics in differential privacy. In the low-dimensional setting, there are various works focusing on this trade-off, including mean estimation (Dwork et al., 2015; Steinke and Ullman, 2016; Bun et al., 2018; Kamath et al., 2019; Cai et al., 2019b; Kamath et al., 2020b), confidence intervals of Gaussian mean (Karwa and Vadhan, 2017) and binomial mean (Awan and Slavković, 2020), linear regression (Wang, 2018; Cai et al., 2019b), generalized linear models Song et al. (2020); Cai et al. (2020); Song et al. (2021), principal component analysis (Dwork et al., 2014; Chaudhuri et al., 2013), convex empirical risk minimization (Bassily et al., 2014), and robust M-estimators (Avella-Medina, 2020; Avella-Medina et al., 2021).
However, in the high-dimensional setting where the dimension is much larger than the sample size, the trade-off between statistical accuracy and privacy is less studied. Most of the existing works focus on relatively standard statistical problems such as the sparse mean estimation and regression. For example, (Steinke and Ullman, 2017) studies the optimal bounds for private top- selection problems. (Cai et al., 2019b) studies near-optimal algorithms for the sparse mean estimation. For the high-dimensional sparse linear regression, (Talwar et al., 2015) obtains a DP LASSO algorithm which is near-optimal in terms of the excess risk; (Cai et al., 2019b) proposes another DP LASSO algorithm with the optimal rate of convergence in estimation. In (Cai et al., 2020), a near-minimax optimal DP algorithm for high-dimensional generalized linear models is introduced.
In the literature of differential privacy, most of the existing works for latent variable models focus on the low-dimensional cases, while the study in the high-dimensional regime is largely lacking. In the classical low-dimensional setting, (Park et al., 2017) introduces a DP EM algorithm, but offers no statistical guarantees/accuracy analysis. (Nissim et al., 2007) provides a result for the low-dimensional Gaussian mixture model based on the sample-aggregate framework and reaches a convergence rate in estimation for the mixture of spherical Gaussian distributions. (Kamath et al., 2020a) considers a more general Gaussian mixture models and studies the total variation distance. (Wang et al., 2020) studies the DP EM algorithm in the classical low-dimensional setting and obtains the estimation error of order . In the current paper, we are going to show this rate can be significantly improved to , obtained by our proposed algorithm in the classic low-dimensional setting.
Organization of this paper. This paper is organized as follows. In Section 2, we introduce the problem formulation as well as some preliminaries of the EM algorithm and differential privacy. In Section 3, we present the main results of this paper and establish the convergence rate of the proposed EM algorithm in high-dimensional settings. In Section 4, we apply the results obtained in Section 3 to three specific models: Gaussian mixture model, mixture of regression, and regression with missing covariates. We present the estimation error bounds for these three models respectively and show the optimality. In Section 5, we consider the DP EM algorithm in the classic low-dimensional setting. In Section 6, simulation studies of the proposed algorithm are conducted to support our theory. Section 7 summarizes the paper and discusses some possible future work. In Appendix A, we provided some supplement materials. We prove the main results in Appendix B, and the proofs of other results and technical lemmas are in the Appendix C.
Notations. Throughout this paper, let be a vector. denotes the set of indices and indicates the restriction of vector on the set . Also, denotes the norm for and specifically denotes the number of non-zero coordinates of , and we also call it the sparsity level of . We denote to be the Hadamard product. Generally, we use to denote the number of samples, to denote the dimension of a vector and to denote the sparsity level of a vector. We also define a truncation function be a function denotes the projection into the ball of radius centered at the origin in . Moreover, we use to denote the gradient of the function . If there is no further specification, this gradient is taken with respect to the first argument. For two sequences and , we write if . We denote if there exist a constant such that and if there exist a constant such that . We also denote if and . In this paper, denote universal constants and their specific values may vary from place to place.
2 Problem Formulation
In this section, we present some preliminaries that are important for the discussions in the rest of the paper. We are going to introduce the EM algorithm in Section 2.1, and the formal definition and some critical properties of differential privacy in Section 2.2.
2.1 The EM algorithm
The EM algorithm is a widely used algorithm to compute the maximum likelihood estimator when there are latent or unobserved variables in the model. We first introduce the standard EM algorithm. Let and be random variables taking values in the sample spaces and . For each pair of data , we assume that only is observed, while remains unobserved. Suppose that the pair has a joint density function , where is the true parameter that we would like to estimate. Let be the marginal density function of the observed variable . Then, we can write by integrating out
| (1) |
The goal of the EM algorithm is to obtain an estimator of through maximizing the likelihood function. Specifically, suppose we have observations of : , we aim to use EM algorithm to maximize the log-likelihood , and get an estimator of . In many latent variable models, it is generally difficult to evaluate the log-likelihood directly, but relatively easy to compute the log-likelihood for the joint distribution . Such situations are in need of EM algorithms. Specifically, for a given parameter , let be the conditional distribution of given the observed variable , that is,
The EM algorithm uses an iterative approach motivated by Jensen’s inequality. Suppose that in the -th iteration, we have obtained and would like to update it to with a larger log-likelihood. The log-likelihood evaluated at can always be lower bounded, as shown in the following expression.
| (2) | ||||
with equality holds when . The basic idea of EM algorithm is to successively maximize the lower bound with respect to in (2). In the E-step, we evaluate the lower bound in (2) at the current parameter . Since the second term in (2) only depends on , which is fixed given the current , we only need to evaluate in the E-step. Then, in the M-Step, we calculate a new parameter which moves towards the direction that maximizes , so the lower bound in (2) becomes larger when we update to . We use the new parameter at the -th iteration and continue the E-step and M-step iteratively until convergence.
In the -th iteration, the M-step in the standard EM algorithm maximizes (Dempster et al., 1977), that is, . However, sometimes it is computationally expensive to compute the maximizer directly. As an alternative, the gradient EM (Balakrishnan et al., 2017) was proposed by taking one-step update of the gradient ascent in the M-step. When is strongly convex with respect to , this gradient EM approach is shown to reach the same statistical guarantee as that of the standard EM approach (Balakrishnan et al., 2017). In the high-dimensional setting, when the data dimension is much larger than the sample size and the true parameter is sparse, people have come up with different variants of EM algorithms. For example, in the M-step, the maximization approach is generalized to the regularized maximization (Yi and Caramanis, 2015; Cai et al., 2019a; Zhang et al., 2020) and the gradient approach is generalized to the truncated gradient (Wang et al., 2015).
2.2 Some basic properties of differential privacy
In this section, we introduce the concepts and properties of differential privacy. These properties will play an important role in the design of the DP EM algorithm. First, the formal definition of differential privacy is given below.
Definition 2.1 (Differential Privacy (Dwork et al., 2006b)).
Let be the sample space for an individual data, a randomized algorithm is -DP if and only if for every pair of adjacent data sets and for any , the inequality below holds:
where we say that two data sets and are adjacent if and only if they differ by one individual datum.
According to the definition, the two parameters control the privacy level. With smaller and , the privacy constraint becomes more stringent. Intuitively speaking, this definition suggests that for a DP algorithm , an adversary cannot distinguish if the original dataset is or when and is adjacent, implying that the information of each individual is protected after releasing .
We then list several useful facts of designing DP algorithms. To create a DP algorithm, the arguably most common strategy is to add random noise to the output. Intuitively, the scale of the noise can not be too large, otherwise the accuracy of the output will be sacrificed. This scale is characterized by the sensitivity of the algorithm.
Definition 2.2.
For any algorithm and two adjacent data sets and , the -sensitivity of is defined as:
For algorithms with finite -sensitivity or -sensitivity, we can achieve differential privacy by adding Laplace noises or Gaussian noises respectively.
Proposition 2.3 (The Laplace Mechanism (Dwork et al., 2006b)).
Let be a deterministic algorithm with . For with coordinates be i.i.d samples drawn from Laplace, is -DP.
Proposition 2.4 (The Gaussian Mechanism (Dwork et al., 2006b)).
Let be a deterministic algorithm with . For with coordinates i.i.d drawn from , is -DP.
These two mechanisms are computationally efficient, and are typically used to build more complicated algorithms. In the following, we introduce the post-processing and composition properties of differential privacy, which enable us to design complicated DP algorithms by combining simpler ones.
Proposition 2.5 (Post-processing Property (Dwork et al., 2006b)).
Let be an -DP algorithm and be an arbitrary function which takes as input, then is also -DP.
Proposition 2.6 (Composition property (Dwork et al., 2006b)).
For , let be -DP algorithm, then is -DP algorithm.
In the following section, we will see that the above two properties are particularly useful in the design of the DP EM algorithm.
3 High-dimensional EM Algorithm
In this section, we develop a novel DP EM algorithm for the (sparse) high-dimensional latent variable models. We are going to first introduce the detailed description of the proposed algorithm in Section 3.1, and then present its theoretical properties in Section 3.2. We will further apply our general method to three specific models in the next section.
3.1 Methodology
Suppose we have data sampled from the latent variable model (1) and aim to use the EM algorithm to find the maximum likelihood estimator in a DP manner. Since the EM algorithm is an iterative approach where the -th iteration takes as input the from the M-step in the last iteration, it suffices to make each differentially private to ensure the privacy guarantee of the final output.
Our algorithm relies on two key designs in the M-step. First, we use the gradient EM approach, and in the gradient update stage, we introduce a truncation step on the gradient to control the sensitivity of the gradient update, and thus we can appropriately determine the scale of noise we need to achieve differential privacy. Secondly, we propose to apply the noisy hard-thresholding algorithm (NoisyHT) (Dwork et al., 2018) to pursue sparsity and achieve privacy at the same time. The NoisyHT algorithm is defined as follows,
In the last step, denotes the operator that makes while preserving . A great advantage of this algorithm is that when the vector has bounded sensitivity , the algorithm is guaranteed to be DP, as we can see in the lemma below.
Lemma 3.1 ((Dwork et al., 2018)).
If for every pair of adjacent data sets . we have , then the noisy hard-thresholding algorithm is -DP.
Another important property of the NoisyHT algorithm is its accuracy. Specifically, for the coordinates that are not chosen by the NoisyHT algorithm, the norm of these coordinates is upper bounded by that of the coordinates with the same size but chosen by the NoisyHT algorithm up to some error term. The formal statement is summarized in the following with the proof given in Appendix C.1.
Lemma 3.2.
Let be the set chosen by the NoisyHT algorithm, be the input vector and be defined as in the NoisyHT algorithm. For every set and such that and for every , we have:
After introducing the NoisyHT algorithm, we now proceed to the development of the DP EM algorithm. We update the estimator based on the NoisyHT algorithm in each M-step after truncation. Such a modified M-step guarantees that the output is sparse and differentially private in each iteration. We also note here that we use the sample-splitting in the algorithm, which makes independent with the batch of samples in -th iteration and helps control the sensitivity of the gradient. The algorithm is summarized below:
In the above algorithm, the truncation operator with truncation level is defined as , where , and denotes some generic truncation function with norm upper bounded by . Later in the application to different specific models, we will specify the form of for each model. The next lemma shows Algorithm 2 is -DP.
Lemma 3.3.
The output of high-dimensional DP EM algorithm (Algorithm 2) is -DP.
The proof of Lemma 3.3 is given in the Appendix C.2. In theory, we shall take the truncation level and number of iterations to be the order of and , respectively, as we will show in the next section. For the sparsity level , we should choose it to have the same order of the true sparsity level . While the true parameter is unknown in practice, could be chosen through cross-validation. Given the differential privacy guarantees, we are going to analyze the utility of this algorithm in the next section.
3.2 Theoretical gaurantees
In this section, we analyze the theoretical properties of the proposed high-dimensional DP EM algorithm. Before we lay out the main results, we first introduce four technical conditions. The first three conditions are standard in the literature of EM algorithms; for example, see (Balakrishnan et al., 2017; Wang et al., 2015; Zhu et al., 2017; Wang et al., 2020). The fourth condition is needed to control the sensitivity in the design of DP algorithms. We will verify these four conditions in the specific models in the next section.
Condition 3.4 (Lipschitz-Gradient).
For the true parameter and any , where denotes a region in the parameter space. We have
This condition implies that if is close to the true parameter , then the gradients and should also be close, which implies gradient stability.
Condition 3.5 (Concavity-Smoothness ).
For any , is -smooth such that
and -strongly concave such that
The Concavity-Smoothness condition indicates that when the second argument of is , is a well-behaved convex function that it can be upper bounded and lower bounded by two quadratic functions. This condition ensures the geometric decay of the optimization error in the statistical analysis.
Condition 3.6 (Statistical-Error).
For any fixed and , we have with probability at least ,
In this condition, the statistical error is quantified by the norm between the population quantity and its sample version . Such a bound is different from the norm bound considered in the classic low-dimensional DP EM algorithms (Wang et al., 2020). In the high-dimensional setting, although for each index, the statistical error is small, the norm can still be quite large. This fine-grained bound enables us to iteratively quantify the statistical accuracy when using the NoisyHT in the M-step.
Condition 3.7 (Truncation-Error).
For any and , there exists a non-incresaing function , such that for the truncation level , with probability ,
The Truncation-Error condition quantifies the error caused by the truncation step in Algorithm 2. Intuitively, when is large, the truncation error can be very small, while leading to larger sensitivity and larger injected noise to ensure privacy. We need to carefully choose to strike a balance between the statistical accuracy and privacy cost. Below we show the main result of this section, with the detailed proof given in Section B.1.
Theorem 3.8.
Suppose the true parameter is sparse with . We define with for some . We assume the Concavity-Smoothness holds and the initialization satisfies . We further assume that the Lipschitz-Gradient holds and define . In Algorithm 2, we let the step size , the number of iterations , the sparsity level where is a constant greater than 1 and . We assume the condition Truncation-Error() holds with and . Moreover, we assume the condition Statistical-Error holds and assume that and there exists a constant , and , also . Then there exist constants , it holds that
| (3) |
with probability . Specifically, for the output in Algorithm 2, it holds that
with probability .
To interpret this result, let us discuss the four terms in (3). The first term, , is the optimization error. With , this term shrinks to zero at a geometric rate when the iteration number is sufficiently large. The second term is of order when is chosen as the same order of , this is the statistical error caused by finite samples. We will further show that in some specific models, is of the order and makes the second term to be . The third term can be seen as the cost of privacy, as this error is introduced by the additional requirement that the output needs to be -DP. This term becomes larger when the privacy constraint becomes more stringent ( become smaller). Typically, in practice, we choose for some and a small constant. This implies that when and satisfy , the cost of privacy will be negligible comparing to the statistical error. In this case, we can gain privacy for free in terms of convergence rate. The fourth term is due to the truncation of the gradient. Under the Truncation-Error condition with an appropriately chosen truncation parameter, this term reaches a convergence rate dominated by the statistical error up to logarithm factors.
4 DP EM Algorithm in Specific Models
In this section, we apply the results developed in Section 3 to specific statistical models and establish concrete convergence rates. We will discuss three models, the Gaussian mixture model, mixture of regression model and regression with missing covariates, in Sections 4.1, 4.2 and 4.3 respectively. Further, for each statistical model, we establish the minimax lower bound of the convergence rate, and demonstrate that our algorithm obtains a near minimax optimal rate of convergence.
4.1 Gaussian mixture model
In this subsection, we first apply the results in Section 3 to the Gaussian mixture model. By verifying the conditions in Theorem 3.8, we establish the convergence rate of the DP estimation in the Gaussian mixture model.
In a standard Gaussian mixture model, we assume:
| (4) |
where is a -dimensional output and . In this model, and are the -dimensional vectors representing the population means of each class, and is a class indicator variable with and . Note that is a hidden variable and independent of . In the high dimensional setting, we assume to be sparse.
Let be samples from the Gaussian mixture model. Using the framework of the EM method introduced in Section 3, we need to calculate
where
Then, for the -step in the -th iteration given , the update rule is given by
Given this expression, we now present the DP estimation in the high-dimensional Gaussian mixture model by applying Algorithm 2. The algorithm is presented in Algorithm 3.
To derive the converge rate of , we need to first verify Conditions 3.4-3.7. Conditions 3.4-3.6 are standard in the literature of EM algorithms (Balakrishnan et al., 2017; Wang et al., 2015). We adapt them into our setting and state the results altogether below.
Lemma 4.1.
Suppose we can always find a sufficiently large constant to be the lower bound of the signal-to-noise ratio, . Then
The detailed proof of Lemma 4.1 is given in Appendix C.3. Given these verified conditions, the following theorem establishes the results for the DP estimation in the high-dimensional Gaussian mixture model.
Theorem 4.2.
We implement Algorithm 3 to the observations generated from the Gaussian mixture model (4). Let defined the same way as in Lemma 4.1. We assume for a sufficiently large constant . Let the initialization satisfy and . Also, set the sparsity level with be a constant and . The step size is chosen as . We choose the number of iterations , and let truncation level . We further assume that . Then, the proposed Algorithm 3 is -DP. Also, we can show that there exist sufficient large constants , it holds that
| (5) |
with probability , where are constants.
The proof of Theorem 4.2 is given in Section B.2. Similar to the interpretation for the results in (3), the first and the second items are respectively the statistical error and the cost of privacy.
In the following, we present the minimax lower bound for the estimation in the high-dimensional Gaussian mixture model with differential privacy constraints, indicating the convergence rate obtained above is near optimal.
Proposition 4.3.
Suppose be the data set of samples observed from the Gaussian mixture model (4) and let be any algorithm such that , where be the set of all -DP algorithms for the estimation of the true parameter . Then there exists a constant , if for some fixed , and for some fixed , we have
4.2 Mixture of regression model
We continue to demonstrate the proposed algorithm in the mixture of regression model, where we assume the following data generative process
| (6) |
where is the response, is an indicator variable with , , , and is a -dimensional coefficients vector, we also require to be sparse in the high-dimensional setting. Note that are independent with each other.
Let be the observed samples from the mixture of regression model. Then, to use the EM algorithm, we need to compute
where
According to the gradient EM update rule, for the -th iteration , we update by
Similar to the Gaussian Mixture model, to apply Algorithm 2, we need to specify the truncation operator . Rather than using truncation on the whole gradient, we perform the truncation on , and respectively, which leads to a more refined analysis and improved rate in the statistical analysis. Specifically, we define
Due to space constraints, we present the full algorithm for mixture of regression model in section A.1. We also verify Conditions 3.4-3.7 in the mixture of regression model, and summarize the results in Lemma A.1. In the following, we show the theoretical guarantees for the high-dimensional DP EM algorithm on the mixture of regression model, with proof given in Section B.4.
Theorem 4.4.
We implement the Algorithm 5 to the sample generated from the mixture of regression model (6). Let defined as in Lemma A.1. We assume for a sufficiently large . Let the initialization and . Also, set the sparsity level with be a constant and . The step size is chosen as . We choose the number of iterations , and let the truncation level . We assume that . Then, the proposed Algorithm 5 is -DP, there exist constants , it holds that
| (7) |
with probability , where are constants.
Theorem 4.4 achieves a similar rate consisting of statistical error and privacy cost as we have discussed above in the general private EM algorithm and the Gaussian mixture model. The proposition below shows the lower bound in the mixture of regression model.
Proposition 4.5.
4.3 Regression with missing covariates
The last model we discuss in this section is the regression with missing covariates. For the model setup, we assume the following data generative process
where is the response, , and are independent. is a -dimensional coefficient vector, and we require to be sparse in the high-dimensional setting with . Let be samples generated from the above model. For each , we assume the missing completely at random model such that each coordinate of is missing independently with probability . Specifically, for each , we denote be the observed covariates such that , where denotes the Hadamard product and is a -dimensional Bernoulli random vector with if is observed and if is missing. Then, by the EM algorithm, we compute
Here, and are defined as
Then, according to the gradient EM update, for the -th iteration , the update rule for the estimation of is given below
Similar as before, to apply Algorithm 2, we also need to specify the truncation operator . According to the definition of , when is close to , we find that is close to , so we propose to truncate on and . Specifically, let
We present the full DP algorithm for regression with missing covariates model in section A.2, and verify Conditions 3.4-3.7 in the regression with missing covariates model. The results are summarized as Lemma A.2. In the following, we show the theoretical guarantees for the high-dimensional DP EM algorithm on the mixture of regression model, with the proof given in Section B.6.
Theorem 4.6.
We implement Algorithm 6 to the samples generated from the regression with missing covariates model. Let are defined as in Lemma A.2, and assume the initialization satisfies and . Also, set the sparsity level with be a constant and . We choose the step size , the number of iterations , and the truncation level . We further assume that . Then, the proposed Algorithm 6 is -DP, there exist constants , it holds that
with probability where are constants.
This results is similar as before, as the convergence rate in the DP estimation in the regression with missing covariates consists of the statistical error and the privacy cost . Again, we show the minimax lower bound for the estimation in the regression with missing covariates with differential privacy constraints.
Proposition 4.7.
Suppose be the data set of samples observed from the regression with missing covariates discussed above and let and defined as in Proposition 4.3. Then there exists a constant , if for some fixed , and for some fixed , we have
5 Low-dimensional DP EM Algorithm
In this section, we extend the technical tools we developed in Section 3 to the classic low-dimensional setting, and propose the DP EM algorithm in this low-dimensional regime. We will further apply our proposed algorithm to the Gaussian mixture model as an example, and show that the proposed algorithm obtains a near-optimal rate of convergence.
For the low-dimensional case, instead of using the noisy hard-thresholding algorithm, here we use the Gaussian mechanism in the M-step for each iteration. Similar to the high-dimensional setting, we use the sample splitting in each iteration, and the truncation step in each M-step to ensure bounded sensitivity. The algorithm is summarized below.
Lemma 5.1.
The output of the low dimensional DP EM algorithm (Algorithm 4) is -DP.
Given the privacy guarantee, we then analyze the statistical accuracy of this algorithm. Before that, we need to modify the Condition 3.6 and Condition 3.7 to fit into the low-dimensional setting.
Condition 5.2 (Statistical-Error-2 ).
For any fixed , we have that with probability at least ,
A difference between the high-dimensional and low-dimensional cases is that in the low-dimensional case, the dimension of , noted as , can be much smaller than the sample size , so rather than using the infinity norm, the statistical error can be directly measured in norm to reflect the accumulated difference between each index of the true and .
Condition 5.3 (Truncation-Error-2 ).
For any , there exists a non-increasing function , such that for the truncation level , with probability ,
Below is the main theorem for the low-dimensional DP EM algorithm.
Theorem 5.4.
For the Algorithm 4, we define and . We assume the Lipschitz-Gradient and the Concavity-Smoothness hold. Define . For the parameters, we choose the step size , the truncation level , and the number of iterations . We assume that and . For the sample size, there exists a constant , and . Then, under the conditions Statistical-Error-2 and Truncation-Error-2, there exists sufficient large constant , such that it holds that with probability ,
| (8) |
Specifically, for the output in Algorithm 4, it holds that
The proof of Theorem 5.4 is given in Section B.7. There are three terms in the result (8), and their interpretations align with the high-dimensional cases. The first term is the optimization error, which converges to zero at a geometric rate. When the number of iterations is large, this term is small. The second term is the cost of privacy caused by the Gaussian noise added in each iteration to achieve DP. When the privacy constraint becomes more stringent ( become smaller), this term becomes larger. The third term reflects the truncation error and the statistical error. On one hand, by choosing an appropriate , nearly every index is below the threshold in each iteration, so the truncation costs few accuracy loss. On the other hand, the statistical error is caused by the finite samples. With proper choice of and sufficiently large , the third term can be quite small.
The result in Theorem 5.4 is obtained for the general latent variables model. The convergence rates of and are unspecified in this general case, which may vary according to different specific models. To show the theoretical guarantees of the proposed algorithm, as an example, we apply the algorithm to the Gaussian mixture model and leave the results of the other two specific models in the Appendix A.4.1 and A.4.2.
Theorem 5.5.
For the Algorithm 4 in the Gaussian mixture model, let the truncation of the gradient be the same as the truncation of gradient in Algorithm 3. Then, we define and . Define as in Lemma 4.1 and . For the choice of parameters, the step size is chosen as , the truncation level is chosen to be and the number of iterations is chosen as . For the sample size , it is sufficiently large that there exists constants , such that and . Then, there exists sufficient large constant , such that it holds that with probability ,
We remark here that in the literature, (Wang et al., 2020) also analyzed the Gaussian mixture model and obtained a rate of convergence. Our result in Theorem 5.5 has faster rate of convergence than that. In the following, we are going to show that such a rate cannot be improved further up to logarithm factors.
Proposition 5.6.
Suppose be the data set of samples observed from the Gaussian mixture model and let be any algorithm such that , where be the set of all -DP algorithms for the estimation of the true parameter in the low-dimensional setting. Then there exists a constant , if and for some fixed with and , we have
6 Numerical Experiments
In this section, we investigate the numerical performance of the proposed DP EM algorithms. Specifically, in the high-dimensional setting, for the illustration purpose, we investigate the Gaussian mixture model (Algorithm 3) in Section 6.1 on the simulated data sets in details. Due to space constraints, an additional simulation for Mixture of regression model is presented in Supplement materials A.3. Then, in the low-dimensional case, we compare our Algorithm 4 with the algorithm in (Wang et al., 2020) under the Gaussian mixture model in Section 6.2. Further, in Section 6.3, we demonstrate the numerical performance of the proposed algorithm on real datasets.
6.1 Simulation results for Gaussian mixture model
For the DP EM algorithm in the high-dimensional Gaussian mixture model, the simulated data set is constructed as follows. First, we set to be a unit vector, where the first indices equal to and the rest of the indices are zero. For , we generate , where and with . We consider the following three settings:
-
1.
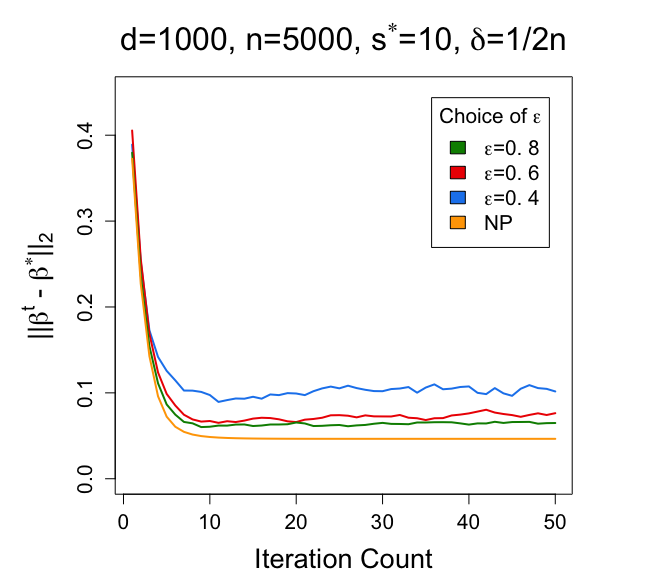
Fix . Compare the results of Algorithm 3 when , respectively.
-
2.
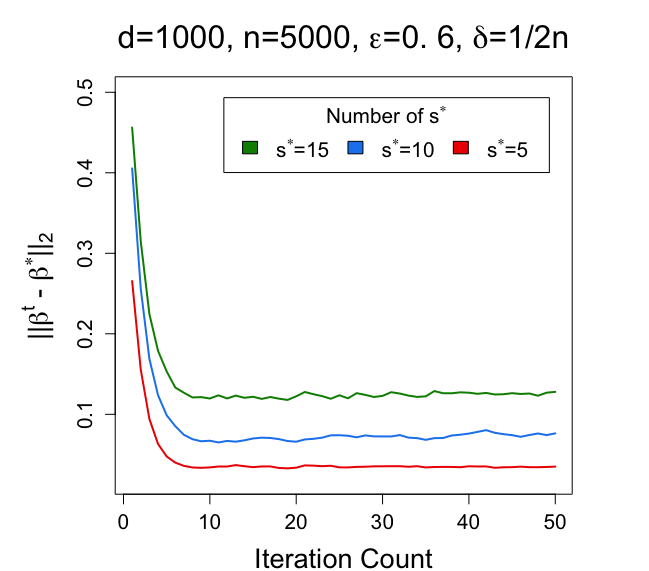
Fix . Compare the results of Algorithm 3 when , respectively.
-
3.
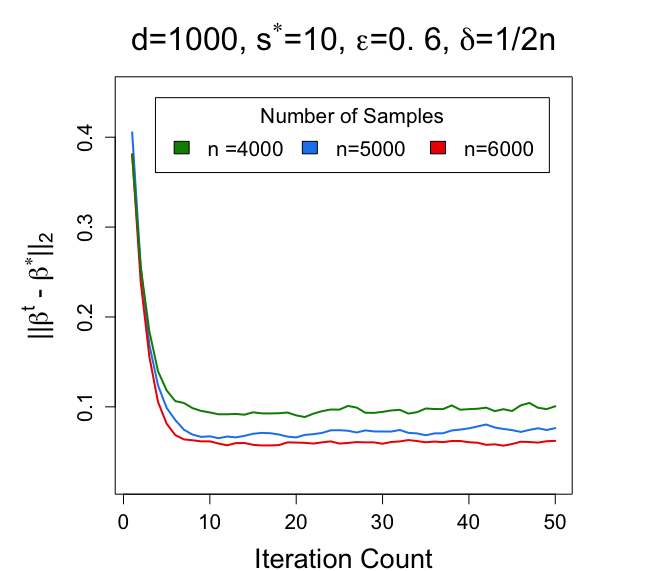
Fix . Compare the results of Algorithm 3 when , respectively.
For each setting, we repeat the experiment for 50 times and report the average of the estimation error . For each experiment, we set the step size to be 0.5. The results are plotted in Figure 1.
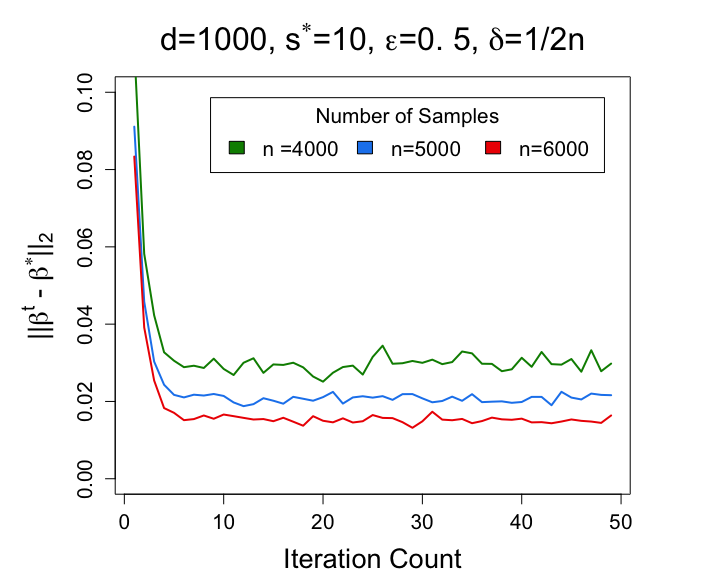
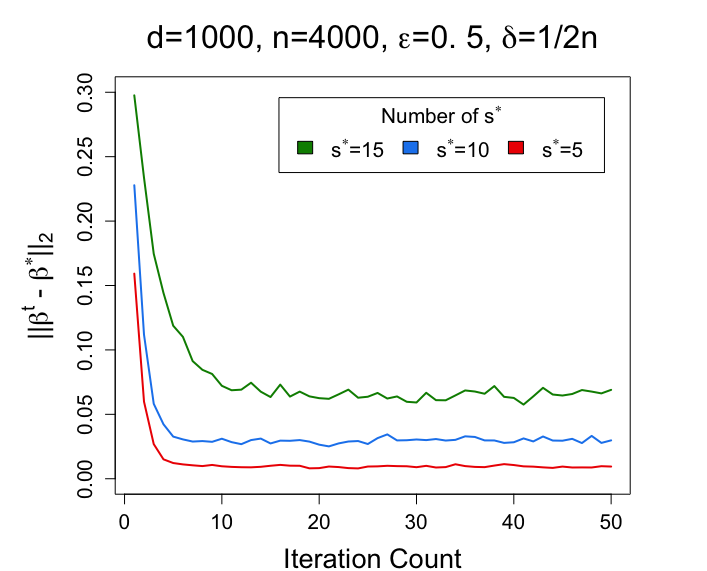
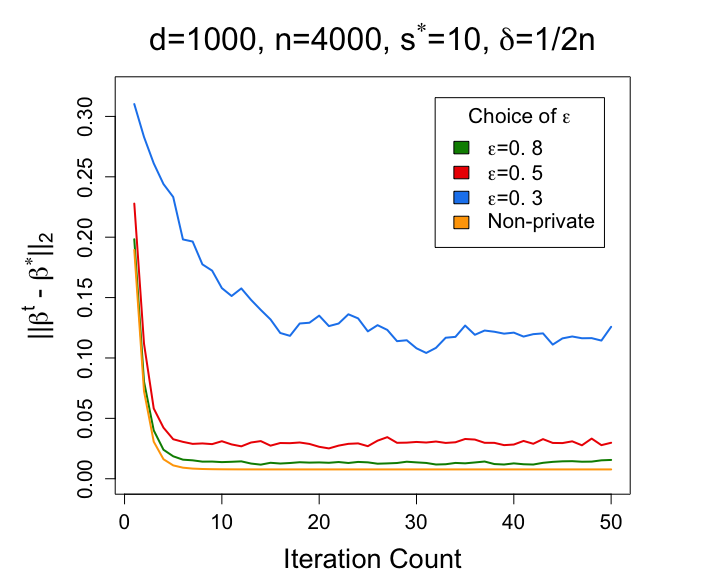
From Figure 1, we can clearly discover the relationship between different choices of and the performance of proposed algorithm in the Gaussian mixture model. The left figure in Figure 1 shows that the estimation of becomes more accurate when becomes larger. The middle figure in Figure 1 shows that when becomes smaller, the estimation error becomes smaller. The right figure in Figure 1 shows that when becomes larger (the privacy constraints are more relaxed), the cost of privacy becomes smaller, and therefore the estimator achieves a smaller estimation error. With the becomes large enough, the estimator becomes closer to the non-private setting.
6.2 Comparison with other algorithms
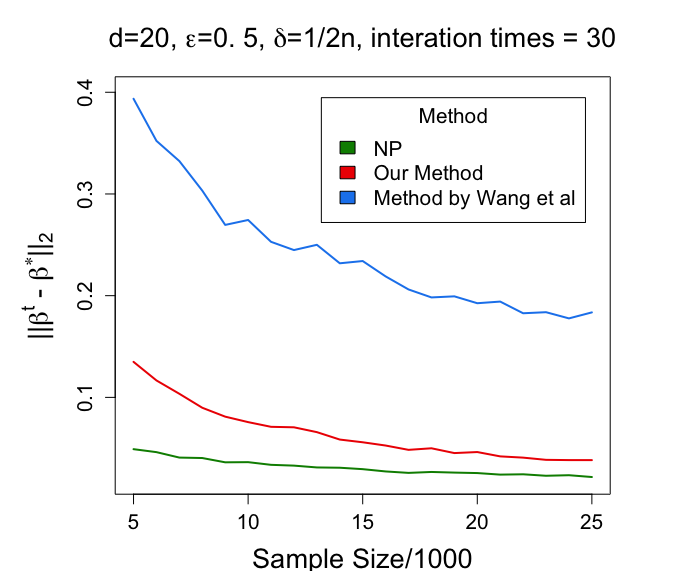
In the literature, (Wang et al., 2020) also studied the DP EM algorithm in the classic low-dimensional latent variable models. In this section, we compare our proposed method with 1). the algorithm proposed in (Wang et al., 2020), and 2). the standard (non-private) gradient EM algorithm (Balakrishnan et al., 2017).
The synthetic data is generated as follows. We first set the true parameter to be a unit vector with each element equal to . Then we simulate the Gaussian mixture model with satisfying and sample a multivariate Gaussian variable with . At last, we compute .
We consider the following two settings. In the first setting, we fix and vary from 5000 to 25000; in the second setting, we fix and vary from 5 to 25. For each setting, we report the average estimation error among 50 repetitions. The simulation results are summarized in Figure 2. The results indicate that although there is always a gap between our algorithm with the non-private EM algorithm (due to the cost of privacy), our algorithm has a much smaller error than that produced by that in (Wang et al., 2020).
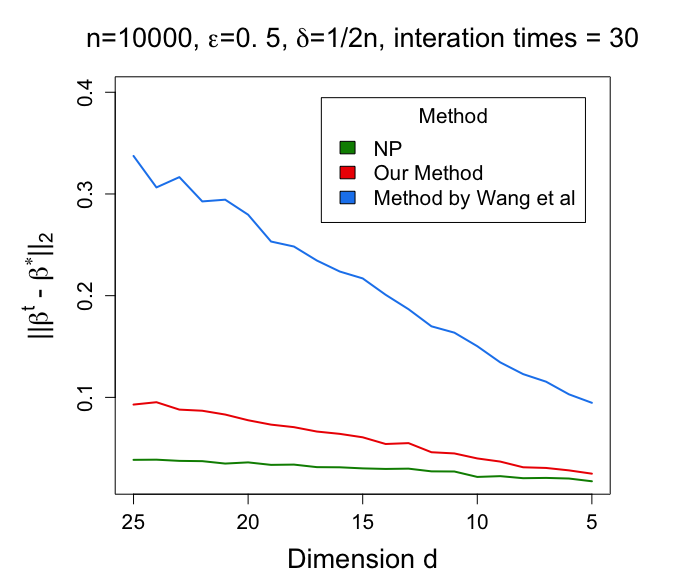
6.3 Real data analysis
In this section, we apply the proposed DP EM algorithm for high-dimensional Gaussian mixture to the Breast Cancer Wisconsin (Diagnostic) Data Set, which is available at the UCI Machine Learning Repository (https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)) (Dua and Graff, 2017). This data set contains 569 instances and 30 attributes. Each instance describes the diagnostic result for an individual as ‘Benign’ or ‘Malignant’. In the dataset, there are 212 instances labeled as ‘Malignant’ while the rest 357 instances labeled as ‘Benign’. Such a medical diagnose data set often contains personal sensitive information and serves as a suitable data set to apply our privacy-preserving algorithms.
In our experiment, all the attributes are normalized to have zero mean and unit variance. Moreover, to make the dataset symmetric, we first randomly drop out 145 data points in the ‘Benign’ class and compute the overall sample mean. Then for each data point, we subtract the overall sample mean from it. After preprocessing, the data is randomly split into two parts, where 70% of the instances are used for training and 30% of instances are used for testing.
In the training stage, we estimate the parameter using the proposed algorithm for high-dimensional Gaussian mixture model (Algorithm 3). We run Algorithm 3 for 50 iterations with step size . The initialization is chosen as the unit vector where all indexes equal . We fix , and choose various sparsity level and privacy parameter as displayed in Table 3. In the testing stage, we classify each testing data as ‘Benign’ or ‘Malignant’ according to the distance closeness between its attributes and with the distance between its attributes and . Then we compute the misclassification rate by comparing with the true diagnostic outcome. For each choice of parameters, we repeat the whole training and testing stages for 50 times, and report the average misclassification rate and the standard error. To compare with the non-private setting, for each choice of parameters, we also use the Algorithm described in (Wang et al., 2015) as the baseline for the non-private setting (shown as in the table below). The results are summarized in the following Table 3.
| 0.14(.07) | 0.12(.05) | 0.10(.04) | |
| 0.08(.02) | 0.07(.02) | 0.07(.01) | |
| 0.07(.02) | 0.06(.02) | 0.06(.01) |
The results suggest that when the privacy requirements become more stringent, the classification accuracy drops in a mild way. Considering the significance to achieve privacy guarantees, such loss of accuracy could be acceptable.
7 Conclusion
In this paper, we introduce a novel DP EM algorithm in both high-dimensional and low-dimensional settings. In the high-dimensional setting, we propose an algorithm based on noisy iterative hard thresholding and show this method is minimax rate-optimal up to logarithm factors in three specific models: Gaussian mixture, mixture of regression, and regression with missing covariates. In the low-dimensional setting, an algorithm based on Gaussian mechanism is also developed and shown to be near minimax optimal.
References
- Abowd [2016] John M Abowd. The challenge of scientific reproducibility and privacy protection for statistical agencies. Census Scientific Advisory Committee, 2016.
- Avella-Medina [2020] Marco Avella-Medina. Privacy-preserving parametric inference: a case for robust statistics. J. Am. Stat. Assoc., pages 1–15, 2020.
- Avella-Medina et al. [2021] Marco Avella-Medina, Casey Bradshaw, and Po-Ling Loh. Differentially private inference via noisy optimization. arXiv preprint arXiv:2103.11003, 2021.
- Awan and Slavković [2020] Jordan Awan and Aleksandra Slavković. Differentially private inference for binomial data. Journal of Privacy and Confidentiality, 10(1):1–40, 2020.
- Bafna and Ullman [2017] Mitali Bafna and Jonathan Ullman. The price of selection in differential privacy. In COLT, pages 151–168. PMLR, 2017.
- Balakrishnan et al. [2017] Sivaraman Balakrishnan, Martin J Wainwright, and Bin Yu. Statistical guarantees for the em algorithm: From population to sample-based analysis. Ann Stat, 45(1):77–120, 2017.
- Bassily et al. [2014] Raef Bassily, Adam Smith, and Abhradeep Thakurta. Private empirical risk minimization: Efficient algorithms and tight error bounds. In FOCS, pages 464–473. IEEE, 2014.
- Bun et al. [2018] Mark Bun, Jonathan Ullman, and Salil Vadhan. Fingerprinting codes and the price of approximate differential privacy. SIAM J. Comput., 47(5):1888–1938, 2018.
- Cai et al. [2019a] T Tony Cai, Jing Ma, and Linjun Zhang. Chime: Clustering of high-dimensional gaussian mixtures with em algorithm and its optimality. Ann Stat., 47(3):1234–1267, 2019a.
- Cai et al. [2019b] T Tony Cai, Yichen Wang, and Linjun Zhang. The cost of privacy: Optimal rates of convergence for parameter estimation with differential privacy. arXiv preprint arXiv:1902.04495, 2019b.
- Cai et al. [2020] T Tony Cai, Yichen Wang, and Linjun Zhang. The cost of privacy in generalized linear models: Algorithms and minimax lower bounds. arXiv preprint arXiv:2011.03900, 2020.
- Chaudhuri et al. [2013] Kamalika Chaudhuri, Anand D Sarwate, and Kaushik Sinha. A near-optimal algorithm for differentially-private principal components. J Mach Learn Res, 14, 2013.
- Daskalakis et al. [2017] Constantinos Daskalakis, Christos Tzamos, and Manolis Zampetakis. Ten steps of em suffice for mixtures of two gaussians. In COLT, pages 704–710. PMLR, 2017.
- Dempster et al. [1977] Arthur P Dempster, Nan M Laird, and Donald B Rubin. Maximum likelihood from incomplete data via the em algorithm. J R Stat Soc Series B, 39(1):1–22, 1977.
- Ding et al. [2017] Bolin Ding, Janardhan Kulkarni, and Sergey Yekhanin. Collecting telemetry data privately. In NeurIPS, pages 3574–3583, 2017.
- Ding and Song [2016] Wei Ding and Peter X-K Song. Em algorithm in gaussian copula with missing data. Comput Stat Data Anal, 101:1–11, 2016.
- Dua and Graff [2017] Dheeru Dua and Casey Graff. UCI machine learning repository, 2017. URL http://archive.ics.uci.edu/ml.
- Dwork and Feldman [2018] Cynthia Dwork and Vitaly Feldman. Privacy-preserving prediction. In COLT, pages 1693–1702. PMLR, 2018.
- Dwork and Roth [2014] Cynthia Dwork and Aaron Roth. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci., 9(3-4):211–407, 2014.
- Dwork et al. [2006a] Cynthia Dwork, Krishnaram Kenthapadi, Frank McSherry, Ilya Mironov, and Moni Naor. Our data, ourselves: Privacy via distributed noise generation. In Eurocrypt, pages 486–503. Springer, 2006a.
- Dwork et al. [2006b] Cynthia Dwork, Frank McSherry, Kobbi Nissim, and Adam Smith. Calibrating noise to sensitivity in private data analysis. In TCC, pages 265–284. Springer, 2006b.
- Dwork et al. [2010] Cynthia Dwork, Guy N Rothblum, and Salil Vadhan. Boosting and differential privacy. In FOCS, pages 51–60. IEEE, 2010.
- Dwork et al. [2014] Cynthia Dwork, Kunal Talwar, Abhradeep Thakurta, and Li Zhang. Analyze gauss: optimal bounds for privacy-preserving principal component analysis. In STOC, 2014.
- Dwork et al. [2015] Cynthia Dwork, Adam Smith, Thomas Steinke, Jonathan Ullman, and Salil Vadhan. Robust traceability from trace amounts. In FOCS, pages 650–669. IEEE, 2015.
- Dwork et al. [2017] Cynthia Dwork, Adam Smith, Thomas Steinke, and Jonathan Ullman. Exposed! a survey of attacks on private data. Annu. Rev. Stat. Appl., 4:61–84, 2017.
- Dwork et al. [2018] Cynthia Dwork, Weijie J Su, and Li Zhang. Differentially private false discovery rate control. arXiv preprint arXiv:1807.04209, 2018.
- Erlingsson et al. [2014] Úlfar Erlingsson, Vasyl Pihur, and Aleksandra Korolova. Rappor: Randomized aggregatable privacy-preserving ordinal response. In CCS’14, pages 1054–1067, 2014.
- Jagannathan et al. [2009] Geetha Jagannathan, Krishnan Pillaipakkamnatt, and Rebecca N Wright. A practical differentially private random decision tree classifier. In ICDM. IEEE, 2009.
- Kadir et al. [2014] Shabnam N Kadir, Dan FM Goodman, and Kenneth D Harris. High-dimensional cluster analysis with the masked em algorithm. Neural Comput, 26(11):2379–2394, 2014.
- Kamath et al. [2019] Gautam Kamath, Jerry Li, Vikrant Singhal, and Jonathan Ullman. Privately learning high-dimensional distributions. In COLT, pages 1853–1902. PMLR, 2019.
- Kamath et al. [2020a] Gautam Kamath, Or Sheffet, Vikrant Singhal, and Jonathan Ullman. Differentially private algorithms for learning mixtures of separated gaussians. In ITA, pages 1–62. IEEE, 2020a.
- Kamath et al. [2020b] Gautam Kamath, Vikrant Singhal, and Jonathan Ullman. Private mean estimation of heavy-tailed distributions. In COLT, pages 2204–2235. PMLR, 2020b.
- Karwa and Vadhan [2017] Vishesh Karwa and Salil Vadhan. Finite sample differentially private confidence intervals. arXiv preprint arXiv:1711.03908, 2017.
- Kifer et al. [2020] Daniel Kifer, Solomon Messing, Aaron Roth, Abhradeep Thakurta, and Danfeng Zhang. Guidelines for implementing and auditing differentially private systems. arXiv preprint arXiv:2002.04049, 2020.
- Kwon and Caramanis [2020] Jeongyeol Kwon and Constantine Caramanis. The EM algorithm gives sample-optimality for learning mixtures of well-separated gaussians. In COLT. PMLR, 2020.
- Kwon et al. [2019] Jeongyeol Kwon, Wei Qian, Constantine Caramanis, Yudong Chen, and Damek Davis. Global convergence of the em algorithm for mixtures of two component linear regression. In COLT, pages 2055–2110. PMLR, 2019.
- Kwon et al. [2020] Jeongyeol Kwon, Nhat Ho, and Constantine Caramanis. On the minimax optimality of the em algorithm for learning two-component mixed linear regression. arXiv preprint arXiv:2006.02601, 2020.
- McLachlan and Krishnan [2007] Geoffrey J McLachlan and Thriyambakam Krishnan. The EM algorithm and extensions, volume 382. John Wiley & Sons, 2007.
- Mirshani et al. [2019] Ardalan Mirshani, Matthew Reimherr, and Aleksandra Slavković. Formal privacy for functional data with gaussian perturbations. In ICML, pages 4595–4604. PMLR, 2019.
- Nissim et al. [2007] Kobbi Nissim, Sofya Raskhodnikova, and Adam Smith. Smooth sensitivity and sampling in private data analysis. In STOC, pages 75–84, 2007.
- Park et al. [2017] Mijung Park, James Foulds, Kamalika Choudhary, and Max Welling. Dp-em: Differentially private expectation maximization. In AISTATS, pages 896–904. PMLR, 2017.
- Quost and Denoeux [2016] Benjamin Quost and Thierry Denoeux. Clustering and classification of fuzzy data using the fuzzy em algorithm. Fuzzy Sets Syst, 286:134–156, 2016.
- Rana et al. [2015] Santu Rana, Sunil Kumar Gupta, and Svetha Venkatesh. Differentially private random forest with high utility. In ICDM2015, pages 955–960. IEEE, 2015.
- Ranjan et al. [2016] Rishik Ranjan, Biao Huang, and Alireza Fatehi. Robust gaussian process modeling using em algorithm. J Process Control, 42:125–136, 2016.
- Song et al. [2020] Shuang Song, Om Thakkar, and Abhradeep Thakurta. Characterizing private clipped gradient descent on convex generalized linear problems. arXiv preprint arXiv:2006.06783, 2020.
- Song et al. [2021] Shuang Song, Thomas Steinke, Om Thakkar, and Abhradeep Thakurta. Evading the curse of dimensionality in unconstrained private glms. In AISTATS. PMLR, 2021.
- Steinke and Ullman [2016] Thomas Steinke and Jonathan Ullman. Between pure and approximate differential privacy. Journal of Privacy and Confidentiality, 7(2):3–22, 2016.
- Steinke and Ullman [2017] Thomas Steinke and Jonathan Ullman. Tight lower bounds for differentially private selection. In FOCS, pages 552–563. IEEE, 2017.
- Talwar et al. [2015] Kunal Talwar, Abhradeep Thakurta, and Li Zhang. Nearly-optimal private lasso. In NeurIPS, pages 3025–3033, 2015.
- Wang et al. [2020] Di Wang, Jiahao Ding, Zejun Xie, Miao Pan, and Jinhui Xu. Differentially private (gradient) expectation maximization algorithm with statistical guarantees. arXiv preprint arXiv:2010.13520, 2020.
- Wang [2018] Yu-Xiang Wang. Revisiting differentially private linear regression: optimal and adaptive prediction & estimation in unbounded domain. arXiv preprint arXiv:1803.02596, 2018.
- Wang et al. [2015] Zhaoran Wang, Quanquan Gu, Yang Ning, and Han Liu. High dimensional em algorithm: Statistical optimization and asymptotic normality. NeurIPS, 28:2512, 2015.
- Wu [1983] CF Jeff Wu. On the convergence properties of the em algorithm. Ann Stat., pages 95–103, 1983.
- Xu et al. [2016] Ji Xu, Daniel J Hsu, and Arian Maleki. Global analysis of expectation maximization for mixtures of two gaussians. NeurIPS, 29, 2016.
- Yan et al. [2017] Bowei Yan, Mingzhang Yin, and Purnamrita Sarkar. Convergence of gradient em on multi-component mixture of gaussians. NeurIPS, 2017.
- Yi and Caramanis [2015] Xinyang Yi and Constantine Caramanis. Regularized em algorithms: A unified framework and statistical guarantees. arXiv preprint arXiv:1511.08551, 2015.
- Yi et al. [2014] Xinyang Yi, Constantine Caramanis, and Sujay Sanghavi. Alternating minimization for mixed linear regression. In ICML, pages 613–621. PMLR, 2014.
- Zhang et al. [2020] Linjun Zhang, Rong Ma, T Tony Cai, and Hongzhe Li. Estimation, confidence intervals, and large-scale hypotheses testing for high-dimensional mixed linear regression. arXiv preprint arXiv:2011.03598, 2020.
- Zhao et al. [2020] Ruofei Zhao, Yuanzhi Li, and Yuekai Sun. Statistical convergence of the em algorithm on gaussian mixture models. Electron. J. Stat., 14(1):632–660, 2020.
- Zhu et al. [2017] Rongda Zhu, Lingxiao Wang, Chengxiang Zhai, and Quanquan Gu. High-dimensional variance-reduced stochastic gradient expectation-maximization algorithm. In ICML, pages 4180–4188. PMLR, 2017.
Appendix A Supplement materials
A.1 DP Algorithm and theories for Mixture of Regression Model in high-dimensional settings
By applying Algorithm 2, the DP estimation algorithm in the high-dimensional mixture of regression is presented in the following in details:
For the truncation step on line 3 of Algorithm 5, rather than using truncation on the whole gradient, we perform the truncation on , and respectively, which leads to a more refined analysis and improved rate in the statistical analysis. Specifically, we define
Lemma A.1.
Suppose we can always find a sufficiently large constant to be the lower bound of the signal-to-noise ratio, . Then
A.2 DP Algorithm and theories for Regression with missing covariates Model in high-dimensional settings
By applying Algorithm 2, we present in the following the DP estimation in the high-dimensional regression with missing covariate model.
For the term on line 3 of Algorithm 5, we design a truncation step specifically for this model. According to the definition of , when is close to , we find that is close to , so we propose to truncate on and . Specifically, let
Lemma A.2.
Suppose the signal-to-noise ratio with be some constant. Also, for the probability that each coordinate of is missing, we have with and be a constant.
A.3 Simulation results for mixture of regression model
For the DP EM algorithm in the high-dimensional mixture of regression model, the simulated dataset is constructed as follows. First, we set to be a unit vector, where the first indices equal to and the rest of the indices are zero. For , we let , where , and with . We consider the following three experimental settings:
-
•
Fix . Compare the results of Algorithm 5 when , respectively.
-
•
Fix . Compare the results of Algorithm 5 when , respectively.
-
•
Fix . Compare the results of Algorithm 5 when , respectively.
For each setting, we repeat the experiment for 50 times and report the average error . For each experiment, the choice of initialized should be close to the true and the step size is set to be 0.5. The results are shown in Figure 4.
From the results in Figure 4, we also discover the relationship between different choices of and the performance of the proposed DP EM algorithm on the mixture of regression model. Similar to the results under the Gaussian mixture model, with larger , smaller and larger , the estimator has a smaller error in estimating .
A.4 Results for specific models in Low-dimensional settings
In this subsection, we will show results for DP algorithm for the mixture of regression model and regression with missing covariates in low-dimensional settings. we will list the algorithm and the theorem below. Since the proofs of these two specific models are highly similar to the proof of the high dimensional setting Theorem 4.4, Proposition 4.5, Theorem 4.6, Proposition 4.7 and also the low dimensional setting for Gaussian mixture Model Theorem 5.5 and Proposition 5.6, we omit the proofs here.
A.4.1 Algorithm and theories for Mixture of Regression Model in low-dimensional settings
The algorithm is listed as below:
where the truncation on the gradient is the same as the truncation in Algorithm 5
Theorem A.3.
For the Algorithm 7 in the Mixture of Regression Model, we define and . Define as in Lemma A.1 and . For the choice of parameters, the step size is chosen as , the truncation level is chosen as and the number of iterations is chosen as . For the sample size , it is sufficiently large that there exists constants , such that and . Then, there exists sufficient large constant , it holds that with probability :
Theorem A.4.
Suppose be the data set of samples observed from the Mixture of Regression Model discussed above and let be any corresponding -differentially private algorithm for the estimation of the true parameter . Then there exists a constant , if and for some fixed , we have:
A.4.2 Algorithm and theories for Regression with Missing Covariates in low dimension cases
The algorithm is listed as below:
where the truncation on the gradient is the same as the truncation in Algorithm 6
Theorem A.5.
For Algorithm 8, we define and . Define as in Lemma A.2 and . For the choice of parameters, the step size is chosen as , the truncation level is chosen to be and the number of iterations is chosen as . For the sample size , it is sufficiently large that there exists constants , such that and . Then, there exists sufficient large constant , it holds that with probability :
Theorem A.6.
Suppose be the data set of samples observed from the Regression with Missing covariates discussed above and let be any corresponding -differentially private algorithm for the estimation of the true parameter . Then there exists a constant , if and for some fixed , we have:
Therefore, both the low-dimensioanl EM algorithm on Mixture of Regression Model and Regression with missing covariates attain a near-optimal rate of convergence up to a log factor.
Appendix B Proofs of main results
B.1 Proof of Theorem 3.8
Assume that the step size is chosen, by Lemma 3.3, we can claim the privacy is guaranteed. Then we can start the proof. For simplicity, we denote . During the -th iteration, we can write the iterated two steps in the following way:
| (9) |
where is the set of indices selected by the private peeling algorithm, and is the vector of Laplace noises with support on . Furthermore, let us introduce the following notations, we define:
| (10) |
Then, before continue the proof, we will first introduce two lemmas:
Lemma B.1.
Suppose we have
| (11) |
for some . Also, for the sparsity level, we have that We assume that and also . We further assume . Then, it holds that, there exists a constant :
| (12) |
with probability , for all in .
Lemma B.2.
For , and defined in the Theorem 3.8, the following inequality holds:
| (13) |
The detailed proof of Lemma B.1 is in Appendix C.6 and the proof for Lemma B.2 is in Lemma 5.2 from [Wang et al., 2015]. Then, by the two lemmas discussed above:
| (14) |
First, we notice that for the term (1) in (B.1):
| (15) |
Second, for the term (2) in (B.1), by Lemma B.1 and Lemma B.2, we have:
| (16) |
Third, for the term , notice that for any , , by the concentration of Laplace Distribution, for every , we have:
| (17) |
here, in this case, , let , we have there exists a constant , such that with probability , we have:
| (18) |
By a union bound and the choice of to be , we find that with probability , we have:
| (19) |
According to our assumption, we find that is o(1). Thus, by combining the results from (B.1)(B.1)(B.1), we find that:
| (20) |
Denote . Then, if , by our assumption in the theorem that , we have . thus we have .
On the other hand, we find that by the assumption we also have . Further more, by the assumptions, we also have that are for any , and with probability , where .
| (21) |
which guarantees that if , we also have . Iterate this, we can get the connection between and :
| (22) |
which finishes the proof for the theorem.
B.2 Proof of Theorem 4.2
The proof of theorem 4.2 consists of three parts. The first part is the privacy guarantees. The second part is to verify the conditions for is satisfied. The third part is to find the convergence rate of , for any on the iteration path. Let us begin the proof with the first part.
For the privacy guarantee, notice that for two adjacent data sets, let and be the difference between these two data sets.
| (23) |
Then, by Lemma 3.3, we can claim that the private Gaussian Mixture Model is -differentially private.
Also, for the conditions of is Theorem 3.8, we find that is roughly and also by the assumption that , we can claim that is actually , thus the condition can be satisfied. Therefore, we can find a constant , such that:
| (24) |
Then, to finish the proof, it suffices to show that for each , , we can claim is . Then we can follow the proof of Theorem 3.8 to finish the proof of Theorem 4.2.
B.3 Proof of Proposition 4.3
Suppose be the data set of samples observed from the Gaussian Mixture Model and let be any corresponding -differentially private algorithm. Suppose we have another model where there are no hidden variables where . Suppose be the data set of samples observed from the latter model and let be any corresponding -differentially private algorithm. Then the estimation of true can be seen as a mean-estimation problem. By Lemma 3.2 and Theorem 3.3 from [Cai et al., 2019b], we have that:
Since the no hidden variables model can be seen as a special case where all hidden variables equals 1, so we have:
By combining the two inequalities together, we finish the proof.
B.4 Proof of Theorem 4.4
Similar to the proof for Theorem 4.2, the proof consists of three parts. The first part is the privacy guarantees. The second part is to verify the conditions of . The third part is to find the convergence of . Here, the verification of is similar to the proof of Theorem 4.2, so we omit the proof here.
For the privacy guarantee, notice that for two adjacent data sets, let and be the difference between these two data sets.
| (25) |
Next, let us find the convergence rate for the truncation error. By Lemma A.1, for the truncation error, we have obtained that with probability , therefore, for any , we have:
| (26) |
By a union bound on , and if we take the times of iteration , we have:
| (27) |
Thus, we can get the result that for all , with probability , , thus follows the proof of Theorem 3.8, we finish the proof of Theorem 4.4.
B.5 Proof of Proposition 4.5
Suppose we have the traditional linear regression model where there are no hidden variables where . Suppose be the data set of samples observed from the linear regression model and let be any corresponding -differentially private algorithm. Then by Lemma 4.3 and Theorem 4.3 in [Cai et al., 2019b], we have that:
Since the no hidden variables model can be seen as a special case where all hidden variables equals 1, so we have:
By combining the two inequalities together, we finish the proof.
B.6 Proof of Theorem 4.6
In the proof of Theorem 4.6, we also need to verify two properties. First is the privacy guarantees. The second part is to find the convergence of .
For the privacy guarantee, notice that for two adjacent data sets, let and be the difference between these two data sets. For the ease of notation, we denote and . Then:
| (28) |
From Lemma A.2, we have that under the truncation condition, with probability , for any , we have:
| (29) |
Again, by a union bound on , and if we take the times of iteration , we have:
| (30) |
Thus, we can get the result that for all , with probability , , thus by Theorem 3.8, we finish the proof of Theorem 4.6.
B.7 Proof of Theorem 5.4
Before the proof, let us first introduce a lemma:
Lemma B.3.
The detailed proof for B.3 is in Theorem 3 from [Balakrishnan et al., 2017]. Then for , we have:
| (31) |
In the above equality, if by choosing , from the assumption, with probability , for any , . Also, by Condition 5.2, for a single , with probability , , then by a union bound, for all , we have with probability , . Then, if , which means that . Then if satisfies that , then we can have .
On the other hand, and if we choose and the times of rotation to be . Notice that for each , . . Then we find that actually follows a chi-square distribution . By the concentration of chi-square distribution, there exists constants , such that:
| (32) |
Then with probability , we can derive that, their exists a constant such that:
By a union bound, we find that with probability , we can derive that, their exists a constant such that:
Then, we properly choose such that . Thus, when , we can also guarantee that , thus we can iterate the conclusions in (B.7), and we can get:
B.8 Proof of Theorem 5.5 and Proposition 5.6
For the proof of Theorem 5.5, we are more focusing on two parts. The first part is the convergence of , which has already been shown in Corollary 9 from [Balakrishnan et al., 2017], which shows that when , . So we will later show the convergence rate of the truncation error.
Follow the proof in Lemma 4.1, we could observe that for the vector , in the low dimensional settings. Thus if we choose . We can find that for a constant :
By the definition of in the Gaussian Mixture Model, we found that the truncation error does not rely on the choice of , thus for all , by probability , , which finishes the proof of Theorem 5.5.
Appendix C Proof of lemmas
C.1 Proof of Lemma 3.2
C.2 Proof of Lemma 3.3
To prove this result, we first prove that for each iteration, we can gain a -differentially private algorithm. Suppose the data points we have gathered is , and if one individual of the data point, say, is replaced by , then define be the gradient taken with respect to , we can show that:
| (33) |
where the last inequality follows from the definition of . Then by Lemma 3.1 we can get the result that for each iteration, we can obtain a -differentially private algorithm. Next, we will show that for an iterative algorithm with data-splitting, the whole algorithm is also a -differentially private algorithm. Let us start from the simple case, a two step iterative algorithm.
Let denote the data set and be the adjacent data set of . Assume the data set are split into two data sets where and . Then let be a -differentially private algorithm with output . also be a -differentially private algorithm with any given . Then we define , we claim that is also -differentially private. To prove this claim, we should use the definition of differential privacy. Since and are two adjacent data sets and differ by only one individual data. Thus, or . We will discuss these two cases one by one. For the first case, . from the definition, we have:
From the definition, we could claim that is -differentially private. Then, for the second case, we have:
For the second case, we also claim that is -differentially private. Then, when the data set is split into subsets, we could use the induction to show that for an iterative algorithm with data-splitting and each iteration being -differentially private, the combined algorithm is also a -differentially private algorithm, which finish the proof of this lemma.
C.3 Proof of Lemma 4.1
The proof consists of three parts, for the first proposition of verification of Condition 3.4 and Condition 3.5, the proof is slight different with the proof for Corollary 1 in [Balakrishnan et al., 2017]. The difference is that for the Lipschitz-Gradient condition, instead the Lipschitz-Gradient-1 condition in [Balakrishnan et al., 2017], we are using Lipschitz-Gradient. However, because the population level satisfies:
So obviously,
Also, let , then we find that,
so in the case of Gaussian Mixture Model, , follow the proof of Corollary 1 in [Balakrishnan et al., 2017], the Lipschitz-Gradient holds when taking . For the second proposition of Condition 3.6, see detailed proof of Lemma 3.6 in [Wang et al., 2015]. For the third proposition of Condition 3.7, by the proof in (B.1) for Theorem 3.8, we find that we only need to bound with the support on . Where is the set of indexes chosen by the NoisyHT algorithm during the -th iteration. Thus, for any , since:
Thus, we have:
| (34) |
where is the response of the Gaussian Mixture model on the population level. Then for any , we can obtain that:
| (35) |
Then since for any , and . Denote the density function of as , the density function of as , the density function of as , we can get:
| (36) |
For the first term in the above result (C.3), by Fubini theorem:
| (37) |
By the tail bound of Gaussian distributions, we can have:
| (38) |
Insert the tail bound from (38) into (C.3), we can obtain:
| (39) |
If we choose and analyze the second term in similar approach in (C.3), we can find that . Then, according to (C.3), we can claim that for sufficiently large , . So if we choose . We can find that for a constant :
which finished the proof of the third proposition in Lemma 4.1. Thus, we complete the proof of Lemma 4.1.
C.4 Proof of Lemma A.1
For the first proposition in Lemma A.1, see detailed proof in Corollary 3 from [Balakrishnan et al., 2017], for the second proposition in Lemma A.1, see detailed proof in Lemma 3.9 from [Wang et al., 2015]. In this section, our major focus is the third proposition, which verifies Condition 3.7 for the Truncation-error. Before we start the proof of third proposition, let us first introduce two lemmas, which are significant in the following analysis.
Lemma C.1.
Let be a sub-gaussian random variable on with mean zero and variance . Then, for the choice of , if , we have . Further, we also have .
Lemma C.2.
Let be a sub-gaussian random vector and be a sub-gaussian random variable. Also, let be realizations of and be realizations of . Suppose we have an index set with . Let , then it holds that, there exists constants :
| (40) |
with probability greater than .
The proof of Lemma C.1 and Lemma C.2 can be found in the Appendix C.7 and C.8. Then we could start the proof of Lemma A.1. Similar to Gaussian Mixture Model, we also assume that for any , has support . Then let for the ease of notation, we can break into two parts:
| (41) |
Since , and are all gaussian random variables. So by the conclusion from Lemma C.2, we could conclude that both the term and the term are all with probability , therefore, for any , we have:
| (42) |
which finishes the proof of the third proposition in Lemma A.1.
C.5 Proof of Lemma A.2
For the first proposition, The detailed proof is in Corollary 6 from [Balakrishnan et al., 2017]. For the second proposition Lemma A.2, the proof is in Lemma 3.12 from [Wang et al., 2015]. Then, we will focus on the proof of the third proposition.
Then, similar to the previous approach, we assume that for any , has support . Denote , then we can break it into three parts. For the ease of notation, we denote and .
| (43) | |||
| (44) | |||
| (45) |
Then, to analysis (43), (44) and (45), we should first introduce a lemma below.
Lemma C.3.
Under the conditions of Theorem 4.6, the random vector is sub-gaussian with a constant parameter.
The detailed proof of Lemma C.3 is in the proof for Lemma 10 in [Balakrishnan et al., 2017]. Then by the definition of sub-gaussian random vector, we can also claim that is sub-gaussian.
Further, for the term , we also claim that, for any unit vector , , so is also a sub-gaussian vector. Similarly, we also have be sub-gaussian random variables. So by the conclusion from Lemma C.2, we could conclude that both the term , the term and the term are all with probability , therefore, for any , we have:
| (46) |
which completes the proof of Lemma A.2.
C.6 Proof of Lemma B.1
By assumption (11), we have
| (47) |
Then, for the simplicity of the proof, we can denote that
We can find that both and are unit vectors. Further, we denote the sets and as the follows
where , the support of . And be the set of indexes chosen by the NoisyHT algorithm during the -th iteration. Let for , respectively. Then, we define , so the results below holds:
| (48) |
By Cauchy-Schwartz inequality, we have
| (49) |
Then, let be a set of indexes for the smallest indexes in , this is possible, since by the assumption, we have , thus . Then, by Lemma 3.2, define , we have for any :
| (50) |
Then by the fact that according to the choice of , and also a standard inequality when . Thus, we have:
| (51) |
Therefore,
| (52) |
Then, we denote . Further, we define that
Thus we have, with probability :
Similarly, we also have that:
Define , which implies that
| (53) |
where the second inequality is by plugging (52) into the inequality. Plugging (C.6) into (C.6), we have
| (54) |
After solving in (54), we can obtain the inequality below:
| (55) |
The final inequality is due to the inequality . By a properly chosen satisfies that , we have . In the following, we will prove that the right hand side of (55) is upper bounded by .
By the assumptions from this lemma, we first observe that and . We can also find that for , by Lemma A.1 from [Cai et al., 2019b], we can claim that, there exists constants , such that, with probability :
Thus, if we let be the maximum of for all the iterations, then by a union bound, if we let be the total number of iterations, then with probability :
Therefore,
| (56) |
by the assumptions of this Lemma, we have , thus for , we find that:
| (57) |
The first term and the third term of (C.6) are all o(1), plug this result into (55), we have that,
By a properly chosen , we can attain that , so,
| (58) |
In the following steps, we will prove that the right hand side of (C.6) is upper bounded by . Such bound holds if we have:
| (59) |
To prove (59), we first note that , which holds because:
| (60) |
where the second inequality is due to the assumptions in the lemma and the final inequality is due to the fact that:
| (61) |
and
| (62) |
By combining (61) and (62), we can finish the proof of (60). Then, we can verify that (59) holds. By (60), we have
| (63) |
The above inequality implies that . Then, for the right hand side of (59), we observe that:
| (64) |
Thus, we can claim that
| (65) |
Furthermore, from (C.6), we have:
noticing that , thus,
By solving from the above inequality, and by the fact that , we have:
| (66) |
where the third inequality is due to (58). Therefore, by (58) and (C.6), we can combine the result as follows:
| (67) |
Note by the definition of , we can find that:
| (68) |
Therefore, we have:
| (69) |
Define . Combining the results from (69) and (67), we observe that:
| (70) |
Then, note the definition of , we can bound the term by:
| (71) |
Then, for the term , we have
| (72) |
Then, we can plug (C.6) and (72) into (70), we can get the following results:
| (73) |
Then, notice that is obtained by truncating , so we have , plug this fact into (73), we get the following results:
| (74) |
By taking square root on both sides of (74) and by the fact that for , , we can find a constant , such that:
| (75) |
Then, the lemma is proved.
C.7 Proof of Lemma C.1
Since is a sub-gaussian random variable with mean zero and variance , then by the definition of sub-gaussian random variables, we have:
| (76) |
Thus, with this tail bound, we can calculate directly, suppose the density function of is , then, according to the definition of , we have:
| (77) |
Then, we will analyze these two terms in (77) separately. For the first term, we have:
| (78) |
Then, by choosing , we have . By the similar approach, we can also attain that . Thus, we claim that .
For the second part proof of this lemma, we can also calculate that:
| (79) |
Same as the first part, we will also analyze these two terms in (79) separately. For the first term, we have:
| (80) |
Then, by choosing , we have . By the similar approach, we can also attain that . Thus, we claim that . Thus finishes the proof of this lemma.
C.8 Proof of Lemma C.2
First, we could separate the left hand side of (40) as follows:
| (81) |
For the term , denote the distribution of as , then , which follows a Gaussian distribution.Then by Lemma C.1 we have, if we choose , we have , thus .
Then, let us analyze on the term , we have for any :
| (82) |
By Lemma C.1, we have that when we choose , , which means that the term . Therefore, for the term .
Finally, let us analyze the term , for any :
| (83) |
Then again, by Lemma C.1, we can also obtain that both and are , insert this analysis into (C.8), we can claim that .
Therefore, if we choose , we have:
| (84) |
Thus finishes the proof.