High-fidelity, quasi-deterministic entanglement generation using phase-matched spectral islands in a zero-added-loss multiplexing architecture
Abstract
While photonic entanglement generation and distribution are well developed, their demonstrated rates are far below what is needed for a quantum internet. The present paper proposes and analyzes a scheme for spectral multiplexing that provides entanglement-distribution rates well in excess of the state of the art. It builds on the idea presented by Chen et al. [Phys. Rev. Appl. 19, 054209 (2023)], who proposed zero-added-loss multiplexing (ZALM) as a means for high-fidelity, quasi-deterministic entanglement generation. Unfortunately, Chen et al.’s ZALM requires a large number (800) of spectral channels to achieve its claimed high-fidelity, quasi-deterministic, high-rate entanglement generation. Our modified version of ZALM affords major performance improvements over the original. It draws on Morrison et al. [APL Photon. 7, 066102 (2022)], who domain engineered a crystal to realize a biphoton wave function with 8 discrete and spectrally-factorable frequency bins. Our ZALM SPDCs each have a modest number ( 800) of these phase-matched spectral islands each generating two-mode squeezed-vacuum states, permitting our analysis, unlike Chen et al.’s, to account for multipairs of all orders, losses in the partial BSM, and propagation losses en route to the receivers. A major innovation in our proposal is to employ both same-island heralding and cross-island heralding, which allows the entanglement-delivery rate to scale as rather than in the weak squeezing regime required for the reception of photon pairs with a high Bell-state fidelity under realistic losses. This heralding scheme uses an order of magnitude fewer spectral channels, which may enable near-term implementations of satellite-to-ground or fiber-optic based ZALM architectures.
I Introduction
Qubit teleportation [1, 2, 3] is a key primitive for quantum communication because it affords error-free, repeaterless transmission of quantum states over pure-loss bosonic channels with transmissivities, viz., links with zero quantum capacity [4]. At power levels below the onset of nonlinear effects, and employing post-propagation dispersion compensation, -km-long transmission over standard single-mode fiber at 1.55 m wavelength may be regarded as a pure-loss channel [5] with transmissivity . Hence its quantum capacity vanishes for km. Because the fiber channel’s classical capacity is not subject to this catastrophic collapse, the internet’s fiber backbone uses erbium-doped fiber amplifiers (EDFAs)—spaced 80–100 km apart—in lieu of classical repeaters. Thus, because co-locating quantum repeaters with those amplifiers is highly desirable for efficient build-out [7] of a quantum internet [8, 9, 10], transmission via qubit teleportation becomes necessary, and that requires creating reservoirs of shared qubit entanglement between these EDFA sites.
Spontaneous parametric down-converters (SPDCs) have long been workhorses for generating polarization-entangled [11, 12, 13, 14] and time-bin entangled [15, 16, 17] photon pairs. Polarization entanglement is preferable for satellite-to-ground entanglement distribution, because atmospheric turbulence is not depolarizing [18]. For terrestrial entanglement distribution over optical fiber, however, time-bin entanglement is the right choice, because standard fiber does not preserve polarization and polarization-maintaining fiber is currently too lossy for long-distance operation. Sadly, in both cases, record-setting demonstrations leave much to be desired with respect to entanglement distribution over long distances. For example, Neumann et al. [19] realized only a 9 s-1 distribution rate over 248 km of deployed fiber, while Yin et al. [20] achieved only a 1.1 s-1 distribution rate from the Micius satellite to a pair of ground stations separated by 1200 km.
The preceding demonstrations used bidirectionally-pumped Sagnac SPDCs [21, 22], which are renowned for their excellent stability and high efficiency. Nevertheless, a Sagnac SPDC—like SPDCs in general—is intrinsically probabilistic, a characteristic that adversely impacts its entanglement-distribution rate. In particular, to suppress unwanted multipair events, SPDCs are typically operated at low brightness, e.g., an average of 0.01 entangled pairs per pump pulse. Multiplexing an array of SPDCs could push up the entangled-pair generation rate to near-deterministic, or at least quasi-deterministic, performance. But multiplexing schemes that rely on path switching at the source, such as Mower et al. [23] and Dhara et al. [24], suffer significant performance penalties from their switch losses. Chen et al.’s zero-added-loss multiplexing (ZALM) [25] is different. ZALM uses the equivalent of two Sagnac sources [26] and partial Bell-state measurements (BSMs) [27] to herald the generation of polarization-entangled biphotons across a large number of frequency-multiplexed signal channels that collectively span the down-converters’ multi-THz phase-matching bandwidth [28]. According to Chen et al., this arrangement has the potential to keep multipair emissions negligible on a per-channel basis while approaching quasi-deterministic performance over the SPDCs’ full phase-matching bandwidth.
ZALM uses a source-in-the-middle configuration, which has higher efficiency than its meet-in-the-middle and sender-receiver alternatives [29]. For the quantum internet’s fiber backbone, every classical-internet EDFA site would contain a ZALM quantum transmitter (QTX) to distribute entangled photon pairs to ZALM quantum receivers (QRXs) at that site’s nearest neighbors, Alice and Bob. As in Thomas et al. [6], classical traffic—including the identities of the frequency channels containing the heralded biphotons—could be confined to the C-band, while optical transmission of the heralded biphotons could occur in the O-band. Alice and Bob’s QRXs would then employ quantum mode conversion—frequency conversion [30, 31] and bandwidth compression [32]—to efficiently couple the biphoton received in each heralded channel to intracavity color-center quantum memories.
Chen et al. [25] presented a broad treatment of ZALM, including its source, mode-conversion, and memory-loading characteristics, as well as its overall performance scaling. Their ZALM relied on a burst of pump pulses to generate a striped frequency-domain biphoton wave function over a very broad (10 THz) bandwidth that, together with narrowband (1 GHz) filtering in the partial BSM and suitable (12.5 GHz) channelization at the receivers, led to a large number (800) of channels whose frequency-domain biphoton wave functions each approximated that of a spectrally-factorable, i.e., single-temporal-mode, state. Such near single-temporal-mode biphoton generation ensured the production of high-fidelity ( 99%) biphotons, and the 800 channels provided quasi-deterministic ( 25% generation probability per pump burst) operation. Unfortunately, Chen et al.’s analysis did not fully account for the combined effects of multipair events and losses.
To overcome these limitations, we take the essence of Chen et al.’s approximately-factorable channelized biphoton wave function to its ideal limit. Motivated by Morrison et al. [33], who domain engineered a crystal, pumped by a transform-limited Gaussian pulse with an appropriately chosen bandwidth, to realize a biphoton wave function with 8 discrete and spectrally factorable frequency bins, we assume the ZALM source’s SPDCs each have a modest number ( 800) of phase-matched spectral islands that each generate two-mode squeezed-vacuum states. As a result, our analysis is able to go well beyond Chen et al.’s, in that ours includes multipair events of all orders, losses in the partial BSM and in propagation to Alice and Bob’s QRXs, and the use of both same-island and cross-island heralding. More importantly, it shows that entangled photon pairs can be generated and delivered with high ( 99%) Bell-state fidelity and very high ( 99.9%) Bell-state fraction despite losses in the partial BSM and in propagation. Furthermore, the generation rate can be quasi-deterministic ( 25% generation probability per pump pulse) with a modest number ( 800) of islands.
The remainder of the paper is organized as follows. Section II introduces the islands-based ZALM source and shows that in ideal, i.e., lossless, operation it can easily generate entanglement that has high fidelity and is near-deterministic. Section III extends our treatment of islands-based ZALM to include losses in the partial BSM and in the signal photons’ propagation to Alice and Bob’s QRXs. Here, same-island plus cross-island heralding permits the QTX’s entanglement generation to be quasi-deterministic, while delivering entangled pairs to Alice and Bob’s QRXs with high Bell-state fidelity and very high Bell-state fraction even with 1% QTX-to-QRX transmissivity. Concluding remarks are presented in Sec. IV, and derivations underlying the performance metrics reported in Secs. III.1 and III.2 appear in Appendices A and B, respectively.
II Lossless ZALM with phase-matched spectral islands
To set the stage, we first introduce and analyze islands-based ZALM in the ideal case of lossless operation. Modifying figures from our previous treatment of dense wavelength-division multiplexed (DWDM) ZALM using type-0 phase matching [34], islands-based ZALM’s QTX is shown schematically in Figs. 1 and 2 and explained below.
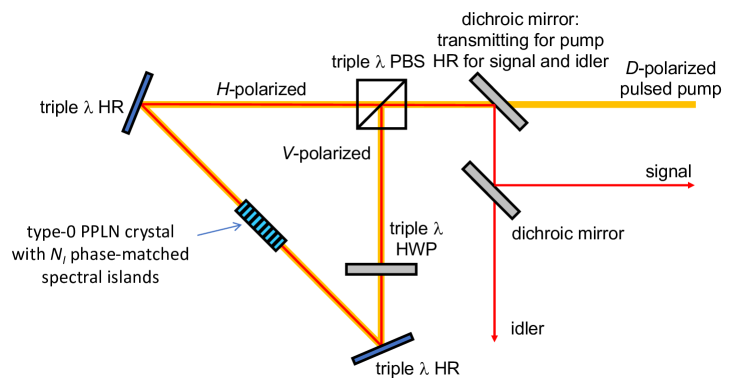
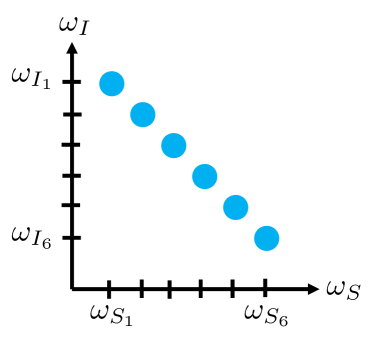
Islands-based ZALM’s QTX uses a pair of Sagnac sources that employ identical periodically-poled lithium niobate (PPLN) crystals each with phase-matched spectral islands. The SPDCs’ islands are type-0 phase matched and pulse-pumped in phase to produce signal-idler pairs from each island that, except for their island-dependent signal and idler center frequencies, are in identical temporal modes. To achieve such a state, the spectral islands must be identical, nonoverlapping, and spectrally factorable, i.e., expressible as a product of functions of the signal frequency and the idler frequency [35] as sketched in Fig. 3 for 6 islands.
Restricting our attention to the foregoing temporal modes, and assuming operation in the SPDCs’ usual no-pump-depletion regime, we have that the output states from Sagnacs resulting from a single pump pulse are the following tensor products of two-mode squeezed-vacuum (TMSV) states,
| (1) |
Here: is the -photon Fock state of the -polarized () signal () and idler () modes emitted by the th phase-matching island; and
| (2) |
is the Bose-Einstein probability distribution with being the squeezing gain, so that is the average number of signal-idler pairs emitted per SPDC-island per pump pulse. The joint signal-idler state of the two Sagnacs is then
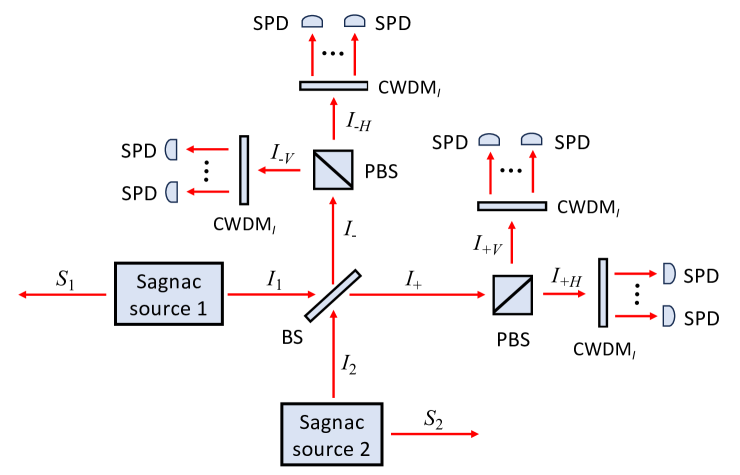
Figure 2’s partial-BSM setup first combines the idlers from the two Sagnacs on a 50–50 beam splitter, after which it separates their horizontal () and vertical () polarization components with polarizing beam splitters (PBSs). Coarse wavelength-division multiplexing (CWDM) filters then perfectly separate the modes from the different phase-matching islands, and the CWDM filters’ outputs illuminate single-photon detectors (SPDs) that have partial number-resolution (PNR), i.e., 0, 1, or , capability and no dark counts. A same-island herald from a particular pump pulse is declared for the th island when exactly two idler photons are detected from the th island, with one being polarized and the other polarized. If those detections both occur in Fig. 2’s branch or in its branch, the signal modes’ heralded state is the polarization Bell-state triplet [34]
| (3) |
Alternatively, if one of those detections occurs in Fig. 2’s branch, while the other occurs in its branch, the signal modes’ heralded state is the polarization Bell-state singlet
| (4) |
Because here we are assuming lossless optics and unit-efficiency, PNR-capable detectors with no dark counts in our partial-BSM apparatus, it is clear that we will get an th-island herald from a particular pump pulse if and only if two th-island idler photons enter the partial-BSM apparatus with one being -polarized and the other being -polarized. There are four ways—all equally likely—in which this th-island heralding event, , can occur: Sagnacs 1 and 2 emit, respectively, an th-island -polarized idler photon and an th-island -polarized idler photon, or vice versa; and Sagnac 1 emits an th-island -polarized idler photon and an th-island -polarized idler photon with no th-island emission from Sagnac 2, or vice versa. The probability of an th-island herald from a particular pump pulse is therefore
| (5) |
and independent of because we have assumed all modes have the same squeezing gain, cf. Eq. (1). Note that only the first two th-island heralding possibilities are true heralds, i.e., heralds for which the heralded state is indeed the one that is transmitted to Alice and Bob. The second two th-island heralding possibilities are called false heralds, viz., they result in two th-island signal photons being sent to Alice and none to Bob, or vice versa. Both the true and false th-island heralds arise because the partial-BSM’s 50–50 beam splitter erases which-path information from the ZALM QTX’s two Sagnacs.
At this point we introduce the three metrics by which we will measure the ZALM QTX’s performance. The first is the per-pump-pulse probability that Alice and Bob are sent a true th-island herald, , which, like , is independent of . The second is the Bell-state fraction, , of the state transmitted after a true th-island herald, i.e., the probability that this state lies in the Hilbert space spanned by those modes’ polarization Bell states. The third is the Bell-state fidelity, , viz., the conditional probability that the state sent to Alice and Bob is the state that was heralded, given a true th-island herald has occurred and the state sent to Alice and Bob lies in the polarization Bell-state Hilbert space.
To evaluate these metrics for same-island heralding we will assume the ZALM QTX sends at most one herald per pump pulse, in keeping with a ZALM QRX architecture that allocates only one qubit of quantum memory to each pump pulse. The probability that Alice and Bob are sent a true th-island herald on a particular pump pulse in this case is therefore
| (6) |
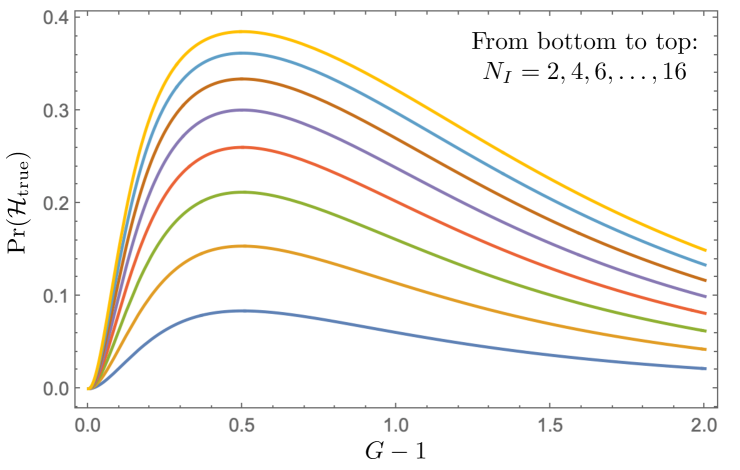
i.e., half the probability that at least one island heralds. Our assumption of lossless QTX optics and unit-efficiency, PNR-capable SPDs with no dark counts immediately implies, from Eq. (1), that a true herald results in a biphoton being transmitted. So, the ideal islands-based ZALM QTX with same-island heralding realizes unit Bell-state fraction () and unit Bell-state fidelity (). Figure 4 plots the per-pump-pulse probability of a true herald versus the average number of signal-idler pairs per SPDC island per pump pulse for islands.
The preceding results tell us that the ideal ZALM QTX with same-island heralding and at most one herald per pump pulse is near perfect, i.e., it has unit Bell-state fraction and unit Bell-state fidelity with a true-herald per-pump-pulse probability that exceeds 0.25 for 8 islands at , and is more than 80% of that metric’s ultimate (0.5) limit for 16 islands at . In contrast, the lossless ZALM QTX from Chen et al. [25] needed 800 channels to achieve high-fidelity operation with 0.25 per-pump-pulse probability of a true herald.
III Lossy ZALM with phase-matched spectral islands
Having painted such a rosy picture for islands-based ZALM QTX with ideal equipment, same-island heralding, and at most one herald per pump pulse, it behooves us to explore how rapidly that QTX’s performance degrades in non-ideal operation. We should also quantify the quality of the state delivered to Alice and Bob after loss in propagation from the ZALM QTX to their QRXs. Thus, in this section, we first consider a lossy QTX whose losses are symmetrically distributed on the idler paths through the partial-BSM setup and lumped together into sub-unit quantum efficiencies, , at each SPD [37], but with no losses in the Sagnac sources’ signal paths. The second case we treat augments the preceding partial-BSM losses with symmetrically-distributed sub-unit signal-path transmissivities, , from the ZALM QTX to Alice and Bob’s QRXs.
The per-pump-pulse th-island heralding probabilities for both cases described above coincide, because they depend only on the reduced density operator for the four idler modes entering the partial BSM and the SPDs’ quantum efficiency. From Eq. (1), the signal-idler mode pairs, are in independent, identically-distributed (iid) two-mode squeezed-vacuum states. Tracing out the signal states leaves the modes in iid thermal states with average photon number . Passing those idler modes through Fig. 2’s 50–50 beam splitter produces idler modes, , that are also in iid thermal states with average photon number . The well-known result for thermal-state photodetection with sub-unit quantum efficiency then gives
| (7) |
for the per-pump-pulse probability that an th-island -polarized idler photon and an th-island -polarized photon are detected. Moreover, as before, half of these detections are false heralds. Furthermore, continuing to assume that the ZALM QTX transmits at most one herald per pump pulse, we have that the per-pump-pulse probability of an th-island true herald is given by Eq. (6) with now from Eq. (7) instead of Eq. (5).
There is no need to replot for a lossy partial BSM; we need only change to on Fig. 4’s abscissa. That said, before using to get for an 8-island QTX with a sub-unit , we must evaluate that transmissivity’s impact on the Bell-state fraction and Bell-state fidelity. This need arises because multipair events are increasingly important as increases, and implies that the SPDs do not completely ward them off. Finding and for a sub-unit is the task of Sec. III.1.
III.1 Islands-based ZALM with partial-BSM loss
Our path to finding the Bell-state fraction and Bell-state fidelity for a ZALM QTX with sub-unit detection efficiency runs through the transform domain, starting from the anti-normally-ordered characteristic function associated with , the density operator for the signal, , and idler, , modes of a single island,
| (8) |
where, for convenience, we suppress the island index, . In Eq. (8): and with
| (9) |
and
| (10) |
being four-dimensional (4D) row vectors of complex-valued parameters and photon creation operators, respectively. The density operator can be recovered from its anti-normally-ordered characteristic function via the 16D operator-valued inverse Fourier transform [38],
| (11) |
A standard squeezed-state calculation, using the th-island state from Eq. (1), gives [4]
| (12) |
Appendix A uses the mode transformation for 50–50 beam splitting and the mode transformation that accounts for sub-unit detector efficiency to obtain the anti-normally-ordered characteristic function associated with the conditional density operator for the modes, , given that an herald has occurred:
| (13) |
Here: are the efficiency- detected idler modes of the single island under consideration; and Using the operator-valued inverse Fourier transform of this characteristic function, Appendix A goes on to show that
| (14) |
and
| (15) |
are the polarization Bell-state probabilities implied by .
Taken together, Eqs. (14) and (15) imply that, given there has been an herald, the state sent to Alice and Bob has unit Bell-state fidelity. To see that this is so, remember that an herald tells Alice and Bob to expect a state. Thus Eqs. (14) and (15) show that this polarization Bell-state singlet is the only Bell state transmitted to them when that herald occurs. Multipair events do not affect the Bell-state fidelity of a lossy partial BSM because, at this point, we have assumed there are no losses in the signal paths. Note too that, as outlined in Appendix A, the other three heralding possibilities— and —also result in states with unit Bell-state fidelity. Unlike the Bell-state fidelity, however, the Bell-state fraction of the ZALM QTX’s output state is adversely impacted by a sub-unit , as we now show.
There are two classes of output states that are outside the polarization Bell-states’ Hilbert space: output states due to false heralds, and output states due to multipair events in which signal photons are sent to both Alice and Bob. Defining a memory-loadable output state to be one that sends signal photons to both Alice and Bob, the partial-BSM’s Bell-state fraction, given an herald, is . From Eqs. (14) and (15) we have that
| (16) |
In Appendix A we show that
| (17) |
Moreover, these probabilities also apply to the other heralding possibilities, and . It follows that the lossy partial-BSM’s Bell-state fraction is
| (18) |
Figure 5 plots the Bell-state fraction, , for a lossy partial BSM versus the average number of signal-idler pairs per SPDC island per pump pulse, , for (top to bottom) . It shows the high premium placed on the having to maintain a high Bell-state fraction at the partial-BSM’s output. Indeed, whereas for lossless operation resulted in quasi-deterministic () performance with unit Bell-state fidelity and unit Bell-state fraction, when we need to realize . Although that Bell-state fraction is accompanied by a unit Bell-state fidelity, it takes a wildly unrealistic 1381 islands in order to reach with same-island heralding when .
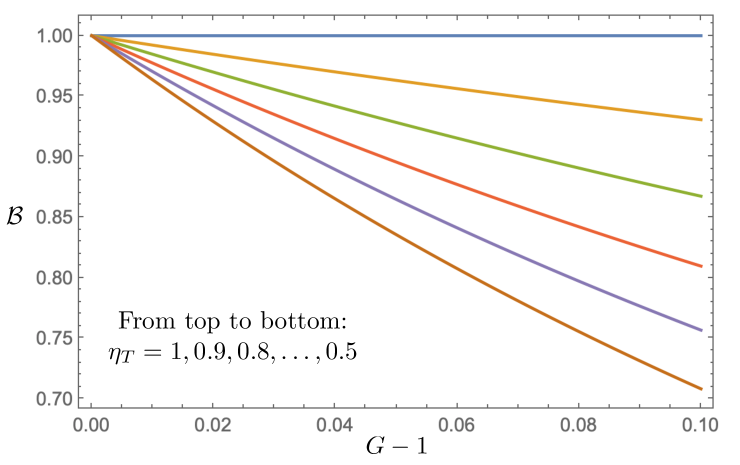
The explosive growth of the number of islands needed to achieve and with same-island heralding that is incurred in going from to can be avoided by employing cross-island together with same-island heralding. We call such a heralding scheme same-plus-cross-island (SPCI) heralding. Same-island heralding requires detection of an -polarized photon and a -polarized photon from the same island. Thus same-island heralding offers only island-choice possibilities. Because, as shown in Eq. (1), the states generated by each island are iid TMSV states, detecting an -polarized photon from the th island and a -polarized photon from the th island, with , also provides a suitable herald. Now, with SPCI heralding, Alice and Bob need to be told which island had the detection and which had the detection, and their QRXs must implement polarization-dependent frequency conversion in their mode-conversion modules.
With both same-island and cross-island heralds being employed the probability of an th-island, th-island herald—regardless of whether or —is
| (19) |
with half of them being false heralds. Continuing our assumption of allowing at most one herald per pump pulse, the per-pump-pulse probability of a true herald when both same-island and cross-island heralds are used is then
| (20) |
because there are now island-pair choices for the and detections. So, using same-island and cross-island heralding, 38 islands suffice to get with and from a lossy partial BSM when , and 82 islands suffice to achieve that same performance when .
III.2 Islands-based ZALM with partial-BSM loss and propagation loss
The final task in this paper is to study the effects of signal-path losses on islands-based ZALM. In the previous subsection we presumed the ZALM QTX’s signal paths were lossless. Taking signal-path losses to be symmetrically distributed, they can be accounted for by subjecting the QTX’s th-island heralded outputs to sub-unit transmissivities . Furthermore, with the assumed source-in-the-middle architecture, it is not unreasonable—at least for an initial study—to lump together the ZALM QTX’s signal path losses with symmetrically-distributed propagation losses en route to Alice and Bob’s QRXs. That case is considered in Appendix B, where beam-splitter mode transformations, with transmissivity , are first used to obtain the anti-normally-ordered characteristic function for the and modes, i.e., the modes arriving at Alice and Bob’s QRXs. Appendix B then parallels what was done in Appendix A to arrive at the following results for ZALM’s Bell-state probabilities, given an herald, with partial-BSM loss and propagation loss:
| (21) |
and
| (22) |
where denotes the signal modes arriving at Alice and Bob’s QRXs, and
From Eqs. (21) and (22)—and the fact that the corresponding results for the other three herald possibilities coincide with these -herald results—we get the Bell-state fidelity curves in Figs. 6 and 7 when there is both partial-BSM loss and propagation loss. Figure 6 shows that and results in Bell-state fidelities exceeding 0.97 for QTX-to-QRX losses as high as 30 dB. Figure 7 shows that gives when and , while does the same when and .
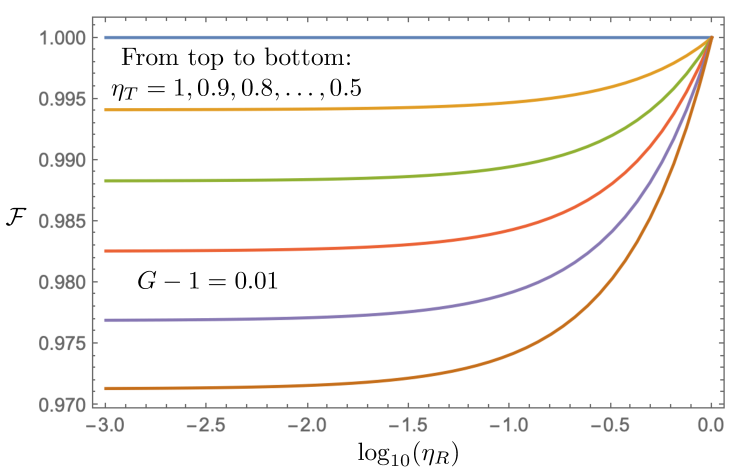
Next on our agenda is evaluating islands-based ZALM’s Bell-state fraction when there is both partial-BSM loss and propagation loss. From Eqs. (21) and (22) we have
| (23) |
and from Appendix B we have
| (24) |
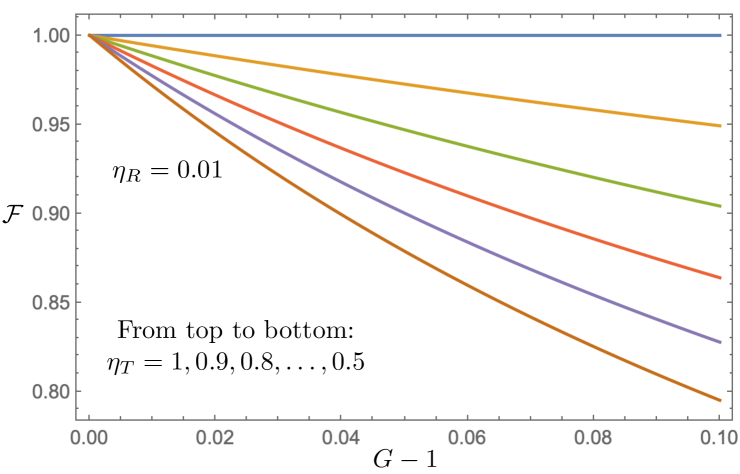
The preceding results also apply to the other three herald possibilities and lead to the Bell-state fraction behaviors in Figs. 8 and 9. They show that very lossy propagation with gives exceedingly high Bell-state fraction for , and for the Bell-state fraction increases as decreases. Let us see what this behavior, combined with what we have already exhibited for the Bell-state fidelity, has to say about delivering high-quality entanglement through very lossy propagation with quasi-deterministic per-pump-pulse probability of a true herald.
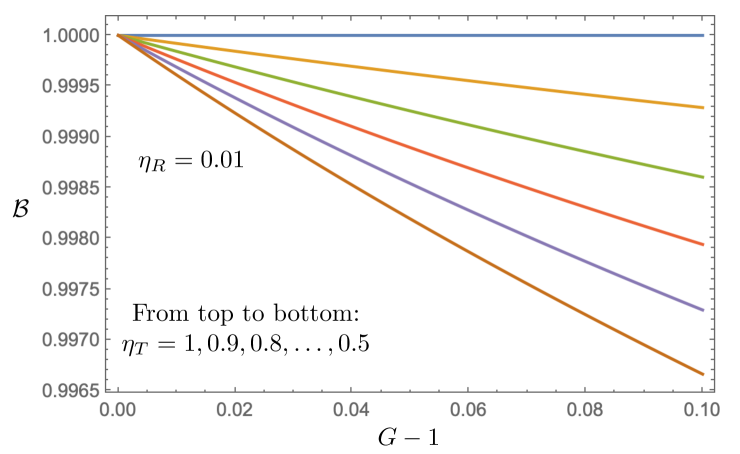
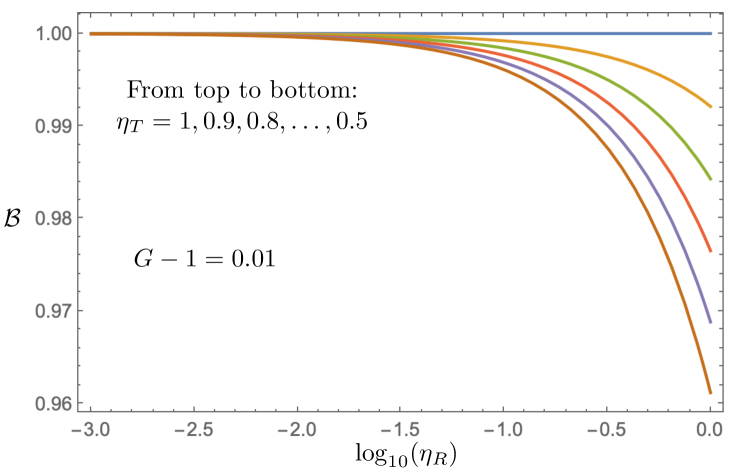
We noted earlier that gives when and , and does the same when and . We can now say that gives when and , and does the same when and . In simple terms, these average numbers of signal-idler pairs per island per pump pulse result in delivery of an state—from a lossy partial BSM through very lossy propagation—that is essentially confined to the Bell states’ Hilbert space. Furthermore, with SPCI heralding exceeds 0.25 when for , and for when and we use the values given above. So, whereas Chen et al. [25] used 800 channels to achieve high-fidelity, quasi-deterministic operation with same-channel heralding, we have demonstrated that far fewer phase-matched spectral islands are needed to do the same with SPCI heralding.
Some additional results from Appendix B deserve mention at this point. There we show that
| (25) |
and
| (26) |
implying that, given an herald, the projection of into , where is the Bell-state Hilbert space, is diagonal in the Bell basis. As explained in Appendix B, the same Bell-state diagonality occurs for the other possible heralds. The near-unit Bell-state fractions of the previous paragraph’s examples then let us say that
| (27) |
Here: denotes a conditional probability given a herald; is given by the right-hand side of Eq. (21); and are given by the right-hand side of Eq (22); and
| (28) |
is a normalization constant.
Note that the right-hand side of Eq. (27) is an exact result for , the projection of on to , regardless of the Bell-state fraction. Thus, we can find the states’ Bell-state purity, , from Eq. (27). When , this result becomes the full state’s purity.
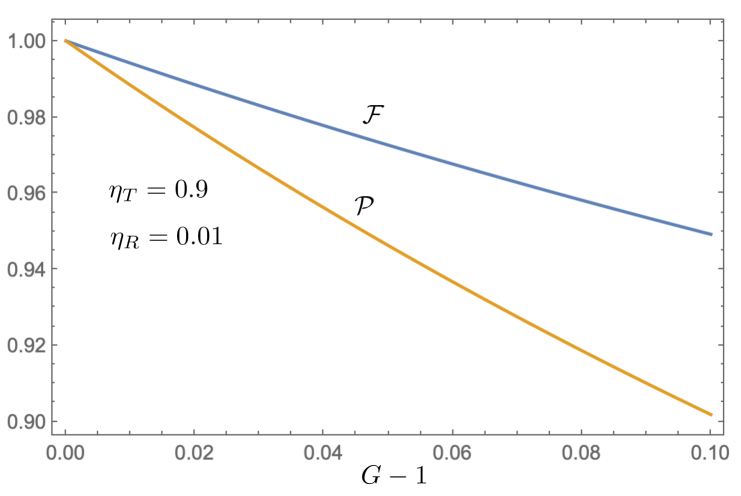
Figure 10 plots the Bell-state fidelity and the Bell-state purity versus the average number of signal-idler pairs per island per pump pulse for and We see that fidelity is greater than the purity— versus when —something that we had previously seen for lossless operation of DWDM-channelized ZALM [34].
IV Conclusions and Discussion
Chen et al. [25] proposed ZALM as a means to avoid the ill-effects of switch losses at the source in multiplexing SPDCs, and thus achieve high-fidelity ( 99%), quasi-deterministic ( 25% per-pump-pulse probability) entanglement generation. Their proposal relies on a burst of pump pulses to generate a striped frequency-domain biphoton wave function over a very broad (10 THz) bandwidth that, together with narrowband (1 GHz) filtering in the partial BSM and suitable (12.5 GHz) channelization at the receivers, leads to the need for a large number (800) of channels whose frequency-domain biphoton wave functions each approximate that of a spectrally factorable, i.e., single-temporal-mode, state. Chen et al.’s ZALM comes, however, with a heavy technological burden in that an 800-channel system requires a partial-BSM apparatus containing 3200 high quantum-efficiency SPDs, which would typically be cryo-cooled superconducting-nanowire single-photon detectors. Temporal multiplexing of the detection process could reduce the number of required SPDs, but that comes at the expense of reducing the maximum pump-pulse rate that can be employed. (In that regard, note that Chen et al. had assumed a pump-pulse rate.) Furthermore, Chen et al.’s analysis did not fully account for multipair events and losses in the partial BSM and in propagation from the ZALM QTX to Alice and Bob’s QRXs.
In seeking a better alternative for the ZALM QTX, as well as providing a more comprehensive analysis, we drew inspiration from Morrison et al.’s demonstration of an SPDC producing a biphoton wave function comprised of 8 near-ideal single-temporal-mode spectral islands [33]. Thus, we assumed SPDCs whose nonlinear crystals had ideal spectral islands, and then derived the anti-normally-ordered characteristic functions for the output signals’ state from a lossy partial BSM, and for the joint state delivered, after lossy propagation, to Alice and Bob’s QRXs. From these characteristic functions we obtained analytic results for the Bell-state fidelities and Bell-state fractions of the output signals’ state and the joint state arriving at Alice and Bob’s QRXs. Then, assuming at most one herald is sent to Alice and Bob per pump pulse and SPCI heralding, we found that 99% Bell-state fidelity, 99.98% Bell-state fraction, and 25% per-pump-pulse probability of a true herald can be obtained with 28 islands if the partial BSM is 90% efficient, and with 62 islands if the partial BSM is 80% efficient. If the number of islands is limited by practical considerations to, for example, 14, then a 95% efficient partial BSM will give 99% Bell-state fidelity, 99.98% Bell-state fraction, and 25% per-pump-pulse probability of a true herald.
The rate, , at which islands-based ZALM delivers heralded polarization-entangled photon pairs to Alice and Bob is this paper’s final takeaway. It is given by [39]
| (29) |
where is the pump’s pulse rate, and , the per-pump-pulse herald probability, includes both true and false heralds. Assuming SPCI heralding with at most one herald sent to Alice and Bob per pump pulse, and , we get when , , , and . Reducing to 0.8 and to while increasing to 62, the delivery rate drops to . Both of these examples provide 99% Bell-state fidelity and 99.98% Bell-state fraction in the presence of propagation loss commensurate with: (a) 100 km fiber connections between the ZALM QTX and Alice and Bob’s QRXs; or (b) 1500-km-long satellite-to-ground free-space (no absorption, scattering, or turbulence) links at 1.55 m wavelength between a ZALM QTX with 10-cm-diameter optics and Alice and Bob’s QRXs with 1-m-diameter optics.
These preceding rates are admittedly optimistic, but, because they are orders-of-magnitude higher than current state of the art and with lower equipment burden than DWDM-channelized ZALM, they strongly suggest continued study of islands-based ZALM. There are a variety of theoretical directions in which such follow-on work could be pursued. One is a more comprehensive exploration of the Bell-state fidelity and Bell-state fraction as functions of , , , and the available . Such an exploration, in conjunction with a capabilities assessment of domain engineering PPLN, could set realistic goals for an initial islands-based ZALM source.
Another theory area to study is the Duan-Kimble loading [40] of Alice and Bob’s pair of intracavity color-center quantum memories. Islands-based ZALM affords an extremely high Bell-state fraction, permitting us to assume that Bell states are the only loadable states arriving at Alice and Bob’s QRXs. For Bell-state illumination we can use results from Raymer et al. [41] and Shapiro et al. [34] to obtain the density operator for the loaded memories. In particular, Shapiro et al. already showed that narrowband operation—in which the ZALM QRXs’ bandwidth-compression module is such that the quantum memories’ state-dependent reflectivities are constant across the photon bandwidth—leads to a perfect transfer of the incoming biphoton state from DWDM-channelized ZALM to the memories. It turns out that such is not the case for narrowband loading of the Bell state received from islands-based ZALM unless the memories are completely lossless [42]. Nevertheless, Shapiro et al.’s loading analysis establishes a route to quantifying islands-based ZALM’s Duan-Kimble loading both inside and outside the narrowband regime.
The just-mentioned follow-on studies are natural progressions from Chen et al., Raymer et al., Shapiro et al., and the present paper. A somewhat different tack, but nonetheless an important one, is to consider replacing the Sagnac sources and partial BSM with a new alternative, proposed by Chahine et al. [43], for heralded production of polarization-entangled Bell states. Chahine et al.’s proposal uses only two SPDCs and has a simpler heralding procedure than the dual-Sagnac arrangement considered here. For islands-based ZALM it then offers the possibility of lower loss in the heralding, which could increase the value at which high Bell-state fidelity and high Bell-state fraction are obtained from which an increased delivery rate would follow. That said, the Chahine proposal’s joint density operator for the signal states sent to Alice and Bob does not match what we have derived in this paper unless the ZALM QTX is lossless, so an analysis of its performance metrics is needed to see whether it truly offers an improvement over what we have found in this paper for the dual-Sagnac source.
Acknowledgements.
This work was supported by the Engineering Research Centers Program of the National Science Foundation under Grant #1941583 to the NSF-ERC Center for Quantum Networks. The authors thank Franco Wong for encouragement and advice in our pursuit of a ZALM source capable of high-purity, quasi-deterministic entanglement distribution, and we thank Yousef Chahine for alerting us to his new concept for a heralded source of polarization-entangled Bell states.Appendix A Islands-based ZALM partial-BSM loss: Derivations
In this appendix we derive the performance metrics for islands-based ZALM with a lossy partial-BSM apparatus, i.e., one whose inefficiencies have been lumped together into a sub-unit quantum efficiency, , for each of its SPDs. The initial quantities of interest are the conditional Bell-state output probabilities from Eqs. (14) and (15) given an herald has occurred. We begin by reworking Eq. (12)’s expression for the anti-normally-ordered characteristic function associated with the joint signal-idler density operator, , of a single island.
As a first step, it is easily seen that Eq. (12) factors into
| (30) |
where and are the real and imaginary parts of . To proceed further, we rewrite the exponents in Eq. (30) as
| (31) |
and
| (32) |
where
| (33) |
and
| (34) |
with
| (35) |
and
| (36) |
for being the 4D identity matrix.
Next, we introduce the beam-splitter relations that convert the modes into the modes, i.e.,
| (37) |
that allow us to obtain the following anti-normally-ordered characteristic function for , viz.,
| (38) |
where
| (39) |
and
| (40) |
with
| (41) |
At this point we account for the SPDs’ sub-unit quantum efficiency by recognizing that detection of the modes is equivalent to unit quantum efficiency detection of the modes whose annihilation operators are
| (42) |
where the modes are in their vacuum states. It now follows that the anti-normally-ordered characteristic function of is
| (43) |
where
| (44) |
and
| (45) |
with
| (46) |
and
| (47) |
We are almost but not quite ready to start evaluating the conditional Bell-state output probabilities for the case of an herald. What we need is to recast in a form that will permit 16D polynomial-weighted inverse Fourier transforms of it to be performed analytically. Toward that end we define
| (48) |
and
| (49) |
where
| (50) |
| (51) |
and
| (52) |
The upshot of what we have just done is that is now given by
| (53) | ||||
| (54) |
where and are the probability density functions (pdfs) for 8D, real-valued, zero-mean Gaussian random vectors with covariance matrices and , respectively. Now, using standard results for Gaussian random vectors and , we get our final rewrite of :
| (55) |
Here, and are the marginal pdfs of and , i.e., 4D zero-mean, covariance-matrix , real-valued Gaussian random vectors. On the other hand, and are, respectively, the conditional pdfs for given and for given . Those probability densities are 4D Gaussians with conditional mean vectors
| (56) |
and
| (57) |
where
| (58) |
and with conditional covariance matrices
| (59) | ||||
| (60) |
With the preceding results in hand we can now find , the density operator for the ZALM source’s signal modes conditioned on there having been an herald. Once that is done, the desired conditional Bell-state output probabilities, viz., Eqs. (14) and (15), are easily obtained. Before proceeding, however, it is worth clarifying a point about the probability densities appearing in the equations above. They do not mean that the random vectors and have physical interpretations. Instead, identifying terms in as Gaussian pdfs allows us to derive analytic performance results for islands-based ZALM with a lossy partial BSM. These derivations are accomplished by means of Gaussian moment factoring, with each derivation in effect performing a 16D integral over a real-valued function.
Now to work. The unnormalized conditional density operator for the the ZALM source’s signal modes, conditioned on there having been an herald, is
| (61) |
Replacing with the operator-valued inverse Fourier transform of , cf. Eq. (11), and evaluating the inner products we get
| (62) |
Using Eq. (55), evaluating the expectations over the conditional probability densities, employing from Eq. (50), and coalescing terms we arrive at
| (63) |
where , as given in Sec. III.1. Because is the probability of getting an herald, it is immediately obvious that
| (64) |
is the conditional density operator of the ZALM source’s output modes given there has been an herald. This result shows that
| (65) |
is the associated anti-normally-ordered characteristic function, as given in Eq. (13).
At last we are ready to go after the conditional Bell-state output probabilities of islands-based ZALM with a lossy partial BSM given an herald. These are , , and , where
| (66) |
and
| (67) |
Employing Eq. (64) now results in
| (68) |
and
| (69) |
Multiplying out the polynomial terms Eqs. (68), (69) and using complex-Gaussian moment factoring [44], which applies because is the joint pdf for 4 iid circulo-complex Gaussian random variables with variance , we verify Eqs. (14) and (15). To handle the remaining possible herald events we start from Eq. (55) and parallel what we did to get and . The results we obtain are
| (70) |
and
| (71) |
Evaluating the conditional Bell-state output probabilities for these heralds, again using complex-Gaussian moment factoring, gives us
| (72) |
with all the others equaling zero. Thus, regardless of what herald occurs the output state from a ZALM QTX with a lossy partial BSM but lossless signal paths has unit Bell-state fidelity.
Turning now to Bell-state fraction for the lossy partial BSM, we already have the Bell-state output probabilities, so we need only find the conditional probability that the output state is loadable, i.e., sends at least one photon to Alice and at least one to Bob. We will do so for the case of an herald, because the other heralds give the same result, as we found for the output-state probabilities.
The unnormalized density operator, , for the loadable ) output states under the preceding conditioning is
| (73) |
where , for , is the vacuum state of the modes and is the vacuum state of the modes. We then have that
| (74) |
Using Eq. (64) and taking the trace in the coherent-state basis results in four integral terms each of which can be evaluated via complex-Gaussian moment factoring. The result is
| (75) |
Appendix B Islands-based ZALM with partial-BSM loss and propagation loss: Derivations
The principal goals of this appendix are to derive the Bell-state fidelity and the Bell-state fraction for islands-based ZALM with a lossy partial-BSM apparatus and lossy propagation. Fortunately, all the heavy lifting has already been done in Appendix A, so we can proceed quickly.
When the modes resulting from an herald propagate to Alice and Bob’s QRXs via transmissivity- channels, the modes arriving there have annihilation operators given by
| (76) |
and
| (77) |
where the modes are all in their vacuum states. With denoting the modes, we then have that
| (78) |
where , for , and . For loss in both the partial BSM and the propagation we now have that
| (79) |
and
| (80) |
Multiplying out the polynomial terms and using complex-Gaussian moment factoring we obtain Eqs. (21) and (22).
The Bell-state probabilities for the other three heralds are obtained in a like manner from
| (81) |
| (82) |
| (83) |
| (84) |
| (85) |
and
| (86) |
The results gotten in this manner are
| (87) |
and
| (88) |
Out next task in this appendix is to find the Bell-state fraction of . Given that we already have the Bell-state probabilities in hand, we need only find, cf. Eqs. (73) and (74),
| (89) |
where
| (90) |
Taking the operator-valued inverse Fourier transform of Eq. (78) to obtain , and then evaluating the Eq. (90)’s trace in the coherent-state basis results in four integral terms. Each of these integrals can be done analytically via complex-Gaussian moment factoring, with their sum being Eq. (24). The same procedure can be repeated for the other three herald possibilities leading to results given by the right-hand side of Eq. (24).
Finally, let us sketch how the Bell-state diagonality reported in Sec. III.2 can be obtained. We have that
| (91) |
and
| (92) |
Multiplying out the polynomials and doing the complex-Gaussian moment factoring we find that these off-diagonal Bell-state elements of vanish. A similar procedure for the other off-diagonal Bell-state elements of this density operator shows that they vanish too. Indeed, this procedure can be applied to the and to show that their off-diagonal Bell-state elements also vanish. We omit the details.
References
- [1] C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wootters, Teleporting an unknown quantum state via dual classic and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
- [2] D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, and A. Zeilinger, Experimental quantum teleportation, Nature 390, 575 (1997).
- [3] M. Riebe, H. Häffner, C. F. Roos, W. Hänsel, J. Benhelm, G. P. T. Lancaster, T. W. Körber, C. Becher, F. Schmidt-Kaler, D. F. V. James, and R. Blatt, Deterministic quantum teleportation with atoms, Nature 429, 734 (2004).
- [4] C. Weedbrook, S. Pirandola, R. García-Patrön, N. J. Cerf, T. C. Ralph, J. H. Shapiro, and S. Lloyd, Gaussian quantum information, Rev. Mod. Phys. 84, 621 (2012).
- [5] Quantum communication over dark fiber readily satisfies the assumption of a pure-loss channel because nonlinear effects will be negligible for its single-photon transmissions. Efficient build-out of a quantum internet, however, will entail sharing the classical internet’s fiber backbone, implying that a pure-loss quantum channel must strongly suppress cross talk from classical traffic. A recent teleportation experiment [6] has demonstrated how this can be done over a 30.2 km fiber link by using the O-band for quantum communication and the C-band for classical traffic.
- [6] J. M. Thomas, F. I. Yeh, J. H. Chen, J. J. Mambretti, S. J. Kohlert, G. S. Kanter, and P. Kumar, Quantum teleportation coexisting with classical communications in optical fiber, Optica 11, 1700 (2024).
- [7] F. Toudeh-Fallah, Long distance quantum-secured optical channels in operational environments, Proc. SPIE 13148, 1314803 (2024).
- [8] S. Lloyd, J. H. Shapiro, F. N. C. Wong, P. Kumar, S. M. Shahriar, and H. P. Yuen, Infrastructure for a quantum internet, Comput. Commun. Rev. 34, 9 (2004).
- [9] H. J. Kimble, The quantum internet, Nature 453, 1023 (2008).
- [10] S. Wehner, D. Elkouss, and R. Hanson, Quantum internet: A vision for the road ahead, Science 362, eaam9288 (2018).
- [11] P. G. Kwiat, K. Mattle, H. Weinfurter, A. Zeilinger, A. V. Sergienko, and Y. Shih, New high-intensity source of polarization-entangled photon pairs, Phys. Rev. Lett. 75, 4337 (1995).
- [12] P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard, Ultrabright source of polarization-entangled photons, Phys. Rev. A 60, R773 (1999).
- [13] Y.-H. Kim, S. P. Kulik, and Y. Shih, Bell-state preparation using pulsed nondegenerate two-photon entanglement, Phys. Rev. A 63, 060301(R) (2001).
- [14] C. Kurtsiefer, M. Oberparleiter, and H. Weinfurter, High-efficiency entangled photon pair collection in type-II parametric fluorescence Phys. Rev. A 64, 023802 (2001).
- [15] J. Brendel, N. Gisin, W. Tittel, and H. Zbinden, Pulsed energy-time entangled twin-photon source for quantum communication, Phys. Rev. Lett. 82, 2594 (1999).
- [16] I. Marcikic, H. de Riedmatten, W. Tittel, V. Scarani, H. Zbinden, and N. Gisin, Time-bin entangled qubits for quantum communication created by femtosecond pulses, Phys. Rev. A 66, 062308 (2002).
- [17] I. Marcikic, H. de Riedmatten, W. Tittel, H. Zbinden, M. Legré, and N. Gisin, Distribution of time-bin entangled qubits over 50 km of optical fiber, Phys. Rev. Lett. 93, 180502 (2004).
- [18] L. C. Andrews and R. L. Phillips, Laser Beam Propagation through Random Media (SPIE, Bellingham, 1998).
- [19] S. P. Neumann, A. Buchner, L. Bulla, M. Bohmann, and R. Ursin, Continuous entanglement distribution over a transnational 248 km fiber link, Nat. Commun. 13, 6134 (2022).
- [20] J. Yin, et al., Satellite-based entanglement distribution over 1200 kilometers, Science 356, 1140 (2017).
- [21] T. Kim, M. Fiorentino, and F. N. C. Wong, Phase-stable source of polarization-entangled photons using a polarization Sagnac interferometer, Phys. Rev. A 73, 012316 (2006).
- [22] F. N. C. Wong, J. H. Shapiro, and T. Kim, Efficient generation of polarization-entangled photons in a nonlinear crystal, Laser Phys. 16, 1517 (2006).
- [23] J. Mower and D. Englund, Efficient generation of single and entangled photons on a silicon photonic integrated chip, Phys. Rev. A 84, 052326 (2011).
- [24] P. Dhara, S. J. Johnson, C. N. Gagatsos, P. G. Kwiat, and S. Guha, Heralded-multiplexed high-efficiency cascaded source of dual-rail polarization-entangled photon pairs using spontaneous parametric down conversion, Phys. Rev. Appl. 17, 034071 (2022).
- [25] K. C. Chen, P. Dhara, M. Heuck, Y. Lee, W. Dai, S. Guha, and D. Englund, Zero-added-loss entangled-photon multiplexing for ground- and space-based quantum networks, Phys. Rev. Appl. 19, 054029 (2023).
- [26] Chen et al. [25] describe their QTX as containing two sources of polarization entanglement each comprised of a pair of coherently-combined spontaneous parametric downconverters. Wong et al.’s Sagnac configuration generates such entanglement with stability superior to that of alternative setups [22].
- [27] S. L. Braunstein and A. Mann, Measurement of the Bell operator and quantum teleportation, Phys. Rev. A 51, R1727 (1995).
- [28] Sagnac sources can also be configured to create time-bin entanglement.
- [29] C. Jones, D. Kim, M. T. Rakher, P. G. Kwiat, and T. D. Ladd, Design and analysis of communication protocols for quantum repeater networks, New J. Phys. 18, 083015 (2016).
- [30] P. Kumar, Quantum frequency conversion, Opt. Lett. 15, 1476 (1990).
- [31] J. M. Huang and P. Kumar, Observation of quantum frequency conversion, Phys. Rev. Lett. 68, 2153 (1992).
- [32] M. Karpinski, M. Jachura, L. J. Wright, and B. J. Smith, Bandwidth manipulation of quantum light by an electrooptic time lens, Nat. Photon. 11, 53 (2017).
- [33] C. L. Morrison, F. Graffitti, P. Barrow, A. Pickston, J. Ho, and A. Fedrizzi, Frequency-bin entanglement from domain-engineered down-conversion, APL Photon. 7, 066102 (2022).
- [34] J. H. Shapiro, M. G. Raymer, C. Embleton, F. N. C. Wong, and B. J. Smith, Entanglement source and quantum memory analysis for zero-added-loss multiplexing, Phys. Rev. Appl. 22, 044014 (2024); Erratum, Phys. Rev. Appl. 23, 029901 (2024).
- [35] W. P. Grice and I. A. Walmsley, Spectral information and distinguishability in type-II down-conversion with a broadband pump, Phys. Rev. A 56, 1627 (1997).
- [36] We assume that our ZALM QTX’s Sagnac SPDC sources use PPLN crystals because of their high nonlinearity and 10 THz phase-matching bandwidth.
- [37] We will continue to assume the SPDs have no dark counts.
- [38] Here, and in all that follows, integrals without limits are from to in all their dimensions.
- [39] We include both true and false heralds in ’s heralding-probability factor because is calculated from the density operator that includes both true and false heralds.
- [40] L.-M. Duan and H. J. Kimble, Scalable quantum computation through cavity-assisted interactions, Phys. Rev. Lett. 92, 127902 (2004).
- [41] M. G. Raymer, C. Embleton, and J. H. Shapiro, The Duan-Kimble cavity-atom quantum memory loading scheme revisited, Phys. Rev. Appl. 22, 044013 (2024).
- [42] The discrepancy between narrowband loading for DWDM-channelized ZALM and narrowband loading for islands-based ZALM is due to the former’s containing only and states, whereas the latter’s contains all four polarization Bell states. Note that DWDM-channelized ZALM’s density operator is a perturbative result, whereas islands-based ZALM’s density operator includes multipairs of all orders.
- [43] Y. K. Chahine, E. J. Katz, A. J. Fallon, and J. D. Lekki, Heralded entanglement source analysis for cascaded parametric down-conversion, in Digest of 2025 Quantum 2.0 (Optica, Washington DC), paper QW3A.17.
-
[44]
Complex-Gaussian moment factoring gives us
for with , and
for