High-Order Topological Phase Diagram Revealed by Anomalous Nernst Effect in Janus ScClI Monolayer
Abstract
Higher-order topological properties of two-dimensional(2D) magnetic materials have recently been proposed. In 2D ferromagnetic Janus materials, we find that ScClI is a second-order topological insulator (SOTI). Using the tight-binding approximation, we develop a multi-orbital model that adequately describes the high-order topological states of ScClI. Further, we give the complete high-order topological phase diagram of ScClI, based on the external field modulation of the magneto-valley coupling and energy levels. 2D ScClI has a pronounced valley polarization. This type of magneto-valleytronics results in different insulating phases to exhibit completely different anomalous Nernst conductance. Through valleytronics, we establish a link between the topological insulator and the valley Nernst effect, thus constructing an anomalous valley nernst conductance map that corresponds to the topological phase diagram. We utilize the characteristics of valley electronics to link higher-order topological materials with the anomalous Nernst effect, which has potential implications for high-order topological insulators and valley electronics.
I Introduction
Recently, two-dimensional high-order topological insulator(HOTI) have received great attention [1, 2, 3, 4, 5, 6]. Prior to this, higher order topological states in three-dimensional , and have received attention [7, 8, 9, 10, 11]. However, higher-order topological corner state hidden in the 2D transition metal family have only recently been discovered [1, 2, 3]. They are all protected by space inversion symmetry and have non-zero topological corner charge [12, 13, 14]. The analogous higher-order topological properties can also be extended to 2D ferromagnetic and ferroelectric materials [15, 16]. However, there is still a need for more detailed and comprehensive analysis of high-order topological multiorbital systems and phase transition processes, as well as a stronger connection to valleytronics. Moreover, compared to photonic and phononic crystals, which are highly manipulated [17, 18], there are still relatively few electronic materials with higher-order topologies. Therefore, finding new 2D HOTI materials has important value and significance.
Two-dimensional materials with honeycomb structure have strong energy valley properties [19, 20, 21]. For 2D ferromagnetic materials, the intrinsic ferromagnetic order couples with the energy valleys to produce giant valley polarization [4, 22] and leads to large differences in the Berry curvature of the K/K’ valleys. Since the Berry curvature is analogous to an equivalent magnetic field [23], the anomalous velocity imparted to the electrons leads to valley currents [21, 22, 23, 24]. Applications on this basis consist of the valley Hall effect [24] and the anomalous Nernst effect [22]. In particular, the anomalous Nernst effect has been widely measured and applied experimentally [25, 26, 27, 28, 29, 30, 31]. The anomalous Nernst effect on family materials was discussed early by Yu [31]. It can be predicted that there is a certain connection between the topological properties and the valley Nernst effect. Such a connection has rarely been mentioned. Consequently, associating topological phase transitions with the anomalous valley Hall effect holds significant physical significance.
In this work, we discover that monolayer ScClI is a SOTI, exhibiting second-order topological corner states in a 2D triangular quantum dot. Using the multi-orbital tight-binding approximation theory, we learn that the -orbitals of the halogen elements are indispensable for higher-order topology. It is not possible to show this by only considering the -orbitals. Next, by applying external field to change the magneto-valley coupling strength and energy level difference, we provide the complete topological phase diagram of 2D Janus ScClI. ScClI mainly undergoes the topological phase transition process of SOTI, quantum anomalous valley Hall insulators (QAVHI), and normal insulators (NI). Due to the strong valley electronic properties of ScClI, the phenomena of SOTI, QAVHI, and NI exhibit distinct characteristics in the thermally induced anomalous Nernst effect. Based on this foundation, we provide anomalous Nernst conductance maps that correspond to the higher-order topological phase diagram. Our results effectively link high-order topology with the anomalous Nernst effect of thermal excitation, which is of great significance for the measurement and application of experimental electronic devices.
Methods
First-principles calculations based on density functional theory (DFT) are conducted using the Vienna Simulation Package (VASP) [32, 33]. The electronic exchange-correlation interactions are treated using the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA) [34, 35]. For two-dimensional materials, a minimum of 15 Å vacuum layer is included. The energy cutoff for the plane-wave basis is set to 500 eV, and a k-mesh is employed for Brillouin-zone sampling. The convergence threshold for the maximum force during structural optimization is set to be less than 0.01 eV/Å, and the energy convergence criterion is set to be eV. We apply GGA + U method to correct the Coulomb repulsion interactions of the Sc atom’s orbitals, with a typical value of U = 3 eV [36, 37]. The parity of the occupied states is calculated using the IrRep program [38]. Additionally, a tight-binding model based on maximally localized Wannier functions (MLWFs) is constructed using the and packages [39, 40].
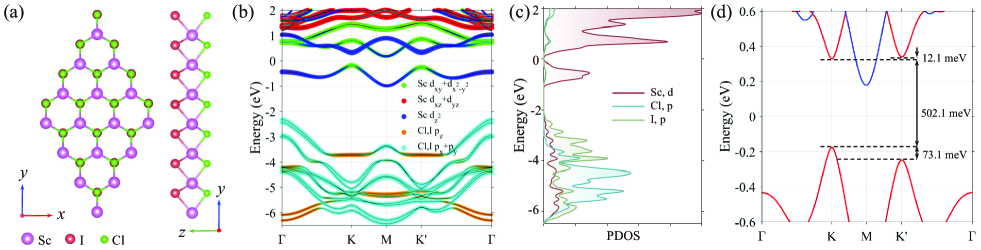
II RESULTS AND DISCUSSION
The crystal structure of the two-dimensional Janus honeycomb material ScClI is shown in Fig. 1(a). And its fatband reveals a predominant contribution from the orbitals of Sc in the vicinity of the Fermi energy level. From PDOS, it can be seen that the low energy states dominated by p-orbitals also contain contributions of d-orbitals from Sc, as shown in Fig. 1(c). In the out-of-plane ferromagnetic state, magneto-valley coupling induces polarization at K and K’, as illustrated in Fig. 1(d). The measured energy level difference between valence electrons in the K and K’ valleys is 73.1 meV, and the band gap in the spin-up energy band of the K valley is determined to be 502.1 meV. Although the system is an indirect bandgap insulator in its fully relaxed state, it can be transformed into a direct bandgap insulator by applying strain.
To verify the high-order topological properties of ScClI, we first calculate the higher order topological indices of the system, which is protected by the symmetry of the rotation symmetry. For the rotation eigenvalues calculation of all occupied states on the high symmetry points in the Brillouin zone, one can take , where denotes the counting about the symmetry eigenvalues at the points K and . The eigenvalues of the rotations are defined as . The topological indices [12, 13] of the HOTI are
| (1) |
where is the charge of the free electron. The upper indicator (3) represents symmetry. By performing DFT calculations, we obtain the wave functions of all occupied Bloch states below the Fermi level. Afterwards, utilizing the IrRep program [38] , we calculate the symmetry eigenvalues of these wave functions upon application of the rotation operator. With them, the topological indicator and the nonzero corner charge is obtained. So, we can conclude that the in-gap corner states of the system is topologically protected.
For this system, the magneto-valley coupling gives rise to a giant valley polarization. This depends on the magnitude of the magnetic moment outside the surface, and the valley polarization disappears when a magnetic moment inside the surface is applied. This is illustrated in Fig. S4 (a,b,c) of the Supplementary Material[41]. Then, to comprehensively capture the essential physical characteristics of higher-order topology, we develop a simplified multi-orbit tight-binding (TB) model based on the Wannier functions. To provide a complete representation of HOTI, the TB model incorporates the entire set of five -orbitals and six -orbitals (from Sc, Cl and I, respectively), with a focus on the nearest-neighbor orbital hopping. From Wannier fitting, the system shows both spin-orbit coupling (SOC) and valley polarization due to intrinsic magnetism. Thus, the Hamiltonian can be written as:
| (2) |
where represents the electron creation (annihilation) operator for the orbital located at position . denotes the strength of the SOC, and represents the magnetic moment direction with intensity. is the Pauli matrix.
Under this TB model, we have successfully identified higher-order topological corner states in the fully relaxed structure of ScClI. The electronic band structure of the triangular quantum dot is depicted in Fig. 2(b), where the presence of red color in the middle of the band gap represents the corner states. The wave functions of the corner states are localized on the corners of the quantum dots. Higher order topological corner states are the result after full consideration of the orbitals. Conversely, if we focus solely on the -orbital contribution from Sc atom, the presence of only one occupied band below the Fermi level results in the corner charge . In this way, we will not obtain in-gap corner states that are topologically protected, as shown in Fig. S2. Moreover, from the PDOS, it can be seen that there is a certain coupling between the and orbitals. So, establishing a TB model for multiple orbits is effective.
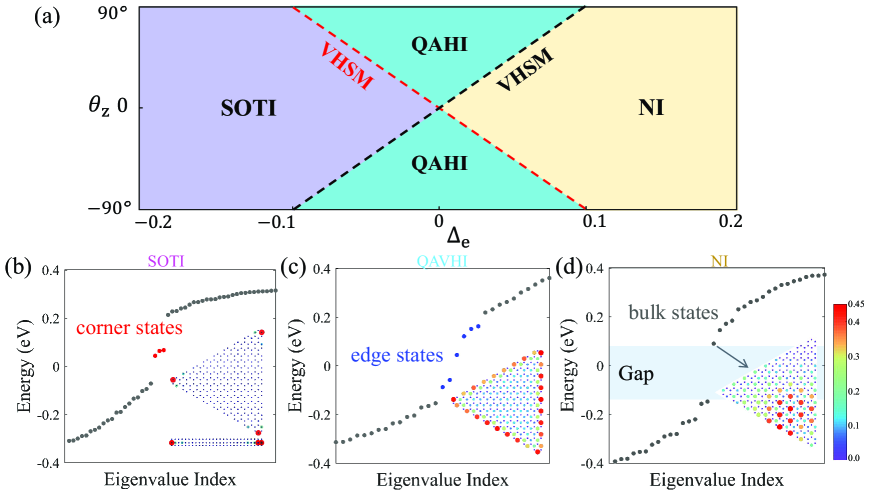
Next, we can achieve higher-order topological phase transitions by tuning the angle of the magnetic moment and the energy level difference between the and orbitals at the K-valley vertex. The angle primarily influences the magnitude of valley polarization, while induces band inversions, leading to a transition from a SOTI to a QAVHI. Due to the magneto-valley coupling, after the first band inversion, the system becomes a QAVHI with Chern number . Following the second band inversion, the system transforms into a trivial insulator. Notably, at the critical point of the topological phase transition, the system manifests a valley-hall semimetal phase at the K valley during the initial inversion and at the K’ valley during the subsequent inversion. Fig. 2(a) displays the complete phase diagram, showing the progression SOTI-VHSM-QAVHI-VHSM-NI.
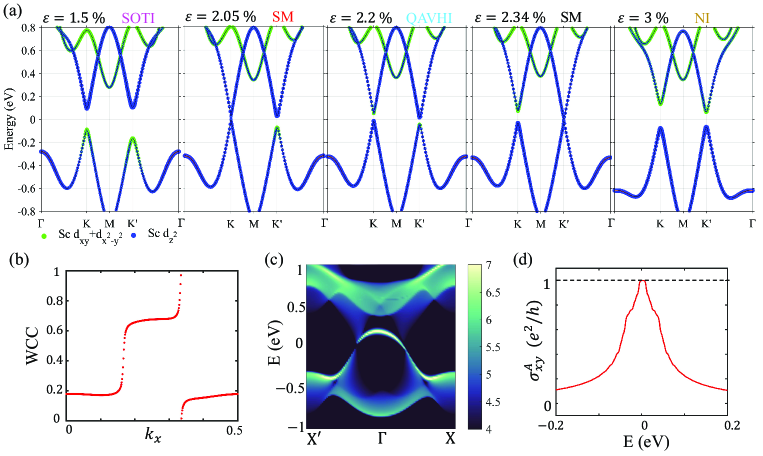
For the above topological phase transition process, we can realize it by applying tensile strain. After experiencing the first energy band inversion in the K valley, the system becomes QAVHI. At this time, the energy spectrum of the triangular quantum dots undergoes a transformation, wherein the band gap disappears and is supplanted by a continuum of edge states, as shown in Fig. 2(c). With increasing strain, the second energy band inversion occurs in the K’ valley. The system behaves as a normal insulator. The corresponding energy spectrum exhibits a band gap with no corner states or edge states within it. Additionally, both sides of the bandgap show localized features within the body, as shown in Fig. 2(d). At tensile strain magnitudes of and , the system reaches the phase boundary, transitioning into a Valley-half Semi-metal, as shown in Fig. 3(a). In both strain ranges, the Chern number of the system is 1, and Fig. 3(b) illustrates the Wannier charge center (WCC) of the system. The surface states and quantum anomalous Hall conductance platform of QAVHI are shown in Fig. 3(c, d), respectively.
The giant valley polarization property, due to the intrinsic magnetism of the system, has attracted our attention because it will bring about a difference in the Berry curvature at the valley of K/K’. Berry curvature is the same as adding an equivalent magnetic field to the system, which causes the electrons to acquire anomalous velocities [23]. We can exploit this property to obtain tunable valley flows.
Since the Berry curvature induced valley flow depends on the neighborhood of the Fermi energy level and related to the valley degree of freedom, we can use the two-band k-p model to characterize the physical properties of valley locking. The Hamiltonian of the two-band can be written as:
| (3) |
where is the valley index, is the lattice constant, is the hopping integral. denotes the strength of the magneto-valley coupling. is the Pauli matrix. The absence of a spin indicator is attributed to the spin polarization in the vicinity of the Fermi energy level. Effective mass . The energy eigenvalues are
| (4) |
where , denoting the conduction and valence bands, respectively. According to the definition of Berry curvature , where is the periodic part of the Bloch wave function. We can obtain the Berry curvature associated with the valley
| (5) |
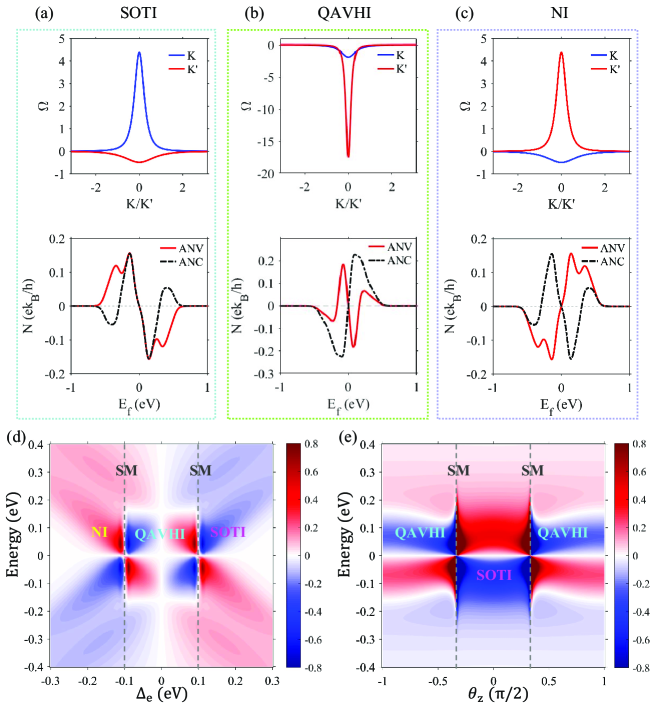
By tuning the bandgap and the magneto-valley coupling strength, we obtained the Berry curvature for the three phases SOTI, QAVHI and NI, respectively. They are shown in Fig. 4(a-c), respectively, matching the results of the DFT calculations. It is worth noting that the valley polarization is reflected by the difference in Berry curvature. One of the distinguishable traits of the Quantum Anomalous Valley Hall Effect (QAVHI) is the evident shift from opposite polarities to consistent polarities in the Berry curvature of the K/K’ valleys during a phase transition.
For characterizing the nature of the valleys matching the phase diagram, we can reveal it through the anomalous Nernst effect of thermal excitation. The valley-dependent anomalous Nernst conductivities is defined as:
| (6) |
where is the entropy density, denotes the Fermi distribution function. At 300 K temperature, we can obtain the anomalous valley Nernst conductance (ANV) and the anomalous charge Nernst conductance (ANC):
| (7) |
Figure 4(a-c) shows the anomalous Nernst conductivities for each of the three phases. In the context of QAVHI, the ANC intersects the zero energy level just once, whereas for SOTI and NI, the ANC crosses the zero point three times. Therefore, the ANC does not perfectly distinguish between individual insulation phases. On the other hand, the ANVs of the three phases differ from each other. The ANV of QAVHI has three intersections with the Fermi energy level. The ANVs of SOTI and NI has only one intersection with the Fermi energy level, and they have opposite signs. Therefore, ANV is a perfect choice to distinguish the insulating phases. When the magnetic moment is perpendicular to the plane, the magneto-valley coupling strength reaches its maximum. By adjusting the gap size, the contour plot of the ANV with respect to energy and gap is obtained, as shown in Fig. 4(d), with this process accompanied by a fixed magnetic moment direction . Fig. 4(e) corresponds to a fixed energy level difference of eV, with magnetic moment direction adjustment, resulting in a QAVHI-SOTI-QAVHI phase transition that perfectly matches the phase diagram.
III CONCLUSIONS
In summary, we employ the multi-orbital tight-binding method to analyze the high-order topological properties of the 2D Janus ScClI. We give the complete phase diagram of ScClI’s high-order topology, which is controlled by the magnetic moment direction and the orbital energy level interpolation . The theoretical predicted phase transition process of SOTI-VHSM-QAVHI-VHSM-NI has been verified and realized from the DFT calculation results under strain engineering. Meanwhile, due to the valley polarization characteristics of the system, the three types of insulators, SOTI, QAVHI, and NI, have different anomalous Nernst conductivity. By exploiting the anomalous Nernst effect, we construct an ANV map that corresponds to the topological phase diagram. Our findings can be extended to other same type of two-dimensional materials, paving a way for the future measurements and characterizations of higher-order topological phases in a broader range of materials.
ACKNOWLEDGMENTS
We acknowledge the financial support by the National Natural Science Foundation of China (No. 11874113) and the Natural Science Foundation of Fujian Province of China (No. 2020J02018).
References
- Costa et al. [2023] M. Costa, B. Focassio, L. M. Canonico, T. P. Cysne, G. R. Schleder, R. B. Muniz, A. Fazzio, and T. G. Rappoport, Connecting higher-order topology with the orbital hall effect in monolayers of transition metal dichalcogenides, Phys. Rev. Lett. 130, 116204 (2023).
- Qian et al. [2022] S. Qian, G.-B. Liu, C.-C. Liu, and Y. Yao, -symmetric higher-order topological crystalline insulators in atomically thin transition metal dichalcogenides, Phys. Rev. B 105, 045417 (2022).
- Zeng et al. [2021] J. Zeng, H. Liu, H. Jiang, Q.-F. Sun, and X. C. Xie, Multiorbital model reveals a second-order topological insulator in transition metal dichalcogenides, Phys. Rev. B 104, L161108 (2021).
- Li et al. [2023a] R. Li, N. Mao, X. Wu, B. Huang, Y. Dai, and C. Niu, Robust second-order topological insulators with giant valley polarization in two-dimensional honeycomb ferromagnets, Nano Lett. 23, 91 (2023a).
- Lee et al. [2023] J. Lee, J. Kwon, E. Lee, J. Park, S. Cha, K. Watanabe, T. Taniguchi, M.-H. Jo, and H. Choi, Spinful hinge states in the higher-order topological insulators wte2, Nat. Commun. 14, 1801 (2023).
- Guo et al. [2022] Z. Guo, J. Deng, Y. Xie, and Z. Wang, Quadrupole topological insulators in (m= ni, pd) monolayers, npj Quantum Mater. 7, 87 (2022).
- Schindler et al. [2018a] F. Schindler, Z. Wang, M. G. Vergniory, A. M. Cook, A. Murani, S. Sengupta, A. Y. Kasumov, R. Deblock, S. Jeon, I. Drozdov, et al., Higher-order topology in bismuth, Nat. phys. 14, 918 (2018a).
- Zhang et al. [2020] R.-X. Zhang, F. Wu, and S. Das Sarma, Möbius insulator and higher-order topology in , Phys. Rev. Lett. 124, 136407 (2020).
- Xu et al. [2019] Y. Xu, Z. Song, Z. Wang, H. Weng, and X. Dai, Higher-order topology of the axion insulator , Phys. Rev. Lett. 122, 256402 (2019).
- Schindler et al. [2018b] F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. Parkin, B. A. Bernevig, and T. Neupert, Higher-order topological insulators, Sci.adv. 4, eaat0346 (2018b).
- Chen et al. [2022] C. Chen, X.-T. Zeng, Z. Chen, Y. X. Zhao, X.-L. Sheng, and S. A. Yang, Second-order real nodal-line semimetal in three-dimensional graphdiyne, Phys. Rev. Lett. 128, 026405 (2022).
- Benalcazar et al. [2017a] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators, Phys. Rev. B 96, 245115 (2017a).
- Benalcazar et al. [2019] W. A. Benalcazar, T. Li, and T. L. Hughes, Quantization of fractional corner charge in -symmetric higher-order topological crystalline insulators, Phys. Rev. B 99, 245151 (2019).
- Benalcazar et al. [2017b] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Quantized electric multipole insulators, Science 357, 61 (2017b).
- Cai et al. [2023] L. Cai, R. Li, X. Wu, B. Huang, Y. Dai, and C. Niu, Second-order topological insulators and tunable topological phase transitions in honeycomb ferromagnets, Phys. Rev. B 107, 245116 (2023).
- Mao et al. [2023] N. Mao, R. Li, X. Zou, Y. Dai, B. Huang, and C. Niu, Ferroelectric higher-order topological insulator in two dimensions, Phys. Rev. B 107, 045125 (2023).
- Zhang et al. [2023] Y. Zhang, J. Tang, X. Dai, and Y. Xiang, Flexible dimensional hierarchy of higher-order topology in the stacked kagome-chain acoustic crystal, Commun. Phys. 6, 130 (2023).
- Wang et al. [2021] H.-X. Wang, L. Liang, B. Jiang, J. Hu, X. Lu, and J.-H. Jiang, Higher-order topological phases in tunable c3 symmetric photonic crystals, Photon. Res. 9, 1854 (2021).
- Ezawa [2015] M. Ezawa, Monolayer topological insulators: Silicene, germanene, and stanene, J Phys. Soc. Jpn 84, 121003 (2015).
- Jana and Muralidharan [2022] K. Jana and B. Muralidharan, Robust all-electrical topological valley filtering using monolayer 2d-xenes, npj 2D Mater. Appl. 6, 19 (2022).
- Xiao et al. [2012] D. Xiao, G.-B. Liu, W. Feng, X. Xu, and W. Yao, Coupled spin and valley physics in monolayers of and other group-vi dichalcogenides, Phys. Rev. Lett. 108, 196802 (2012).
- Zhou et al. [2021] X. Zhou, R.-W. Zhang, Z. Zhang, W. Feng, Y. Mokrousov, and Y. Yao, Sign-reversible valley-dependent berry phase effects in 2d valley-half-semiconductors, npj Comput. Mater. 7, 160 (2021).
- Qi et al. [2015] J. Qi, X. Li, Q. Niu, and J. Feng, Giant and tunable valley degeneracy splitting in , Phys. Rev. B 92, 121403 (2015).
- Tong et al. [2016] W.-Y. Tong, S.-J. Gong, X. Wan, and C.-G. Duan, Concepts of ferrovalley material and anomalous valley hall effect, Nat. commun. 7, 13612 (2016).
- Tanaka et al. [2023] H. Tanaka, T. Higo, R. Uesugi, K. Yamagata, Y. Nakanishi, H. Machinaga, and S. Nakatsuji, Roll-to-roll printing of anomalous nernst thermopile for direct sensing of perpendicular heat flux, Adv. Mater. , 2303416 (2023).
- Li et al. [2023b] M. Li, H. Pi, Y. Zhao, T. Lin, Q. Zhang, X. Hu, C. Xiong, Z. Qiu, L. Wang, Y. Zhang, et al., Large anomalous nernst effects at room temperature in fe3pt thin films, Adv. Mater. , 2301339 (2023b).
- Roychowdhury et al. [2023] S. Roychowdhury, K. Samanta, P. Yanda, B. Malaman, M. Yao, W. Schnelle, E. Guilmeau, P. Constantinou, S. Chandra, H. Borrmann, et al., Interplay between magnetism and topology: Large topological hall effect in an antiferromagnetic topological insulator, eucuas, J. Am. Chem. Soc. (2023).
- Pan et al. [2022] Y. Pan, C. Le, B. He, S. J. Watzman, M. Yao, J. Gooth, J. P. Heremans, Y. Sun, and C. Felser, Giant anomalous nernst signal in the antiferromagnet ybmnbi2, Nat. mater. 21, 203 (2022).
- Li et al. [2023c] Y. Li, J. Zhou, M. Li, L. Qiao, C. Jiang, Q. Chen, Y. Li, Q. Tao, and Z.-A. Xu, Enhanced anomalous nernst effect by tuning the chemical potential in the topological kagome ferromagnet , Phys. Rev. Appl. 19, 014026 (2023c).
- Sawahata et al. [2023] H. Sawahata, N. Yamaguchi, S. Minami, and F. Ishii, First-principles calculation of anomalous hall and nernst conductivity by local berry phase, Phys. Rev. B 107, 024404 (2023).
- Yu et al. [2015] X.-Q. Yu, Z.-G. Zhu, G. Su, and A.-P. Jauho, Thermally driven pure spin and valley currents via the anomalous nernst effect in monolayer group-vi dichalcogenides, Phys. Rev. Lett. 115, 246601 (2015).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci. 6, 15 (1996).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Perdew et al. [1998] J. P. Perdew, K. Burke, and M. Ernzerhof, Perdew, burke, and ernzerhof reply:, Phys. Rev. Lett. 80, 891 (1998).
- Jia et al. [2023] K. Jia, X.-J. Dong, S.-S. Li, W.-X. Ji, and C.-W. Zhang, Spontaneous valley polarization and valley-nonequilibrium quantum anomalous hall effect in janus monolayer scbri, Nanoscale 15, 8395 (2023).
- Guo et al. [2023] X.-S. Guo, S.-D. Guo, S.-N. Si, K. Cheng, K. Wang, and Y. S. Ang, Janus monolayer scxy (x,y = cl, br and i) for piezoelectric and valleytronic application: a first-principle prediction, J Phys.-Condens. Mat. 35, 405501 (2023).
- Iraola et al. [2022] M. Iraola, J. L. Mañes, B. Bradlyn, M. K. Horton, T. Neupert, M. G. Vergniory, and S. S. Tsirkin, Irrep: Symmetry eigenvalues and irreducible representations of ab initio band structures, Comput. Phys. Commun. 272, 108226 (2022).
- Mostofi et al. [2008] A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, and N. Marzari, wannier90: A tool for obtaining maximally-localised wannier functions, Comput. Phys. Commun. 178, 685 (2008).
- Wu et al. [2018] Q. Wu, S. Zhang, H.-F. Song, M. Troyer, and A. A. Soluyanov, Wanniertools: An open-source software package for novel topological materials, Comput. Phys. Commun.s 224, 405 (2018).
- [41] See supplemental material for () orbital verification of high-order topology, () robustness of high-order topology, () magnetic valley coupling effects and other dft results, () valley related anomalous nernst conductivity and anc map., .