High-precision mass measurement of ¹⁰³Sn restores smoothness of the mass surface

C. M. Ireland ireland@frib.msu.edu Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA F. M. Maier Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA G. Bollen Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA S. E. Campbell Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA X. Chen Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA H. Erington Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA N. D. Gamage Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA M. J. Gutiérrez Institut für Physik, Universität Greifswald, 17487 Greifswald, Germany GSI Helmholtzzentrum für Schwerionenforschung, D-64291 Darmstadt, Germany C. Izzo Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA E. Leistenschneider Nuclear Science Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA E. M. Lykiardopoulou Nuclear Science Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA R. Orford Nuclear Science Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA W. S. Porter Department of Physics and Astronomy, University of Notre Dame, Notre Dame, IN, USA D. Puentes Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA M. Redshaw Department of Physics, Central Michigan University, Mount Pleasant, Michigan 48859, USA R. Ringle Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA S. Rogers Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA S. Schwarz Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA L. Stackable Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA C. S. Sumithrarachchi Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA A. A. Valverde Physics Divison, Argonne National Laboratory, Argonne, IL, USA A. C. C. Villari Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA I. T. Yandow Facility for Rare Isotope Beams, East Lansing, Michigan, 48824, USA Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA

(August 2, 2025)

Abstract

As a step towards the ultimate goal of a high-precision mass measurement of doubly-magic ¹⁰⁰Sn, the mass of ¹⁰³Sn was measured at the Low Energy Beam and Ion Trap (LEBIT) located at the Facility for Rare Isotope Beams (FRIB). Utilizing the time-of-flight ion cyclotron resonance (ToF-ICR) technique, a mass uncertainty of 3.7 keV was achieved, an improvement by more than an order of magnitude compared to a recent measurement performed in 2023 at the Cooler Storage Ring (CSRe) in Lanzhou. Although the LEBIT and CSRe mass measurements of ¹⁰³Sn are in agreement, they diverge from the experimental mass value reported in the 2016 version of the Atomic Mass Evaluation (AME2016), which was derived from the measured $Q_{\beta^{+}}$ value and the mass of ¹⁰³In. In AME2020, this indirectly measured ¹⁰³Sn mass was classified as a ‘seriously irregular mass’ and replaced with an extrapolated value, which aligns with the most recent measured values from CSRe and LEBIT. As such, the smoothness of the mass surface is confidently reestablished for ¹⁰³Sn. Furthermore, LEBIT’s mass measurement of ¹⁰³Sn enabled a significant reduction in the mass uncertainties of five parent isotopes which are now dominated by uncertainties in their respective $Q$ -values.

^†^†preprint: APS/123-QED

I I. Introduction

Atomic nuclei composed of specific numbers of protons and neutrons known as magic numbers show particularly energetically favorable configurations. For example, the binding energy of these nuclei is significantly higher than what the semi-empirical mass formula [1], derived from the liquid drop model of the nucleus, would predict. Understanding the microscopic origins of this phenomenon, known as nuclear shell evolution, is a central focus of contemporary nuclear physics [2, 3]. The isotope ¹⁰⁰Sn is often referred to as the ‘holy grail of nuclear structure research’, as it is the heaviest known proton-bound nucleus among the self-conjugate ( $N=Z$ ) nuclei, which is expected to be doubly magic with neutron and proton shell closures at $N=50$ and $Z=50$ , respectively. Comprehensive reviews of the existing literature on ¹⁰⁰Sn can be found in Refs. [4, 5]. Significant experimental efforts are underway to measure the properties of ¹⁰⁰Sn. Its proximity to the proton drip-line makes it one of the rarest nuclei to study. As such, only its half-life, $\beta$ -endpoint energy and mass are known so far [6, 7]. Unfortunately, the limited precision of the latter does not provide sufficient clarity regarding the nuclear shell evolution along the proton drip-line.

The properties of nuclei close to ¹⁰⁰Sn are also of high interest for nuclear structure studies, see e.g. recent discussions in Refs. [8, 9, 10, 11, 12, 13]. The isotopes located northeast of ¹⁰⁰Sn on the nuclear chart form an island of enhanced $\alpha$ and proton decay whose existence originates from the double magicity of ¹⁰⁰Sn and the proximity to the proton drip-line [14]. They show a large Gamow-Teller $\beta$ -decay strength [6], super-allowed $\alpha$ decay [15, 16, 17, 18, 19, 20], and potentially cluster [21, 22, 23] and two-proton emission [24, 25]. Moreover, these isotopes play a role in stellar nucleosynthesis as the astrophysical rapid proton (rp) capture process dies out in this region [14, 26, 27, 28, 29, 30]. Precise knowledge of their binding energies, and thus their masses, are necessary to establish the energy balances of the relevant decays and transitions in this process.

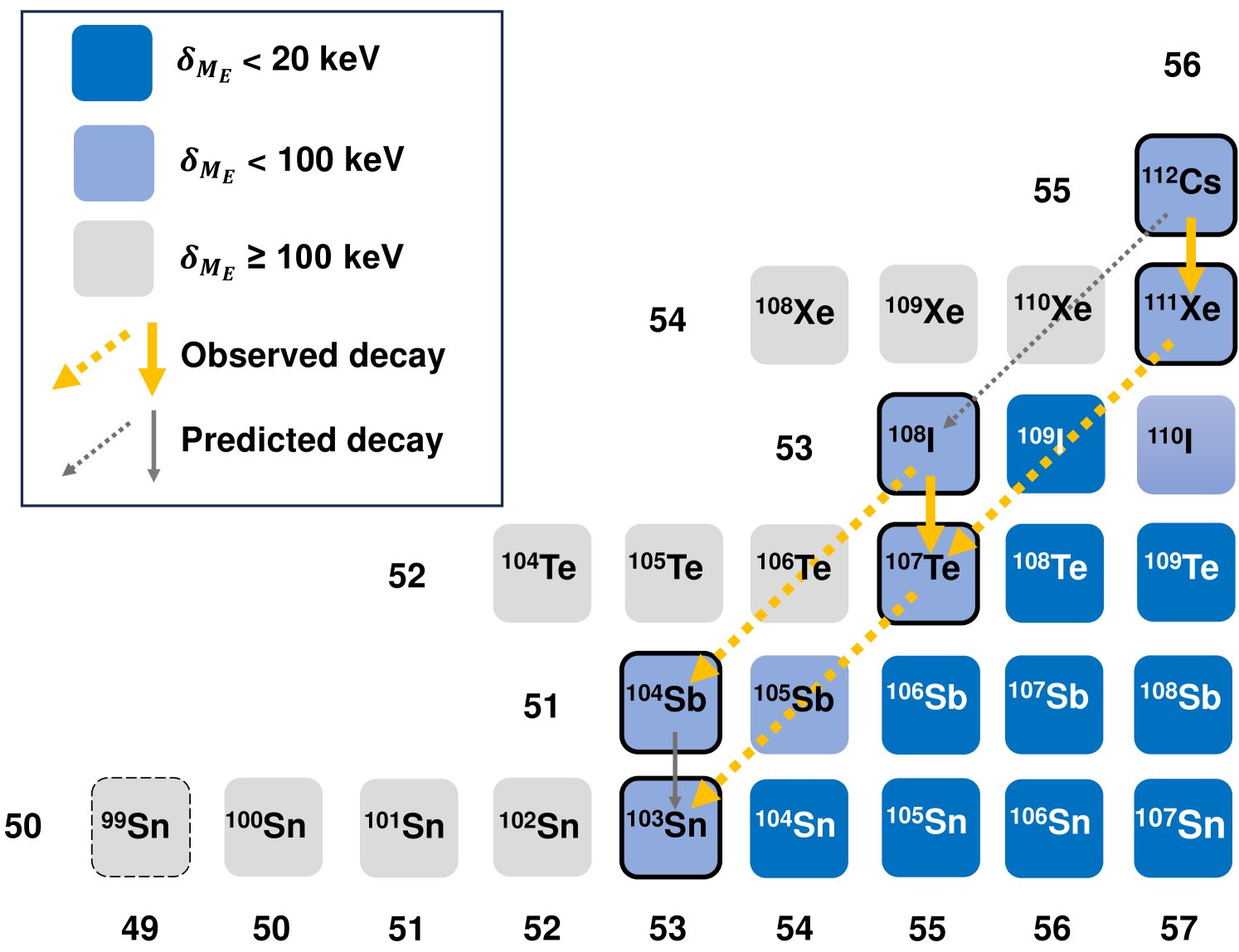
Since the decay chains of ¹⁰⁴Sb, ¹⁰⁷Te, ¹⁰⁸I, ¹¹¹Xe, and ¹¹²Cs are terminated in ¹⁰³Sn (see Fig. 1), a precise knowledge of the mass of ¹⁰³Sn is required to determine the masses of these five isotopes based on their respective $Q$ -values known from decay spectroscopy [31]. However, the mass of ¹⁰³Sn has been a topic of debate. The 2016 version of the Atomic Mass Evaluation (AME2016) [32] reported an experimental mass excess of $-66970(70)$ keV for ¹⁰³Sn derived from the $Q_{\beta^{+}}$ value and the mass of ¹⁰³In, but significant inconsistencies with theoretical predictions, see e.g. Ref. [8], and mass surface trends led to its replacement with an extrapolated value of $-67090(100)$ keV in AME2020 [31]. A subsequent direct mass measurement at the Cooler Storage Ring (CSRe) in Lanzhou in 2023 yielded a mass excess of $-67138(68)$ keV [33], which is in good agreement with the extrapolated value in AME2020, restoring confidence in the smoothness of the mass surface. An independent and more precise mass measurement of ¹⁰³Sn would further validate this finding and would serve as a crucial anchor for the masses of ¹⁰⁴Sb, ¹⁰⁷Te, ¹⁰⁸I, ¹¹¹Xe, and ¹¹²Cs.

Refer to caption — Figure 1: The nuclear landscape in the region of ¹⁰⁰Sn. Individual isotopes are colored based on their mass excess uncertainties $\delta_{M_{E}}$ prior to this work. A dashed border around an isotope refers to an extrapolated mass. The mass excesses of isotopes marked with a thick solid border were improved in this work. Directly observed and predicted decay chains are illustrated by thick orange and thin grey arrows, respectively, representing either proton (solid) or alpha (dashed) decay.

In this work, we report on high-precision Penning trap mass measurements of ¹⁰³Sn performed at the Low Energy Beam and Ion Trap (LEBIT) [34] located at the Facility of Rare Isotope Beams (FRIB) using the time-of-flight ion cyclotron (ToF-ICR) technique [35, 36, 37]. Beyond its relevance to nuclear structure and astrophysics, the high precision mass measurement of ¹⁰³Sn serves as a step towards a measurement of ¹⁰⁰Sn. With the ongoing ramp-up of beam intensity [38], FRIB is expected to produce ¹⁰⁰Sn, as well as many of its neighbors, at rates of a few ions per second in the near future, paving the way for exceptional research opportunities and deeper insights into the evolution of the nuclear shells in the vicinity of doubly magic ¹⁰⁰Sn.

II II. Experimental Method and Analysis

A beam of radioactive ¹⁰³Sn was produced via projectile fragmentation. A ¹²⁴Xe primary beam was accelerated in FRIB’s superconducting Linear Accelerator [39] to an energy of 228 MeV/u and sent to a 2.015 mm thick ¹²C target, creating a cocktail of ion species that was passed to the Advanced Rare Isotope Separator (ARIS) [40] for purification. In preparation for stopping the ions in a gas stopper, the momentum of the purified beam was compressed using an Al wedge of 1004 $\mu$ m thickness at an angle of 2.67 mrad, followed by a 611 $\mu$ m thick Al degrader. An optimal degrader angle of 17 degrees was determined adjusting the effective thickness seen by the incoming beam. This process prepared the beam for acceptance into the Advanced Cryogenic Gas Stopper (ACGS) [41], which utilizes helium buffer gas to stop the beam. After stopping, radio-frequency (RF) carpet surfing [42] was used to guide the ions to an extraction orifice. After extraction, the ions passed through an RF quadrupole for differential pumping and were accelerated to 30 keV. A dipole magnet with resolving power $\approx$ 1500 selected all ion species with a mass-to-charge ratio $A/$ Q=51.5, including ¹⁰³Sn²⁺. The choice of a half-integer $A/$ Q was motivated by the increased purity of the beam delivered to LEBIT. At LEBIT, the continuous ion beam was injected into a linear buffer-gas-filled Paul trap cooler-buncher [43] for accumulation, cooling and bunching of the ion beam. Following the extraction of the ions from the Paul trap as well-defined ion bunches with reduced emittance, the ions were guided into LEBIT’s 9.4 T hyperbolic Penning trap [44].

In the Penning trap, the ions were confined in three-dimensions by a homogeneous magnetic field $B$ and a quadrupolar electrostatic field. The motion of an ion in a Penning trap is characterized by three eigenfrequencies: an axial frequency $\nu_{z}$ and two radial frequencies, $\nu_{-}$ (magnetron frequency) and $\nu_{+}$ (reduced-cyclotron frequency), where typically $\nu_{-}\ll\nu_{z}<\nu_{+}$ . For an ideal trap, the cyclotron frequency $\nu_{c}$ of an ion can be approximated as the sum of its radial frequencies [45],

\nu_{c}=\nu_{+}+\nu_{-}.

(1)

Penning traps enable a precise determination of the mass $m$ of the ion of interest by measuring its cyclotron frequency $\nu_{c}=qB/(2\pi m)$ relative to that of a well-known reference ion $\nu_{c,\mathrm{ref}}=q_{\mathrm{ref}}B/(2\pi m_{\mathrm{ref}})$ . The cyclotron frequency ratio $R$ is given by

R=\frac{\nu_{c}}{\nu_{c,\textrm{ref}}}=\frac{q\cdot m_{\textrm{ref}}}{q_{\textrm{ref}}\cdot m},

(2)

where $q$ and $q_{\mathrm{ref}}$ are the charges and $m$ and $m_{\mathrm{ref}}$ are the masses of the ion of interest and the reference ion, respectively.

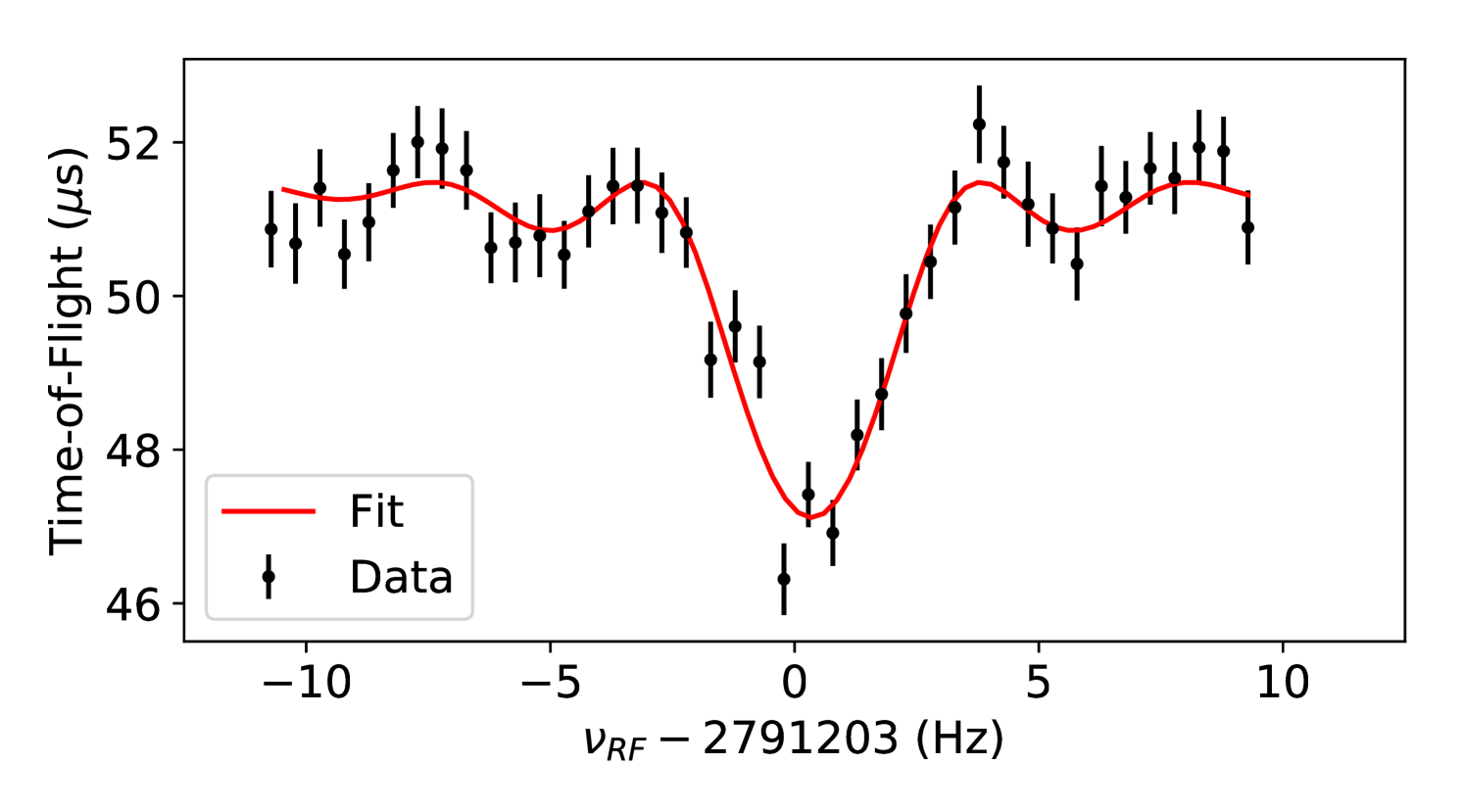
In this work, the mass of ¹⁰³Sn²⁺ was determined using the ToF-ICR technique [35, 37, 36]. Extracted ions from the cooler-buncher were steered off-axis relative to trap center upon injection into the Penning trap using a Lorentz steerer [46], inducing initial magnetron motion. The remaining isobaric contaminants at $A/$ Q = 51.5 were cleaned using dipolar RF excitation applied to the central ring electrode near their respective reduced cyclotron frequencies [47]. A quadrupolar RF pulse applied for a chosen 250 ms of excitation time within a frequency range near that of the expected cyclotron frequency for ¹⁰³Sn²⁺ converted the slow magnetron motion to fast reduced cyclotron motion. The ions were subsequently ejected and their time-of-flight to a microchannel plate (MCP) detector was recorded. Figure 2 shows the ions’ time-of-flight as a function of the applied quadrupolar frequency $\nu_{RF}$ . When $\nu_{RF}$ approached $\nu_{c}$ , the ions’ radial energy increased, resulting in a shorter flight time to the detector. This led to a time-of-flight minimum when $\nu_{RF}=\nu_{c}$ . Measurements of the ion of interest for 250 ms of quadrupolar excitation time and measurements of the stable molecular reference ¹²\ceC3¹\ceH2¹⁴\ceN1⁺ for 500 ms of excitation time were interleaved to yield the average ratio $\bar{R}$ , weighted by each measurement’s uncertainty. The mass of ¹⁰³Sn was determined according to Eq. 2 accounting for the mass of the missing electron(s). The electron’s binding energy itself is neglected, as it is smaller than the statistical uncertainty of $\bar{R}$ .

III III. Results

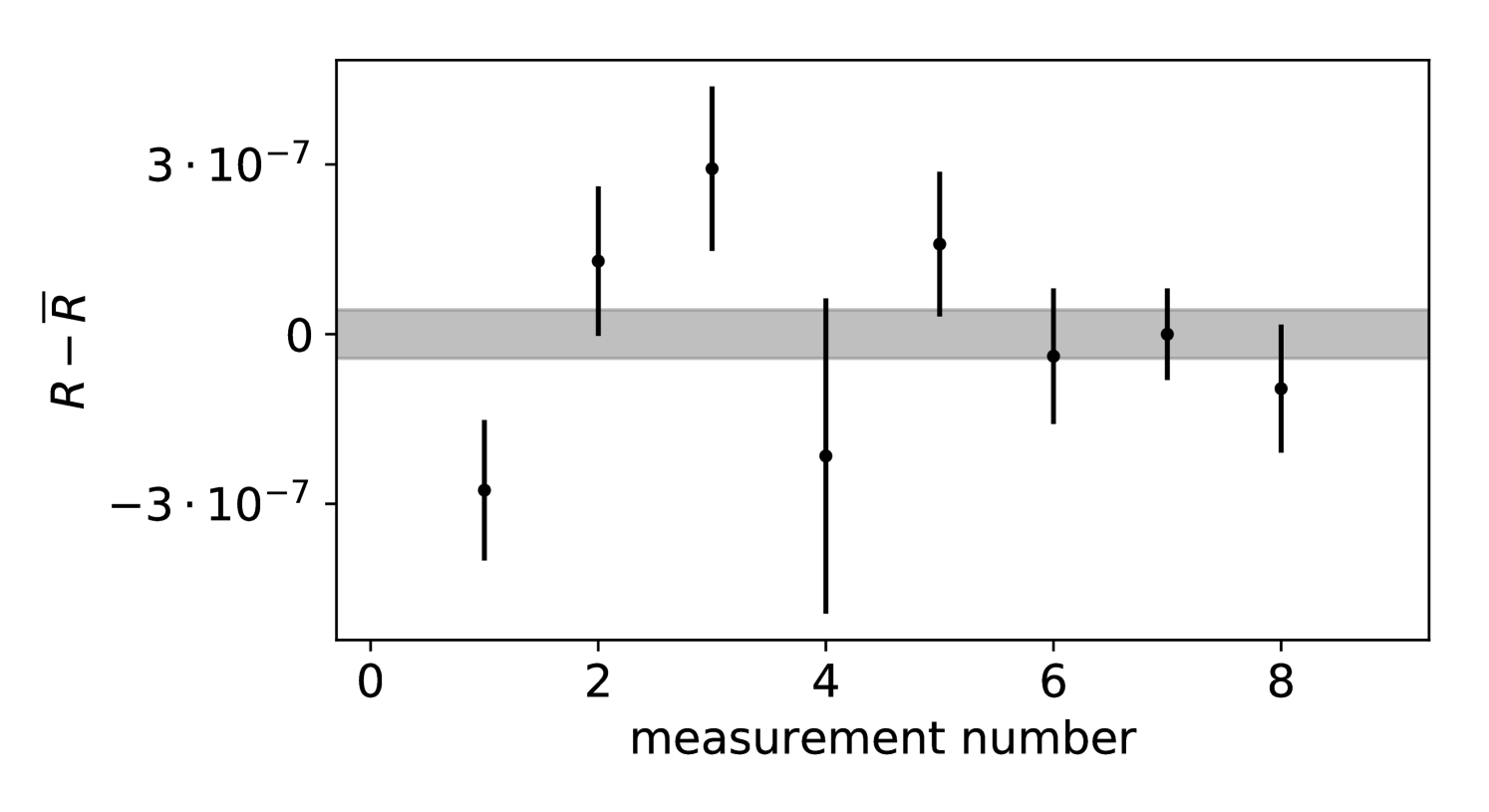
Eight ToF-ICR measurements of ¹⁰³Sn²⁺ were taken over the course of approximately eight hours. The measured frequency ratios of the individual measurements are shown in Fig. 3 relative to that of the stable reference. The weighted average mass ratio $\bar{R}=1.010779605(29)$ corresponds to a mass excess of $-67125.9(3.7)$ keV for ¹⁰³Sn.

Several systematic effects add an uncertainty $\delta_{R}$ to $\bar{R}$ . Mass-dependent shifts related to inhomogeneity in the magnetic field and trap imperfections were studied at LEBIT in detail and are known to add an uncertainty of $\delta_{R}\approx 2\times 10^{-10}/u$ [48]. Additionally, non-linear temporal shifts in the magnetic field at LEBIT contribute $\delta_{R}<10^{-9}$ per hour [49]. To counter these, regular reference measurements were performed. The maximum ion cutoff $\leq 5$ also allowed the uncertainty due to ion-ion interactions to be $\delta_{R}\approx 10^{-8}$ . These various uncertainties are negligible in comparison to the statistical precision of the measurement ( $\approx 10^{-7}$ ). The cyclotron frequency ratio $R$ was periodically checked against the expected $R$ determined from masses obtained from AME2020 as measurements were performed to verify that it did not correspond to (molecular) isobars within the uncertainty of the measurement. No such isobars were plausible, providing confirmation that what was measured was indeed ¹⁰³Sn²⁺.

IV IV. Discussion

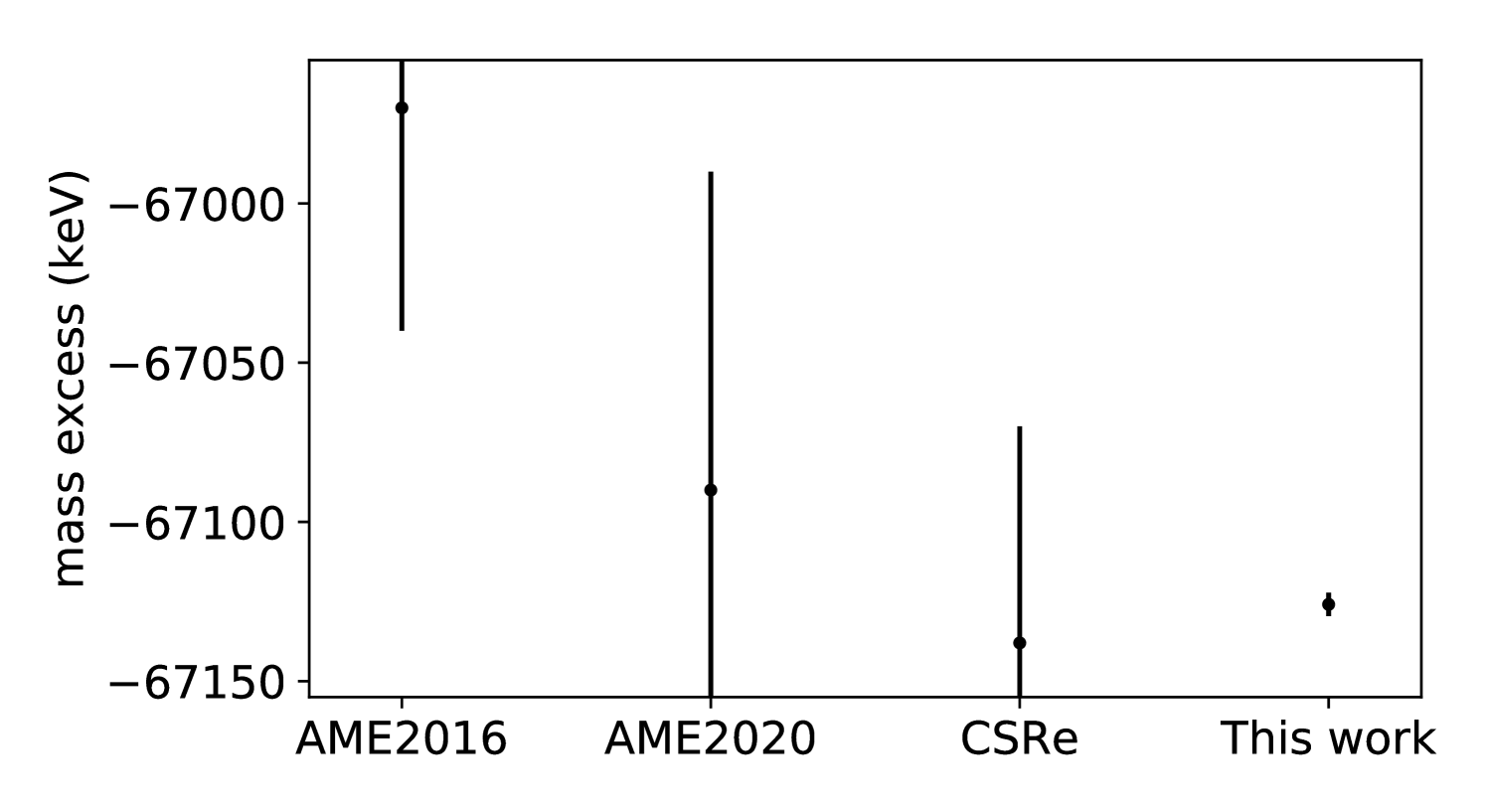
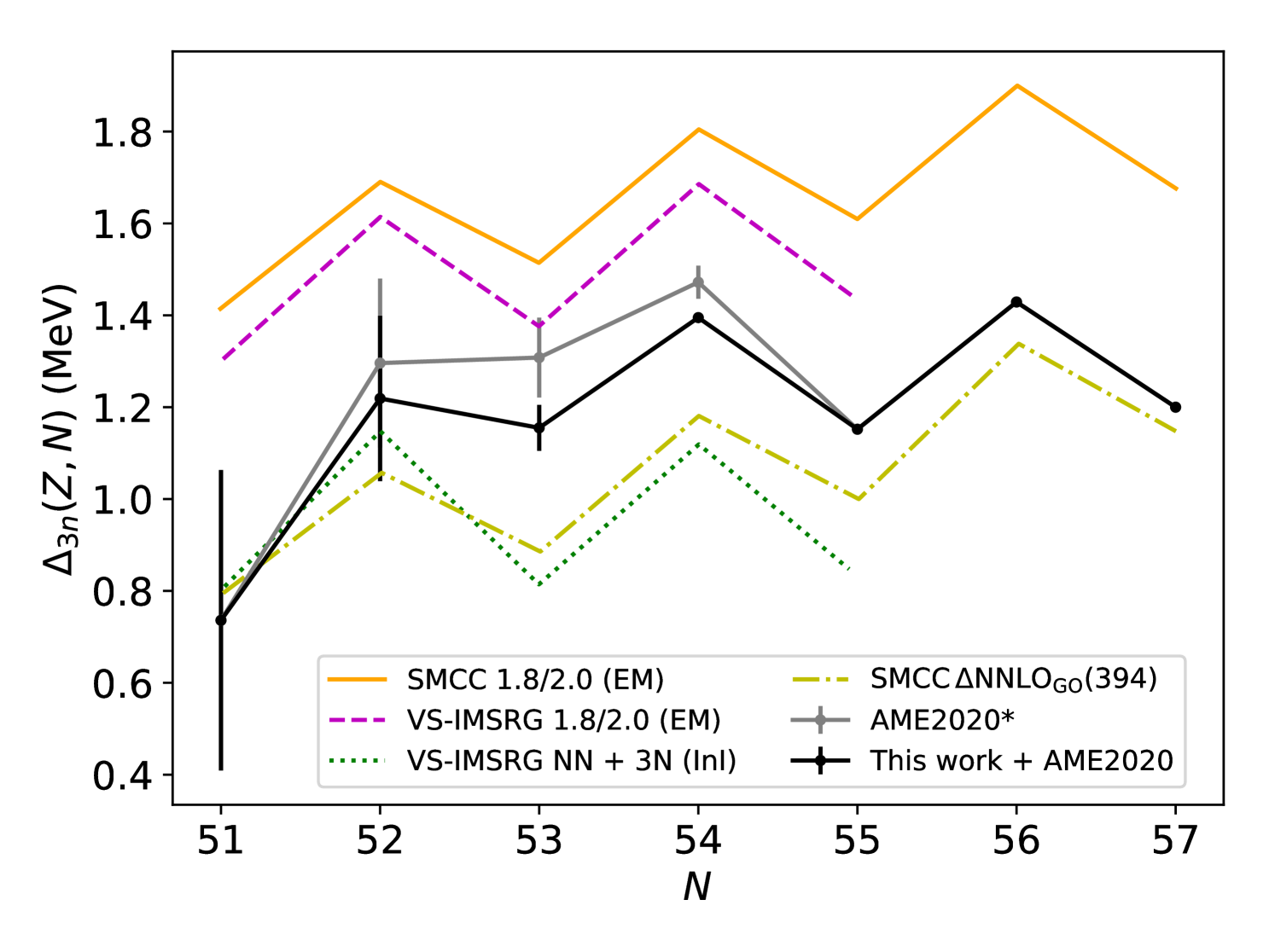
Our mass value of ¹⁰³Sn agrees with the previous measurement conducted at CSRe [33], while improving the precision by more than an order of magnitude, see Fig. 4. However, both of these measurements deviate from the mass reported experimentally in AME2016 [32], which was derived indirectly from the known mass of ¹⁰³In and the $\beta$ -decay energy $Q_{\beta^{+}}$ between ¹⁰³Sn and ¹⁰³In [32, 50, 51]. Assuming that the atomic mass $M$ of ¹⁰³In is well known, we calculate a new $Q_{\beta^{+}}$ value based on our measured mass of ¹⁰³Sn and the AME2020 mass of ¹⁰³In [31], $Q_{\beta^{+}}=M(^{103}\mathrm{Sn})-M(^{103}\mathrm{In})$ . Our updated $Q_{\beta^{+}}$ value is 7506(10) keV, compared to the previous value of 7660(70) keV. This discrepancy indicates a limited understanding of the full decay processes, possibly due to internal gamma conversion or undetected weak decay branches in Refs. [50, 51]. In AME2020 [31], the mass of ¹⁰³Sn was classified as a ‘seriously irregular mass’ and replaced by an extrapolated value, which perfectly matches our new measurement. Consequently, the smoothness of the mass surface around ¹⁰³Sn is confidently restored. Taking our new mass value of ¹⁰³Sn into account, the experimental trend of the three-point estimator for the odd-even staggering $\Delta_{3n}(Z,N)=0.5\cdot(-1)^{N}[M_{E}(Z,N-1)-2M_{E}(Z,N)+M_{E}(Z,N+1)]$ along the tin isotopic chain is relatively well reproduced by various theoretical models that are discussed in detail in Ref. [8], see Fig. 5. This increases confidence in the predictive power of these theoretical calculations for ¹⁰⁰Sn.

Furthermore, our new high-precision mass measurement of ¹⁰³Sn significantly reduces the mass uncertainty of the alpha and proton emitters ¹⁰⁴Sb, ¹⁰⁷Te, ¹⁰⁸I, ¹¹¹Xe and ¹¹²Cs, which are located northeast of the nuclear chart with respect to ¹⁰⁰Sn, see Fig. 1. The mass excesses of these five isotopes were calculated based on our high-precision ¹⁰³Sn measurement and the respective $Q$ -values, see Tab. 1,

\begin{split}M_{E}(^{107}\mathrm{Te})&=M_{E}(^{103}\mathrm{Sn})+M_{E}(\alpha)+Q_{\alpha}(^{107}\mathrm{Te}),\\ M_{E}(^{111}\mathrm{Xe})&=M_{E}(^{107}\mathrm{Te})+M_{E}(\alpha)+Q_{\alpha}(^{111}\mathrm{Xe}),\\ M_{E}(^{112}\mathrm{Cs})&=M_{E}(^{111}\mathrm{Xe})+M_{E}(p)+Q_{p}(^{112}\mathrm{Cs}),\\ M_{E}(^{108}\mathrm{I})&=M_{E}(^{107}\mathrm{Te})+M_{E}(p)+Q_{p}(^{108}\mathrm{I})\text{ and}\\ M_{E}(^{104}\mathrm{Sb})&=M_{E}(^{108}\mathrm{I})-M_{E}(\alpha)-Q_{\alpha}(^{108}\mathrm{I}).\\ \end{split}

(3)

The respective mass excesses can be found in Tab. 2. Their uncertainties are now dominated by the uncertainties of the respective $Q$ -values and not by the uncertainty in the mass excess of ¹⁰³Sn. Since the astrophysical rp-process is terminated in this region [14, 26, 27, 28, 29, 30], these isotopes play a vital role in our understanding of stellar nucleosynthesis. Precise mass determinations, and ideally direct mass measurements in the future, aid in establishing the energy balances of the relevant decays and transitions.

Table 1: Measured

Q

-values as reported in AME2020 [31] and used for the mass excess calculation of the five parent isotopes of ¹⁰³Sn presented in Tab. 2.

	$Q$ -value (keV)	references
$Q_{p}$ (¹⁰⁸I)	597(13)	Ref. [26]
$Q_{p}$ (¹¹²Cs)	816(4)	Refs. [52, 53]
$Q_{\alpha}$ (¹⁰⁷Te)	4010(5)	Refs. [54, 55, 26, 56]
$Q_{\alpha}$ (¹⁰⁸I)	4099(5)	Refs. [52, 26]
$Q_{\alpha}$ (¹¹¹Xe)	3710(60)	Refs. [54, 57, 55, 56]

Table 2: Measured mass excess of ¹⁰³Sn and calculated mass excesses based on the ¹⁰³Sn measurement from this work (left) compared to the result from CSRe [33] (right).

	$M_{E,\mathrm{LEBIT}}$ (keV)	$M_{E,\mathrm{CSRe}}$ (keV)
¹⁰³Sn	$-67125.9(3.7)$	$-67138(68)$
¹⁰⁴Sb	$-59329(15)$	$-59340(70)$
¹⁰⁷Te	$-60691(6)$	$-60700(70)$
¹⁰⁸I	$-52805(14)$	$-52820(70)$
¹¹¹Xe	$-54556(60)$	$-54570(90)$
¹¹²Cs	$-46451(60)$	$-46460(90)$

V V. Conclusions

The first Penning trap mass measurement of ¹⁰³Sn was performed at LEBIT [34] and a mass excess of $-67125.9(3.7)$ keV was obtained. This value improves the precision of the previous measurement [33] by more than an order of magnitude and restores confidence in the smoothness of the nuclear mass surface. Furthermore, the masses of five parent alpha/proton emitters calculated from this improved measurement of ¹⁰³Sn have become well-anchored and their mass uncertainties are now dominated by their respective $Q$ -values. The closed neutron and proton shells at $N=50$ and $Z=50$ of ¹⁰⁰Sn provide a unique testing ground for our understanding of nuclear forces and shell evolution. Our measurement of ¹⁰³Sn, just three neutrons away from ¹⁰⁰Sn, lays the foundation for future high-precision mass measurements of ¹⁰⁰Sn.

VI Acknowledgements

This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics and used resources of the Facility for Rare Isotope Beams (FRIB) Operations, which is a DOE Office of Science User Facility under Award Number DE-SC0023633. This work was conducted with the support of Michigan State University, the US National Science Foundation under contracts nos. PHY-1565546 and PHY-2111185, the DOE, Office of Nuclear Physics under contract no. DE-AC02-06CH11357, DE-AC02-05CH11231, DE-SC0022538, and DE-SC0022538. S.E.C. acknowledges support from the DOE NNSA SSGF under DE-NA0003960.

References

Benzaid et al. [2020] D. Benzaid, S. Bentridi, A. Kerraci, and N. Amrani, Bethe–Weizsäcker semiempirical mass formula coefficients 2019 update based on AME2016, Nuclear Science and Techniques 31, 9 (2020).
Sorlin and Porquet [2008] O. Sorlin and M.-G. Porquet, Nuclear magic numbers: New features far from stability, Progress in Particle and Nuclear Physics 61, 602 (2008).
Kanungo [2013] R. Kanungo, A new view of nuclear shells, Physica Scripta 2013, 014002 (2013).
Faestermann et al. [2013] T. Faestermann, M. Górska, and H. Grawe, The structure of ¹⁰⁰Sn and neighbouring nuclei, Progress in Particle and Nuclear Physics 69, 85 (2013).
Górska [2022] M. Górska, Trends in the Structure of Nuclei near ¹⁰⁰Sn, Physics 4, 364 (2022).
Hinke et al. [2012] C. Hinke, M. Böhmer, P. Boutachkov, T. Faestermann, H. Geissel, J. Gerl, R. Gernhäuser, M. Górska, A. Gottardo, H. Grawe, et al., Superallowed Gamow–Teller decay of the doubly magic nucleus ¹⁰⁰Sn, Nature 486, 341 (2012).
Chartier et al. [1996] M. Chartier, G. Auger, W. Mittig, A. Lépine-Szily, L. K. Fifield, J. M. Casandjian, M. Chabert, J. Fermé, A. Gillibert, M. Lewitowicz, M. Mac Cormick, M. H. Moscatello, O. H. Odland, N. A. Orr, G. Politi, C. Spitaels, and A. C. C. Villari, Mass Measurement of ¹⁰⁰Sn, Phys. Rev. Lett. 77, 2400 (1996).
Mougeot et al. [2021] M. Mougeot, D. Atanasov, J. Karthein, R. N. Wolf, P. Ascher, K. Blaum, K. Chrysalidis, G. Hagen, J. D. Holt, W. J. Huang, G. R. Jansen, I. Kulikov, Y. A. Litvinov, D. Lunney, V. Manea, T. Miyagi, T. Papenbrock, L. Schweikhard, A. Schwenk, T. Steinsberger, S. R. Stroberg, Z. H. Sun, A. Welker, F. Wienholtz, S. G. Wilkins, and K. Zuber, Mass measurements of ^99-101In challenge ab initio nuclear theory of the nuclide ¹⁰⁰Sn, Nature Physics 17, 1099 (2021).
Nies et al. [2023] L. Nies, D. Atanasov, M. Athanasakis-Kaklamanakis, M. Au, K. Blaum, J. Dobaczewski, B. S. Hu, J. D. Holt, J. Karthein, I. Kulikov, Y. A. Litvinov, D. Lunney, V. Manea, T. Miyagi, M. Mougeot, L. Schweikhard, A. Schwenk, K. Sieja, and F. Wienholtz, Isomeric excitation energy for ${{}^{99}\mathrm{In}}^{m}$ from mass spectrometry reveals constant trend next to doubly magic ${}^{100}\mathrm{Sn}$ , Phys. Rev. Lett. 131, 022502 (2023).
Park et al. [2020] J. Park, R. Krücken, A. Blazhev, D. Lubos, R. Gernhäuser, M. Lewitowicz, S. Nishimura, D. S. Ahn, H. Baba, B. Blank, P. Boutachkov, F. Browne, I. Čeliković, G. de France, P. Doornenbal, T. Faestermann, Y. Fang, N. Fukuda, J. Giovinazzo, N. Goel, M. Górska, H. Grawe, S. Ilieva, N. Inabe, T. Isobe, A. Jungclaus, D. Kameda, G. D. Kim, Y.-K. Kim, I. Kojouharov, T. Kubo, N. Kurz, Y. K. Kwon, G. Lorusso, K. Moschner, D. Murai, I. Nishizuka, Z. Patel, M. M. Rajabali, S. Rice, H. Sakurai, H. Schaffner, Y. Shimizu, L. Sinclair, P.-A. Söderström, K. Steiger, T. Sumikama, H. Suzuki, H. Takeda, Z. Wang, H. Watanabe, J. Wu, and Z. Y. Xu, Spectroscopy of ${}^{99}\mathrm{Cd}$ and ${}^{101}\mathrm{In}$ from $\beta$ decays of ${}^{99}\mathrm{In}$ and ${}^{101}\mathrm{Sn}$ , Phys. Rev. C 102, 014304 (2020).
Reponen et al. [2021] M. Reponen, R. P. de Groote, L. Al Ayoubi, O. Beliuskina, M. L. Bissell, P. Campbell, L. Cañete, B. Cheal, K. Chrysalidis, C. Delafosse, A. de Roubin, C. S. Devlin, T. Eronen, R. F. Garcia Ruiz, S. Geldhof, W. Gins, M. Hukkanen, P. Imgram, A. Kankainen, M. Kortelainen, Á. Koszorús, S. Kujanpää, R. Mathieson, D. A. Nesterenko, I. Pohjalainen, M. Vilén, A. Zadvornaya, and I. D. Moore, Evidence of a sudden increase in the nuclear size of proton-rich silver-96, Nature Communications 12, 4596 (2021).
Hornung et al. [2020] C. Hornung, D. Amanbayev, I. Dedes, G. Kripko-Koncz, I. Miskun, N. Shimizu, S. Ayet San Andrés, J. Bergmann, T. Dickel, J. Dudek, J. Ebert, H. Geissel, M. Górska, H. Grawe, F. Greiner, E. Haettner, T. Otsuka, W. R. Plaß, S. Purushothaman, A.-K. Rink, C. Scheidenberger, H. Weick, S. Bagchi, A. Blazhev, O. Charviakova, D. Curien, A. Finlay, S. Kaur, W. Lippert, J.-H. Otto, Z. Patyk, S. Pietri, Y. K. Tanaka, Y. Tsunoda, and J. S. Winfield, Isomer studies in the vicinity of the doubly-magic nucleus ¹⁰⁰Sn: Observation of a new low-lying isomeric state in ⁹⁷Ag, Physics Letters B 802, 135200 (2020).
Karthein et al. [2023] J. Karthein, C. Ricketts, R. Ruiz, J. Billowes, C. Binnersley, T. Cocolios, J. Dobaczewski, G. Farooq-Smith, K. Flanagan, G. Georgiev, et al., Electromagnetic properties of indium isotopes elucidate the doubly magic character of ¹⁰⁰Sn, arXiv preprint arXiv:2310.15093 (2023).
Cartegni et al. [2012] L. Cartegni, C. Mazzocchi, R. Grzywacz, I. G. Darby, S. N. Liddick, K. P. Rykaczewski, J. C. Batchelder, L. Bianco, C. R. Bingham, E. Freeman, C. Goodin, C. J. Gross, A. Guglielmetti, D. T. Joss, S. H. Liu, M. Mazzocco, S. Padgett, R. D. Page, M. M. Rajabali, M. Romoli, P. J. Sapple, J. Thomson, and H. V. Watkins, Experimental study of the decays of ¹¹²Cs and ¹¹¹Xe, Phys. Rev. C 85, 014312 (2012).
Auranen et al. [2018] K. Auranen, D. Seweryniak, M. Albers, A. D. Ayangeakaa, S. Bottoni, M. P. Carpenter, C. J. Chiara, P. Copp, H. M. David, D. T. Doherty, J. Harker, C. R. Hoffman, R. V. F. Janssens, T. L. Khoo, S. A. Kuvin, T. Lauritsen, G. Lotay, A. M. Rogers, J. Sethi, C. Scholey, R. Talwar, W. B. Walters, P. J. Woods, and S. Zhu, Superallowed $\alpha$ decay to doubly magic ${}^{100}\mathrm{Sn}$ , Phys. Rev. Lett. 121, 182501 (2018).
Macfarlane and Siivola [1965] R. D. Macfarlane and A. Siivola, New region of alpha radioactivity, Phys. Rev. Lett. 14, 114 (1965).
Seweryniak et al. [2006] D. Seweryniak, K. Starosta, C. N. Davids, S. Gros, A. A. Hecht, N. Hoteling, T. L. Khoo, K. Lagergren, G. Lotay, D. Peterson, A. Robinson, C. Vaman, W. B. Walters, P. J. Woods, and S. Zhu, $\alpha$ decay of ${}^{105}\mathrm{Te}$ , Phys. Rev. C 73, 061301 (2006).
Liddick et al. [2006] S. N. Liddick, R. Grzywacz, C. Mazzocchi, R. D. Page, K. P. Rykaczewski, J. C. Batchelder, C. R. Bingham, I. G. Darby, G. Drafta, C. Goodin, C. J. Gross, J. H. Hamilton, A. A. Hecht, J. K. Hwang, S. Ilyushkin, D. T. Joss, A. Korgul, W. Królas, K. Lagergren, K. Li, M. N. Tantawy, J. Thomson, and J. A. Winger, Discovery of ${}^{109}\mathrm{Xe}$ and ${}^{105}\mathrm{Te}$ : Superallowed $\alpha$ decay near doubly magic ${}^{100}\mathrm{Sn}$ , Phys. Rev. Lett. 97, 082501 (2006).
Janas et al. [2005] Z. Janas, C. Mazzocchi, L. Batist, A. Blazhev, M. Górska, M. Kavatsyuk, O. Kavatsyuk, R. Kirchner, A. Korgul, M. La Commara, K. Miernik, I. Mukha, A. Płochocki, E. Roeckl, and K. Schmidt, Measurements of ¹¹⁰Xe and ¹⁰⁶Te decay half-lives, The European Physical Journal A - Hadrons and Nuclei 23, 197 (2005).
Capponi et al. [2016] L. Capponi, J. F. Smith, P. Ruotsalainen, C. Scholey, P. Rahkila, K. Auranen, L. Bianco, A. J. Boston, H. C. Boston, D. M. Cullen, X. Derkx, M. C. Drummond, T. Grahn, P. T. Greenlees, L. Grocutt, B. Hadinia, U. Jakobsson, D. T. Joss, R. Julin, S. Juutinen, M. Labiche, M. Leino, K. G. Leach, C. McPeake, K. F. Mulholland, P. Nieminen, D. O’Donnell, E. S. Paul, P. Peura, M. Sandzelius, J. Sarén, B. Saygi, J. Sorri, S. Stolze, A. Thornthwaite, M. J. Taylor, and J. Uusitalo, Direct observation of the ${}^{114}\mathrm{Ba}\rightarrow^{110}\mathrm{Xe}\rightarrow^{106}\mathrm{Te}\rightarrow^{102}\mathrm{Sn}$ triple $\alpha$ -decay chain using position and time correlations, Phys. Rev. C 94, 024314 (2016).
Florescu and Insolia [1995] A. Florescu and A. Insolia, Microscopic calculation for $\alpha$ and heavier cluster emissions from proton rich Ba and Ce isotopes, Phys. Rev. C 52, 726 (1995).
Kumar and Gupta [1994] S. Kumar and R. K. Gupta, Measurable decay modes of barium isotopes via exotic cluster emissions, Phys. Rev. C 49, 1922 (1994).
Kumar et al. [1995] S. Kumar, D. Bir, and R. K. Gupta, ${}^{100}\mathrm{daughter}$ $\alpha$ -nuclei cluster decays of some neutron-deficient Xe to Gd parents: Sn radioactivity, Phys. Rev. C 51, 1762 (1995).
Dobaczewski and Nazarewicz [1995] J. Dobaczewski and W. Nazarewicz, Limits of proton stability near ${}^{100}\mathrm{Sn}$ , Phys. Rev. C 51, R1070 (1995).
Olsen et al. [2013] E. Olsen, M. Pfützner, N. Birge, M. Brown, W. Nazarewicz, and A. Perhac, Landscape of two-proton radioactivity, Phys. Rev. Lett. 110, 222501 (2013).
Auranen et al. [2019] K. Auranen, D. Seweryniak, M. Albers, A. Ayangeakaa, S. Bottoni, M. Carpenter, C. Chiara, P. Copp, H. David, D. Doherty, J. Harker, C. Hoffman, R. Janssens, T. Khoo, S. Kuvin, T. Lauritsen, G. Lotay, A. Rogers, C. Scholey, J. Sethi, R. Talwar, W. Walters, P. Woods, and S. Zhu, Proton decay of ¹⁰⁸I and its significance for the termination of the astrophysical rp-process, Physics Letters B 792, 187 (2019).
Schatz et al. [2001] H. Schatz, A. Aprahamian, V. Barnard, L. Bildsten, A. Cumming, M. Ouellette, T. Rauscher, F.-K. Thielemann, and M. Wiescher, End point of the $\mathit{rp}$ process on accreting neutron stars, Phys. Rev. Lett. 86, 3471 (2001).
Elomaa et al. [2009] V.-V. Elomaa, G. K. Vorobjev, A. Kankainen, L. Batist, S. Eliseev, T. Eronen, J. Hakala, A. Jokinen, I. D. Moore, Y. N. Novikov, H. Penttilä, A. Popov, S. Rahaman, J. Rissanen, A. Saastamoinen, H. Schatz, D. M. Seliverstov, C. Weber, and J. Äystö, Quenching of the snsbte cycle in the $rp$ process, Phys. Rev. Lett. 102, 252501 (2009).
Grawe et al. [2007] H. Grawe, K. Langanke, and G. Martínez-Pinedo, Nuclear structure and astrophysics, Reports on Progress in Physics 70, 1525 (2007).
Mazzocchi et al. [2007] C. Mazzocchi, R. Grzywacz, S. N. Liddick, K. P. Rykaczewski, H. Schatz, J. C. Batchelder, C. R. Bingham, C. J. Gross, J. H. Hamilton, J. K. Hwang, S. Ilyushkin, A. Korgul, W. Królas, K. Li, R. D. Page, D. Simpson, and J. A. Winger, $\alpha$ Decay of ${}^{109}\mathrm{I}$ and Its Implications for the Proton Decay of ${}^{105}\mathrm{Sb}$ and the Astrophysical Rapid Proton-Capture Process, Phys. Rev. Lett. 98, 212501 (2007).
Wang et al. [2021] M. Wang, W. Huang, F. Kondev, G. Audi, and S. Naimi, The AME 2020 atomic mass evaluation (II). Tables, graphs and references*, Chinese Physics C 45, 030003 (2021).
Meng et al. [2017] W. Meng, G. Audi, F. G. Kondev, W. Huang, S. Naimi, and X. Xing, The AME2016 atomic mass evaluation (II). Tables, graphs and references, Chinese Physics C 41, 030003 (2017).
Xing et al. [2023] Y. M. Xing, C. X. Yuan, M. Wang, Y. H. Zhang, X. H. Zhou, Y. A. Litvinov, K. Blaum, H. S. Xu, T. Bao, R. J. Chen, C. Y. Fu, B. S. Gao, W. W. Ge, J. J. He, W. J. Huang, T. Liao, J. G. Li, H. F. Li, S. Litvinov, S. Naimi, P. Shuai, M. Z. Sun, Q. Wang, X. Xu, F. R. Xu, T. Yamaguchi, X. L. Yan, J. C. Yang, Y. J. Yuan, Q. Zeng, M. Zhang, and X. Zhou, Isochronous mass measurements of neutron-deficient nuclei from ${}^{112}\mathrm{Sn}$ projectile fragmentation, Phys. Rev. C 107, 014304 (2023).
Ringle et al. [2013] R. Ringle, S. Schwarz, and G. Bollen, Penning trap mass spectrometry of rare isotopes produced via projectile fragmentation at the lebit facility, International Journal of Mass Spectrometry 349-350, 87 (2013), 100 years of Mass Spectrometry.
Bollen et al. [1990] G. Bollen, R. B. Moore, G. Savard, and H. Stolzenberg, The accuracy of heavy‐ion mass measurements using time of flight‐ion cyclotron resonance in a penning trap, Journal of Applied Physics 68, 4355 (1990), https://doi.org/10.1063/1.346185 .
Becker et al. [1990] S. Becker, G. Bollen, F. Kern, H.-J. Kluge, R. Moore, G. Savard, L. Schweikhard, and H. Stolzenberg, Mass measurements of very high accuracy by time-of-flight ion cyclotron resonance of ions injected into a penning trap, International Journal of Mass Spectrometry and Ion Processes 99, 53 (1990).
König et al. [1995] M. König, G. Bollen, H.-J. Kluge, T. Otto, and J. Szerypo, Quadrupole excitation of stored ion motion at the true cyclotron frequency, International Journal of Mass Spectrometry and Ion Processes 142, 95 (1995).
Wei et al. [2022] J. Wei, H. Ao, B. Arend, S. Beher, G. Bollen, N. Bultman, F. Casagrande, W. Chang, Y. Choi, S. Cogan, C. Compton, M. Cortesi, J. Curtin, K. Davidson, X. Du, K. Elliott, B. Ewert, A. Facco, A. Fila, K. Fukushima, V. Ganni, A. Ganshyn, J. Gao, T. Glasmacher, J. Guo, Y. Hao, W. Hartung, N. Hasan, M. Hausmann, K. Holland, H. C. Hseuh, M. Ikegami, D. Jager, S. Jones, N. Joseph, T. Kanemura, S.-H. Kim, P. Knudsen, B. Kortum, E. Kwan, T. Larter, R. E. Laxdal, M. Larmann, K. Laturkar, J. LeTourneau, Z.-Y. Li, S. Lidia, G. Machicoane, C. Magsig, P. Manwiller, F. Marti, T. Maruta, A. McCartney, E. Metzgar, S. Miller, Y. Momozaki, D. Morris, M. Mugerian, I. Nesterenko, C. Nguyen, W. O’Brien, K. Openlander, P. N. Ostroumov, M. Patil, A. S. Plastun, J. Popielarski, L. Popielarski, M. Portillo, J. Priller, X. Rao, M. Reaume, H. Ren, K. Saito, M. Smith, M. Steiner, A. Stolz, O. B. Tarasov, B. Tousignant, R. Walker, X. Wang, J. Wenstrom, G. West, K. Witgen, M. Wright, T. Xu, Y. Xu, Y. Yamazaki, T. Zhang, Q. Zhao, S. Zhao, K. Dixon, M. Wiseman, M. Kelly, K. Hosoyama, and S. Prestemon, Accelerator commissioning and rare isotope identification at the facility for rare isotope beams, Modern Physics Letters A 37, 2230006 (2022), https://doi.org/10.1142/S0217732322300063 .
York et al. [2009] R. York, G. Bollen, C. Compton, A. Crawford, M. Doleans, T. Glasmacher, W. Hartung, F. Marti, J. Popielarski, J. Vincent, et al., Frib: A new accelerator facility for the production of rare isotope beams, SRF2009, Berlin, September (2009).
Hausmann et al. [2013] M. Hausmann, A. Aaron, A. Amthor, M. Avilov, L. Bandura, R. Bennett, G. Bollen, T. Borden, T. Burgess, S. Chouhan, et al., Design of the advanced rare isotope separator aris at frib, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 317, 349 (2013).
Lund et al. [2020] K. Lund, G. Bollen, D. Lawton, D. Morrissey, J. Ottarson, R. Ringle, S. Schwarz, C. Sumithrarachchi, A. Villari, and J. Yurkon, Online tests of the advanced cryogenic gas stopper at nscl, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 463, 378 (2020).
Bollen [2011] G. Bollen, “ion surfing” with radiofrequency carpets, International Journal of Mass Spectrometry 299, 131 (2011).
Schwarz et al. [2016] S. Schwarz, G. Bollen, R. Ringle, J. Savory, and P. Schury, The lebit ion cooler and buncher, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 816, 131 (2016).
Ringle et al. [2009] R. Ringle, G. Bollen, A. Prinke, J. Savory, P. Schury, S. Schwarz, and T. Sun, The LEBIT 9.4T Penning trap mass spectrometer, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 604, 536 (2009).
Gabrielse [2009] G. Gabrielse, Why is sideband mass spectrometry possible with ions in a Penning trap?, Phys. Rev. Lett. 102, 172501 (2009).
Ringle et al. [2007a] R. Ringle, G. Bollen, A. Prinke, J. Savory, P. Schury, S. Schwarz, and T. Sun, A “lorentz” steerer for ion injection into a penning trap, International Journal of Mass Spectrometry 263, 38 (2007a).
Blaum et al. [2004] K. Blaum, D. Beck, G. Bollen, P. Delahaye, C. Guénaut, F. Herfurth, A. Kellerbauer, H.-J. Kluge, D. Lunney, S. Schwarz, L. Schweikhard, and C. Yazidjian, Population inversion of nuclear states by a Penning trap mass spectrometer, Europhysics Letters 67, 586 (2004).
Gulyuz et al. [2015] K. Gulyuz, J. Ariche, G. Bollen, S. Bustabad, M. Eibach, C. Izzo, S. J. Novario, M. Redshaw, R. Ringle, R. Sandler, S. Schwarz, and A. A. Valverde, Determination of the direct double- $\beta$ -decay Q value of ⁹⁶Zr and atomic masses of ^90-92,94,96Zr and^92,94-98,100Mo, Phys. Rev. C 91, 055501 (2015).
Ringle et al. [2007b] R. Ringle, T. Sun, G. Bollen, D. Davies, M. Facina, J. Huikari, E. Kwan, D. J. Morrissey, A. Prinke, J. Savory, P. Schury, S. Schwarz, and C. S. Sumithrarachchi, High-precision penning trap mass measurements of ${}^{37,38}\mathrm{Ca}$ and their contributions to conserved vector current and isobaric mass multiplet equation, Phys. Rev. C 75, 055503 (2007b).
Mukha et al. [2004] I. Mukha, L. Batist, F. Becker, A. Blazhev, A. Brüchle, J. Döring, M. Gorska, H. Grawe, T. Faestermann, C. Hoffman, et al., Studies of $\beta$ -delayed proton decays of N $\approx$ Z nuclei around ¹⁰⁰Sn at the GSI-ISOL facility, Nuclear Physics A 746, 66 (2004).
Kavatsyuk et al. [2005] O. Kavatsyuk, M. Kavatsyuk, L. Batist, A. Banu, F. Becker, A. Blazhev, W. Brüchle, J. Döring, T. Faestermann, M. Górska, H. Grawe, Z. Janas, A. Jungclaus, M. Karny, R. Kirchner, M. La Commara, S. Mandal, C. Mazzocchi, I. Mukha, S. Muralithar, C. Plettner, A. Płochocki, E. Roeckl, M. Romoli, M. Schädel, R. Schwengner, and J. Żylicz, Beta decay of ¹⁰³Sn, The European Physical Journal A - Hadrons and Nuclei 25, 211 (2005).
Page et al. [1994] R. D. Page, P. J. Woods, R. A. Cunningham, T. Davinson, N. J. Davis, A. N. James, K. Livingston, P. J. Sellin, and A. C. Shotter, Decays of odd-odd N-Z=2 nuclei above ${}^{100}\mathrm{Sn}$ : The observation of proton radioactivity from ${}^{112}\mathrm{Cs}$ , Phys. Rev. Lett. 72, 1798 (1994).
Wady et al. [2012] P. T. Wady, J. F. Smith, E. S. Paul, B. Hadinia, C. J. Chiara, M. P. Carpenter, C. N. Davids, A. N. Deacon, S. J. Freeman, A. N. Grint, R. V. F. Janssens, B. P. Kay, T. Lauritsen, C. J. Lister, B. M. McGuirk, M. Petri, A. P. Robinson, D. Seweryniak, D. Steppenbeck, and S. Zhu, $\gamma$ -ray spectroscopy of the odd-odd $N=Z+2$ deformed proton emitter ¹¹²Cs, Phys. Rev. C 85, 034329 (2012).
Schardt et al. [1979] D. Schardt, R. Kirchner, O. Klepper, W. Reisdorf, E. Roeckl, P. Tidemand-Petersson, G. Ewan, E. Hagberg, B. Jonson, S. Mattsson, and G. Nyman, Alpha decay studies of tellurium, iodine, xenon and cesium isotopes, Nuclear Physics A 326, 65 (1979).
Heine et al. [1991] F. Heine, T. Faestermann, A. Gillitzer, J. Homolka, M. Köpf, and W. Wagner, Proton and alpha radioactivity of very neutron deficient Te, I, Xe and Cs isotopes, studied after electrostatic separation, Zeitschrift für Physik A Hadrons and Nuclei 340, 225 (1991).
Capponi et al. [2020] L. Capponi, J. F. Smith, P. Ruotsalainen, C. Scholey, P. Rahkila, L. Bianco, A. J. Boston, H. C. Boston, D. M. Cullen, X. Derkx, M. C. Drummond, T. Grahn, P. T. Greenlees, L. Grocutt, B. Hadinia, U. Jakobsson, D. T. Joss, R. Julin, S. Juutinen, M. Labiche, M. Leino, K. G. Leach, C. McPeake, K. F. Mulholland, P. Nieminen, D. O’Donnell, E. S. Paul, P. Peura, M. Sandzelius, J. Sarén, B. Saygi, J. Sorri, S. Stolze, A. Thornthwaite, M. J. Taylor, and J. Uusitalo, Delayed or absent $\pi{({h}_{11/2})}^{2}$ alignment in ${}^{111}\mathrm{Xe}$ , Phys. Rev. C 101, 014313 (2020).
Schardt et al. [1981] D. Schardt, T. Batsch, R. Kirchner, O. Klepper, W. Kurcewicz, E. Roeckl, and P. Tidemand-Petersson, Alpha decay of neutron-deficient isotopes with 52 $\leq$ Z $\leq$ 55, including the new isotopes ¹⁰⁶Te (T_1/2 = 60 $\mu$ s) and ¹¹⁰Xe, Nuclear Physics A 368, 153 (1981).

High-precision mass measurement of 103Sn restores smoothness of the mass surface