High-Throughput VLSI architecture for Soft-Decision decoding with ORBGRAND
Abstract
Guessing Random Additive Noise Decoding (GRAND) is a recently proposed approximate Maximum Likelihood (ML) decoding technique that can decode any linear error-correcting block code. Ordered Reliability Bits GRAND (ORBGRAND) is a powerful variant of GRAND, which outperforms the original GRAND technique by generating error patterns in a specific order. Moreover, their simplicity at the algorithm level renders GRAND family a desirable candidate for applications that demand very high throughput. This work reports the first-ever hardware architecture for ORBGRAND, which achieves an average throughput of up to Gbps for a code length of at an SNR of dB. Moreover, the proposed hardware can be used to decode any code provided the length and rate constraints. Compared to the state-of-the-art fast dynamic successive cancellation flip decoder (Fast-DSCF) using a 5G polar code, the proposed VLSI implementation has more average throughput while maintaining similar decoding performance.
Index Terms— Guessing Random Additive Noise Decoding (GRAND), Ordered Reliability Bits GRAND (ORBGRAND), Maximum Likelihood Decoding (MLD).
1 Introduction
Channel coding techniques are an integral part of all modern communications systems. Since their inception [1], a lot of effort was focused on finding practical channel coding schemes that could approach channel capacity. Over time, various capacity-approaching codes have been designed, such as Turbo codes [2] and LDPC codes [3]. Polar codes [4], proposed in 2009, are able to asymptotically achieve the channel capacity. Each of these aforementioned channel coding techniques, along with many others, require a dedicated decoder. However, there exists an alternate paradigm of decoders that do not rely on the underlying channel code and hence can be used to decode any code.
Guessing Random Additive Noise Decoding (GRAND) is a recently proposed approximate Maximum Likelihood (ML) decoding technique for linear error-correcting codes [5]. Instead of decoding the received codeword, GRAND attempts to guess the noise present in the codeword. Hence, GRAND can be used for any linear block code. GRAND relies on the generation of putative test error patterns that are successively applied to the received vector and checked for codebook membership using the parity check matrix of the underlying code. The order in which these putative test error patterns are generated is the key difference between different variants of GRAND. Among its variants, GRAND with ABandonment (GRANDAB) [5] is a hard decision version of GRAND which generates the test error patterns in the increasing Hamming weight order, up to weight . Symbol Reliability GRAND [6] is another variant, which uses thresholding on the input LLRs, to differentiate between reliable and unreliable bits of the received codeword.
Concomitant with the discovery of the GRAND algorithm, applications that require short frames are emerging, such as machine-to-machine communications. Thus, the implementation of the ORBGRAND algorithm is particularly appealing, since it can approach the ML performance, while only requiring a fraction of its complexity [7]. ORBGRAND is a soft-input version of GRAND, which generates test error patterns in the logistic weight () order rather than in the Hamming weight (HW) order. The logistic weight corresponds to the sum of the indices that are being flipped. The complexity of ORBGRAND is directly dependent on the number of putative test error patterns. ORBGRAND utilizes the soft information associated with the channel observation more efficiently than SRGRAND, which makes it an attractive choice for implementation. In this paper, we investigate parameters that impact the ORBGRAND decoding performance as well as the computational complexity for the polar code studied in [8]. Furthermore, this work presents the first-ever high throughput hardware architecture for ORBGRAND which can achieve an average throughput of Gbps for a code of length at an SNR of dB.
The remainder of this paper is structured as follows: Section 2 provides an overview of the ORBGRAND algorithm. In Section 3, logistic weights and their impact on complexity and performance are investigated. In Section 4, the proposed hardware architecture is detailed and the implementation results are compared. Finally, concluding remarks are drawn in Section 5.
2 Background
Algorithm 1 depicts the pseudo-code of ORBGRAND. The inputs to the algorithm are the vector of channel LLRs of size , a parity check matrix of the code , a matrix such that is the identity matrix, with a generator matrix of the code, and the maximum logistic weight considered . We note that .
First, the indices are sorted in the ascending order of their absolute value LLRs (). The obtained permutation vector is denoted by (line 1). Then, for each logistic weight, all the integer partitions are generated (line 4). These integer partitions and the permutation vector of the sorted LLRs are used to generate the test error patterns (line 6). Finally, the hard decision obtained from the LLRs () is combined with the current test error pattern, and the resulting word is queried for codebook membership (line 7). If the word considered is a codeword, the message is recovered (line 8) and the process is terminated. Otherwise, following error patterns or larger logistic weights are considered.
3 ORBGRAND Simplification
3.1 Generating the Integer Partitions
An integer partition of a positive integer , noted , where , is the breakdown of into a sum of strictly positive integers . If all are different, the partition is called distinct. In the ORBGRAND algorithm, each represents an index to be flipped, and therefore it requires distinct integer partitions only. The generated test error pattern obtained from an integer partition with elements has a Hamming weight of .
Hardware generation of the integer partitions was proposed in [9]. However, their approach cannot be applied directly to our proposed ORBGRAND as the generated partitions are not distinct. In addition, their partition generation is sequential, which is not desirable for parallelized, high-throughput architectures. We noticed that when considering a specific logistic weight convenient patterns appear. For example, for , the distinct integer partitions are . If the listing order is followed for (i.e. the subset ), the first integer descends while the second ascends. Similar trends can be observed for higher-order partitions such as : the first integer descends while the second ascends as the third integer remains fixed until all iterations for the first two integers are complete. Inspired from this trend, we propose an arrangement of shift registers to come up with a way of generating integer partitions of a particular size, that is described in Section 4.
Without loss of generality, , when an integer is partitioned into parts, and assuming that are ordered, the maximum value for each is bounded by
| (1) |
The first value of can be found using . The associated proof for (1) is omitted due to the lack of space.
3.2 Impact of the Parameters
The maximum logistic weight () has a strong impact on both the maximum number of codebook membership queries (and essentially, the worst-case complexity) and the decoding performance. Fig. 1 plots the frame error rate (FER) performance for ORBGRAND decoding of 5G CRC-aided polar code (128, 105+11) [8, 10], with BPSK modulation over an AWGN channel. The SNR in dB is defined as . For values of 128, 96 and 64, the maximum number of required queries are , , and , respectively. When is reduced from to , a performance degradation of dB is observed at FER = . On the other hand, the complexity is reduced by as a result of this reduction. In addition to restricting the , the number of elements () in can also be limited. For example, for the considered polar code with , the degradation in error correction performance is negligible with when compared to an unlimited . As a result of these simplifications, the maximum number of queries is reduced to . In addition to reducing complexity, appropriate selection of parameters and helps design simple hardware implementations.
In comparison with the hard decision variant of GRANDAB (AB=3), ORBGRAND results in a FER gain of at least 2 dB for FER lower than . Moreover, ORBGRAND with parameters and results in a similar performance as the state-of-the-art Dynamic SC-Flip (DSCF) polar code decoder [11], which is also an iterative decoder. The number of attempts () parameter for DSCF is set to 50 and the maximum bit-flipping order is set to 2.
4 VLSI Architecture for ORBGRAND
In [12], a VLSI architecture for GRANDAB (AB=3) was proposed. The VLSI architecture uses the linearity property of the underlying code to combine one bit flip error syndrome ( with ) to generate an error pattern with the Hamming weight of . However, the VLSI architecture proposed in [12] can only tackle up to 3-bit flips and the error patterns are tested in an ascending order of their Hamming weights. Thus, profound changes must be made to be able to consider soft-inputs, to generate error patterns in increasing order of their logistic weight, and to consider larger Hamming weights.
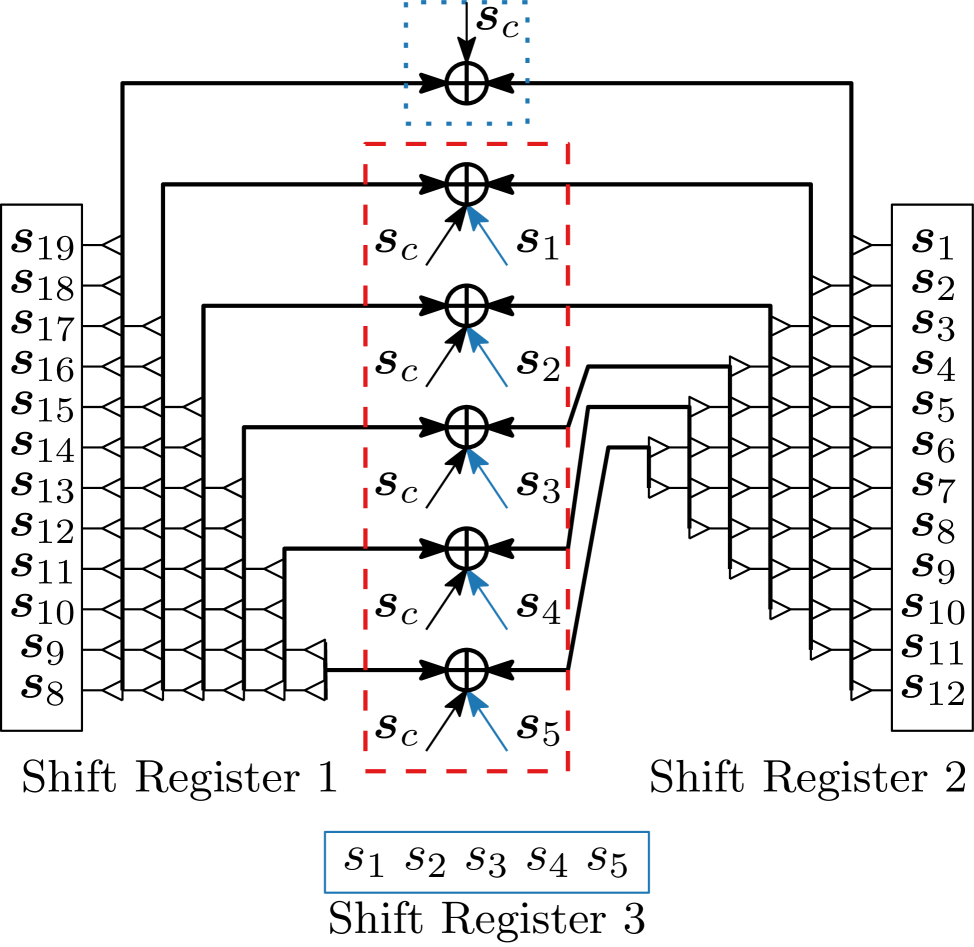
4.1 Principle, Scheduling and Details
The VLSI architecture for the GRANDAB algorithm [12] is articulated around shift registers storing syndromes of 1-bit flip error patterns. Since this approach allows us to move the data very slightly to compute different syndromes, we use this approach as the baseline for the proposed architecture for ORBGRAND. The number of shift registers has a direct impact on the Hamming weight of error patterns, that can be computed in parallel. However, if too many shift registers are used, the amount of interconnections become problematic. Therefore, we decide to consider 3 shift registers corresponding to an integer partition of size 3 ().
During ORBGRAND decoding, for each (), integer partitions are generated with size (). We propose to generate these integer partitions in ascending order of their size. This modification does not impact the FER performance, however, it helps for a simpler hardware implementation. In our proposed architecture, , , are mapped to first, second and third shift register. The third shift register is a bit shift register, where value is given by (1). Whereas first and second shift registers have a size of bits. Since we have , is stored at the th index of the first shift register; whereas for the second and third shift registers is stored at the th index.
An example of the content and the interconnection of the three shift registers corresponding to is presented in Fig. 2. The elements of the shift register 1 and 2 are connected to arrays of -wide XOR gates whereby a collection of these connections is defined as a bus. The busses, each originating from a shift register, are used to feed the -wide XOR gate arrays for computing the syndromes of the error patterns. The first array of XOR gates (dotted rectangle) is responsible to check for 2-bit flips error patterns by combining the syndromes of the received codewords with all the elements of the first and second register (the first bus of each shift register). Similarly, the remaining five XOR gate arrays combine the remaining buses ( the selected elements of the shift register 1 and 2) with the elements of the shift register 3 to check for 3-bit flips error patterns (dashed rectangle).
Due to the described layout of the 3 shift registers, all the error patterns corresponding to an integer partition of sizes 2 and 3 for a specific are checked in one time-step. For generating test error patterns corresponding to integer partitions of sizes , a controller is used in conjunction with the shift registers. The controller is able to combine syndromes together, noted . Hence, when is fixed, only one time-step is required to generate all possible combinations of using the shift registers with adequately chosen shifting values. Therefore, the number of time steps required to generate all integer partitions of size for a specific is given by:
| (2) |
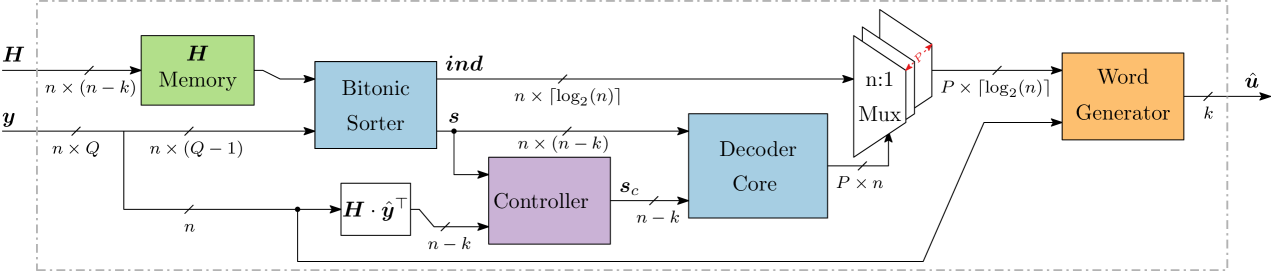
The proposed VLSI architecture for ORBGRAND is presented in Fig. 3. The control and clock signals are not depicted for simplicity. Any matrix can be loaded into the H memory of size at any time to support different codes and rates. To achieve high throughput, a bitonic sorter [13] is considered to sort the incoming LLRs.
At the first step of decoding, a syndrome check is performed on the hard decided word . If the syndrome is verified, decoding is assumed to be successful. Otherwise, the bitonic sorter is invoked to sort the LLR values. The bitonic sorter is pipelined to stages and hence it takes cycles to sort the LLRs values. While indices of the sorted LLR are forwarded to the multiplexers for later use by the word generator module, the sorted one bit-flip syndromes are passed to the decoder core, as depicted in Fig. 2. After the sorting operation, all the one bit-flip syndromes (,) are checked in one time-step. Next, error patterns are checked in the ascending logistic weight order. If any of the tested syndromes combinations verify the parity check constraint, a 2D priority encoder along with the controller module is used to forward the respective indices to the word generator module, where multiplexers are used to translate the sorted index values to their correct bit flip locations.
GRANDAB [12] ORBGRAND DSCF [14] Parameters AB=3 LW64, P6 , Technology (nm) 65 65 65 Supply (V) 0.9 0.9 0.9 Max. Frequency (MHz) 500 454 426 Area (mm2) 0.25 1.82 0.22 W.C. Latency (ns) 8196 9308 6103 Avg. Latency (ns) 2 2.47 122 W.C. T/P (Mbps) 12.8 11.3 17.2 Avg. T/P (Gbps) 52.5 42.5 0.86 Code compatible Yes Yes No
4.2 Implementation Results
The proposed ORBGRAND architecture has been implemented in Verilog HDL and synthesized using the general-purpose TSMC 65 nm CMOS technology, using post-synthesis verified test vectors. Table 1 presents the synthesis results for the proposed decoder with , code rates between and , , . Inputs are quantized on 5 bits, including 1 sign bit and 3 bits for the fractional part.
The ORBGRAND implementation supports a maximum frequency of . Since no pipelining strategy is used for the decoder core, one clock cycle corresponds to one time-step. For , cycles are required in the worst-case (W.C.) scenario, resulting in a W.C. latency of 9.3s. The average latency, however, is only of 2.47ns at SNR dB (target FER of ), which results in an average decoding information throughput of Gbps for a (128,105) 5G-NR CRC-Aided polar code. In comparison with the hard decision-based GRANDAB decoder (AB=3) [12], ORBGRAND has area overhead, and and higher W.C. and average latency. This translates into and lower W.C. and average decoding throughput, respectively. However, the FER performance of ORBGRAND, being a soft decision decoder, surpasses GRANDAB (AB=3) decoder by at least dB for target FER lower than , as shown in Fig. 1.
The proposed ORBGRAND is also compared with the state-of-the-art iterative Dynamic SC-Flip (DSCF) polar code decoder with similar performance [14], considering a quantization of 6 and 7 bits for channel and internal LLRs, respectively. In comparison with DSCF, ORBGRAND has area overhead, in addition to overhead in worst-case latency. However, proposed ORBGRAND results in lower average latency and higher average throughput than the DSCF at a target FER of . Moreover, the proposed ORBGRAND is code and rate compatible, while DSCF can only decode polar codes.
5 Conclusion
In this paper, we presented the first high throughput hardware architecture for the ORBGRAND algorithm. Due to the code-agnostic nature of GRAND, the proposed architecture for ORBGRAND can decode any code, given the length and rate constraints. We suggest modifications in the ORBGRAND algorithm to assist hardware implementation as well as reducing the complexity. ASIC synthesis results showed that an average decoding throughput of Gbps can be achieved for a code-length of for a target FER of . In comparison with the state-of-the-art DSCF decoder for polar codes, the proposed VLSI implementation results in decoding throughput for a 5G CA (128,105) polar code at an SNR of dB. Moreover, the proposed architecture serves as the first step towards the hardware implementation of soft-input decoders from GRAND family.
References
- [1] R. W. Hamming, “Error detecting and error correcting codes,” Bell System Technical Journal, vol. 29, pp. 147–160, 1950.
- [2] C. Berrou, A. Glavieux, and P. Thitimajshima, “Near shannon limit error-correcting coding and decoding: Turbo-codes. 1,” in Proceedings of ICC ’93 - IEEE International Conference on Communications, 1993, vol. 2, pp. 1064–1070 vol.2.
- [3] R. Gallager, “Low-density parity-check codes,” IRE Transactions on information theory, vol. 8, no. 1, pp. 21–28, 1962.
- [4] E. Arikan, “Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels,” IEEE Transactions on Information Theory, vol. 55, no. 7, pp. 3051–3073, 2009.
- [5] K. R. Duffy, J. Li, and M. Médard, “Capacity-achieving guessing random additive noise decoding,” IEEE Transactions on Information Theory, vol. 65, no. 7, pp. 4023–4040, 2019.
- [6] K. R. Duffy and M. Médard, “Guessing random additive noise decoding with soft detection symbol reliability information - SGRAND,” in 2019 IEEE International Symposium on Information Theory (ISIT), 2019, pp. 480–484.
- [7] K. R. Duffy, “Ordered reliability bits guessing random additive noise decoding,” arXiv preprint arXiv:2001.00546, 2020.
- [8] K. R. Duffy, A. Solomon, K. M. Konwar, and M. Médard, “5G NR CA-Polar maximum likelihood decoding by GRAND,” in 2020 54th Annual Conference on Information Sciences and Systems (CISS). IEEE, 2020, pp. 1–5.
- [9] J. Butler and T. Sasao, “High-speed hardware partition generation,” ACM Transactions on Reconfigurable Technology and Systems, vol. 7, pp. 1–17, 01 2014.
- [10] 3GPP, “NR; Multiplexing and Channel Coding,” Tech. Rep. TS 38.212, April 2020, Rel. 16.1.
- [11] L. Chandesris, V. Savin, and D. Declercq, “Dynamic-scflip decoding of polar codes,” IEEE Transactions on Communications, vol. 66, no. 6, pp. 2333–2345, 2018.
- [12] S. M. Abbas, T. Tonnellier, F. Ercan, and W. J. Gross, “High-throughput VLSI architecture for GRAND,” in 2020 IEEE Workshop on Signal Processing Systems (SiPS), 2020, pp. 1–6.
- [13] K. E. Batcher, “Sorting networks and their applications,” in Proceedings of the April 30–May 2, 1968, Spring Joint Computer Conference, New York, NY, USA, 1968, AFIPS ’68 (Spring), p. 307–314, Association for Computing Machinery.
- [14] F. Ercan, T. Tonnellier, N. Doan, and W. J. Gross, “Practical dynamic SC-flip polar decoders: Algorithm and implementation,” IEEE Transactions on Signal Processing, vol. 68, pp. 5441–5456, 2020.