Higher Energy Composite Fermion Levels in the Fractional Quantum Hall Effect

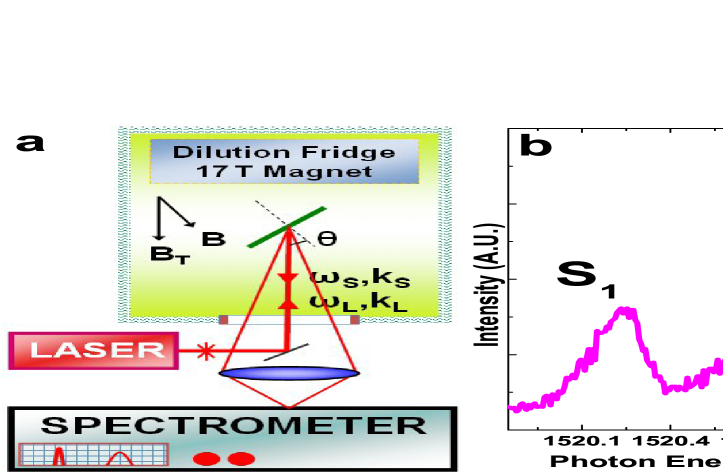
Collective states of matter have proved enormously important both because of the conceptual structures they reveal and the role they play in technological innovation. The fractional quantum Hall (FQH) liquid, which emerges as a result of interactions between electrons when the dimensionality is reduced to two and the Hilbert space is further restricted by application of an intense magnetic field Stormer et al. (1999), represents a cooperative behavior that does not subscribe to concepts such as Bose-Einstein condensation, diagonal or off-diagonal long range order, and Landau order parameter. It is the realization of a topological quantum state of matter, the understanding of which has influenced development in a wide variety of fields, such as topological insulators, cold atoms, graphene, generalized particle statistics, quantum cryptography, and more Levin and Stern (2009); Nayak et al. (2008); Du et al. (2009); Bolotin et al. (2009); Callan et al. (1995); Lin et al. (2009).

Neutral excitations provide a window into the physics of the FQH liquid. Early theoretical treatments of the lowest neutral collective mode of the FQH state at $\nu$=1/3 employed a single mode approximation Girvin et al. (1985), as well as exact diagonalization studies on small systems Haldane and Rezayi (1985), and showed a minimum in the dispersion, which, following the terminology used in superfluid Helium, is called a “magneto-roton.” Subsequently, the collective modes at this and other fractions were understood in terms of CFs, quasiparticles that result from a binding of electrons and an even number of quantized vortices Jain (1989). Despite their complex collective character, CFs act as almost free particles insofar as the low energy behavior is concerned Stormer et al. (1999). They experience an effective magnetic field and form their own Landau-like levels, which are called “$\Lambda$ levels.” (The CF “$\Lambda$ levels reside within the lowest electronic Landau level.) The neutral excitations are described as inter-$\Lambda$-level exciton collective modes of CFs Dev and Jain (1992); Platzman and He (1994); He et al. (1994); Scarola et al. (2000), in close analogy to the electronic collective modes of the integral Hall states.

We report the excitation spectrum of the FQH fluid at $\nu$=1/3 in an unexplored energy range. Our main finding is the existence of several well defined collective modes at energies substantially exceeding those of the highest before reported spin-conserving (SC) and spin-flip (SF) modes Groshaus et al. (2008); Murthy (2009); Davies et al. (1997). Further, we provide compelling evidence, supported by a detailed comparison between theory and experiment, that these neutral modes represent a new family of excitations involving CF transitions across several $\Lambda$ levels. The direct experimental observation of the integrity of $\Lambda$ levels at energies far above the Fermi energy demonstrates that CFs are more robust than previously thought, bolstering the expectation that the quasiparticles of other topological states of CFs, such as the nonabelian quasiparticles of the Pfaffian state at 5/2 Nayak et al. (2008); Stern (2010), will also have comparably robust character.

The collective excitations of the FQH systems are measured by ILS. The experiments are performed in a backscattering geometry with windows for direct optical access to the sample, as shown in Fig. 1a. The 2D electron system studied here is formed in an asymmetrically doped, 33 nm wide GaAs single quantum well (QW). The electron density is n=5.6$\times$10¹⁰cm^-2, with mobility, $\mu$=7$\times$10⁶cm²Vs at T=300 mK. Samples are mounted on the cold finger of a dilution refrigerator with a base temperature of 40 mK that is inserted into the cold bore of a 17 T superconducting magnet. The energy of the incident photons, $\omega_{L}$, is continuously tunable to be close to singlet ($S_{1}$) and triplet ($T_{B}$) fundamental optical transitions of the GaAs, seen in emission spectra shown in Fig. 1b Groshaus et al. (2008). The power density is kept below 10^-4Wcm^-2. Scattered light is dispersed by a Spex 1404 double Czerny Turner spectrometer with holographic master gratings. Spectra are acquired by optical multichannel detection. The combined resolution of the system is about 20$\mu$eV. Spectra can be taken with the linear polarization of $\omega_{L}$ parallel (polarized) or perpendicular (depolarized) to the detected scattered photon polarization.

The wave vector transferred from the photons to the 2D system is $q=(2\omega_{L}/c)\sin\theta$, much smaller than $1/\emph{l}$, where l=$\sqrt{\hbar c/eB}$ is magnetic length. However, weak short-range disorder induces a breakdown of wave vector conservation Groshaus et al. (2008); Davies et al. (1997); Marmorkos and Das Sarma (1992); not , which allows ILS to detect the critical points in the exciton dispersion, such as the rotons, because of van Hove singularities in the density of states at these energies.

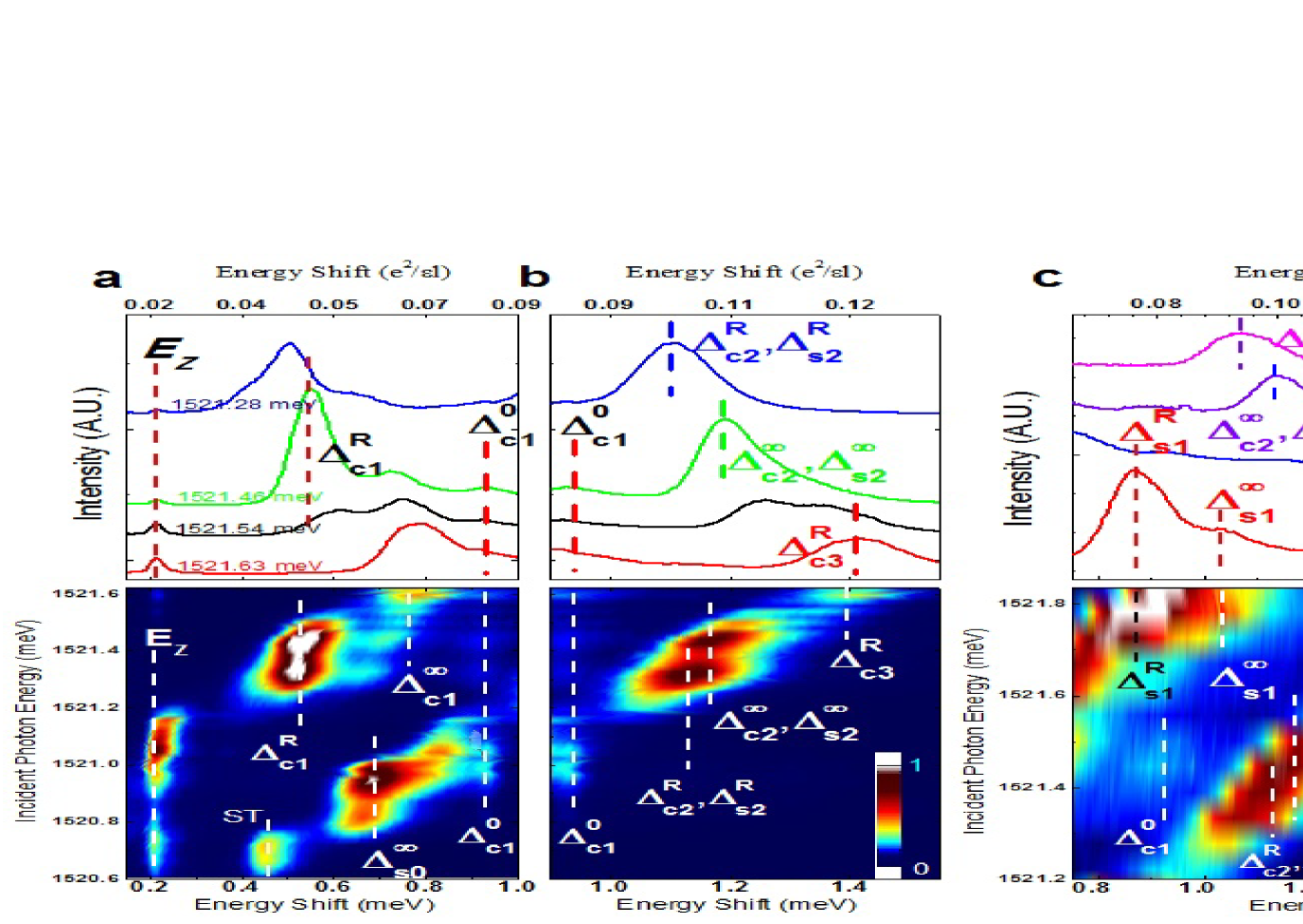
The intensity of the ILS at $\nu$=1/3 is displayed in Fig. 2 as a function of the energy transfer $\omega=\omega_{L}-\omega_{S}$. Each peak indicates the presence of a collective mode. The collective mode energies are marked by vertical linescom . The previously observed modes lie at energies below $\sim$1 meV, as seen in Fig. 2a. The striking feature of the spectra shown in Fig. 2b and 2c is the existence of several new modes up to 1.6 meV, the largest energy exchange accessed in our experiments.

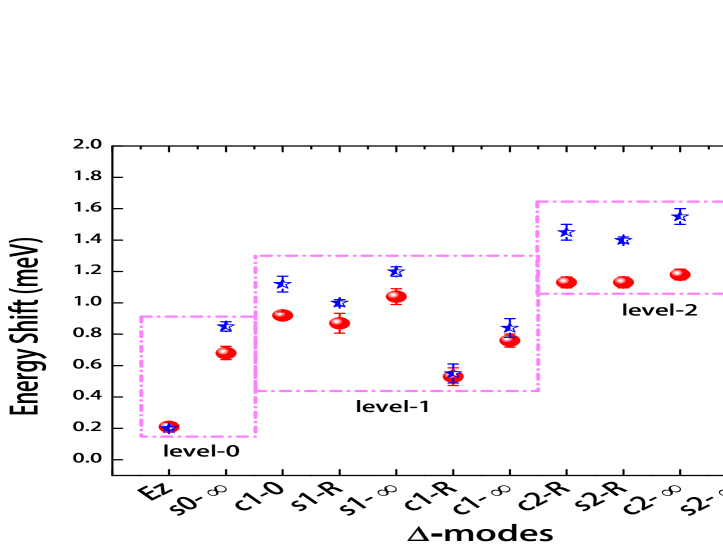
It is natural to interpret these new modes in terms of excitations of CFs across K levels, referred to below as “level-K excitons.” Previous experiments at $\nu=1/3$ had reported only level-1 SC excitons and level-0 SF excitons Groshaus et al. (2008); Davies et al. (1997); Pinczuk et al. (1993); Hirjibehedin et al. (2005). Level-2 and level-3 CF excitons were recently investigated theoreticallyMujumder et al. (2009) in the context of the splitting of the 1/3 collective mode at small but nonzero wave vectors Hirjibehedin et al. (2005). Because the modes may also involve spin reversal, we adopt the notation in which we denote the level-$K$ spin-conserving modes by $\Delta_{cK}^{\alpha}$ and the level-$K$ spin-flip modes by $\Delta_{sK}^{\alpha}$. The superscript indicates the position of the mode: we have $\alpha=0$ for the zero wave vector mode, $\alpha=\infty$ for the large wave vector limit, and $\alpha=$R for a roton mode. Identifications of the various modes shown on Fig. 2 are based on the analysis below.

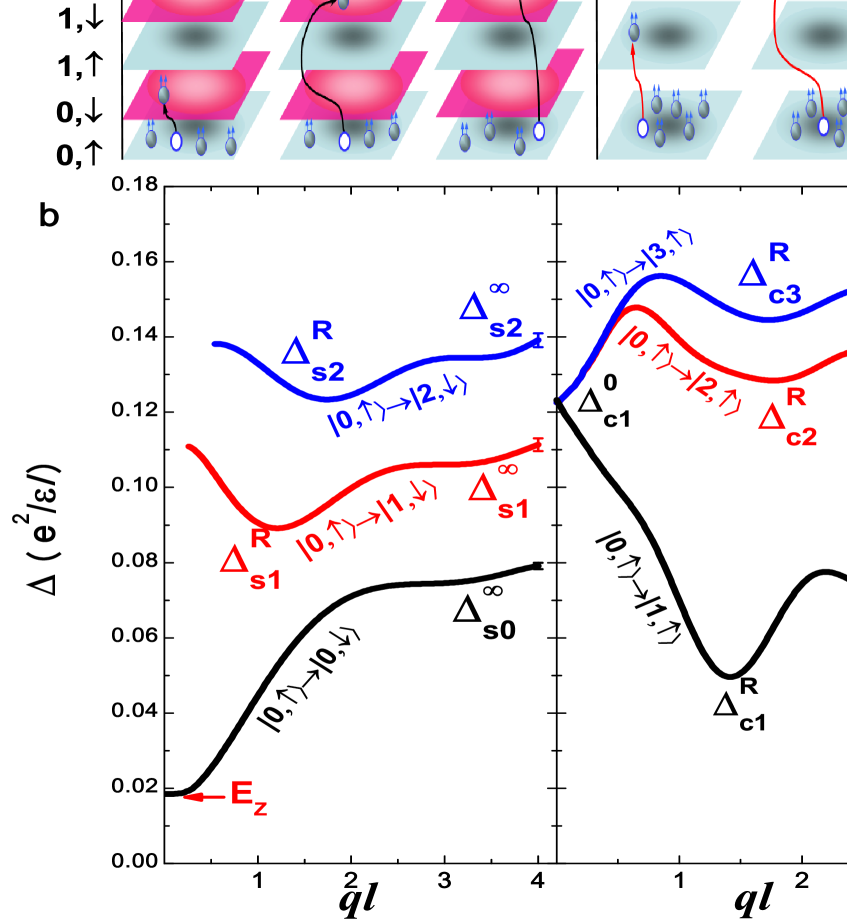
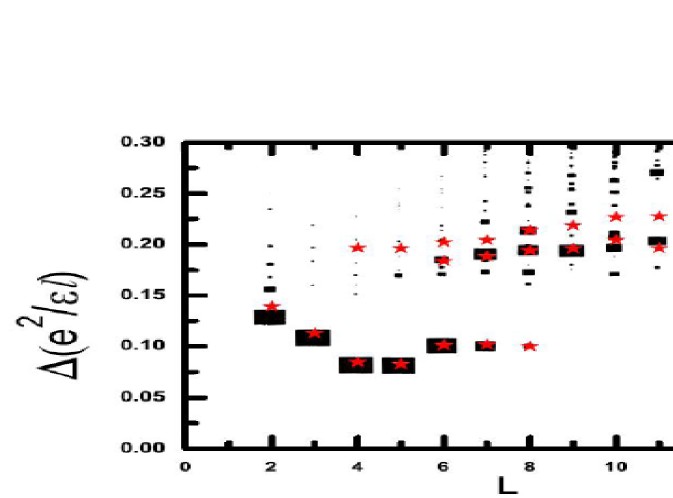
The dispersions of the SC and SF excitons are obtained by the method of CF diagonalization (without Landau level mixing and disorder) CFDiag1 . For a more accurate comparison, we have included here two realistic effects: The finite width modification of the interaction is incorporated via a self-consistent local density approximation. We also allow $\Lambda$ level mixing by considering the five lowest energy CF excitons. A combination of these two effects results in a 20 $\%$ reduction of the energy of the level-2 and level-3 excitons, and a smaller ($\sim$ 10 $\%$) reduction in the energy of the level-1 exciton. Figure 3 shows the full theoretical dispersions of the CF exciton branches for SC and SF modes. To avoid clutter, only the lowest three branches are shown. The calculations are performed for 200 (100) particles for SC (SF) modes and reflect the thermodynamic behavior. The three dispersion curves indicated in Fig. 3b are assigned as level-0, level-1 and level-2 for SF modes and level-1, level-2 and level-3 for SC modes, in order of increasing energy. The residual interaction between CFs in principle mixes the different “unperturbed” level-K excitations; however, the modes do not mix significantly at large $ql$, which allows us to continue to use the level-K nomenclature even for mixed modes. Figure 4 shows a comparison of the CF excitons with exact diagonalization studies on a finite system.

Level-1 SC modes and level-0 SF modes have been identified in previous experiments Hirjibehedin et al. (2005); Groshaus et al. (2008); Davies et al. (1997). Of interest here are the higher lying modes. We proceed by sorting the experimental values of the new modes in ascending order and match them up with theoretical values. The resulting comparison between theory and experiment is shown in Fig. 5. The theoretical results for the energies of level-1 excitons are in excellent agreement with the experimental results. The only exception is the long wavelength collective mode $\Delta^{0}_{c1}$, for which the discrepancy is closer to 35$\%$, but a $\sim$20$\%$ agreement is achieved when screening of the single exciton by two-roton excitations is taken into account Park and Jain (2000). This correction, not included in the calculation shown in Fig. 3, is incorporated in Fig. 5.

It is significant that mode energies predicted by theory agree to within 0.2-0.3 meV with measured energies, which translates into a better than 20$\%$ agreement. It should be stressed that a similar level of deviation between the theoretical and experimental values of the excitation energies has been found in the past for other excitations, and attributed to disorder. We judge the overall comparison between theory and experiment to be good, and take it as a strong support of the identification of the high energy collective modes ranging from about 1.0 meV to 1.6 meV in terms of transitions of CFs into higher levels.

We note that due to the presence of a large number of modes, sometimes two or more modes happen to lie at very nearby energies, and thus may not be resolved in our experiments. For example, for SC modes, the energy of the level-3 roton overlaps with the small q (ql $\sim$ 0.6) critical point of the level-2 exciton (see Fig. 3b). As another example, the small q (ql $\sim$ 0.8) critical point of the level-3 exciton overlaps in energy with the large wave vector limit of the level-3 exciton. When encountering such a situation, we have, for simplicity, arbitrarily assigned one of the possible labels to the observed mode ($\Delta^{R}_{c3}$ and $\Delta^{\infty}_{c3}$, respectively, for the above two cases). The assignment remains tentative in such cases, and more sensitive experiments in the future may reveal further finer structure.

Our work sets the stage for further investigations in other FQH states in GaAs, and also in other 2D systems, such as graphene, where the FQH physics is in its infancy Du et al. (2009); Bolotin et al. (2009). The high energy excitations should also be accessible to other experimental methods such as optical absorptionKukushkin et al. (2009) and time domain capacitance spectroscopyDial et al. (2010); these probes are likely to provide important further insight into the physics discussed above.

Acknowledgments - T.D.R. and A.P. were supported by the National Science Foundation (NSF) under grants DMR-0352738 and DMR-0803445; by the Dept. of Energy under grant DE-AIO2-04ER46133; and by the Nanoscale Science and Engineering Initiative of the NSF under award CHE-0641523. J.K.J. was supported in part by the NSF under DMR-1005536. The computation was performed at the Dept. of Theoretical Physics, Indian Assoc. for the Cultivation of Science.