Higher-order Topological Anderson Insulators
Abstract
We study disorder effects in a two-dimensional system with chiral symmetry and find that disorder can induce a quadrupole topological insulating phase (a higher-order topological phase with quadrupole moments) from a topologically trivial phase. Their topological properties manifest in a topological invariant defined based on effective boundary Hamiltonians, the quadrupole moment and zero-energy corner modes. We find gapped and gapless topological phases and a Griffiths regime. In the gapless topological phase, all the states are localized, while in the Griffiths regime, the states at zero energy become multifractal. We further apply the self-consistent Born approximation to show that the induced topological phase arises from disorder renormalized masses. We finally introduce a practical experimental scheme with topolectrical circuits where the predicted topological phenomena can be observed by impedance measurements. Our work opens the door to studying higher-order topological Anderson insulators and their localization properties.
I Introduction
Traditional topological phases usually feature the bulk-boundary correspondence that -dimensional gapless boundary states exist for an -dimensional topological system. Recently, topological phases have been generalized to the case where there exist -dimensional (instead of ) gapless boundary states with for an -dimensional system Taylor2017Science ; Fritz2012PRL ; ZhangFan2013PRL . In the past few years, the higher-order topological phenomena have drawn tremendous attention, and various higher-order topological states have been discovered Taylor2017Science ; Fritz2012PRL ; ZhangFan2013PRL ; Slager2015PRB ; FangChen2017PRL ; Brouwer2017PRL ; Bernevig2018SciAdv ; Brouwer2019PRX ; Roy2019PRB ; SYang2019PRL ; Vincent2020PRL ; Haiping2020PRL ; Yanbin2020PRR ; Tiwari2020PRL , such as quadrupole topological phases with zero-energy corner modes Taylor2017Science and its type-II cousin Yanbin2020PRR and second-order topological insulators with chiral hinge modes Bernevig2018SciAdv . It has also been shown that higher-order topological insulators (HOTIs) are robust against weak disorder Hatsugai2019PRB ; Jiang2019CPB ; Franca2019PRB ; CALi2020PRB ; Agarwala2020PRR ; XRWang2020 .
Disorder plays an important role in quantum transport, such as Anderson localization and metal-insulator transitions Evers2008RMP . In the context of first-order topological phases, it has been shown that they are usually stable against weak symmetry preserving disorder. But disorder is not always detrimental to first-order topological phases. Ref. Sheng2009PRL theoretically predicted that disorder can drive a topological phase transition from a metallic trivial phase to a quantum spin Hall insulator; topological insulators induced by disorder are called topological Anderson insulators (TAIs) Sheng2009PRL ; Beenakker2009PRL . Since their discovery, there has been great interest and advancement in the study of TAIs Jiang2009PRB ; Franz2010PRL ; Altland2014PRL ; Prodan2014PRL ; Rafael2015PRL ; SZhang2017PRL . In addition, disorder can drive a transition from a Weyl semimetal to a 3D quantum anomalous Hall state Xie2015PRL . Remarkably, the TAI has been experimentally observed in a photonic waveguide array Szameit2018Nat and disordered cold atomic wire Gadway2018Science .
Disorder, topology and symmetry are closely connected, which can be seen from classification theories. For example, random matrix theories are classified based on three internal symmetries, explaining universal transport properties of disordered physical systems Altland1997PRB ; Beenakker1997RMP ; HaakeBook . Similarly, the classification of topological phases is made according to these internal symmetries Ludwig2010NJP . Among these symmetries, chiral symmetry plays an important role in disordered systems and many peculiar properties have been found, such as the divergence of density of states (DOS) and localization length at energy Dyson ; Cohen1976PRB ; Eggarter1978PRB ; Eilmes1998EPJB ; Brouwer1998PRL . In 2D, first-order topological phases are not allowed in a system with only chiral symmetry. Yet, it has been reported that a second-order topological phase can exist in a 2D system with chiral symmetry Okugawa2019PRB ; Qibo2020PRB and thus provides an ideal platform to study the interplay between disorder and topology.
Here we study the interplay between disorder and higher-order topology in a 2D system with chiral symmetry. We prove that the quantization of the quadrupole moment is maintained by chiral symmetry irrespective of crystalline symmetries, indicating that the quadrupole topological insulator can exist in a system with chiral symmetry without the requirement of any crystalline symmetry. This also gives us an opportunity to explore the effects of off-diagonal disorder respecting chiral symmetry. We theoretically predict the existence of a disorder induced HOTI [dubbed higher-order topological Anderson insulator (HOTAI)] with zero-energy corner modes, which arises through the localization-delocalization-localization phase transition. We further apply the self-consistent Born approximation (SCBA) to show that the induced phase appears due to the disorder renormalized masses. Besides, we find gapped and gapless HOTAIs and a Griffiths regime. In the gapless regime, all the states are localized, while in the Griffiths regime, the states at zero energy become multifractal. In addition, we study the disorder effects on a HOTI and show the existence of gapped and gapless topological phases and a Griffiths regime. Finally, we propose an experimental scheme using topolectrical circuits to realize and detect the HOTAI.
II Model Hamiltonian
We start by considering the following higher-order Hamiltonian
| (1) |
where with () being a creation (annihilation) operator at the th site in a unit cell described by with and being integers (suppose that the lattice constants are equal to one), and . Here
| (2) |
depicts the intra-cell hopping, and
| (3) |
describe the inter-cell hopping along and , respectively [also see Fig. 1(a) for the hopping parameters]. The system parameters , , , , , , and all take real values. For simplicity without loss of generality, we take the inter-cell hopping magnitude as energy units so that . In this case, and with and being a identity matrix. For a clean system with , the system respects a generalized symmetry as detailed in Appendix A.
To show that the Hamiltonian (1) describes a higher-order phase supporting zero-energy corner modes in the clean case with and , we write the Hamiltonian in momentum space as
| (4) |
Here
| (5) |
where with being the Pauli matrices and being a identity matrix. To see the presence of zero-energy corner modes in the system, we recast the Hamiltonian (5) to a form in continuous real space by replacing by and by () so that . Considering semi-infinite boundaries along and , if and are zero-energy edge modes of and , respectively, is a zero-energy mode of localized at a corner.
Since the system contains only the nearest-neighbor hopping, it respects chiral symmetry, i.e., , where is the first-quantization Hamiltonian and is a unitary matrix. But this system breaks the time-reversal symmetry and thus the particle-hole symmetry, because is complex. In contrast, if we generalize the Benalcazar-Bernevig-Hughes (BBH) model Taylor2017Science to the disordered case, it still respects the time-reversal, particle-hole and chiral symmetries. However, these two models are connected through a local transformation and thus have similar topological and localization properties as proved in Appendix B. The equivalence also tells us that our system supports zero-energy corner modes and has quantized quadrupole moments Cho2018arXiv ; Wheeler2018arXiv protected by reflection symmetries. But with disorder breaking the reflection symmetry, one may wonder whether the quadrupole moment is still quantized. Here we prove the quantization of the quadrupole moment maintained by chiral symmetry (see Appendix C), indicating that chiral symmetry can protect a quadrupole topological insulator. We remark that in three dimensions (3D) chiral symmetry maintains the quantization of the octupole moment as proved in Appendix C, indicating that chiral symmetry can protect the third-order topological insulator with zero-energy corner modes in 3D.
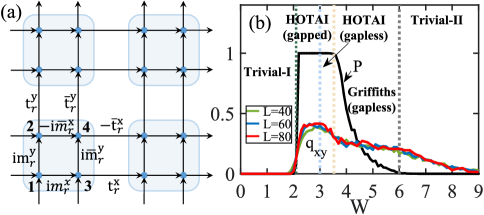
To study the disorder effects, we consider the disorder in the intra-cell hopping, that is, and with , where and are uniformly randomly distributed in without correlation. Here and represent the disorder strength. For simplicity, we take . Because of the random character, we perform the average over 200-2000 sample configurations for numerical calculation.
III Higher-order topological Anderson insulators
We map out the phase diagram in Fig. 1(b), showing remarkably the presence of a disorder-induced higher-order topological phase transition. To characterize the phase transition, we evaluate the polarization () of effective boundary Hamiltonians at a -normal (-normal) boundary at half filling. In one dimension, the polarization is equivalent to the Berry phase in a translation invariant system, which can be used as a topological invariant Resta . In fact, the polarization as a topological invariant can be evaluated in real space for a system without translational symmetries based on Resta’s formula Resta ; Prodan2014PRL . For the quadrupole topological phase, we define a topological invariant based on and as
| (6) |
When , the system is in a higher-order topologically nontrivial phase, and when , it is in a trivial phase (see Appendix D for its justification for a clean system).
We now generalize it to the disordered case. Specifically, we evaluate the average polarization of the effective boundary Hamiltonian at the -normal boundary (similarly for -normal one) by , where Resta with , being the particle number operator at the site , and being the length of the system along (we also deduct the atomic positive charge contribution). Here is the ground state at half filling of the boundary Hamiltonian with being the th boundary Green’s function obtained by Dai2008PRB ; Oppen2017PRB
| (7) |
where is the Hamiltonian for the th layer and is the coupling between the th and th layer. We note that is quantized to be either or for each iteration since also preserves chiral symmetry. The polarization is evaluated at even steps of Green’s function given that there are two different layers in the clean limit. In the disordered case, the intra-cell hopping parts in and are randomly generated for each iteration (see Appendix D). The topological invariant is finally determined.
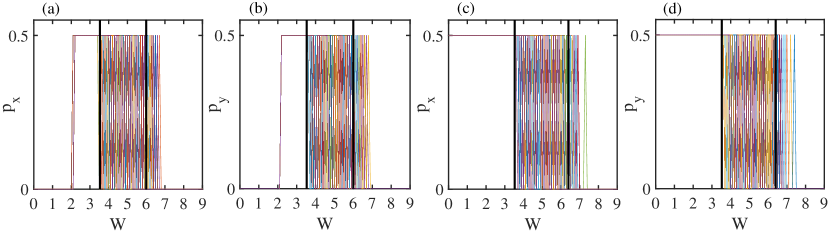
In Fig. 1(b), we plot the topological invariant as the disorder magnitude increases. We see that suddenly jumps to when , indicating the occurrence of a topological phase transition. remains quantized to be until , where it begins decreasing continuously. This regime corresponds to the Griffiths phase where topologically trivial and nontrivial sample configurations coexist (see Appendix E). When , vanishes, showing that the system reenters into a trivial phase.
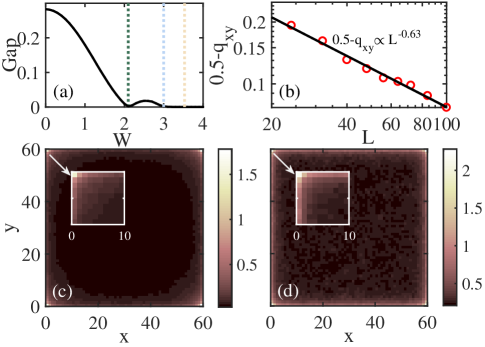
To further identify that the induced topological phase is a quadrupole topological phase, we calculate the quadrupole moment, which can be used as a topological invariant since its quantization is protected by chiral symmetry (see Appendix C). Figure 1(b) shows that the quadrupole moment qualitatively agrees with the results of . Yet, conspicuous discrepancy can be observed. The quadrupole moment over many samples is not quantized to in the regime where [ for most disorder configurations and for other configurations (see Fig. C1 in Appendix C)] and the Griffiths regime is much larger. We attribute this to the finite-size effects, given that for the quadrupole moment, we can only perform a computation for a system with its size up to , while to determine , we consider a system with its size up to and iterations up to . To be more quantitative, we plot as the system size increases when in Fig. 2(b), showing a power law decay and thus suggesting that approaches in the thermodynamic limit.
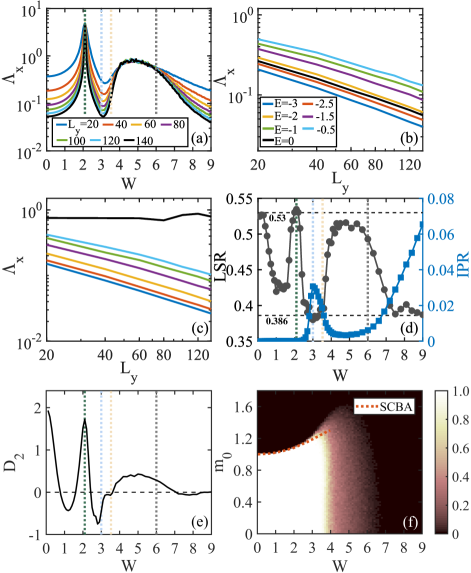
The higher-order topological phase transition occurs as the bulk energy gap closes at and reopens, as shown in Fig. 2(a). In fact, the transition is associated with the divergence of the localization length at [see Fig. 3(a)]. When is further increased, the energy gap closes again and remains closed due to the strong disorder scattering, leading to the gapless HOTAI. Even in the gapless regime, the topological invariant can still be quantized as shown in Fig. 1(b). In fact, in this phase, all the states are localized corresponding to an Anderson insulator (see the following discussion).
To further confirm that the TAI is a higher-order topological state, in Fig. 2(c-d), we display the local density of states (LDOS) at for two typical values of corresponding to a gapped and gapless topological phase, respectively, clearly showing the presence of zero-energy states localized at corners. The evidence above definitely suggests the existence of HOTAIs.
IV Localization properties
We now study the localization properties of energy bands in different phases by evaluating their localization length, adjacent level-spacing ratio (LSR), inverse participation ratio (IPR) and fractal dimensions. The LSR is defined as
| (8) |
where with being the th eigenenergy sorted in an ascending order and denotes the sum over an energy bin around the energy with energy levels counted. For localized states, corresponding to the Poisson statistics and for extended states of symmetric real Hamiltonians, corresponding to the Gaussian orthogonal ensemble (GOE) Huse2007PRB .
The localization property can also be characterized by the real space IPR defined as
| (9) |
This quantity evaluates how much a state in an energy bin around energy is spatially localized. For an extended state in 2D, with being the size of a system, which goes zero in the thermodynamic limit; for a state localized in a single unit cell, it is one. It is well known that at the critical point between localized and delocalized phases, the state exhibits multifractal behavior with fractal dimensions defined through Castellani1986 . Clearly, and indicates that a state is extended and localized, respectively, in the thermodynamic limit; intermediate values of suggests the multifractal state.
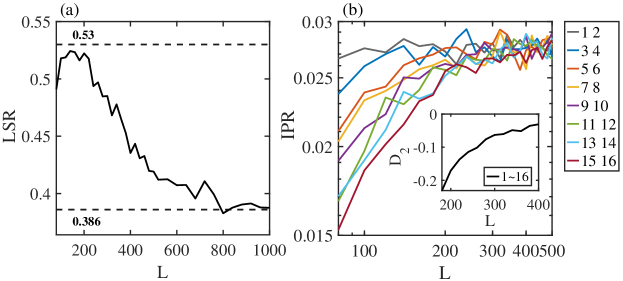
In Fig. 3(a), we plot the normalized localization length (similarly for ) with respect to the disorder strength at for distinct , where () is the localization length along calculated by the transfer matrix method Kramer1983 . In the gapless HOTAI and trivial-II phases, we see the decrease of as is increased, suggesting that the states at are localized. The decline can also be clearly seen in Fig. 3(b) where versus is plotted for for distinct energies. In fact, all states are localized in these two phases as detailed in the following discussion. This shows that even in the higher-order case, the topology can be carried by localized bulk states. Being localized for the states in these regimes is also evidenced by their relatively large IPR and the LSR approaching [see Fig. 3(d)]. In these regimes, the fractal dimension becomes negative or approaches zero [see Fig. 3(e)], further indicating that the states around zero energy are localized. We note that the negative arises from finite-size effects. It indicates that the IPR rises with increasing the system size, suggesting that the states are localized (see Appendix F for the finite-size analysis).
Figure 3(a) also demonstrates the existence of a regime (corresponding to the Griffiths regime) where at remains almost unchanged as increases, suggesting a multifractal phase in this regime. The multifractal phase resides between two localized phases, which is very different from the conventional wisdom that a multifractal phase lives at the critical point between delocalized and localized phases. In fact, only the states at or very near become multifractal, and all other states remain localized [see Fig. 3(c)]. The multifractal properties are also evidenced by the fractal dimension of the states around zero energy as shown in Fig. 3(e).
In the gapped regime, there are trivial-I and gapped HOTAI phases. In the trivial phase, the states at the band edge around zero energy exhibit the LSR close to [see Fig. 3(d)], suggesting the localized property of these states. The localized property is also evidenced by the negative (in the region around ) [see Fig. 3(e)]. We note that near the phase transition points of and , the states exhibit delocalized properties due to the large localization length. In the gapped HOTAI, Fig. 3(d) and (e) illustrate that the LSR experiences a drop from around to and drops from to negative values, suggesting that the states at the band edge undergo a phase transition from delocalized to localized ones.
The above results indicate that for strong disorder, all states are localized in the gapless HOTAI and the trivial-II phase. Yet in the Griffiths phase, all states are localized except at where the states become multifractal. For weak disorder, all states can be localized in the topological regime. In the trivial-I phase, the states at the band edge around zero energy are localized.
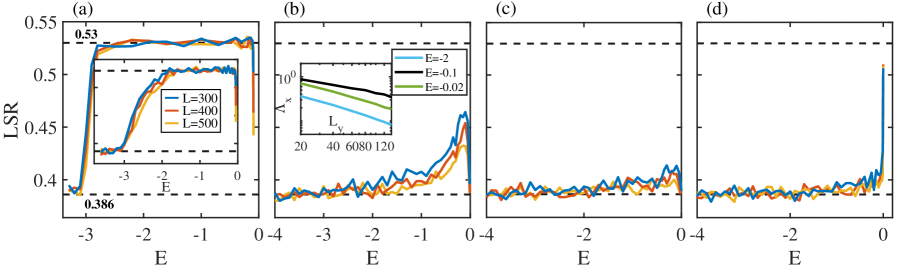
In the following, we provide more evidence on localization properties. Figure 4 shows the LSR as a function of energy for five different disorder amplitudes. For small corresponding to the trivial-I phase [Fig. 4(a) and its inset], the LSR remains around except at the lower band edge where it exhibits a sudden drop towards , indicating that the states at the band edge are localized. But we cannot claim the existence of mobility edges in the trivial-I phase given that it is very possible that the delocalized behavior is caused by the finite-size effects, which is very difficult to identify since the localization length is huge for the weak disorder. In the gapped HOTAI, while we cannot conclusively determine that all states are localized when is near the transition point, we show that this occurs when is larger. For instance, when , Fig. 4(b) illustrates that the LSR decreases towards with the increase of the system size. We also plot the normalized localization length with respect to for different energies, the fall of which clearly suggests that the states are localized. These indicators show that all the states are localized. Similarly, Fig. 4(c) indicates that all the states are localized in the gapless HOTAI phase. But in the Griffiths regime, all the states are localized except at where the LSR remains unchanged as the system size is increased [see Fig. 4(d)].
We also compute the density of states (DOS) at with respect to the disorder strength as shown in Fig. 5(a). The DOS is defined as , which is normalized to one, i.e., . Here describes the LDOS, where denotes the spatial eigenstate of the system with periodic boundaries corresponding to the eigenenergy , and denotes the average over different samples. The DOS rises to the maximum in the multifractal phase and then fall in the trivial-II phase. Specifically, we see the development of a very narrow peak of the DOS at in this regime [Fig. 5(b)].
V Self-consistent Born approximation
We now explain the disorder induced quadrupole topological insulator based on the self-consistent Born approximation (SCBA) Beenakker2009PRL . As introduced in Sec. II, we consider a disordered system by adding the following random intra-cell hopping terms at each unit cell
| (10) | ||||
where , , , , and , , , . Here we have changed the notation in Sec. II by , , and for convenience. Since we are interested in disorder without correlations, we require
| (11) | |||||
| (12) |
for with denoting the average over disorder ensembles.
Based on the self-consistent Born approximation, the effective Hamiltonian at is given by where the self-energy in the presence of disorder can be calculated through the following self-consistent equation
| (13) |
where . At energy , we find numerically that the self-energy can be expanded as
| (14) |
with being real numbers. It is clear to see that the topological masses and associated with topological properties are renormalized by disorder to new values
| (15) | ||||
| (16) |
Based on Eq. (13), we first approximate the self-energy by taking in the right-hand side of the equation, yielding
| (17) |
where
| (18) | |||||
| (19) |
with . When and , both and are negative due to the positive integrands, leading to a topological phase transition when the disorder strength is sufficiently large so that and . We also numerically solve the Eq. (13) self-consistently to determine and and plot the results in Fig. 3(f). For weak disorder, the results agree very well with the numerical phase boundary.
VI Disorder effects on HOTIs
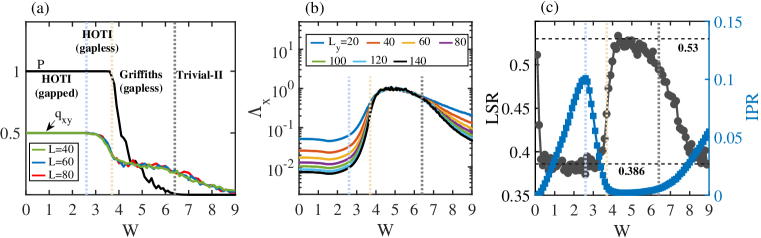
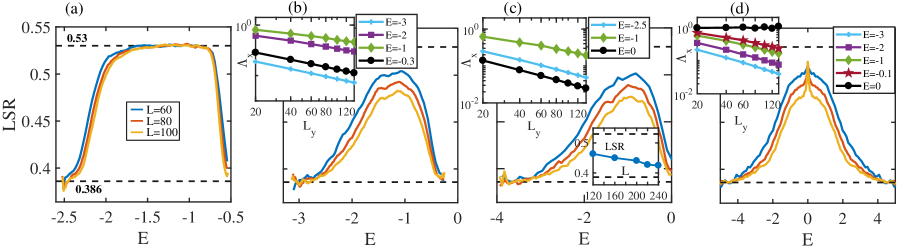
In this section, we study the effects of disorder on HOTIs. Specifically, we consider corresponding to a HOTI in the clean limit. We find that the topological phase is stable against weak disorder as evidenced by the quantized topological invariant in Fig. 6(a). When the disorder strength becomes sufficiently strong, it enters into a Griffiths regime with fractional and finally becomes a trivial phase. The strong disorder also closes the energy gap when . In the gapless HOTI and trivial-II phases, all states are localized, as evidenced by the normalized localization length, LSR and IPR [see Fig. 6(b) and (c)]. In the Griffiths regime, the states at are multifractal and all other states are localized [see Fig. 6(b)]. In the disordered gapped HOTI, we find that for weak disorder, the states near the band edge are localized as shown by the LSR around in Fig. 6(c). For larger disorder, all the states become localized in this phase.
Figure 7 further plots the LSR with respect to for four different disorder strength. When the disorder is weak, e.g., , the LSR shows that the states near the band edge are localized in the gapped HOTI [Fig. 7(a)]. Yet, when , the LSR of all the states decreases towards with the increase of the system size, reflecting that all the states are localized. The localized property is also signalled by the decline of the normalized localization length with increasing [Fig. 7(b)]. Similarly, in the gapless HOTI, all the states are localized as shown in Fig. 7(c). In this case, the LSR at decreases towards as the system size is increased, providing further evidence for localization. In the Griffiths regime, the LSR becomes smaller for larger system sizes except at where it remains unchanged, suggesting that the states at are multifractal and all other states are localized. The multifractal property is also reflected by the unchanged property of the normalized localization length as is increased [Fig. 7(d)].
VII Experimental realization
The BBH model has been experimentally realized in several metamaterials, such as microwave, phononic, photonic and topolectrical circuit systems Huber2018Nature ; Bahl2018Nature ; Thomale2018NP ; Hafezi2019NP . In fact, some systems, such as silicon ring resonators Hafezi2019NP , have demonstrated the robustness of zero-energy corner modes to certain disorders. The HOTAI can be easily realized in these systems when the off-diagonal hopping disorder is considered in the experimentally realized BBH model. The BBH model has also been implemented in topolectrical circuits, and zero-energy corner modes are probed by measuring two-point impedances Thomale2018NP . One can involve disorder in the system by tuning the capacitance of capacitors and inductance of inductors to realize the HOTAI, as we have proved that this model is equivalent to our model in topological and localization properties (see Appendix B). In the following, we discuss in detail an experimental scheme to realize the Hamiltonian (1) using topolectrical circuits and show that the HOTAI phase can be detected by two-point impedance measurements.
Let us consider an electric network composed of different nodes and electric element connecting nodes, as shown in Fig. 8(a). We denote the input current and voltage of each node by and , respectively. According to Kirchhoff’s law, the circuit at a frequency of should satisfy the relation
| (20) |
where is the admittance of the corresponding electric element between the node and , and is the admittance of the electric element between the node and the ground. We can rewrite the above equation into a compact form as
| (21) |
where and are -component column vectors with components and for nodes, respectively. Here the matrix is the circuit Laplacian. Then we can simulate our Hamiltonian with the Laplacian at a proper frequency through
| (22) |
Each node in the circuit represents one lattice site in our Hamiltonian, and each electric element linking two nodes represents the corresponding hopping between the sites, which can be either a capacitor, or an inductor, or a negative impedance converter with current inversion (INIC). For two nodes in the circuit, the electric element between them is determined according to the corresponding matrix element between the site and in our Hamiltonian, as illustrated in Fig. 8(a). Specifically, for two neighboring sites in our Hamiltonian, if is a positive (negative) real number, the electric element between and should be an inductor (a capacitor) with inductance (capacitance) (). For the case that is an imaginary number, we should connect the two nodes using an INIC with resistance and proper direction. In addition, we connect every node with the ground by appropriate electric elements to eliminate the extra diagonal terms in the Laplacian.
Similar to the experimental work Thomale2018NP , we utilize the two-point impedance measurement in the circuit to characterize the zero-energy corner modes in the HOTAI phase. The two-point impedance between node and is defined as
| (23) |
where is the component for the node of the th eigenvector of with eigenvalue . We define the impedance of each unit cell as the average two-point impedance between nearest-neighbor nodes within each unit cell as
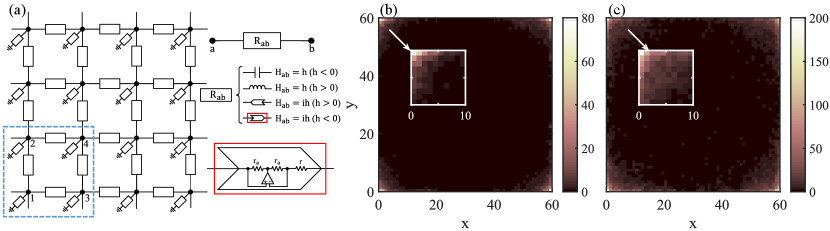
| (24) |
where denotes the two-point impedance between the th node and th node of the unit cell . Fig. 8(b) and (c) plot the magnitude of averaged over random samples under open boundary conditions for two values of within HOTAI regime for , which clearly show the impedance resonance near the corners corresponding to the presence of zero-energy corner modes of the Hamiltonian.
VIII Conclusion
In summary, we have discovered the HOTAI in a 2D disordered system with chiral symmetry. Specifically, we show that a topologically trivial phase can transition into a quadrupole topological phase, when disorder is added. We find gapped and gapless HOTAIs and a Griffiths regime. In the gapless HOTAI, all the states are localized, while in the Griffiths regime, the states at zero energy are multifractal and other states are localized. The Griffiths regime corresponds to a critical regime between two localized phases: a gapless HOTAI and a trivial phase. We also propose an experimental scheme with topolectrical circuits to realize the HOTAI. Our results demonstrate that disorder can induce quadrupole topological insulators with peculiar localization properties from a trivial phase and thus opens a new avenue for studying the role of disorder in higher-order topological phases.
Acknowledgements.
We thank Y.-L. Tao and N. Dai for helpful discussion. Y.B.Y., K.L. and Y.X. are supported by the National Natural Science Foundation of China (11974201), the start-up fund from Tsinghua University and the National Thousand-Young-Talents Program. We acknowledge in addition support from the Frontier Science Center for Quantum Information of the Ministry of Education of China, Tsinghua University Initiative Scientific Research Program, and the National key Research and Development Program of China (2016YFA0301902).Note added: Recently, we became aware of two related work Shen2020PRL ; Zhang2020arXiv .
Appendix A: Generalized symmetry
In the clean case, when and , the Hamiltonian (1) in the main text respects a generalized symmetry,
| (A1) |
where
| (A2) |
with
| (A3) |
and being a rotation operator such that .
In momentum space, let us write with . The generalized symmetry takes the following form
| (A4) |
where and
| (A5) |
Appendix B: Equivalence between our model and the disordered BBH model
In this Appendix, we will prove that our model is equivalent to the BBH model in topological and localization properties. The BBH model reads
| (B1) |
where is a real matrix expressed as
| (B2) |
This model respects the time-reversal, particle-hole and chiral symmetries.
While the two Hamiltonians have different symmetries, they are closely related by a local transformation , that is, , and . Specifically, one can transform in Eq. (1) to by the transformation . In other words, if is a spatial eigenstate of , then with , , and is an eigenstate of corresponding to the same energy . Here and are the first-quantization Hamiltonians of and , respectively. Therefore, and have the same energy spectrum and density profiles, indicating identical localization properties that they possess. In addition, this local phase transformation does not change the topological property, and thus the two Hamiltonians have the same topology. Under open boundary conditions, the two models are connected by the transformation irrelevant of the system size. Yet, under periodic boundary conditions, the transformation works well only when and are integer multiples of four. For topological property, the two models should be equivalent irrelevant of a system size given that the topology does not depend on a specific system size. For localization property, we have also calculated the IPR and LSR of the two Hamiltonians with their sizes being odd and find similar results, showing that their localization properties are irrelevant of the parity of a system size.
Appendix C: Quantization of quadrupole moments by chiral symmetry
In this Appendix, we will prove that the quadrupole moment is protected to be quantized by chiral symmetry and thus can be used as a topological invariant. Note that the quadrupole moment may not characterize the physical quadrupole moment, we here are only interested in the formula as a topological invariant. We consider the quadrupole moment defined by Wheeler2018arXiv ; Cho2018arXiv
| (C1) | ||||
where with () denoting the -position (-position) operator for electron with (the number of occupied states in our model) at half filling, and is the many-body ground state of electrons in the system. Here is the contribution from occupied electrons, and is the contribution from the background positive charge distribution where denotes the position of the th atomic orbital. Here, is the total number of atomic orbitals so that the single-particle Hamiltonian is a matrix. At half filling, .
Let us write the many-body wave function of occupied electrons in real space representation as
| (C6) |
where represents the th occupied eigenstate of a first-quantization Hamiltonian. Then, the quadrupole moment of occupied electrons can be evaluated through
| (C7) |
where
| (C8) |
and . Let us define which is a matrix representing the occupied states of electrons. Then we can express the quadrupole moment of occupied electrons as
| (C9) |
where we define a diagonal matrix with denoting the position of -th atomic orbital.
For a generic Hamiltonian in real space with chiral (sublattice) symmetry, , if is an eigenstate of corresponding to energy , is also an eigenstate of with energy , corresponding to an unoccupied state. The set therefore constitutes the unoccupied states. We then define representing the unoccupied states of electrons. The quadrupole moment for the unoccupied states is
| (C10) | ||||
| (C11) |
Clearly, commutes with the chiral (sublattice) symmetry transformation , i.e., ,
| (C12) |
Let us define . Then we will have
| (C13) |
Next we will prove that , i.e., .
Proof.
We define a unitary matrix . It can be easily seen that
| (C14) | ||||
| (C15) | ||||
| (C16) |
Then we have the following relations
| (C17) | |||||
In the derivation, we have utilized the orthonormal properties , and . ∎
Therefore, we have the following relation
| (C18) |
Combined with the relation that , we get the conclusion that , namely, is quantized to or up to an integer. The result is consistent with our numerical results where all disorder configurations exhibit quantized quadrupole moments. We note that this proof remains valid when we replace and in the definition of with and , respectively where is a general function so that the newly defined quantity is also quantized by chiral symmetry like the quadrupole moment. In addition, one can use the same procedure to prove the quantization of the octupole moment in 3D protected by chiral symmetry.
We note that while we have proved that the quadrupole moment is quantized to either or for each disorder configuration protected by chiral symmetry, for a disorder system, we need to consider many distinct samples and perform the average of the quadrupole moment over these samples. In this case, the averaged quadrupole moment may not be quantized since for some samples the quadruple moments are equal to and for others they are equal to when a system size is not large as shown in Fig. C1.
It is worth mentioning that Ref. Agarwala2020PRR has found that quadrupole topological insulators with quantized quadrupole moments can still exist even in amorphous systems without crystalline symmetries. We now can understand that the quantized quadrupole moment found in Ref. Agarwala2020PRR is protected by chiral symmetry.
Appendix D: Effective boundary Hamiltonian
In this section, we follow the transfer matrix method introduced in Ref. Oppen2017PRB to derive the effective boundary Hamiltonian of our system in the clean case. We will show that the effective boundary Hamiltonian at the -normal (-normal) edges are proportional to [] up to a nonzero factor, implying that the higher-order topology can be characterized by the topological invariant introduced in the main text.
Specifically, let us write the Hamiltonian as where with the index denoting the th layer consisting of sites along and reads
| (D1) |
with denoting the coupling between the th and th layer. In disordered systems, the parameters in and describing the intra-cell hopping are randomly generated.
In the clean case, the system has the translational invariance of period 2 and thus there are two different layers described by the Hamiltonian and , respectively. If we view these two layers as a unit cell, we use and to describe the intra-cell and inter-cell layer coupling, respectively. Now can be simplified as
| (D2) |
Considering the periodic boundaries along , we write , , and in momentum space as , and . When , it is clear to see that the effective boundary Hamiltonian is . When , we obtain the following two transfer matrices at energy
| (D3) | ||||
where the transfer matrices connect the eigenstate in neighboring layers through
| (D4) | ||||
with and is the component in the th layer of an eigenstate with the energy .
We now define the total transfer matrix at zero energy as
| (D5) |
where . This matrix can be reduced to a diagonal block form through an elementary interchange transformation,
| (D6) |
where
| (D7) | ||||
Evidently, and have the same eigenvalues. Since is a symplectic matrix, its eigenvalues show up in pairs as . Suppose that () is an eigenvalue of , then
| (D10) | ||||
| (D15) |
where is made up of eigenvectors of and . Then, the fixed-point boundary Green’s function is given by
| (D16) |
where can be chosen as any invertible matrix. By calculating eigenvectors of and , we obtain the effective boundary Hamiltonian along
| (D17) |
where and ( is not considered as it corresponds to a phase boundary). Let us further prove that for all . Suppose , then , we have
| (D18) | |||||
where we have used . If , then ; otherwise, we have , giving . Similarly,
| (D19) |
where and with and .
Evidently, the higher-order topological phase arises when these effective boundary Hamiltonians become topological and thus can be characterized by the topological invariant .
Appendix E: Griffiths regime
In the main text, we have shown the existence of a Griffiths phase where topologically nontrivial and trivial samples coexist, leading to the topological invariant that is not quantized. In Fig. D1, we plot the polarizations in different iteration steps corresponding to different sample configurations. We see that in the Griffiths regime, some results show the polarization of and others zero.
Appendix F: The finite-size analysis of the LSR and IPR
In the main text, we have shown that the LSR at the band edge around zero energy in the region around is close to , indicating that the states are localized. Here we further plot the LSR for with respect to the system size in Fig. F1(a), illustrating that the LSR approaches as the system size increases. We have also shown in the main text that for the localized states, the fractal dimension can take negative values due to finite-size effects. Here we plot the IPR with respect to the system size in Fig. F1(b), showing the increase of the IPR with respect to the system size for a system with moderate sizes. Such an increase gives a negative fractal dimension. Yet, the increase slope declines as the system size is raised, indicating that approaches zero in the thermodynamic limit.
References
- (1) W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Quantized electric multipole insulators, Science 357, 61 (2017).
- (2) M. Sitte, A. Rosch, E. Altman, and L. Fritz, Topological Insulators in Magnetic Fields: Quantum Hall Effect and Edge Channels with a Nonquantized Term, Phys. Rev. Lett. 108, 126807 (2012).
- (3) F. Zhang, C. L. Kane, and E. J. Mele, Surface State Magnetization and Chiral Edge States on Topological Insulators, Phys. Rev. Lett. 110, 046404 (2013).
- (4) R.-J. Slager, L. Rademaker, J. Zaanen, and L. Balents, Impurity-bound states and Green’s function zeros as local signatures of topology, Phys. Rev. B 92, 085126 (2015).
- (5) Z. Song, Z. Fang, and C. Fang, -Dimensional Edge States of Rotation Symmetry Protected Topological States, Phys. Rev. Lett. 119, 246402 (2017).
- (6) J. Langbehn, Y. Peng, L. Trifunovic, F. von Oppen, and P. W. Brouwer, Reflection-Symmetric Second-Order Topological Insulators and Superconductors, Phys. Rev. Lett. 119, 246401 (2017).
- (7) F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Higher-order topological insulators, Sci. Adv. 4, eaat0346 (2018).
- (8) L. Trifunovic and P. W. Brouwer, Higher-order bulk-boundary correspondence for topological crystalline phases, Phys. Rev. X 9, 011012 (2019).
- (9) D. Călugăru, V. Juričić, and B. Roy, Higher-order topological phases: A general principle of construction, Phys. Rev. B 99, 041301(R) (2019).
- (10) X.-L. Sheng, C. Chen, H. Liu, Z. Chen, Z.-M. Yu, Y. X. Zhao, and S. A. Yang, Two-Dimensional Second-Order Topological Insulator in Graphdiyne, Phys. Rev. Lett. 123, 256402 (2019).
- (11) B. Huang and W. V. Liu, Floquet Higher-Order Topological Insulators with Anomalous Dynamical Polarization, Phys. Rev. Lett. 124, 216601 (2020).
- (12) H. Hu, B. Huang, E. Zhao, and W. V. Liu, Dynamical Singularities of Floquet Higher-Order Topological Insulators, Phys. Rev. Lett. 124, 057001 (2020).
- (13) Y.-B. Yang, K. Li, L.-M. Duan, and Y. Xu, Type-II quadrupole topological insulators, Phys. Rev. Res. 2, 033029 (2020).
- (14) A. Tiwari, M.-H. Li, B. A. Bernevig, T. Neupert, and S. A. Parameswaran, Unhinging the Surfaces of Higher-Order Topological Insulators and Superconductors, Phys. Rev. Lett. 124, 046801 (2020).
- (15) H. Araki, T. Mizoguchi, and Y. Hatsugai, Phase diagram of a disordered higher-order topological insulator: A machine learning study, Phys. Rev. B 99, 085406 (2019).
- (16) Z. Su, Y. Kang, B. Zhang, Z. Zhang, and H. Jiang, Disorder induced phase transition in magnetic higher-order topological insulator: A machine learning study, Chin. Phys. B 28, 117301 (2019).
- (17) S. Franca, D. V. Efremov, and I. C. Fulga, Phase-tunable second-order topological superconductor, Phys. Rev. B 100, 075415 (2019).
- (18) C.-A. Li and S.-S. Wu, Topological states in generalized electric quadrupole insulators, Phys. Rev. B 101, 195309 (2020).
- (19) A. Agarwala, V. Juričić, and B. Roy, Higher-order topological insulators in amorphous solids, Phys. Rev. Res. 2, 012067(R) (2020).
- (20) C. Wang and X. R. Wang, Disorder-induced quantum phase transitions in three-dimensional second-order topological insulators, Phys. Rev. Res. 2, 033521 (2020).
- (21) F. Evers and A. D. Mirlin, Anderson transitions, Rev. Mod. Phys. 80, 1355 (2008).
- (22) J. Li, R.-L. Chu, J. K. Jain, and S.-Q. Shen, Topological Anderson Insulator, Phys. Rev. Lett. 102, 136806 (2009).
- (23) C. W. Groth, M. Wimmer, A. R. Akhmerov, J. Tworzydło, and C. W. J. Beenakker, Theory of the Topological Anderson Insulator, Phys. Rev. Lett. 103, 196805 (2009).
- (24) H. Jiang, L. Wang, Q.-F. Sun, and X. C. Xie, Numerical study of the topological Anderson insulator in HgTe/CdTe quantum wells, Phys. Rev. B 80, 165316 (2009).
- (25) H.-M. Guo, G. Rosenberg, G. Refael, and M. Franz, Topological Anderson Insulator in Three Dimensions, Phys. Rev. Lett. 105, 216601 (2010).
- (26) A. Altland, D. Bagrets, L. Fritz, A. Kamenev, and H. Schmiedt, Quantum Criticality of Quasi-One-Dimensional Topological Anderson Insulators, Phys. Rev. Lett. 112, 206602 (2014).
- (27) I. Mondragon-Shem, T. L. Hughes, J. Song, and E. Prodan, Topological Criticality in the Chiral-Symmetric AIII Class at Strong Disorder, Phys. Rev. Lett. 113, 046802 (2014).
- (28) P. Titum, N. H. Lindner, M. C. Rechtsman, and G. Refael, Disorder-Induced Floquet Topological Insulators, Phys. Rev. Lett. 114, 056801 (2015).
- (29) C. Liu, W. Gao, B. Yang, and S. Zhang, Disorder-Induced Topological State Transition in Photonic Metamaterials, Phys. Rev. Lett. 119, 183901 (2017).
- (30) C.-Z. Chen, J. Song, H. Jiang, Q.-F. Sun, Z. Wang, and X. C. Xie, Disorder and Metal-Insulator Transitions in Weyl Semimetals, Phys. Rev. Lett. 115, 246603 (2015).
- (31) S. Stützer, Y. Plotnik, Y. Lumer, P. Titum, N. H. Lindner, M. Segev, M. C. Rechtsman, and A. Szameit, Photonic topological Anderson insulators, Nature (London) 560, 461 (2018).
- (32) E. J. Meier, F. A. An, A. Dauphin, M. Maffei, P. Massignan, T. L. Hughes, and B. Gadway, Observation of the topological Anderson insulator in disordered atomic wires, Science 362, 929 (2018).
- (33) A. Altland and M. R. Zirnbauer, Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures, Phys. Rev. B 55, 1142 (1997).
- (34) C. W. J. Beenakker, Random-matrix theory of quantum transport, Rev. Mod. Phys. 69, 731 (1997).
- (35) F. Haake, Quantum Signatures of Chaos (Springer-Verlag, Berlin, Heidelberg, 2006).
- (36) S. Ryu, A. P. Schnyder, A. Furusaki, and A. W. W. Ludwig, Topological insulators and superconductors: tenfold way and dimensional hierarchy, New J. Phys. 12, 065010 (2010).
- (37) F. J. Dyson, The Dynamics of a Disordered Linear Chain, Phys. Rev. 92, 1331 (1953).
- (38) G. Theodorou and M. H. Cohen, Extended states in a one-demensional system with off-diagonal disorder, Phys. Rev. B 13, 4597 (1976).
- (39) T. P. Eggarter and R. Riedinger, Singular behavior of tight-binding chains with off-diagonal disorder, Phys. Rev. B 18, 569 (1978).
- (40) A. Eilmes, R. A. Römer, and M. Schreiber, The two-dimensional Anderson model of localization with random hopping, Eur. Phys. J. B 1, 29 (1998).
- (41) P. W. Brouwer, C. Mudry, B. D. Simons, and A. Altland, Delocalization in Coupled One-Dimensional Chains, Phys. Rev. Lett. 81, 862 (1998).
- (42) R. Okugawa, S. Hayashi, and T. Nakanishi, Second-order topological phases protected by chiral symmetry, Phys. Rev. B 100, 235302 (2019).
- (43) Q.-B. Zeng, Y.-B. Yang, and Y. Xu, Higher-order topological insulators and semimetals in generalized Aubry-André-Harper models, Phys. Rev. B 101, 241104(R) (2020).
- (44) B. Kang, K. Shiozaki, and G. Y. Cho, Many-body order parameters for multipoles in solids, Phys. Rev. B 100, 245134 (2019).
- (45) W. A. Wheeler, L. K. Wagner, and T. L. Hughes, Many-body electric multipole operators in extended systems, Phys. Rev. B 100, 245135 (2019).
- (46) R. Resta, Quantum-Mechanical Position Operator in Extended Systems, Phys. Rev. Lett. 80, 1800 (1998).
- (47) X. Dai, T. L. Hughes, X.-L. Qi, Z. Fang, and S.-C. Zhang, Helical edge and surface states in HgTe quantum wells and bulk insulators, Phys. Rev. B 77, 125319 (2008).
- (48) Y. Peng, Y. Bao, and F. von Oppen, Boundary Green functions of topological insulators and superconductors, Phys. Rev. B 95, 235143 (2017).
- (49) V. Oganesyan and D. A. Huse, Localization of interacting fermions at high temperature, Phys. Rev. B 75, 155111 (2007).
- (50) C. Castellani and L. Peliti, Multifractal wavefunction at the localisation threshold, J. Phys. A 19, L429 (1986).
- (51) A. MacKinnon and B. Kramer, The scaling theory of electrons in disordered solids: Additional numerical results, Z. Phys. B 53, 1 (1983).
- (52) M. Serra-Garcia, V. Peri, R. Süsstrunk, O. R. Bilal, T. Larsen, L. G. Villanueva, and S. D. Huber, Observation of a phononic quadrupole topological insulator, Nature (London) 555, 342 (2018).
- (53) C. W. Peterson, W. A. Benalcazar, T. L. Hughes, and G. Bahl, A quantized microwave quadrupole insulator with topologically protected corner states, Nature (London) 555, 346 (2018).
- (54) S. Imhof, C. Berger, F. Bayer, J. Brehm, L. W. Molenkamp, T. Kiessling, F. Schindler, C. H. Lee, M. Greiter, T. Neupert, and R. Thomale, Topolectrical-circuit realization of topological corner modes, Nat. Phys. 14, 925 (2018).
- (55) S. Mittal, V. V. Orre, G. Zhu, M. A. Gorlach, A. Poddubny, and M. Hafezi, Photonic quadrupole topological phases, Nat. Photon. 13, 692 (2019).
- (56) C.-A. Li, B. Fu, Z.-A. Hu, J. Li, and S.-Q. Shen, Topological Phase Transitions in Disordered Electric Quadrupole Insulators, Phys. Rev. Lett. 125, 166801 (2020).
- (57) W. Zhang, D. Zou, Q. Pei, W. He, J. Bao, H. Sun, and X. Zhang, Experimental Observation of Higher-Order Topological Anderson Insulators, arXiv:2008.00423.