Highly Efficient Knowledge Graph Embedding Learning
with Orthogonal Procrustes Analysis
Abstract
Knowledge Graph Embeddings (KGEs) have been intensively explored in recent years due to their promise for a wide range of applications. However, existing studies focus on improving the final model performance without acknowledging the computational cost of the proposed approaches, in terms of execution time and environmental impact. This paper proposes a simple yet effective KGE framework which can reduce the training time and carbon footprint by orders of magnitudes compared with state-of-the-art approaches, while producing competitive performance. We highlight three technical innovations: full batch learning via relational matrices, closed-form Orthogonal Procrustes Analysis for KGEs, and non-negative-sampling training. In addition, as the first KGE method whose entity embeddings also store full relation information, our trained models encode rich semantics and are highly interpretable. Comprehensive experiments and ablation studies involving 13 strong baselines and two standard datasets verify the effectiveness and efficiency of our algorithm.
1 Introduction

The recent growth in energy requirements for Natural Language Processing (NLP) algorithms has led to the recognition of the importance of computationally cheap and eco-friendly approaches (Strubell et al., 2019). The increase in computational requirements can, to a large extent, be attributed to the popularity of massive pre-trained models, such as Language Models (e.g., BERT (Devlin et al., 2019) and GPT-3 (Brown et al., 2020)) and Knowledge Graph Embeddings (KGEs, e.g., SACN (Shang et al., 2019)), that require significant resources to train. A number of solutions have been proposed such as reducing the number of parameters the model contains. For instance, Sanh et al. (2019) introduced a distilled version of BERT and Zhang et al. (2019) decreased the parameters used for training KGEs with the help of the quaternion. In contrast with previous work, this paper explores algorithmic approaches to the development of efficient KGE techniques.
Knowledge Graphs are core to many NLP tasks and downstream applications, such as question answering (Saxena et al., 2020), dialogue agents (He et al., 2017), search engines (Dong et al., 2014) and recommendation systems (Guo et al., 2020). Facts stored in a knowledge graph are always in the format of tuples consisting of one head entity, one tail entity (both are nodes in knowledge graphs) and a relation (an edge in knowledge graphs) between them. KGEs learn representations of relations and entities in a knowledge graph, which are then utilised in downstream tasks like predicting missing relations (Bordes et al., 2013; Sun et al., 2019; Tang et al., 2020). The application of deep learning has led to significant advances in KGE (Rossi et al., 2020). Nonetheless, such approaches are computationally expensive with associated environmental costs. For example, training the SACN model (Shang et al., 2019) can lead to emissions of more than 5.3kg (for more data of other algorithms, see Tab. 2).
To alleviate the computational cost we introduce ProcrustEs, a lightweight, fast, and eco-friendly KGE training technique. ProcrustEs is built upon three novel techniques. First, to reduce the batch-wise computational overhead, we propose to parallelise batches by grouping tuples according to their relations, which ultimately enables efficient full batch learning. Second, we turn to a closed-form solution for Orthogonal Procrustes Problem to boost the embedding training, which has never been explored in the context of KGEs. Third, to break though the bandwidth bottleneck, our algorithm is allowed to be trained without negative samples.
To verify the effectiveness and efficiency of our proposed method, we benchmark two popular datasets (WN18RR and FB15k-237) against 13 strong baselines. Experimental results show that ProcrustEs yields performance competitive with the state-of-the-art while also reducing training time by up to 98.4% and the carbon footprint by up to 99.3%. In addition, we found that our algorithm can produce easily interpretable entity embeddings with richer semantics than previous approaches. Our code is available at https://github.com/Pzoom522/ProcrustEs-KGE.
Our contribution is three-fold: (1) We introduce three novel approaches to substantially reduce computational overhead of embedding large and complex knowledge graphs: full batch learning based on relational matrices, closed-form Orthogonal Procrustes Analysis for KGEs, and non-negative-sampling training. (2) We systemically benchmark the proposed algorithm against 13 strong baselines on two standard datasets, demonstrating that it retains highly competitive performance with just order-of-minute training time and emissions of less than making two cups of coffee. (3) We successfully encode both entity and relation information in a single vector space for the first time, thereby enriching the expressiveness of entity embeddings and producing new insights into interpretability.
2 Methodology
We propose a highly efficient and lightweight method for training KGEs called ProcrustEs, which is more efficient in terms of time consumption and emissions than previous counterparts by orders of magnitude while retaining strong performance. This is achieved by introducing three novel optimisation strategies, namely, relational mini-batch, closed-form Orthogonal Procrustes Analysis, and non-negative sampling training.
2.1 Preliminaries: Segmented Embeddings
Our proposed ProcrustEs model is built upon segmented embeddings, a technique which has been leveraged by a number of promising recent approaches to KGE learning (e.g., RotatE (Sun et al., 2019), SEEK (Xu et al., 2020), and OTE (Tang et al., 2020)). In contrast to conventional methods for KGEs where each entity only corresponds to one single vector, algorithms adopting segmented embeddings explicitly divide the entity representation space into multiple independent sub-spaces. During training each entity is encoded as a concatenation of decoupled sub-vectors (i.e., different segments, and hence the name). For example, as shown in Fig. 1, to encode a graph with 7 entities, the embedding of the th entity is the row-wise concatenation of its sub-vectors (i.e., ), where and denote the dimensions of entity vectors and sub-vectors, respectively. Employing segmented embeddings permits parallel processing of the structurally separated sub-spaces, and hence significantly boosts the overall training speed. Furthermore, segmented embeddings can also enhance the overall expressiveness of our model, while substantially reducing the dimension of matrix calculations. We provide detailed discussion on the empirical influence of segmented embedding setups in § 3.4.
2.2 Efficient KGE Optimisation
Full batch learning via relational matrices.
Segmented embeddings can speed up training process by parallelising tuple-wise computation. In this section, we propose a full batch learning technique via relational matrices, which can optimise batch-wise computation to further reduce training time. This idea is motivated by the observation that existing neural KGE frameworks all perform training based on random batches constructed from tuples consisting of different types of relations Bordes et al. (2013); Trouillon et al. (2016); Schlichtkrull et al. (2018); Chami et al. (2020). Such a training paradigm is based on random batches which, although straightforward to implement, is difficult to parallelise. This is due to the nature of computer process scheduling: during the interval between a process reading and updating the relation embeddings, they are likely to be modified by other processes, leading to synchronisation errors and consequently result in unintended data corruption, degraded optimisation, or even convergence issues.
To tackle this challenge, we propose to construct batches by grouping tuples which contain the same relations. The advantage of this novel strategy is two-fold. For one thing, it naturally reduces the original tuple-level computation to simple matrix-level arithmetic. For another and more importantly, we can then easily ensure that the embedding of each relation is only accessible by one single process. Such a training strategy completely avoids the data corruption issue. In addition, it makes the employment of the full batch learning technique (via relational matrices) possible, which offers a robust solution for parallelising the KGEs training process and hence can greatly enhance the training speed. To the best of our knowledge, this approach has never been explored by the KGE community.
As illustrated in Fig. 1, we first separate the embedding space into segments (cf. § 2.1) and arrange batches based on relations. After that, for each training step, the workflow of ProcrustEs is essentially decomposed into parallel optimisation processes, where is the number of relation types. Let and denote the indices of relation types and sub-spaces, respectively, then the column-wise concatenations of the th sub-vectors of all tuples of th relations can be symbolised as (for head entities) and (for tail entities). Similarly, denotes the corresponding relation embedding matrix in the th sub-space. The final objective function of ProcrustEs becomes
| (1) |
Orthogonal Procrustes Analysis.
Our key optimisation objective, as formulated in Eq. (1), is to minimise the Euclidean distance between the head and tail matrices for each parallel process. In addition, following Sun et al. (2019) and Tang et al. (2020), we restrict the relation embedding matrix to be orthogonal throughout model training, which has been shown effective in improving KGE quality. Previous KGE models use different approaches to impose orthogonality. For instance, RotatE (Sun et al., 2019) takes advantage of a corollary of Euler’s identity and defines its relation embedding as
| (2) |
which is controlled by a learnable parameter . Although Eq. (2) holds orthogonality and retains simplicity, it is essentially a special case of segmented embedding where equals 2. As a result, is always two-dimensional, which greatly limits the modelling capacity (see § 3.4 for discussion on the impact of dimensionality). To overcome this limitation, OTE (Tang et al., 2020) explicitly orthogonalises using the Gram-Schmidt algorithm per back-propagation step (see Appendix A for details). However, while this scheme works well for a wide range of (i.e., the dimension for the sub-vector), similar to RotatE, OTE finds a good model solution based on gradient descent, which is computationally very expensive.
We address the computational issue by proposing a highly efficient method utilising the proposed parallelism of full batch learning. With full batch learning, comparing with existing methods which deal with heterogeneous relations, ProcrustEs only needs to optimise one single in each process, which becomes a simple constrained matrix regression task. More importantly, through Singular Value Decomposition (SVD), we can derive an closed-form solution (Schönemann, 1966) as
| (3) |
where denotes the optima. During each iteration, ProcrustEs can directly find the globally optimal embedding for each relation given the current entity embeddings by applying Eq. (3). Then, based on the calculated , ProcrustEs updates entity embeddings through the back propagation mechanism (NB: the relation embeddings do not require gradients here). This process is repeated until convergence. As the optimisation of relation embeddings can be done almost instantly per iteration thanks to the closed-form Eq. (3), ProcrustEs is significantly (orders of magnitude) faster than RotatE and OTE. In addition, compared with entity embeddings of all other KGE models which are updated separately with relation embedding, entity embeddings trained by ProcrustEs can be used to restore relation embeddings directly (via Eq. (3)). In other words, ProcrustEs can encode richer information in the entity space than its counterparts (see § 3.5).
Further optimisation schemes.
As recently surveyed by Ruffinelli et al. (2020), existing KGE methods employ negative sampling as a standard technique for reducing training time, where update is performed only on a subset of parameters by calculating loss based on the generated negative samples. With our proposed closed-form solution (i.e., Eq. (3)), computing gradients to update embeddings is no longer an efficiency bottleneck for ProcrustEs. Instead, the speed bottleneck turns out to be the extra bandwidth being occupied due to the added negative samples. Therefore, for ProcrustEs, we do not employ negative sampling but rather update all embeddings during each round of back propagation with positive samples only, in order to further optimise the training speed (see Appendix B for bandwidth comparisons against baselines which adopts negative sampling).
We also discovered that if we do not apply any additional conditions during training, ProcrustEs tends to fall into a trivial optimum after several updates, i.e., , with all values in , and being zero. In other words, the model collapses with nothing encoded at all. This is somewhat unsurprising as such trivial optima often yields large gradient and leads to this behaviour (Zhou et al., 2019). To mitigate this degeneration issue, inspired by the geometric meaning of orthogonal (i.e., to rotate towards around the coordinate origin, without changing vector length), we propose to constrain all entities to a high-dimensional hypersphere by performing two spherisation steps in every epoch. The first technique, namely centring, respectively translates and so that the column-wise sum of each matrix becomes a zero vector (note that each row denotes a sub-vector of an entity). The second operation is length normalisation, which ensures the row-wise Euclidean norm of and to always be one. Employing these two simple constraints effectively alleviates the trivial optimum issue, as evidenced in our experiments (see § 3).
3 Experiment
3.1 Setups
We assess the performance of ProcrustEs on the task of multi-relational link prediction, which is the de facto standard of KGE evaluation.
| FB15k-237 | WN18RR | |
|---|---|---|
| Entities | 14,541 | 40,943 |
| Relations | 237 | 11 |
| Train samples | 272,115 | 86,835 |
| Validate samples | 17,535 | 3,034 |
| Test samples | 20,466 | 3,134 |
| WN18RR | FB15k-237 | |||||||||||
| MRR | H1 | H3 | H10 |
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/time.png) ○ ○
|
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/CO2.png) ○ ○
|
MRR | H1 | H3 | H10 |
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/time.png) ○ ○
|
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/CO2.png) ○ ○
|
|
| TransE (2013) | .226 | - | - | .501 | 85 | 367 | .294 | - | - | .465 | 96 | 370 |
| DistMult (2015) | .430 | .390 | .440 | .490 | 79 | 309 | .241 | .155 | .263 | .419 | 91 | 350 |
| ComplEx (2016) | .440 | .410 | .460 | .510 | 130 | 493 | .247 | .158 | .275 | .428 | 121 | 534 |
| R-GCN (2018) | .417 | .387 | .442 | .476 | 138 | 572 | .248 | .151 | .264 | .417 | 152 | 598 |
| ConvE (2018) | .430 | .400 | .440 | .520 | 840 | 3702 | .325 | .237 | .356 | .501 | 1007 | 4053 |
| A2N (2019) | .450 | .420 | .460 | .510 | 203 | 758 | .317 | .232 | .348 | .486 | 229 | 751 |
| SACN (2019) | .470 | .430 | .480 | .540 | 1539 | 5342 | .352 | .261 | .385 | .536 | 1128 | 4589 |
| TuckER (2019) | .470 | .443 | .482 | .526 | 173 | 686 | .358 | .266 | .392 | .544 | 184 | 704 |
| QuatE (2019) | .488 | .438 | .508 | .582 | 176 | 880 | .348 | .248 | .382 | .550 | 180 | 945 |
| InteractE (2020) | .463 | .430 | - | .528 | 254 | 1152 | .354 | .263 | - | .535 | 267 | 1173 |
| RotH (2020) | .496 | .449 | .514 | .586 | 192 | 903 | .344 | .246 | .380 | .535 | 207 | 1120 |
| \hdashlineRotatE (2019) | .439 | .390 | .456 | .527 | 255 | 823 | .297 | .205 | .328 | .480 | 343 | 1006 |
| OTE (2020) | .448 | .402 | .465 | .531 | 304 | 1008 | .309 | .213 | .337 | .483 | 320 | 1144 |
| ProcrustEs (ours) | .453 | .408 | .491 | .549 | 14 | 37 | .295 | .241 | .310 | .433 | 9 | 42 |
| \hdashlinew/ NS (ours) | .457 | .411 | .494 | .551 | 44 | 124 | .302 | .245 | .333 | .465 | 37 | 159 |
| w/ TB (ours) | .468 | .417 | .498 | .557 | 92 | 268 | .326 | .247 | .354 | .492 | 56 | 243 |
| w/ NS+TB (ours) | .474 | .421 | .502 | .569 | 131 | 346 | .345 | .249 | .379 | .541 | 85 | 285 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/time.png) ○: training time (minutes); \scalerel*
○: training time (minutes); \scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/CO2.png) ○: carbon dioxide production (grams). NS: negative sampling; TB: traditional batch. The performance results of baselines are coloured heavily and lightly if they are below those of ProcrustEs and “w/ NS+TB”, respectively.
State-of-the-art scores are in bold.
Following Balazevic et al. (2019) and Zhang et al. (2019), for fair comparison, both RotatE and OTE results are reported with conventional negative sampling rather than the self-adversarial one.
○: carbon dioxide production (grams). NS: negative sampling; TB: traditional batch. The performance results of baselines are coloured heavily and lightly if they are below those of ProcrustEs and “w/ NS+TB”, respectively.
State-of-the-art scores are in bold.
Following Balazevic et al. (2019) and Zhang et al. (2019), for fair comparison, both RotatE and OTE results are reported with conventional negative sampling rather than the self-adversarial one.
Datasets.
In this study, following previous works (e.g., baselines in Tab. 2), we employ two benchmark datasets for link prediction: (1) FB15K-237 (Toutanova and Chen, 2015), which consists of sub-graphs extracted from Freebase, and contains no inverse relations; and (2) WN18RR (Dettmers et al., 2018), which is extracted from WordNet. Tab. 1 shows descriptive statistics for these two datasets, indicating that FB15K-237 is larger in size and has more types relations while WN18RR has more entities. We use the same training, validating, and testing splits as past studies.
Evaluation metrics.
Baselines.
We compare ProcrustEs to not only classical neural graph embedding methods, including TransE (Bordes et al., 2013), DistMulti (Yang et al., 2015), and ComplEx (Trouillon et al., 2016), but also embedding techniques recently reporting state-of-the-art performance on either WN18RR or FB15k-237, including R-GCN (Schlichtkrull et al., 2018), ConvE (Dettmers et al., 2018), A2N (Bansal et al., 2019), RotatE (Sun et al., 2019), SACN (Shang et al., 2019), TuckER (Balazevic et al., 2019), QuatE (Zhang et al., 2019), InteractE (Vashishth et al., 2020), OTE (Tang et al., 2020), and RotH (Chami et al., 2020). For all these baselines, we use the official code and published hyper-parameters to facilitate reproducibility.
Implementation details.
All experiments are conducted on a workstation with one NVIDIA GTX 1080 Ti GPU and one Intel Core i9-9900K CPU, which is widely applicable to moderate industrial/academic environments. We use the Experiment Impact Tracker (Henderson et al., 2020) to benchmark the time and carbon footprint of training. To reduce measurement error, in each setup we fix the random seeds, run ProcrustEs and all baselines for three times and reported the average.
The key hyper-parameters of our model is and , which are respectively set at 2K and 20 for both datasets. The detailed selection process is described in § 3.4. We train each model for a maximum of 2K epochs and check if the validation MRR stops increasing every 100 epochs after 100 epochs. For WN18RR and FB15k-237 respectively, we report the best hyperparameters as fixed learning rates of 0.001 and 0.05 (Adam optimiser), and stopping epochs of 1K and 200.
3.2 Main Results

Tab. 2 reports the results of both our ProcrustEs and all other 13 baselines on both WN18RR and FB15k-237 datasets. We analyse these results from two dimensions: (1) Effectiveness: the model performance on link prediction task (MRR is our main indicator); (2) Efficiency: system training time and carbon footprint (i.e., emissions).
Regarding the performance on WN18RR, we found that ProcrustEs performs as good as or even better than previous state-of-the-art approaches. To be concrete, out of all 13 baselines, it beats 11 in H10, (at least) 9 in H3 and 8 in MRR. The models outperformed by ProcrustEs include not only all methods prior to 2019, but also several approaches published in 2019 or even 2020. Notably, when compared with the RotatE and OTE, two highly competitive methods which have similar architectures to ProcrustEs (i.e., with segmented embeddings and orthogonal constraints), our ProcrustEs can learn KGEs with higher quality (i.e., 0.014 and 0.005 higher in MRR, respectively). This evidences the effectiveness of the proposed approaches in § 2 in modelling knowledge tuples.
While ProcrustEs achieves very competitive performance, it requires significantly less time for training: it converges in merely 14 minutes, more than 100 times faster than strong-performing counterparts such as SACN. Moreover, it is very environmentally friendly: from bootstrapping to convergence, ProcrustEs only emits 37g of , which is even less than making two cups of coffee111https://tinyurl.com/coffee-co2. On the contrary, the baselines emit on average 1469g and up to 5342g : the latter is even roughly equal to the carbon footprint of a coach ride from Los Angeles to San Diego222https://tinyurl.com/GHG-report-2019.
As for the testing results on FB15k-237, we found that although ProcrustEs seems less outstanding (we investigate the reasons in § 3.3), it still outperforms at least 7 more complex baselines in H1 and almost all models prior to 2019 in MRR. Furthermore, similar to the observation on WN18RR, it demonstrates great advantage in terms of efficiency. While all baselines need 91 to 1128 minutes to coverage with 350g to 4589g produced, ProcrustEs can learn embeddings of similar quality in just 9 minutes and with 42g emissions. By employing both traditional batch and negative sampling, we show that ProcrustEs can achieve near-state-of-the-art performance on both datasets. We discuss this in detail in § 3.3.
To provide a unified comparisons between ProcrustEs and the most strong-performing baselines on both effectiveness and efficiency, we further investigate the following question: How much performance gain can we obtain by spending unit time on training or making unit emissions? We did analysis by calculating MRR/(training time) and MRR/(carbon footprint) and the results are presented in Fig. 2. It is obvious that among all competitive KGE models, ProcrustEs is the most economic algorithm in terms of performance-cost trade-off: it is more than 20 times more efficient than any past works, in terms of both performance per unit training time and per unit emissions.
We also investigate baseline performance with a shorter training schedule. From scratch, we train RotH, the best performing algorithm on WN18RR, and stop the experiment when MRR reaches the performance of ProcrustEs. On WN18RR, RotH takes 50 minutes (3.6 ProcrustEs) and emits 211g (5.7 ProcrustEs); on FB15k-237 RotH takes 45 minutes (5.0 ProcrustEs) and emits 218g (5.2 ProcrustEs). These results once again highlight the efficiency superiority of our approach.
3.3 Ablation Studies
To better understand the performance difference of ProcrustEs on WN18RR and FB15k-237, we dive deeply into the dataset statistics in Tab. 1. Goyal et al. (2017) and Hoffer et al. (2017) found that although full batch learning can boost training speed and may benefit performance, when the data distribution is too sparse, it may be trapped into sharp minimum. As the average number of samples linked to each relation is significantly smaller for FB15k-237 than for WN18RR (1148 vs 7894), the distribution of the former is likely to be more sparse and the generalisability of ProcrustEs may thus be harmed. For another, FB15k-237 has finer-grained relation types (237 vs. 11 of WN18RR), so intuitively the likelihood of tuples sharing similar relations rises. However, as ProcrustEs omits negative sampling to trade for speed, sometimes it maybe be less discriminative for look-alike tuples.
To validate the above hypotheses, we additionally conduct ablation studies by switching back to traditional batch mode and/or adding negative sampling modules333Following Sun et al. (2019), we set the batch size at 1024 and the negative sample size at 128.. Configurations where the closed-form optimisation, Eq. (3), is replaced by gradient descent are omitted since the resulting architecture is very similar to OTE. As shown in the lower section of Tab. 2, both using either traditional or negative sampling (i.e., w/ NS and w/ TB) can improve the performance of ProcrustEs for all metrics. For example, on WN18RR our approach (w/ NS+TB) outperforms most baselines and is close to the performance of QuatE and RotH, but thanks to the Orthogonal Procrustes Analysis, the computational cost of our approach is significantly less. Compared to WN18RR, the gain of our model on FB15k-237 by adopting negative sampling and traditional batch is even more significant, achieving near-state-of-the-art performance (i.e., compared to TuckER, the MRR is only 1.3% less with merely 4.9% of the computational time). These observations verify our aforementioned hypotheses. We also found out that traditional batch is more effective than negative sampling for ProcrustEs in terms of improving model performance. On the other hand, however, adding these two techniques can reduce the original efficiency of ProcrustEs to some extend.
Nevertheless, as Eq. (3) is not only fast but also energy-saving (as only basic matrix arithmetic on GPUs is involved), even ProcrustEs with the “w/ NS+TB” configuration preserves great advantage in training time and carbon footprint. Moreover, it achieves near-state-of-the-art effectiveness on both datasets (cf. Tab. 2) and still exceeds strong baselines in training efficiency with large margins (cf. Fig. 2). One interesting observation is that, while the training time of RotH is merely 1.47 of that of ProcrustEs (w/ NS+TB), their emission levels are drastically different. This is because RotH implements 24-thread multiprocessing by default while our approach creates only one process. Within similar training time, methods like RotH will thus consume a lot more power and emit a lot more . Therefore, for effectiveness-intensive applications, we recommend training ProcrustEs in transitional batches with negative sampling, as it can then yield cutting-edge performance without losing its eco-friendly fashion.
3.4 Impacts of Dimensionality
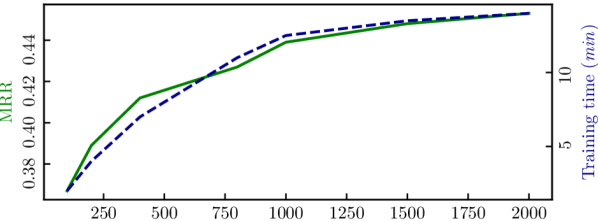
Our experiments also indicate that the selection of two dimensional hyper-parameters has substantial influence on both effectiveness and efficiency of ProcrustEs. For the dimension of the entire embedding space, we follow the recommendation of Tang et al. (2020) and set at 20. We then train ProcrustEs with and plotted results based on the validation set, as shown in Fig. 3. It is evident that with the increase of , the model performance (indicated by MRR) grows but the training time also rises. Observing the curvature of training time almost saturates when 1K, we decide 2K as the best setting for both WN18RR and FB15k-237 given the 11GB graphics memory limit of our hardware. For the dimension of sub-embeddings, we fix at 2K and enumerated . For algorithm performance, the pattern we witnessed is on par with that reported by Tang et al. (2020), i.e., before reaches 20 or 25 the effectiveness jumps rapidly, but after that the model slowly degrades, as the learning capacity of the network reduces. Coincidentally, the training speed also climbs its peak when is 20, making it indisputably become our optimal choice.


| A1 | chittagong, cartagena, pittsburghofthesouth, lehavre, nanning, stuttgart, kolkata, houston, windycity, |
| A2 | yellowstoneriver, atlasmountains, sanfernandovalley, sambreriver, nileriver, susquehannariver, rhineriver, |
| A3 | sudan, balkanshealps, eastmalaysia, loweregypt, kalimantan, turkistan, tobago, lowlandsofscotland, sicily, |
| B1 | mefoxin, metharbita, valium, amobarbital, procaine, nitrostat, tenormin, minortranquillizer, cancerdrug, |
| B2 | epinephrine, steroidhormone, internalsecretion, alkaloid, gallamine, prolactin, luteinizinghormone, |
| C1 | militaryformation, retreat, tactics, strategicwarning, peacekeepingoperation, unauthorizedabsence, |
| C2 | commando, sailorboy, outpost, saddam’smartyrs, militaryadvisor, battlewagon, commander, |
| D | plaintiff, remitment, franchise, summons, falsepretens, suspect, amnesty, legalprinciple, disclaimer, affidavit, |
| E | genusambrosia, gloxinia, saintpaulia, genuscestrum, genuseriophyllum, valerianella, genuschrysopsis, |
| F | moneyer, teacher, researcher, president, primeminister, wheelerdealer, houseservant, victualler, burglar, |
3.5 Interpreting Entity Embeddings
Building on the fact that ProcrustEs marry entity information and relation information (in other words, for a specific entity, the information of the entity itself and of its corresponding relations is encoded in a single vector), the location of a entity is more expressive and, thus, the related entity embedding is more interpretable. Picking up on that, we do visualisation study on the trained entity embeddings. To this end, we conduct dimension reduction on the embeddings using Principal Components Analysis (PCA), which reduces the dimensionality of an entity embedding from 2K to three444We disable axes and grids for visualisation’s clarity. Please see the original figure in Appendix C.. Fig. 3 shows the visualisation result, from which we see a diagram with 6 “arms”. This is far distinct from the distributional topology of conventional semantic representations, e.g., word embeddings (Mikolov et al., 2013) (see Appendix C).
In Fig. 3, we also list the representative entities that fall in some clusters on each arm. Each cluster is referred by an ID (from A1 to F2). When we zoom into this list, we observe something interesting: First, entities on the same arm are semantically similar, or, in other words, these entities belong to the same category. Concretely, entities on arm A are locations, those on arm B are biochemical terms, and those on arm C are military related entities. Entities on arm D, E, and F consists of entities refer to concepts of law, botany, and occupation, respectively. Second, significant differences exist between each cluster/position on a arm. One example is that, for arm A, A1 are entities for cities, such as Stuttgart, Houston, Nanning; A2 is about entities for rivers, mountains, etc.; and A3 contains entities referring to countries or regions. Similarly, while B1 mainly consists of medicine names, entities in B2 obviously relate to chemical terms. Last, ProcrustEs can also put the “nick name” of a entity into the correct corresponding cluster. For example, Windy City (i.e., Chicago) and Pittsburgh of the South (i.e, Birmingham) were successfully recognised as names for cities.
4 Related Work
KGE techniques.
In recent years, a growing body of studies has been conducted on the matter of training KGEs. Roughly speaking, these KGE methods fall into two categories: distance-based models and semantic matching models.
The line of researches regarding distance-based models, which measures plausibility of tuples by calculating distance between entities with additive functions, was initialised the KGE technique proposed by Bordes et al. (2013), namely, TransE. After that, a battery of follow-ups have been proposed, including example models like TransH (Wang et al., 2014), TransR (Lin et al., 2015), and TransD (Ji et al., 2015). These algorithms have enhanced ability on modelling complex relations by means of projecting entities into different (more complex) spaces or hyper-planes. More recently, a number of studies attempt to further boost the quality of KGEs through a way of adding orthogonality constraints (Sun et al., 2019; Tang et al., 2020) for maintaining the relation embedding matrix being orthogonal, which is also the paradigm we follow in the present paper (see § 2).
In contrast, semantic matching models measure the plausibility of tuples by computing the similarities between entities with multiplicative functions. Such an similarity function could be realised using, for example, a bilinear function or a neural network. Typical models in this line includes DistMult (Yang et al., 2015), ComplEx (Trouillon et al., 2016), ConvE (Dettmers et al., 2018), TuckER (Balazevic et al., 2019), and QuatE (Zhang et al., 2019).
Accelerating KGE training.
All those KGE approaches share the same issue of their low speed in both training and inference phases (see Rossi et al. (2020) for a controlled comparison of the efficiency across different methodologies). In response to this issue, some state-of-the-art KGE algorithms attempted to accelerate their inference speed either through making use of the high-speed of the convolutional neural networks (Dettmers et al., 2018) or through reducing the scale of parameters of the model (Zhang et al., 2019; Zhu et al., 2020).
As for the acceleration of model training, a number of attempts have been conducted in a mostly engineering way. These well-engineered systems adopt linear KGE methods to multi-thread versions in other to make full use of the hardware capacity (Joulin et al., 2017; Han et al., 2018), which accelerates training time of, for example, TransE, from more than an hour to only a couple of minutes. Nonetheless, this line of work has two major issues: one is that training models faster in this way does not necessarily mean they also emit less, as process scheduling of a multi-thread system can be energy-consuming. The other is that they are all extensions of linear KGE models only (also noting that linear models are naturally much faster than other non-linear models) without any algorithmic contribution, which leading to the performance of the resulting models limited by the upper bound of linear models (e.g., recent state-of-the-art methods in Tab. 2, such as RotH, are nonlinear approaches).
5 Conclusion
In this paper, we proposed a novel KGE training framework, namely ProcrustEs, which is eco-friendly, time-efficient and can yield very competitive or even near-state-of-the-art performance. Extensive experiments show that our method is valuable especially considering its significant and substantial reduction on training time and carbon footprint.
Broader Impact
We provided a efficient KGE training framework in this paper. The resulting KGEs, akin to all previous KGE models, might have been encoded with social biases, e.g., the gender bias (Fisher, 2019). We suggest this problem should always be looked at critically. For whoever tend to build their applications grounding on our KGEs, taking care of any consequences caused by the gender bias is vital since, in light of the discussion in Larson (2017), mis-gendering individuals/entities is harmful to users Keyes (2018). Additionally, as having been proven in this paper, our method emits less greenhouse gases and therefore, has less negative environmental repercussions than any other KGE approaches.
Acknowledgements
This work is supported by the award made by the UK Engineering and Physical Sciences Research Council (Grant number: EP/P011829/1) and Baidu, Inc. We would also like to express our sincerest gratitude to Chen Li, Ruizhe Li, Xiao Li, Shun Wang, and the anonymous reviewers for their insightful and helpful comments.
References
- Balazevic et al. (2019) Ivana Balazevic, Carl Allen, and Timothy Hospedales. 2019. TuckER: Tensor factorization for knowledge graph completion. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 5185–5194, Hong Kong, China. Association for Computational Linguistics.
- Bansal et al. (2019) Trapit Bansal, Da-Cheng Juan, Sujith Ravi, and Andrew McCallum. 2019. A2N: Attending to neighbors for knowledge graph inference. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 4387–4392, Florence, Italy. Association for Computational Linguistics.
- Bordes et al. (2013) Antoine Bordes, Nicolas Usunier, Alberto García-Durán, Jason Weston, and Oksana Yakhnenko. 2013. Translating embeddings for modeling multi-relational data. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, pages 2787–2795.
- Brown et al. (2020) Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel Ziegler, Jeffrey Wu, Clemens Winter, Chris Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. 2020. Language models are few-shot learners. In Advances in Neural Information Processing Systems, volume 33, pages 1877–1901. Curran Associates, Inc.
- Chami et al. (2020) Ines Chami, Adva Wolf, Da-Cheng Juan, Frederic Sala, Sujith Ravi, and Christopher Ré. 2020. Low-dimensional hyperbolic knowledge graph embeddings. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 6901–6914, Online. Association for Computational Linguistics.
- Dettmers et al. (2018) Tim Dettmers, Pasquale Minervini, Pontus Stenetorp, and Sebastian Riedel. 2018. Convolutional 2d knowledge graph embeddings. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, Louisiana, USA, February 2-7, 2018, pages 1811–1818. AAAI Press.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Computational Linguistics.
- Dong et al. (2014) Xin Dong, Evgeniy Gabrilovich, Geremy Heitz, Wilko Horn, Ni Lao, Kevin Murphy, Thomas Strohmann, Shaohua Sun, and Wei Zhang. 2014. Knowledge vault: a web-scale approach to probabilistic knowledge fusion. In The 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’14, New York, NY, USA - August 24 - 27, 2014, pages 601–610. ACM.
- Fisher (2019) Joseph Fisher. 2019. Measuring social bias in knowledge graph embeddings. arXiv preprint arXiv:1912.02761.
- Goyal et al. (2017) Priya Goyal, Piotr Dollár, Ross Girshick, Pieter Noordhuis, Lukasz Wesolowski, Aapo Kyrola, Andrew Tulloch, Yangqing Jia, and Kaiming He. 2017. Accurate, large minibatch sgd: Training imagenet in 1 hour. In International Conference on Learning Representations.
- Guo et al. (2020) Qingyu Guo, Fuzhen Zhuang, Chuan Qin, Hengshu Zhu, Xing Xie, Hui Xiong, and Qing He. 2020. A survey on knowledge graph-based recommender systems. arXiv preprint arXiv:2003.00911.
- Han et al. (2018) Xu Han, Shulin Cao, Xin Lv, Yankai Lin, Zhiyuan Liu, Maosong Sun, and Juanzi Li. 2018. OpenKE: An open toolkit for knowledge embedding. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, pages 139–144, Brussels, Belgium. Association for Computational Linguistics.
- He et al. (2017) He He, Anusha Balakrishnan, Mihail Eric, and Percy Liang. 2017. Learning symmetric collaborative dialogue agents with dynamic knowledge graph embeddings. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1766–1776, Vancouver, Canada. Association for Computational Linguistics.
- Henderson et al. (2020) Peter Henderson, Jieru Hu, Joshua Romoff, Emma Brunskill, Dan Jurafsky, and Joelle Pineau. 2020. Towards the systematic reporting of the energy and carbon footprints of machine learning.
- Hoffer et al. (2017) Elad Hoffer, Itay Hubara, and Daniel Soudry. 2017. Train longer, generalize better: closing the generalization gap in large batch training of neural networks. In Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 1731–1741.
- Ji et al. (2015) Guoliang Ji, Shizhu He, Liheng Xu, Kang Liu, and Jun Zhao. 2015. Knowledge graph embedding via dynamic mapping matrix. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 687–696, Beijing, China. Association for Computational Linguistics.
- Joulin et al. (2017) Armand Joulin, Edouard Grave, Piotr Bojanowski, Maximilian Nickel, and Tomas Mikolov. 2017. Fast linear model for knowledge graph embeddings. arXiv preprint arXiv:1710.10881.
- Keyes (2018) Os Keyes. 2018. The misgendering machines: Trans/hci implications of automatic gender recognition. Proc. ACM Hum.-Comput. Interact., 2.
- Larson (2017) Brian Larson. 2017. Gender as a variable in natural-language processing: Ethical considerations. In Proceedings of the First ACL Workshop on Ethics in Natural Language Processing, pages 1–11, Valencia, Spain. Association for Computational Linguistics.
- Lin et al. (2015) Yankai Lin, Zhiyuan Liu, Maosong Sun, Yang Liu, and Xuan Zhu. 2015. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, January 25-30, 2015, Austin, Texas, USA, pages 2181–2187. AAAI Press.
- Mikolov et al. (2013) Tomás Mikolov, Ilya Sutskever, Kai Chen, Gregory S. Corrado, and Jeffrey Dean. 2013. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, pages 3111–3119.
- Rossi et al. (2020) Andrea Rossi, Donatella Firmani, Antonio Matinata, Paolo Merialdo, and Denilson Barbosa. 2020. Knowledge graph embedding for link prediction: A comparative analysis. arXiv preprint arXiv:2002.00819.
- Ruffinelli et al. (2020) Daniel Ruffinelli, Samuel Broscheit, and Rainer Gemulla. 2020. You CAN teach an old dog new tricks! on training knowledge graph embeddings. In 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020. OpenReview.net.
- Sanh et al. (2019) Victor Sanh, Lysandre Debut, Julien Chaumond, and Thomas Wolf. 2019. Distilbert, a distilled version of bert: smaller, faster, cheaper and lighter. arXiv preprint arXiv:1910.01108.
- Saxena et al. (2020) Apoorv Saxena, Aditay Tripathi, and Partha Talukdar. 2020. Improving multi-hop question answering over knowledge graphs using knowledge base embeddings. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 4498–4507, Online. Association for Computational Linguistics.
- Schlichtkrull et al. (2018) Michael Schlichtkrull, Thomas N Kipf, Peter Bloem, Rianne Van Den Berg, Ivan Titov, and Max Welling. 2018. Modeling relational data with graph convolutional networks. In European Semantic Web Conference. Springer.
- Schönemann (1966) Peter Schönemann. 1966. A generalized solution of the orthogonal procrustes problem. Psychometrika.
- Shang et al. (2019) Chao Shang, Yun Tang, Jing Huang, Jinbo Bi, Xiaodong He, and Bowen Zhou. 2019. End-to-end structure-aware convolutional networks for knowledge base completion. In The Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, Hawaii, USA, January 27 - February 1, 2019, pages 3060–3067. AAAI Press.
- Strubell et al. (2019) Emma Strubell, Ananya Ganesh, and Andrew McCallum. 2019. Energy and policy considerations for deep learning in NLP. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3645–3650, Florence, Italy. Association for Computational Linguistics.
- Sun et al. (2019) Zhiqing Sun, Zhi-Hong Deng, Jian-Yun Nie, and Jian Tang. 2019. Rotate: Knowledge graph embedding by relational rotation in complex space. In 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, May 6-9, 2019. OpenReview.net.
- Tang et al. (2020) Yun Tang, Jing Huang, Guangtao Wang, Xiaodong He, and Bowen Zhou. 2020. Orthogonal relation transforms with graph context modeling for knowledge graph embedding. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 2713–2722, Online. Association for Computational Linguistics.
- Toutanova and Chen (2015) Kristina Toutanova and Danqi Chen. 2015. Observed versus latent features for knowledge base and text inference. In Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality, pages 57–66, Beijing, China. Association for Computational Linguistics.
- Trouillon et al. (2016) Théo Trouillon, Johannes Welbl, Sebastian Riedel, Éric Gaussier, and Guillaume Bouchard. 2016. Complex embeddings for simple link prediction. In Proceedings of the 33nd International Conference on Machine Learning, ICML 2016, New York City, NY, USA, June 19-24, 2016, volume 48 of JMLR Workshop and Conference Proceedings, pages 2071–2080. JMLR.org.
- Vashishth et al. (2020) Shikhar Vashishth, Soumya Sanyal, Vikram Nitin, Nilesh Agrawal, and Partha Talukdar. 2020. Interacte: Improving convolution-based knowledge graph embeddings by increasing feature interactions. In Proceedings of the AAAI Conference on Artificial Intelligence.
- Wang et al. (2014) Zhen Wang, Jianwen Zhang, Jianlin Feng, and Zheng Chen. 2014. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, July 27 -31, 2014, Québec City, Québec, Canada, pages 1112–1119. AAAI Press.
- Xu et al. (2020) Wentao Xu, Shun Zheng, Liang He, Bin Shao, Jian Yin, and Tie-Yan Liu. 2020. SEEK: Segmented embedding of knowledge graphs. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 3888–3897, Online. Association for Computational Linguistics.
- Yang et al. (2015) Bishan Yang, Wen-tau Yih, Xiaodong He, Jianfeng Gao, and Li Deng. 2015. Embedding entities and relations for learning and inference in knowledge bases. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings.
- Zhang et al. (2019) Shuai Zhang, Yi Tay, Lina Yao, and Qi Liu. 2019. Quaternion knowledge graph embeddings. In Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 2731–2741.
- Zhou et al. (2019) Mo Zhou, Tianyi Liu, Yan Li, Dachao Lin, Enlu Zhou, and Tuo Zhao. 2019. Toward understanding the importance of noise in training neural networks. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA, volume 97 of Proceedings of Machine Learning Research, pages 7594–7602. PMLR.
- Zhu et al. (2020) Yushan Zhu, Wen Zhang, Hui Chen, Xu Cheng, Wei Zhang, and Huajun Chen. 2020. Distile: Distiling knowledge graph embeddings for faster and cheaper reasoning. arXiv preprint arXiv:2009.05912.
Appendix A Gram-Schmidt Process of Tang et al. (2020)
The Gram-Schmidt process takes a set of tensor for and generates an orthogonal set that spans the same dimensional subspace of as , such that
| (A.1) |
where and denotes the inner product of and . Its complexity is and the parallelisation is not trivial.
Appendix B Bandwidth Comparison
To further ascertain the efficiency advantage of ProcrustEs by ruling out factors such as numbers of all epochs, we pick four frameworks with strongest MRR performance and estimate their bandwidth during training, as illustrated in Fig. B.1.

We can see that although some baselines have been engineered for enhanced computational efficiency, e.g., by default RotH creates 24 threads for multiprocessing, on both datasets they still substantially underperform ProcrustEs with huge margins in terms of bandwidth.
Appendix C Visualisation Comparisons


![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/water.png) ○ Guanyi Chen
○ Guanyi Chen![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/2b65b8ce-a584-47fe-9878-55977d5ae04c/leaf.png) ○ Chenghua Lin
○ Chenghua Lin