Holographic cold dense matter constrained by neutron stars
Abstract
The equation of state (EoS) for cold dense matter inside neutron stars is investigated by using holographic QCD models in the framework of the Einstein-Maxwell-dilaton (EMD) system and the improved Karch-Katz-Son-Stephanov (KKSS) action for matter part. This method of describing holographic nuclear matter in the EMDKKSS framework is different from that by using the Dirac-Born-Infeld (DBI) action and the Chern-Simons (CS) terms. Combining with the Hebeler-Lattimer-Pethick-Schwenk (HLPS) intermediate equation of state (EoS), the hybrid EoS inside the neutron stars is constructed. The obtained hybrid EoS is located in the range that is defined by the low-density chiral effective theory, the high-density perturbative QCD, and the polytropic interpolations between them, and is constrained by the astrophysics observations. The square of the sound velocity reaches a maximum value larger than in the region of times the saturation baryon number density and approaches the conformal limit at the high baryon density range. The mass-radius relation and the tidal deformability of the neutron stars are in agreement with astrophysical measurements. The possible maximum mass for the neutron star is about and the radius is about then. It is noticed that the holographic quark matter branch in the mass-radius relation is always unstable and the holographic nuclear matter can produce a stable branch. These results indicate that even in the core of the NS, the matter is still in the confinement phase and the quark matter is not favored.
I Introduction
Quantum chromodynamics (QCD) is believed to be the basic theory of the strong interaction. However, the strong interaction is non-perturbative at low energy scale. Thus many phenomena such as hadron and glueball spectra, chiral phase transition and confinement-deconfinement phase transition, the equation of state (EoS) of the strong interaction matter under extreme conditions (high temperature, high baryon number density, rapid rotation, and strong magnetic field) can’t be explained from the first principle until now. Therefore many efforts have been paid on developing non-perturbative methods, such as lattice QCD [1, 2, 3], chiral effective theory [4], Nambu–Jona-Lasinio (NJL) model [5, 6], QCD sum rule [7, 8, 9, 10, 11, 12, 13, 14], Dyson Schwinger equations (DSE) and functional renormalization group (FRG) [15], and recently holographic QCD method [16, 17, 18, 19, 20, 21, 22, 23, 24].
Exploring the equation of state (EoS) and phase structure of quantum chromodynamics (QCD) at high density is boosted both by neutron star (NS) and heavy ion collisions. Relativistic heavy ion collision (RHIC) can produce the quark-gluon plasma (QGP) with high temperature and/or high baryon number density, and strong magnetic field. Besides that, the QGP with rapid rotation can also be produced in non-central heavy ion collisions. That is the most extreme environment created in the laboratory. It has been theoretically predicted that there exists a critical end point (CEP) for QCD at finite baryon density. The search of the CEP has been one of the most important targets for the beam energy scan program at RHIC as well as for the future accelerator facilities at Facility for Antiproton and Ion Research (FAIR) in Darmstadt and Nuclotron-based Ion Collider Facility (NICA) in Dubna.
In the nature, the early universe and the compact stars are also in extreme conditions. All these provide good platforms to investigate the non-perturbative features of strong interaction and the properties of the QCD matter.
The neutron star (NS) is a kind of compact star, which is the remnant after a massive super-giant star collapses. From August 1967 on, when the existence of NSs was confirmed by the discovery of radio pulsars, more than 2700 radio pulsars have been detected. It has been wondered for more than a half-century what’s the internal structure of NSs. Whether quark matter exists inside the core of NSs [25, 26]? Is there any exotic matter in NSs? Do strange stars exist? We can’t answer these questions yet. There are just a few of the open questions [27]. The strong interaction matter in the core of the NS is extremely dense, the baryon number density of which can reach as high as , where is the nuclear saturation density. Although the surface of the NS is hot and the temperature can reach several hundred thousand Kelvin [28, 29], compared with the QCD energy scale this temperature is still very low and can be neglected. Thus we can regard the matter in the NS as cold dense QCD matter.
On the experimental side, there are some observations of the NSs, including the mass measurements through the general relativistic Shapiro delay [30] and other methods [31, 32, 33, 34, 35, 36], the mass and radius measurements through the detection of thermal emission from the surface of the stars [37, 38, 39, 40], and the radius, EoS, and tidal deformability measurements through the gravitational wave signals of the binary systems [41, 42]. We will discuss these observations in detail in Sec. II.
Recent developments in the field of observational astronomy, e.g. the currently operating satellites, the Neutron star Interior Composition Explorer (NICER), and the gravitational-wave laser interferometers (Advanced LIGO, Virgo, and KAGRA) have provided tight constraints on neutron star masses and radii, which in turn, put strict constraints on the equation of state of dense matter.
The difficulties to predict the cold QCD matter from the theoretical side come from the awkward energy scale of the QCD matter in NS : the baryon number density in the neutron star is high so that exceeds the appropriate range where the traditional nuclear physics theories validate; however it is still not high enough to adapt the perturbative method.
Although it’s very hard to directly study the EoS of cold dense QCD matter inside the NSs, we can still derive some useful information when we combine the results of the traditional nuclear theories in the low energy scale and the results of the perturbative QCD at the high energy scale with the observation data. Under the constraints from the observation data, there are two approaches to derive the allowed range of the EoS for the cold QCD matter in the whole range of : the “direct interpolation approach” [43, 44] and the “causality and thermodynamic stability constraint approach” [45, 46]. In the former approach, combining the observation data, a generic family of neutron-star-matter EoSs, which interpolate between theoretical results at low and high baryon density, are obtained. In the latter one, utilizing the thermodynamic stability and causality, it is found that - calculations in QCD at high densities, as complementary to the astrophysical observations, provide significant and nontrivial information about the EoS of matter in the cores of the neutron star.
To directly calculate the NS interior composition, from the theoretical side, normally Nambu-Jona-Lasinio (NJL) model [47, 48, 49, 50, 51, 52, 53] has been used for quark matter. The holographic QCD model [54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69] has been developed at finite baryon density over recent years.
There are many efforts to describe the EoS of cold dense matter inside the neutron star in the holographic frame. The main approach is to use the background action in the holographic models to describe the holographic quark matter. Then the phase equilibrium conditions can be used to connect the EoS of the holographic quark matter and the EoS calculated in effective theories adapted at low energy scale. This kind of hybrid EoSs can describe the NSs. However, the problem is that the branch that corresponds to the holographic quark matter in the mass-radius relation is unstable according to the Bardeen-Thorne-Meltzer (BTM) stable criterion stated in Refs. [70, 71]. The BTM stable criterion is stated in the following. As one moves along the - curve, where is the mass of the NS as one observes from outside and is its radius, to make sure the value of the internal energy density at the center of the star increases, all configurations remain stable until one reach the first extreme value (maximum or minimum) of . The fundamental mode of radial oscillation becomes unstable at the first extreme value point. Between the first extreme value point and the second one, all configurations contain one unstable radial mode. At the second extreme value point, and also at each succeeding extreme value point, the stability of one more mode of radial oscillation changes. How the - curve bends as it passes through the extreme value point determines how the stability changes. One previously stable radial mode becomes unstable at the critical point if the direction of the bend is counter-clockwise (with increasing ). One previously unstable mode becomes stable at the critical point if the direction of the bend is clockwise.
The key point to produce the stable branch in the holographic method is to consider the holographic nuclear matter. In Refs. [72, 60, 61, 62, 63, 64, 65, 66], the Dirac-Born-Infeld (DBI) action and the Chern-Simons (CS) terms has been used to describe the baryons, where the solitons are regarded as baryons. The authors in Refs. [60, 61, 62] used the V-QCD bottom-up model action [73, 74, 75] to describe the background. In Refs. [63, 64, 65], the authors chose the Witten-Sakai-Sugimoto model [76, 20, 21] in top-down approach as the background. In Ref. [66], the authors used the hard-wall AdS/QCD model action to describe the background. They all obtained the stable branch that corresponds to the holographic nuclear matter.
In this work, different from the topological description of the baryons, we use the improved Karch-Katz-Son-Stephanov (KKSS) action [24, 77, 78, 79, 80] to introduce the contribution of the hadrons and treat it as a probe. Then we can calculate the EoS of the holographic nuclear matter. This article is organized in the following. In Sec. II, we briefly summarize the observation data of the mass and radius of the NSs. In Sec. III, we first introduce three holographic models. Then, we solve the Einstein-Maxwell-dilaton (EMD) system to derive the thermodynamics of the background and plot the phase diagram for the confinement-deconfinement phase transition in the three models. We also compare the deformed background metric in the three models with that in the space-time. In Sec. IV we consider the thermodynamic contribution made by the KKSS action and calculate the EoS of the holographic nuclear matter. Combined with the Hebeler-Lattimer-Pethick-Schwenk (HLPS) intermediate EoS, we then construct the hybrid EoS of the cold strong interaction matter. In Sec. V, we use the hybrid EoSs to calculate some properties of the neutron stars, such as mass-radius relation and tidal deformability. We also compare our results with the observation data. Finally, we give the conclusion and some discussions in Sec. VI.
II The measurement of the mass and radius of neutron stars
PSR J1614-2230 is a recycled millisecond pulsar with a very low inferred magnetic field, the magnetic induction intensity of which is . It was discovered in a completed search of 56 unidentified mid-latitude EGRET -ray sources for pulsations using the Parkes telescope and the multibeam receiver in 2004 [82]. In 2010, the authors in Ref. [31] presented radio timing observations of the binary millisecond pulsar PSR J1614-2230. The detection of the general relativistic Shapiro delay [30] implied the pulsar mass is , which made it the heaviest known NS at that time. In 2016, the authors in Ref. [32] analyzed 24 binary radio pulsars in the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) nine-year data set and made 14 significant measurements of the Shapiro delay. They presented the mass of PSR J1614-2230 is at credibility.
PSR J0348+0432 is a mildly partially recycled binary pulsar with and low magnetic field (), in a orbit with a low-mass companion, which was detected in 2012 in a Drift-scan Survey using the Robert C. Byrd Green Bank Telescope with the goal of finding new radio pulsars, especially millisecond pulsars that can be timed to high precision [83]. PSR J0348+0432 is only the second NS with a precisely determined mass around , after PSR J1614-2230. In 2013, the authors in Ref. [33] reported on radio-timing observations of the pulsar J0348+0432 and phase-resolved optical spectroscopy of its white-dwarf companion and then derived a NS mass in the range from to at confidence or to at confidence.
In 2014, 67 new radio pulsars including J0741+66 () were discovered in the Green Bank Northern Celestial Cap (GBNCC) survey, which surveys the entire sky visible to the Robert C. Byrd Green Bank Radio Telescope (GBT) at 350 MHz for radio pulsars and fast radio transients [84]. In 2018, the pulsar J0741+66 was renamed J0740+6620 in Ref. [85]. In 2019, by combining data from the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) 12.5-yr data set with orbital phase-specific observations using the Green Bank Telescope, the authors in Ref. [34] measured the mass of the millisecond pulsars (MSP) J0740+6620 to be at credibility interval or at credibility interval. In 2021, the authors in Ref. [35] used the data set that consisted of combined pulse arrival-time measurements made with the Green Bank Telescope and the Canadian Hydrogen Intensity Mapping Experiment telescope. They presented the model-averaged result of the mass of PSR J0740+6620 is at credible interval, which is reduced by about compared to the result given in Ref. [34]. This model-averaged value remains the largest of all other precisely measured pulsar masses determined with the Shapiro delay to date.
There is also a special class of MSPs called black widows (and redbacks), the masses of which are higher. In black-widow systems, a millisecond pulsar is accompanied by a low-mass, few companion, which is bloated and strongly irradiated by the pulsar, leading to outflows strong enough to eclipse the pulsar signal for significant fractions of the orbit [36]. The authors in Ref. [36] present evidence that the black-widow pulsar, PSR B1957+20, has a high mass. Their best-fit pulsar mass is . However, as it was stated in Ref. [81], there are many difficulties to obtain accurate measurements from these ablated companions, and the possibility of even more massive NSs than J0348+0432 is not yet as robust as the results from radio timing.
These mass measurements provide a strict restriction on the EoS of the cold QCD matter, which can’t be too “soft” and should lead to the maximum mass of NSs is about times the solar mass. Otherwise, the high masses of the above NSs cannot be explained. Many soft EoSs have already been ruled out through these mass measurements.
The measurements of the radii of the NSs are more difficult than that of the masses. In the past decade, several different techniques have been employed in the NS radius measurements. Almost all of the methods that are currently used base on the detection of thermal emission from the surface of the stars. People either measure its apparent angular size or detect the effects of the NS space-time on this emission to extract the information of the radius. These methods can be divided into two kinds: spectroscopic measurements and timing measurements. The ongoing NASA’s NS Interior Composition Explorer Mission (NICER) [86] uses the latter method (pulse profile modeling) where a large number of counts from a small number of rotation-powered pulsars which emit thermally from their polar caps are collected. Combined with the refined theoretical models that have been developed to analyze these waveforms, those data will provide the measurement of radii and EoSs of the NSs. The results have been published in Refs. [37, 38, 39, 40], in which they also use the data from the XMM-Newton telescope.
In 2019, the authors in Ref. [37] derived that for the isolated millisecond pulsar PSR J0030+0451, the estimated equatorial circumferential radius is and the gravitational mass is at credible level. In the same year, another group presented different values for PSR J0030+0451, inferred mass and equatorial radius of which are and , respectively, where the credible interval bounds are approximately the and quantiles in marginal posterior mass, given relative to the median [38].
In 2021, the authors in Ref. [39] found that the equatorial circumferential radius of PSR J0740+6620 is at credibility based on fits of rotating hot spot patterns to NS Interior Composition Explorer (NICER) and X-ray Multi-Mirror (XMM-Newton) X-ray observations. On the same day, another group constrained the equatorial radius and mass of PSR J0740+6620 to be and , respectively, each reported as the posterior credible interval bounded by the and quantiles [40].
There is another way to study the NSs, in which people observe the binary merger events involving NSs. On August 17, 2017, the Advanced LIGO and Advanced Virgo gravitational-wave detectors made their first observation of a binary NS inspiral [87]. The signal, GW170817, was detected. Thereafter the multi-messenger observations of this binary NS merger are finished by telescopes and observatories ranging basically over the whole spectrum of electromagnetic waves [88]. In 2018, under the hypothesis that both bodies in the GW170817 event are NSs that are described by the same equation of state and have spins within the range observed in Galactic binary NSs, the authors in Refs. [41] employed two methods to give an analysis of the radii and EoS of the NSs. From the LIGO and Virgo data alone and using equation-of-state-insensitive relations between various macroscopic properties of the NSs, they measured the two NS radii as for the heavier one and for the lighter one at the credible level. Using an efficient parametrization of the defining function of the equation of state itself and requiring that the equation of state supports NSs with masses larger than , they further derived for the heavier one and for the lighter one at the credible level. They also obtained constraints on at supranuclear densities, with pressure at twice nuclear saturation density measured at at the level. The tidal deformability of a -NS could be estimated to be at the level when a common but unknown EoS is imposed. This measurement value of is very interesting: contrary to the constraint from the mass measurement, it suggests that “soft” EoSs such as APR4 are favored over “stiff” EoSs such as H4 or MS1. So for an EoS that satisfies both the mass measurement and the tidal deformability measurement, it should be stiff but not too stiff.
First identified in data from two detectors, LIGO Livingston and Virgo on 2019 August 14, GW190814 is the signal of a compact binary coalescence with the most unequal mass ratio yet measured with gravitational waves: [42]. The primary component of GW190814 is conclusively a black-hole (BH) with mass . Due to the lack of measurable tidal deformations and the absence of an electromagnetic counterpart, the secondary component may be an NS or a BH. However, comparing with the maximum NS mass predicted by studies of GW170817’s remnant indicate it’s an NS by current knowledge of the NS equation of state, and by electromagnetic observations of NSs in binary systems [42]. If it’s true, this source with the mass of is the heaviest NS ever observed in a double compact-object system. Then the corresponding constraints on the radius and tidal deformability of a canonical -NS are and [42].
III The holographic framework and the background of the holographic models
Firstly we introduce the framework of the Einstein-Maxwell-dilaton (EMD) system, which comes back to the gravity-dilaton coupling system at zero chemical potential. As the background action, the EMD system is widely used in the holographic QCD models. It can be used to describe the QCD confinement-deconfinement phase diagram [89, 90], the effect of the magnetic field on the QCD phase transition [91], the rotating effect on deconfinement phase transition [92], the thermodynamic properties of QCD and the location of the critical endpoint (CEP) [93], the critical behavior near the CEP [94, 95], and the spectra glueballs and corresponding EoS [96].
Including hadrons excitation, the total action of the -dimensional holographic QCD model is
| (1) |
where is the action for the background in the string frame, and is the action that describes hadrons in the string frame.
The EMD action in the string frame is denoted by :
| (2) | |||||
where denotes the string frame, , is the -dimensional Newton constant. is the determinant of the metric in the string frame: . The metric tensor in the string frame can be extracted from
| (3) |
where is the curvature radius of the asymptotic space-time. For simplicity and without loss of generality, we assume in the following calculations. is the Ricci curvature scalar in the string frame. The -dimensional scalar field is the dilaton field that depends only on the coordinate . is the field strength of the gauge field :
| (4) |
The -dimensional vector field is dual to the baryon number current. The function describes the coupling strength of in the theory, and the function represents the potential of the dilaton field in the string frame. and are the functions that depend only on the value of .
III.1 The Einstein-Maxwell-dilaton system
As discussed in Ref. [97], it is more convenient to choose the string frame when solving the vacuum expectation value of the loop operator, and it is more convenient to choose the Einstein frame to work out the gravity solution and to study the equation of state. So we apply the following Weyl transformation [98, 99] to Eq. (2):
| (5) |
where is the metric tensor in the Einstein frame. The capital letter ’E’ denotes the Einstein frame. Then, Eq. (2) becomes
| (6) | |||||
where the function .
The coefficient of the kinetic term of the dilaton field is in Eq. (6), which is not canonical. So we define a new dilaton field :
| (7) |
Now the action Eq. (6) becomes
| (8) |
where is the Lagrangian density in the Einstein frame:
| (9) |
The function , and . According to Eqs. (3), (5) and (7), we then derive the line element of the space-time in the Einstein frame:
| (10) |
where
| (11) |
Using the variation method, we can derive the Einstein field equations and the equations of motion of and from Eq. (8)-(9):
| (12) |
where is the energy-momentum tensor:
| (13) | |||||
It’s safe to suppose all the components of the vector field are zero except the -component . After substituting the metric Eq. (10) into the equations of motion (EoMs) Eq. (12), we then get the EoMs for the components of the fields:
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) |
Only 4 equations are independent in the above 5 equations. So we choose Eq. (18) as a constraint and use it to check the solutions of the EoMs.
III.2 The matter part action in the holographic model
As mentioned earlier, in Eq. (1) is the action that describe hadrons in the string frame. Here we use the improved KKSS action:
| (19) |
where
| (20) |
is the covariant derivative of the -dimensional scalar field ,
| (21) |
is the potential of the -dimensional scalar field . The parameter describe the coupling strength between the matter part and the background in the action. , , , and are the generators of the and group, respectively. . describes the baryons. The original KKSS action is proposed in Ref. [24]. It is modified in Refs. [77, 78, 79, 80] to describe the chiral phase transition and meson spectra.
According to the AdS/CFT dictionary [23], the bulk scalar field and the chiral gauge fields are dual to the relevant QCD operators at the ultraviolet (UV) boundary . The bulk scalar field can be decomposed as
| (22) |
where is the pseudoscalar meson field and is the scalar meson field. The field is related to the vacuum expectation value (VEV):
| (23) |
where is the identity matrix. The -dimensional bulk gauge field can be recombined into the vector field and the axial-vector field :
| (24) |
The field-strength tensor for the vector field and the axial-vector field are
| (25) | |||
| (26) |
According to mass-dimension relationship and , , the -dimensional mass square of the bulk field is .
The action that describes the matter part can be decomposed as
| (27) |
where
| (28) |
is the action for the VEV . The -dimensional fields that dual to the mesons and baryons tower are perturbations compared with the field . The contribution made by and to the thermodynamics is believed to be small compared with that from . Thus we will neglect and in the calculation in this article.
The EoM of the field can be obtained from the action Eq. (19):
| (29) |
The asymptotic expansion of the field in the UV region is
| (30) |
where [100] is the current quark mass, is the chiral condensate, is the normalization constant.
III.3 Three different holographic models
In this work, we take three different holographic models.
III.3.1 Model I
Model I is a variant of Gubser model [101]. The potential for the dilation field and the function are taken from Ref. [93]:
| (31) |
| (32) |
where , , , , and . The -dimensional Newtonian constant is . The characteristic energy scale [102] of the EMD system is . The Eqs. (31)-(32) and the values of the above parameters are taken from Ref. [93], which can give the thermodynamic properties in good agreement with the lattice simulations for the system of dynamical quarks with physical masses [103].
Besides those parameters, , , . The critical value of baryon chemical potential is . The meaning of this parameter will be interpreted in Subsec. IV.1.
III.3.2 Model II
In model II, the potential for the dilation field is
| (33) |
and the function is
| (34) |
where , , . The function are taken from Ref. [104]. The -dimensional Newtonian constant is . The characteristic energy scale [102] of the EMD system is .
Besides those parameters, , , . The critical value of baryon chemical potential is .
III.3.3 Model III
In model III, the dilation field is
| (35) |
and the function is
| (36) |
where and . The -dimensional Newtonian constant is . The value of the parameter is taken from Ref. [96], which can produce good results for the glueballs/oddballs spectra compared with those of the lattice QCD simulation, as “Model III, IV(1)” in Table III in Ref. [96]. The form of the function is inspired by Refs. [105, 106].
Besides those parameters, , , . The critical value of baryon chemical potential is .
III.4 phase diagram for the confinement-deconfinement phase transition
We can get the black-hole solution from the EoMs Eq. (14)-(18). The temperature of the black-hole is
| (37) |
where is the location of the horizon for the black-hole. The entropy density of the black-hole is
| (38) |
According to the AdS/CFT dictionary, the temperature and the entropy density of the QCD matter are and , respectively.
According to the AdS/CFT dictionary, the chemical potential is
| (39) |
and the baryon number density is
| (40) |
where is the Lagrangian density in the Einstein frame in Eq. (9). From the Euler-Lagrange equation of the field :
| (41) |
we then derive that
| (42) |
Eq. (42) is actually the EoM of Eq. (14). Thus, we get the conserved Gauss charge associated with the field :
| (43) |
Then we derive
| (44) |
Sometimes the following expression of which is related to the quantities at the black-hole horizon is more convenient in the calculation:
| (45) |
The internal energy density and the free energy density are
| (46) |
The differential relation of the above equations are
| (47) |
From Eq. (47), we can calculate the pressure and the internal energy density . The trace anomaly is
| (48) |
The square of the speed of sound is
| (49) |
Here all the thermodynamic quantities are labeled with “b”, which denotes “background”. The corresponding phase transition is the confinement-deconfinement phase transition.
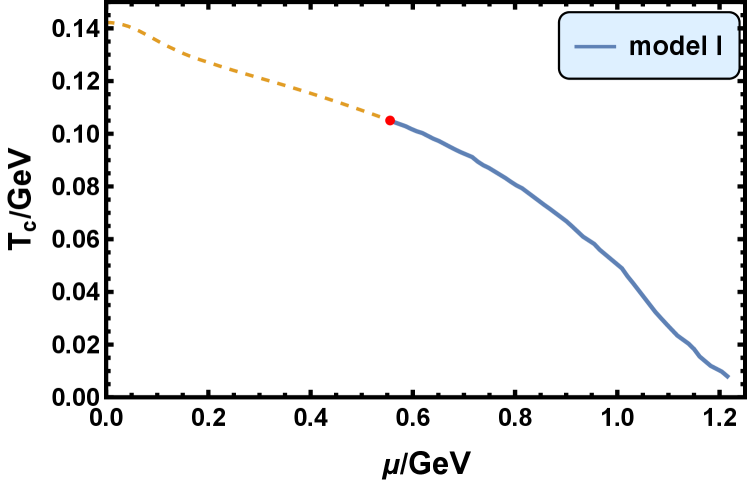
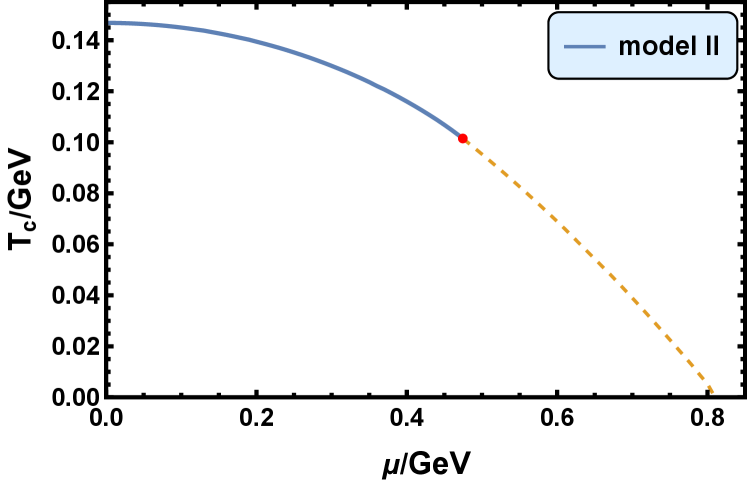
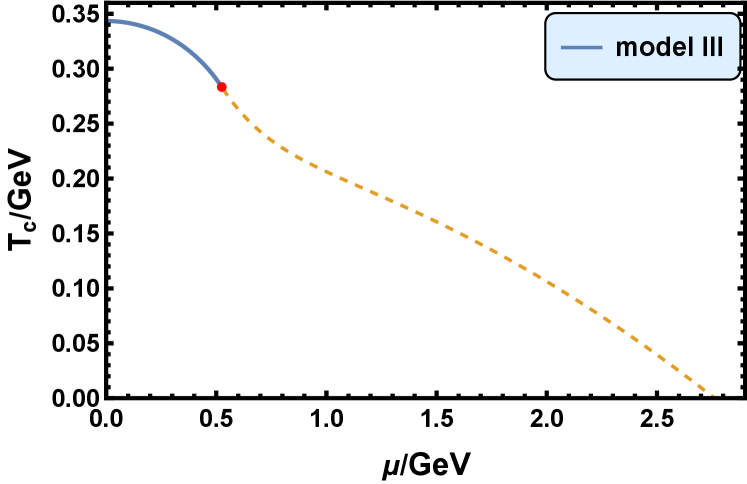
The phase diagrams for the confinement-deconfinement phase transition in model I, II, and III are shown in in Fig. 1. is the critical temperature of the confinement-deconfinement phase transition, is the baryon chemical potential. The blue full line represents that the confinement-deconfinement phase transition is first order transition, and the tan dashed line represents that it’s the cross-over behavior.
It is noticed that the confinement-deconfinement phase transition is the cross-over behavior at low baryon chemical potential range and a first order phase transition at high baryon chemical potential range in model I. The CEP is located at , which is close to the FRG result in Ref. [107] and that of the rPNJL model [108]. The confinement-deconfinement phase transition is a first order phase transition at low baryon chemical potential range and the cross-over behavior at high baryon chemical potential range in model II and model III, which contrasts with that in model I. The CEP is located at in model II and in model III.
When , the critical temperature is , , and in model I, II and III, respectively. When , the critical baryon chemical potential is about , , and in model I, II and III, respectively. In Subsec. IV.1 we will see that these critical chemical potentials will be changed when we consider the contribution made by the matter part action.
III.5 Metric deformation in the three models
To understand the system described by model I, model II, and model III, before we calculate the EoS of the quark matter, we compare the backgrounds in the three models with the space-time.
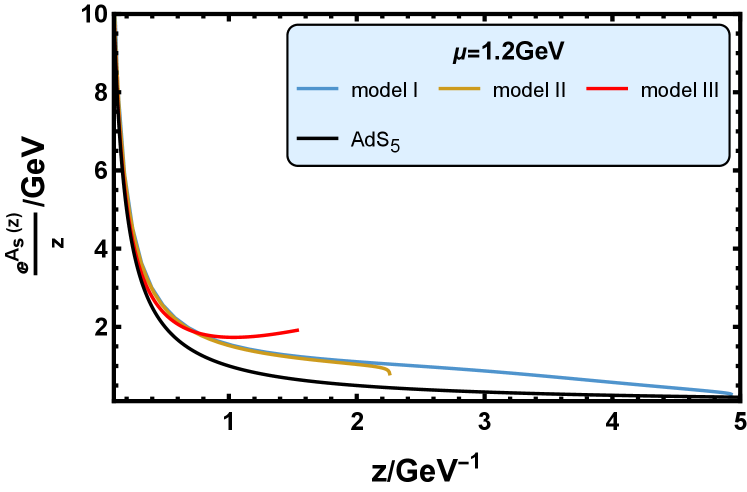
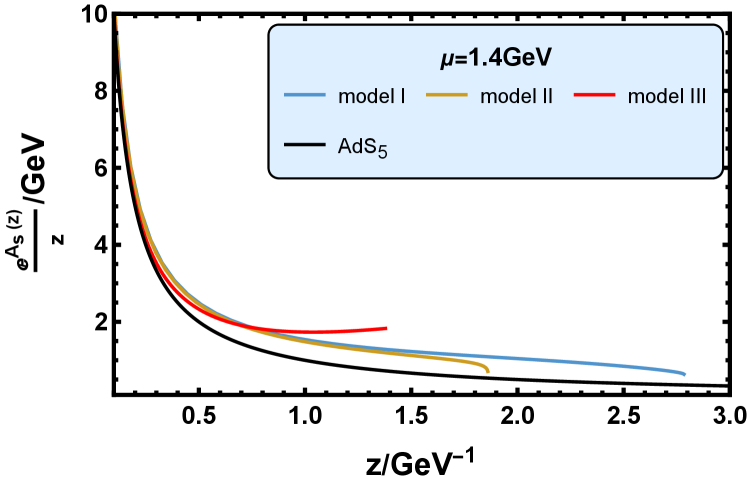
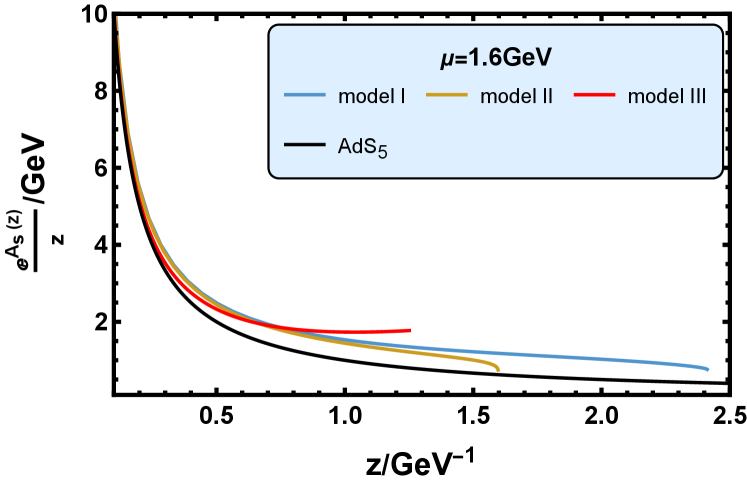
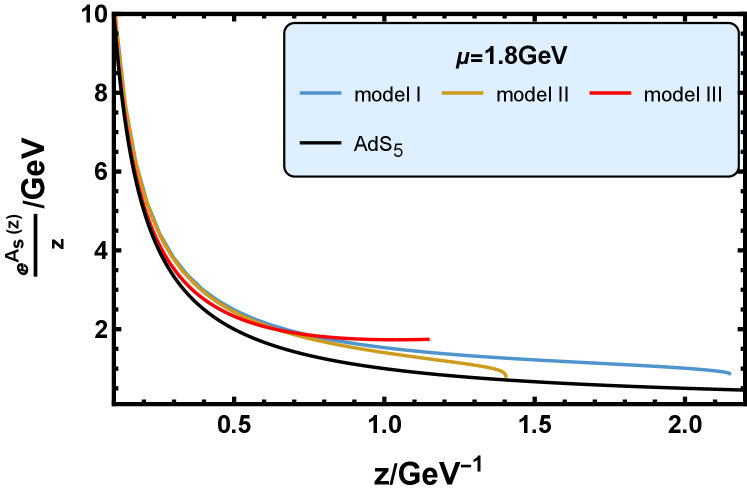
In Fig. 2, we plot the function in the deformed metric in three models at four different values of baryon chemical potential: , , , and at . In the space-time, , which is shown by the black solid line. So the deviation of the lines in Fig. 2 from the black lines shows the deformation of the metric in the three holographic models.
We can see from Fig. 2 that the function in the three models are all located above the case. As mentioned in Subsec. III.3, under the parameter values in model I, the EMD system can derive the thermodynamics that is consistent with the lattice QCD result of the system of dynamical quarks with physical masses [93, 103]. Thus, we think the background of model I describes the flavor system. The parameters in model III can produce good results of the glueballs/oddballs spectra compared with those of the lattice QCD simulation [96]. Thus, the background of model III is considered to describe the pure gluon system. Fig. 2 shows that the pure gluon system is most deformed in the infrared (IR) range.
In Subsec. V.1 we will see that the astrophysical observations of neutron star prefer model I and model III than model II. So we surmise that the background, the function of which is located between the steel blue line and the red line in Fig. 2, can produce neutron star properties that are consistent with the astrophysical observations.
IV Equation of state for the cold QCD matter
IV.1 Nuclear matter
In this subsection, we introduce how to describe nuclear matter in the holographic model. The total pressure consists of the contribution made by the background part and that made by the matter part:
| (50) |
As discussed in Subsec. III.4, the background part of the pressure can be calculated from the confined solutions of the EoMs Eq. (14)-(18). But the matter part of the pressure is obtained through calculating the on-shell Euclidean action :
| (51) |
When we calculate the on-shell Euclidean action for the matter part, we neglect the contribution from the and :
| (52) |
As mentioned in Subsec. III.2, the pressure density from -dimensional fields that dual to the mesons and baryons tower are perturbations compared with that from the field . So we think the contribution to the Euclidean on-shell action from and are negligible.
Now we use model I as the example to illustrate how to describe nuclear matter and then to calculate the EoS of nuclear matter. From Fig. 1, we can see that there is a intersection point between the curve and the horizontal axis, the position of which is denoted as . When and , the background is the thermal-gas solutions, the line element for which in Einstein frame is
| (53) |
In this case, the values of , , , are all . Thus, from Eqs. (50)-(52) the total pressure is
| (54) |
When and , although the thermal-gas solutions also exist, the black-hole solutions are more stable, and the corresponding line element in the Einstein frame is Eq. (10).
In principle, the calculation should be implemented in the case of . However, it’s very difficult to calculate the solutions in strict zero temperature. Thus, we calculate the EoS of cold strong interaction matter in a very low temperature, such as for quark matter. When we calculate the total pressure , we choose a critical value of baryon chemical potential, , so that . This value is slightly different from the in Sec. “Baryons from a homogeneous bulk gauge field” in Ref. [60].
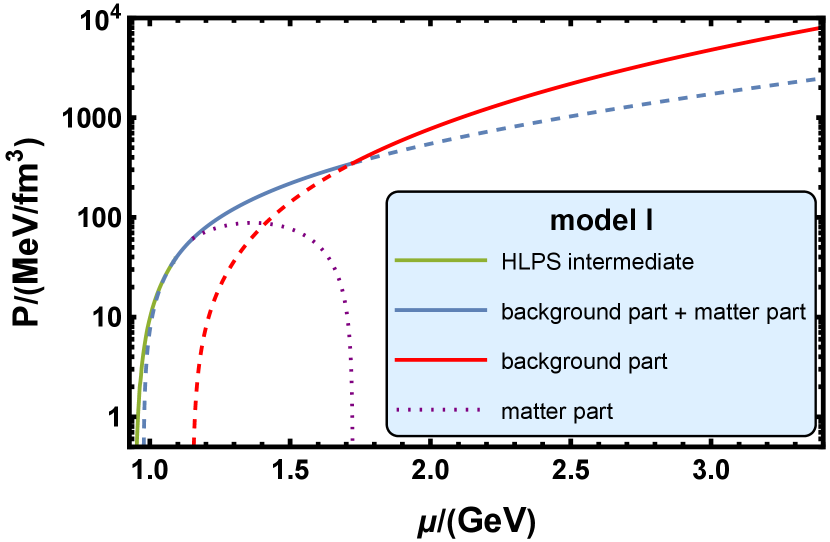
We then plot the function as the silver lake blue line in Fig. 3. There are also other three different colors in Fig. 3: the olive green line represents the HLPS intermediate case [109], the red line, which is calculated in Subsec. III.4, represents the holographic result which contains only the contribution made by the background part, and the dotted purple line represents the contribution made by the matter part. There is an intersection between the olive green line and the silver lake blue line, where the baryon chemical potential is . The intersection represents a second-order phase transition, where and is continuous, but are different at both side of this critical values of .
Similarly, the intersection between the silver lake blue line and the red line, where , represents a first order transition. The value of are different at both side of this critical values of . We regard this phase transition as the confinement-deconfinement phase transition in QCD. It is noticed that after considering the contribution made by the matter part action, the critical chemical potential is different from that in Subsec. III.4. Thus, the silver lake blue line is the EoS for the holographic nuclear matter and the red line is the EoS for the holographic quark matter.
We note that the silver lake blue line is full line only when . It means the free energy, in this case, is minimal between the three cases (the olive green line, the silver lake blue line, and the red line) and it is thermodynamic stable when . When , the nuclear matter with the HLPS intermediate EoS is stable. When , the holographic quark matter is stable.
After we get the pressure of the nuclear matter , we can calculate the entropy and the baryon number density of the nuclear matter using the differential relation:
| (55) |
Then we can derive all other thermodynamic quantities of the nuclear matter. That’s why all the thermodynamic quantities here are labeled with “NM”, which denotes “nuclear matter”.
IV.2 Hybrid equation of state for neutron stars
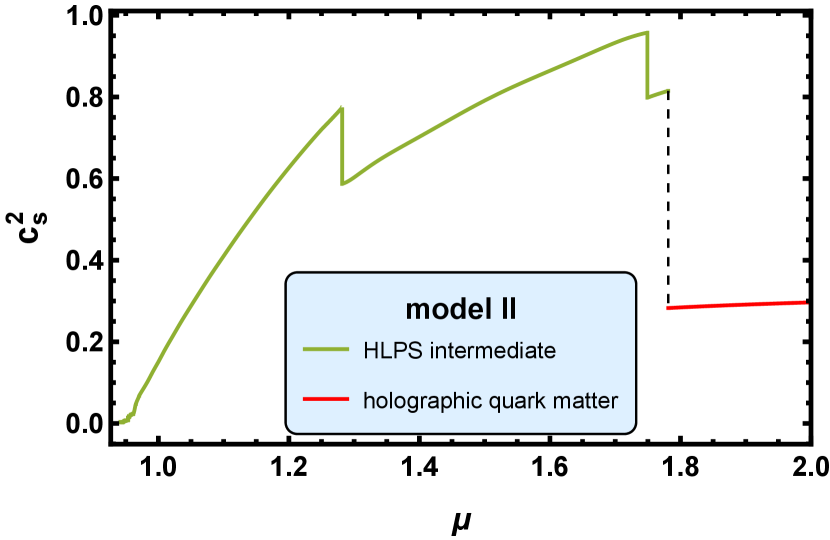
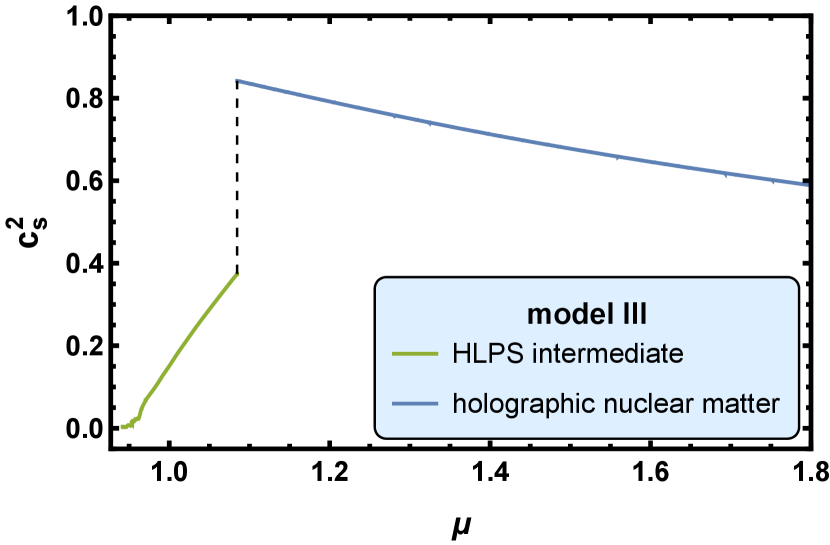
We show the final results of the hybrid EoS for cold QCD matter from model I, II and III in Fig. 4, and the corresponding square of the speed of sound in Fig. 5 and Fig. 6.
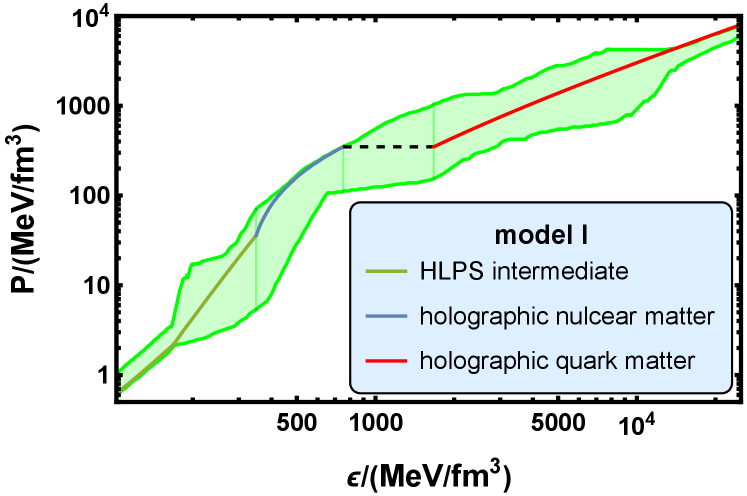
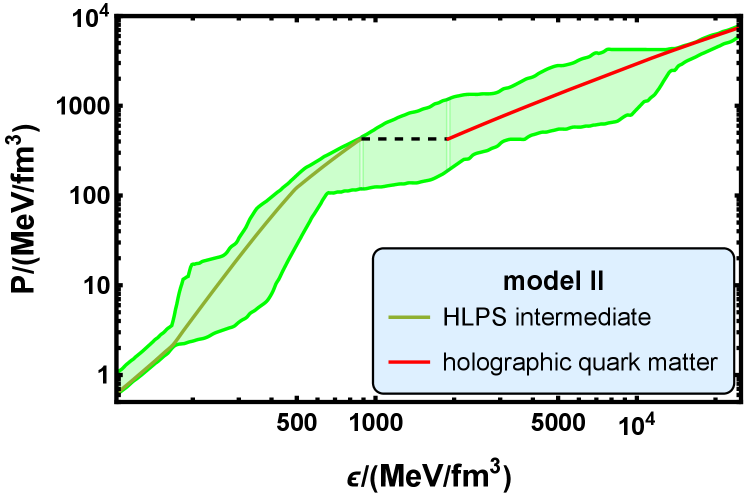
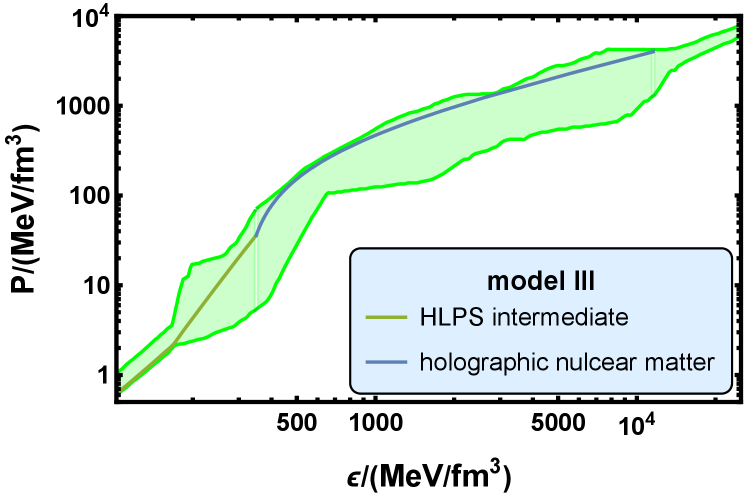
The hybrid EoS of model I includes three parts, i.e., the HLPS intermediate EoS [109], the holographic nuclear matter EoS, and the holographic quark matter EoS. The hybrid EoS of model II includes the HLPS intermediate EoS and the holographic quark matter EoS. The hybrid EoS of model III includes the HLPS intermediate EoS and the holographic nuclear matter EoS.
It is observed that the EoSs in the three models all fall in the green band, which is taken from Ref. [43], is the “allowed” range of the EOS for cold QCD matter. It is defined by the low-density chiral effective theory, the high-density perturbative QCD, and the polytropic interpolations between them, and is constrained by the astrophysics observations.
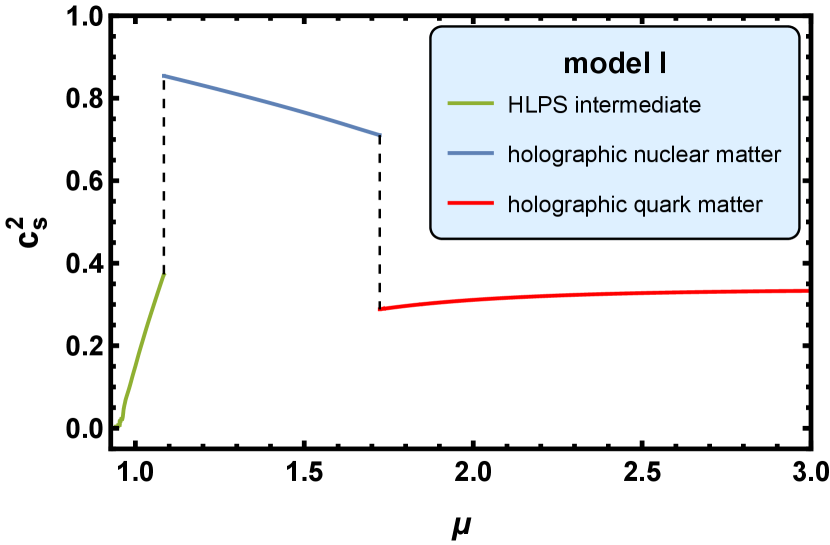
In Fig. 5, the corresponding square of the speed of sound is shown as a function of the chemical potential. We can observe that the square of the speed of sound increases from a small value at zero chemical potential to a relatively large value more than , then decreases to a smaller value at the high baryon chemical potential range. The violation of sound velocity bound in neutron stars has been discussed in much literature, e.g. Refs. [110, 111]. The sound velocity in model I and model III reaches maximum in holographic nuclear matter. However, the maximum sound velocity in model II lies in the HLPS intermediate part.
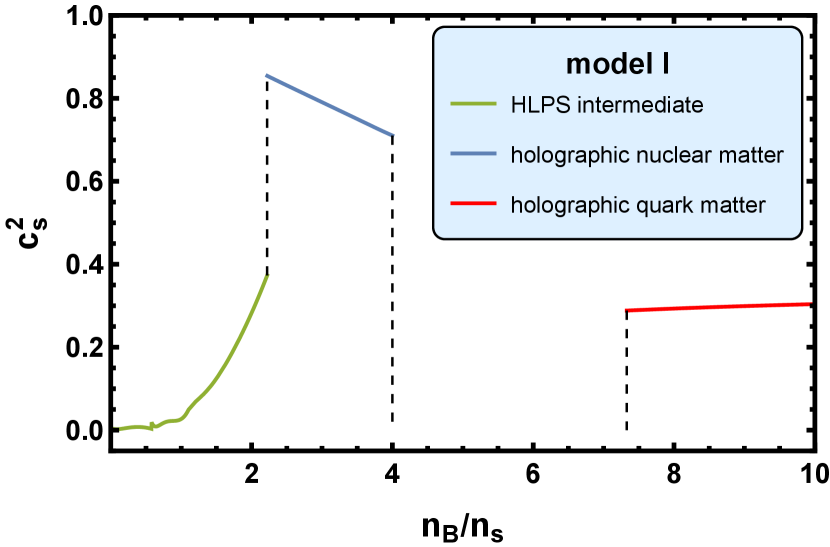
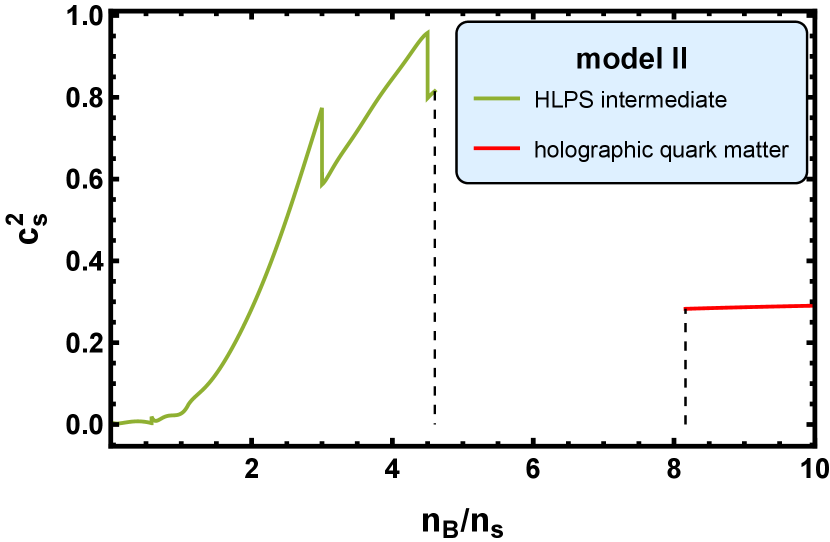
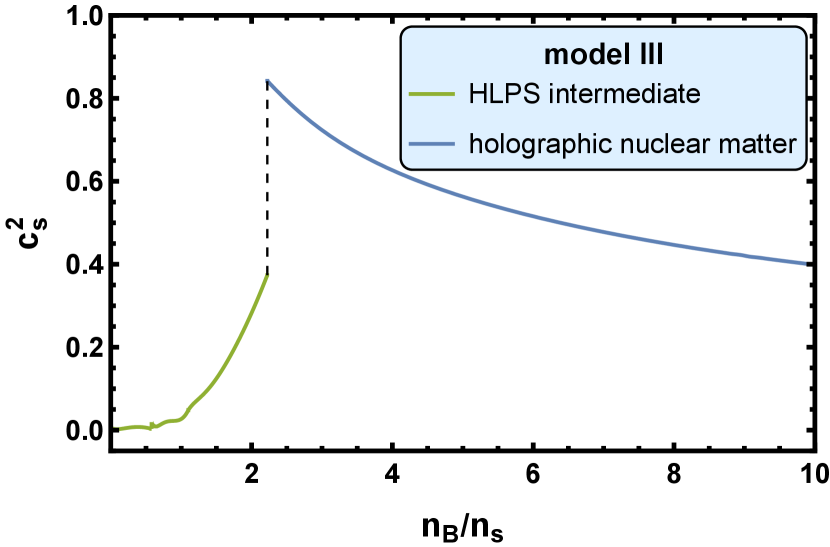
In Fig. 6, we show the square of the speed of sound as a function of the scaled baryon number density , where is the nuclear saturation baryon number density.
From Figs. 4-6, we clearly observe that in model I, there are two phase transition. The first one is a second order transition. At this phase transition, the baryon number density , the baryon chemical potential , the internal energy density , and the pressure . This phase transition connects the HLPS intermediate nuclear matter with the holographic nuclear matter.
The HLPS intermediate nuclear matter and the holographic nuclear matter may be in the same QCD deconfinement phase. So they should be joined together smoothly. However, in practice calculation, the two EoSs come from different models and we have tried our best to use a second order phase transition to join them together. The square of the speed of sound, , jumps from to through this second order transition. Another possible interpretation for the holographic nuclear matter is that it’s in the quarkyonic phase [112, 90] which is in confinement with chiral symmetry restoration. We don’t investigate the quarkyonic phase further here and leave it in future work.
The second one is a first order transition, which is interpreted as the confinement-deconfinement phase transition in Subsec. IV.1 and is located at and . The value of jumps from to , the value of jumps from to , and the value of jumps from to through this first order transition. At , the baryon number density reaches , which is a very high value, and . We will see in Subsec. V.1 that this first order transition leads to the branch that corresponds to the holographic quark matter is unstable in the mass-radius figure of the NS.
In model II, there is a first order phase transition, which is interpreted as the confinement-deconfinement phase transition and located at and . The value of jumps from to , the value of jumps from to , and the value of jumps from to through this first order transition. At , the baryon number density reaches and . Being similar to the case in model I, this first order phase transition here also leads to the unstable branch that corresponds to the holographic quark matter.
In model III, there is a second order phase transition. The parameter values of this phase transition are , , , and . The square of the speed of sound, , jumps from to through this second order transition. At , the baryon number density reaches and .
V The neutron star
V.1 Mass-radius relation
The Tolman-Oppenheimer-Volkoff (TOV) equation [113, 114, 115] describes the structure of a spherically symmetric and isotropic object in static gravitational equilibrium:
| (56) |
where is the radial coordinate, is the pressure, and is the internal energy density of the material at the radius . is the Newtonian constant. is the total mass inside the sphere with radius measured by the gravitational field felt by a distant observer. It satisfies
| (57) | |||
| (58) |
The metric inside the object can be obtained from the element:
| (59) |
where obeys the following equation:
| (60) |
If the sphere is in the vacuum, the metric outside it is the Schwarzschild metric:
| (61) |
where is the total mass of the object measured by the gravitational field felt by a distant observer, is the radius coordinate of the boundary of the object.
To make sure the metric is continuous at the boundary , we impose the boundary condition
| (62) |
Two other boundary conditions are the zero pressure condition at the boundary of the object
| (63) |
and the given internal energy density at
| (64) |
The NS consists of cold QCD matter. We only consider the spherical symmetric and isotropic neutron star in the vacuum without rotation. The EoS of the cold QCD matter can be written in the form
| (65) |
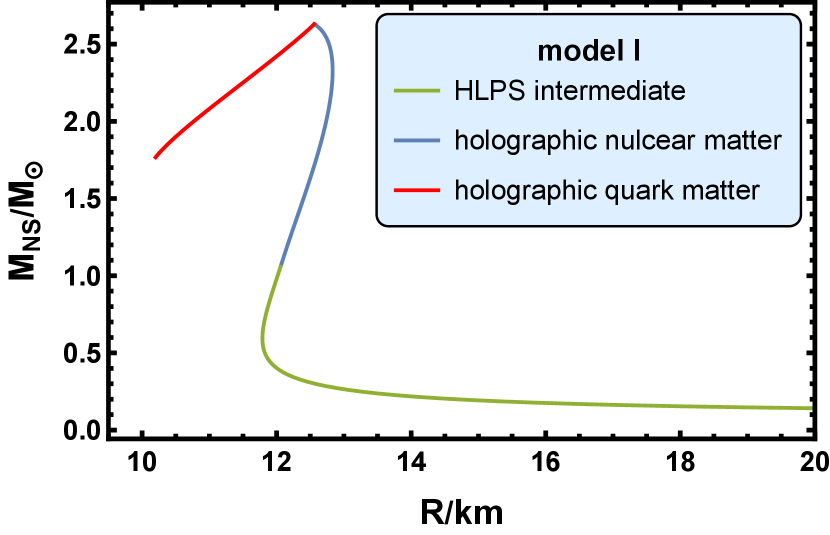
From Fig 7, we observe that in model I, the radius for the -NS is . The max possible radius for the NS is , which correspond a -NS. The max possible mass for the NS is , which correspond a -NS.
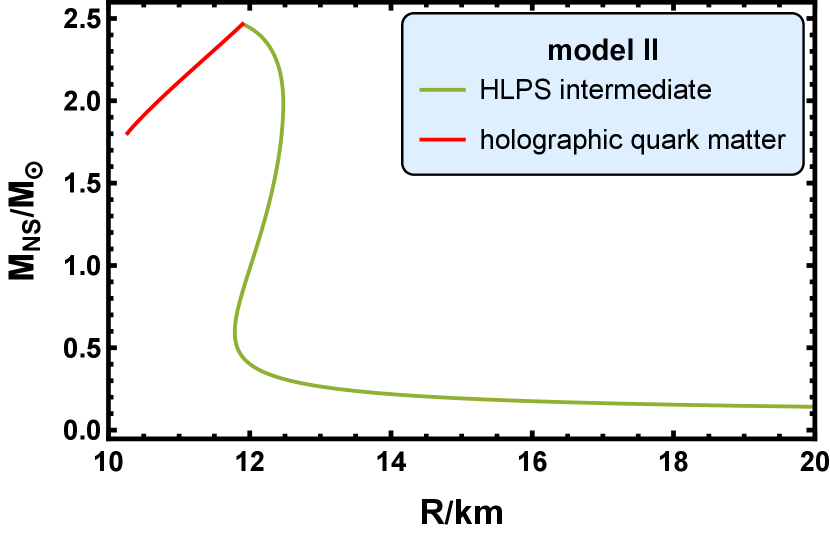
In model II, the radius for the -NS is . The max possible radius for the NS is , which correspond a -NS. The max possible mass for the NS is , which correspond a -NS.
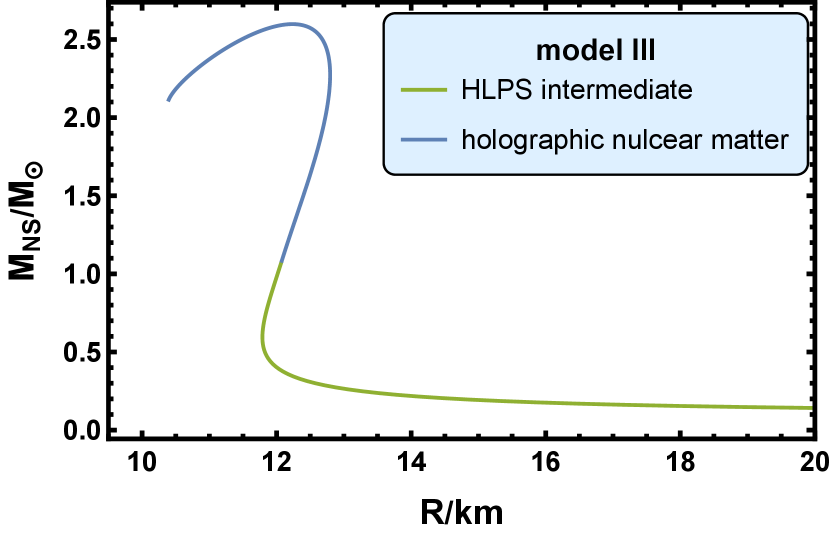
In model III, the radius for the -NS is . The max possible radius for the NS is , which correspond a -NS. The max possible mass for the NS is , which correspond a -NS.
In conclusion, the max possible mass for the neutron star is about and the radius is about then. It is noticed that the branch that corresponds to the holographic quark matter is always unstable, and the holographic nuclear matter can produce the stable branch. These results indicate that even in the core of the NS, the matter is still in the confinement phase and the quark matter is not favored. This is consistent with the conclusion in Ref. [116], in which the authors combined the input from the gauge-gravity duality and the input from various - methods for the nuclear matter at low density and analyzed families of hybrid equations of state of cold QCD matter. Their prediction is that all neutron stars are fully hadronic without quark matter cores.
V.2 Tidal deformability
At last, we investigate the tidal deformability of the NSs. We consider a static, spherically symmetric object in a static external quadrupolar tidal field [117, 118, 119]. Then the tidal deformability is defined to linear order as
| (66) |
where is the quadrupole moment. The dimensional tidal deformability is also related to the dimensionless tidal Love number :
| (67) |
The asymptotic expansion of the component of the full metric outside the object at a large distance from the object is
| (68) |
The right hand side (r.h.s.) of Eq. (68) includes two leading-order terms of the perturbative expansions. The second one describes an external tidal field increasing with and the first one describes the resulting tidal distortion decreasing with .
Introducing a linear perturbation on the object leads to a static, even-parity perturbation on the metric [118, 119] in the Regge-Wheeler gauge [120]:
| (69) |
where
| (70) |
The corresponding perturbations of the stress-energy tensor of the perfect fluid are
| (71) |
| (72) |
The function obeys the following differential equation:
| (73) |
Being similar to the method of solving the moment of inertia in the slow rotation approximation [121], we can calculate the tidal perturbation for a given EoS [119].
| (74) | |||
| (75) |
The boundary conditions are
| (76) | |||
| (77) |
The constant determines the extent of deformation of the object and will be canceled in the calculation of the Love number. Eq. (74)-(77) can be solved together with the TOV system Eq. (56), Eq. (57), Eq. (60), Eq. (65), Eq. (58), Eq. (62), Eq. (63), and Eq. (64).
The Love number is [119]
| (78) |
where
| (79) |
and
| (80) |
is the compactness of the object. From Eq. (67), we then define a dimensionless tidal deformability [64]:
| (81) |
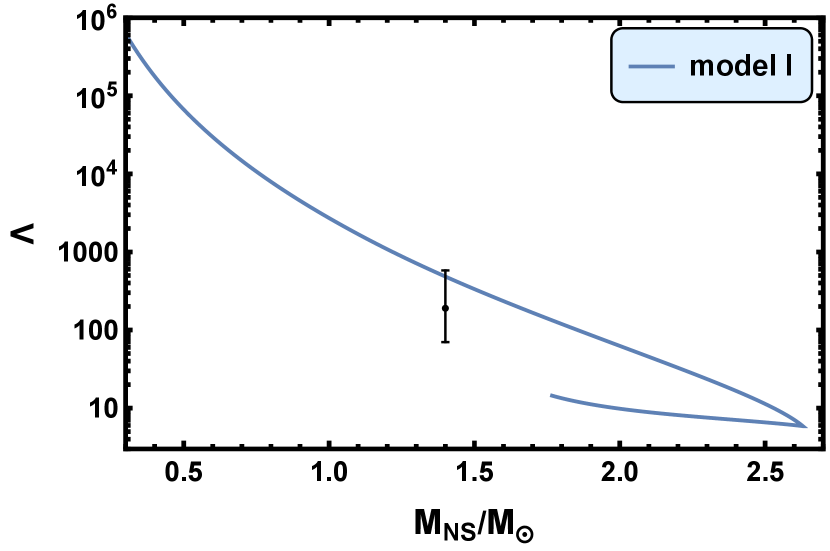
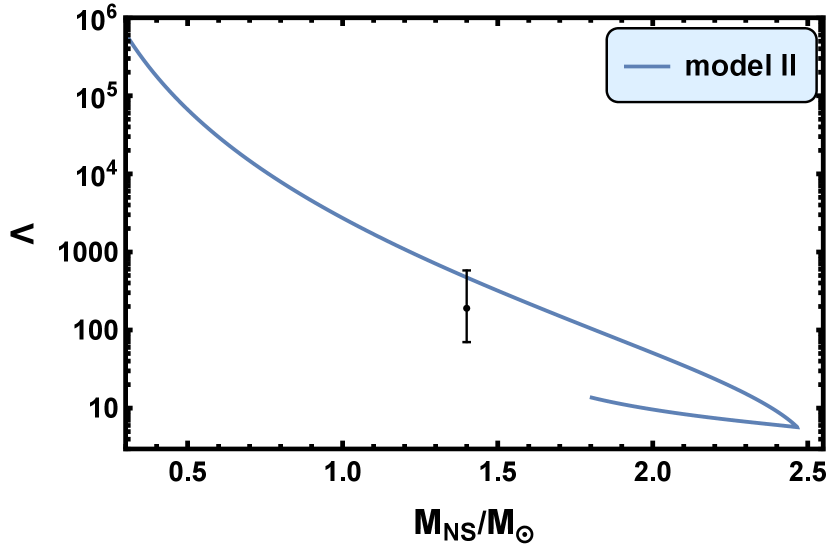
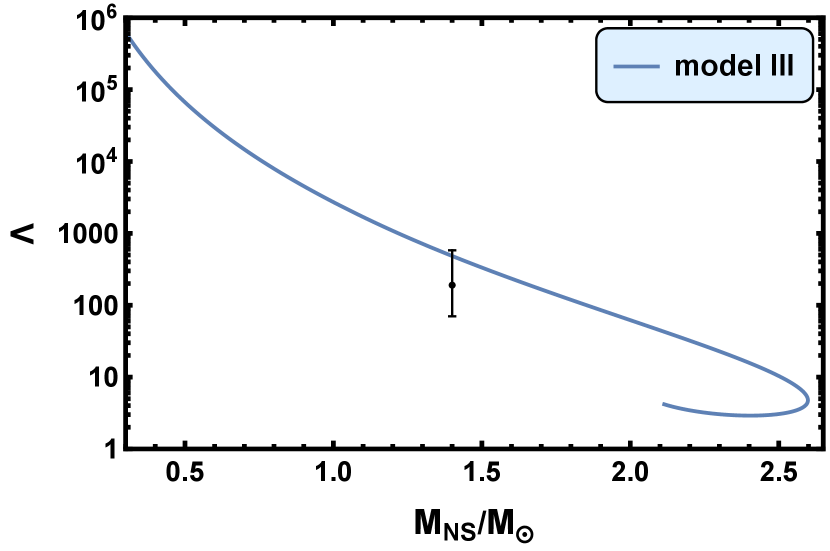
The tidal deformability as a function of the mass ratio between the neutron star and the sun calculated in model I, model II, and model III are shown in Fig. 8. The black dot with error bar is the tidal deformability of a -NS, estimated in Ref. [41]: . In model I, our calculation result for the tidal deformability of a -NS is . In model II, . In model III, . Our results of the tidal deformability in all three models are consistent with this experiment data.
In Ref. [42], the authors gave that the radius of a canonical NS is and the tidal deformability is by assuming that the secondary of GW190814 proves to be a NS. Because the secondary mass of GW190814 is , that assumption requires that the max possible mass of the NS should be no less than . Model I and model III satisfy this requirement. Actually, we find the results of and given by the three models are all consistent with those from Ref. [42].
VI Conclusion and discussion
We construct the hybrid equations of state (EoSs) of the cold strong interaction matter using three holographic models in this work. In the low baryon number density range, the HLPS intermediate EoS is used to describe the nuclear matter. At the intermediate range, we use the holographic QCD to calculate the EoS. The EoS from the holographic QCD is connected with the HLPS EoS through the phase equilibrium condition. The key point is to describe the nuclear matter in the holographic frame, the EoS of which can be connected with the HLPS EoS through a second order phase transition. It is found that the branch that corresponds to the holographic nuclear matter is stable in the mass-radius relation of the NS.
The holographic action consists of two parts: the Einstein-Maxwell-dilaton (EMD) system for the background and the KKSS action for the matter part. The EMD system is solved to get the background metric which is used to calculate the EoS. For holographic nuclear matter, the thermodynamic contribution made by the KKSS action is also included to calculate the EoS. From the previous study in Ref. [90], most probably the holographic nuclear matter is in the quarkyonic phase [112] in which the chiral symmetry is restored but the quarks and gluons are still confined. We will study the quarkyonic phase and its relationship with the NS in our holographic models in the future. There are already some articles [72, 60, 61, 62, 63, 64, 65, 66] to describe the baryons by introducing the Dirac-Born-Infeld (DBI) action and the Chern-Simons (CS) terms, where the solitons are regarded as baryons. However, the method to calculate the EoS of the holographic nuclear matter here is new and hadn’t been used within the holographic QCD yet.
The hybrid EoSs we constructed are located in the “allowed” range constrained by interpolating the results of nuclear physics and the results of perturbative QCD with the constraint of the astrophysical observations. Then we calculate the properties of the neutron star, including the mass-radius relation and the tidal deformability.
We use three different holographic models here. In model I, the radius for the -NS is . The max possible radius for the NS is , which correspond a -NS. The max possible mass for the NS is , which correspond a -NS. In model II, the radius for the -NS is . The max possible radius for the NS is , which correspond a -NS. The max possible mass for the NS is , which correspond a -NS. In model III, the radius for the -NS is . The max possible radius for the NS is , which correspond a -NS. The max possible mass for the NS is , which correspond a -NS.
The branch that corresponds to the holographic quark matter is always unstable, and the holographic nuclear matter can produce the stable branch. These results indicate that even in the core of the NS, the matter is still in the confinement phase and the quark matter is not favored. This is consistent with the conclusion in Ref. [116], in which the authors combined the input from the gauge-gravity duality and the input from various - methods for the nuclear matter at low density and analyzed families of hybrid equations of state of cold QCD matter. Their prediction is that all neutron stars are fully hadronic without quark matter cores.
In model I, our calculation result for the tidal deformability of a -NS is . In model II, . In model III, . Our results of the tidal deformability in all three models are consistent with that estimated in Ref. [41]. In Ref. [42], the authors gave that the radius of a canonical NS is and the tidal deformability is by assuming that the secondary of GW190814 proves to be a NS. Because the secondary mass of GW190814 is , that assumption requires that the max possible mass of the NS should be no less than . Model I and model III satisfy this requirement. Actually, we find the results of and given by the three models are all consistent with those from Ref. [42].
For future studies, we will investigate the relation between the chiral phase transition and confinement-deconfinement phase transition, and figure out whether the stable holographic nuclear matter is in the quarkyonic phase. Currently, the EMD system and the KKSS action are solved separately, which means we use the “probe approximation” here. The KKSS action is regarded as a probe and its back-reaction to the background EMD system is neglected. We will investigate this holographic model beyond the probe approximation and solve it consistently in the future. Also, as we stated in the introduction, the “allowed” range of the EoS we used here is derived by the “direct interpolation approach” [43, 44]. However the “causality and thermodynamic stability constraint approach” proposed in Refs. [45, 46] will give more strict constraints on the EoS of cold QCD matter. We will consider these constraints in future works.
Acknowledgements.
We thank Minghua Wei and Yidian Chen for helpful discussions. This work is supported in part by the National Natural Science Foundation of China (NSFC) Grant Nos. 11725523 and 11735007, the Strategic Priority Research Program of Chinese Academy of Sciences under Grant Nos XDB34030000 and XDPB15, the start-up funding from University of Chinese Academy of Sciences(UCAS), and the Fundamental Research Funds for the Central Universities.References
- [1] John B. Kogut. An Introduction to Lattice Gauge Theory and Spin Systems. Rev. Mod. Phys., 51:659, 1979.
- [2] John B. Kogut. A Review of the Lattice Gauge Theory Approach to Quantum Chromodynamics. Rev. Mod. Phys., 55:775, 1983.
- [3] Heng-Tong Ding, Frithjof Karsch, and Swagato Mukherjee. Thermodynamics of strong-interaction matter from Lattice QCD. Int. J. Mod. Phys. E, 24(10):1530007, 2015.
- [4] Steven Weinberg. Phenomenological Lagrangians. Physica A, 96(1-2):327–340, 1979.
- [5] Yoichiro Nambu and G. Jona-Lasinio. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. 1. Phys. Rev., 122:345–358, 1961.
- [6] Yoichiro Nambu and G. Jona-Lasinio. DYNAMICAL MODEL OF ELEMENTARY PARTICLES BASED ON AN ANALOGY WITH SUPERCONDUCTIVITY. II. Phys. Rev., 124:246–254, 1961.
- [7] C. A. Dominguez and N. Paver. LOCAL DUALITY CONSTRAINTS ON SCALAR GLUONIUM. Z. Phys. C, 31:591, 1986.
- [8] C. A. Dominguez and N. Paver. Tensor Gluonium Spectrum in QCD. Z. Phys. C, 32:391, 1986.
- [9] J. I. Latorre, Stephan Narison, and S. Paban. 0++ TRIGLUONIUM SUM RULES. Phys. Lett. B, 191:437–441, 1987.
- [10] Stephan Narison and G. Veneziano. QCD Tests of (1.6) = Glueball. Int. J. Mod. Phys. A, 4:2751, 1989.
- [11] Stephan Narison. Masses, decays and mixings of gluonia in QCD. Nucl. Phys. B, 509:312–356, 1998.
- [12] Stephan Narison. Masses, decays and mixings of gluonia in QCD. Nucl. Phys. B Proc. Suppl., 64:210–219, 1998.
- [13] Tao Huang, Hong-Ying Jin, and Ai-Lin Zhang. Determination of the scalar glueball mass in QCD sum rules. Phys. Rev. D, 59:034026, 1999.
- [14] Stephan Narison. Light scalar mesons in QCD. Nucl. Phys. B Proc. Suppl., 186:306–311, 2009.
- [15] Wei-jie Fu. QCD at finite temperature and density within the fRG approach: An overview. 5 2022.
- [16] Juan Martin Maldacena. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys., 2:231–252, 1998.
- [17] S. S. Gubser, Igor R. Klebanov, and Alexander M. Polyakov. Gauge theory correlators from noncritical string theory. Phys. Lett. B, 428:105–114, 1998.
- [18] Edward Witten. Anti-de Sitter space and holography. Adv. Theor. Math. Phys., 2:253–291, 1998.
- [19] Martin Kruczenski, David Mateos, Robert C. Myers, and David J. Winters. Towards a holographic dual of large N(c) QCD. JHEP, 05:041, 2004.
- [20] Tadakatsu Sakai and Shigeki Sugimoto. Low energy hadron physics in holographic QCD. Prog. Theor. Phys., 113:843–882, 2005.
- [21] Tadakatsu Sakai and Shigeki Sugimoto. More on a holographic dual of QCD. Prog. Theor. Phys., 114:1083–1118, 2005.
- [22] Leandro Da Rold and Alex Pomarol. Chiral symmetry breaking from five dimensional spaces. Nucl. Phys. B, 721:79–97, 2005.
- [23] Joshua Erlich, Emanuel Katz, Dam T. Son, and Mikhail A. Stephanov. QCD and a holographic model of hadrons. Phys. Rev. Lett., 95:261602, 2005.
- [24] Andreas Karch, Emanuel Katz, Dam T. Son, and Mikhail A. Stephanov. Linear confinement and AdS/QCD. Phys. Rev. D, 74:015005, 2006.
- [25] J. M. Lattimer and M. Prakash. The physics of neutron stars. Science, 304:536–542, 2004.
- [26] Eemeli Annala, Tyler Gorda, Aleksi Kurkela, Joonas Nättilä, and Aleksi Vuorinen. Evidence for quark-matter cores in massive neutron stars. Nature Phys., 16(9):907–910, 2020.
- [27] Werner Becker et al. Neutron stars and pulsars, volume 357. Springer, 2009.
- [28] Pawel Haensel, Aleksander Yu Potekhin, and Dmitry G Yakovlev. Neutron Stars 1. Springer, 2007.
- [29] Bulent Kiziltan. Reassessing the fundamentals: On the evolution, ages and masses of neutron stars. University of California, Santa Cruz, 2010.
- [30] Irwin I. Shapiro. Fourth Test of General Relativity. Phys. Rev. Lett., 13:789–791, 1964.
- [31] Paul Demorest, Tim Pennucci, Scott Ransom, Mallory Roberts, and Jason Hessels. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature, 467:1081–1083, 2010.
- [32] Emmanuel Fonseca et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J., 832(2):167, 2016.
- [33] John Antoniadis et al. A Massive Pulsar in a Compact Relativistic Binary. Science, 340:6131, 2013.
- [34] H. T. Cromartie et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nature Astron., 4(1):72–76, 2019.
- [35] E. Fonseca et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett., 915(1):L12, 2021.
- [36] M. H. van Kerkwijk, R. Breton, and S. R. Kulkarni. Evidence for a Massive Neutron Star from a Radial-Velocity Study of the Companion to the Black Widow Pulsar PSR B1957+20. Astrophys. J., 728:95, 2011.
- [37] M. C. Miller et al. PSR J0030+0451 Mass and Radius from Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett., 887(1):L24, 2019.
- [38] Thomas E. Riley et al. A View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett., 887(1):L21, 2019.
- [39] M. C. Miller et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett., 918(2):L28, 2021.
- [40] Thomas E. Riley et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett., 918(2):L27, 2021.
- [41] B. P. Abbott et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett., 121(16):161101, 2018.
- [42] R. Abbott et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett., 896(2):L44, 2020.
- [43] Eemeli Annala, Tyler Gorda, Aleksi Kurkela, and Aleksi Vuorinen. Gravitational-wave constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett., 120(17):172703, 2018.
- [44] Eemeli Annala, Tyler Gorda, Evangelia Katerini, Aleksi Kurkela, Joonas Nättilä, Vasileios Paschalidis, and Aleksi Vuorinen. Multimessenger Constraints for Ultradense Matter. Phys. Rev. X, 12(1):011058, 2022.
- [45] Oleg Komoltsev and Aleksi Kurkela. How Perturbative QCD Constrains the Equation of State at Neutron-Star Densities. Phys. Rev. Lett., 128(20):202701, 2022.
- [46] Tyler Gorda, Oleg Komoltsev, and Aleksi Kurkela. Ab-initio QCD calculations impact the inference of the neutron-star-matter equation of state. 4 2022.
- [47] Klaus Schertler, Stefan Leupold, and Jurgen Schaffner-Bielich. Neutron stars and quark phases in the NJL model. Phys. Rev. C, 60:025801, 1999.
- [48] S. Lawley, Wolfgang Bentz, and Anthony William Thomas. Neutron star properties from an NJL model modified to simulate confinement. Nucl. Phys. B Proc. Suppl., 141:29–33, 2005.
- [49] Takahide Kambe, Tetsuya Katayama, and Koichi Saito. Equation of State for Neutron Star Matter with NJL Model and Dirac–Brueckner–Hartree–Fock Approximation. JPS Conf. Proc., 14:020807, 2017.
- [50] German Malfatti, Milva Orsaria, Gustavo A. Contrera, and Fridolin Weber. Quark-hadron Phase Transition in Proto-Neutron Stars Cores based on a Non-local NJL Model. Int. J. Mod. Phys. Conf. Ser., 45:1760039, 2017.
- [51] T. Yazdizadeh and G. H. Bordbar. The structure of cold neutron star with a quark core within the MIT and NJL models. Iran. J. Sci. Technol. A, 43(5):2691–2698, 2019.
- [52] Takuya Minamikawa, Toru Kojo, and Masayasu Harada. Chiral condensates for neutron stars in hadron-quark crossover: From a parity doublet nucleon model to a Nambu–Jona-Lasinio quark model. Phys. Rev. C, 104(6):065201, 2021.
- [53] Takuya Minamikawa, Toru Kojo, and Masayasu Harada. Chiral condensates for neutron stars in hadron-quark crossover; from a parity doublet nucleon model to an NJL quark model. 2 2022.
- [54] Jan de Boer, Kyriakos Papadodimas, and Erik Verlinde. Holographic Neutron Stars. JHEP, 10:020, 2010.
- [55] Kazuo Ghoroku, Kouki Kubo, Motoi Tachibana, Tomoki Taminato, and Fumihiko Toyoda. Holographic cold nuclear matter as dilute instanton gas. Phys. Rev. D, 87(6):066006, 2013.
- [56] Kazuo Ghoroku, Kouki Kubo, Motoi Tachibana, and Fumihiko Toyoda. Holographic cold nuclear matter and neutron star. Int. J. Mod. Phys. A, 29:1450060, 2014.
- [57] Carlos Hoyos, David Rodríguez Fernández, Niko Jokela, and Aleksi Vuorinen. Holographic quark matter and neutron stars. Phys. Rev. Lett., 117(3):032501, 2016.
- [58] Niko Jokela, Matti Järvinen, and Jere Remes. Holographic QCD in the Veneziano limit and neutron stars. JHEP, 03:041, 2019.
- [59] Luis A. H. Mamani, Cesar V. Flores, and Vilson T. Zanchin. Phase diagram and compact stars in a holographic QCD model. Phys. Rev. D, 102(6):066006, 2020.
- [60] Takaaki Ishii, Matti Järvinen, and Govert Nijs. Cool baryon and quark matter in holographic QCD. JHEP, 07:003, 2019.
- [61] Niko Jokela, Matti Järvinen, Govert Nijs, and Jere Remes. Unified weak and strong coupling framework for nuclear matter and neutron stars. Phys. Rev. D, 103(8):086004, 2021.
- [62] Matti Järvinen. Holographic modeling of nuclear matter and neutron stars. Eur. Phys. J. C, 82(4):282, 2022.
- [63] Nicolas Kovensky and Andreas Schmitt. Isospin asymmetry in holographic baryonic matter. SciPost Phys., 11(2):029, 2021.
- [64] Nicolas Kovensky, Aaron Poole, and Andreas Schmitt. Building a realistic neutron star from holography. Phys. Rev. D, 105(3):034022, 2022.
- [65] Nicolas Kovensky, Aaron Poole, and Andreas Schmitt. Predictions for neutron stars from holographic nuclear matter. SciPost Phys. Proc., 6:019, 2022.
- [66] Lorenzo Bartolini, Sven Bjarke Gudnason, Josef Leutgeb, and Anton Rebhan. Neutron stars and phase diagram in a hard-wall AdS/QCD model. Phys. Rev. D, 105(12):126014, 2022.
- [67] Sitthichai Pinkanjanarod and Piyabut Burikham. Massive neutron stars with holographic multiquark cores. Eur. Phys. J. C, 81(8):705, 2021.
- [68] Sitthichai Pinkanjanarod, Piyabut Burikham, and Supakchai Ponglertsakul. Tidal deformation and radial pulsations of neutron star with holographic multiquark core. Eur. Phys. J. C, 82(2):141, 2022.
- [69] Piyabut Burikham, Sitthichai Pinkanjanarod, and Supakchai Ponglertsakul. Slowly rotating neutron star with holographic multiquark core: I-Love-Q relations. Phys. Rev. D, 105(10):104018, 2022.
- [70] David W Meltzer and Kip S Thorne. Normal modes of radial pulsation of stars at the end point of thermonuclear evolution. The Astrophysical Journal, 145:514, 1966.
- [71] James M Bardeen, Kip S Thorne, and David W Meltzer. A catalogue of methods for studying the normal modes of radial pulsation of general-relativistic stellar models. The Astrophysical Journal, 145:505, 1966.
- [72] Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, and Shinichiro Yamato. Baryons from instantons in holographic QCD. Prog. Theor. Phys., 117:1157, 2007.
- [73] Matti Jarvinen and Elias Kiritsis. Holographic Models for QCD in the Veneziano Limit. JHEP, 03:002, 2012.
- [74] U. Gursoy and E. Kiritsis. Exploring improved holographic theories for QCD: Part I. JHEP, 02:032, 2008.
- [75] U. Gursoy, E. Kiritsis, and F. Nitti. Exploring improved holographic theories for QCD: Part II. JHEP, 02:019, 2008.
- [76] Edward Witten. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys., 2:505–532, 1998.
- [77] Zhen Fang, Yue-Liang Wu, and Lin Zhang. Chiral phase transition and meson spectrum in improved soft-wall AdS/QCD. Phys. Lett. B, 762:86–95, 2016.
- [78] Zhen Fang, Yue-Liang Wu, and Lin Zhang. Chiral Phase Transition with 2+1 quark flavors in an improved soft-wall AdS/QCD Model. Phys. Rev. D, 98(11):114003, 2018.
- [79] Zhen Fang, Yue-Liang Wu, and Lin Zhang. Chiral phase transition and QCD phase diagram from AdS/QCD. Phys. Rev. D, 99(3):034028, 2019.
- [80] Zhen Fang, Yue-Liang Wu, and Lin Zhang. Octet meson spectra and chiral phase diagram in the improved soft-wall AdS/QCD model. Phys. Rev. D, 100(5):054008, 2019.
- [81] Feryal Özel and Paulo Freire. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys., 54:401–440, 2016.
- [82] Jason Hessels, Scott Ransom, Mallory Roberts, Victoria Kaspi, Margaret Livingstone, Cindy Tam, and Fronefield Crawford. Three new binary pulsars discovered with Parkes. ASP Conf. Ser., 328:395, 2005.
- [83] Ryan S. Lynch et al. The Green Bank Telescope 350 MHz Drift-scan Survey II: Data Analysis and the Timing of 10 New Pulsars, Including a Relativistic Binary. Astrophys. J., 763:81, 2013.
- [84] K. Stovall et al. The Green Bank Northern Celestial Cap Pulsar Survey - I: Survey Description, Data Analysis, and Initial Results. Astrophys. J., 791(1):67, 2014.
- [85] Ryan S. Lynch et al. The Green Bank North Celestial Cap Pulsar Survey III: 45 New Pulsar Timing Solutions. Astrophys. J., 859(2):93, 2018.
- [86] Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, volume 8443 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, September 2012.
- [87] B. P. Abbott et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett., 119(16):161101, 2017.
- [88] B. P. Abbott et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett., 848(2):L12, 2017.
- [89] Rong-Gen Cai, Song He, and Danning Li. A hQCD model and its phase diagram in Einstein-Maxwell-Dilaton system. JHEP, 03:033, 2012.
- [90] Xun Chen, Danning Li, Defu Hou, and Mei Huang. Quarkyonic phase from quenched dynamical holographic QCD model. JHEP, 03:073, 2020.
- [91] Song He, Yi Yang, and Pei-Hung Yuan. Analytic Study of Magnetic Catalysis in Holographic QCD. 4 2020.
- [92] Xun Chen, Lin Zhang, Danning Li, Defu Hou, and Mei Huang. Gluodynamics and deconfinement phase transition under rotation from holography. JHEP, 07:132, 2021.
- [93] Rong-Gen Cai, Song He, Li Li, and Yuan-Xu Wang. Probing QCD critical point and induced gravitational wave by black hole physics. 1 2022.
- [94] Zhibin Li, Yidian Chen, Danning Li, and Mei Huang. Locating the QCD critical end point through the peaked baryon number susceptibilities along the freeze-out line. Chin. Phys. C, 42(1):013103, 2018.
- [95] Xun Chen, Danning Li, and Mei Huang. Criticality of QCD in a holographic QCD model with critical end point. Chin. Phys. C, 43(2):023105, 2019.
- [96] Lin Zhang, Chutian Chen, Yidian Chen, and Mei Huang. Spectra of glueballs and oddballs and the equation of state from holographic QCD. Phys. Rev. D, 105(2):026020, 2022.
- [97] Danning Li, Song He, Mei Huang, and Qi-Shu Yan. Thermodynamics of deformed AdS5 model with a positive/negative quadratic correction in graviton-dilaton system. JHEP, 09:041, 2011.
- [98] Hermann Weyl and Henry L Brose. Raum–zeit–materie [space–time–matter]. Lectures on General Relativity (in German)(Springer, Berlin, 1921), 1921.
- [99] H Weyl and J Ehlers. Space, time, matter: Lectures on general relativity. Berlin, Germany: Springer, 1993.
- [100] M. Tanabashi, K. Hagiwara, K. Hikasa, et al. Review of particle physics. Phys. Rev. D, 98:030001, Aug 2018.
- [101] Oliver DeWolfe, Steven S. Gubser, and Christopher Rosen. A holographic critical point. Phys. Rev. D, 83:086005, 2011.
- [102] Renato Critelli, Jorge Noronha, Jacquelyn Noronha-Hostler, Israel Portillo, Claudia Ratti, and Romulo Rougemont. Critical point in the phase diagram of primordial quark-gluon matter from black hole physics. Phys. Rev. D, 96(9):096026, 2017.
- [103] S. Borsányi, Z. Fodor, J. N. Guenther, R. Kara, S. D. Katz, P. Parotto, A. Pásztor, C. Ratti, and K. K. Szabó. Lattice QCD equation of state at finite chemical potential from an alternative expansion scheme. Phys. Rev. Lett., 126(23):232001, 2021.
- [104] Yuta Hamada, Elias Kiritsis, and Francesco Nitti. Holographic Theories at Finite -Angle, CP-Violation, Glueball Spectra and Strong-Coupling Instabilities. Fortsch. Phys., 69(2):2000111, 2021.
- [105] Song He, Shang-Yu Wu, Yi Yang, and Pei-Hung Yuan. Phase Structure in a Dynamical Soft-Wall Holographic QCD Model. JHEP, 04:093, 2013.
- [106] David Dudal and Subhash Mahapatra. Thermal entropy of a quark-antiquark pair above and below deconfinement from a dynamical holographic QCD model. Phys. Rev. D, 96(12):126010, 2017.
- [107] Wei-jie Fu, Jan M. Pawlowski, and Fabian Rennecke. QCD phase structure at finite temperature and density. Phys. Rev. D, 101(5):054032, 2020.
- [108] Zhibin Li, Kun Xu, Xinyang Wang, and Mei Huang. The kurtosis of net baryon number fluctuations from a realistic Polyakov–Nambu–Jona-Lasinio model along the experimental freeze-out line. Eur. Phys. J. C, 79(3):245, 2019.
- [109] K. Hebeler, J. M. Lattimer, C. J. Pethick, and A. Schwenk. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J., 773:11, 2013.
- [110] Paulo Bedaque and Andrew W. Steiner. Sound velocity bound and neutron stars. Phys. Rev. Lett., 114(3):031103, 2015.
- [111] Len Brandes, Wolfram Weise, and Norbert Kaiser. Inference of the sound speed and related properties of neutron stars. 8 2022.
- [112] Larry McLerran and Sanjay Reddy. Quarkyonic Matter and Neutron Stars. Phys. Rev. Lett., 122(12):122701, 2019.
- [113] Richard C. Tolman. Effect of imhomogeneity on cosmological models. Proc. Nat. Acad. Sci., 20:169–176, 1934.
- [114] Richard C. Tolman. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev., 55:364–373, 1939.
- [115] J. R. Oppenheimer and G. M. Volkoff. On massive neutron cores. Phys. Rev., 55:374–381, 1939.
- [116] Niko Jokela, Matti Järvinen, and Jere Remes. Holographic QCD in the NICER era. Phys. Rev. D, 105(8):086005, 2022.
- [117] Eanna E. Flanagan and Tanja Hinderer. Constraining neutron star tidal Love numbers with gravitational wave detectors. Phys. Rev. D, 77:021502, 2008.
- [118] Tanja Hinderer. Tidal Love numbers of neutron stars. Astrophys. J., 677:1216–1220, 2008.
- [119] Tanja Hinderer, Benjamin D. Lackey, Ryan N. Lang, and Jocelyn S. Read. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D, 81:123016, 2010.
- [120] Tullio Regge and John A. Wheeler. Stability of a Schwarzschild singularity. Phys. Rev., 108:1063–1069, 1957.
- [121] James B. Hartle and Kip S. Thorne. Slowly Rotating Relativistic Stars. III. Static Criterion for Stability. Astrophys. J. , 158:719, November 1969.
- [122] Yong-Liang Ma and Mannque Rho. Sound velocity and tidal deformability in compact stars. Phys. Rev. D, 100(11):114003, 2019.
- [123] A. Kanakis-Pegios, P. S. Koliogiannis, and Ch. C. Moustakidis. Speed of sound constraints from tidal deformability of neutron stars. Phys. Rev. C, 102(5):055801, 2020.
- [124] Alkiviadis Kanakis-Pegios, Polychronis Koliogiannis, and Charalampos Moustakidis. Constraints on the speed of sound of dense nuclear matter through the tidal deformability of neutron stars. EPJ Web Conf., 252:05005, 2021.
- [125] Won-Gi Paeng, Thomas T. S. Kuo, Hyun Kyu Lee, Yong-Liang Ma, and Mannque Rho. Scale-invariant hidden local symmetry, topology change, and dense baryonic matter. II. Phys. Rev. D, 96(1):014031, 2017.
- [126] Yong-Liang Ma, Hyun Kyu Lee, Won-Gi Paeng, and Mannque Rho. Pseudoconformal equation of state in compact-star matter from topology change and hidden symmetries of QCD. Sci. China Phys. Mech. Astron., 62(11):112011, 2019.
- [127] Yong-Liang Ma and Mannque Rho. Pseudoconformal structure in dense baryonic matter. Phys. Rev. D, 99(1):014034, 2019.