Holographic heat engine in Horndeski model with the -essence sector
Abstract
We study the extended thermodynamical properties of the charged black hole in Horndeski model with the -essence sector. Then we define a holographic heat engine via the black hole. We compute the engine efficiency in the large temperature limit and compare the results with the exact ones. With the given specified parameters in the rectangular engine, the higher order coupling suppresses the engine efficiencies.
pacs:
04.20.Gz, 04.20.-q, 03.65.-wI Introduction
Thermodynamics of the anti de Sitter (AdS) black holes are important fields for us to understand the nature of quantum gravity and it has been attracting much attention in the development of holographic gauge/gravity duality Maldacena:1997re ; Gubser:1998bc ; Witten:1998qj . Recently, one of the most significant progress in the study of black hole thermodynamic is extending the study into a more general case by treating the cosmological constant, , as the pressure of the thermal black hole systemKastor:2009wy ; Dolan:2010ha ; Cvetic:2010jb ; Dolan:2011xt . In this synopsis, the thermodynamical volume is defined as the conjugation of the pressure or , and it usually satisfies the Reverse Isoperimetric InequalityCvetic:2010jb ; Altamirano:2014tva with a counterexample proposed in Hennigar:2014cfa . And the standard smarr formula also has to be modified such that the mass of the black hole plays the role of the enthalpy of the thermodynamical systemKastor:2009wy . Phenomena in the extended thermodynamic of black hole including Van der Waals like phase transition, triple points and reentrant phase transition and so on have been investigated. Readers can refer to the review paper Kubiznak:2016qmn and therein for references.
Besides, based on the extended thermodynamic of AdS black hole, the author of Johnson:2014yja proposed to define a traditional heat engine via an AdS black hole, which is realized by a circle in the pressure-volume phase space of the black hole. The defined engine is also called holographic heat engine because the engine circle represents a process defined on the space of the dual field theory living in one dimension lower than the bulk. In this engine, the input of heat, the exhaust of heat and the mechanical work all can be determined from the gravitational system, so the engine efficient can directly be evaluated in the bulk. The studies of holographic engine were soon extended in other modified gravitational model, such as with Gauss-Bonnet correctionJohnson:2015ekr , in Born-Infeld corrected black holeJohnson:2015fva , in rotational black holeHennigar:2017apu ; Johnson:2017ood , in three dimensional black holeMo:2017nhw and so onLiu:2017baz ; Wei:2016hkm ; Mo:2018hav ; Xu:2017ahm ; Zhang:2018vqs , and many remarkable properties of engine efficiency were observed. More recently, it was addressed in Johnson:2018amj that the holographic heat engines defined via AdS black hole can be seen as a working substance correspond to specific combinations of conform field theory flows and deformations.
Since our world is far from being ideal, so it is more realistic to study the heat engine defined via black holes with momentum relaxation. The engine efficiency modified by mass of graviton, which breaks the diffimophism system in the bulk and so introduces the momentum relaxation in the dual theoryDavison:2013jba , has been carefully studied in Mo:2017nes ; Hendi:2017bys . One of us studied the heat engine in the Einstein-Maxwell-Axions theoryFang:2017nse , where the momentum relaxation is introduced by the linear massless axion fieldsAndrade:2013gsa .
The aim of this paper is to continue to construct holographic heat engine with momentum relaxation. We will work in the Horndeski gravity with the -essence sector proposed in Cisterna:2017jmv . In this theory, besides the minimal coupling of axions term, , the authors included nonlinear terms in the form of an arbitrary power of and got the exact black hole solution. So this paper can be treated as the extension of our previous work Fang:2017nse . Note that with the use of holography, it is found in Cisterna:2017jmv that the nonlinear terms modifies the dc conductivities. So we also expect that the terms will enrich the properties of the dual heat engine.
Following is the plan of this paper. We briefly review the AdS black hole solution in Horndeski model with the -essence sector in section II and then study the extended thermodynamics in section III. In section IV, we define the holographic engine and get its general efficiency while in section V, we compute the engine efficiency in large temperature limit and then compare the results with the exact results. Section VI is our conclusions and discussions. In this paper, we will work in the units with .
II Horndeski model with the -essence sector
We shall briefly review the four-dimensional Horndeski gravity with the -essence sector proposed in Cisterna:2017jmv . The action was given by
| (1) |
where the cosmological constant is with the AdS radius and with . are massless scalar field and is the field strength of Maxwell field. The above action goes back to that for the minimally coupled Einstein-Maxwell-axions gravity studied in Bardoux:2012aw ; Andrade:2013gsa . The equations of motions derived from the action are the Klein-Gordon equation
| (2) |
the Maxwell equation
| (3) |
and the Einstein equation
| (4) |
The above equations of motion admit the following exact black hole solution
| (5) | |||||
| (6) |
and the matter fields
| (7) | |||||
| (8) |
where are integral constants which are connected with the physical quantities of the black hole and the integral constant is to guarantee the regular condition of Maxwell field at the horizon. So this solution is not exactly the one presented in Cisterna:2017jmv where they had the Coulomb form . We note that as pointed out in Cisterna:2017jmv , the coupling parameter is required to be positive to avoid phantom contributions. And the null energy condition, finite ADM mass and asymptotically matching the GR black hole solution requires the restriction in the solution.
III The extended thermodynamics
The usual thermodynamical analysis has been achieved via the Euclidean approach in Cisterna:2017jmv . Here, we will analyze the extended thermodynamical properties of the black hole solution (5)-(8). To this end, we connect the cosmological constant and the pressure of the system via Kastor:2009wy ; Dolan:2010ha ; Cvetic:2010jb ; Dolan:2011xt
| (9) |
where the thermodynamic quantity conjugate to the pressure is defined as the thermodynamic volume of black holes.
Defining the location of horizon, , which satisfies in (6), the integral constant is solved as
| (10) |
where we have used (9). The Hawking temperature of the black hole is given by,
| (11) |
and the entropy is
| (12) |
The mass and charge of the black hole are connected with the parameters asBHMASS
| (13) |
where is the volume of the two dimensional flat space. Subsequently, the thermodynamical volume as the conjugation of the pressure is
| (14) |
and the electric potential of the black hole isCaldarelli:1999xj ; Cvetic:1999ne
| (15) |
It is straightforward to verify that the first law of thermodynamics
| (16) |
is satisfied.
According to the dimensional analysisKastor:2009wy , we obtain that the modified Smarr relation for the black hole is111We thank Yen Chin Ong for the helpful discussion on the Smarr formula.
| (17) |
where is the conjugation of with dimension
| (18) |
It is obvious that without the higher order coupling, i.e, or , the Smarr formula is standard which goes back to the result found in Fang:2017nse . The above Smarr like relation leads us to consider the role of the mass from internal energy to enthalpy, and so the first law of black hole thermodynamics (16) should be modified as
| (19) |
From the expression of temperature, we get the state equation
| (20) |
In the right hand side of (20), all terms are positive since can only be positive, so we can not observe the criticality in the extended phase space proposed in Chamblin:1999tk ; Chamblin:1999hg ; Kubiznak:2012wp . This is not necessary to construct dual heat engine to the black hole, which we will study in next sections.
IV Holographic heat engine and its general efficiency
We will study the holographic heat engine built via the black hole solution described in previous section. Before the construction, we have to exact two important thermodynamical physical quantities, the specific heat with the constant volume, , and the specific heat with constant pressure, , of the black hole. The general specific heat is defined as , so we can treat both and as functions of the horizon to achieve the calculation.
Differentiation of (12) gives us
| (21) |
The differentiation to the expression of temperature (11) is
| (22) |
from which we obtain
| (23) |
Then the general formula of the specific heat is
| (24) |
In the case with constant volume which means also constant via (14), the state equation (20) gives us . Thus, the specific heat at constant volume is reduced to
| (25) |
which implies that adiabats and isochores are equivalent. We will see soon that this is a helpful property in the construction of the cycle of the holographic heat engine.
In the case with constant pressure, we have , so the specific heat at constant pressure, , is
| (26) |
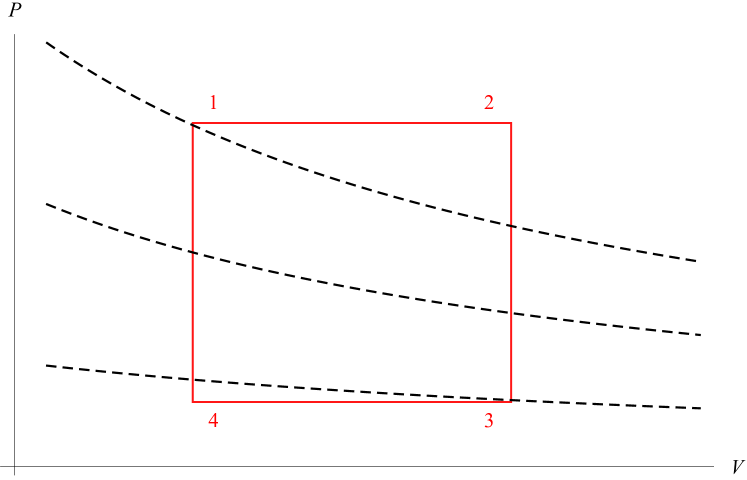
Now, we are ready to define a heat engine dual to the black hole. Following Johnson:2015fva ; Hennigar:2017apu ; Xu:2017ahm ; Johnson:2017ood ; Mo:2017nhw ; Liu:2017baz ; Wei:2016hkm ,we consider a rectangle cycle in the plane. The cycle is consisted by two isobars and two isochores as shown in figure 1 where are four corners in the thermal flow cycle. We will express the relevant quantities evaluated with the use the subscripts at the related corners. The engine efficiency is computed by
| (27) |
where is the work done by the engine and is the input of the heat due to the equivalence of adiabats and isochores in the circle, respectively. It is noticed that in plane, the isotherms at temperatures and with give the Carnot efficiency and for our engine, it is
| (28) |
The effect of the momentum on the engine efficiency has been studied by one of us in Fang:2017nse . So here we will mainly study the engine efficiency modified by the higher terms of the axions field . We will set and the volume without loss of generality.
V Engine efficiency in large temperature limit
To evaluate the efficiency, in general, we can cancel in (26) using (11) to rewrite as a function of and then applying the definition (27). However, the integration is difficult to proceed. So in order to study the efficiency directly from the definition. We consider the large temperature limit, i.e., , which means that can be treated as a small quantity. Solving in term of large from (11), we obtain
| (29) | |||||
Then from (14) and (26), we get the thermodynamic volume and the specific heat at constant pressure in large limit as
| (30) | |||||
| (31) | |||||
respectively.
Subsequently, we can substitute the above expression of and into (27) to calculate the efficiency of the engine. Considering the relations of each corner in the circle, we find is finally determined by the values of and we will not write down the detailed expression due to the complexity.
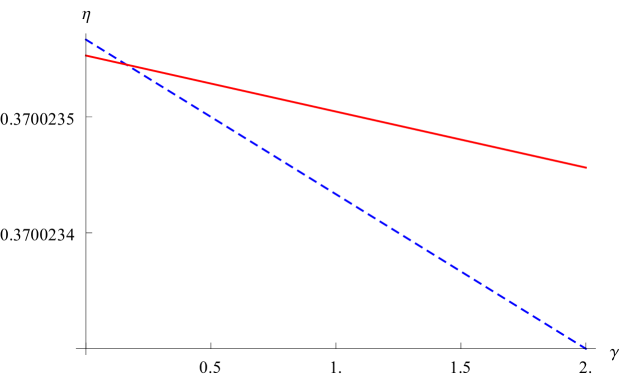
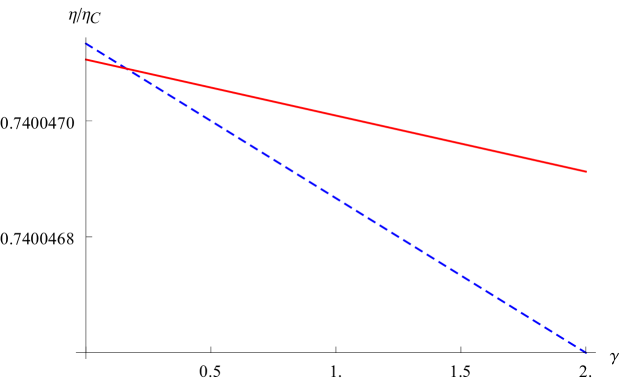
We now study the affection of higher terms of axions on . It was addressed in Johnson:2014yja that one can process by choose different schemes on the given specified quantities. Here, we will work with given specified because in this scheme the Carnot efficiency will not change with parameters. Recalling the state equation (20), we can calculate via and via and , respectively. Then we can further calculate via . The efficiencies and change as are shown by dashed lines in figure 2 which shows that and are both suppressed by increasing the coupling parameter. is always lower than the Carnot efficiency which is expected because Carnot cycle is the most efficient. We also list the related efficiency for samples of exponent in table 1. As increases, increases slowly, so does .
| 0.37002343 | 0.74004687 | |
| 0.37002355 | 0.74004712 | |
| 0.37002357 | 0.74004713 |
In order to examine whether the above results in large limit are reliable, we shall double check them with the exact formula of efficiency
| (32) |
proposed in Johnson:2016pfa where denote the related mass of the black hole evaluated at each corner in the cycle, i.e., the values of (13) computed at each corner. With the same setup, the results of and evaluated by (32) are shown by solid lines in figure 2. Comparing with the dashed and solid lines in the plots, though the results in large limit have derivation from the exact results, but the rules are the same. The agreement is also fulfilled for different power exponent .
VI Conclusion
In this paper, we focused on the charged AdS black hole in Horndeski gravity with the -essence sector proposed in Cisterna:2017jmv where higher order couplings of axions field were introduced. We studied the extended thermodynamics of the black hole and derived the modified smarr formula as well as the generalized first law of thermodynamic. We found that the coupling parameter should be treated as a thermodynamical quantity to achieve them.
Then based on the extended thermodynamics, we built the holographic heat engine by the AdS black hole. We especially studied the effect of higher order couplings on the efficiency of heat engine in large temperature limit. With the given specified , the efficiency is always lower than the Carnot efficiency as we expect, and it is suppressed by the stronger coupling parameter. Moreover, as the exponent of higher coupling increases, the efficiency is enhanced slowly. Finally, we also calculated the exact efficiencies by the method proposed Johnson:2016pfa and it was shown that our results in large temperature somehow is reliable. It is notable that it is also interesting to study the heat engine with momentum relaxation constructed via black string or p-brane exactly solved in Cisterna:2017qrb .
In this paper, we have focused on the rectangular engine shown in figure 1, the studies on how the momentum relaxations terms affect on the engine efficiency in circular engine Chakraborty:2016ssb and axially symmetric engine as well as riangular type engineRosso:2018acz , can be further extended. As claimed in Johnson:2018amj that the holographic heat engines can be seen as a working substance correspond to specific combinations of conform field theory flows and deformations, so it would be significant to investigate from holography that the role of the higher couplings in the flows, which may help us understand the deep physic of the phenomena we observed. We shall study this issue in the near future.
Acknowledgement
This work is supported by the Natural Science Foundation of China under Grant No.11705161 and Natural Science Foundation of Jiangsu Province under Grant No.BK20170481. Xiao-Mei Kuang appreciates Li-Qing Fang for the related collaborations and she also appreciates Adolfo Cisterna for nice correspondence. We thank Bo Liu and group members in CGC of YZU (http://www.cgc-yzu.cn) for helpful discussions.
References
- (1) J. M. Maldacena, “ The Large N limit of superconformal field theories and supergravity”, Int. J. Theor. Phys. 38, 1113 (1999) [Adv. Theor. Math. Phys. 2, 231 (1998)] [hep-th/9711200].
- (2) S. S. Gubser, I. R. Klebanov and A. M. Polyakov, “ Gauge theory correlators from noncritical string theory”, Phys. Lett. B 428, 105 (1998) [hep-th/9802109].
- (3) E. Witten, “Anti-de Sitter space and holography”, Adv. Theor. Math. Phys. 2, 253 (1998) [hep-th/9802150].
- (4) D. Kastor, S. Ray and J. Traschen, “Enthalpy and the Mechanics of AdS Black Holes,” Class. Quant. Grav. 26, 195011 (2009) [arXiv:0904.2765 [hep-th]].
- (5) B. P. Dolan, “The cosmological constant and the black hole equation of state,” Class. Quant. Grav. 28, 125020 (2011) [arXiv:1008.5023 [gr-qc]].
- (6) M. Cvetic, G. W. Gibbons, D. Kubiznak and C. N. Pope, “Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume,” Phys. Rev. D 84, 024037 (2011) [arXiv:1012.2888 [hep-th]].
- (7) B. P. Dolan, “Pressure and volume in the first law of black hole thermodynamics,” Class. Quant. Grav. 28, 235017 (2011) [arXiv:1106.6260 [gr-qc]].
- (8) N. Altamirano, D. Kubiznak, R. B. Mann and Z. Sherkatghanad, “Thermodynamics of rotating black holes and black rings: phase transitions and thermodynamic volume,” Galaxies 2, 89 (2014) [arXiv:1401.2586 [hep-th]].
- (9) R. A. Hennigar, D. Kubiz and R. B. Mann, “Entropy Inequality Violations from Ultraspinning Black Holes,” Phys. Rev. Lett. 115, no. 3, 031101 (2015) [arXiv:1411.4309 [hep-th]].
- (10) D. Kubiznak, R. B. Mann and M. Teo, “Black hole chemistry: thermodynamics with Lambda,” Class. Quant. Grav. 34, no. 6, 063001 (2017) [arXiv:1608.06147 [hep-th]].
- (11) C. V. Johnson, “Holographic Heat Engines,” Class. Quant. Grav. 31, 205002 (2014) [arXiv:1404.5982 [hep-th]].
- (12) C. V. Johnson, “Gauss-Bonnet black holes and holographic heat engines beyond large ,” Class. Quant. Grav. 33, no. 21, 215009 (2016) [arXiv:1511.08782 [hep-th]].
- (13) C. V. Johnson, “Born-Infeld AdS black holes as heat engines,” Class. Quant. Grav. 33, no. 13, 135001 (2016) [arXiv:1512.01746 [hep-th]].
- (14) R. A. Hennigar, F. McCarthy, A. Ballon and R. B. Mann, “Holographic heat engines: general considerations and rotating black holes,” Class. Quant. Grav. 34, no. 17, 175005 (2017) [arXiv:1704.02314 [hep-th]].
- (15) C. V. Johnson, “Taub-Bolt heat engines,” Class. Quant. Grav. 35, no. 4, 045001 (2018) [arXiv:1705.04855 [hep-th]].
- (16) J. X. Mo, F. Liang and G. Q. Li, “Heat engine in the three-dimensional spacetime,” JHEP 1703, 010 (2017) [arXiv:1701.00883 [gr-qc]].
- (17) H. Xu, Y. Sun and L. Zhao, “Black hole thermodynamics and heat engines in conformal gravity,” Int. J. Mod. Phys. D 26, no. 13, 1750151 (2017) [arXiv:1706.06442 [gr-qc]].
- (18) H. Liu and X. H. Meng, “Effects of dark energy on the efficiency of charged AdS black holes as heat engines,” Eur. Phys. J. C 77, no. 8, 556 (2017) [arXiv:1704.04363 [hep-th]].
- (19) S. W. Wei and Y. X. Liu, “Implementing black hole as efficient power plant,” arXiv:1605.04629 [gr-qc].
- (20) J. X. Mo and S. Q. Lan, “Phase transition and heat engine efficiency of phantom AdS black holes,” arXiv:1803.02491 [gr-qc].
- (21) J. Zhang, Y. Li and H. Yu, arXiv:1801.06811 [hep-th].
- (22) C. V. Johnson and F. Rosso, “Holographic Heat Engines, Entanglement Entropy, and Renormalization Group Flow,” arXiv:1806.05170 [hep-th].
- (23) R. A. Davison, “Momentum relaxation in holographic massive gravity,” Phys. Rev. D 88, 086003 (2013) [arXiv:1306.5792 [hep-th]].
- (24) J. X. Mo and G. Q. Li, “Holographic Heat engine within the framework of massive gravity,” JHEP 1805, 122 (2018) [arXiv:1707.01235 [gr-qc]].
- (25) S. H. Hendi, B. Eslam Panah, S. Panahiyan, H. Liu and X.-H. Meng, “Black holes in massive gravity as heat engines,” Phys. Lett. B 781, 40 (2018) [arXiv:1707.02231 [hep-th]].
- (26) L. Q. Fang and X. M. Kuang, “Holographic heat engine with momentum relaxation,” Sci. China Phys. Mech. Astron. 61, 080421 (2018) [arXiv:1710.09054 [hep-th]].
- (27) T. Andrade and B. Withers, “A simple holographic model of momentum relaxation,” JHEP 1405, 101 (2014) [arXiv:1311.5157 [hep-th]].
- (28) A. Cisterna, M. Hassaine, J. Oliva and M. Rinaldi, “Axionic black branes in the k-essence sector of the Horndeski model,” Phys. Rev. D 96, no. 12, 124033 (2017) [arXiv:1708.07194 [hep-th]].
- (29) Y. Bardoux, M. M. Caldarelli and C. Charmousis, “Shaping black holes with free fields,” JHEP 1205, 054 (2012) [arXiv:1202.4458 [hep-th]].
- (30) R. C. Myers and J. Z. Simon, Phys. Rev. D 38, 2434 (1988); L. F. Abbott and S. Deser, Nucl. Phys. B 195, 76 (1982).
- (31) M. M. Caldarelli, G. Cognola and D. Klemm, “Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories,” Class. Quant. Grav. 17, 399 (2000) [hep-th/9908022].
- (32) M. Cvetic and S. S. Gubser, “Phases of R charged black holes, spinning branes and strongly coupled gauge theories,” JHEP 9904, 024 (1999) [hep-th/9902195].
- (33) A. Chamblin, R. Emparan, C. V. Johnson and R. C. Myers, “Charged AdS black holes and catastrophic holography,” Phys. Rev. D 60, 064018 (1999) [hep-th/9902170].
- (34) A. Chamblin, R. Emparan, C. V. Johnson and R. C. Myers, “Holography, thermodynamics and fluctuations of charged AdS black holes,” Phys. Rev. D 60, 104026 (1999) [hep-th/9904197].
- (35) D. Kubiznak and R. B. Mann, “P-V criticality of charged AdS black holes,” JHEP 1207, 033 (2012) [arXiv:1205.0559 [hep-th]].
- (36) C. V. Johnson, “An Exact Efficiency Formula for Holographic Heat Engines,” Entropy 18, 120 (2016) [arXiv:1602.02838 [hep-th]].
- (37) A. Cisterna and J. Oliva, “Exact black strings and p-branes in general relativity,” Class. Quant. Grav. 35, no. 3, 035012 (2018) [arXiv:1708.02916 [hep-th]].
- (38) A. Chakraborty and C. V. Johnson, “Benchmarking Black Hole Heat Engines,” arXiv:1612.09272 [hep-th].
- (39) F. Rosso, “Holographic heat engines and static black holes: a general efficiency formula,” arXiv:1801.07425 [hep-th].