Homogeneous crystallization in cyclically sheared frictionless grains
Abstract
Many experiments over the past half century have shown that, for a range of protocols, granular materials compact under pressure and repeated small disturbances. A recent experiment on cyclically sheared spherical grains showed significant compaction via homogeneous crystallization (Rietz et al., 2018). Here we present numerical simulations of frictionless, purely repulsive spheres undergoing cyclic simple shear with dissipative Newtonian dynamics at fixed vertical load. We show that for sufficiently small strain amplitudes, cyclic shear gives rise to homogeneous crystallization at a volume fraction . This result indicates that neither friction nor gravity is essential for homogeneous crystallization in driven granular media.
Loose granular materials will compact under a range of different protocols of small repeated disturbances while under the influence of gravity and/or external pressure. In the half century following the pioneering work of J.D. Bernal [1] and G.D. Scott [2] around 1960, the existence of a barrier to compaction has been confirmed for many types of disturbances [3, 4, 5, 6], but not for cyclic shear for which the systems compacted via wall-induced crystallization [7]. Walls that inhibit nucleation and precision measurements of the positions of the spherical grains recently enabled Rietz et al. [8] to observe homogeneous crystallization in a granular material undergoing cyclic shear.
Using Newtonian overdamped dynamics, we numerically simulate purely repulsive spherical grains undergoing cyclic simple shear strain dynamics to model granular crystallization in the Rietz et al. experiment [8]. The simulations allow us to tune the grain interactions, gravity, and boundary conditions to understand the essential physics that gives rise to homogeneous crystallization.
Our simulations reveal the essential physical requirements needed for crystallization in driven dissipative granular materials: volume exclusion, system confinement, and small disturbances that allow grain rearrangements. In particular, gravity, friction, and energy conservation are not required to yield homogeneous crystallization. The simulations use deterministic dynamics in contrast with the probabilistic evolution equations used in classical nucleation theory [9] to model crystallization in atomic and molecular systems.
From the simulations we show that the volume fraction at the onset of crystallization becomes independent of the shear amplitude for sufficiently small amplitudes, rad, consistent with Rietz et al. [8], who used rad. The volume fraction at the onset of crystallization is also within the range of jamming volume fractions found for different packing generation protocols for frictionless hard spheres [11].
Methods. We simulate cyclic simple shear of frictionless monodisperse spheres in three spatial dimensions using a discrete element method (see Supplemental Materials (SM), Sec. B [10]). Figure 1(a) shows the simulation shear cell, designed to mimic the parallelepiped shear cell used in experiments [7] with two sidewalls that tilt with respect to the vertical axis by a variable angle in the - plane, and a bottom wall that oscillates horizontally and can move vertically under an applied load. The system is periodic in the -direction. The initial jammed packing is prepared via gravitational deposition by pouring the grains into a static container and allowing the dissipative forces to remove the kinetic energy in the system. A subsystem, of size in the -, -, and -directions, is cut out from the initial packing, where is the grain diameter (see Fig.1(b)). Grains with center positions less than away from all of the surfaces of the subsystem except the two in the direction are then fixed to form the walls. Wall-induced crystallization is suppressed since the grains forming the walls are randomly positioned. Simulations were run for cells with edge lengths , , , and containing, respectively, , , , and grains. The selection of the simulation time step size is discussed in SM Sec. B.3 [10].
The grains are modeled as frictionless spheres interacting via the pairwise, purely repulsive linear spring force,
| (1) |
where is the spring constant (see SM Sec. B.1 [10]), is the intergrain overlap, is the center-to-center separation between grains and , is the Heaviside step function, and is the unit vector pointing from the center of grain to the center of grain . The interaction between the fixed wall grains and the interior grains follows the same force law as that between pairs of interior grains. Under gravity in the -direction, Newton’s equation of motion for each interior grain is given by
| (2) |
where is the acceleration due to gravity, , , and are the mass, acceleration, and velocity of grain , is the number of grains overlapping grain , and is the damping constant. The damping force arises from Stokes drag with the assumption of the existence of fluid in the cell, as in the experiment of Rietz et al. We consider two forms for for the Stokes drag; see SM Sec. B.2 [10]. The equations of motion are integrated using a modified velocity-Verlet scheme. We are interested in simulating grains in the hard sphere limit; the relationship between the spring constant and the interparticle overlap is discussed in SM Sec. B.1 [10]).
To shear the packing, the bottom wall oscillates in the -direction (see Fig. 1 (a)) as the two sidewalls tilt with an angle that evolves with time as
| (3) |
where is the shear amplitude and is the angular frequency. We study shear amplitudes , , , , , and rad. The oscillating bottom wall consists of grains and is subjected to a force from interior grains. The motion of the bottom wall due to the applied pressure can be obtained by solving
| (4) |
where is the total mass of grains in the bottom wall and and are the acceleration and velocity of the bottom wall, which is constrained to move along the direction, , at time . The values of the simulation parameters are listed in Table 1.
An alternative energy relaxation method was also considered, closer to that used in the experiment of Rietz et al. [8]. Simulations with amplitude rad were carried out with the grains allowed to come to rest after each cycle of the walls, instead of moving the walls and dissipating energy continuously. Fig. S4 in Supplemental Material Sec. B.4 shows that the results for the fraction of crystallized grains versus volume fraction using the two relaxation methods is similar until .
| Parameter | Value |
|---|---|
| Grain mass | kg |
| Grain diameter | m |
| Spring constant | N/m |
| Damping constant | kg/s |
| Pressure | Pa |
| Angular frequency | rad/s |
| Simulation steps per cycle | 45600 |
| Gravitational acceleration | 9.81 m/s2 |
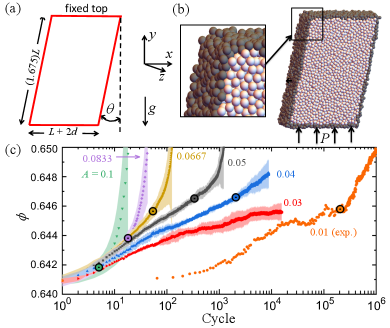

Results. Intuitively, the global volume fraction of a collection of grains in a container is the sum of the volumes of the grains divided by the volume of the container. If one partitions the volume of the container by the Voronoi cells of the grains, one has a useful local version, the local volume fraction for that Voronoi cell or grain. Our grains are slightly deformable so there is some choice in how to assign a volume to them. We are interested in modeling asymptotically hard grains, as in the experiment Rietz et al, so we define the volume of a grain to be , where is the maximum of the ‘overlap’ volume of that sphere with its neighbors (see Supplemental Material Sec. B.1). The global volume fraction of a collection of grains is then the mean of the local volume fractions of all the ‘free’ grains, that is, the grains which are fixed as part of the boundary are not counted.
The results for the global volume fraction obtained in our simulations for shear amplitudes , , , , , and rad are shown in Fig. 1(c), along with results from the experiment of Rietz et al. [8] for rad. The volume fraction increases in a similar way for each shear amplitude for the first few shear cycles (i.e., ), while subsequently the increase in volume fraction is more rapid for larger shear amplitudes, as seen already by Scott experimentally [7].
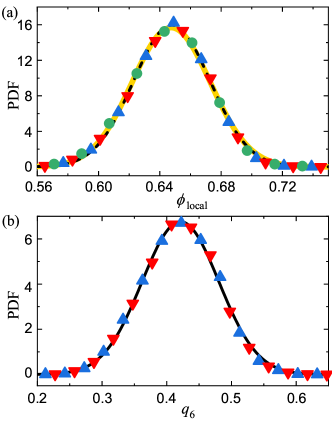
At low shear amplitudes and for sufficiently small cycle numbers, the system remains disordered. Figure 2(a) shows, for rad and several cycle numbers, probability distribution functions for the local volume fraction . These probability distributions become time-invariant after shear cycles. Figure 2(b) shows time invariance also in the probability distribution functions for the local bond orientational order [12], which we use to identify crystallization; see Supplemental Material Sec. A for background. Similarly, the experiment with rad reached a persistent state at shear cycles (see Fig. 1(c)).
The simulations with amplitudes rad do not give rise to a persistent state, as can be seen in Fig. 1(c). Further, Fig. 3 shows that for the probability distribution function for the local density starts as a Gaussian with a peak near . With an increasing number of shear cycles, the height of this peak decreases and its width increases. With continued shearing, a second peak emerges at in both the experiment with rad and in the simulations with rad. (Thus, the persistent state in the simulations at rad begins to disappear for shear amplitudes in the range and is absent for larger .) The second peak in the probability distribution at corresponds to the formation of HCP and FCC crystallites.
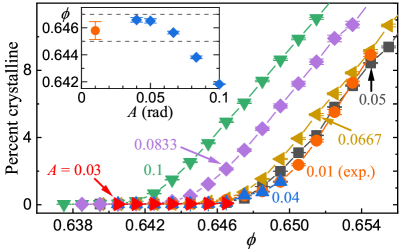
Figure 4 presents results for the fraction of the system that is crystalline in simulations with different amplitudes . (The identification of crystalline grains is discussed in SM Sec. A [10].) The similarity between the results from the simulation for rad and the experiment for rad is remarkable considering the many differences between the simulation model and the laboratory experiment. For rad (i.e., , , and rad), the crystallization onset occurs for a smaller volume fraction than the onset observed in the experiment.
We have considered several methods for obtaining an accurate estimate for the volume fraction at the onset of crystallization in a system satisfying the limits of small shear amplitude and large system size. The method used for the inset of Fig. 4 is to determine the critical cluster size for each shear amplitude and identify the associated value of the volume fraction; see Supplemental Material Sec. C for a comparison with an alternative method for determining the volume fraction at the onset of crystallization. Both methods are in quantitative agreement, yielding the results in the inset of Fig. 4.
Discussion. The results obtained from the simulations of the deterministic equations of motion for frictionless monodisperse spheres in a container undergoing periodic shear reveal the onset of homogeneous crystallization that depends on the shear amplitude and on the number of grains in the system. However, the simulations show that there is a well-defined volume fraction, , above which homogeneous crystallization occurs in the limit of small amplitude, rad (see inset of Fig. 4(a)) and large system size, . This characteristic volume fraction agrees well with the experimental value found in Rietz et al. [8], where rad and .
Note that there are multiple differences between the experiment by Rietz et al. and the simulations, including the form of the dissipation, which in the experiment arises from Stokes drag on the motion of the grains relative to the viscous refractive-index-matching fluid surrounding the grains, from the inelasticity of the grains, and from the static and dynamic friction between grains in contact. In contrast, in the simulations only Stokes dissipation is included; the static and kinetic friction coefficients are zero. Still, the results for the onset of crystallization in the simulations and the Rietz et al. experiment agree in the limits of hard-sphere interactions, low driving amplitude, and large system size.
The random close packed (RCP) limit, which has been discussed in more than one thousand papers in the past half century, has never been unambiguously defined and may well be different for different physical compaction protocols [13]. However, for cyclic simple shear (in the quasistatic limit), we find a well-defined value of the global volume fraction, at the onset of crystallization. This value, which is in the reported range for RCP, 0.62-0.66, is robust to friction, gravity, and amplitude changes in the small amplitude limit. To avoid confusion we refer to the value we obtain as the ‘crystallization volume fraction’ for asymptotically small shear amplitudes.
There are compaction protocols, such as cyclic shear coupled with horizontal and vertical shaking, for which the particles or grains possess significant kinetic energy that is slowly drained during the compaction process. For such protocols, it is possible as noted above, that the volume fraction for the onset of crystallization may occur at a different value than the one found here. One method to investigate this question is to carry out simulations of cyclic shear for underdamped, frictionless grains with weak damping, in addition to weak horizontal vibrations. Then the onset of crystallization could be determined as a function of the damping coefficient [14] as well as in the limit of small shear and vibration amplitudes.
Physical nongranular crystallization experiments and their modeling, in particular the homogeneous freezing of molecular fluids [9], should be compared with the homogeneous crystallization in the present simulations and in Rietz et al. [8] and [15]. In particular, persistent states play an important role in classical nucleation theory but seem to play a marginal role in these simulations and experiment, disappearing with growing shear amplitude.
Acknowledgements We acknowledge support from NSF Grant Nos.
CBET-2002782 (C.O.), CBET-2002797 (M.S.), and DMR-1119826 (W.J.) and
from the Army Research Laboratory under Grant No. W911NF-17-1-0164
(C.O.). This work was also supported by the High Performance Computing
facilities operated by Yale’s Center for Research Computing and
computing resources provided by the Army Research Laboratory Defense
University Research Instrumentation Program Grant No. W911NF1810252.
∗microwei.jin@gmail.com ∗∗shattuck@ccny.cuny.edu
References
- [1] J.D. Bernal, A geometrical approach to the structure of liquids, Nature (London) 183, 141 (1959).
- [2] G.D. Scott, Packing of equal spheres, Nature (London) 188, 908 (1960) .
- [3] J. B. Knight, C. G. Fandrich, C. N. Lau, H. M. Jaeger, and S. R. Nagel, Density relaxation in a vibrated granular material, Phys. Rev. E 51, 3957 (1995); P. Richard, M. Nicodemi, R. Delannay, P. Ribiere, and D. Bideau, Slow relaxation and compaction of granular systems, Nat. Mater. 4, 121 (2005).
- [4] S. R. Liber, S. Borohovich, A. V. Butenko, A. B. Schofield, and E. Sloutskin, Dense colloidal fluids form denser amorphous sediments, PNAS 110, 5769 (2013).
- [5] K. Chen, J. Cole, C. Conger, J. Draskovic, M. Lohr, K. Klein, T. Scheidemantel, and P. Schiffer, Packing grains by thermal cycling, Nature (London) 442, 257 (2006).
- [6] M. Schröter, D. I. Goldman, and H. L. Swinney, Stationary state volume fluctuations in a granular medium, Phys. Rev. E 71, 030301 (2005).
- [7] G.D. Scott, A.M. Charlesworth, and M.K. Mak, On the random packing of spheres, J. Chem. Phys. 40, 611 (1964); M. Nicolas, P. Duru and O. Pouliquen, Compaction of a granular material under cyclic shear, Eur. Phys. J. E 3, 309 (2000).
- [8] F. Rietz, C. Radin, H. Swinney and M. Schröter, Nucleation in sheared granular matter, Phys. Rev. Lett. 120, 055701 (2018).
- [9] F. F. Abraham, Homogeneous Nucleation Theory (Academic Press, New York, 1974); P. Debenedetti, Metastable Liquids (Princeton University Press, Princeton, NJ, 1996).
- [10] See the Supplemental Material at http://link.aps.org/supplemental/XX/PhysRevLett.XX for discussions of the identification of the crystalline grains (Sec. A); the computational method, including the dependence on the spring constant magnitude (Sec. B.1), drag force (Sec. B.2), simulation timestep size (Sec. B.3), and the protocol used for energy relaxation (Sec. B.4); the determination of the critical cluster size (Sec. C); the role of gravity (Sec. D); and the homogeneity of the nucleation process (Sec. E).
- [11] P. Chaudhuri, L. Berthier, and S. Sastry, Jamming transitions in amorphous packings of frictionless spheres occur over a continuous range of volume fractions, Phys. Rev. Lett. 104, 165701 (2010).
- [12] P. J. Steinhardt, D.R. Nelson, and M. Ronchetti, Bond-orientation order in liquids and crystals. Phys. Rev. B 28, 784 (1983).
- [13] S. Torquato, T. M. Truskett, and P. G. Debenedetti, Is random close packing of spheres well defined?, Phys. Rev. Lett. 84 2064 (2000); C. Radin, Random close packing of granular matter, J. Stat. Phys. 131 567 (2008); Y. Jin and H. A. Makse, A first-order phase transition defines the Random close packing of hard spheres, Physica A 389 5362 (2010).
- [14] S. S. Ashwin, J. Blawzdziewicz, C. S. O’Hern, and M. D. Shattuck, Calculations of the basin volumes for mechanically stable packings, Phys. Rev. E 85, 061307 (2012).
- [15] C. Radin and H. L. Swinney, Phases of granular matter, J. Stat. Phys. 175, 542 (2019).