Hot Jupiters in binary star systems
Abstract
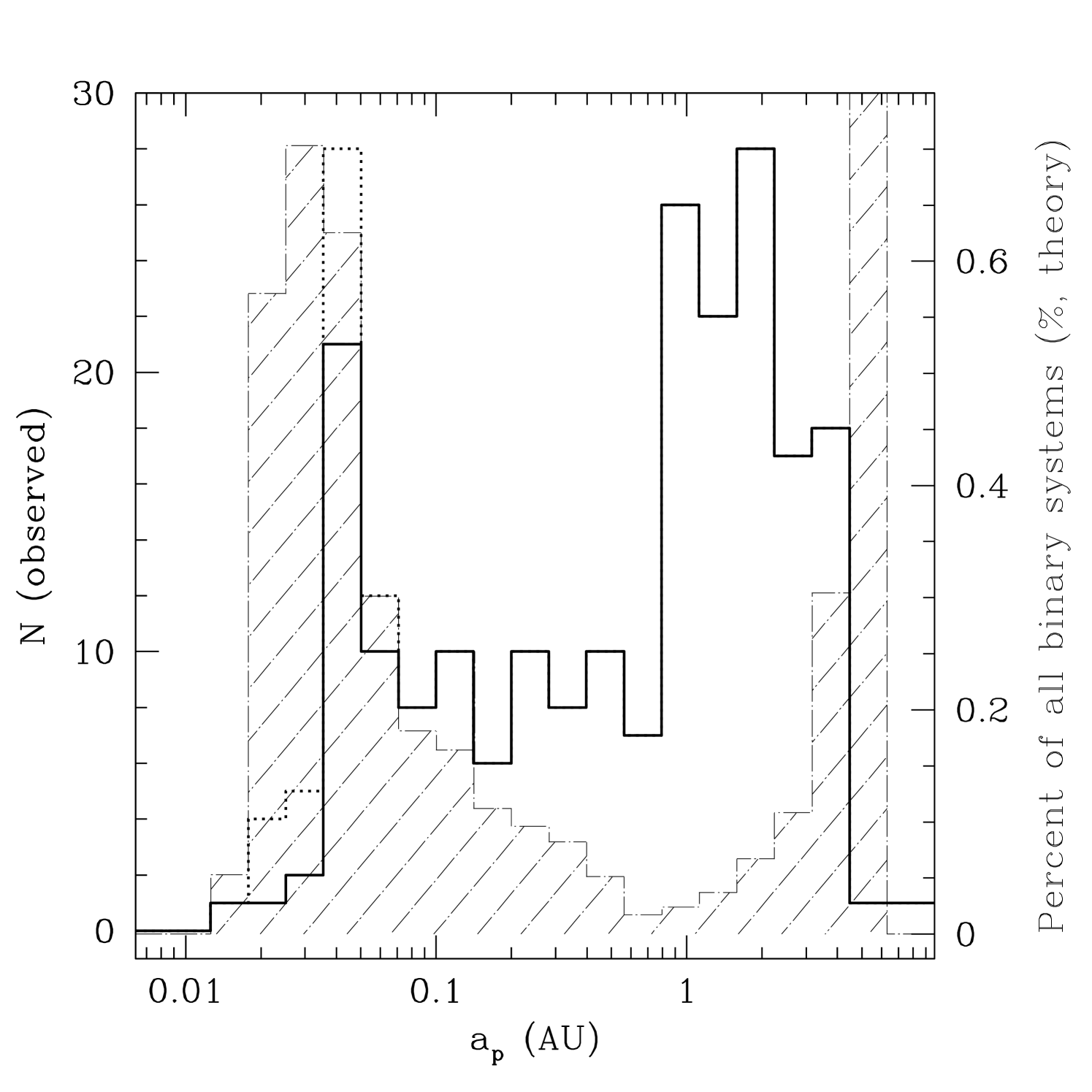
Radial velocity surveys find Jupiter mass planets with semi-major axes less than 0.1 AU around of solar-type stars; counting planets with as large as 5 AU, the fraction of stars having planets reaches (Marcy et al., 2005; Butler et al., 2006). An examination of the distribution of semi-major axes shows that there is a clear excess of planets with orbital periods around 3 or 4 days, corresponding to AU, with a sharp cutoff at shorter periods (see Figure 1). It is believed that Jupiter mass planets form at large distances from their parent stars; some fraction then migrate in to produce the short period objects. We argue that a significant fraction of the ‘hot Jupiters’ (AU) may arise in binary star systems in which the orbit of the binary is highly inclined to the orbit of the planet. Mutual torques between the two orbits drive down the minimum separation or periapse between the planet and its host star (the Kozai mechanism). This periapse collapse is halted when tidal friction on the planet circularizes the orbit faster than Kozai torque can excite it. The same friction then circularizes the planet orbit, producing hot Jupiters with the peak of the semimajor axis distribution lying around 3 days. For the observed distributions of binary separation, eccentricity and mass ratio, roughly of planets with initial semimajor axis will migrate to within of their parent star. Kozai migration could account for or more of the observed hot Jupiters.
Subject headings:
binaries:general;planetary systems;celestial mechanics1. Introduction to Kozai Migration
Statistics from radial velocity planet searches (Marcy et al., 2005; Butler et al., 2006) show that the occurrence rate of giant planets within 0.1 AU (“hot-Jupiters”) is ; extrapolating to 20 AU the occurrence is . There is a clear ”pile-up” of planets with orbital periods near 3 days (Fig. 1). Transit observations yield a similar fraction of hot Juptiers (Gould et al., 2006; Fressin et al., 2007). What migration mechanisms can produce the observed feature in semi-major axis distributions represented by hot Jupiters? In this article we focus on the mechanism known as Kozai migration.
Consider a planet circling a star that is a member of a binary system. The mutual torques between the binary and planetary orbits transfer angular momentum between the two while leaving the orbital energies nearly unchanged. For mutual inclinations a resonance between the precession rate of the planet’s nodal and apsidal lines greatly enhances the effectiveness of this exchange of angular momentum, producing large oscillations in the planet’s angular momentum (Kozai cycles, Kozai, 1962). The planet eccentricity () and periapse () oscillate with a characteristic timescale (Holman et al., 1997)
| (1) |
where and are the masses of the central and companion stars, while and are the periods of the binary and planetary orbits, respectively. The binary eccentricity is denoted by . Holman et al. (1997) and Takeda & Rasio (2005), among others, have studied the role of these Kozai cycles in producing the eccentricities observed in known exo-planets.
For sufficiently large , can reach very small values, allowing tidal dissipation to erode the orbit of the planet. Eggleton & Kiseleva-Eggleton (2001) were the first to propose that Kozai cycles, in combination with tidal friction, can shrink the orbit of a inner binary in a hierarchical triple system, leading to the formation of contact binaries. Wu & Murray (2003, hereafter WM03) have studied Kozai migration in application to exo-planets and found it to be the only plausible explanation for the migration of the planetary object HD80606b.
In the absence of any other modification of the gravitational potential, the minimum may fall below the Roche radius () and the planet may be destroyed. However, there are a number of competing torques that can limit the amount of angular momentum that the Kozai torque can extract from the orbit of the planet, including general relativistic (GR) corrections to Newtonian gravity, and torques associated with the extended mass distribution of both the primary star and the planet. The latter includes rotationally induced planetary oblateness, the tidal bulge raised by the star on the planet, the misalignment of this bulge produced by friction, and the stellar counterparts of all these. These torques can halt the Kozai-induced collapse in and promote planetary survival.
Which torque becomes competitive with the Kozai torque depends on the system; for systems with very large binary semi-major axis () and therefore very weak Kozai torque, the GR precession can halt the reduction of before tides become important. However, for tighter or more inclined binaries, tidal friction sets the minimum . Since the tidal torques depend strongly on , binary systems with a wide range of will be stalled at essentially the same , leading to a pile-up of hot Jupiters at when the planet orbits are later circularized.
2. Numerical Experiments
We quantify the effect of Kozai migration by considering an ensemble of binary systems following that in Takeda & Rasio (2005). These binaries are initially comprised of a solar-mass host star, a jupiter-mass planet () orbiting at AU with an eccentricity of , and a binary companion of mass – this is the peak of the observed mass ratio distribution in the solar neighbourhood (Duquennoy & Mayor, 1991). The distribution in binary separation () is assumed flat in logarithmic ( ranging from to AU). We set , a thermal distribution often adopted in binary population synthesis. This latter choice hardly affects the results. The last ansatz, our most sensitive yet most uncertain assumption, takes to be isotropically distributed. Based on studies of stellar spin and binary orbits (Hale, 1994), this seems reasonable for AU, but may be less appropriate for tighter binaries; polarimetry studies of protostellar disks suggest that the circumstellar disk and the binary plane are correlated for up to a few hundred AU (Jensen et al., 2004; Monin et al., 2006). However, polarimetry estimates only the projected angle between the two planes, and is strongly plagued by interstellar polarization. The results should be taken with caution at present.
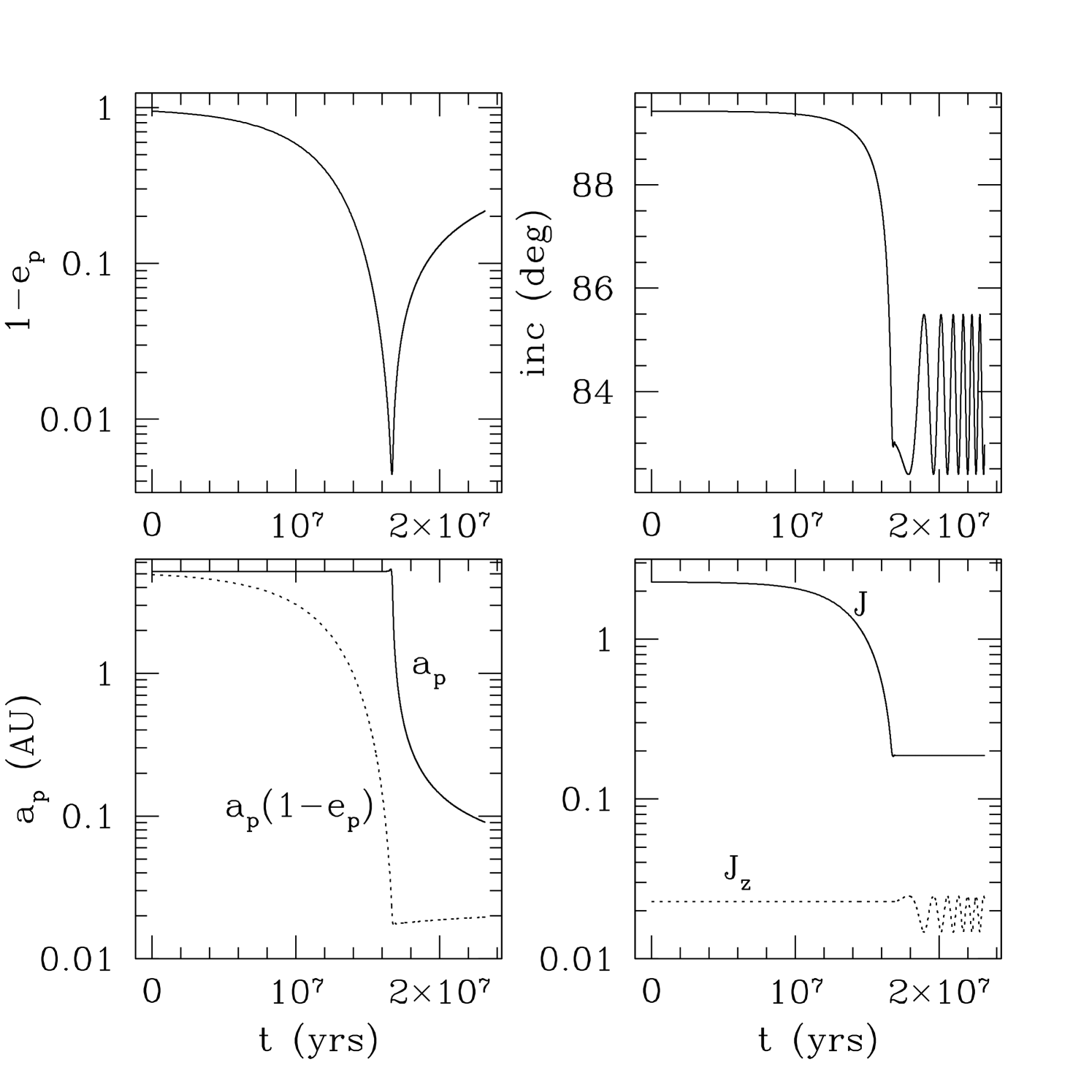
We produce an ensemble of systems. Out of these we select systems that can potentially perturb the planet to AU. To reach this distance, a planet starting at semi-major axis (with a small eccentricity) will have to attain . Ignoring tidal dissipation,111Tidal dissipation increases the Kozai integral and slightly raises the minimum requirement on (WM03). the Kozai integral (the planet’s orbital angular momentum in the normal of the binary plane) . Taking a minimum during the Kozai cycles (see, e.g., Holman et al., 1997), this yields a minimum initial inclination required for producing hot Jupiters: . This value is independent of the binary separation or mass. The fraction of isotropically inclined systems that have such a misalignment is .
We then weed out planets that are likely dynamically unstable according to the following fitting formula
| (2) |
This expression is obtained by integrating the orbits of our initial system for binary orbits, taking . This non-coplanar stability limit is to more restrictive than the coplanar stability limit found by Holman & Wiegert (1999). It is used here as a rough proxy for systems that either eject their planets quickly after formation, or are unable to form planets due to the strong tidal influence of the companion. This proceedure eliminates many systems with AU; we are left with of the original ensemble that could potentially reach AU, if they are not stalled by other torques at larger distances.
These remaining systems are integrated using secular equations obtained by averaging over the orbital motions of both the planet and the binary companion (Eggleton & Kiseleva-Eggleton, 2001). These equations include the effects of Kozai perturbation, tidal dissipation, GR precession, and tidal and rotational bulge precessions.222In this study, we rely exclusively on these secular equations. The actual dynamics may deviate due to short term noises and mean-motion perturbations and should be studied with N-body integration codes. We use a Runge-Kutta integrator with an adaptive step size set to keep the integration error below a preset limit. We follow the procedure described in WM03, which also lists values for the various parameters involved. In particular, we choose the initial stellar spin direction to be aligned with the initial orbit normal for the planet.
The integration is stopped after Gyrs have passed, or when million timesteps are exhausted, or when . The last condition roughly corresponds to the planet overflowing its Roche lobe; however, none of the planet in our simulation reached this state.333This is due to the strong dependence of the tidal timescale on ; tidal distortions act as a barrier, maintaining . The limit on the number of integration timesteps is usually reached if Kozai oscillations have been effectively halted by rapid tidal or other precessions; in that case the subsequent dynamical evolution of the planet simply reduces . We then use a simplified code, including only the effects of tidal dissipation on the planet orbit and planet/stellar spins, to finish integrating to Gyrs.
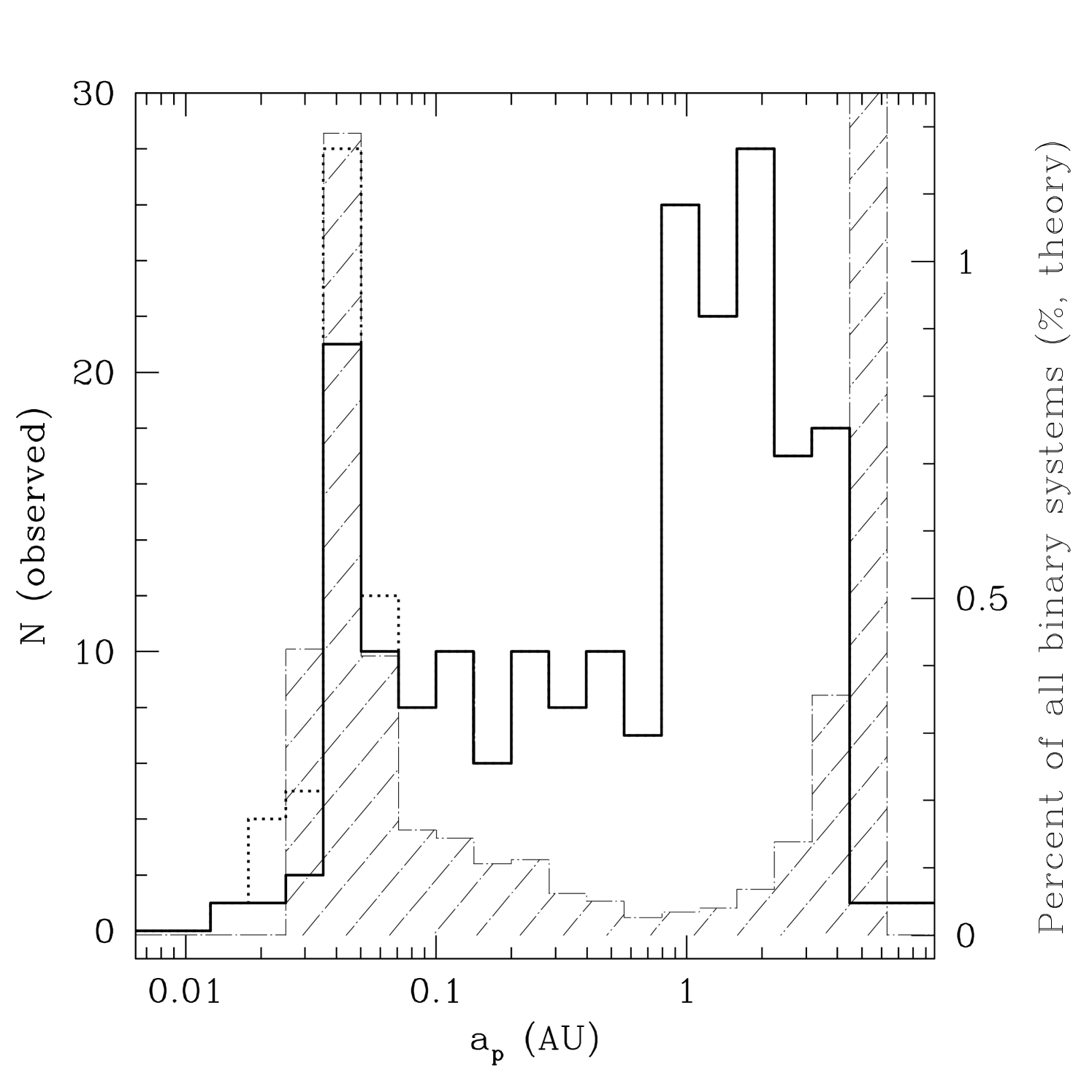
We find that about of our ensemble eventually migrate inward of AU. The distribution of final semi-major axes is concentrated between AU and AU with a peak at AU. Our hot Jupiters exhibit a pile-up at day periods similar to the observed population (Fig. 1).
Given the same initial , tighter binaries produce a closer-in hot Jupiter in a shorter amount of time. Many of the hot Jupiters are tidally ensnared on their first close approach to the host star (Fig. 3), with the Kozai period between to yrs. Tidal circularization of these orbits then takes upward of years.
The 3-day feature in the computed distribution appears wider than the observed distribution. However, as just noted, closer-in planets are migrated in earlier, so they still have larger radii and larger stalling peraipses. Experimenting with the following time evolution of planet radius,
| (3) |
with taken to be , we find that the 3-day bump narrows significantly (Fig. 2).
3. Discussion
3.1. Stalling Radius and the 3-day Pile-up
The periapse of a Kozai-migrating planet is stalled at a distance where the eccentricity forcing due to the binary companion is counteracted by the eccentricity damping by tidal dissipation. Kozai forcing yields (Eggleton & Kiseleva-Eggleton, 2001)
| (4) |
where , . The rate of tidal eccentricity damping depends strongly on the periapse distance. Considering only tides raised on the planet, we obtain(Hut, 1981)
| (5) |
where is the planet’s tidal Love number, its tidal dissipation factor and its radius (see WM03). The mass ratio . Equating the two rates, we obtain the stalling periapse value,
| (6) | |||||
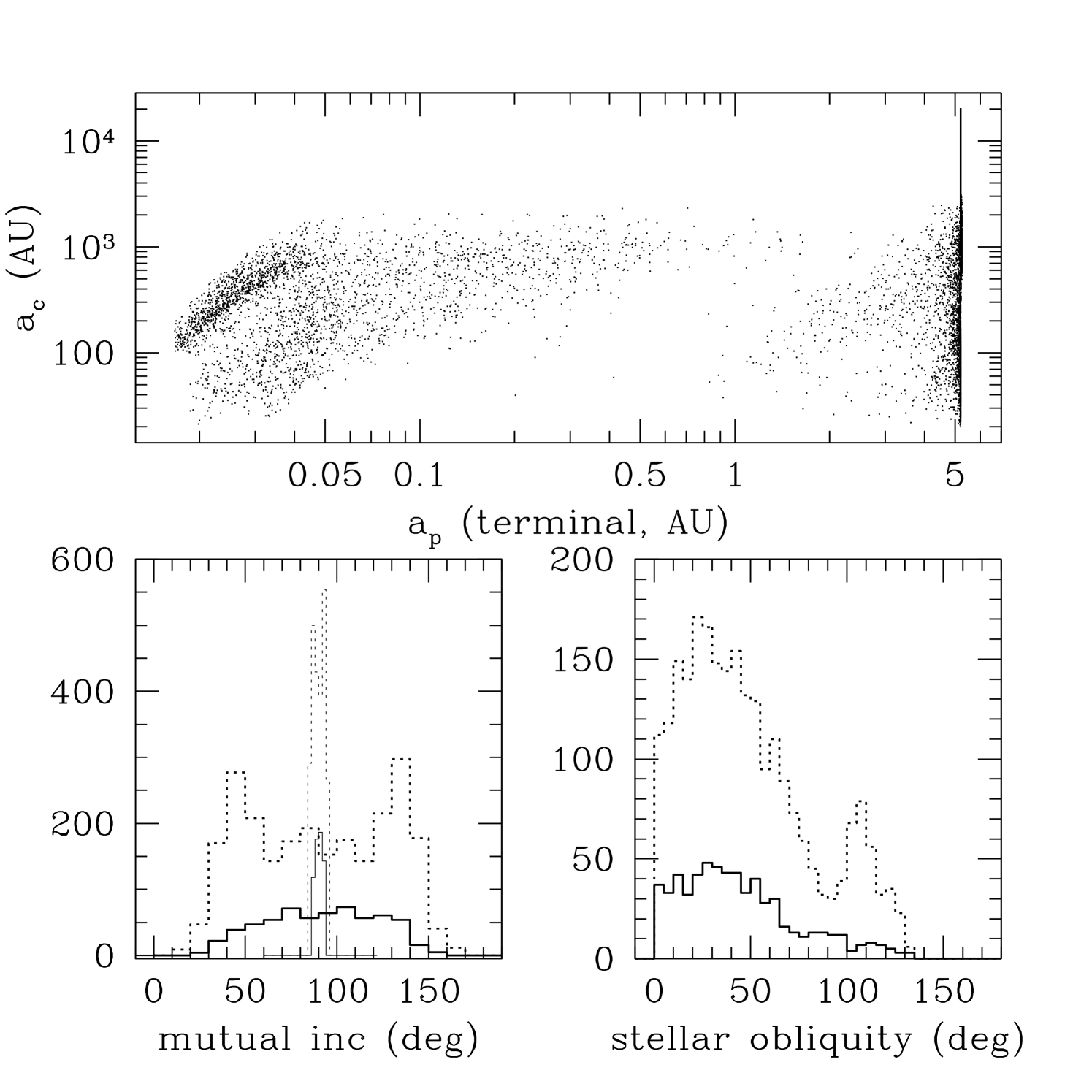
where we have scaled variables by their representative values ( is the radius of Jupiter). Coincidentally, , and it depends little on a variety of parameters, including stellar mass, companion mass, planet mass, planet tidal factor, and planet initial orbit. This justifies our choices for these parameters in the numerical experiment. 444This mechanism works for other types of planets like hot Neptunes or super-earths. Substituting into Eq. (6) values appropriate for Neptune and Earth, we obtain similar values for . In our simulation, most binaries that give rise to hot Jupiters have AU (Fig. 4) and we have scaled here by roughly the median value. Tighter binaries are relatively unimportant – planets in many of these systems are dynamically unstable and are excluded from our study.
In the subsequent tidal circularization, orbital angular momentum is roughly conserved and the final AU.
The fraction of stars with Kozai migrated hot Jupiters is given by
| (7) |
where is the fraction of stars in binary systems, is the fraction of solar type stars with Jupiter mass planets formed at a few AU, and is the fraction of planets in binary star systems that undergo Kozai migration to AU. Taking (Duquennoy & Mayor, 1991), (Marcy et al., 2005), and (this work), we suggest that, at a minimum, of the known hot Jupiters may be due to Kozai migration. The most uncertain number is . The value of we have quoted is the observed fraction in the Keck sample, which is substantially complete up to . Assuming the number of planets per is flat up to gives and . There is some indication that the number of planets per is an increasing function of . If , more than half the hot Jupiters could be produced by the Kozai mechanism.
3.2. Predictions of the Kozai Migration Scenario
The number of hot Jupiters produced by Kozai migration can be determined by observations in the near future, since Kozai migrated planets must have a number of attributes. First, candidate Kozai hot Jupiters will reside in binary star systems, although the binary mass ratio may well be small; a brown dwarf companion can be dynamically as effective as a solar-type companion (eq. [6]). The study by Duquennoy & Mayor (1991) establishes that of the stars in the solar neighbourhood are actually binary or triple systems. While radial velocity surveys select against close binaries, studies by Raghavan et al. (2006) show that at least of radial velocity planet hosts have stellar companions. The discoveries of brown-dwarf companions to the planet bearing stars HD 3651 (Mugrauer et al., 2006) and HD 89744 (Mugrauer et al., 2004) highlight the possibility that the existence of dim companions will increase the known binary fraction of planet bearing stars significantly. The Kozai scenario predicts that the binary fraction of hot Jupiters will be higher than that of systems with more distant planets. Binary-induced radial velocity trends induced on the primary by a stellar companion will be of order
| (8) |
where is the sine of the angle between the line of sight and the stellar velocity. This is clearly detectable at the current sensitivity of radial velocity surveys (Wright et al., 2007). The companion will also induce an astrometric acceleration of a few micro-arcsecond/yr/yr, detectable by SIM or GAIA.
Second, Kozai systems have , with not uncommon (Fig. 4). In transiting systems the binary orbit will be in or near the plane of the sky. This can be tested via both radial velocity and astrometry.
Third, the angle between the spin axis of the primary star (assumed to be the orbit normal of the planet at formation) and the present-day planet orbit normal will range from 0 to 130 degrees (Fig. 4) with the values between 0 and 50 degrees being preferred. This angle can be determined if both the spin period of the star as well as its rotational velocity can be independently measured. The angle projected onto the plane of the sky, measurable using the Rossiter-McLaughlin effect, will have a similar range.
Fourth, the semimajor axis ratio with any second planet will be small. This results from the requirement that the precession rate induced by the second planet not break the Kozai resonance (Wu & Murray, 2003). Radial velocity measurements can constrain the mass and semimajor axis of any nearby planetary companions to hot Jupiters (Wright et al., 2007). A corollary is that the fraction of multiplanet systems having hot Jupiters will be smaller than the fraction of single planet systems with hot Jupiters.
Kozai-migrated planets dissipate many times their own binding energy during tidal circularization. Ogilvie & Lin (2004) find that tidally dissipated energy is deposited throughout the bulk of the planet, raising the possibility that the planet will expand catastrophically. In contrast, Wu (2005) concludes that energy is deposited exclusively near the photosphere, which would leave the planet intact.
The theoretical situation is unclear, but the existence of hot Jupiters suggests an answer. A plot of versus strongly suggests that the low ’s of the hot Jupiters are the result of tidal circularization, as the observed ’s follow closely the upper-bound set by the tidal process (see, e.g., Fig. 1 of Wu, 2003). If so, most or all hot Jupiters have experienced rapid tidal heating and survived.
Another concern with the Kozai picture is raised by the Rossiter-McLaughlin measurement of stellar obliquity, currently available for 5 transiting planets (see Table 2 of Fabrycky & Tremaine, 2007). All are consistent with zero obliquity. Taken at face value, this is at variance with the above Kozai prediction. 555HD147506 (Winn et al., 2007; Loeillet et al., 2007), a star with a massive planet, may have experienced tidal synchronization in its surface-layer that would alter its apparent rotation axis.
3.3. Alternatives to Kozai Migration
In Kozai migration, it is important that evolves on a time scale no shorter than the tidal precession time scale; if were to suddenly plunge from above to below the Roche radius, as for example would be the case if two planets suffered a close encounter, the inward scattered planet would not be stalled outside . Instead it would suffer rapid mass loss and likely be lost. In that case there will be a cut-off in the distribution of at (Ford & Rasio, 2006), but not a pile-up.
Migration in a gas disk may also produce hot Jupiters. If the disk extends all the way to the star, one would observe a cut-off at ; if the disk is truncated, e.g., by stellar magnetic fields (Lin et al., 1996), a feature will appear at an orbital period half that of the inner edge of the disk. However, spin periods and magnetic fields of accreting stars show a substantial dispersion, which would lead to a rather broad distribution in the disk inner radii, and hence a smeared out feature in the distribution of planetary semimajor axis.
We have studied the role of a binary companion in increasing and causing a gradual collapse in . But it is also plausible that soft planet-planet scattering can gradually decrease (Juric & Tremaine, 2007; Chatterjee et al., 2007). Moreover, Kozai oscillations can also be excited by a second planet,666This second planet can be placed on a highly inclined orbit by, e.g., planet-planet scattering. in the absence of a binary stellar companion. As long as these or other processes produce gentle eccentricity driving on to year timescales, tidal effects will halt the periapse evolution when . Tidal circularization then pushes the planets out to and produces a narrow pile-up of hot Jupiters there.
References
- Butler et al. (2006) Butler, R. P., Wright, J. T., Marcy, G. W., Fischer, D. A., Vogt, S. S., Tinney, C. G., Jones, H. R. A., Carter, B. D., Johnson, J. A., McCarthy, C., & Penny, A. J. 2006, ApJ, 646, 505
- Chatterjee et al. (2007) Chatterjee, S., Ford, E. B., & Rasio, F. A. 2007, ArXiv Astrophysics e-prints
- Duquennoy & Mayor (1991) Duquennoy, A. & Mayor, M. 1991, A&A, 248, 485
- Eggleton & Kiseleva-Eggleton (2001) Eggleton, P. P. & Kiseleva-Eggleton, L. 2001, ApJ, 562, 1012
- Fabrycky & Tremaine (2007) Fabrycky, D. & Tremaine, S. 2007, ArXiv e-prints, 705
- Ford & Rasio (2006) Ford, E. B. & Rasio, F. A. 2006, ApJ, 638, L45
- Fressin et al. (2007) Fressin, F., Guillot, T., Morello, V., & Pont, F. 2007, ArXiv e-prints, 704
- Gould et al. (2006) Gould, A., Dorsher, S., Gaudi, B. S., & Udalski, A. 2006, Acta Astronomica, 56, 1
- Hale (1994) Hale, A. 1994, AJ, 107, 306
- Holman et al. (1997) Holman, M., Touma, J., & Tremaine, S. 1997, Nature, 386, 254
- Holman & Wiegert (1999) Holman, M. J. & Wiegert, P. A. 1999, AJ, 117, 621
- Hut (1981) Hut, P. 1981, A&A, 99, 126
- Jensen et al. (2004) Jensen, E. L. N., Mathieu, R. D., Donar, A. X., & Dullighan, A. 2004, ApJ, 600, 789
- Juric & Tremaine (2007) Juric, M. & Tremaine, S. 2007, ArXiv Astrophysics e-prints
- Kozai (1962) Kozai, Y. 1962, AJ, 67, 591
- Lin et al. (1996) Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606
- Loeillet et al. (2007) Loeillet, B., Shporer, A., Bouchy, F., Pont, F., Mazeh, T., Beuzit, J. L., Boisse, I., Bonfils, X., Da Silva, R., Delfosse, X., Desort, M., Ecuvillon, A., Forveille, T., Galland, F., Gallenne, A., Hebrard, G., Lagrange, A. M., Lovis, C., Mayor, M., Moutou, C., Pepe, F., Perrier, C., Queloz, D., Segransan, D., Sivan, J. P., Santos, N. C., Tsodikovich, Y., Udry, S., & Vidal-Madjar, A. 2007, ArXiv e-prints, 707
- Marcy et al. (2005) Marcy, G., Butler, R. P., Fischer, D., Vogt, S., Wright, J. T., Tinney, C. G., & Jones, H. R. A. 2005, Progress of Theoretical Physics Supplement, 158, 24
- Monin et al. (2006) Monin, J.-L., Ménard, F., & Peretto, N. 2006, A&A, 446, 201
- Mugrauer et al. (2004) Mugrauer, M., Neuhäuser, R., Mazeh, T., Guenther, E., & Fernández, M. 2004, Astronomische Nachrichten, 325, 718
- Mugrauer et al. (2006) Mugrauer, M., Seifahrt, A., Neuhäuser, R., & Mazeh, T. 2006, MNRAS, 373, L31
- Ogilvie & Lin (2004) Ogilvie, G. I. & Lin, D. N. C. 2004, ApJ, 610, 477
- Raghavan et al. (2006) Raghavan, D., Henry, T. J., Mason, B. D., Subasavage, J. P., Jao, W.-C., Beaulieu, T. D., & Hambly, N. C. 2006, ApJ, 646, 523
- Takeda & Rasio (2005) Takeda, G. & Rasio, F. A. 2005, ApJ, 627, 1001
- Winn et al. (2007) Winn, J. N., Asher Johnson, J., Peek, K. M. G., Marcy, G. W., Bakos, G. A., Enya, K., Narita, N., Suto, Y., Turner, E. L., & Vogt, S. S. 2007, ArXiv e-prints, 707
- Wright et al. (2007) Wright, J. T., Marcy, G. W., Fischer, D. A., Butler, R. P., Vogt, S. S., Tinney, C. G., Jones, H. R. A., Carter, B. D., Johnson, J. A., McCarthy, C., & Apps, K. 2007, ApJ, 657, 533
- Wu (2003) Wu, Y. 2003, Scientific Frontiers in Research on Extrasolar Planets, 294, 213
- Wu (2005) Wu, Y. 2005, ApJ, 635, 688
- Wu & Murray (2003) Wu, Y. & Murray, N. 2003, ApJ, 589, 605