How different are shadows of compact objects with and without horizons?

In 1918, Lense and Tirring proposed an approximate solution to describe a slow rotating large-distance stationary isolated body in the framework of the vacuum Einstein equations [62], which takes

	$\displaystyle ds^{2}=$	$\displaystyle-$	$\displaystyle\left[1-\frac{2M}{r}+\mathcal{O}\left(\frac{1}{r^{2}}\right)\right]dt^{2}-\left[\frac{4J\sin^{2}\theta}{r}+\mathcal{O}\left(\frac{1}{r^{2}}\right)\right]d\phi dt$		(2.1)
		$\displaystyle+$	$\displaystyle\left[1+\frac{2M}{r}+\mathcal{O}\left(\frac{1}{r^{2}}\right)\right]\left[dr^{2}+r^{2}\left(d\theta^{2}+\sin^{2}\theta d\phi^{2}\right)\right]\,$

where $M$ and $J$ are the mass and the angular momentum, respectively. $\mathcal{O}(r^{-2})$ denotes the subdominant terms. By properly regulating the specific forms of $\mathcal{O}(r^{-2})$, one can obtain various metrics with the same asymptotic limit at large distances, which are physically different from each other. Recently, Baines et al. constructed an explicit Painlevé-Gullstrand variant of the –Lense-Thirring spacetime [63], for which the metric is

$\displaystyle ds^{2}=-dt^{2}+\left(dr+\sqrt{\frac{2M}{r}}dt\right)^{2}+r^{2}\left[d\theta^{2}+\sin^{2}\theta\left(d\phi-\frac{2J}{r^{3}}dt\right)^{2}\right]\,.$

(2.2)

There are three solid advantages for this new version of the –Lense-Thirring spacetime, of which the first is that the metric reduces to the Painlevé–Gullstrand version of the Schwarzschild black hole solution when $J=0$; the second is that the azimuthal dependence takes a partial Painlevé-Gullstrand form, that is, $g_{\phi\phi}(d\phi-v^{\phi}dt)^{2}=g_{\phi\phi}(d\phi-\omega dt)^{2}$, where $v^{\phi}$ is minus the azimuthal component of the shift vector in the ADM formalism denoting the “flow ” of the space in the azimuthal direction and $\omega=g_{t\phi}/g_{\phi\phi}$ is the angular velocity of the spacetime; and the third is that all the spatial dependence is in exact Painlevé-Gullstrand type form, which implies that the spatial hypersurface $t=\text{const}$ is flat. These exciting features make the Painlevé-Gullstrand variant much easier to calculate with respect to the tetrads, the curvature components, and the geodesic analysis than any other variant of the Lense-Thirring spacetime [64, 65].

On the other hand, from the original asymptotic form in Eq. (2.1), we can see that the Lense-Thirring metric should make sense only in the region $r>r_{s}$. The metric in Eq. (2.1) has a coordinate singularity $r=2M$ when neglecting the subdominant terms so that the Lense-Thirring spacetime should be valid when the condition $r_{s}>2M$ holds. Moreover, for a slowly rotating object, we must have $J/r_{s}^{2}\ll 1$. Thus, we should also impose the conditions $J/r_{s}^{2}\ll 1,r_{s}>2M$ on the Painlevé-Gullstrand version of the Lense-Thirring spacetime when investigating the properties of the Painlevé-Gullstrand form.

In this subsection, we review the geodesics in the Painlevé-Gullstrand form of the Lense-Thirring spacetime, which has been carefully studied in [65]. Similar to the Kerr spacetime, there are also four conserved quantities along the geodesics of free particles: the mass $m$, the energy $E$, the axial angular momentum $L$, and the Carter constant $C$. For simplicity and without loss of generality, we set $m=0$ for photons and $m=1$ for time-like particles. Then, the four-momentum $p^{a}$ reads

$\displaystyle p^{a}=\dot{t}\left(\frac{\partial}{\partial t}\right)^{a}+\dot{r}\left(\frac{\partial}{\partial r}\right)^{a}+\dot{\theta}\left(\frac{\partial}{\partial\theta}\right)^{a}+\dot{\phi}\left(\frac{\partial}{\partial\phi}\right)^{a}\,,$

(2.3)

with “ $\dot{}$ ” denoting the derivative with respect to the affine parameter $\tau$. Considering $p^{a}p_{a}=0$ for photons and $p^{a}p_{a}=-1$ for time-like particles, $\tau$ can be seen as the proper time for time-like worldliness. Then, the conserved quantities $E,L,C$ can be written as

		$\displaystyle E$	$\displaystyle=-p_{t}=\left(1-\frac{2M}{r}-\frac{4J^{2}\sin^{2}\theta}{r^{4}}\right)\dot{t}-\sqrt{\frac{2M}{r}}\dot{r}+\frac{2J\sin^{2}\theta}{r}\dot{\phi}\,,$		(2.4)
		$\displaystyle L$	$\displaystyle=p_{\phi}=r^{2}\sin^{2}\theta\left(\dot{\phi}-\frac{2J}{r^{3}}\dot{t}\right)\,,\quad C=r^{4}\dot{\theta}^{2}+\frac{L^{2}}{\sin^{2}\theta}\,,$

explicitly. For time-like particles, $E$ and $L$ can now be treated as the energy per unit mass and the angular momentum per unit mass. Then, combined with the condition $-p^{a}p_{a}=m\in\{0,1\}$, one can obtain the exact expressions of the components of the four momentum $p^{a}$ as follows:

	$\displaystyle\dot{r}$	$\displaystyle=$	$\displaystyle S_{r}\sqrt{R(r)}\,,$
	$\displaystyle\dot{t}$	$\displaystyle=$	$\displaystyle\frac{E-2JL/r^{3}+S_{r}\sqrt{(2M/r)R(r)}}{(1-2M/r)}\,,$
	$\displaystyle\dot{\theta}$	$\displaystyle=$	$\displaystyle S_{\theta}\frac{\sqrt{\Theta(\theta)}}{r^{2}}\,,$
	$\displaystyle\dot{\phi}$	$\displaystyle=$	$\displaystyle\frac{L}{r^{2}\sin^{2}\theta}+2J\frac{E-2JL/r^{3}+S_{\phi}\sqrt{(2M/r)R(r)}}{r^{3}(1-2M/r)}\,,$		(2.5)

where we define

	$\displaystyle R(r)$	$\displaystyle=$	$\displaystyle\left(E-\frac{2JL}{r^{3}}\right)^{2}-\left(m+\frac{C}{r^{2}}\right)\left(1-\frac{2M}{r}\right)\,,$		(2.6)
	$\displaystyle\Theta(\theta)$	$\displaystyle=$	$\displaystyle C-\frac{L^{2}}{\sin^{2}\theta}\,,$		(2.7)

as the effective potential functions governing the radial and polar motions, and

	$\displaystyle S_{r}$	$\displaystyle=$	$\displaystyle\begin{cases}+1\>\>\>\text{outgoing geodesic}\\ -1\>\>\>\text{ingoing geodesic}\end{cases}\;$
	$\displaystyle S_{\theta}$	$\displaystyle=$	$\displaystyle\begin{cases}+1\>\>\>\text{increasing declination geodesic}\\ -1\>\>\>\text{decreasing declination geodesic}\end{cases}\;$
	$\displaystyle S_{\phi}$	$\displaystyle=$	$\displaystyle\begin{cases}+1\>\>\>\text{prograde geodesic}\\ -1\>\>\>\text{retrograde geodesic}\end{cases}\,$		(2.8)

following the conventions in [65]. The context for each equation in Eq. (2.2) denotes the corresponding physical interpretation. Here, we want to stress that $S_{r}$ and $S_{\phi}$ appear separately in the $t$-motion and $\phi$-motion due to the Painlevé-Gullstrand form; however, for geodesic equations of Kerr spacetime in Boyer-Lindquist coordinates, $S_{r}$ comes up only in the radial motion, and $S_{\phi}$ is not necessarily introduced. Then, one can explore the properties of null and time-like geodesics by adequately manipulating the equations in (2.2).

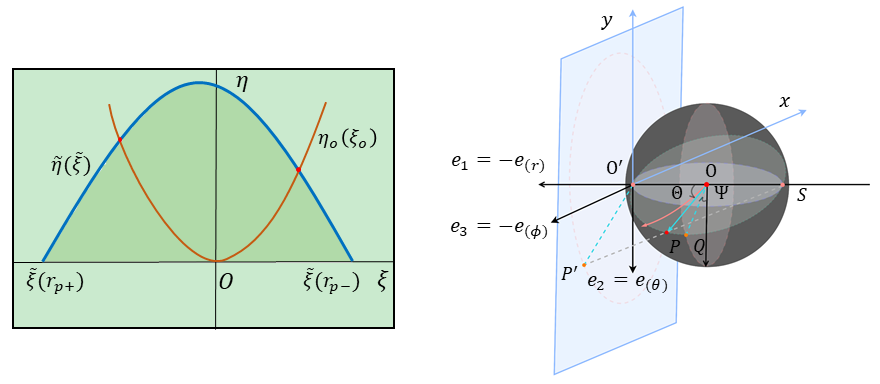
Before we discuss the shadows of the COs, we first review the shadows of ordinary black holes. To determine the shadow of a black hole, in addition to the photon region, there is a second condition related to the observational angle. For a certain observational angle $\theta_{o}$, we can see that the term under the square root $\Theta(\theta_{o})\geq 0$ must be satisfied in polar motion, which produces

$\displaystyle\Theta(\theta_{o})=\eta_{o}-\frac{\xi_{o}^{2}}{\sin^{2}\theta_{o}}\geq 0\,,$

(3.6)

and a new function $\eta_{o}(\xi_{o})=\frac{\xi_{o}^{2}}{\sin^{2}\theta_{o}}$. That is, the photons can reach the observer if their impact parameters satisfy the above condition. Combining the critical impact parameters $\tilde{\eta}(\tilde{\xi})$ with the constraint $\Theta(\theta_{o})\geq 0$, one can fix the photons exactly that have critical impact parameters and those that can escape to observers if they are perturbed. As a result, the shadow curve is formed by these photons since the surface of the black hole, that is, the horizon, is always inside the photon region.

In the study of shadows of COs, including black holes, we find it convenient to define the observational photon region (OPR) and possible observational photon region (POPR). The OPR is defined as the set of impact parameters for which the photons with these impact parameters precisely determine the shadow curve for observers with a specific observational angle. The POPR is defined as the union of the OPRs at all possible observational angles. Thus, for the case of black holes, the POPR is composed of the critical impact parameters $\tilde{\eta}(\tilde{\xi})$, and the elements of the OPR are the critical impact parameters $\tilde{\eta}(\tilde{\xi})$, which also satisfy the condition $\Theta(\theta_{o})\geq 0$. In the left panel of Fig. 1, we present the functions of $\tilde{\eta}(\tilde{\xi})$ and $\eta_{o}(\xi_{o})$ in the $\xi O\eta$ plane and find that the two functions have two intersections. The OPR corresponds to the segment of $\tilde{\eta}(\tilde{\xi})$ between the two intersections, and the POPR corresponds to a piece of $\tilde{\eta}(\tilde{\xi})$ above the $\xi$-axis.

Then, one can calculate the shadow curve by standard methods, that is, introducing the celestial coordinates and obtaining the projections on the screen of observers. In this work, we employ the stereographic projection method, which has been used in our previous work [66]. We also bring Fig. 11 from the work [66] into the right panel of Fig. 1 to give a deep intuition on the celestial coordinates and Cartesian coordinates $(x,y)$ in the local rest frame of the observers.

In terms of the metric in Eq. (2.2), the local rest frame of observers can be defined as

	$\displaystyle e_{0}$	$\displaystyle=$	$\displaystyle\hat{e}_{(t)}=\partial_{t}-\sqrt{\frac{2M}{r}}\partial_{r}+\frac{2J}{r^{3}}\partial_{\phi}\,,$		(3.7)
	$\displaystyle e_{1}$	$\displaystyle=$	$\displaystyle-\hat{e}_{(r)}=-\partial_{r}\,,$		(3.8)
	$\displaystyle e_{2}$	$\displaystyle=$	$\displaystyle\hat{e}_{(\theta)}=\frac{1}{r}\partial_{\theta}\,,$		(3.9)
	$\displaystyle e_{3}$	$\displaystyle=$	$\displaystyle-\hat{e}_{(\phi)}=-\frac{1}{r\sin\theta}\partial_{\phi}\,.$		(3.10)

It is not hard to verify that these bases are normalized and orthogonal to each other. Moreover, since $\hat{e}_{(t)}\cdot\partial_{\phi}=0$, the observer with the 4-velocity $\hat{u}=e_{0}$ in this local rest frame has zero angular momentum for infinity. Therefore, this frame is usually called the ZAMO reference frame. In our model, the relation between the celestial coordinates $(\Theta,\Psi)$ and the 4-momentum of the OPR takes

$\displaystyle\Theta=\arccos\left(\sqrt{\frac{2M}{r_{0}}}+\frac{\dot{\tilde{r}}_{o}}{\dot{\tilde{t}}_{o}}\right)\,,\quad\Psi=-\arctan\left(\frac{\tilde{\xi}}{\sqrt{\tilde{\eta}\csc^{2}\theta_{o}-\tilde{\xi}^{2}}}\right)\,,$

(3.11)

where “ $\sim$ ” means evaluated with critical impact parameters $\tilde{\xi}$ and $\tilde{\eta}$, and the subscript “ _o ” means evaluated at the observer with coordinates $(0,r_{o},\theta_{o},0)$. Then, the Cartesian coordinates $(x,y)$ on the screen can be defined as

$\displaystyle x=-2\tan\frac{\Theta}{2}\sin\Psi\,,\quad y=-2\tan\frac{\Theta}{2}\cos\Psi\,,$

(3.12)

where we have chosen the energy of the photon observed by the ZAMOs to be unity, considering that the trajectories of photons are independent of the energies.

In this subsection, we study the shadows of COs, which have no horizon. For simplicity, we assume that the COs are nonluminous bodies, and they neither transmit nor reflect light. We recall that the spacetime outside a CO that we consider in this work is modeled by the Painlevé-Gullstrand form of the Lense-Thirring spacetime, and we investigate the shadows in three situations, (1) $2M<r_{s}<r_{p-}$, (2) $r_{s}>r_{p+}$, and (3) $r_{p-}<r_{s}<r_{p+}$.

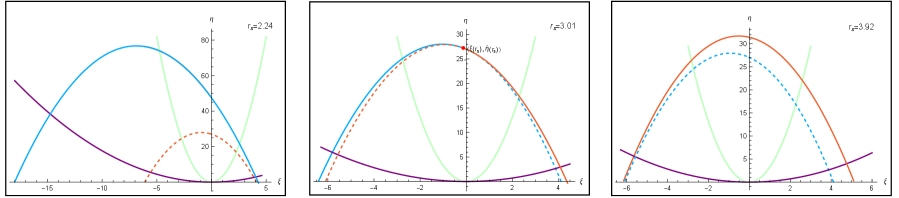
As mentioned above, the shadow is clear if we find the corresponding OPR. Thus, the main task is to look for the OPR for each case. Since the CO is regarded as a dark body in our work, the effect on lights is equivalent to that of the event horizon of a black hole; that is, the photons cannot return if they meet the surface of the CO. As a result, the incoming photons, which have two turning points in the radial motion, cannot escape to infinity if the outer turning point is inside the surface of the CO. Thus, if $r_{s}$ is not less than $\tilde{r}_{p-}$, the part of the photon region inside the surface of the CO has no contribution to the POPR. More precisely, from $R(r_{s})=0$, we can obtain a new relation between $\xi_{s}$ and $\eta_{s}$ as follows:

$\displaystyle\eta_{s}=-\frac{(r_{s}-2J\xi_{s})^{2}}{(2M-r_{s})r_{s}^{3}}-\xi_{s}^{2}\,,$

(3.13)

where the subscript “ $s$ ” means evaluated at $r=r_{s}$. Considering that the radius of the surface $r_{s}$ can be the inner or outer turning point, which corresponds to different values of $(\xi_{s},\eta_{s})$, $\eta_{s}(\xi_{s})$ becomes the new critical parameter when $r_{s}>\tilde{r}$, where $\tilde{r}$ is the radius of the photon region with $\tilde{\eta}(\tilde{\xi})$. In Fig. 2, we give examples of $\tilde{\eta}(\tilde{\xi})$, $\eta_{s}(\xi_{s})$ and $\eta_{o}(\xi_{o})$ for three cases at the observational angles $\theta_{o}=17^{\circ}$ and $\theta=80^{\circ}$ with the mass and the angular momentum of the CO chosen as $M=1$ and $J=0.5$ here and after this. By numerically solving the equation $\tilde{\eta}=0$, we find

$\displaystyle r_{p-}\simeq 2.47\,,\quad r_{p+}\simeq 3.56\,.$

(3.14)

In addition, assuming $R=\partial_{r}R=\partial_{r}^{2}R=0$ for prograde time-like particles , we can find the radius of the innermost stable circular orbit $r_{I}\simeq 4.29$. Considering that the horizon is at $r_{h}=2$, we set $r_{s}=\frac{r_{h}+r_{p-}}{2}\simeq 2.24<r_{p-}$, $r_{p-}<r_{s}=\frac{r_{p-}+r_{p+}}{2}\simeq 3.01<r_{p+}$ and $r_{s}=\frac{r_{p+}+r_{I}}{2}\simeq 3.92>r_{p+}$ for the plots from left to right in Fig. 2. In addition, for each plot, the dashed line denotes $\tilde{\eta}(\tilde{\xi})$, the other curve with a downward opening indicated by a solid line denotes $\eta_{s}(\xi_{s})$, the curve with an upward opening drawn in green is $\eta_{o}(\xi_{o})$ with $\theta_{o}=17^{\circ}$, and the other curve with an upward opening drawn in purple is $\eta_{o}(\xi_{o})$ with $\theta_{o}=80^{\circ}$. For the middle plot in Fig. 2 with $r_{p-}<r_{s}<r_{p+}$, there is an intersection point $(\tilde{\xi}(r_{s}),\tilde{\eta}(r_{s}))$ of $\tilde{\eta}(\tilde{\xi})$ and $\eta_{s}(\xi_{s})$, which means that the two turning points of photons coincide with the radius $r=r_{s}$. When $\xi>\tilde{\xi}(r_{s})$, we find that $r_{s}$ is the outer turning point of $R(r_{s})=0$ and $r_{s}>\tilde{r}$. In contrast, when $\xi<\tilde{\xi}(r_{s})$, we find that $r_{s}$ is the inner turning point of $R(r_{s})=0$ and $r_{s}<\tilde{r}$. Therefore, the red line is the POPR. The impact parameters that are not in POPR are shown in blue. Moreover, combined with the condition from the observer at $\theta_{o}=17^{\circ}$ ($\theta_{o}=80^{\circ}$), the POR is the segment of the red line between the intersections of the red and green (purple) lines. For the left plot in Fig. 2 with $r_{s}<r_{p-}$, we can see that the POPR is still determined by $\tilde{\eta}(\tilde{\xi})$, which is the same as that in black hole spacetime since the surface of the CO is always hidden in the photon region. The OPR is the segment of $\tilde{\eta}(\tilde{\xi})$ between the intersections of the red line $\tilde{\eta}(\tilde{\xi})$ and the green line $\eta_{o}(\xi_{o})$. For the right plot in Fig. 2 with $r_{s}>r_{p+}$, we can see that the POPR is determined by the solid line $\eta_{s}(\xi_{s})$ since the photon region is completely encapsulated by the surface of the CO. The OPR is now given by the segment of the red line $\eta_{s}(\xi_{s})$ between the intersections of $\eta_{s}(\xi_{s})$ and $\eta_{o}(\xi_{o})$.

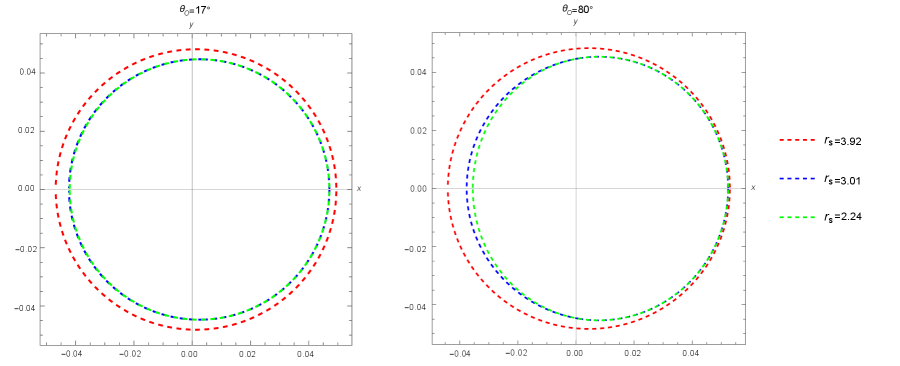
Then, the shadows of COs without horizons can be calculated with the help of Eqs. (3.11) and (3.12). In Fig. 3, we show the shadow curves with dashed lines at $\theta_{o}=17^{\circ}$ for the left plot and $\theta=80^{\circ}$ for the right plot. The red, blue and green lines correspond to $r_{s}=3.92>r_{p+}$, $r_{p-}<r_{s}=3.01<r_{p+}$ and $r_{s}=2.24<r_{p-}$, respectively. As we have discussed above, the shadow curve is exactly determined by the OPR, and we note that in Fig. 2, the dashed line in each plot represents the same photon region, that is, $\tilde{\eta}(\tilde{\xi})$, and thus, the segment of $\tilde{\eta}(\tilde{\xi})$ between the intersections of $\tilde{\eta}(\tilde{\xi})$ and $\eta_{o}(\xi_{o})$ remains invariable in the three plots. As a result, we find that for the case of $\theta_{o}=17^{\circ}$, the blue line and the green line almost coincide in Fig. 3, since from the middle plot in Fig. 2, one can see that the OPR with $r_{s}=3.01$ coincides with the OPR with $r_{s}=2.24$ when $\xi<\tilde{\xi}(r_{s})$ and only has a tiny difference from the OPR with $r_{s}=2.24$ when $\xi>\tilde{\xi}(r_{s})$. Similarly, the difference between the red and green lines in the case of $\theta_{o}=17^{\circ}$ is visible in Fig. 3 since one can see that the difference in their OPRs is evident from the right plot in Fig. 2. Moreover, from the right plot in Fig. 3, we can see that the difference between the green and blue lines becomes significant on the right, and the three lines are very close in the left part. The reason can be easily found in Fig. 2, where the opening of the parabola $\eta_{o}(\xi_{o})$ increases when $\theta_{o}$ goes from $17^{\circ}$ to $80^{\circ}$. Furthermore, in the middle plot of Fig. 2, the difference in the OPRs becomes larger at $\theta_{o}=80^{\circ}$, and in the right plot of Fig. 2, the red and blue lines intersect very closely with the purple line since $r_{s}=3.92$ is near $r_{p+}=3.56$.

Therefore, qualitatively, we can conclude that when $r_{s}<r_{p-}$, the shadow of the CO is the same as that of the black hole; when $r_{p-}<r_{s}<r_{p+}$, the shadow of the CO is larger than that of the black hole, and the shadow of the CO becomes slightly larger as $\theta_{o}$ increases from $0^{\circ}$ to $90^{\circ}$ with parts of the shadow curves overlapping; and when $r_{s}>r_{p+}$, the shadow of the CO becomes significantly larger, and each point of the CO shadow curve is outside the corresponding end of the black hole shadow curve.

In this subsection, we give a quantitative study of the variation of the shadow concerning the radius of the surface of a CO. Following the work [67, 68], we use the average radius $\bar{R}$ as the characteristic length of a shadow.

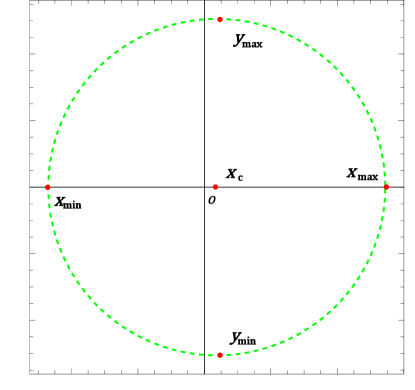
In Fig. 4, we present a diagram to show the coordinates of points at which the shadow curve intersects two axes. $O$ is the origin of the Cartesian coordinates on the screen. Considering the $\mathcal{Z}_{2}$ symmetry of the spacetime, the center of the shadow can be defined as $\left(x_{c}=\frac{x_{\text{min}}+x_{\text{max}}}{2},\frac{y_{\text{min}}+y_{\text{max}}}{2}=0\right)$. Then, let $(x_{c},0)$ be the center, and we can introduce polar coordinates $(R,\psi)$ with $R=\sqrt{(x-x_{c})^{2}+y^{2}}$. The parameter $\bar{R}$ can be defined as

$\displaystyle\bar{R}=\int_{0}^{2\pi}\frac{R(\psi)}{2\pi}d\psi\,,$

(3.15)

which denotes the average radius of the shadow curve. It is convenient to introduce a dimensionless parameter

$$\sigma=\frac{\bar{R}}{\bar{R}_{0}}-1\,,$$

(3.16)

where we use $\bar{R}_{0}$ to represent the average radius of the shadow curve when $r_{h}<r_{s}<r_{p-}$. In Fig. 5, we show the variation in $\sigma$ concerning the radius of the CO surface, where we fix $M=1$ and $J=0.5$ and set $r_{s}=2.07+0.4(i-1)$ with $i=1,2,\dots,14$. We find that the average radius of the shadow curve increases slowly as the radius of the CO surface increases from $r_{p-}$ to $r_{p+}$, because $r_{p+}-r_{p-}=1.09$ is small. When $r_{s}>r_{p+}$, the average radius of the shadow curve increases quickly as the radius of the CO surface increases, and the change is almost linear. In addition, we can see that the average radius of the shadow curve at $\theta_{o}=80^{\circ}$ is always larger than that at $\theta_{o}=17^{\circ}$ for a fixed $r_{s}$ in the range $r_{s}>r_{p-}$, which agrees well with our analysis in the last subsection.