How Material Heterogeneity Creates Rough Fractures
Abstract
Fractures are a critical process in how materials wear, weaken, and fail whose unpredictable behavior can have dire consequences. While the behavior of smooth cracks in ideal materials is well understood, it is assumed that for real, heterogeneous systems, fracture propagation is complex, generating rough fracture surfaces that are highly sensitive to specific details of the medium. Here we show how fracture roughness and material heterogeneity are inextricably connected via a simple framework. Studying hydraulic fractures in brittle hydrogels that have been supplemented with microbeads or glycerol to create controlled material heterogeneity, we show that the morphology of the crack surface depends solely on one parameter: the probability to perturb the front above a critical size to produce a step-like instability. This probability scales linearly with the number density, and as heterogeneity size to the power. The ensuing behavior is universal and is captured by the 1D ballistic propagation and annihilation of steps along the singular fracture front.
As a crack moves through a material, it leaves in its wake a fracture surface that preserves the time history of the shape of the crack front. For many materials this surface is rough, a remnant of the crack’s tortuous path. Roughness is intrinsically three-dimensional, indicating the distortion of a spatially-extended, singular, crack tip line. Idealized fractures advance when the flux of released elastic stress at the crack tip is greater than the energetic cost of breaking the material and generating new surface Lawn et al. (1993), therefore, rougher cracks require more energy to produce. Once cracks exists within a material, they fundamentally alter its characteristics, with their roughness affecting properties including fluid transport Tsang and Witherspoon (1983); Aydin (2000); Bunger and Lecampion (2017) and frictional stability Brodsky et al. (2011); Brodsky and Mori (2007); Candela et al. (2011); Dieterich and Kilgore (1994); Greenwood and Williamson (1966); Persson (2001).
For slow brittle fractures, the crack front is largely straight and forms flat, mirror-like surfaces. Nevertheless, a close inspection of these surfaces often reveals the presence one of the most prominent components of brittle fracture roughness: long, step-like discontinuities called step lines. This class of fractographic features is found in a wide array of both hard Sommer (1969); Hull (1995); Cooke and Pollard (1996) and soft Baumberger et al. (2008); Tanaka et al. (1996, 1998); Kolvin et al. (2017, 2018a); Goldstein and Osipenko (2012) brittle materials. Unlike microbranches, which appear at significant fractions of the Rayleigh wave speed Sharon and Fineberg (1996), step lines form on slow, quasi-static fractures as well.
Step lines arise from a critical twisting, or mixed mode I + III loading, of the fracture front Sommer (1969). Rather than reorient the entire front, an instability mediates the formation of a step-like defect, locally accounting for the twist, while the rest of the crack remains flat Sommer (1969); Ronsin et al. (2014); Lazarus et al. (2001a, b); Leblond et al. (2019); Chen et al. (2015); Pons and Karma (2010); Lin et al. (2010); Pham and Ravi-Chandar (2016, 2017); Kolvin et al. (2018a). Mixed mode loading at the crack tip can result from applied boundary conditions Sommer (1969); Lazarus et al. (2001a, b); Hull (1993, 1995, 1999), but is also understood to arise from material heterogeneity Leblond and Ponson (2016); Ravi-Chandar and Knauss (1984). However, the connection between heterogeneity and roughness has not been resolved because it is difficult to systematically control or measure heterogeneity in an experimental sample. Moreover, it is assumed that rough fracture surfaces result from complex crack behavior that is highly sensitive to the details of the medium.
In this work we show that heterogeneity and fracture roughness are inextricably linked through a simple framework where the evolution of the system depends solely on one parameter: the probability that the heterogeneity perturbs the front enough to produce a step line. By analyzing the broken surfaces of hydrogels prepared with controlled, discrete heterogeneities, we show that increasing either the size or amount of heterogeneities present leads to a marked increase in the density of step lines on the fracture surface. After step lines form, they continuously drift laterally along the front Tanaka et al. (1998); Kolvin et al. (2018a), leading them to interact in a manner that, on average, reduces the number of steps. Eventually, step creation and annihilation rates balance, leading to a steady state. We identify the relationship between the scale of a heterogeneity and the probability of step nucleation on a crack front, connecting the material heterogeneity to the excess energy required to propagate a crack. We also show that our framework can be extended to complex backgrounds of non-discrete, inhomogeneity, indicating that the resultant roughness of a fracture is invariant to the specific process that perturbs the crack front. Finally, when heterogeneities are present at high densities and on many different scales, interactions between steps and the complex background result in fracture surfaces resembling those observed in natural systems.

Hydraulic fractures in hydrogels are an excellent model system in which to study fracture mechanics. Hydraulically-driven fractures generate large, reproducible surfaces Sommer (1969), while hydrogels offer unique flexibility in tuning material properties and geometry. In this study, experiments are performed by flowing a dyed fluid into a small pre-fracture in a 1x1x1 inch brittle, chemically cross-linked hydrogel (for details, see Section S3). This fracture then grows until it reaches the sample edge, as shown in Figure 1A.
While the gel fracture surfaces are nominally flat and smooth, they are pervasively segmented by long curved step lines, which separate two otherwise largely flat planes, as shown in Figure 1B and C. When steps nucleate they drift laterally along the front, either left or right, at a rate equal to that of crack propagation, causing step lines to maintain a 45-degree angle to the crack front Tanaka et al. (1998); Kolvin et al. (2018a). For the curved crack fronts in our experiment, this results in arched step lines. Steps drift in both directions along the front, leading to pairwise interactions as they meet. These interactions result in zero, one, or two outgoing steps, and can only reduce the number of steps. Thus, nucleations increase the number of steps on the front, while interactions, on average, reduce the number of steps.
For each surface we measure the number of step nucleations, (including new steps that branch off existing steps) per unit area, , as well as the total length of lines, or mileage, per unit area on the fracture surface (excluding the region near the crack origin), , as shown in Figure 2A and B. Step lines reach a steady-state height Kolvin et al. (2018a), thus is equivalent to the excess surface energy required to generate the fracture compared to a perfectly smooth crack.
When the gel is supplemented with a low number (1 wt) of rigid microbeads, acting as local heterogeneities, the density of step lines on the surface increases significantly. Systematically increasing the number of beads, , leads to a monotonic increase in both the number of step nucleations, and , by up to a factor of six, as shown in Figure 2C and D.
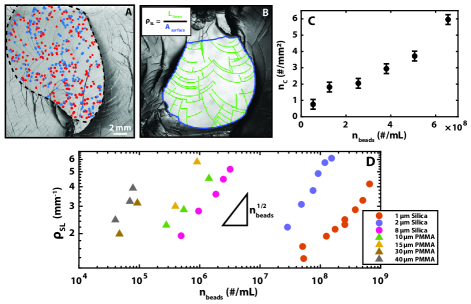
The number of discrete steps created per unit area, , grows linearly with , as shown in Figure 2C, indicating that the probability of a step nucleating along the front, , scales linearly with the density of heterogeneities. By comparison, grows sub-linearly for a range of bead sizes between 1-40 m and does not depend on the material properties of the beads. The number of beads required to generate a similar decreases significantly with increasing radius, , as shown in Figure 2D. This indicates that is a strong function of , and thus, takes the form
| (1) |
Step interactions require two steps and, on average, result in fewer than two outgoing steps. By contrast, when the front interacts with a bead, it nucleates a step, increasing the number of steps on the front. is proportional to the density of beads, suggesting that the beads are well dispersed, and thus act independently. By contrast, the probability of an interaction between steps increases with the density of steps present on the front at a given time, .
Steps are confined to move continuously on the singular fracture front. Thus, from a statistical physics point of view, our system is equivalent to ballistic particles in one dimension. If the locations and drift directions of steps are random, the probability of two steps interacting at a given time should scale as . This leads to a framework where as a crack front propagates, the creation rate remains constant while the probability of interactions grows. Because interactions reduce the number of steps, the interaction rate will continue to grow until the rate of nucleations and annihilations through interaction are equal. As a result, the system reaches a steady-state density of steps, , such that is proportional to . Indeed, outside of the immediate area where the fracture initiates, the density of steps lines is broadly consistent, as shown in Figure S1. Combining this with Eq. 1, we find:
| (2) |
When the front advances a fixed distance, , each step creates the same amount of mileage, , due to the constant front angle. Thus, the rate at which mileage is generated is proportional to the instantaneous number of steps on the front. Assuming the total mileage is measured on a surface produced predominantly at steady state, . Thus,
| (3) |
or
| (4) |
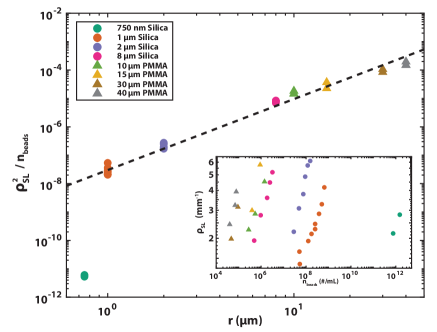
Plotting as a function of collapses the data onto a single line, as shown by Figure 3. This suggests that by neglecting the area around crack initiation, we capture a surface that is predominately at steady state. In addition, the slope of this line indicates that scales as . Therefore the complete scaling function for the probability of nucleating a step is given by:
| (5) |
And for , a measure of the excess surface energy due to heterogeneity, is given by:
| (6) |
The scaling regime for , described by Eq 6, breaks down sharply below m, with the rescaled data for 750 nm beads falling 4 orders of magnitude below the trend for 1-40 m beads. Previous work has shown that a critical ratio of mode I/III loading is required to generate a step line Sommer (1969). We therefore suspect that beads below 1 m do not generate a large enough perturbation of the front to nucleate a step. Instead, the minor roughness increase we do observe is likely the result of bead clustering. Surprisingly, this 1 m cutoff indicates the presence of a length scale for a system governed by linear elastic fracture mechanics, which has classically considered to be scale-invariant. This is consistent with recent work showing that heterogneities significantly smaller than the size of the fracture process zone do not affect the dynamics or fracture energy of a crack Taureg and Kolinski (2020).
This framework fully captures the connection between heterogeneity and surface roughness for systems with well defined, discrete heterogeneities. However, a key assumption for quantifying the size and number of heterogeneities is that they are well distributed, and as a result, the front is locally straight. Many natural systems do not have localized, dominant defects, and instead have smoother backgrounds of inhomogeneity, exhibiting non-local correlations on multiple scales. In these systems step nucleation and interactions may not necessarily be a local process. Our framework relates the heterogeneity of the intact material to the excess energy required to generate a rough surface through the probability of nucleating steps, and thus does not necessitate specific knowledge of the nature of the heterogeneity. We show this by analyzing hydrogels with imhomogeneity that is controlled chemically.
Gels without any beads still produce a small number of step lines. The value of for these experiments, , is approximately . There are a number of proposed mechanisms that cause structural heterogeneity in hydrogels Seiffert (2017), including differences in the rate of monomer and crosslinker consumption during gelation, local fluctuations in polymer concentration, which become ”frozen” in the polymer network during gelationSakai (2014), and microsyneresis. We theorized that the addition of a second phase to the solvent could accentuate these effects, creating inhomogeneity in polymer density that is more gradual and does not exhibit a sharp phase boundary compared to the highly-localized rigid beads.
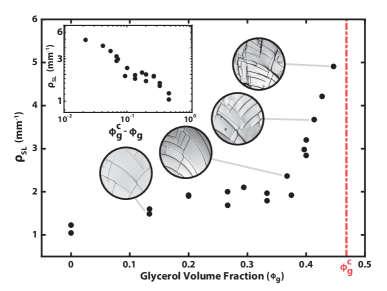
Indeed, when gels are polymerized in a solvent of glycerol and water, there is a continuous increase in up to a factor of 5 as a function of distance from the critical solubility limit, , (46.5% for PEGMEMA in glycerol-water), as shown in Figure 4. This is a clear indication that solubility drives the formation of the inhomogeneity. However, even very close to the solubility limit, the gels are fully transparent, showing no optical aberrations indicative of this inhomogeneity, and attempts to measure either the scale or amount of heterogeneity present via static light scattering were unsuccessful, making a full characterization impossible 111Attempts to measure heterogeneity of glycerol-supplemented hydrogels via static light scattering were unsuccessful due to natural heterogeneity present in the base materials. Private communications with S. Seiffert.
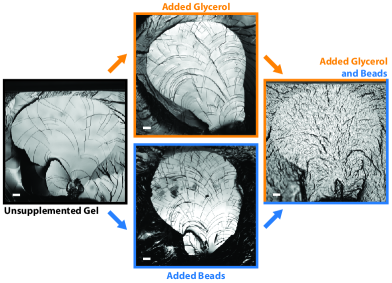
Surprisingly, the fracture surfaces of glycerol-supplemented gels are indistinguishable from those in bead-supplemented ones, as shown in Figure 5, suggesting that fracture roughness does not depend on the nature of the heterogneity or the specific process that perturbs the front, only on the probability of nucleating a step.
Steps produced in unsupplemented gels are caused by a low amplitude background of inhomogeneity. A large enough bead creates a strong localized perturbation to the stress field, which overwhelms the subtle effect of the background. Indeed, the scaling discussed above for the bead-supplemented hydrogels does not include , suggesting that in this regime, the stability of the fracture front is set exclusively by the dominant perturbation. However, as the amplitude of the background increases, a new regime emerges where neither discrete heterogeneity created by beads, nor more gradual inhomogeneity due to glycerol dominate. The resulting fracture surfaces look fundamentally different, and resemble those observed in more complex brittle materials Bahat (1991); Christensen and Hatch (2019); Kimura et al. (1977); Issa and Hammad (1994); Carpinteri et al. (1999), as shown in Figure 5. This complex fracture morphology may be due to beads and/or steps interacting through the background, or additionally, at high enough densities of steps along the front, interactions may no longer be simple and pairwise. Regardless, realistic fracture topographies can be generated through the creation and interaction of step lines, potentially leading to previously observed self-affine fracture roughness Mandelbrot et al. (1984); Ponson et al. (2006).
We have developed a simple model that connects material heterogeneity to fracture roughness. For ideal, brittle materials, linear elastic fracture mechanics successfully predicts crack propagation, but it was commonly assumed that for heterogeneous materials, fractures are extremely sensitive to the details of the medium. We have shown that at least for quasi-static fractures, this is not the case. Instead, the evolution of the system depends solely on the probability to perturb the front enough to produce a step. The ensuing behavior is universal and results from the effectively 1D ballistic propagation and annihilation of steps along the fracture front.
The evolution of step lines on crack fronts is nearly identical to the seemingly unrelated system of decay kinetics in chemically reactive ideal gases. Extensively examined since the 1980s and named ballistic annihilation, this theoretical framework considers the annihilation reaction of ballistic particles. In one dimension, an exact solution Elskens and Frisch (1985) shows that the concentration of ballistic particles decays as , while a mean field approximation predicts a scaling. This discrepancy highlights that this seemingly simple system is in effect quite difficult to analyze Biswas and Leyvraz (2021); Burdinski et al. (2019), hinting at why an understanding of fracture roughness has been so elusive. While the theoretical analysis of this system has been extended to partial annihilation Kafri (2001), to our knowledge, there has been no investigation of a system that includes the creation of ballistic particles. As a result, the possibility of reaching a steady state has not been considered.
Linear elastic fracture mechanics is a scaleless theory, yet prior observations have provided strong indirect evidence for the existence of a material-dependent length scale Dugdale (1960); Chen et al. (2017); Taureg and Kolinski (2020); Livne et al. (2008); Kolvin et al. (2017). It has been suggested that this length is related to the size of the fracture process zone and is important in determining the toughness of soft materialsChen et al. (2017). The sharp breakdown in scaling for beads below 1 m in our system is the most direct experimental evidence yet for a critical microscopic length scale in brittle fracture mechanics.
Our framework demonstrates how steady state fracture roughness results from a balance between step nucleations and interactions, providing a scaffold for a complete theory that would require detailed descriptions of each behavior. However, these processes are inherently three-dimensional and dynamic, necessitating both measurement and theory that capture this dimensionality. Importantly, it is impossible to reduce the dimensionality of the system to a single 2D plane, highlighting the distinction between mixed mode I/II Gao and Rice (1989); Gao et al. (1991); Rice et al. (1994); Taureg and Kolinski (2020) and the current case of mixed mode I/III loading Pons and Karma (2010); Leblond et al. (2019); Lazarus et al. (2001a, b). The complexity of step interactions arises from the fact that in spite of their intricate three-dimensional morphologySommer (1969); Hull (1995); Baumberger et al. (2008); Kolvin et al. (2018b), steps are topologically bound to the same one-dimensional fracture front-line, constraining their motion and interactions with other steps Tanaka et al. (1998). In addition, these interactions occur dynamically during crack growth, so their geometry may also affect both local and global fracture propagation. A full description of the rules and dynamics that govern step nucleation and interaction, completing the framework presented above, will offer a pathway to fully understanding of how real materials break.
I Acknowledgements
The authors would like to thank Tom Kodger, Dmitry Garagash, and Robert Viesca for helpful discussions, and Sebastian Seiffert for preliminary optical measurements of hydrogel heterogeneity. This work was supported by the National Science Foundation through the Harvard Materials Research Science and Engineering Center (DMR-1420570). S. M. R. acknowledges support from the Alfred P. Sloan Research Foundation (FG-2016-6925).
References
- Lawn et al. (1993) B. Lawn, Lawn, and T. R. Wilshaw, Fracture of Brittle Solids (Cambridge University Press, 1993).
- Tsang and Witherspoon (1983) Y. W. Tsang and P. A. Witherspoon, Journal of Geophysical Research 88, 2359 (1983).
- Aydin (2000) A. Aydin, Marine and Petroleum Geology 17, 797 (2000).
- Bunger and Lecampion (2017) A. Bunger and B. Lecampion, Four critical issues for successful hydraulic fracturing applications, Rock Mechanics and Engineering (2017).
- Brodsky et al. (2011) E. E. Brodsky, J. J. Gilchrist, A. Sagy, and C. Collettini, Earth and Planetary Science Letters 302, 185 (2011).
- Brodsky and Mori (2007) E. E. Brodsky and J. Mori, Geophysical Research Letters 34 (2007), 10.1029/2007GL030917.
- Candela et al. (2011) T. Candela, F. Renard, J. Schmittbuhl, M. Bouchon, and E. E. Brodsky, Geophysical Journal International 187, 959 (2011).
- Dieterich and Kilgore (1994) J. H. Dieterich and B. D. Kilgore, Pure Appl. Geophys , 283 (1994).
- Greenwood and Williamson (1966) J. A. Greenwood and J. B. P. Williamson, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 295, 300 (1966).
- Persson (2001) B. N. J. Persson, The Journal of Chemical Physics 115, 3840 (2001).
- Sommer (1969) E. Sommer, Engineering Fracture Mechanics 1, 539 (1969).
- Hull (1995) D. Hull, International Journal of Fracture 70, 59 (1995).
- Cooke and Pollard (1996) M. L. Cooke and D. D. Pollard, Journal of Geophysical Research: Solid Earth 101, 3387 (1996).
- Baumberger et al. (2008) T. Baumberger, C. Caroli, D. Martina, and O. Ronsin, Physical Review Letters 100, 178303 (2008), arXiv:0801.1557 .
- Tanaka et al. (1996) Y. Tanaka, K. Fukao, Y. Miyamoto, H. Nakazawa, and K. Sekimoto, Journal of the Physical Society of Japan 65, 2349 (1996).
- Tanaka et al. (1998) Y. Tanaka, K. Fukao, Y. Miyamoto, and K. Sekimoto, EPL (Europhysics Letters) 43, 664 (1998).
- Kolvin et al. (2017) I. Kolvin, J. Fineberg, and M. Adda-Bedia, Physical Review Letters 119, 215505 (2017).
- Kolvin et al. (2018a) I. Kolvin, J. M. Kolinski, J. P. Gong, and J. Fineberg, Physical Review Letters 121, 135501 (2018a), arXiv:1808.07902 .
- Goldstein and Osipenko (2012) R. V. Goldstein and N. M. Osipenko, Doklady Physics 57, 281 (2012).
- Sharon and Fineberg (1996) E. Sharon and J. Fineberg, Physical Review B 54, 7128 (1996).
- Ronsin et al. (2014) O. Ronsin, C. Caroli, and T. Baumberger, EPL (Europhysics Letters) 105, 34001 (2014).
- Lazarus et al. (2001a) V. Lazarus, J.-B. Leblond, and S.-E. Mouchrif, Journal of the Mechanics and Physics of Solids 49, 1399 (2001a).
- Lazarus et al. (2001b) V. Lazarus, J.-B. Leblond, and S.-E. Mouchrif, Journal of the Mechanics and Physics of Solids 49, 1421 (2001b).
- Leblond et al. (2019) J.-B. Leblond, A. Karma, L. Ponson, and A. Vasudevan, Journal of the Mechanics and Physics of Solids 126, 187 (2019).
- Chen et al. (2015) C.-H. Chen, T. Cambonie, V. Lazarus, M. Nicoli, A. J. Pons, and A. Karma, Physical Review Letters 115, 265503 (2015).
- Pons and Karma (2010) A. J. Pons and A. Karma, Nature 464, 85 (2010).
- Lin et al. (2010) B. Lin, M. E. Mear, and K. Ravi-Chandar, International Journal of Fracture 165, 175 (2010).
- Pham and Ravi-Chandar (2016) K. H. Pham and K. Ravi-Chandar, International Journal of Fracture 199, 105 (2016).
- Pham and Ravi-Chandar (2017) K. H. Pham and K. Ravi-Chandar, International Journal of Fracture 206, 229 (2017).
- Hull (1993) D. Hull, International Journal of Fracture 62, 119 (1993).
- Hull (1999) D. Hull, Fractography: Observing, Measuring and Interpreting Fracture Surface Topography (Cambridge University Press, 1999).
- Leblond and Ponson (2016) J.-B. Leblond and L. Ponson, Comptes Rendus Mécanique 344, 521 (2016).
- Ravi-Chandar and Knauss (1984) K. Ravi-Chandar and W. G. Knauss, International Journal of Fracture 26, 65 (1984).
- Taureg and Kolinski (2020) A. Taureg and J. M. Kolinski, arXiv:2004.04137 [cond-mat] (2020), arXiv:2004.04137 [cond-mat] .
- Sakai (2014) T. Sakai, Polymer Journal 46, 517 (2014).
- Seiffert (2017) S. Seiffert, Polymer Chemistry 8, 4472 (2017).
- Note (1) Attempts to measure heterogeneity of glycerol-supplemented hydrogels via static light scattering were unsuccessful due to natural heterogeneity present in the base materials. Private communications with S. Seiffert.
- Bahat (1991) D. Bahat, Tectonofractography (Springer Berlin Heidelberg, Berlin, Heidelberg, 1991).
- Christensen and Hatch (2019) A. M. Christensen and G. M. Hatch, Journal of Forensic Radiology and Imaging 18, 37 (2019).
- Kimura et al. (1977) T. Kimura, K. Ogawa, and M. Kamiya, Zeitschrift fur Rechtsmedizin 79 (1977), 10.1007/BF00201173.
- Issa and Hammad (1994) M. Issa and A. Hammad, Cement and Concrete Research 24, 325 (1994).
- Carpinteri et al. (1999) A. Carpinteri, B. Chiaia, and S. Invernizzi, Theoretical and Applied Fracture Mechanics 31, 163 (1999).
- Mandelbrot et al. (1984) B. B. Mandelbrot, D. E. Passoja, and A. J. Paullay, Nature 308, 721 (1984).
- Ponson et al. (2006) L. Ponson, D. Bonamy, and E. Bouchaud, Physical Review Letters 96, 035506 (2006).
- Elskens and Frisch (1985) Y. Elskens and H. L. Frisch, Physical Review A 31, 3812 (1985).
- Biswas and Leyvraz (2021) S. Biswas and F. Leyvraz, The European Physical Journal B 94, 240 (2021), arXiv:2106.15758 .
- Burdinski et al. (2019) D. Burdinski, S. Gupta, and M. Junge, Latin American Journal of Probability and Mathematical Statistics 16, 1077 (2019).
- Kafri (2001) Y. Kafri, Journal of Physics A: Mathematical and General 34, 1957 (2001).
- Dugdale (1960) D. Dugdale, Journal of the Mechanics and Physics of Solids 8, 100 (1960).
- Chen et al. (2017) C. Chen, Z. Wang, and Z. Suo, Extreme Mechanics Letters 10, 50 (2017).
- Livne et al. (2008) A. Livne, E. Bouchbinder, and J. Fineberg, Physical Review Letters 101, 264301 (2008), arXiv:0807.4866 .
- Gao and Rice (1989) H. Gao and J. R. Rice, Journal of Applied Mechanics 56, 828 (1989).
- Gao et al. (1991) H. Gao, J. R. Rice, and J. Lee, Journal of Geophysical Research: Solid Earth 96, 21535 (1991).
- Rice et al. (1994) J. R. Rice, Y. Ben-Zion, and K.-S. Klm, Journal of the Mechanics and Physics of Solids 42, 813 (1994).
- Kolvin et al. (2018b) I. Kolvin, G. Cohen, and J. Fineberg, Nature Materials 17, 140 (2018b).