How Much Privacy Does Federated Learning with Secure Aggregation Guarantee?

Ahmed Roushdy Elkordy aelkordy@usc.edu University of Southern CaliforniaUSA , Jiang Zhang jiangzha@usc.edu University of Southern CaliforniaUSA , Yahya H. Ezzeldin yessa@usc.edu University of Southern CaliforniaUSA , Konstantinos Psounis kpsounis@usc.edu University of Southern CaliforniaUSA and Salman Avestimehr avestime@usc.edu University of Southern CaliforniaUSA

(2023)

Abstract.

Federated learning (FL) has attracted growing interest for enabling privacy-preserving machine learning on data stored at multiple users while avoiding moving the data off-device. However, while data never leaves users’ devices, privacy still cannot be guaranteed since significant computations on users’ training data are shared in the form of trained local models. These local models have recently been shown to pose a substantial privacy threat through different privacy attacks such as model inversion attacks. As a remedy, Secure Aggregation (SA) has been developed as a framework to preserve privacy in FL, by guaranteeing the sever can only learn the global aggregated model update but not the individual model updates. While SA ensures no additional information is leaked about the individual model update beyond the aggregated model update, there are no formal guarantees on how much privacy FL with SA can actually offer; as information about the individual dataset can still potentially leak through the aggregated model computed at the server. In this work, we perform a first analysis of the formal privacy guarantees for FL with SA. Specifically, we use Mutual Information (MI) as a quantification metric, and derive upper bounds on how much information about each user’s dataset can leak through the aggregated model update. When using the FedSGD aggregation algorithm, our theoretical bounds show that the amount of privacy leakage reduces linearly with the number of users participating in FL with SA. To validate our theoretical bounds, we use an MI Neural Estimator to empirically evaluate the privacy leakage under different FL setups on both the MNIST and CIFAR10 datasets. Our experiments verify our theoretical bounds for FedSGD, which show a reduction in privacy leakage as the number of users and local batch size grow, and an increase in privacy leakage as the number of training rounds increases. We also observe similar dependencies for the FedAvg and FedProx protocol.

^†^†copyright: none^†^†journalyear: 2023^†^†doi: XXXXXXX.XXXXXXX^†^†conference: Proceedings on Privacy Enhancing Technologies; July 10–14, 2023; Lausanne, Switzerland

1. Introduction

Federated learning (FL) has recently gained significant interest as it enables collaboratively training machine learning models over locally private data across multiple users without requiring the users to share their private local data with a central server (Bonawitz et al., 2017; Kairouz et al., 2019; McMahan et al., 2017). The training procedure in FL is typically coordinated through a central server who maintains a global model that is frequently updated locally by the users over a number of iterations. In each training iteration, the server firstly sends the current global model to the users. Next, the users update the global model by training it on their private datasets and then push their local model updates back to the server. Finally, the server updates the global model by aggregating the received local model updates from the users.

In the training process of FL, users can achieve the simplest notion of privacy in which users keep their data in-device and never share it with the server, but instead they only share their local model updates. However, it has been shown recently in different works (e.g., (Zhu et al., 2019a; Geiping et al., 2020; Yin et al., 2021)) that this alone is not sufficient to ensure privacy, as the shared model updates can still reveal substantial information about the local datasets. Specifically, these works have empirically demonstrated that the private training data of the users can be reconstructed from the local model updates through what is known as the model inversion attack.

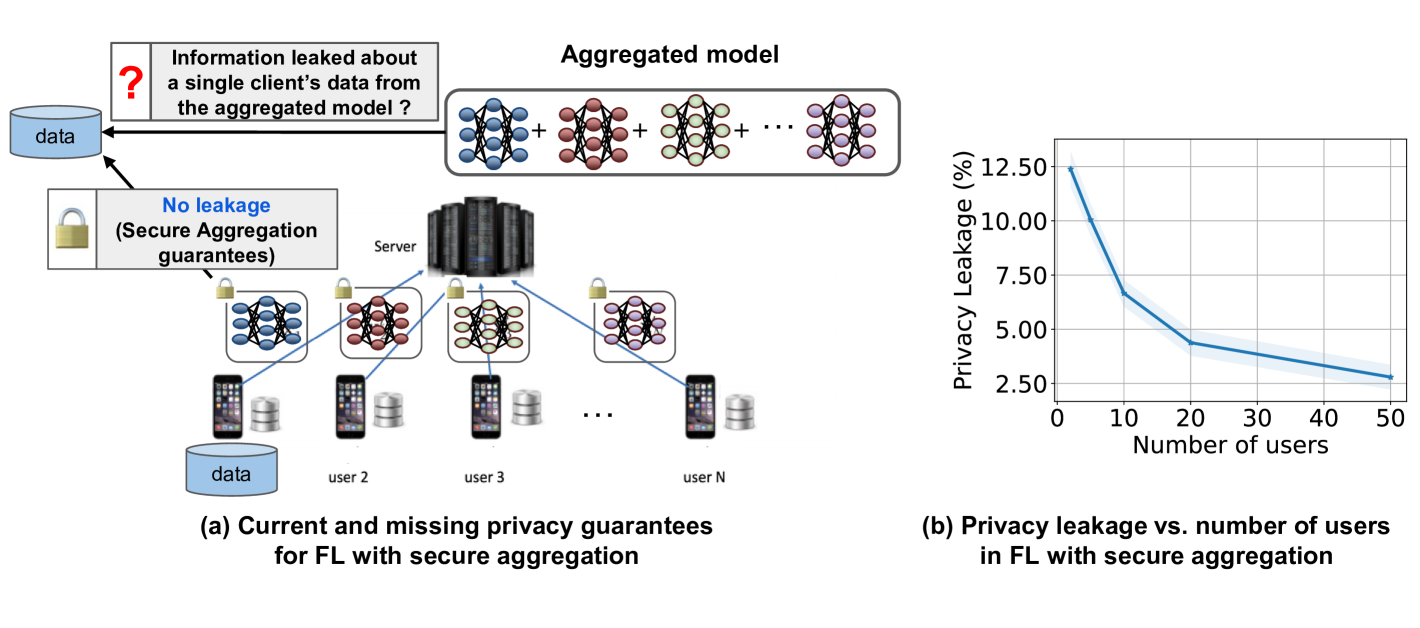
Refer to caption — Figure 1. Figure (a) illustrates the current formal privacy guarantee of FL with SA protocols and sheds light on the missing privacy guarantee on the aggregated model information leakage which is studied in this paper. Figure (b) gives a preview of the behavior of the privacy leakage through the global aggregated model for a CNN model as a function of the number of users in FL. The privacy leakage follows a $\mathcal{O}(1/N)$ decay as proved in our theoretical bounds.

To prevent such information leakage from the individual models that are shared during the training process of FL, Secure Aggregation (SA) protocols have emerged as a remedy to address these privacy concerns by enabling the server to aggregate local model updates from a number of users, without observing any of their model updates in the clear. As shown in Fig. 1a, in each training round, users encrypt their local model updates before sending it to the server for aggregation. Thus, SA protocols formally guarantee that: 1) both the server and other users have no information about any user’s clear model update from the encrypted update in the information theoretic sense; 2) the server only learns the aggregated model. In other words, secure aggregation ensures that only the aggregated model update is revealed to the server. Note that these SA guarantees allow for its use as a supporting protocol for other privacy-preserving approaches such as differential privacy (Dwork et al., 2006). In particular, these approaches can benefit from SA by reducing the amount of noise needed to achieve a target privacy level (hence improving the model accuracy) as demonstrated in different works (e.g., (Truex et al., 2019; Kairouz et al., 2021)).

However, even with these SA guarantees on individual updates, it is not yet fully understood how much privacy is guaranteed in FL using SA, since the aggregated model update may still leak information about an individual user’s local dataset. This observation leads us to the central question that this work addresses:

In this paper, we tackle this question by studying how much privacy can be guaranteed by using FL with SA protocols. We highlight that this work does not propose any new approaches to tackle privacy leakage but instead analyzes the privacy guarantees offered by state-of-the-art SA protocols, where updates from other users can be used to hide the contribution of any individual user. An understanding of this privacy guarantee may potentially assist other approaches such as differential privacy, such that instead of introducing novel noise to protect a user’s model update, the randomized algorithm can add noise only to supplement the noise from other users’ updates to the target privacy level. We can summarize the contributions of the work as follows.

Contributions. In this paper, we provide information-theoretic upper bounds on the amount of information that the aggregated model update (using FedSGD (Bonawitz et al., 2017)) leaks about any single user’s dataset under an honest-but-curious threat model, where the server and all users follow the protocol honestly, but can collude to learn information about a user outside their collusion set. Our derived upper bounds show that SA protocols exhibit a more favorable behavior as we increase the number of honest users participating in the protocol at each round. We also show that the information leakage from the aggregated model decreases by increasing the batch size, which has been empirically demonstrated in different recent works on model inversion attacks (e.g., (Zhu et al., 2019a; Geiping et al., 2020; Yin et al., 2021)), where increasing the batch size limits the attack’s success rate. Another interesting conclusion from our theoretical bounds is that increasing the model size does not have a linear impact on increasing the privacy leakage, but it depends linearly on the rank of the covariance matrix of the gradient vector at each user.

In our empirical evaluation, we conduct extensive experiments on the CIFAR10 (Krizhevsky, 2009) and MNIST (LeCun et al., 2010) datasets in different FL settings. In these experiments, we estimate the privacy leakage using a mutual information neural estimator (Belghazi et al., 2018) and evaluate the dependency of the leakage on different FL system parameters: number of users, local batch size and model size. Our experiments show that the privacy leakage empirically follows similar dependencies to what is proven in our theoretical analysis. Notably, as the number of users in the FL system increase to 20, the privacy leakage (normalized by the entropy of a data batch) drops below $5\%$ when training a CNN network on the CIFAR10 dataset (see Fig. 1b. We also show empirically that the dependencies, observed theoretically and empirically for FedSGD, also extend when using the FedAvg (Bonawitz et al., 2017) FL protocol to perform multiple local training epochs at the users.

2. Preliminaries

We start by discussing the basic federated learning model, before introducing the secure aggregation protocol and its state-of-the-art guarantees.

2.1. Basic Setting of Federated Learning

Federated learning is a distributed training framework (McMahan et al., 2017) for machine learning, in which a set of users $\mathcal{N}=[N]$ ( $|\mathcal{N}|=N$ ), each with its own local dataset $\mathcal{D}_{i}$ ( $\forall i\in[N]$ ), collaboratively train a $d$ -dimensional machine learning model parameterized by $\bm{\theta}\in\mathbb{R}^{d}$ , based on all their training data samples. For simplicity, we assume that users have equal-sized datasets, i.e., $D_{i}=D$ for all $i\in[N]$ . The typical training goal in FL can be formally represented by the following optimization problem:

(1)

\bm{\theta}^{*}=\arg\min_{\bm{\theta}\in\mathbb{R}^{d}}\left[C(\bm{\theta}):=\frac{1}{N}\sum_{i=1}^{N}C_{i}(\bm{\theta})\right],

where $\bm{\theta}$ is the optimization variable, $C(\bm{\theta})$ is the global objective function, $C_{i}(\bm{\theta})$ is the local loss function of user $i$ . The local loss function of user $i$ is given by

(2)

C_{i}(\bm{\theta})=\frac{1}{D}\sum_{(x,y)\in\mathcal{D}_{i}}\ell_{i}(\bm{\theta},(x,y)),

where $\ell_{i}(\bm{\theta},(x,y))\in\mathbb{R}$ denotes the loss function at a given data point $(x_{i},y_{i})\in\mathcal{D}_{i}$ . The dataset $\mathcal{D}_{i}$ at user $i\in[N]$ is sampled from a distribution $\mathcal{P}_{i}$ .

To solve the optimization problem in (1), an iterative training procedure is performed between the server and distributed users, as illustrated in Fig. 2. Specifically, at iteration $t$ , the server firstly sends the current global model parameters, $\bm{\theta}^{(t)}$ , to the users. User $i\in[N]$ then computes its model update $\mathbf{x}_{i}^{(t)}$ and sends it to the server. After that, the model updates of the $N$ users are aggregated by the server to update the global model parameters into $\bm{\theta}^{(t+1)}$ for the next round according to

(3)

\bm{\theta}^{(t+1)}=\bm{\theta}^{(t)}-\eta^{(t)}\frac{1}{N}\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i}.

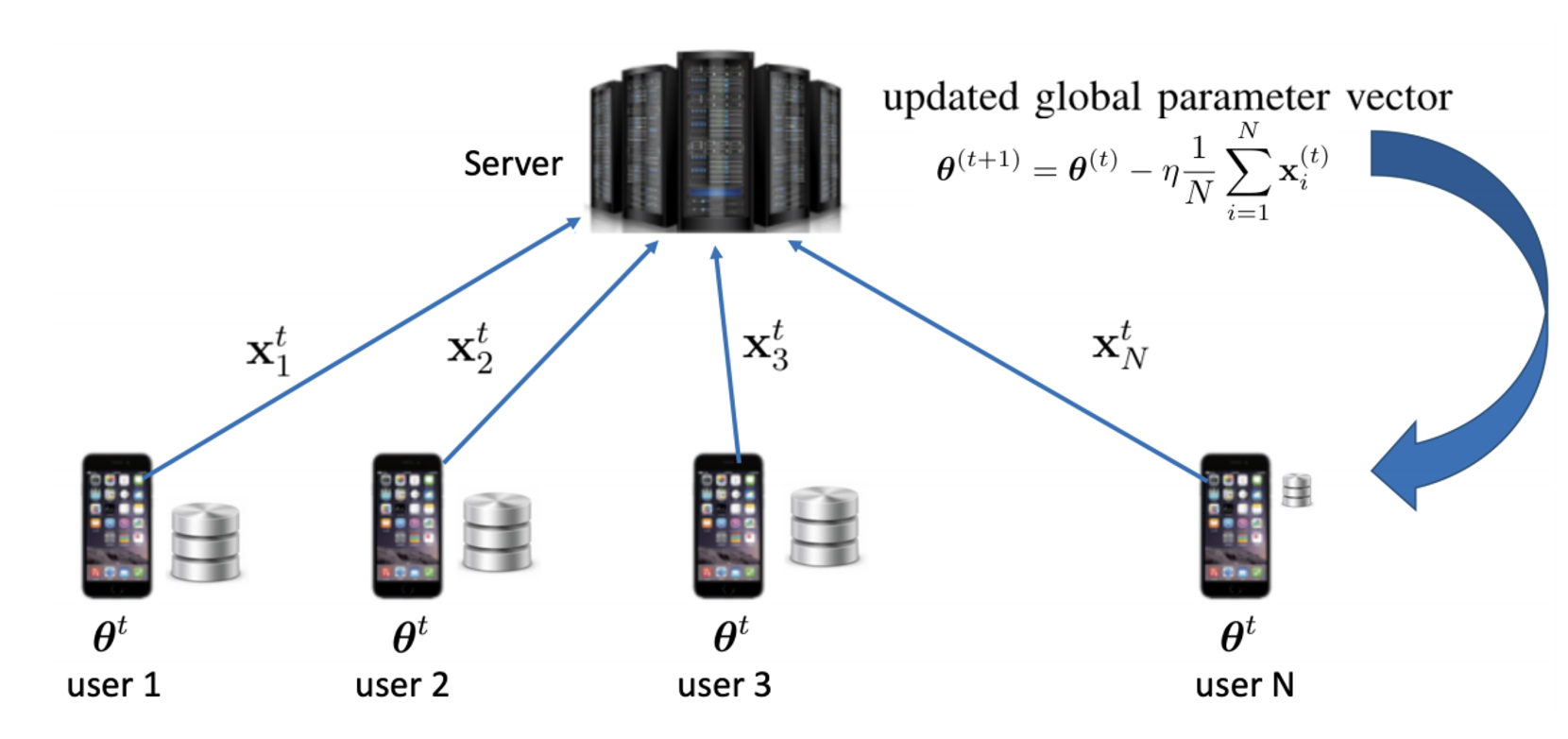
There are two common protocols for computing the model update $\mathbf{x}_{i}$ : FedSGD and FedAvg (McMahan et al., 2017). Specifically, in FedSGD, each user uses a data batch $\mathcal{B}_{i}^{(t)}$ of size $B$ sampled uniformly at random from it local dataset $\mathcal{D}_{i}$ to compute the model update as follows:

(4)

\mathbf{x}_{i}^{(t)}=\frac{1}{B}\sum_{b\in\mathcal{B}_{i}^{(t)}}g_{i}(\bm{\theta}^{(t)},b),

where $g_{i}(\bm{\theta}^{(t)})$ is the stochastic estimate of the gradient $\nabla C_{i}(\bm{\theta}^{(t)})$ of the local loss function $C_{i}$ of user $i$ computed based on a random sample $b$ (corresponding to $(x_{b},y_{b})$ ) drawn uniformly from $\mathcal{D}_{i}$ without replacement. In FedAvg, each user will run $E$ complete local training rounds over its local dataset $\mathcal{D}_{i}$ to get its model update $\mathbf{x}_{i}^{(t)}$ . Specifically, during each training round, each user will use all their mini-batches sampled from $\mathcal{D}_{i}$ to perform multiple stochastic gradient descent steps.

2.2. Secure Aggregation Protocols for Federated Learning

Recent works (e.g., (Zhu et al., 2019a; Geiping et al., 2020; Yin et al., 2021)) have empirically shown that some of the local training data of user $i$ can be reconstructed from the local model update $\mathbf{x}_{i}$ , for $i\in[N]$ . To prevent such data leakage, different SA protocols (Aono et al., 2017; Truex et al., 2019; Dong et al., 2020; Xu et al., 2019; Bell et al., 2020; So et al., 2021a; Kadhe et al., 2020; Zhao and Sun, 2021; So et al., 2022; Elkordy and Salman Avestimehr, 2022; Mugunthan et al., 2019; So et al., 2021b) have been proposed to provide a privacy-preserving FL setting without sacrificing the training performance. In the following, we discuss the threat model used in these SA protocols.

2.2.1. Threat Model in Secure Aggregation for Federated Learning

Most of SA protocols consider the honest-but-curious model (Bonawitz et al., 2017) with the goal of uncovering users’ data. In this threat model, the server and users honestly follow the SA protocol as specified. In particular, they will not modify their model architectures to better suit their attack, nor send malicious model update that do not represent the actually learned model. However, the server and the participating users are assumed to be curious and try to extract any useful information about the training data of any particular user. The extraction of the information is done by storing and analyzing the different data received during the execution of the protocol.

On the other hand, the threat model in theses SA protocols assumes that the server can collude with any subset of users $\mathcal{T}\subset[N]$ by jointly sharing any data that was used during the execution of the protocol (including their clear model updates $\mathbf{x}_{i}$ , for all $i\in\mathcal{T}$ ) that could help in breaching the data privacy of any target user $i\in[N]/\mathcal{T}$ . Similarly, this threat model also assumes that users can collude with each other to get information about the training data of other users.

2.2.2. Secure Aggregation Guarantees

In general, SA protocols that rely on different encryption techniques; such as homomorphic encryption (Aono et al., 2017; Truex et al., 2019; Dong et al., 2020; Xu et al., 2019), and secure multi-party computing (MPC) (Bell et al., 2020; So et al., 2021a; Kadhe et al., 2020; Zhao and Sun, 2021; So et al., 2022; Elkordy and Salman Avestimehr, 2022; Mugunthan et al., 2019; So et al., 2021b), are all similar in the encryption procedure in which each user encrypts its own model update $\mathbf{y}^{(t)}_{i}=\text{Enc}(\mathbf{x}^{(t)}_{i})$ before sending it to the server. This encryption is done such that these protocols achieve: 1) Correct decoding of the aggregated model under users’ dropout; 2) Privacy for the local model update of the users from the encrypted model. In the following, we formally describe each of these guarantees.

Correct decoding. The encryption guarantees correct decoding for the aggregated model of the surviving users even if a subset $\mathcal{U}\subset[N]$ of the users dropped out during the protocol execution. In other words, the server should be able to decode

(5)

\text{Dec}\left(\sum_{i\in\mathcal{V}}\mathbf{y}^{(t)}_{i}\right)=\sum_{i\in\mathcal{V}}\mathbf{x}^{(t)}_{i},

where $\mathcal{V}$ is the set of surviving users (e.g., $\mathcal{U}\cup\mathcal{V}=[N]$ and $\mathcal{U}\cap\mathcal{V}=\phi$ ).

Privacy guarantee. Under the collusion between the server and any strict subset of users $\mathcal{T}\subset[N]$ , we have the following

(6)

I\left({\{\mathbf{y}}^{(t)}_{i}\}_{i\in[N]};\{\mathbf{x}^{(t)}_{i}\}_{i\in[N]}\middle|\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i},\mathbf{z}_{\mathcal{T}}\right)=0,

where $\mathbf{z}_{\mathcal{T}}$ is the collection of information at the users in $\mathcal{T}$ . In other words, (6) guarantees that under a given subset of colluding users $\mathcal{T}$ with the server, the encrypted model updates $\{\mathbf{y}^{(t)}_{i}\}_{i\in[N]}$ leak no information about the model updates $\{\mathbf{x}^{(t)}_{i}\}_{i\in[N]}$ beyond the aggregated model $\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i}$ . We note that the upper bound on the size of the colluding set $\mathcal{T}$ such that (6) is always guaranteed has been analyzed in the different SA protocols. Assuming that $|\mathcal{T}|\leq\frac{N}{2}$ is widely used in most of the works (e.g., (So et al., 2022; So et al., 2021b)).

Remark 1.

Recently, there have been also some works that enable doing secure model aggregation by using Trusted Execution Environments (TEE) such as Intel SGX (e.g., (Kuznetsov et al., 2021; Zhang et al., 2021)). SGX is a hardware-based security mechanism to protect applications running on a remote server. These TEE-based works are also designed to give the same guarantee in (6).

In the following, we formally highlight the weakness of the current privacy guarantee discussed in (6).

2.2.3. Our Contribution: Guarantees on Privacy Leakage from the Aggregated Model

Different SA protocols guarantee that the server doesn’t learn any information about the local model update $\mathbf{x}^{(t)}_{i}$ of any user $i$ from the received encrypted updates $\{\mathbf{y}^{(t)}_{i}\}_{i\in\mathcal{N}}$ , beyond the aggregated model as formally shown in (6). However, it is not clear how much information the aggregated model update itself leaks about a single user’s local dataset $\mathcal{D}_{i}$ . In this work, we fill this gap by theoretically analyzing the following term.

(7)

\displaystyle I_{\rm priv/data}=\max_{i\in[N]}\ I\left(\mathcal{D}_{i};\left\{\frac{1}{N}\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i}\right\}_{t\in[T]}\right).

The term in (7) represents how much information the aggregated model over $T$ global training rounds could leak about the private data $\mathcal{D}_{i}$ of any user $i\in[N]$ . In the following section, we theoretically study this term and discuss how it is impacted by the different FL system parameters such as model size, number of users , etc. In Section 5, we support our theoretical findings by empirically evaluating $I_{\rm priv/data}$ in real-world datasets and different neural network architectures.

3. Theoretical Privacy Guarantees of FL with Secure Aggregation

In this section, we theoretically quantify the privacy leakage in FL when using secure aggregation with the FedSGD protocol.

3.1. Main Results

For clarity, we first state our main results under the honest-but-curious threat model discussed in Section 2.2.1 while assuming that there is no collusion between the server and users. We also assume that there is no user dropout. Later in Section 3.3, we discuss the general result with user dropout and the collusion with the server.

Our central result in this section characterizes the privacy leakage in terms of mutual information for a single round of FedSGD, which for round $t$ is defined as

(8)

I_{\rm priv}^{(t)}=\max_{i\in[N]}I\left(\mathbf{x}^{(t)}_{i};\sum_{i=1}^{N}\mathbf{x}_{i}^{(t)}\middle|\left\{\sum_{i=1}^{N}\mathbf{x}_{i}\right\}_{k\in[t-1]}\right)

and then extends the privacy leakage bound to multiple rounds. Before stating our main result in Theorem 1 below, we first define two key properties of random vectors that will be used in stating our theorem and formally state our operational assumptions.

Definition 1 (Independent under whitening).

We say that a random vector $\mathbf{v}$ with mean $\mu_{v}$ and non-singular covariance matrix $\mathbf{K}_{v}$ is independent under whitening, if the whitened vector $\widehat{\mathbf{v}}$ is composed of independent random variables, where $\widehat{\mathbf{v}}=\mathbf{K}_{v}^{-1/2}\left(\mathbf{v}-\mu_{v}\right)$ .

Definition 2 (Uniformly $\sigma$ -log concave).

A random vector $\mathbf{v}$ with covariance $\mathbf{K}_{v}$ is uniformly $\sigma$ -log concave if it has a probability density function $e^{-\phi(\mathbf{v})}$ satisfying $\nabla^{2}\phi(\mathbf{v})\succeq\mathbf{I}$ and $\exists\ \sigma>0$ , such that $\mathbf{K}_{q}\succeq\sigma\mathbf{I}$ .

Assumption 1 (IID data distribution).

Throughout this section, we consider the case where the local dataset $\mathcal{Z}_{i}$ are sampled IID from a common distribution, i.e., the local dataset of user $i$ consists of IID data samples from a distribution $\mathcal{P}_{i}$ , where $\mathcal{P}_{i}=\mathcal{P}$ for $\forall i\in[N]$ . This implies that the distribution of the gradients $g_{i}(\bm{\theta}^{(t)},b)$ , for $i\in[N]$ , conditioned on the last global model $\bm{\theta}^{(t)}$ is also IID. For this common conditional distribution, we will denote its mean with $\mu_{G}^{(t)}$ and the covariance matrix $\mathbf{K}_{G}^{(t)}$ in the $t$ -th round.

With the above definitions and using Assumption 1, we can now state our main result below, which is proved in Appendix A.

Theorem 1 (Single Round Leakage).

Let $d^{*}\leq d$ be the rank of the gradient covariance matrix $\mathbf{K}_{G}^{(t)}$ , and let $\mathcal{S}_{g}$ denote the set of subvectors of dimension $d^{*}$ of $g(\bm{\theta}^{(t-1)},b)$ that have a non-singular covariance matrices. Under Assumption 1, we can upper bound $I_{\rm priv}^{(t)}$ for FedSGD in the following two cases:
Case. 1 If $\exists\bar{g}\in\mathcal{S}_{g}$ , such that $\bar{g}$ is independent under whitening (see Def. 1), and ${\rm E}|\bar{g}_{i}|^{4}<\infty,\forall i\in[d^{*}]$ , then $\exists\ C_{0,\bar{g}}>0$ , such that

(9)

\displaystyle I_{\rm priv}^{(t)}\leq\frac{C_{0,\bar{g}}\ d^{*}}{(N-1)B}+\frac{d^{*}}{2}\log\left(\frac{N}{N-1}\right),

Case. 2 If $\exists\bar{g}\in\mathcal{S}_{g}$ , such that $\bar{g}$ is $\sigma$ -log concave under whitening (see Def. 2) then we have that

(10)

\displaystyle I_{\rm priv}^{(t)}\leq\frac{d^{*}C_{1,\bar{g}}-C_{2,\bar{g}}}{(N-1)B\sigma^{4}}+\frac{d^{*}}{2}\log\left(\frac{N}{N-1}\right),

where: the constants $C_{1,\bar{g}}=2\left(1+\sigma+\log(2\pi)-\log(\sigma)\right)$ and $C_{2,\bar{g}}=4\left(h(\bar{g})-\frac{1}{2}\log(|\Sigma_{\bar{g}}|\right)$ , with $\Sigma_{\bar{g}}$ being the covariance matrix of the vector $\bar{g}$ .

Remark 2 (Simplified bound).

Note that each $\bar{g}\in\mathcal{S}_{g}^{(t)}$ satisfying Case 1 or Case 2 gives an upper bound on $I_{\rm priv}^{(t)}$ . Let $\mathcal{S}_{g,c}^{(t)}$ be the set of $\bar{g}\in\mathcal{S}_{g}^{(t)}$ satisfying either Case 1 or Case 2. Then, we can combine these different bounds in Theorem 1 as follows

(11)

\displaystyle I_{\rm priv}^{(t)}\leq\frac{d^{*}}{2}\log\left(\!\frac{N}{N{-}1}\!\right)+\dfrac{\displaystyle\min_{\bar{g}\in\mathcal{S}_{g,c}^{(t)}}\left\{d^{*}\widehat{C}_{1,\bar{g}}-\widehat{C}_{2,\bar{g}}\right\}}{(N-1)B},

where

\displaystyle(\widehat{C}_{1,\bar{g}},\widehat{C}_{2,\bar{g}})=\begin{cases}\left(C_{0,\bar{g}},0\right),&\text{if $\bar{g}$ satisfies Case 1},\\ \left(\frac{C_{1,\bar{g}}}{\sigma^{4}},\frac{C_{2,\bar{g}}}{\sigma^{4}}\right),&\text{if $\bar{g}$ satisfies Case 2},\end{cases}

where $C_{0,\bar{g}},C_{1,\bar{g}}$ and $C_{2,\bar{g}}$ are defined as in Theorem 1.

Remark 3.

(Why the IID assumption?) Our main result in Theorem 1 relies on recent results on the entropic central (Eldan et al., 2020; Bobkov et al., 2014) for the sum of independent and identically random variables/vectors. Note that the IID assumption in the entropic central limit theorem can be relaxed to independent (but not necessarily identical) distributions, however, in this case, the upper bound will have a complex dependency on the moments of the $N$ distributions in the system. In order to high-light how the privacy guarantee depends on the different system parameters (discussed in the next subsection), we opted to consider the IID setting in our theoretical analysis.

Remark 4.

(Independence under whitening) One of our key assumptions in Theorem 1 is the independence under whitening assumption for stochastic gradient descent (SGD). This assumption is satisfied if the SGD vector can be approximated by a distribution with independent components or by a multivariate Gaussian vector. Our adoption of this assumption is motivated by recent theoretical results for analyzing the behaviour of SGD. These results have demonstrated great success in approximating the practical behaviour of SGD, in the context of image classification problems, by modeling the SGD with (i) a non-isotropic Gaussian vector (Zhu et al., 2019b), or, (ii) $\alpha$ -stable random vectors with independent components (Simsekli et al., 2019). For both these noise models, the independence under whitening assumption in Theorem 1 is valid. However, a key practical limitation for the aforementioned SGD models (and thus of the independence under whitening assumption) is assuming a smooth loss function for learning. This excludes deep neural networks that make use of non-smooth activation and pooling functions (e.g., ReLU and max-pooling).

Now using the bounds in Theorem 1, in the following corollary, we characterize the privacy leakage of the local training data $\mathcal{D}_{i}$ of user $i$ after $T$ global training rounds of FedSGD, which is defined as

(12)

I_{\rm priv/data}=\max_{i\in[N]}I\left(\mathcal{D}_{i};\left\{\frac{1}{N}\sum_{i\in[N]}\mathbf{x}^{(t)}_{i}\right\}_{t\in[T]}\right),

Corollary 0.

Assuming that users follow the FedSGD training protocol and the same assumptions in Theorem 1, we can derive the upper bound of the privacy leakage $I_{\rm priv/data}$ after $T$ global training rounds of FedSGD in the following two cases:
Case. 1: Following the assumptions used in Case 1 in Theorem 1, we get

(13)

\displaystyle I_{\rm priv/data}\leq T\left[\frac{C_{0,\bar{g}}d^{*}}{(N-1)B}+\frac{d^{*}}{2}\log\left(\frac{N}{N-1}\right)\right],

Case. 2: Following the assumptions used in Case 2 in Theorem 1, we get

(14)

\displaystyle I_{\rm priv/data}\leq T\left[\!\frac{d^{*}C_{1,\bar{g}}-C_{2,\bar{g}}}{(N-1)B\sigma^{4}}+\frac{d^{*}}{2}\log\left(\frac{N}{N{-}1}\right)\!\right].

We prove Corollary 1 in Appendix B. Note that, we can combine the bounds in Corollary 1 similar to the simplification in (11) from Theorem 1.

3.2. Impact of System Parameters

3.2.1. Impact of Number of Users (N)

As shown in Theorem 1 and Corollary 1, the upper bounds on information leakage from the aggregated model update decrease in the number of users $N$ . Specifically, the leakage dependency on $N$ is at a rate of $\mathcal{O}(1/N)$ .

3.2.2. Impact of Batch Size (B)

Theorem 1 and Corollary 1 show that the information leakage from the aggregated model update could decrease when increasing the batch size that is used in updating the local model of each user.

3.2.3. Impact of Model Size (d)

Given our definition of $d^{*}$ in Theorem 1, where $d^{*}$ represents the rank of the covariance matrix $K_{G^{(t)}}$ and $d^{*}\leq d$ ( $d$ is the model size), the leakage given in Theorem 1 and Corollary 1 only increases with increasing the rank of the covariance matrix of the gradient. This increase happens at a rate of $\mathcal{O}(d^{*})$ . In other words, increasing the model size $d$ (especially when the model is overparameterized) does not have a linear impact on the leakage. The experimental observation in Section 4 supports these theoretical findings.

3.2.4. Impact of Global Training Rounds (T)

Corollary 1 demonstrates that the information leakage from the aggregated model update about the private training data of the users increases with increasing the number of global training rounds. This result reflects the fact as the training proceed, the model at the server start to memorize the training data of the users, and the data of the users is being exposed multiple times by the server as $T$ increases, hence the leakage increases. The increase of the leakage happens at a rate of $\mathcal{O}(T)$ .

3.3. Impact of User Dropout, Collusion, and User Sampling

In this section, we extend the results given in Theorem 1 and Corollary 1 to cover the more practical FL scenario that consider, user dropout, the collusion between the server and the users and user sampling. We start by discussing the impact of user dropout and collusion.

3.3.1. Impact of User Dropout and Collusion with the Server

Note that, in the case of user dropouts, this is equivalent to a situation where the non-surviving users send a deterministic update of zero. As a result, their contribution can be removed from the aggregated model, and we can, without loss of generality, consider an FL system where only the surviving subset $\mathcal{N}_{s}\subset[N]$ users participate in the system.

Similarly, when a subset of users colludes with the server, then the server can subtract away their contribution to the aggregated model in order to unmask information about his target user $i$ . As a result, we can again study this by considering only the subset of non-colluding (and surviving, if we also consider dropout) users in our analysis. This observation gives us the following derivative of the result in Theorem 1 which can summarized by the following corollary.

Corollary 0.

In FedSGD, under the assumptions used in Theorem 1, if there is only a subset $\mathcal{N}_{s}^{(t)}\subset[N]$ of non-colluding and surviving users in the global training round $t$ , then, we have the following bound on $I_{\rm priv}^{(t)}$

(15)

\displaystyle I_{\rm priv}^{(t)}\leq\frac{d^{*}}{2}\log\left(\!\frac{|\mathcal{N}_{s}|}{|\mathcal{N}_{s}|{-}1}\!\right)+\dfrac{\displaystyle\min_{\bar{g}\in\mathcal{S}_{g,c}^{(t)}}\left\{d^{*}\widehat{C}_{1,\bar{g}}-\widehat{C}_{2,\bar{g}}\right\}}{(|\mathcal{N}_{s}|-1)B},

where the maximization in $I_{\rm priv}^{(t)}$ (given in (8)) is only over the set of non-colluding surviving and non-colluding users; and the constants $\widehat{C}_{1,\bar{g}}$ and $\widehat{C}_{2,\bar{g}}$ are given in Remark 2.

This implies that the per round leakage increases when we have a smaller number of surviving and non-colluding users. Similarly, we can modify the bound in Corollary 1 to take into account user dropout and user collusion by replacing $N$ with $|\mathcal{N}_{s}|$ .

3.3.2. Impact of User Sampling

In Theorem 1 and Corollary 1, we assume that all $N$ users in the FL system participate in each training round. If instead $K$ users are chosen each round, then all leakage upper bound will be in terms of $K$ , the number of users in each round, instead of $N$ . Furthermore, through Corollary 1, we can develop upper bounds for each user $i$ , depending on the number of rounds $T_{i}$ that the user participated in. For example, taking into account selecting $K$ users in each round denoted by $\mathcal{K}^{(t)}$ , then the upper bound in (13) is modified to give the following information leakage for user $i$

		$\displaystyle I_{\rm priv/data}(i)=I\left(\mathcal{D}_{i};\left\{\frac{1}{K}\sum_{i\in\mathcal{K}^{(t)}}\mathbf{x}^{(t)}_{i}\right\}_{t\in[T]}\right)$
(16)			$\displaystyle\leq T_{i}\left[\frac{C_{0,\bar{g}}d^{}}{(K-1)B}+\frac{d^{}}{2}\log\left(\frac{K}{K-1}\right)\right],$

where $T_{i}=K/N$ if the set of $K$ users are chosen independently and uniformly at random in each round.

Thus user sampling would improve the linear dependence of the leakage on $T$ (Section 3.2.4), but increase the per round leakage due to a smaller number of users in each round (Section 3.2.1).

4. Experimental Setup

4.1. MI Estimation

In order to estimate the mutual information in our experiments, we use Mutual Information Neural Estimator (MINE) which is the state-of-the-art method (Belghazi et al., 2018) to estimate the mutual information between two random vectors (see Appendix D for more details). In our experiments, at the $t$ -th global training round, we use MINE to estimate $I(\mathbf{x}^{(t)}_{i};\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i}|\bm{\theta}^{(t-1)})$ , i.e., the mutual information between model update of the $i$ -th user $\mathbf{x}^{(t)}_{i}$ and the aggregated model update from all users $\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i}$ . Our sampling procedure is described as follows: 1) at the beginning of the global training round $t$ , each user will first update its local model parameters as the global model parameters $\bm{\theta}^{(t-1)}$ . 2) Next, each user shuffles its local dataset. 3) Then, each user will pick a single data batch from its local dataset (if using FedSGD) or use all local data batches (if using FedAvg) to update its local model. 4) Lastly, secure aggregation is used to calculate the aggregated model update. We repeat the above process for $K$ times to get $K$ samples $\{(\mathbf{x}^{(t)}_{i,k};\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i,k})\}_{k=1}^{k=K}$ , where $\mathbf{x}^{(t)}_{i,k}$ represents the model update from the $i$ -th user in the $k$ -th sampling and $\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i,k}$ represents the aggregated model update from the $i$ -th user in the $k$ -th sampling. Note that we use the $K-th$ (last) sample $\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i,K}$ to update the global model.

We repeat the end-to-end training and MI estimation multiple times in order to get multiple MI estimates for each training round $t$ . We use the estimates for each round to report the average MI estimate and derive the confidence interval (95%) for the MI estimation¹¹1During our experiments, we observe that the estimated MI does not change significantly across training rounds. Hence, we average the estimated MI across training rounds when reporting our results..

Lastly, when using MINE to estimate MI, we use a fully-connected neural network with two hidden layers each having 100 neurons each as $T_{\theta}$ (see Appendix D for more details) and we perform gradient ascent for 1000 iterations to train the MINE network.

4.2. Datasets and Models

Datasets. We use MNIST and CIFAR10 datasets in our experiments. Specifically, the MNIST dataset contains 60,000 training images and 10,000 testing images, with 10 classes of labels. The CIFAR10 dataset contains 50,000 training images and 10,000 testing images, with 10 classes of labels. For each of the dataset, we randomly split the training data into 50 local datasets with equal size to simulate a total number of 50 users with identical data distribution. Note that we describe how to generate users with non-identical data distribution when we evaluate the impact of user heterogeneity in Section 5.6.

Moreover, we use MINE to measure the entropy of an individual image in each of these datasets, as an estimate of the maximal potential MI privacy leakage per image. We report that the entropy of an MNIST image is 567 (bits) and the entropy of a CIFAR10 image is 1403 (bits). Note that we will use the entropy of training data to normalize the measured MI privacy leakage in Section 5.

Models. Table 1 reports the models and their number of parameters used in our evaluation. For MNIST dataset, we consider three different models for federated learning. For each of these models, it takes as input a 28 $\times$ 28 image and outputs the probability of 10 image classes. We start by using a simple linear model, with a dimension of 7850. Next, we consider a non-linear model with the same amounts of parameters as the linear model. Specifically, we use a single layer perceptron (SLP), which consists of a linear layer and a ReLU activation function (which is non-linear). Finally, we choose a multiple layer perceptron (MLP) with two hidden layers, each of which contains 100 neurons. In total, it has 89610 parameters. Since the MLP model we use can already achieve more than 95% testing accuracy on MNIST dataset, we do not consider more complicated model for MNIST.

For the CIFAR10 dataset, we also evaluate three different models for FL. For each of these models, it will take as input an 32 $\times$ 32 $\times$ 3 image and outputs the probability of 10 image classes. Similar to MNIST, the first two models we consider are a linear model and a single layer perceptron (SLP), both of which contains 30720 parameters. The third model we consider is a Convolutional Neural Network (CNN) modified from AlexNet (Krizhevsky et al., 2012), which contains a total of 82554 parameters and is able to achieve a testing accuracy larger than 60% on CIFAR. We do not consider larger CNN models due to the limited computation resources.

Models for MNIST
Name	Linear	SLP	MLP
Size ( $d$ )	7890	7850	89610
Models for CIFAR10
Name	Linear	SLP	CNN
Size ( $d$ )	30730	30730	82554

Table 1. Models used for MNIST and CIFAR10 datasets. Note that SLP, MLP, and CNN represent Single Layer Perceptron, Multiple Layer Perceptron, and Convolutional Neural Network, respectively.

5. Empirical Evaluation

In this section, we empirically evaluate how different FL system parameters affect the MI privacy leakage in SA. Our experiments explore the effect of the system parameters on FedSGD, FedAvg and FedProx (Sahu et al., 2018). Note that our evaluation results on FedSGD are backed by our theoretical results in Section 3, while our evaluation results on FedAvg and FedProx are purely empirical.

We start by evaluating the impact of the number of users $N$ on the MI privacy leakage for FedSGD, FedAvg and FedProx (see in Section 5.1). Then, we evaluate the impact of batch size $B$ on the MI privacy leakage for both FedSGD, FedAvg and FedProx (see in Section 5.3). Next, in Section 5.4, we measure the accumulative MI privacy leakage across all global training rounds. We evaluate how the local training rounds $E$ for each user will affect the MI privacy leakage for FedAvg and FedProx in Section 5.5. Finally, the impact of user heterogeneity on the MI privacy leakage for FedAvg is evaluated in Section 5.6.

We would like to preface by noting that FedProx differs from FedAvg by adding a strongly-convex proximal term to the loss used in FedAvg. Thus, we expect similar dependencies on the number of users $N$ , batch-size $B$ and local epochs $E$ , when using FedAvg and FedProx.

5.1. Impact of Number of Users (N)

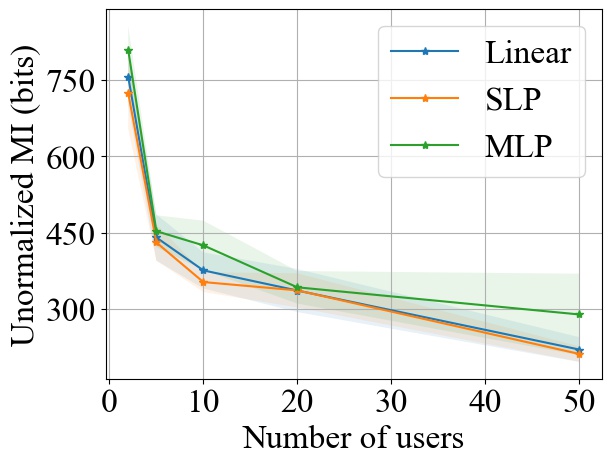
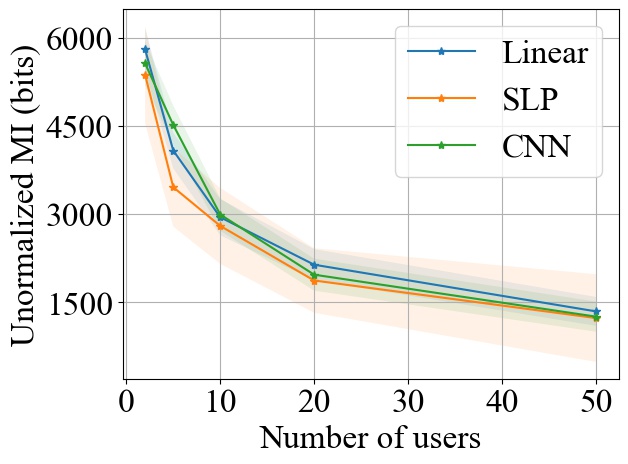
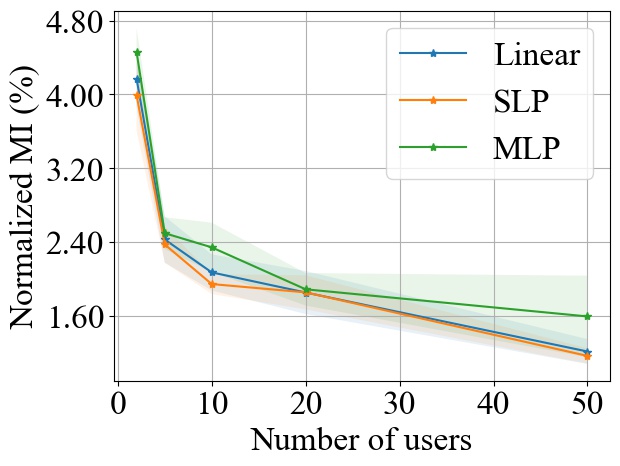
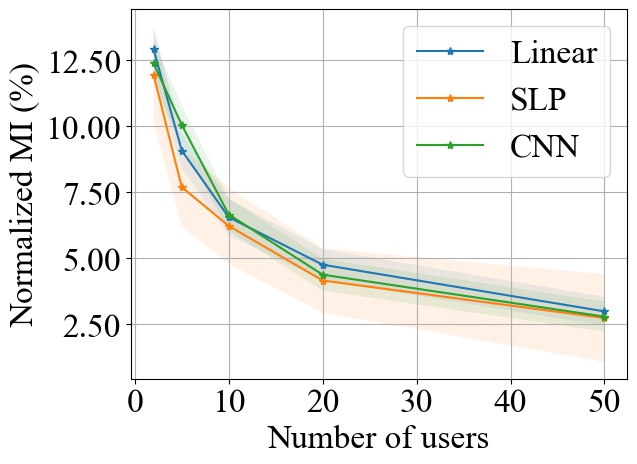
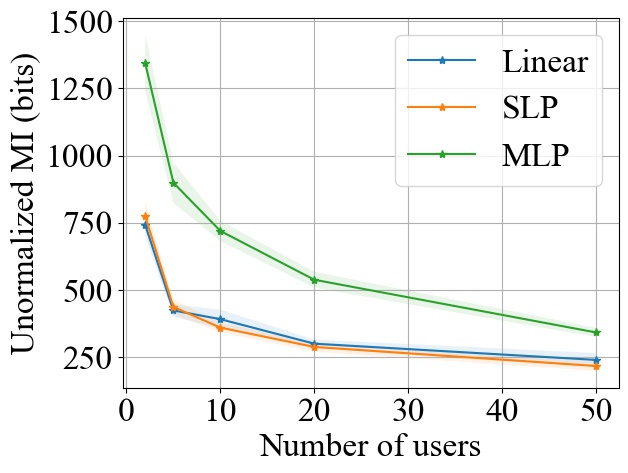
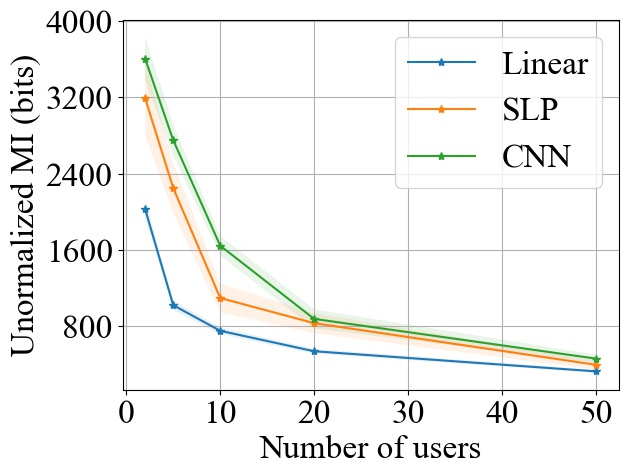
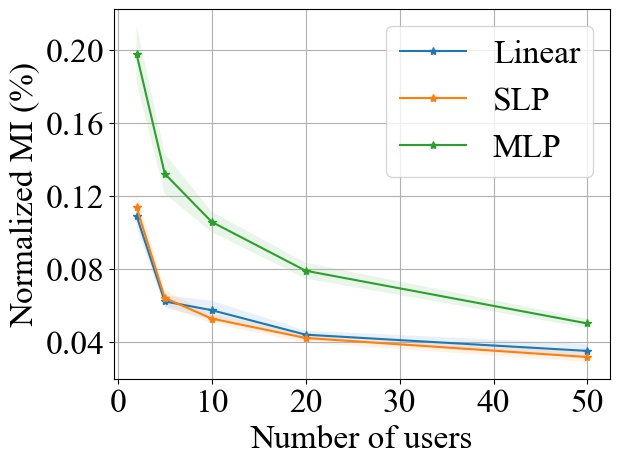
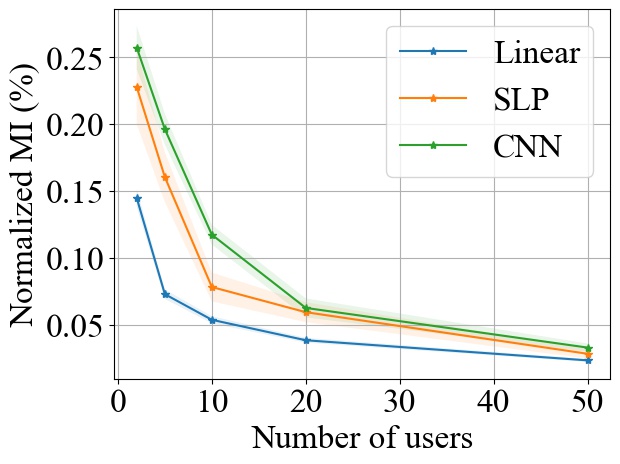
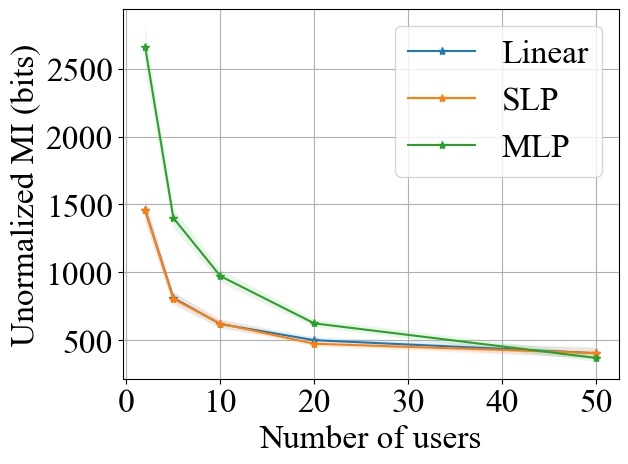
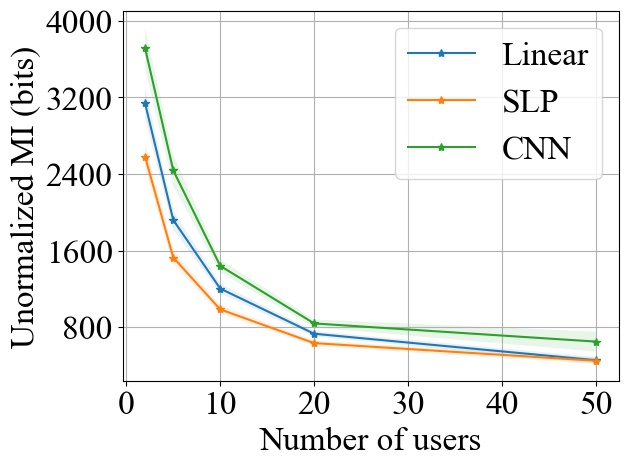
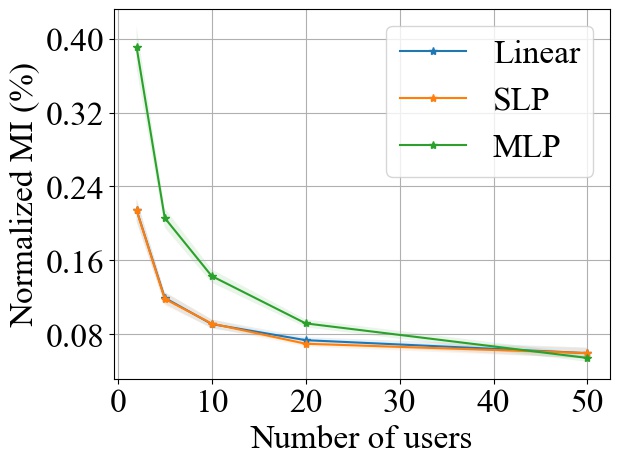
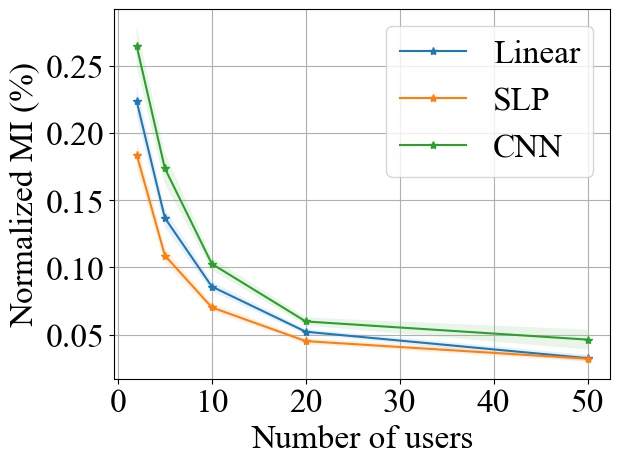
FedSGD. Fig. 3 shows the impact of varying $N$ on MI privacy leakage in FedSGD, where the number of users is chosen from $\{2,5,10,20,50\}$ , and we measure the MI privacy leakage of different models on both MNIST and CIFAR10 datasets. We observe that increasing the number of users participating in FL using FedSGD will decrease the MI privacy leakage in each global training round (see Fig. 3(a) and 3(b)), which is consistent with our theoretical analysis in Section 3.2.1. Notably, as demonstrated in Fig. 3(c) and 3(d), the percentile of MI privacy leakage (i.e. normalized by the entropy of a data batch) can drop below 2% for MNIST and 5% for CIFAR10 when there are more than 20 users.

FedAvg. Fig. 4 shows the impact of varying $N$ on MI privacy leakage in FedAvg. Similar to the results in FedSGD, as the number of users participating in FedAvg increases, the MI privacy leakage in each global training round will decrease (see Fig. 4(a) and 4(b)), and the decreasing rate is approximately $\mathcal{O}(N)$ . Moreover, as shown in Fig. 4(c) and 4(d), the percentile of MI privacy leakage drops below 0.1% on both MNIST and CIFAR10 when there are more than 20 users participating in FL. It is worth noting that we normalize the MI by the entropy of the whole training dataset in FedAvg instead of the entropy of a single batch, since users will iterate over all their data batches to calculate their local model updates in FedAvg. Therefore, although we observe that the unnormalized MI is comparable for FedSGD and FedAvg, the percentile of MI privacy leakage in FedAvg is significantly smaller than that in FedSGD.

FedProx. Similar to FedAvg, Fig. 5 shows how the MI privacy leakage with FedProx varies with the number of users $N$ . As the number of users increase, the MI privacy leakage decreases in each training round at an approximate rate of $O(N)$ . With more than 20 participating users, the percentile of MI leakage drops below 0.12% under both MNIST and CIFAR10. Same as FedAvg, we normalize the MI privacy leakage by the entropy of the whole training dataset of a single user.

In conclusion, while our theoretical analysis on the impact of $N$ in Section 3.2.1 is based on the assumption that the FedSGD protocol is used, our empirical study shows that it holds not only in FedSGD but also in FedAvg and FedProx.

5.2. Impact of Model Size (d)

FedSGD. From Fig. 3, we observe that increasing model size $d$ will increase the MI leakage during each global training round. However, the increase rate of MI leakage is smaller than the increase rate of $d$ . This is expected since the upper bound of MI privacy leakage is proportional to $d^{*}$ (i.e. the rank of the covariance of matrix as proved in Theorem 1), which will not increase linearly with $d$ especially for overparameterized neural networks (see Section 3.2.3). Finally, we observe that the MI privacy leakage on CIFAR10 is generally higher than that on MNIST. Since the input images on CIFAR10 have higher dimension than the images on MNIST, larger model size are required during training. Therefore, we expect that the MI privacy leakage on CIFAR10 is higher than that on MNIST.

FedAvg and FedProx. As shown in Fig. 4 and Fig. 5, increasing the model size will also have a sub-linear impact on the increase of the MI privacy leakage in FedAvg and FedProx, which is consistent with our results in FedSGD.

5.3. Impact of Batch Size (B)

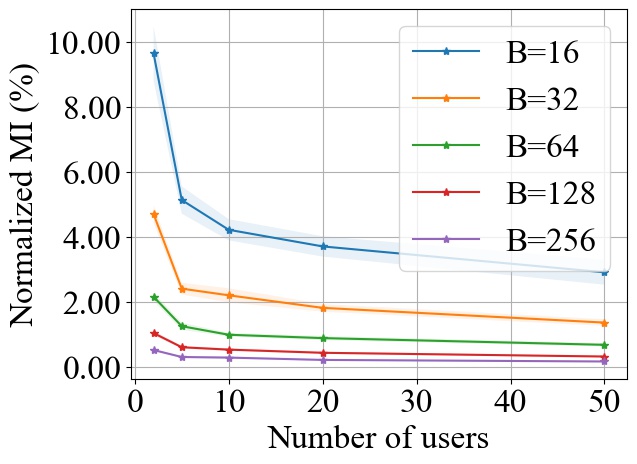
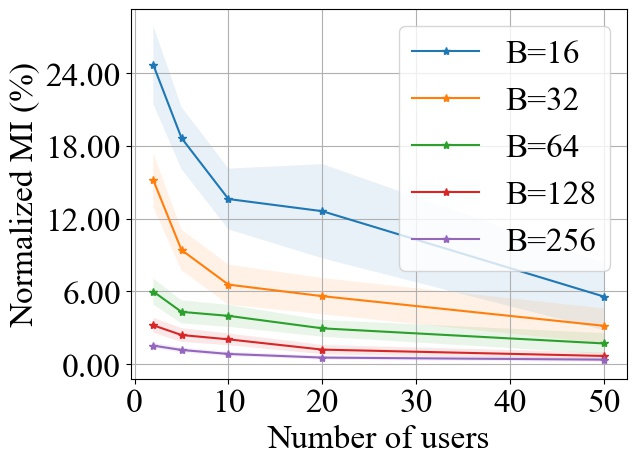
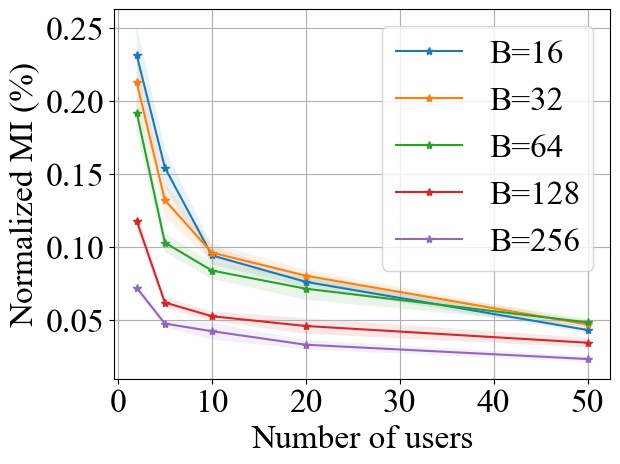
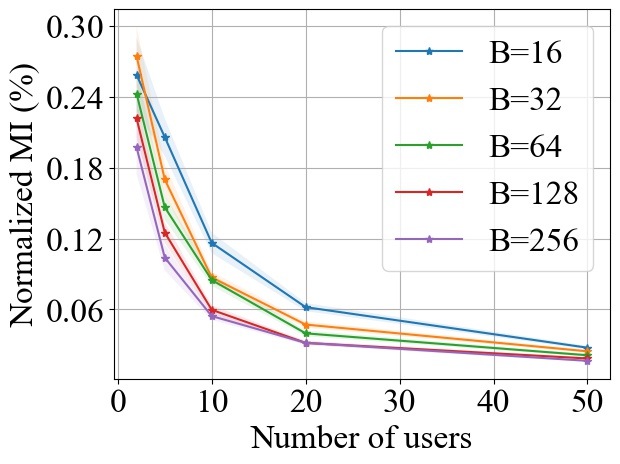
FedSGD. Fig. 6 shows the impact of varying $B$ on the normalized MI privacy leakage in FedSGD, where the batch size is chosen from $\{16,32,64,128,256\}$ and we use MLP model on MNIST and CNN model on CIFAR10 during experiments. Note that we normalize the MI by the entropy of a single data batch used in each training round, which is proportional to the batch size $B$ . On both MNIST and CIFAR10 datasets, we consistently observe that increasing $B$ will decrease the MI privacy leakage in FedSGD, and the decay rate of MI is inversely proportional to batch size $B$ . As demonstrated in Fig. 6, when there are more than 20 users, the percentile of MI privacy leakage for a single training round can be around 4% on MNIST and 12% on CIFAR10 with batch size 16. However, such leakage can drop to less 1% on both MNIST and CIFAR10 with batch size 256, which is significantly reduced.

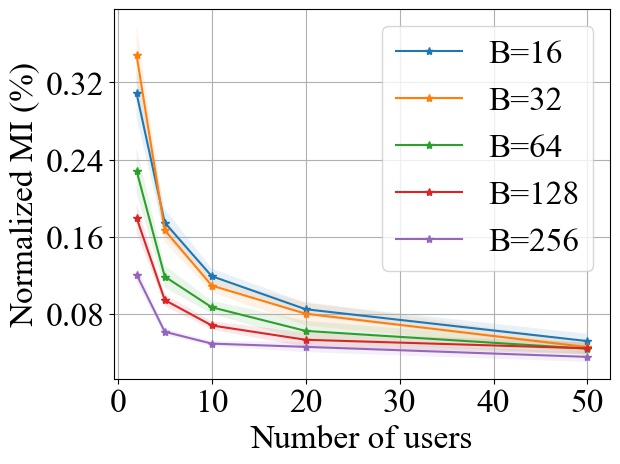
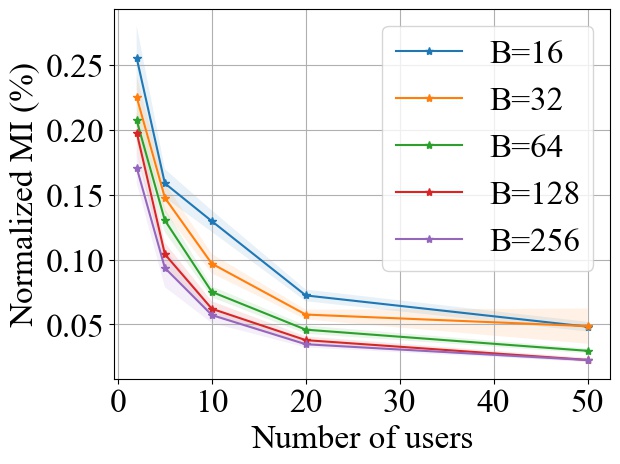
FedAvg and FedProx. Fig. 7 and Fig. 8 show the impact of varying the batch size $B$ on MI privacy leakage in FedAvg and FedProx, respectively, following the same experimental setup as in Fig. 6. Since in both FedAvg and FedProx, each user will transverse their whole local dataset in each local training round, we normalize the MI by the entropy of the target user’s local training dataset. As shown in Fig. 7 and Fig. 8, the impact of $B$ in FedAvg and FedProx is relatively smaller than that in FedSGD. However, we can still observe that increasing $B$ can decrease the MI privacy leakage in both FedAvg and FedProx. For example, with 20 users participating in FedAvg, the percentile of MI privacy leakage at each training round can drop from 0.8% to 0.3% when the batch size increases from 16 to 256, achieving a reduction in privacy leakage by a factor of more than 2 $\times$ . Similarly, in FedProx, this causes a decrease in the MI privacy leakage from 0.09% to 0.04% when the batch size increases from 16 to 256.

In conclusion, we observe that increasing the batch size $B$ can decrease the MI privacy leakage from the aggregated model update in FedSGD, FedAvg and FedProx which verifies our theoretical analysis in Section 3.2.3.

5.4. Accumulative MI leakage

To evaluate how the accumulative MI privacy leakage will accumulate with the number of training round $T$ , we measure the MI between training data and the aggregated model updates across training round. Specifically, given a local training dataset sample $\mathcal{D}_{i}$ , we will concatenate the aggregated model updates $\{\frac{1}{N}\sum_{i\in\mathcal{N}}\mathbf{x}_{i}^{(t)}\}_{t\in[T]}$ across $T$ training rounds in a single vector with dimension $d*T$ . By randomly generating $\mathcal{D}_{i}$ for the target user for $K$ times, we can get $K$ concatenated aggregated model update vectors. Then, we use MINE to estimate $I(\mathcal{D}_{i};\{\frac{1}{N}\sum_{i\in\mathcal{N}}\mathbf{x}_{i}^{(t)}\}_{t\in[T]})$ with these $K$ dataset and concatenated model update samples.

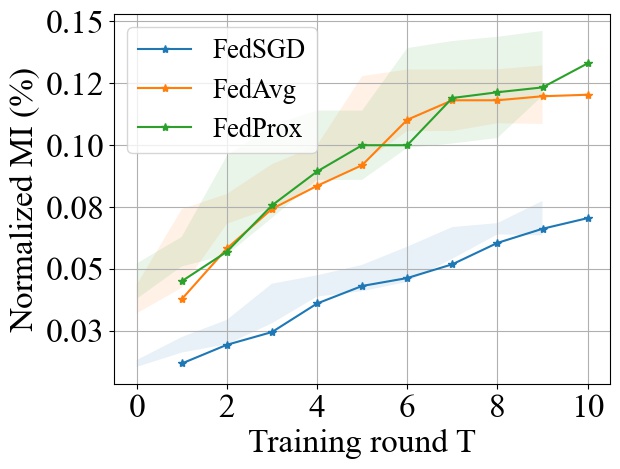
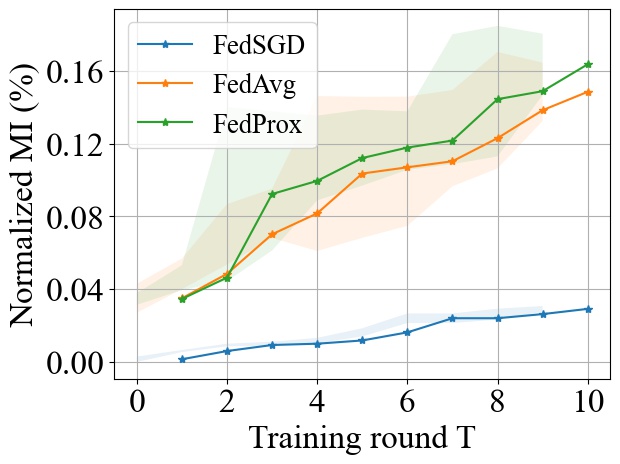
As illustrated in Fig. 9, the MI privacy leakage will accumulate linearly as we increase the global training round $T$ on both MNIST and CIFAR dataset, which is consistent with our theoretical results in Section 3.2.4. That also says, by reducing the times of local model aggregation, the MI privacy leakage of secure aggregation will be reduced. In practice, we can consider using client sampling to reduce the participation times of each client in FL, such that the accumulative MI leakage of individual users can be reduced. Moreover, we can also consider increasing the number of local averaging as much as possible to reduce the aggregation times for local model updates.

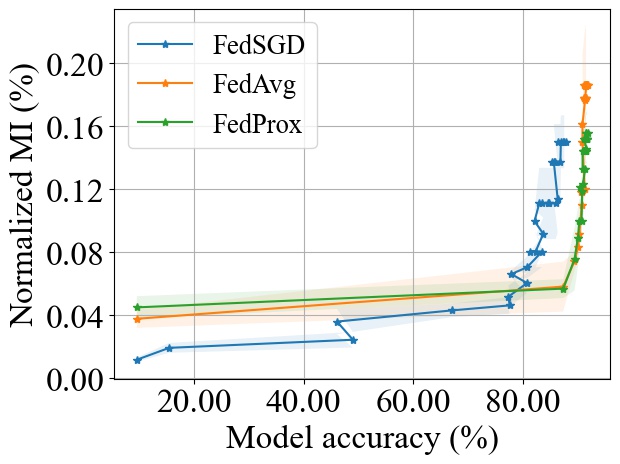
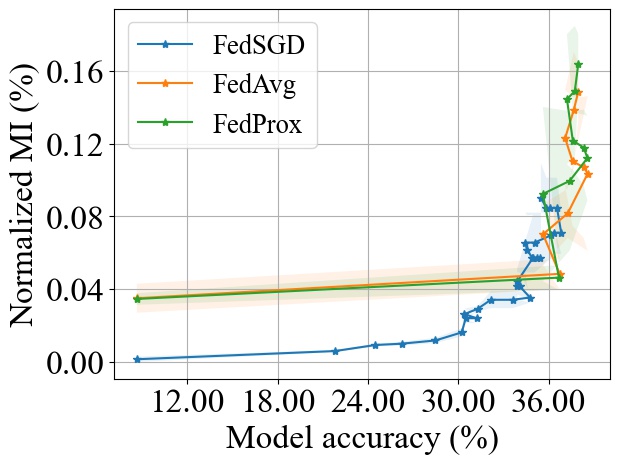
Although, the three aggregation algorithms exhibit a similar trend with $T$ , these algorithms can result in different convergence speeds to a target accuracy. To highlight the effect of convergence rate on the accumulative MI privacy leakage, we show, in Fig. 10, how the accuracy changes with the amount of MI leakage incurred for the three algorithms during the training process up to a maximum of 30 training rounds for FedSGD. We observe that although FedSGD achieves lower MI leakage for a fixed number of rounds (see Fig. 9), its slow convergence rate will make it suffer from more leakage before reaching a target accuracy rate. For example, given a target accuracy of 85% on the MNIST dataset, both FedAvg and FedProx achieve the target accuracy with 0.058% and 0.057% leakage while FedSGD will reach 85% accuracy in later rounds resulting in an accumulative MI leakage of 0.11% (even with smaller leakage per round).

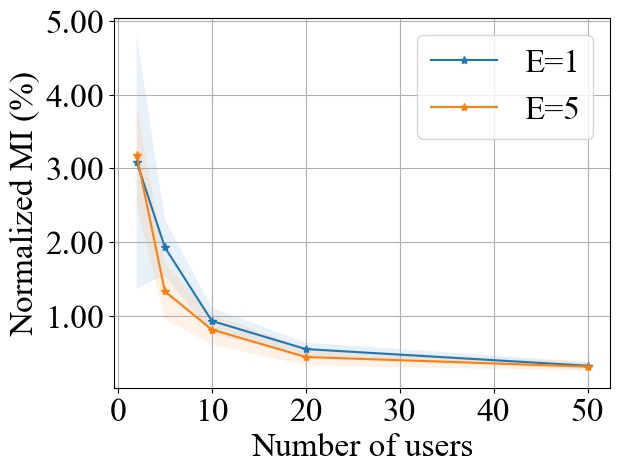
5.5. Impact of Local Training Epochs (E)

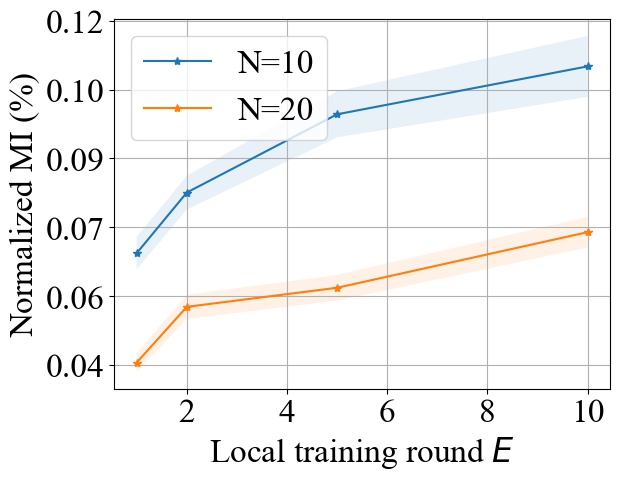
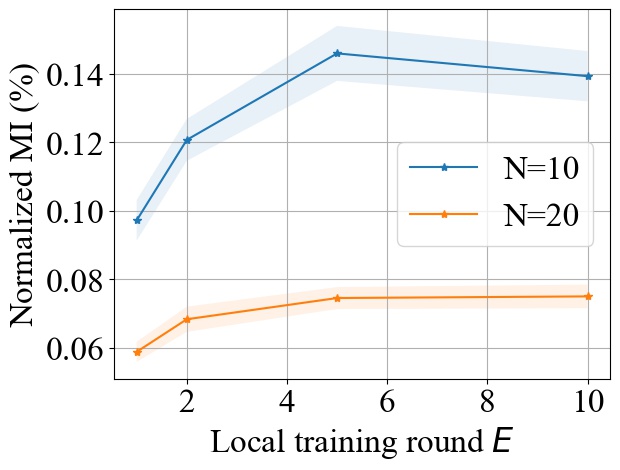
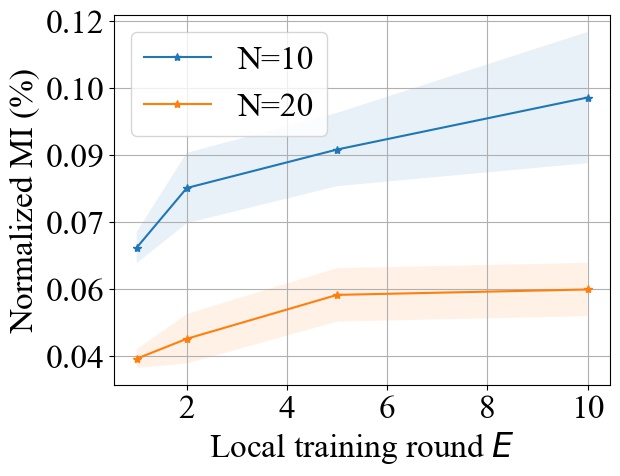
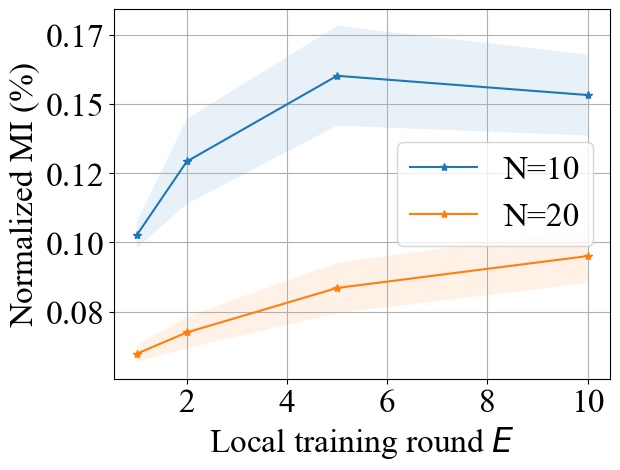
Fig. 11 shows the impact of varying the number of local training epochs $E$ on MI privacy leakage in FedAvg on both MNIST and CIFAR10 datasets. We select $E$ from $\{1,2,5,10\}$ and $N$ from $\{10,20\}$ , and we consider MLP model for MNIST and CNN model for CIFAR10. We observe that increasing the local training round $E$ will increase the MI privacy leakage in FedAvg. An intuitive explanation is that with more local epochs, the local model updates become more biased towards the user’s local dataset, hence it will potentially leak more private information about users’ and make it easier for the server to infer the individual model update from the aggregated update. However, as shown in Fig. 11, increasing the local epochs $E$ will not have a linear impact on the increase of MI privacy leakage. As $E$ increases, the increase rate of MI privacy leakage becomes smaller.

Similar to FedAvg, we observe from Fig. 12 that the local training epochs $E$ has a sub-linear impact on the MI privacy leakage when using FedProx. As aforementioned, this can be attributed to the fact that FedProx represents an application of FedAvg with the original loss function in addition to a convex regularization term.

5.6. Impact of Data Heterogeneity

As discussed in Remark 3 of Section 3, in our theoretical analysis, we considered IID data distribution across users in Theorem 1 in order to make use of entropic central limit theorem results in developing our upper bounds on privacy leakage. However in practice, the data distribution at the users can be heterogeneous. Hence, in this subsection, we analyze the impact of the non-IID (heterogeneous) data distribution across the users’ on the privacy leakage. To measure how user heterogeneity can potentially impact the MI privacy leakage in FedAvg, we consider two different data settings. In the first setting, we create synthetic users with non-IID data distributions following the methodology in (Hsu et al., 2019). For the second setting, we consider FEMNIST (Caldas et al., 2018), a benchmark non-IID FL dataset extended from MNIST, which consists of $62$ different classes of 28 $\times$ 28 images ( $10$ digits, $26$ lowercase letters, $26$ uppercase letters) written by $3500$ users.

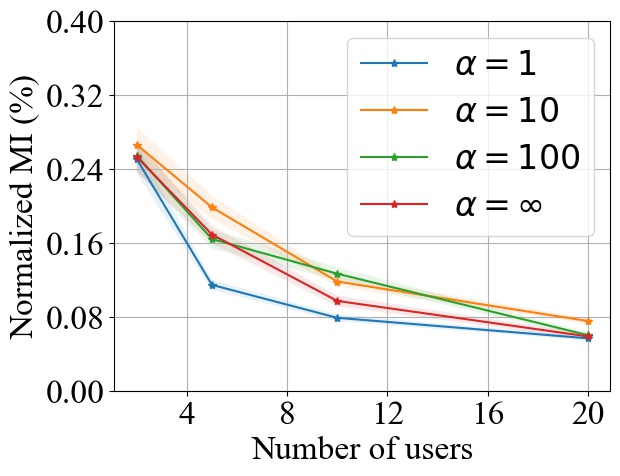
In the first, synthetic non-IID data setting, we use Dirichlet distribution parameterized by $\alpha$ to split the dataset into multiple non-IID distributed local datasets. Smaller $\alpha$ (i.e., $\alpha\rightarrow 0$ ) represents that the users’ datasets are more non-identical with each other, while larger $\alpha$ (i.e., $\alpha\rightarrow\infty$ ) means that the user datasets are more identical with each other. We choose CIFAR10 as the dataset, CNN as the model, and use FedAvg for a case study while using a batch size of $B=32$ . Note that we do not consider FedSGD since it will not be affected by user heterogeneity. During the experiments, we choose the $\alpha$ value from $\{1,10,100,\infty\}$ to create different levels of non-IID user datasets, and we consider $N\in\{2,5,10,20\}$ and $E\in\{1,5\}$ .

Fig. 13 shows how the MI privacy leakage varies with the number of users under different $\alpha$ , where the MI privacy leakage is normalized by the entropy of each user’s local dataset. We notice that the MI privacy leakage will decrease with the number of users consistently under different $\alpha$ , which empirically shows that our theoretical results in Section 3 also holds in the case where users are heterogeneous.

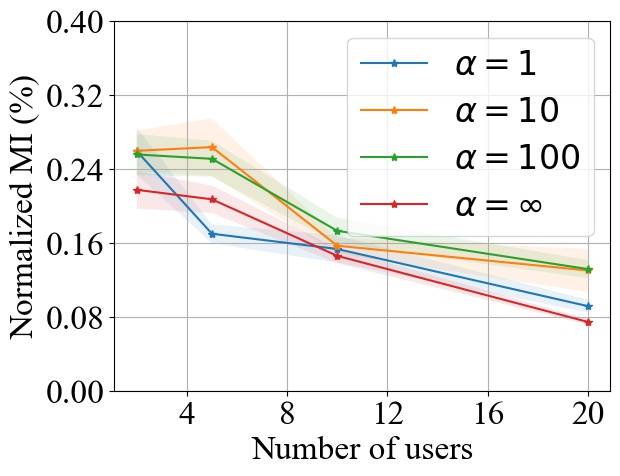
For the second, FEMNIST data setting, we split the dataset by users into 3500 non-overlapping subsets, each of which contains character images written by a specific user. Considering that the size of each subset is small, in order to have enough training data, we choose to sample $N$ users at each training round instead of using a fixed set of $N$ users, which simulates the user sampling scenario in FL. Specifically, at the beginning of each FL training round with $N$ participating users, we use the same target user and randomly pick the other $N-1$ out of 3500 users. Note that we consider $N\in\{2,5,10,20,50\}$ and $E\in\{1,5\}$ , and use the same model (CNN), batch size ( $B=32$ ), and FedAvg algorithm in our evaluation..

Fig. 14 shows how the MI privacy leakage varies with the number of users. Similar to the synthetic non-IID data setting in Fig. 13, the privacy leakage decreases with increasing the number of user $N$ .

5.7. Practical Privacy Implications

Success of Privacy attacks

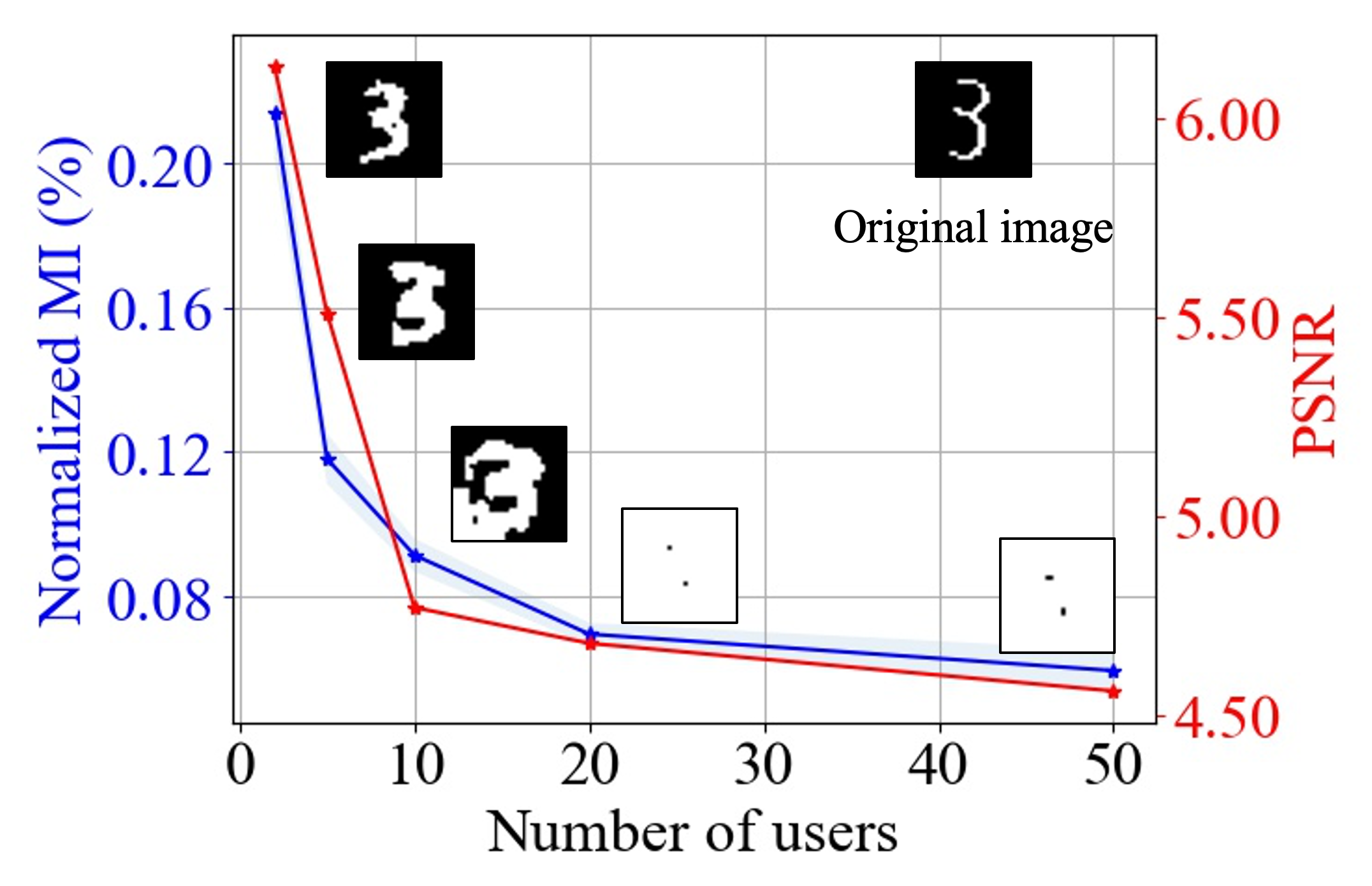
To provide insights on how MI translates to practical privacy implications, we conduct experiments using one of the state-of-the-art data reconstruction attack, i.e., the Deep Leakage from Gradients (DLG) attack from (Zhu et al., 2019a), to show how the MI metric reflects the reconstructed image quality of the attack as we vary system parameters. Specifically, we choose MNIST as the dataset, the same SLP used in Section 4.2 as the model, and FedSGD with batch size of $32$ as training algorithm. For the data distribution across the users, we consider the IID setting. At the end of each training round, each user uses a batch of images with size 32 to calculate their local gradients, which will be securely aggregated by the server. The DLG attack will reconstruct a batch of images with size 32 from the aggregated gradient, making them as similar as possible to the batch of images used by the target user. After that, we apply the same PSNR (Peak Signal-to-noise Ratio) metric used in (Zhu et al., 2019a) to measure the quality of reconstructed images compared with the images used by the target user during training. Note that without loss of generality, we report the PSNR value of reconstructed images by DLG attack for the first training round.

Fig. 15 shows the impact of number of users $N$ on the privacy leakage metric (MI) and the reconstructed image quality of DLG attack (PSNR). We pick the image of digit 3 out of the target $32$ images as an example of reconstructed images. We can observe that increasing the number of users $N$ decreases the MI metric as well as the PSNR at almost the same rate. This demonstrates that the MI metric used in this paper can translate to practical privacy implications well.

MI Privacy leakage under the joint use of DP and SA

To highlight the joint effect of differential privacy with secure aggregation, we conduct experiments on the MNIST dataset with a linear model to measure the MI privacy leakage in the presence of centralized DP noise added at the server after SA. Specifically, following (Abadi et al., 2016), we first clip the aggregated model updates to make its norm bounded by $C$ , and then add Gaussian noise with variance $\sigma^{2}$ to achieve $(\epsilon,\delta)$ -DP. We set $C=1$ , $\delta=1/1200$ , and $\sigma=\sqrt{2\log(\frac{1.25}{\delta})}/\epsilon$ .

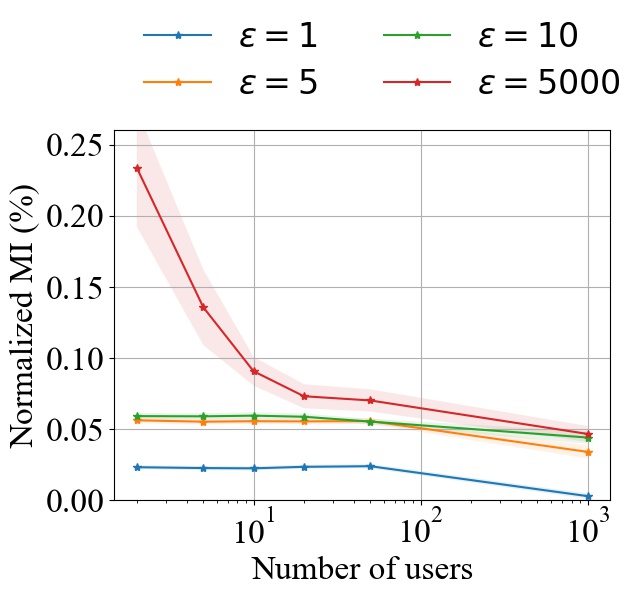
Fig. 16(a) shows the MI privacy leakage for different $(\epsilon,\delta)$ -DP levels with SA ( $\delta$ is fixed at $1/1200$ ). As the number of users increase, SA improves the privacy level (measured in terms of MI leakage) for different levels of DP noise, with the effect being most pronounced for weak DP noise level ( $\epsilon=5000$ in Fig. 16(a)). Our experiments also show that as the number of users increase, the gain from using higher DP noise levels is diminished. In particular, with $N=1000$ users, the MI leakage level for $\epsilon=$ 5, 10 and 5000 are almost the same; MI leakage is only reduced from 0.046% to 0.034% when using $\epsilon=5$ instead of $\epsilon=5000$ . In contrast, we get a reduction from 0.234% to 0.056% when there are $N=2$ users.

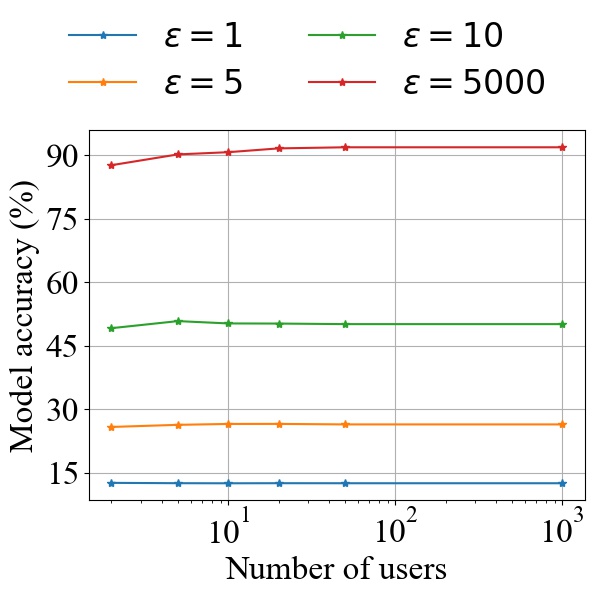
Importantly, the reduction observed in privacy leakage due to applying additional DP noise results in a severe degradation in accuracy as seen in Fig. 16(b), whereas privacy improvement gained by having more users has a negligible effect on the performance of the trained model. For example, consider the case of 1000 users. One may achieve the same level of privacy in terms of MI leakage (lower than 0.05% MI) with either (i) $(\epsilon,\delta)$ -DP with $\epsilon=10$ , which, however, results in unusable model accuracy (less than 50%), or, (ii) by aggregating the 1000 users and using a tiny amount of DP noise (equivalent to $\epsilon=5000$ ), which achieves a model accuracy higher than 90%.

6. Related work

Secure Aggregation in FL. As mentioned secure aggregation has been developed for FL (Bonawitz et al., 2017) to provide protection against model inversion attacks and robustness to user dropouts (due to poor connections or unavailability). There has been a series of works that aim at improving the efficiency of the aggregation protocol (Bell et al., 2020; So et al., 2021a; Kadhe et al., 2020; Zhao and Sun, 2021; So et al., 2022; So et al., 2021b; Elkordy and Salman Avestimehr, 2022). This general family of works using secure aggregation disallow the learning information about each client’s individual model update beyond the global aggregation of updates, however there has not been a characterization of how much information the global aggregation can leak about the individual client’s model and dataset. To the best of our knowledge, in this work, we provide the first characterization of the privacy leakage due to the aggregated model through mutual information for FL using secure aggregation.

Differential Privacy. One way to protect a client’s contributions is to use differential privacy (DP). DP provides a rigorous, worst-case mathematical guarantee that the contribution a single client does not impact the result of the query. Central application of differential privacy was studied in (Bassily et al., 2014; Chaudhuri et al., 2011; Abadi et al., 2016). This form of central application of DP in FL requires trusting the server with individual model updates before applying the differentially private mechanism. An alternative approach studied in FL for an untrusted server entity is the local differential privacy (LDP) model (Kasiviswanathan et al., 2011; Agarwal et al., 2018; Balle et al., 2019) were clients apply a differentially private mechanism (e.g. using the Gaussian mechanism) locally on their update before sending to the central server. LDP constraints imply central DP constraints, however due to local privacy constraints LDP mechanisms significantly perturb the input and reduces globally utility due to the compounded effect of adding noise at different clients.

In this work, we use a mutual information metric to study the privacy guarantees for the client’s dataset provided through the secure aggregation protocol without adding differential privacy noise at the clients. In this case, secure aggregation uses contributions from other clients to mask the contribution of a single client. We will discuss in Section 7 situations where relying only on SA can clearly fail to provide differential privacy guarantees and comment on the prevalence of such situations in practical training scenarios.

Privacy Attacks. There have been some works trying to empirically show that it is possible to recovery some training data from the gradient information. (Phong et al., 2017; Aono et al., 2017; Wang et al., 2019; Yin et al., 2021). Recently, the authors in (Geiping et al., 2020) show that it is possible to recover a batch of images that were used in the training of non-smooth deep neural network. In particular, their proposed reconstruction attack was successful in reconstruction of different images from the average gradient computed over a mini-batch of data. Their empirical results have shown that the success rate of the inversion attack decreases with increasing the batch size. Similar observations have been demonstrated in the subsequent works (Yin et al., 2021). In contrast to this work, we are the first to the best of our knowledge to theoretically quantify the amount of information that the aggregated gradient could leak about the private training data of the users, and to understand how the training parameters (e.g., number of users) affect the leakage. Additionally, our empirical results are different from the ones in (Phong et al., 2017; Aono et al., 2017; Wang et al., 2019; Yin et al., 2021, 2021) in the way of quantifying the leakage. In particular, we use the MINE tool to abstractly quantify the amount of information leakage in bits instead of the number of the reconstructed images. We have also empirically studied the effect of the system parameters extensively using different real world data sets and different neural network architectures.

7. Further Discussion and Conclusions

In this paper, we derived the first formal privacy guarantees for FL with SA using MI as a metric to measure how much information the aggregated model update can leak about the local dataset of each user. We proved theoretical bounds on the MI privacy leakage in theory and showed through an empirical study that this holds in practice after FL settings. Our concluding observations is that by using FL with SA, we get that: 1) the MI privacy leakage will decrease at a rate of $\mathcal{O}(\frac{1}{N})$ ( $N$ is the number of users participating in FL with SA); 2) increasing model size will not have a linear impact on the increase of MI privacy leakage, and the MI privacy leakage only linearly increases with the rank of the covariance matrix of the individual model update; 3) larger batch size during local training can help to reduce the MI privacy leakage. We hope that our findings can shed lights on how to select FL system parameters with SA in practice to reduce privacy leakage and provide an understanding for the baseline protection provided by SA in settings where it is combined with other privacy-preserving approaches such as differential privacy.

Can we provide differential privacy guarantees using SA? Note that when using FL with SA, then from the point of view of an adversary that is interested in the data of the $i$ -th user, the aggregated model in $i^{-}=[N]\backslash\{i\}$ can be viewed as noise that is independent of the gradient $\mathbf{x}_{i}$ given the last global model, which is very similar to an LDP mechanism for the update $\mathbf{x}_{i}^{(t)}$ of user $i$ that adds noise to $\mathbf{x}_{i}^{(t)}$ . This leads to an intriguing question: Can we get LDP-like guarantees from the securely aggregated updates?

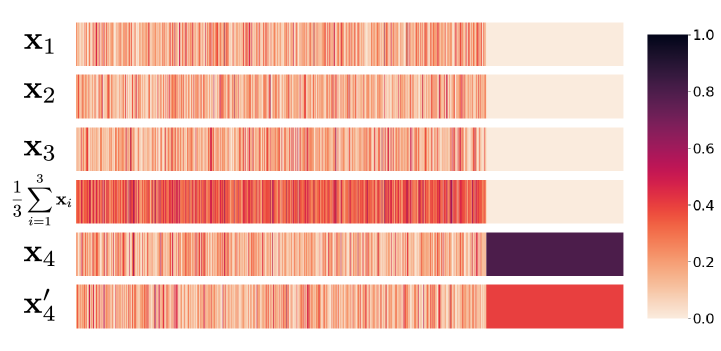
Since DP is interested in a worst-case guarantee, it turns out that their exist model update distributions where it is impossible to achieve an $\epsilon<\infty$ DP guarantee by using other model updates as noise as illustrated in Fig. 17. In this case, the alignment of the sparsity pattern in $x_{1},x_{2}$ and $x_{3}$ allows an adversary to design a perfect detector to distinguish between $x_{4}$ and $x_{4}^{\prime}$ .

Why our MI privacy guarantee can avoid this? Although, the previous example illustrates that DP flavored guarantees are not always possible, in practical scenarios, the worst-case distribution for $\mathbf{x}_{1},\mathbf{x}_{2}$ and $\mathbf{x}_{3}$ that enables the distinguishing between $\mathbf{x}_{4}$ and $\mathbf{x}_{4}^{\prime}$ in Fig. 17 are an unlikely occurrence during training. For instance, in our theoretical analysis, since users have IID datasets, then having the distribution of $x_{1}$ , $x_{2}$ and $x_{3}$ be restricted to a subspace $\mathcal{S}_{x_{i^{-}}}$ , implies also that points generated from $\mathbf{x}_{4}$ would also belong to $\mathcal{S}_{x_{i^{-}}}$ almost surely. This is a key reason why we can get mutual information guarantee in Theorem 1: for an aggregated gradient direction $\sum_{i=1}^{N}\mathbf{x}_{i}$ , where each component is restricted to a common subspace $\mathcal{S}_{x}$ protects the contribution of each individual component $\mathbf{x}_{i}$ as $N$ increases.

In the worst case, where one component is not restricted to the subspace $\mathcal{S}_{x}$ spanned by the remaining components, then we get the privacy leakage discussed in the example above. We highlight that through our experiments and other studies in the literature (Ergun et al., 2021), we observe that such sparsity alignment happens with very low probability. This presents motivation for studying a probabilistic notion of DP that satisfies $(\epsilon,\delta)$ -DP with a probability at least $\gamma$ , instead of the worst-case treatment in current DP notions, but this is beyond the scope of the study in this current work.

Another interesting future direction is to use the results from this work for a providing “privacy metrics” to users to estimate/quantify their potential leakage for participating in a federated learning cohort. Such metrics can be embedded in platforms, such as FedML (He et al., 2020b), to guide users to make informed decisions about their participation in federated learning. Finally, it would also be important to extend the results to model aggregation protocols that are beyond weighted averaging (e.g., in federated knowledge transfer (He et al., 2020a)).

References

(1)
Abadi et al. (2016) Martin Abadi, Andy Chu, Ian Goodfellow, H Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. 2016. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC conference on computer and communications security. 308–318.
Agarwal et al. (2018) Naman Agarwal, Ananda Theertha Suresh, Felix Xinnan X Yu, Sanjiv Kumar, and Brendan McMahan. 2018. cpSGD: Communication-efficient and differentially-private distributed SGD. Advances in Neural Information Processing Systems 31 (2018).
Aono et al. (2017) Yoshinori Aono, Takuya Hayashi, Lihua Wang, Shiho Moriai, et al. 2017. Privacy-preserving deep learning via additively homomorphic encryption. IEEE Transactions on Information Forensics and Security 13, 5 (2017), 1333–1345.
Balle et al. (2019) Borja Balle, James Bell, Adrià Gascón, and Kobbi Nissim. 2019. The privacy blanket of the shuffle model. In Annual International Cryptology Conference. Springer, 638–667.
Bassily et al. (2014) Raef Bassily, Adam Smith, and Abhradeep Thakurta. 2014. Private empirical risk minimization: Efficient algorithms and tight error bounds. In 2014 IEEE 55th Annual Symposium on Foundations of Computer Science. IEEE, 464–473.
Belghazi et al. (2018) Mohamed Ishmael Belghazi, Aristide Baratin, Sai Rajeshwar, Sherjil Ozair, Yoshua Bengio, Aaron Courville, and Devon Hjelm. 2018. Mutual Information Neural Estimation. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 80), Jennifer Dy and Andreas Krause (Eds.). PMLR, 531–540.
Bell et al. (2020) James Henry Bell, Kallista A Bonawitz, Adrià Gascón, Tancrède Lepoint, and Mariana Raykova. 2020. Secure single-server aggregation with (poly) logarithmic overhead. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. 1253–1269.
Bobkov et al. (2014) Sergey G Bobkov, Gennadiy P Chistyakov, and Friedrich Götze. 2014. Berry–Esseen bounds in the entropic central limit theorem. Probability Theory and Related Fields 159, 3-4 (2014), 435–478.
Bonawitz et al. (2017) Keith Bonawitz, Vladimir Ivanov, Ben Kreuter, Antonio Marcedone, H Brendan McMahan, Sarvar Patel, Daniel Ramage, Aaron Segal, and Karn Seth. 2017. Practical secure aggregation for privacy-preserving machine learning. In proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. 1175–1191.
Caldas et al. (2018) Sebastian Caldas, Sai Meher Karthik Duddu, Peter Wu, Tian Li, Jakub Konečnỳ, H Brendan McMahan, Virginia Smith, and Ameet Talwalkar. 2018. Leaf: A benchmark for federated settings. arXiv preprint arXiv:1812.01097 (2018).
Chaudhuri et al. (2011) Kamalika Chaudhuri, Claire Monteleoni, and Anand D Sarwate. 2011. Differentially private empirical risk minimization. Journal of Machine Learning Research 12, 3 (2011).
Cover and Thomas (2006) Thomas M. Cover and Joy A. Thomas. 2006. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing). Wiley-Interscience, USA.
Dong et al. (2020) Ye Dong, Xiaojun Chen, Liyan Shen, and Dakui Wang. 2020. EaSTFLy: Efficient and secure ternary federated learning. Computers & Security 94 (2020), 101824.
Dwork et al. (2006) Cynthia Dwork, Frank McSherry, Kobbi Nissim, and Adam Smith. 2006. Calibrating noise to sensitivity in private data analysis. In Theory of cryptography conference. Springer, 265–284.
Eldan et al. (2020) Ronen Eldan, Dan Mikulincer, and Alex Zhai. 2020. The CLT in high dimensions: quantitative bounds via martingale embedding. The Annals of Probability 48, 5 (2020), 2494–2524.
Elkordy and Salman Avestimehr (2022) Ahmed Roushdy Elkordy and A. Salman Avestimehr. 2022. HeteroSAg: Secure Aggregation with Heterogeneous Quantization in Federated Learning. IEEE Transactions on Communications (2022), 1–1. https://doi.org/10.1109/TCOMM.2022.3151126
Ergun et al. (2021) Irem Ergun, Hasin Us Sami, and Basak Guler. 2021. Sparsified Secure Aggregation for Privacy-Preserving Federated Learning. arXiv preprint arXiv:2112.12872 (2021).
Geiping et al. (2020) Jonas Geiping, Hartmut Bauermeister, Hannah Dröge, and Michael Moeller. 2020. Inverting Gradients – How easy is it to break privacy in federated learning?. In Advances in Neural Information Processing Systems.
He et al. (2020a) Chaoyang He, Murali Annavaram, and Salman Avestimehr. 2020a. Group knowledge transfer: Federated learning of large cnns at the edge. Advances in Neural Information Processing Systems 33 (2020), 14068–14080.
He et al. (2020b) Chaoyang He, Songze Li, Jinhyun So, Xiao Zeng, Mi Zhang, Hongyi Wang, Xiaoyang Wang, Praneeth Vepakomma, Abhishek Singh, Hang Qiu, et al. 2020b. Fedml: A research library and benchmark for federated machine learning. arXiv preprint arXiv:2007.13518 (2020).
Hsu et al. (2019) Tzu-Ming Harry Hsu, Hang Qi, and Matthew Brown. 2019. Measuring the effects of non-identical data distribution for federated visual classification. arXiv preprint arXiv:1909.06335 (2019).
Kadhe et al. (2020) Swanand Kadhe, Nived Rajaraman, O Ozan Koyluoglu, and Kannan Ramchandran. 2020. Fastsecagg: Scalable secure aggregation for privacy-preserving federated learning. arXiv preprint arXiv:2009.11248 (2020).
Kairouz et al. (2021) Peter Kairouz, Ziyu Liu, and Thomas Steinke. 2021. The distributed discrete gaussian mechanism for federated learning with secure aggregation. arXiv preprint arXiv:2102.06387 (2021).
Kairouz et al. (2019) Peter Kairouz, H. Brendan McMahan, Brendan, and et al. 2019. Advances and Open Problems in Federated Learning. preprint arXiv:1912.04977 (2019). arXiv:1912.04977
Kasiviswanathan et al. (2011) Shiva Prasad Kasiviswanathan, Homin K Lee, Kobbi Nissim, Sofya Raskhodnikova, and Adam Smith. 2011. What can we learn privately? SIAM J. Comput. 40, 3 (2011), 793–826.
Krizhevsky (2009) Alex Krizhevsky. 2009. Learning multiple layers of features from tiny images. Technical Report. Citeseer.
Krizhevsky et al. (2012) Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. 2012. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 25 (2012).
Kuznetsov et al. (2021) Eugene Kuznetsov, Yitao Chen, and Ming Zhao. 2021. SecureFL: Privacy Preserving Federated Learning with SGX and TrustZone. In 2021 IEEE/ACM Symposium on Edge Computing (SEC). 55–67. https://doi.org/10.1145/3453142.3491287
LeCun et al. (2010) Yann LeCun, Corinna Cortes, and CJ Burges. 2010. MNIST handwritten digit database. ATT Labs [Online]. Available: http://yann.lecun.com/exdb/mnist 2 (2010).
McMahan et al. (2017) Brendan McMahan, Eider Moore, Daniel Ramage, Seth Hampson, and Blaise Aguera y Arcas. 2017. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (Proceedings of Machine Learning Research, Vol. 54), Aarti Singh and Jerry Zhu (Eds.). 1273–1282.
Mugunthan et al. (2019) Vaikkunth Mugunthan, Antigoni Polychroniadou, David Byrd, and Tucker Hybinette Balch. 2019. Smpai: Secure multi-party computation for federated learning. In Proceedings of the NeurIPS 2019 Workshop on Robust AI in Financial Services.
Phong et al. (2017) Le Trieu Phong, Yoshinori Aono, Takuya Hayashi, Lihua Wang, and Shiho Moriai. 2017. Privacy-preserving deep learning: Revisited and enhanced. In International Conference on Applications and Techniques in Information Security. Springer, 100–110.
Sahu et al. (2018) Anit Kumar Sahu, Tian Li, Maziar Sanjabi, Manzil Zaheer, Ameet Talwalkar, and Virginia Smith. 2018. On the convergence of federated optimization in heterogeneous networks. arXiv preprint arXiv:1812.06127 3 (2018), 3.
Simsekli et al. (2019) Umut Simsekli, Levent Sagun, and Mert Gurbuzbalaban. 2019. A tail-index analysis of stochastic gradient noise in deep neural networks. In International Conference on Machine Learning. PMLR, 5827–5837.
So et al. (2021a) Jinhyun So, Ramy E Ali, Basak Guler, Jiantao Jiao, and Salman Avestimehr. 2021a. Securing secure aggregation: Mitigating multi-round privacy leakage in federated learning. arXiv preprint arXiv:2106.03328 (2021).
So et al. (2021b) Jinhyun So, Başak Güler, and A Salman Avestimehr. 2021b. Turbo-aggregate: Breaking the quadratic aggregation barrier in secure federated learning. IEEE Journal on Selected Areas in Information Theory 2, 1 (2021), 479–489.
So et al. (2022) Jinhyun So, Corey J Nolet, Chien-Sheng Yang, Songze Li, Qian Yu, Ramy E Ali, Basak Guler, and Salman Avestimehr. 2022. Lightsecagg: a lightweight and versatile design for secure aggregation in federated learning. Proceedings of Machine Learning and Systems 4 (2022), 694–720.
Truex et al. (2019) Stacey Truex, Nathalie Baracaldo, Ali Anwar, Thomas Steinke, Heiko Ludwig, Rui Zhang, and Yi Zhou. 2019. A hybrid approach to privacy-preserving federated learning. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security. 1–11.
Wang et al. (2019) Zhibo Wang, Mengkai Song, Zhifei Zhang, Yang Song, Qian Wang, and Hairong Qi. 2019. Beyond inferring class representatives: User-level privacy leakage from federated learning. In IEEE INFOCOM 2019-IEEE Conference on Computer Communications. IEEE, 2512–2520.
Xu et al. (2019) Runhua Xu, Nathalie Baracaldo, Yi Zhou, Ali Anwar, and Heiko Ludwig. 2019. Hybridalpha: An efficient approach for privacy-preserving federated learning. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security. 13–23.
Yin et al. (2021) Hongxu Yin, Arun Mallya, Arash Vahdat, Jose M. Alvarez, Jan Kautz, and Pavlo Molchanov. 2021. See through Gradients: Image Batch Recovery via GradInversion. arXiv,2104.07586 (2021).
Zhang et al. (2021) Yuhui Zhang, Zhiwei Wang, Jiangfeng Cao, Rui Hou, and Dan Meng. 2021. ShuffleFL: gradient-preserving federated learning using trusted execution environment. In Proceedings of the 18th ACM International Conference on Computing Frontiers. 161–168.
Zhao and Sun (2021) Yizhou Zhao and Hua Sun. 2021. Information theoretic secure aggregation with user dropouts. In 2021 IEEE International Symposium on Information Theory (ISIT). IEEE, 1124–1129.
Zhu et al. (2019a) Ligeng Zhu, Zhijian Liu, and Song Han. 2019a. Deep Leakage from Gradients. In Advances in Neural Information Processing Systems, Vol. 32.
Zhu et al. (2019b) Zhanxing Zhu, Jingfeng Wu, Bing Yu, Lei Wu, and Jinwen Ma. 2019b. The Anisotropic Noise in Stochastic Gradient Descent: Its Behavior of Escaping from Sharp Minima and Regularization Effects. In International Conference on Machine Learning. PMLR, 7654–7663.

Appendix A Proof of Theorem 1

Without loss of generality, using permutation of clients indices, we will prove the upper bound for the following term

(17)

I\left(\mathbf{x}^{(t)}_{N};\frac{1}{N}\sum_{i=1}^{N}\mathbf{x}^{(t)}_{i}\middle|\left\{\frac{1}{N}\sum_{i=1}^{N}\mathbf{x}^{(k)}_{i}\right\}_{k\in[t-1]}\right),

where $\mathbf{x}_{N}$ is the mini-batch gradient of node $i$ which is given by

(18)

\mathbf{x}_{i}^{(t)}=\frac{1}{B}\sum_{b\in\mathcal{B}^{(t)}_{i}}g_{i}(\bm{\theta}^{(t)},b),

We will use the following property of vectors with singular covariance matrices in the proof of this theorem.

Property 1.

Given a random vector $\mathbf{q}$ with a singular covariance matrix $\mathbf{K}_{q}$ of rank $d^{*}$ , there exists a sub-vector $\bar{\mathbf{q}}$ of $\mathbf{q}$ with a non-singular covariance matrix $\mathbf{K}_{\bar{q}}$ such that $\mathbf{q}[k]=\mathbf{A}\bar{\mathbf{q}}$ where $\mathbf{A}\in\mathbb{R}^{d\times d^{*}}$ is a deterministic linear transformation matrix.

Let us define $S_{{N}}^{(t)}=\frac{1}{{N}}\sum_{i=1}^{N}\mathbf{x}_{i}^{(t)}$ . We also use the the definition of $\bar{{g}}_{i}(\bm{\theta}^{(t)},b)\in\mathbb{R}^{d^{*}}$ , for $d^{*}\leq d$ where $d$ is the model size, which is the largest sub-vector of the stochastic gradient $g_{i}(\bm{\theta}^{(t)},b)$ such that $\bar{{g}}_{i}(\bm{\theta}^{(t)},b)$ has a non-singular covariance matrix $K_{\bar{G}^{(t)}}$ for all $i\in\mathcal{N}$ . According to the definition of $\bar{{g}}_{i}(\bm{\theta}^{(t)},b)$ , we can rewrite (17) and the term $S_{{N}}^{(t)}$ as follows:

	$\displaystyle\bar{\mathbf{x}}_{i}^{(t)}$	$\displaystyle=\frac{1}{B}\sum_{b\in\mathcal{D}_{i}}\bar{{g}}_{i}(\bm{\theta}^{(t)},b)$
(19)		$\displaystyle\bar{S}_{{N}}^{(t)}$	$\displaystyle=\frac{1}{{N}}\sum_{i\in\mathcal{N}}\bar{\mathbf{x}}_{i}^{(t)}$

Let also define ${F}_{{N}}^{(t)}=\sqrt{N}\bar{S}_{{N}}^{(t)}$ . We can decompose the expression in (17) as follows:

	$\displaystyle I\left(\mathbf{x}^{(t)}_{N};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\overset{(a)}{=}I\left(\sqrt{B}\mathbf{x}_{N}^{(t)};\sqrt{N}S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\overset{(b)}{=}I\left(\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)};F_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=h\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right){+}h\left(\!\!{F}_{{N}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad-h\left(\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)},F_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=h\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right){+}h\left(\!\!{F}_{{N}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad-\!h\left(\!\begin{bmatrix}\mathrm{I}_{d}^{}&\mathrm{0}_{d}^{}\\ \mathrm{I}_{d}^{}\frac{1}{\sqrt{N}}&\frac{\sqrt{N-1}}{\sqrt{N}}\mathrm{I}_{d}^{}\end{bmatrix}\!\!\!\begin{bmatrix}\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\\ {F}_{{N-1}}^{(t)}\end{bmatrix}\!\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\stackrel{{\scriptstyle(c)}}{{=}}h\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right){+}h\left(\!\!{F}_{{N}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad{-}h\!\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!\!k\in[t-1]}\!\right)\!{-}h\!\left(\!{F}_{{N-1}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad-\log\left\|\det\begin{bmatrix}\mathrm{I}_{d}^{}&\mathrm{0}_{d}^{}\\ \mathrm{I}_{d}^{}\frac{1}{\sqrt{N-1}}&\frac{\sqrt{N-1}}{\sqrt{N}}\mathrm{I}_{d}^{}\end{bmatrix}\right\|$
	$\displaystyle\stackrel{{\scriptstyle(d)}}{{=}}h\left(\!F_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right)$
(20)		$\displaystyle\qquad-h\!\left(\!\!{F}_{{N-1}}^{(t)}\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right){+}\frac{d^{*}}{2}\log\left(\!\frac{N}{N-1}\!\right)\!,$

where: $(a)$ follows from the fact that the mutual information is invariant under deterministic multiplication; $(b)$ from Property 1 $(c)$ follows from the property of the entropy of linear transformation of random vectors (Cover and Thomas, 2006) and the fact that $\bar{\mathbf{x}}_{N}^{(t)}$ and ${F}_{{N-1}}^{(t)}$ are conditionally independent given $\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}$ (e.g., the last global model at time $t$ ) ; $(d)$ follows from the Schur compliment of the matrix.

We will now turn our attention to characterizing the entropy term $h\left(F_{M}^{(t)}\middle|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$ for any ${M}$ . Note that

	$\displaystyle h\left(F_{M}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=h\left(\!\!\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{d\in\mathcal{B}_{i}^{(t)}}\bar{g}_{i}(b,\bm{\theta}^{(t)})\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\!\!\right)$
	$\displaystyle\stackrel{{\scriptstyle(i)}}{{=}}h\!\!\left(\frac{\mathbf{K}_{\bar{G}^{(t)}}^{1/2}}{\sqrt{MB}}\sum_{i=1}^{M}\!\sum_{b\in\mathcal{B}_{i}^{(t)}}\!\!\!\widehat{g}_{i}(b,\bm{\theta}^{(t)})\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\stackrel{{\scriptstyle(ii)}}{{=}}\log\left(\|\det\mathbf{K}_{\bar{G}^{(t)}}^{1/2}\|\right)$
(21)		$\displaystyle\qquad{+}\underbrace{h\!\!\left(\!\!\frac{1}{\sqrt{MB}}\!\sum_{i=1}^{M}\!\sum_{b\in\mathcal{B}_{i}^{(t)}}\!\!\!\widehat{g}_{i}(b,\bm{\theta}^{(t)})\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right)}_{H_{M}}\!,$

where: $(i)$ makes use of the fact that the covariance matrix is the same across clients and using the whitening definition (Definition 1) on the vector $\bar{g}_{i}(b,\bm{\theta}^{(t)})$ ; $(ii)$ again uses the property of entropy of linear transformation of random vectors.

Note that the term of $h\left(F_{M}^{(t)}\middle|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$ only depends on $M$ in the second term $H_{M}$ . As a result by substituting (A) in (A), we get that

		$\displaystyle I\left(\mathbf{x}^{(t)}_{N};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
(22)			$\displaystyle=H_{N}-H_{N-1}+\frac{d^{*}}{2}\log\left(\frac{N}{N-1}\right),$

Our final step is to find suitable upper and lower bounds for $H_{M}$ to use in (A). Recall for the following arguments that due to whitening, the vector $\widehat{g}_{b}^{(t)}=\widehat{g}(b,\bm{\theta}^{(t)})$ has zero mean and identity covariance.

A.1. Upper bound on $H_{M}$

The upper bound is the simplest due to basic entropy properties. In particular, the sum $\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{b\in\mathcal{B}_{i}^{(t)}}\widehat{g}_{b}^{(t)}$ has zero mean and $\mathrm{I}_{d^{*}}$ covariance. Thus,

	$\displaystyle H_{M}$	$\displaystyle=h\left(\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{b\in\mathcal{B}_{i}^{(t)}}\widehat{g}_{b}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
(23)			$\displaystyle\overset{(a)}{\leq}\frac{1}{2}d^{*}\log\left(2\pi e\right),$

where $(a)$ follows from the fact that for a fixed first and second moment, Gaussian distribution maximizes the entropy.

The distinction between the proof of the bound in Case 1 and Case 2 in Theorem 1 is in the lower bound on the term $H_{M}$ . We start by providing the lower bound that is used for proving Case 1.

A.2. Lower bound on $H_{M}$ for Case 1 in Theorem 1

For the lower bound, we will rely heavily on the assumption that the elements of $\widehat{g}_{b}^{(t)}$ are independent and the interesting result that gives Berry-Esseen style bounds for the entropic central limit theorem (Bobkov et al., 2014). In particular, in its simplest form, the result states that for IID zero mean random variables $X_{i}$ , the entropy of the normalized sum $T_{m}=\frac{1}{\sqrt{M}}\sum_{i=1}^{M}X_{i}$ approaches the entropy of a Gaussian random variable $\Phi_{\sigma^{2}}$ with the same variance $\sigma^{2}$ as $X_{i}$ , such that the following is always satisfied

(24)

h(\Phi_{\sigma^{2}})-h(T_{M})\leq\tilde{C}\frac{\mathbb{E}|X_{i}|^{4}}{M},

Using (24), we can find a lower bound for $H_{M}$ as follows:

	$\displaystyle H_{M}$	$\displaystyle=h\left(\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{b\in\mathcal{B}_{i}^{(t)}}\widehat{g}_{b}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
		$\displaystyle=\sum_{j=1}^{d^{*}}h\underbrace{\left(\frac{1}{\sqrt{MB}}\sum_{b\in\mathcal{B}_{i}^{(t)}}\sum_{i=1}^{M}\widehat{g}_{b}^{(t)}[j]\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)}_{\text{variance = $1$}}$
(25)			$\displaystyle\stackrel{{\scriptstyle\eqref{eq:berry_esseen_entropy}}}{{\geq}}\!\!\sum_{j=1}^{d^{}}\!\left(\!h(\Phi_{1})-\frac{C_{0,\bar{g}}}{B}\!\right){=}\frac{d^{}}{2}\log\left(2\pi e\right){-}\frac{C_{0,\bar{g}}}{MB}.$

In other words, we have the following bound on $H_{M}$

(26)

\frac{d^{*}}{2}\log\left(2\pi e\right)-\frac{d^{*}C_{0,\bar{g}}}{MB}\leq H_{M}\leq\frac{d^{*}}{2}\log\left(2\pi e\right).

By substituting (26) in (A) (lower bound for $M=N-1$ and upper bound for $M=N$ ), we get that

	$\displaystyle I\left(\mathbf{x}^{(t)}_{N};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$	$\displaystyle=H_{N}-H_{N-1}+d^{*}\log\left(\frac{N}{N-1}\right)$
(27)			$\displaystyle\leq\frac{d^{}}{2}\log\left(\frac{N}{N-1}\right)+\frac{d^{}C_{0,\bar{g}}}{(N-1)B}.$

This concludes the proof of Case 1.

A.3. Lower bound on $H_{M}$ for Case 2 in Theorem 1

The proof of this lower bound relies on the entropic central limit theorem for the vector case (Eldan et al., 2020) and Lemma 1 which will be stated later in this section. We start by giving the entropic central limit theorem for the case of IID random vectos (Eldan et al., 2020).

Theorem 2 (Entropic central limit theorem (Eldan et al., 2020)).

Let $\mathbf{q}$ be a $\sigma$ -uniformly log concave $d$ -dimensional random vector with $\mathbb{E}[\mathbf{q}]=0$ and non-singular covariance matrix $\Sigma$ . Additionally, let $\mathbf{z}\sim\mathcal{N}(0,\Sigma)$ be a Gaussian vector with the same covariance as $\mathbf{q}$ , and let $\gamma\sim\mathcal{N}(0,\mathrm{I}_{d})$ to be a standard Gaussian. The entropy of the normalized sum $T_{M}=\frac{1}{\sqrt{M}}\sum_{i=1}^{M}\mathbf{q}_{i}$ , where $\mathbf{q}_{i}$ ’s are random samples, approaches the entropy of a Gaussian random vector $Z$ , such that the following is always satisfied

(28)

\text{Ent}(T_{M}||\mathbf{z})\leq\frac{2(d+2(\text{Ent}(\sqrt{\sigma}\mathbf{q}||\gamma)}{M\sigma^{4}},

where $\text{Ent}(T_{M}||\mathbf{z})$ is the relative entropy.

Lemma 1.

Given a random vector $\mathbf{q}\in\mathbb{R}^{d}$ with a distribution $f_{\mathbf{q}}(y)$ and Cov $({\mathbf{q}})=\Sigma$ , and defining $\mathbf{z}\sim\mathcal{N}(0,\Sigma)$ to be a Gaussian vector with the same covariance as $\mathbf{q}$ , for $\sigma>0$ , we get

	$\displaystyle\text{Ent}(\sqrt{\sigma}\mathbf{q}\|\|\mathbf{z})$	$\displaystyle=-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
(29)			$\displaystyle+\frac{1}{2}\log(\|\Sigma\|)+\sigma\frac{d}{2}$
(30)		$\displaystyle\text{Ent}(\mathbf{q}\|\|\mathbf{z})$	$\displaystyle=h(\mathbf{z})-h(\mathbf{q})$

Given the assumption that $\widehat{g}_{b}^{(t)}$ has a $\sigma$ -log concave distribution while both the term $\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{b\in\mathcal{B}_{i}^{(t)}}\widehat{g}_{b}^{(t)}$ and $\widehat{g}_{b}^{(t)}$ have an identity covariance matrix $\Sigma=\mathrm{I}_{d^{*}}$ given $\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}$ , we can use (28) with $\mathbf{z}\sim\mathcal{N}(0,\mathrm{I}_{d^{*}})$ . Furthermore, by using Lemma 1, we get

(31)

h(\mathbf{z})-H_{M}\leq\frac{d^{*}C_{1,\bar{g}}-C_{2,\bar{g}}}{MB},

where, $C_{1,\bar{g}}=\frac{2\left(1+\sigma+\log(2\pi)-\log(\sigma)\right)}{\sigma^{4}}$ and $C_{2,\bar{g}}=\frac{4h\left(\widehat{g}(b,\bm{\theta}^{(t)})\right)}{\sigma^{4}}$ , and $h(\widehat{g}(b,\bm{\theta}^{(t)}))$ is the entropy of the random vector $\bar{g}_{i}(b,\bm{\theta}^{(t)})$ after whitening.

Finally, using the fact that the entropy of the Gaussian random vector $\mathbf{z}$ with covariance $\mathrm{I}_{d^{*}}$ is given by $h(\mathbf{z})=\frac{d^{*}}{2}\log(2\pi e)$ , we get the following bound on $H_{M}$

(32)

\frac{d^{*}}{2}\log\left(2\pi e\right)-\frac{d^{*}C_{1,\bar{g}}-C_{2,\bar{g}}}{(N-1)B}\leq H_{M}\leq\frac{d^{*}}{2}\log\left(2\pi e\right).

By substituting (32) in (A) (lower bound for $M=N-1$ and upper bound for $M=N$ ), we can now upper bound the mutual information term as follows

	$\displaystyle I\left(\mathbf{x}^{(t)}_{N};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=H_{N}-H_{N-1}+\frac{d^{*}}{2}\log\left(\frac{N}{N-1}\right)$
(33)		$\displaystyle\leq\frac{d^{}}{2}\log\left(\frac{N}{N-1}\right)+\frac{d^{}C_{1,\bar{g}}-C_{2,\bar{g}}}{(N-1)B}.$

This concludes the proof of Theorem 1.

Appendix B Proof of Corollary 1

In the following, we define $S_{{N}}^{(t)}=\frac{1}{{N}}\sum_{i=1}^{N}\mathbf{x}_{i}^{(t)}$ . Using this notation, we can upper bound $I_{\rm priv/data}$ as follows

	$\displaystyle I_{\rm priv/data}={I}\left(\mathcal{D}_{i};\left\{S_{{N}}^{(k)}\right\}_{k\in[T]}\right)$
	$\displaystyle\overset{(a)}{=}\sum_{t=1}^{T}{I}\left(\mathcal{D}_{i};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\overset{(b)}{\leq}\sum_{t=1}^{T}{I}\left(\mathcal{B}_{i}^{(t)};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
(34)		$\displaystyle\overset{(c)}{\leq}\sum_{t=1}^{T}\!\underbrace{I\!\left(\mathbf{x}_{i}^{(t)}\!\left(\mathcal{B}_{i}^{(t)};\left\{\!S_{{N}}^{(k)}\!\right\}_{\!\!k\in[t-1]}\!\right);S_{{N}}^{(t)}\middle\|\left\{\!S_{{N}}^{(k)}\!\right\}_{k\in[t-1]}\!\right)}_{\text{This is bounded by the result in Theorem 1}}\!.$

where: (a) comes from the chain-rule; (b) from data processing inequality $D_{i}\rightarrow B_{i}^{(t)}\rightarrow\mathbf{x}_{i}^{(t)}$ , where $B_{i}^{(t)}$ is the sampled mini-batch from the data set of node $i$ ; (c) from data processing inequality $B_{i}^{(t)}\rightarrow\mathbf{x}_{i}^{(t)}\rightarrow\frac{1}{N}\sum_{i\in\mathcal{N}}\mathbf{x}^{(t)}_{i}$ ;. Combining the results given in the two cases of Theorem 1 with (B) concludes the proof of Corollary 1.

Appendix C Proof of Lemma 1

	$\displaystyle\text{Ent}(\sqrt{\sigma}\mathbf{q}\|\|\mathbf{Z})=\text{Ent}(\mathbf{q}^{\prime}\|\|\mathbf{Z})=\int f_{\mathbf{q}^{\prime}}(y)\log\frac{f_{\mathbf{q}^{\prime}}(y)}{f_{\mathbf{Z}}(y)}dy$
	$\displaystyle=\int f_{\mathbf{q}^{\prime}}(y)\log f_{\mathbf{q}^{\prime}}dy-\int f_{\mathbf{q}^{\prime}}(y)\log f_{\mathbf{Z}}(y)dy$
	$\displaystyle\overset{(a)}{=}-h(\mathbf{q}^{\prime})+\frac{d}{2}\log(2\pi)$
	$\displaystyle\qquad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\int f_{\mathbf{q}^{\prime}}(y)y^{T}\Sigma^{-1}ydy$
	$\displaystyle\overset{(b)}{=}-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
	$\displaystyle\quad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\int f_{\mathbf{q}^{\prime}}(y)\text{ Tr}(\Sigma^{-1}y^{T}y)dy$
	$\displaystyle\overset{(c)}{=}-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
	$\displaystyle\qquad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\text{ Tr}\left(\Sigma^{-1}\int f_{\mathbf{q}^{\prime}}(y)y^{T}ydy\right)$
	$\displaystyle=-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
	$\displaystyle\qquad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\text{ Tr}\left(\Sigma^{-1}\mathbb{E}_{\mathbf{q}^{\prime}}[\mathbf{q}^{\prime T}\mathbf{q}^{\prime}]\right)$
	$\displaystyle\overset{(d)}{=}-h(\mathbf{q})+\frac{d}{2}\log(\frac{2\pi}{\sigma})+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\sigma\text{ Tr}\left(\Sigma^{-1}\Sigma\right)$
(35)		$\displaystyle=-h(\mathbf{q})+\frac{d}{2}\log(\frac{2\pi}{\sigma})+\frac{1}{2}\log(\|\Sigma\|)+\sigma\frac{d}{2},$

where: $\rm Tr$ represents the trace function; $(a)$ follows from using the multivariate distribution of the Gaussian vector $\mathbf{z}$ ; $(b)$ using the scaling property of the entropy with $\mathbf{q}^{\prime}=\sqrt{\sigma}\mathbf{q}$ ; $(c)$ from follows from using the linearity of the trace function; finally $(d)$ from using the linear transformation of the random vector $\mathbf{q}^{\prime}=\sqrt{\sigma}\mathbf{q}$ and the fact that $\mathbf{q}$ has the same covariance matrix $\Sigma$ as $\mathbf{z}$ .

The proof of (30) follows directly by substituting $\sigma=1$ in the equation (C) and using entropy of a Gaussian vector with covariance $\Sigma$ .

Appendix D Overview of MINE

In our empirical evaluation in Section 5, we use the Mutual Information Neural Estimator (MINE) (Belghazi et al., 2018) to estimate the mutual information, which is the state-of-the-art method for mutual information estimation (Belghazi et al., 2018). Specifically, given random vectors $X$ and $Z$ , and a function family parameterized by a neural network $\mathcal{F}=\{T_{\theta}:X\times Z\rightarrow\mathbb{R}\}_{\theta\in\Theta}$ , the following bound holds:

(36)

I(X;Z)\geq I_{\Theta}(X;Z),

where $I_{\Theta}(X;Z)$ is the neural mutual information measure defined as:

(37)

I_{\Theta}(X;Z)=\sup_{\theta\in\Theta}\mathbb{E}_{\mathbb{P}_{XZ}}[T_{\theta}]-\log(\mathbb{E}_{\mathbb{P}_{X}\otimes\mathbb{P}_{Z}}[e^{T_{\theta}}]),

$\mathbb{P}_{X}$ and $\mathbb{P}_{Z}$ are the marginal distribution of $X$ and $Z$ respectively, $\mathbb{P}_{XZ}$ is the joint distribution of $X$ and $Z$ , and $\mathbb{P}_{X}\otimes\mathbb{P}_{Z}$ is the product of marginals $\mathbb{P}_{X}$ and $\mathbb{P}_{Z}$ . As an empirical estimation of $I_{\Theta}(X;Z)$ , MINE is implemented as

(38)

\widehat{I(X;Z)}_{K}=\sup_{\theta\in\Theta}\mathbb{E}_{\mathbb{P}_{XZ}^{(K)}}[T_{\theta}]-\log(\mathbb{E}_{\mathbb{P}_{X}^{(K)}\otimes\mathbb{P}_{Z}^{(K)}}[e^{T_{\theta}}]),

where $\mathbb{P}_{(\cdot)}^{(K)}$ is the empirical distribution of $\mathbb{P}_{(\cdot)}$ with $K$ IID samples. Finally, solving Eq. 38 (i.e. get the MI estimation) can be achieved by solving the following optimization problem via gradient ascent:

	$\displaystyle\widehat{I(X;Z)}_{K}$
	$\displaystyle=\max_{\theta\in\Theta}\left\{\!\frac{1}{K}\!\sum_{k=1}^{K}T_{\theta}(x_{k},z_{k})-\log\left(\frac{1}{K}\sum_{k=1}^{K}e^{T_{\theta}(x_{k},\bar{z}_{k})}\right)\right\},$

where $(x_{k},z_{k})$ is the $k$ -th sample from $\mathbb{P}_{XZ}$ and $\bar{z}_{k}$ is the $k$ -th sample from $\mathbb{P}_{Z}$ .

	$\displaystyle I\left(\mathbf{x}^{(t)}_{N};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\overset{(a)}{=}I\left(\sqrt{B}\mathbf{x}_{N}^{(t)};\sqrt{N}S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\overset{(b)}{=}I\left(\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)};F_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=h\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right){+}h\left(\!\!{F}_{{N}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad-h\left(\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)},F_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=h\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right){+}h\left(\!\!{F}_{{N}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad-\!h\left(\!\begin{bmatrix}\mathrm{I}_{d}^{}&\mathrm{0}_{d}^{}\\ \mathrm{I}_{d}^{}\frac{1}{\sqrt{N}}&\frac{\sqrt{N-1}}{\sqrt{N}}\mathrm{I}_{d}^{}\end{bmatrix}\!\!\!\begin{bmatrix}\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\\ {F}_{{N-1}}^{(t)}\end{bmatrix}\!\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\stackrel{{\scriptstyle(c)}}{{=}}h\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right){+}h\left(\!\!{F}_{{N}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\!\right\}_{\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad{-}h\!\left(\!\!\!\sqrt{B}\bar{\mathbf{x}}_{N}^{(t)}\!\middle\|\!\left\{\!S_{{N}}^{(k)}\!\right\}_{\!\!k\in[t-1]}\!\right)\!{-}h\!\left(\!{F}_{{N-1}}^{(t)}\!\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!\!k\in[t-1]}\!\right)$
	$\displaystyle\qquad-\log\left\|\det\begin{bmatrix}\mathrm{I}_{d}^{}&\mathrm{0}_{d}^{}\\ \mathrm{I}_{d}^{}\frac{1}{\sqrt{N-1}}&\frac{\sqrt{N-1}}{\sqrt{N}}\mathrm{I}_{d}^{}\end{bmatrix}\right\|$
	$\displaystyle\stackrel{{\scriptstyle(d)}}{{=}}h\left(\!F_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right)$
(20)		$\displaystyle\qquad-h\!\left(\!\!{F}_{{N-1}}^{(t)}\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right){+}\frac{d^{*}}{2}\log\left(\!\frac{N}{N-1}\!\right)\!,$

	$\displaystyle h\left(F_{M}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle=h\left(\!\!\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{d\in\mathcal{B}_{i}^{(t)}}\bar{g}_{i}(b,\bm{\theta}^{(t)})\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\!\!\right)$
	$\displaystyle\stackrel{{\scriptstyle(i)}}{{=}}h\!\!\left(\frac{\mathbf{K}_{\bar{G}^{(t)}}^{1/2}}{\sqrt{MB}}\sum_{i=1}^{M}\!\sum_{b\in\mathcal{B}_{i}^{(t)}}\!\!\!\widehat{g}_{i}(b,\bm{\theta}^{(t)})\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\stackrel{{\scriptstyle(ii)}}{{=}}\log\left(\|\det\mathbf{K}_{\bar{G}^{(t)}}^{1/2}\|\right)$
(21)		$\displaystyle\qquad{+}\underbrace{h\!\!\left(\!\!\frac{1}{\sqrt{MB}}\!\sum_{i=1}^{M}\!\sum_{b\in\mathcal{B}_{i}^{(t)}}\!\!\!\widehat{g}_{i}(b,\bm{\theta}^{(t)})\middle\|\!\left\{S_{{N}}^{(k)}\right\}_{\!k\in[t-1]}\!\right)}_{H_{M}}\!,$

	$\displaystyle H_{M}$	$\displaystyle=h\left(\frac{1}{\sqrt{MB}}\sum_{i=1}^{M}\sum_{b\in\mathcal{B}_{i}^{(t)}}\widehat{g}_{b}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
		$\displaystyle=\sum_{j=1}^{d^{*}}h\underbrace{\left(\frac{1}{\sqrt{MB}}\sum_{b\in\mathcal{B}_{i}^{(t)}}\sum_{i=1}^{M}\widehat{g}_{b}^{(t)}[j]\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)}_{\text{variance = $1$}}$
(25)			$\displaystyle\stackrel{{\scriptstyle\eqref{eq:berry_esseen_entropy}}}{{\geq}}\!\!\sum_{j=1}^{d^{}}\!\left(\!h(\Phi_{1})-\frac{C_{0,\bar{g}}}{B}\!\right){=}\frac{d^{}}{2}\log\left(2\pi e\right){-}\frac{C_{0,\bar{g}}}{MB}.$

	$\displaystyle I_{\rm priv/data}={I}\left(\mathcal{D}_{i};\left\{S_{{N}}^{(k)}\right\}_{k\in[T]}\right)$
	$\displaystyle\overset{(a)}{=}\sum_{t=1}^{T}{I}\left(\mathcal{D}_{i};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
	$\displaystyle\overset{(b)}{\leq}\sum_{t=1}^{T}{I}\left(\mathcal{B}_{i}^{(t)};S_{{N}}^{(t)}\middle\|\left\{S_{{N}}^{(k)}\right\}_{k\in[t-1]}\right)$
(34)		$\displaystyle\overset{(c)}{\leq}\sum_{t=1}^{T}\!\underbrace{I\!\left(\mathbf{x}_{i}^{(t)}\!\left(\mathcal{B}_{i}^{(t)};\left\{\!S_{{N}}^{(k)}\!\right\}_{\!\!k\in[t-1]}\!\right);S_{{N}}^{(t)}\middle\|\left\{\!S_{{N}}^{(k)}\!\right\}_{k\in[t-1]}\!\right)}_{\text{This is bounded by the result in Theorem 1}}\!.$

	$\displaystyle\text{Ent}(\sqrt{\sigma}\mathbf{q}\|\|\mathbf{Z})=\text{Ent}(\mathbf{q}^{\prime}\|\|\mathbf{Z})=\int f_{\mathbf{q}^{\prime}}(y)\log\frac{f_{\mathbf{q}^{\prime}}(y)}{f_{\mathbf{Z}}(y)}dy$
	$\displaystyle=\int f_{\mathbf{q}^{\prime}}(y)\log f_{\mathbf{q}^{\prime}}dy-\int f_{\mathbf{q}^{\prime}}(y)\log f_{\mathbf{Z}}(y)dy$
	$\displaystyle\overset{(a)}{=}-h(\mathbf{q}^{\prime})+\frac{d}{2}\log(2\pi)$
	$\displaystyle\qquad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\int f_{\mathbf{q}^{\prime}}(y)y^{T}\Sigma^{-1}ydy$
	$\displaystyle\overset{(b)}{=}-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
	$\displaystyle\quad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\int f_{\mathbf{q}^{\prime}}(y)\text{ Tr}(\Sigma^{-1}y^{T}y)dy$
	$\displaystyle\overset{(c)}{=}-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
	$\displaystyle\qquad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\text{ Tr}\left(\Sigma^{-1}\int f_{\mathbf{q}^{\prime}}(y)y^{T}ydy\right)$
	$\displaystyle=-h(\mathbf{q})-\frac{d}{2}\log(\sigma)+\frac{d}{2}\log(2\pi)$
	$\displaystyle\qquad+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\text{ Tr}\left(\Sigma^{-1}\mathbb{E}_{\mathbf{q}^{\prime}}[\mathbf{q}^{\prime T}\mathbf{q}^{\prime}]\right)$
	$\displaystyle\overset{(d)}{=}-h(\mathbf{q})+\frac{d}{2}\log(\frac{2\pi}{\sigma})+\frac{1}{2}\log(\|\Sigma\|)+\frac{1}{2}\sigma\text{ Tr}\left(\Sigma^{-1}\Sigma\right)$
(35)		$\displaystyle=-h(\mathbf{q})+\frac{d}{2}\log(\frac{2\pi}{\sigma})+\frac{1}{2}\log(\|\Sigma\|)+\sigma\frac{d}{2},$

How Much Privacy Does Federated Learning with Secure Aggregation Guarantee?

Abstract.

1. Introduction

2. Preliminaries

2.1. Basic Setting of Federated Learning

2.2. Secure Aggregation Protocols for Federated Learning

2.2.1. Threat Model in Secure Aggregation for Federated Learning

2.2.2. Secure Aggregation Guarantees

Remark 1.

2.2.3. Our Contribution: Guarantees on Privacy Leakage from the Aggregated Model

3. Theoretical Privacy Guarantees of FL with Secure Aggregation

3.1. Main Results

Definition 1 (Independent under whitening).

Definition 2 (Uniformly σ\sigma-log concave).

Assumption 1 (IID data distribution).

Theorem 1 (Single Round Leakage).

Remark 2 (Simplified bound).

Remark 3.

Remark 4.

Corollary 0.

3.2. Impact of System Parameters

3.2.1. Impact of Number of Users (N)

3.2.2. Impact of Batch Size (B)

3.2.3. Impact of Model Size (d)

3.2.4. Impact of Global Training Rounds (T)

3.3. Impact of User Dropout, Collusion, and User Sampling

3.3.1. Impact of User Dropout and Collusion with the Server

Corollary 0.

3.3.2. Impact of User Sampling

4. Experimental Setup

4.1. MI Estimation

4.2. Datasets and Models

5. Empirical Evaluation

5.1. Impact of Number of Users (N)

5.2. Impact of Model Size (d)

5.3. Impact of Batch Size (B)

5.4. Accumulative MI leakage

5.5. Impact of Local Training Epochs (E)

5.6. Impact of Data Heterogeneity

5.7. Practical Privacy Implications

Success of Privacy attacks

MI Privacy leakage under the joint use of DP and SA

6. Related work

7. Further Discussion and Conclusions

References

Appendix A Proof of Theorem 1

Property 1.

A.1. Upper bound on HMH_{M}

A.2. Lower bound on HMH_{M} for Case 1 in Theorem 1

A.3. Lower bound on HMH_{M} for Case 2 in Theorem 1

Theorem 2 (Entropic central limit theorem (Eldan et al., 2020)).

Lemma 1.

Appendix B Proof of Corollary 1

Appendix C Proof of Lemma 1

Appendix D Overview of MINE

Definition 2 (Uniformly $\sigma$ -log concave).

A.1. Upper bound on $H_{M}$

A.2. Lower bound on $H_{M}$ for Case 1 in Theorem 1

A.3. Lower bound on $H_{M}$ for Case 2 in Theorem 1