How to determine if a random graph with a fixed degree sequence has a giant component

Let us first describe the result of Molloy and Reed [24]. For every $1\leq i\leq n$, one can explore the component containing a specific initial vertex $i$ of a graph on $\{1,...,n\}$ via breadth-first search. Initially we have $d_{i}$ “open” edges out of $i$. Upon exposing the other endpoint $j$ of such an open edge, it is no longer open, but we gain $d_{j}-1$ open edges out of $j$. Thus, the number of open edges has increased by $d_{j}-2$ (note that this is negative if $d_{j}=1$).

One can generate the random graph $G({\cal D})$ for ${\cal D}=(d_{1},...,d_{n})$ and carry out this exploration at the same time, by choosing each vertex as $j$ with the appropriate probability.

Intuitively speaking, the probability we pick a specific vertex $j$ as the other endpoint of the first exposed edge is proportional to its degree. So, the expected increase in the number of open edges in the first step is equal to $\frac{\sum_{k\in\{1,..,n\},k\neq i}d_{k}(d_{k}-2)}{\sum_{k\in\{1,..,n\},k\neq i}d_{k}}$. Thus, it is positive essentially if and only if the sum of the squares of the degrees exceeds twice the sum of the degrees.

Suppose that this expected increase remains the same until we have exposed a linear number of vertices. It seems intuitively clear that if the expected increase is less than $0$, then the probability that initial vertex $i$ is in a linear order component is $o(1)$, and hence the probability that $G({\cal D})$ has no linear order component is $1-o(1)$. If for some positive constant $\epsilon$, the expected increase is at least $\epsilon$, then there is some $\gamma=\gamma(\epsilon)>0$ such that the probability that $i$ is in a component with at least $\gamma n$ vertices exceeds $\gamma$.

In [24], Molloy and Reed proved, subject to certain technical conditions which required them to discuss sequences of degree sequences rather than one single degree sequence, that we essentially have that (i) if $\frac{\sum_{k=1}^{n}d_{k}(d_{k}-2)}{\sum_{k=1}^{n}d_{k}}>\epsilon$ for some $\epsilon>0$, then the probability that $G({\cal D})$ has a giant component is $1-o(1)$, and (ii) if $\frac{\sum_{k=1}^{n}d_{k}(d_{k}-2)}{\sum_{k=1}^{n}d_{k}}<-\epsilon$ for some $\epsilon>0$, then the probability that $G({\cal D})$ has no giant component is $1-o(1)$. We present their precise result and some of its generalizations later in this introductory section.

It turns out that, absent the imposed technical conditions, the expected increase may change drastically during the exploration process. Consider for example the situation in which $n=k^{2}$ for some large odd integer $k$, $d_{1}=d_{2}=..=d_{n-1}=1$ and $d_{n}=2k$. Then $\frac{\sum_{k=1}^{n}d_{k}(d_{k}-2)}{\sum_{k=1}^{n}d_{k}}=\frac{4k^{2}-4k-(n-1)}{2k+n-1}\approx 3$, and so the Molloy-Reed approach would suggest that with probability $1-o(1)$ there is a giant component. However, with probability $1$, $G({\cal D})$ is the disjoint union of a star with $2k$ leaves and $\frac{n-2k-1}{2}$ components of order $2$ and hence it has no giant component. The problem is that as soon as we explore vertex $n$, the expected increase drops from roughly $3$ to $-1$, so it does not stay positive throughout (the beginning of) the process.

Thus, we see that the Molloy-Reed criterion cannot be extended for general degree sequences. To find a variant which applies to arbitrary degree sequences, we need to characterize those for which the expected increase remains positive for a sufficiently long time.

Intuitively, since the probability that we explore a vertex is essentially proportional to its degree, in lower bounding the length of the period during which the expected increase remains positive, we could assume that the exploration process picks at each step a highest degree vertex that has not been explored yet. Moreover, note that vertices of degree $2$ have a neutral role in the exploration process as exposing such a vertex does not change the number of open edges, provided we assume that our component locally looks like a tree (which turns out to be a good approximation around the critical window). These observations suggest that we should focus on the following invariants of $\mathcal{D}$ defined by considering a permutation $\pi$ of the vertices that satisfies $d_{\pi_{1}}\leq...\leq d_{\pi_{n}}$:

• -

  $j_{\cal D}=\min\left(\Big{\{}j:j\in[n]\mbox{ and }\sum\limits_{i=1}^{j}d_{\pi_{i}}(d_{\pi_{i}}-2)>0\Big{\}}\cup\Big{\{}n\Big{\}}\right)$,

• -

  $R_{\cal D}=\sum\limits_{i=j_{\cal D}}^{n}d_{\pi_{i}}$, and

• -

  $M_{\cal D}=\sum\limits_{i\in[n]:\,d_{i}\neq 2}d_{i}$.

We emphasize that these invariants are determined by the multiset of the degrees given by ${\cal D}$ and are independent from the choice of $\pi$ subject to $d_{\pi_{1}}\leq...\leq d_{\pi_{n}}$.

Our intuition further suggests that in the exploration process, the expected increase in the number of open edges will be positive until we have explored $R_{\cal D}$ edges and will then become negative. Thus, we might expect to explore a component with about $R_{\cal D}$ edges, and indeed we can show this is the case.

This allows us to prove our main result which is that whether $G({\cal D})$ has a giant component essentially depends on whether $R_{\cal D}$ is of the same order as $M_{\cal D}$ or not. There is however a caveat, this is not true if essentially all vertices have degree $2$.

For any function $\lambda:\mathbb{N}\to\mathbb{N}$, we say a degree sequence ${\cal D}$ is $\lambda$-well-behaved or simply well-behaved if $M_{\cal D}$ is at least $\lambda(n)$. Our main results hold for any function $\lambda\to\infty$ as $n\to\infty$.

As we shall see momentarily, previous results in this field apply to sequences of degree sequences, and required that both the proportion of elements of a given degree and the average degree of an element of the degree sequences in the sequence approaches a limit in some smooth way. We can easily deduce results for every sequence of (feasible) degree sequences from the two theorems above, and from our results on degree sequences which are not well-behaved, presented in the next section.

We denote by $\mathfrak{D}=({\cal D}_{n})_{n\geq 1}$ a sequence of degree sequences where $\mathcal{D}_{n}$ has length $n$. We say that $\mathfrak{D}$ is well-behaved if for every $b$, there is an $n_{b}$ such that for all $n>n_{b}$, we have $M_{{\cal D}_{n}}>b$; $\mathfrak{D}$ is lower bounded if for some $\epsilon>0$, there is an $n_{\epsilon}$ such that for all $n>{n_{\epsilon}}$, we have $R_{{\cal D}_{n}}\geq\epsilon M_{{\cal D}_{n}}$; and $\mathfrak{D}$ is upper bounded if for every $\epsilon>0$, there is an $n_{\epsilon}$ such that for all $n>{n_{\epsilon}}$, we have $R_{{\cal D}_{n}}\leq\epsilon M_{{\cal D}_{n}}$.

The following is an immediate consequence of Theorem 1 and 2, and Theorem 6, which will be presented in the next section.

At first glance, it may be surprising that the existence of a giant component depends on the ratio between $R_{\cal D}$ and $M_{\cal D}$ rather than the ratio between $R_{\cal D}$ and $\sum_{i=1}^{n}d_{i}$. It may also be unclear why we have to treat differently degree sequences where the sum of the degrees which are not 2 is bounded.

To clarify why our results are stated as they are, we now highlight the special role of vertices of degree 2.

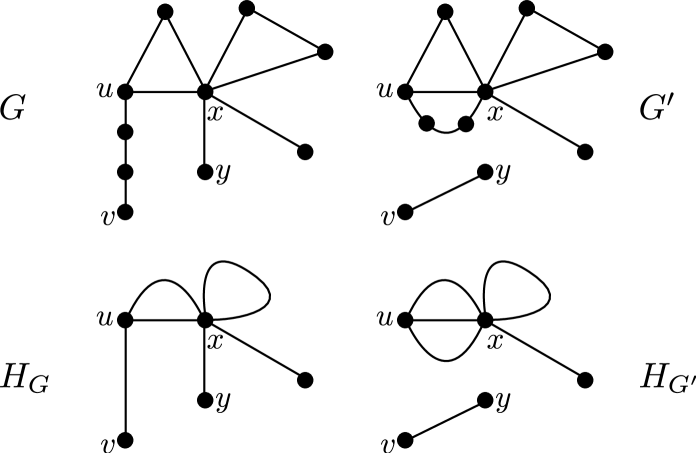
The non-cyclic components²²2A component is cyclic if it is a cycle and non-cyclic if it is not. of $G({\cal D})$ can be obtained by subdividing the edges of a multigraph $H({\cal D})$ none of whose vertices have degree 2 so that every loop is subdivided at least twice, and all but at most one edge of every set of parallel edges is subdivided at least once. Note that $H(\mathcal{D})$ can be obtained from $G(\mathcal{D})$ by deleting all cyclic components and suppressing all vertices of degree $2$.³³3Here and throughout the paper, when we say we suppress a vertex $u$ of degree $2$, this means we delete $u$ and we add an edge between its neighbours. Observe that this may create loops and multiple edges, so the resulting object might not be a simple graph. Clearly, $H({\cal D})$ is uniquely determined by $G({\cal D})$. Moreover, the degree sequence of $H(\mathcal{D})$ is precisely that of $G(\mathcal{D})$ without the vertices of degree $2$.

The number of vertices of a non-cyclic component of $G({\cal D})$ equals the sum of the number of vertices of the corresponding component of $H({\cal D})$ and the number of vertices of degree 2 used in subdividing its edges. Intuitively, the second term in this sum depends on the proportion of the edges in the corresponding component of $H({\cal D})$. Subject to the caveat mentioned above and discussed below, if the number of vertices of degree 2 in $G(\mathcal{D})$ is much larger than the size⁴⁴4As it is standard, we use order and size to denote the number of vertices and the number of edges of a graph, respectively. of $H({\cal D})$, then the probability that $G({\cal D})$ has a giant component is essentially the same as the probability $H({\cal D})$ has a component containing a positive fraction of its edges. The same is true, although not as immediately obvious, even if the number of vertices of degree 2 is not this large.

As we mentioned above, degree sequences which are not well behaved behave differently from well-behaved degree sequences. For instance, suppose that $M_{\cal D}=0$. Then $H({\cal D})$ is empty and $G({\cal D})$ is a uniformly chosen disjoint union of cycles. In this case it is known that the probability of having a giant component is bounded away both from $0$ and $1$. Indeed, the latter statement also holds whenever $M_{\cal D}$ is at most $b$ for any constant $b$.

This theorem both explains why we concentrate on well-behaved degree sequences and sets out how degree sequences which are not well-behaved actually behave (badly obviously). Combining it with Theorem 1 and 2, it immediately implies Theorem 3. We omit the straightforward details.

The study of the existence of a giant component in random graphs with an arbitrary prescribed degree sequence⁵⁵5Random graphs with special degree sequences had been studied earlier (see, e.g. [22, 33])., started with the result of Molloy and Reed [24]. Although they define the concept of asymptotic degree sequences, we will state all the previous results in terms of sequences of degree sequences $\mathfrak{D}=(\mathcal{D}_{n})_{n\geq 1}$. Using a symmetry argument, one can easily translate results for sequences of degree sequences to asymptotic degree sequences, and vice versa. For every $\mathcal{D}_{n}=(d_{1}^{(n)},\dots,d_{n}^{(n)})$, we define $n_{i}=n_{i}(n)=|\{j\in[n]:\,d_{j}^{(n)}=i\}|$. Recall that we only consider degree sequences such that $n_{0}=0$.

Before stating their result, we need to introduce a number of properties of sequences of degree sequences. A sequence of degree sequences $\mathfrak{D}$ is

• -

  feasible, if for every $n\geq 1$, there exists at least one simple graph on $n$ vertices with degree sequence $\mathcal{D}_{n}$.

• -

  smooth, if for every nonnegative integer $i\geq 0$, there exists $\lambda_{i}\in[0,1]$ such that $\lim_{n\to\infty}\frac{n_{i}}{n}=\lambda_{i}$.

• -

  sparse, if there exists $\lambda\in(0,\infty)$ such that $\lim_{n\to\infty}\sum_{i\geq 1}\frac{in_{i}}{n}=\lambda$.

• -

  $f$-bounded, for some function $f:\mathbb{N}\to\mathbb{R}$, if $n_{i}=0$ for every $i>f(n)$.

In particular, observe that random graphs $G(\mathcal{D}_{n})$ arising from a sparse sequence of degree sequences $\mathfrak{D}$ have a linear number of edges, provided that $n$ is large enough.

We say a sequence of degree sequences $\mathfrak{D}$ satisfies the $\mathbf{MR}$-conditions if

1. (a.1)

   it is feasible, smooth and sparse,

2. (a.2)

   it is $n^{1/4-\epsilon}$-bounded, for some $\epsilon>0$,

3. (a.3)

   for every $i\geq 1$, $\frac{i(i-2)n_{i}}{n}$ converges uniformly to $i(i-2)\lambda_{i}$, and

4. (a.4)

   $\lim_{n\to\infty}\sum_{i\geq 1}i(i-2)\frac{n_{i}}{n}$ exists and converges uniformly to $\sum_{i\geq 1}i(i-2)\lambda_{i}$.

For a precise statement of the uniform convergence on conditions (a.3)–(a.4), we refer the reader to [24]. Note that these conditions imply that $\lambda=\sum_{i\geq 1}i\lambda_{i}$.

Now we can precisely state the result of Molloy and Reed [24].

Theorem 7 has been generalized to other sequences of degree sequences, which in particular include the case $Q(\mathfrak{D})=0$. In Section 8, we show that Theorem 3 implies all the criteria for the existence of a giant component in $G(\mathcal{D}_{n})$ introduced below.⁶⁶6Note that some of these results give a more precise description on the order of the largest component. Our results only deal with the existential question.

We say a sequence of degree sequences $\mathfrak{D}$ satisfies the $\mathbf{JL}$-conditions if

1. (b.1)

   is feasible, smooth, and sparse,

2. (b.2)

   $\sum_{i\geq 1}i^{2}n_{i}=O(n)$, and

3. (b.3)

   $\lambda_{1}>0$.

Observe that if $\mathfrak{D}$ satisfies the $\mathbf{JL}$-conditions, then, by (b.2), it is also $O(n^{1/2})$-bounded. Moreover, they also imply that $\lambda=\sum_{i\geq 1}i\lambda_{i}$. Janson and Luczak in [18] showed that one can prove a variant of Theorem 7 obtained by replacing the $\mathbf{MR}$-conditions by the $\mathbf{JL}$-conditions.⁷⁷7Their result gives convergence in probability of the proportion of vertices in the giant component and they also consider the case $Q(\mathfrak{D})=0$. They also note that if $\lambda_{2}=1$, then the criterion based on $Q(\mathfrak{D})$ does not apply. Our results completely describe the case $\lambda_{2}=1$.

We say a sequence of degree sequence $\mathfrak{D}$ satisfies the $\mathbf{BR}$-conditions if

1. (c.1)

   it is feasible, smooth and sparse,

2. (c.2)

   $\sum_{i\geq 3}\lambda_{i}>0$, and

3. (c.3)

   $\lambda=\sum_{i\geq 1}i\lambda_{i}$.

Bollobás and Riordan in [5] proved a version of Theorem 7 for sequences of degree sequences obtained by replacing the $\mathbf{MR}$-conditions by the $\mathbf{BR}$-conditions.⁸⁸8They also proved some results on the distribution of the order of the largest component and also consider the case $Q(\mathfrak{D})=0$.

Theorem 7 and its extensions provide easy-to-use criteria for the existence of a giant component and have been widely used by many researchers in the area of complex networks [2, 4, 27]. However, the technical conditions on $\mathfrak{D}$ to which they can be applied, restrict its applicability, seem to be artificial and are only required due to the nature of the proofs. It turns out to be the case that many real-world networks do not satisfy these conditions. For this reason, researchers have developed both ad-hoc approaches for proving results for specific types of degree sequences and variants of the Molloy-Reed result which require different sets of technical conditions to be satisfied.

An early example of an ad-hoc approach is the work of Aiello, Chung and Lu on Power-Law Random Graphs [1]. They introduce a model depending on two parameters $\alpha,\beta>0$ that define a degree sequence satisfying $n_{i}=\lfloor e^{\alpha}i^{-\beta}\rfloor$. One should think about these parameters as follows: $\alpha$ is typically large and determines the order of the graph (we always have $\alpha=\Theta(\log{n})$), and $\beta$ is a fixed constant that determines the power-decay of the degree distribution. Among other results, the authors prove that there exists $\beta_{0}>0$, such that if $\beta>\beta_{0}$ the probability that there is a component of linear order is $o(1)$ and if $\beta<\beta_{0}$ the probability there is a component of linear order is $1-o(1)$. Here, the previous conditions are only satisfied for certain values of $\beta$ and the authors need to do additional work to determine when a giant component exists for other values of $\beta$. In Section 8 we will show how Theorem 3 also implies Aiello-Chung-Lu results on the existence of a giant component in the model of Power-Law Random Graphs.

Beginning with the early results of Molloy and Reed, the study of the giant component in random graphs with prescribed degree sequence has attracted a lot of attention. Directions of study include determining the asymptotic order of the largest component in the subcritical regime or estimating the order of the second largest component in both regimes [5, 16, 18, 20, 21, 25, 30]. It would be interesting to extend these known results to arbitrary degree sequences.

For example, Theorem 1 and 2 precisely describe the appearance of a giant component when the degree sequence is well-behaved. While bounds on the constant $\gamma$ in terms of $\delta$ and $\epsilon$ respectively, may follow from their respective proofs, these bounds are probably not of the right order of magnitude. Molloy and Reed in [25], precisely determined this dependence for sequences of degree sequences that satisfy the $\mathbf{MR}$-conditions. Precise constants are also given in [5, 14, 18]. We wonder whether it is possible to determine the precise dependence on the parameters for arbitrary degree sequences. It is likely that our methods can be used to find this dependence and to determine the order of the second largest component when a giant one exists.

Another direction is the study of site and bond percolation in $G(\mathcal{D})$ for arbitrary degree sequences $\mathcal{D}$. This problem has been already approached for sequences of degree sequences that satisfy certain conditions similar to the ones presented in Section 1.4 [5, 13, 17, 30].

Motivated by some applications in peer-to-peer networks (see, e.g. [6]), one can study efficient sampling of the random graph $G(\mathcal{D})$. Cooper et al. [8] showed that the switching chain rapidly mixes for $d$-regular graphs for every $3\leq d\leq n-1$. Greenhill [15] recently extended this result to $G(\mathcal{D})$, but, due to some technical reasons, this result only holds if the maximum degree in $\mathcal{D}$ is small enough.

Many other basic properties of $G(\mathcal{D})$, such as determining its diameter [11, 31, 32] or the existence of giant cores [7, 10, 19], have already been studied for certain sequences of degree sequences. We believe that our method can help to extend these results to arbitrary degree sequences.

The proofs of Theorem 4, 5 and 6 are simpler than the remaining proofs and we delay any discussion of these results to Section 6 and 7. By applying them, we see that in order to prove Theorem 1 and 2 it is enough to prove the following results:

The proofs of both theorems analyse an exploration process similar to the one discussed in Section 1.1 by combining probabilistic tools with a combinatorial switching argument. However, we will focus on the edges of $H(\mathcal{D})$ rather than the ones of $G({\cal D})$. Again, we will need to bound the expected increase of the number of open edges throughout the process and prove that the (random) increase is highly concentrated around its expected value. In order to do so, we will need to bound the probability that the next vertex of $H({\cal D})$ explored in the process, is a specific vertex $w$. One of the key applications of our combinatorial switching technique will be to estimate this probability and show that it is approximately proportional to the degree of $w$.

Crucial to this approach is that the degrees of the vertices explored throughout the process are not too high. Standard arguments for proving concentration of a random variable require that the change at each step is relatively small. This translates precisely to an upper bound on the maximum degree of the explored graph. Furthermore, without such a bound on the maximum degree, we cannot obtain good bounds on the probability that a certain vertex $w$ is the next vertex explored in the process. So, a second key ingredient in our proofs will be a preprocessing step which allows us to handle the vertices of high degree, ensuring that we will not encounter them in our exploration process.

We consider a variant of the exploration process where we start our exploration at a non-empty set $S_{0}$ of vertices of $H(\mathcal{D})$, rather than at just one vertex.

Thus, we see that the exploration takes $|V(H(\mathcal{D}))\setminus S_{0}|$ steps and produces sets

where $w_{t}=S_{t}\setminus S_{t-1}$ is either a neighbour of a vertex $v_{t}$ of $S_{t-1}$ or is a randomly chosen vertex in $V(H(\mathcal{D}))\setminus S_{t-1}$ if there are no edges between $S_{t-1}$ and $V(H(\mathcal{D}))\setminus S_{t-1}$.

To specify our exploration process precisely, we need to describe how we choose $v_{t}$ and $w_{t}$. To aid in this process, for each vertex $v\in V(H({\cal D}))$ we will choose a uniformly random permutation of its adjacency list in $G({\cal D})$. For this purpose, an input of our exploration process consists of a graph $G$ equipped with an ordering of its adjacency lists for all vertices $v\in V(H(\mathcal{D}))$. Applying the method of deferred decisions (cf. Section 2.4 in [26]), we can generate these random linear orders as we go along with our process. We note that this yields, in a natural manner, an ordering of the non-loop edges of $H({\cal D})$ which have the vertex $v$ as an endpoint. If there are no edges between $S_{t-1}$ and $V(H(\mathcal{D}))\setminus S_{t-1}$, we choose each vertex of $V(H({\cal D}))\setminus S_{t-1}$ to be $w_{t}$ with probability proportional to its degree. Otherwise we choose the smallest vertex $v_{t}$ of $S_{t-1}$ (with respect to the natural order in $\{1,\dots,n\}$), which has a neighbour in $V(H(\mathcal{D}))\setminus S_{t-1}$. We expose the edge of $H(\mathcal{D})$ from $v_{t}$ to $V(H(\mathcal{D}))\setminus S_{t-1}$ which appears first in our random ordering and let $w_{t}$ be its other endpoint. Furthermore, we expose all the edges of $H(\mathcal{D})$ from $w_{t}$ to $S_{t-1}\setminus\{v_{t}\}$ as well as the loops incident to $w_{t}$. Finally, we expose the paths of $G({\cal D})$ corresponding to the edges of $H({\cal D})$ which we have just exposed and the position in the random permutation of the adjacency list of $w_{t}$ in $G({\cal D})$ of the edges we have just exposed.

Thus, after $t$ iterations of our exploration process we have exposed

• •

  the subgraph of $H({\cal D})$ induced by $S_{t}$,

• •

  the paths of $G({\cal D})$ corresponding to the exposed edges of $H({\cal D})$, and

• •

  where each initial and final edge of such a path appears in the random permutation of the adjacency list of any of its endpoints which is also an endpoint of the path.

We refer to this set of information as the configuration ${\cal C}_{t}$ at time $t$. A configuration can also be understood as a set of inputs. During our analysis of the exploration process, we will consider all the probabilities of events conditional on the current configuration.

An important parameter for our exploration process is the number $X_{t}$ of edges of $H({\cal D})$ between $S_{t}$ and $V(H({\cal D}))\setminus{S}_{t}$. We note that if $X_{t}=0$, then $S_{t}$ is the union of some components of $H({\cal D})$ containing all of $S_{0}$. We note that if $|S_{0}|=1$, then every $X_{t}$ is a lower bound on the maximum size of a component of $H({\cal D})$ (not necessarily the one containing the vertex in $S_{0}$).

We prove Theorem 8 by showing that under its hypotheses for every vertex $v$ of $H({\cal D})$, there is a set $S_{0}=S_{0}(v)$ containing $v$ such that, given we start our exploration process with $S_{0}$, the probability that there is a $t$ with $X_{t}=0$ for which the number of edges within $S_{t}$ is at most $\gamma M_{\cal D}$, is $1-o(M_{\cal D}^{-1})$. Since $H({\cal D})$ has at most $2M_{\cal D}$ vertices, it follows that the probability that $H({\cal D})$ has a component of size at least $\gamma M_{\cal D}$ is $o(1)$. The set $S_{0}\setminus\{v\}$ is a set of highest degree vertices the sum of whose degrees exceeds $R_{\mathcal{D}}$. By the definition of $j_{\cal D}$ and $R_{\cal D}$, this implies that, unless $X_{0}=0$, the expectation of $X_{1}-X_{0}$ is negative. We show that, as the process continues, the expectation of $X_{t}-X_{t-1}$ becomes even smaller. We can prove that the actual change of $X_{t}$ is highly concentrated around its expectation and hence complete the proof, because $S_{0}$ contains all the high degree vertices and so in the analysis of our exploration process we only have to deal with low degree vertices.

We prove (a slight strengthening of) Theorem 9 for graphs without large degree vertices by showing that under its hypotheses and setting $S_{0}$ to be a random vertex $v$ chosen with probability proportional to its degree, with probability $1-o(1)$, there exists some $t$ such that $X_{t}\geq\gamma M_{\cal D}$ (and hence there is a component of $H({\cal D})$ of size at least $\gamma M_{\cal D}$). Key to doing so is that the expected increase of $X_{t}$ is a positive fraction of the increase in the sum of the degrees of the vertices in $S_{t}$ until this sum approaches $R_{\cal D}$. To handle the high degree vertices, we expose the edges whose endpoints are in components containing a high degree vertex. If this number of edges is at least a constant fraction of $M_{\cal D}$, then we can show that in fact all the high degree vertices lie in one component, which therefore contains a constant fraction of the edges of $H({\cal D})$. Otherwise, we show that the conditions of Theorem 9 (slightly relaxed) hold in the remainder of the graph, which has no high degree vertices, so we can apply (a slight strengthening of) Theorem 9 to find the desired component of $H({\cal D})$.