Hyperbolic graphs of small complexity
Abstract.
In this paper we enumerate and classify the “simplest” pairs where is a closed orientable -manifold and is a trivalent graph embedded in .
To enumerate the pairs we use a variation of Matveev’s definition of complexity for -manifolds, and we consider only -irreducible pairs, namely pairs such that any 2-sphere in intersecting transversely in at most points bounds a ball in either disjoint from or intersecting in an unknotted arc. To classify the pairs our main tools are geometric invariants defined using hyperbolic geometry. In most cases, the graph complement admits a unique hyperbolic structure with parabolic meridians; this structure was computed and studied using Heard’s program Orb and Goodman’s program Snap.
We determine all -irreducible pairs up to complexity 5, allowing disconnected graphs but forbidding components without vertices in complexity 5. The result is a list of 129 pairs, of which 123 are hyperbolic with parabolic meridians. For these pairs we give detailed information on hyperbolic invariants including volumes, symmetry groups and arithmetic invariants. Pictures of all hyperbolic graphs up to complexity 4 are provided. We also include a partial analysis of knots and links.
The theoretical framework underlying the paper is twofold, being based on Matveev’s theory of spines and on Thurston’s idea (later developed by several authors) of constructing hyperbolic structures via triangulations. Many of our results were obtained (or suggested) by computer investigations.
2000 Mathematics Subject Classification:
Primary 57M50; Secondary 57M27, 05C30, 57M20.1. Introduction
The study of knotted graphs in -manifolds is a natural generalization of classical knot theory, with potential applications to chemistry and biology (see e.g. [10]). In knot theory, extensive knot tables have been built up through the work of many mathematicians (see e.g. Conway [6] and Hoste–Thistlethwaite–Weeks [21]). There has been much less work on the tabulation of knotted graphs, but some knotted graphs in have been enumerated in order of crossing number by Simon [45], Litherland [27], Moriuchi [38, 39], and Chiodo et. al. [5].
In this paper we classify the simplest trivalent graphs in general closed -manifolds. We first enumerate them using a notion of complexity which extends Matveev’s definition for -manifolds [32], and then we classify them with the help of geometric invariants, mostly defined using hyperbolic geometry.
More precisely, the objects considered in this paper are pairs where is a closed, connected orientable -manifold and is a trivalent graph in . The graph may contain loops and multiple edges, and is possibly disconnected (in particular, can be a knot or a link). To avoid “wild” embeddings we work in the piecewise linear category: thus is a PL-manifold and is a 1-dimensional subcomplex, and we aim to classify graphs up to PL-homeomorphisms of pairs.
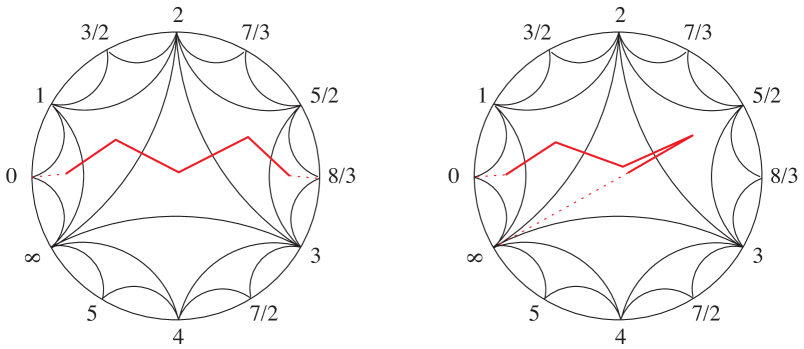
Following [32], a compact polyhedron is called simple if the link of every point of embeds in the 1-skeleton of the tetrahedron (the complete graph with 4 vertices). Points having the whole of this graph as a link are called vertices of . Moreover, as defined in [41], is a spine of a pair if it embeds in so that its complement is a finite union of balls intersecting in the simplest possible ways, as shown in Figure 1.
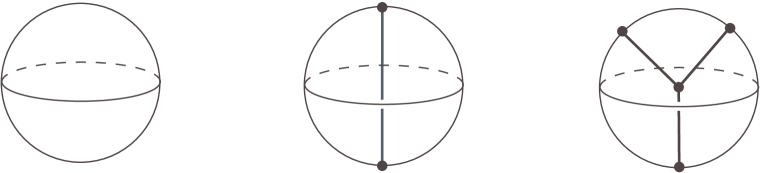
As usual in complexity theory, the complexity is then defined as the minimal number of vertices in a simple spine of . The case considered in [41] is actually that of 3-orbifolds, but the definition of complexity is the same as just given, except that a contribution of the edge labels is also introduced. When we recover the original definition of Matveev, thus getting the equality . In general, we have .
For manifolds, Matveev showed that complexity is additive under connected sum and that it behaves particularly well on irreducible manifolds (i.e. manifolds in which every 2-sphere bounds a 3-ball). In particular, there exist only finitely many irreducible manifolds with given complexity. These facts extend to the context of the pairs described above, with the following notion of irreducibility: is -irreducible if every 2-sphere embedded in and meeting transversely in at most two points bounds a ball intersecting as in Figure 1, left or centre (in particular, there exists no 2-sphere meeting in one point).
This paper is devoted to the enumeration and the geometric investigation of all -irreducible graphs of small complexity. As usual in -dimensional topology, a key role in the study of our graphs is played by invariants coming from hyperbolic geometry, which in particular provided the tools we used in most cases to distinguish the pairs from each other.
While the complement of in very often has no hyperbolic structure with geodesic boundary (for instance, it is often a handlebody), most pairs are indeed hyperbolic in a more general sense, namely they are hyperbolic with parabolic meridians. This means that carries a metric of constant sectional curvature which completes to a manifold with non-compact geodesic boundary having:
-
•
toric cusps at the knot components of ,
-
•
annular cusps at the meridians of the edges of , and
-
•
geodesic 3-punctured boundary spheres at the vertices of .
This hyperbolic structure is the natural analogue of the complete hyperbolic structure on a knot or link complement and is also useful when studying orbifold structures on .
By Mostow-Prasad rigidity, a hyperbolic structure with parabolic meridians is unique if it exists, so its geometric invariants only depend on . One can therefore use the volume and Kojima’s canonical decomposition [24, 25] to distinguish hyperbolic graphs. For the pairs in our list we have constructed and analyzed the hyperbolic structure using the computer program Orb, written by the first named author [19].
Since knots and links have already been widely studied in many contexts, this paper focuses mostly on graphs containing vertices.
Number of hyperbolic graphs
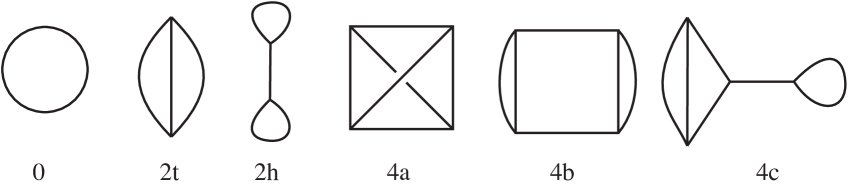
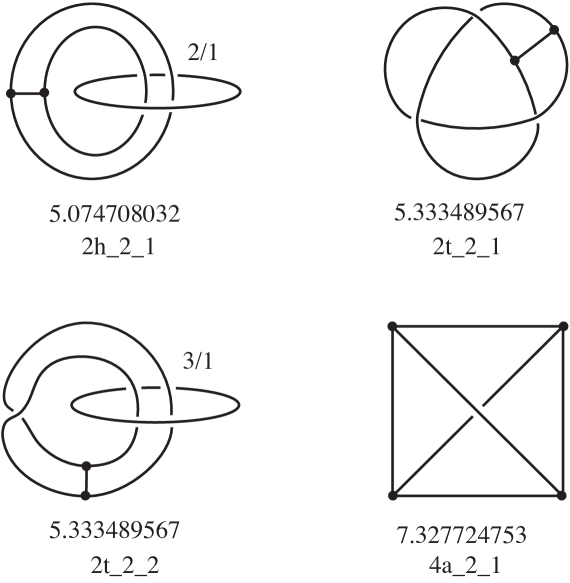
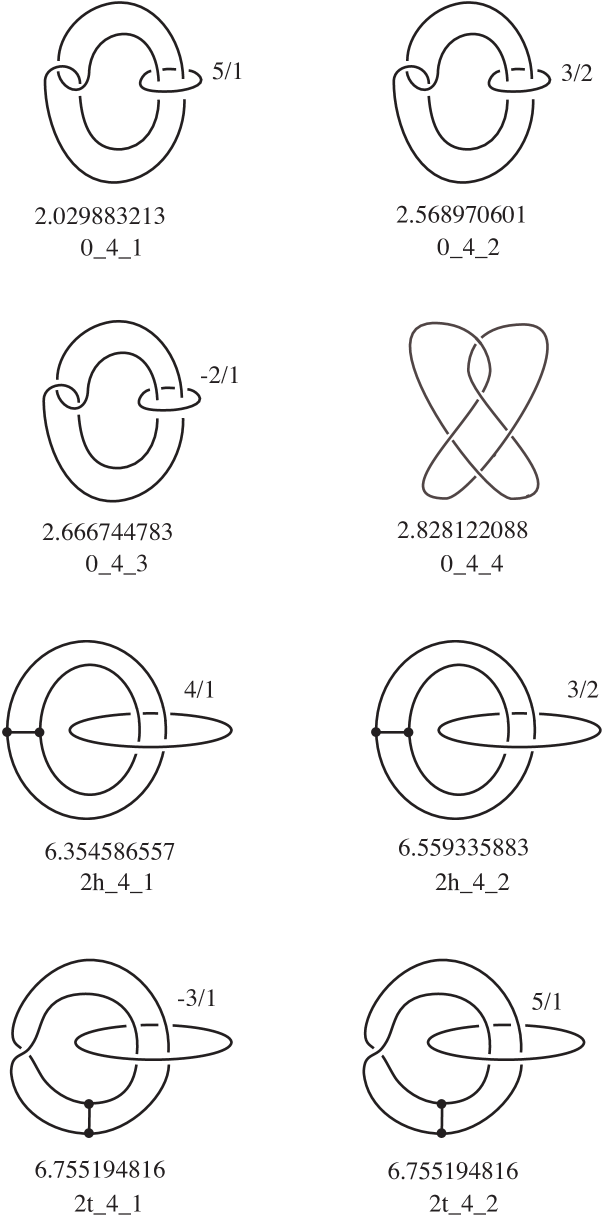
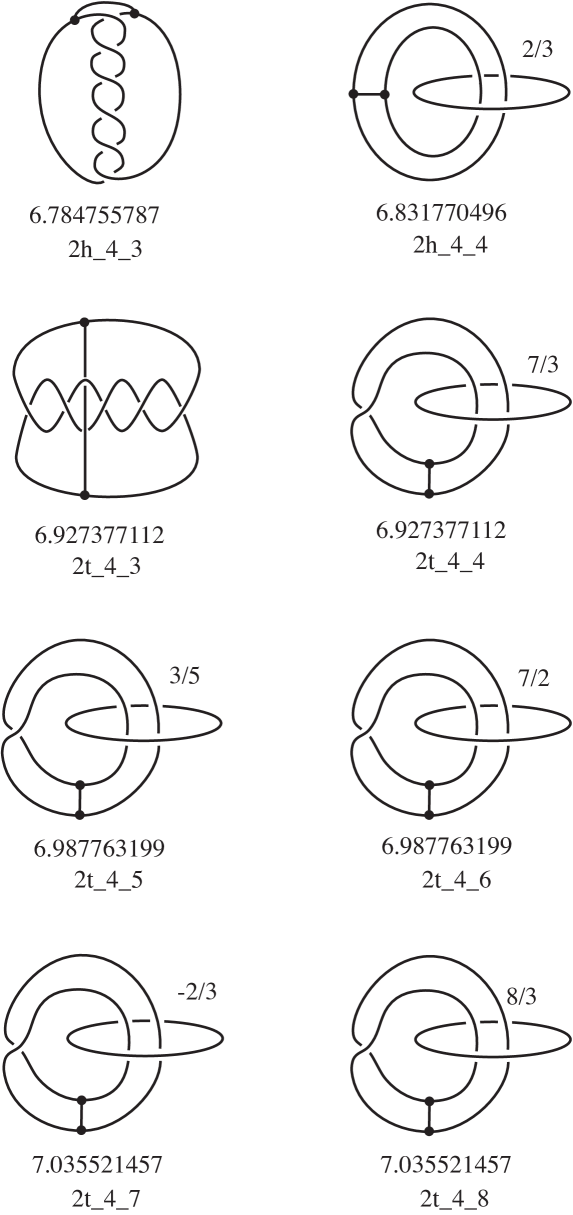
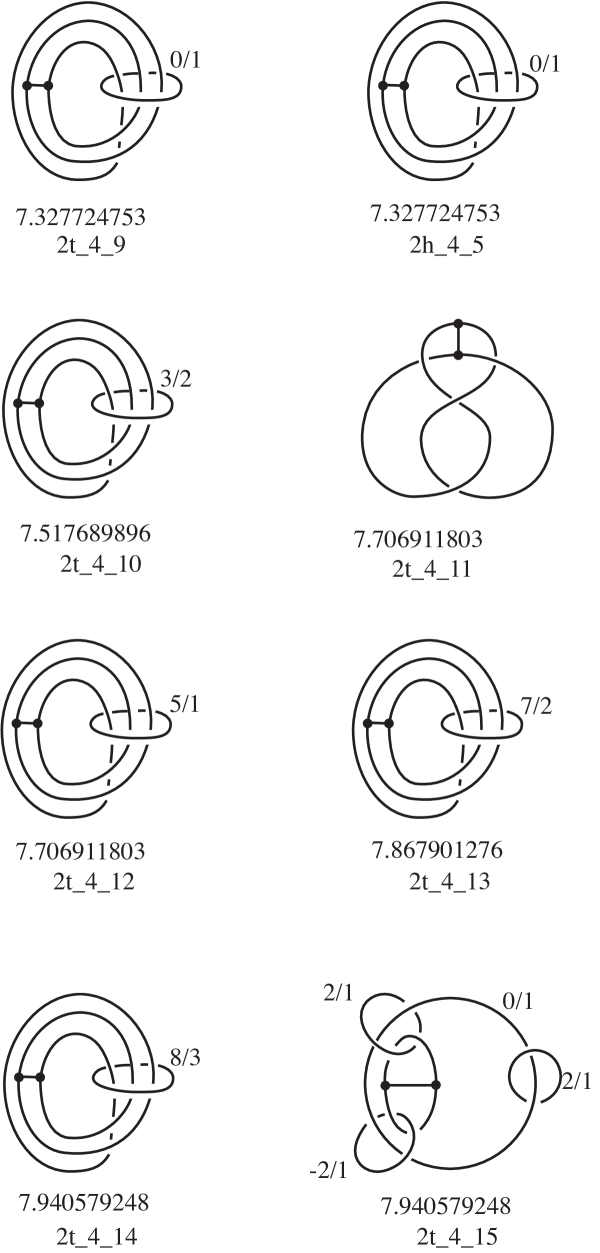
Table 1 gives a summary of our results. Up to complexity our census of hyperbolic graphs is complete and contains elements, consisting of 5 knots, 24 -graphs, 13 handcuffs, and 3 distinct connected graphs with four vertices. The graph types occurring are shown in Figure 2. In complexity 5 we decided to rule out knot components, and we found 78 more hyperbolic graphs. Out of our 123 graphs, 36 lie in .
| type | |||||
|---|---|---|---|---|---|
| knot (in ) | 0 (0) | 0 (0) | 1 (1) | 4 (1) | – (–) |
| (in ) | 0 (0) | 2 (1) | 4 (1) | 18 (4) | 49 (10) |
| (in ) | 1 (1) | 1 (0) | 3 (2) | 8 (2) | 27 (8) |
| (in ) | 0 (0) | 1 (1) | 0 (0) | 0 (0) | 2 (2) |
| (in ) | 0 (0) | 0 (0) | 0 (0) | 1 (1) | 0 (0) |
| (in ) | 0 (0) | 0 (0) | 0 (0) | 1 (1) | 0 (0) |
Complexity and volume
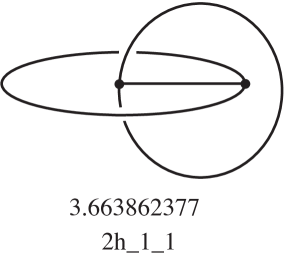
As shown in Table 1, there is a single hyperbolic graph of smallest complexity . It is a handcuff graph in , described in Figure 4 and Example 2.1. It is also the hyperbolic graph with vertices of least volume 3.663862377… This fact confirms the following relationships between complexity and hyperbolic geometry, which have already been verified for closed manifolds [32, 15], cusped manifolds [2, 3, 14, 15], and manifolds with arbitrary (geodesic) boundary [13, 26, 36, 11]:
-
(1)
Objects having complexity zero are not hyperbolic.
-
(2)
Among hyperbolic ones, the objects having lowest volume have the lowest complexity.
Note that complexity and volume may share the same first segments of hyperbolic objects (as they do) but are qualitatively different globally, because in general there are finitely many hyperbolic objects of bounded complexity, while infinitely many ones may have bounded volume thanks to Dehn surgery.
Compact totally geodesic boundary
It may happen that has a hyperbolic metric which completes to a manifold with compact totally geodesic boundary. In this case we say that is hyperbolic with geodesic boundary, which implies that is also hyperbolic (with parabolic meridians), but as mentioned above the converse is often false. By analyzing the graphs in Table 1, we have established the following:
Proposition 1.1.
Non-hyperbolic graphs
The (0,1,2)-irreducible graphs of complexity 0 were detected by theoretical means, see Section 3. There are 3 knots (cores of Heegaard tori in , and ) and the trivial -graph in , and they are all non-hyperbolic. In complexity we have classified all (0,1,2)-irreducible non-hyperbolic graphs, finding only 16 knots and two links. The same phenomenon happens for , where we have shown that only knots and links are (0,1,2)-irreducible and non-hyperbolic. However we refrained from classifying them completely, confining ourselves to those in with . Since our primary interest was in hyperbolic graphs, we decided to rule out knot components in complexity , but quite interestingly we have found some non-hyperbolic examples in this case. Our results are summarized by Table 2 and the next statement:
Proposition 1.2.
The only -irreducible non-hyperbolic graphs with such that has no knot component are the trivial -graph in , which has complexity , and five pairs in complexity , where is a -graph and contains an embedded Klein bottle.
| type | ||||||
|---|---|---|---|---|---|---|
| knot (in ) | 3 (1) | 4 (1) | 12 (1) | – (4) | – (–) | – (–) |
| 2-link (in ) | 0 (0) | 1 (1) | 1 (0) | – (1) | – (–) | – (–) |
| 2t (in ) | 1 (1) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 5 (0) |
Some open problems
We conclude this introduction by suggesting a few problems for further investigation.
-
(1)
Enumerate the first few hyperbolic graphs with parabolic meridians in order of increasing hyperbolic volume.
-
(2)
Enumerate the first few hyperbolic -manifolds of finite volume with (compact or non-compact) geodesic boundary in order of increasing hyperbolic volume.
-
(3)
Enumerate the first few closed hyperbolic 3-orbifolds in order of increasing complexity as defined in [41].
-
(4)
Enumerate the first few closed hyperbolic 3-orbifolds in order of increasing hyperbolic volume.
-
(5)
Determine the exact complexity of infinite families of knotted graphs, for example the torus knots in lens spaces (see Conjecture 6.4 below).
Note that Kojima and Miyamoto [26, 36] have already identified the lowest volume hyperbolic -manifolds with compact and non-compact geodesic boundary. Perhaps the “Mom technology” introduced by Gabai, Meyerhoff and Milley [14, 15] may offer an approach to (1) and (2). Recent work of Martin with Gehring and Marshall [16, 29] has identified the lowest volume orientable hyperbolic 3-orbifold.
2. Hyperbolic geometry
In this section we review the main geometric notions and results we will need in the rest of the paper.
2.1. Hyperbolic structures with parabolic meridians
To help classify knotted graphs, we will study hyperbolic structures analogous to the compete hyperbolic structure on the complement of a knot or link. Given a graph in a closed orientable -manifold , let be the manifold obtained from by removing an open regular neighbourhood of the vertex set of . Thus is a non-compact -manifold with boundary consisting of 3-punctured spheres, one corresponding to each vertex of . Then we say that has a hyperbolic structure with parabolic meridians if admits a complete hyperbolic metric of finite volume with geodesic boundary (with toric and annular cusps). Equivalently, the double of admits a complete hyperbolic metric of finite volume (with toric cusps). Such a hyperbolic structure on is unique by a standard argument using Mostow-Prasad rigidity [46] and Tollefson’s classification [49] of involutions with 2-dimensional fixed point set (see [47] and also [12]).
Example 2.1.
The simplest hyperbolic handcuff graph can be obtained from one tetrahedron with the two front faces folded together and the two back faces folded together giving a triangulation of with the graph contained in the 1-skeleton as shown in Figure 4.

If we truncate the vertices of the tetrahedron until all edge lengths are zero, the result can be realized geometrically by a regular ideal octahedron in hyperbolic space, as shown in Figure 5. We can then glue the 4 unshaded faces together in pairs so that the other 4 shaded faces form two totally geodesic 3-punctured spheres.
This gives a hyperbolic structure with parabolic meridians for with hyperbolic volume 3.663862377… The work of Miyamoto and Kojima [26, 36] shows that this is the smallest volume for trivalent graphs. Their work also implies that a trivalent graph having this volume is obtained by identifying the unshaded faces of an ideal octahedron as above, and hence has complexity . Therefore the handcuff graph in Figure 4 is the unique graph of minimal volume.
We next describe topological conditions for the existence of a hyperbolic structure with parabolic meridians. Let denote the graph exterior, i.e., the compact manifold obtained from by removing an open regular neighbourhood of the graph . Then is a disjoint union of pairs of pants (corresponding to the vertices of ) and a collection of annuli and tori (corresponding to the edges and knots in ). Thurston’s hyperbolization theorem for pared -manifolds [37, 23] implies the following:
Theorem 2.2.
admits a hyperbolic structure with parabolic meridians if and only if
-
•
is irreducible and homotopically atoroidal,
-
•
consists of incompressible annuli and tori,
-
•
there is no essential annulus , and
-
•
is not a product where is a pair of pants.
This hyperbolic structure is unique up to isometry.
Remark 2.3.
To obtain a hyperbolic structure with geodesic boundary on a general pared manifold , we would need to add the requirements that incompressible and is acylindrical (i.e., every annulus is homotopic into ). But these conditions follow here since consists of -punctured spheres (see [1, pp. 243-244]).
The conditions for hyperbolicity simplify considerably when is -irreducible, as defined in the introduction. To elucidate the notion, we say that is:
-
•
0-irreducible if every 2-sphere in disjoint from bounds a 3-ball in disjoint from ;
-
•
1-irreducible if there exists no 2-sphere in meeting transversely in a single point;
-
•
2-irreducible if every 2-sphere in meeting transversely in two points bounds a ball in that intersects in a single unknotted arc.
Then a graph is -irreducible if it is -irreducible for .
Theorem 2.4.
admits a hyperbolic structure with parabolic meridians if and only if
-
•
is -irreducible,
-
•
is homotopically atoroidal and is not a solid torus or the product of a torus with an interval, and
-
•
is not the trivial -graph in .
Proof.
It is easy to check that the conditions listed are necessary for hyperbolicity. To show that they are sufficient, first note that -irreducibility of implies that is irreducible, and -irreducibility implies that is incompressible or is a solid torus, but the latter possibility is excluded. Moreover is not a product where is a pair of pants, because is not the trivial -graph in . According to the previous theorem we are only left to show that there cannot exist an essential annulus . Suppose the contrary and note that each of the two components of is incident to either an annular or a toric component of . We show that the existence of such an annulus is impossible by considering the three possibilities:
-
(1)
If is only incident to annuli of , we readily see that -irreduciblity is violated.
-
(2)
If is incident to an annular component of and a torus component of , then the boundary of a regular neighbourhood of is another annulus incident to only. Again we see that -irreducibility is violated, since the resulting sphere does not bound a ball containing a single unknotted arc.
-
(3)
If is incident to toric components only, proceeding as in the previous case we find one or two tori, depending on whether the toric components are distinct or not. Homotopic atoroidality implies that these tori must be compressible or boundary parallel in . Using irreducibility of and incompressibility of , we find that is Seifert fibred with the core circle of as a fibre and base space either a pair of pants, an annulus with at most one singular point, or a disc with at most two singular points. By homotopic atoroidality, we deduce that is the product of a torus and an interval or a solid torus, contrary to our assumptions.
∎
Corollary 2.5.
If is a trivalent graph containing at least one vertex, then is hyperbolic with parabolic meridians if and only if is -irreducible, geometrically atoroidal and not the trivial -graph in .
2.2. Hyperbolic structures with geodesic boundary
Let be a graph, and let denote the graph exterior as above. Let us define as the manifold obtained by mirroring in its non-toric boundary components, so is either closed or bounded by tori. Then minus its toric boundary components has a hyperbolic structure with totally geodesic boundary if and only if the interior of has a complete hyperbolic structure. By Thurston’s hyperbolization theorem [37, 23] and Mostow-Prasad rigidity (see [47, p. 14]) we then have:
Theorem 2.6.
minus its toric boundary components admits a hyperbolic structure with totally geodesic boundary if and only if is irreducible, boundary incompressible, homotopically atoroidal, and acylindrical. This hyperbolic structure is unique up to isometry.
2.3. Hyperbolic orbifolds
One of the initial motivations of our work was the study of hyperbolic -orbifolds, but the analysis of graphs turned out to be interesting enough by itself, so we decided to leave orbifolds for the future. However we mention them briefly here.
Given a trivalent graph in a closed -manifold , we obtain an orbifold associated to by attaching an integer label to each edge or circle of . Note that we do not impose any restrictions on the labels of the edges incident to a vertex , so from a topological viewpoint gives rise either to an interior point of (if ) or to a boundary component of — a 2-orbifold of type .
We will say that is hyperbolic if admits an incomplete hyperbolic metric whose completion has a cone angle along each edge or circle in . Depending on whether is positive, zero or negative, a vertex with incoming labels gives rise to an interior point of to which the singular metric extends, to a cusp of , or to a totally geodesic boundary component of .
The main connections between orbifold hyperbolic structures and those we deal with in this paper are as follows:
-
•
If has a hyperbolic orbifold structure for some choice of labels , then admits a hyperbolic structure with parabolic meridians.
-
•
If admits a hyperbolic structure with parabolic meridians then the corresponding orbifolds are hyperbolic provided all labels are sufficiently large; moreover the structure with parabolic meridians can be regarded as the limit of the orbifold hyperbolic structures as all labels tend to infinity.
2.4. Algorithmic search for hyperbolic structures
As already mentioned, the hyperbolic structures and related invariants on the 123 pairs of our census have been obtained using the computer program Orb [19]. More details on this program will be provided below, but we outline here the underlying theoretical idea (due to Thurston [46]) of the algorithmic construction of a hyperbolic structure with geodesic boundary on a pared manifold , where is compact but not closed and is a collection of tori and annuli on .
The starting point is a (suitably defined) ideal triangulation of , namely a realization of as a gluing of generalized ideal tetrahedra. Each of these is a tetrahedron with its vertices removed and, depending on its position with respect to and , perhaps entire edges and/or open regular neighbourhoods of vertices also removed. The next step is to choose a realization of each of these tetrahedra as a geodesic generalized ideal tetrahedron in hyperbolic -space. These realizations are parameterized by certain moduli, and the condition that the hyperbolic structures on the individual tetrahedra match up to give a hyperbolic structure on translates into equations in the moduli. The algorithm then consists of changing the initial moduli using Newton’s method until the (unique) solution of the equations is found.
When is closed one can search for its hyperbolic structure using a similar method, starting from a decomposition of into compact tetrahedra [4].
2.5. Canonical cell decompositions
Whenever a hyperbolic manifold is not closed, it admits a canonical decomposition into geodesic hyperbolic polyhedra, which allows one to very efficiently compute its symmetry group and compare it for equality with another such manifold. The decomposition was defined by Epstein and Penner [9] when but has cusps, and by Kojima [24, 25] when . We will now briefly outline the latter construction.
Begin with the geodesic boundary components of and very small horospherical cross sections of any torus cusps of , and expand these surfaces at the same rate until they bump to give a 2-complex (the cut locus of the initial boundary surfaces). Then dual to this complex is the Kojima canonical decomposition of into generalized ideal hyperbolic polyhedra. This is independent of the choice of horosphere cross sections provided they are chosen sufficiently small, and gives a complete topological invariant of the manifold.
Thus two finite volume hyperbolic -manifolds with geodesic boundary are isometric (or, equivalently, homeomorphic) if and only if their Kojima canonical decompositions are combinatorially the same; and the symmetry group of isometries of such a manifold is the group of combinatorial automorphisms of the canonical decomposition. Similarly, two graphs admitting hyperbolic structures with parabolic meridians are equivalent if and only if there is a combinatorial isomorphism between their canonical decompositions taking meridians to meridians; and the group of symmetries of such a graph is the group of combinatorial automorphisms of the canonical decomposition taking meridians to meridians.
2.6. Arithmetic invariants
Let us first note that a hyperbolic structure on an orientable -manifold without boundary corresponds to a realization of the manifold as the quotient of hyperbolic space under the action of a discrete group of orientation-preserving isometries of . If the manifold has boundary, should be replaced by a -invariant intersection of closed half-spaces in . Moreover for any given hyperbolic -manifold, the group is well-defined up to conjugation within the full group of orientation-preserving isometries of , which is isomorphic to .
If is a discrete subgroup of , then the invariant trace field is the field generated by the traces of the elements of lifted to . This is a commensurability invariant of (unchanged if is replaced by a finite index subgroup). Further, if has finite volume then it follows from Mostow-Prasad rigidity that is a number field, i.e., a finite degree extension of the rational numbers . (See [28] for an excellent discussion and proofs.)
If a trivalent graph admits a hyperbolic structure with parabolic meridians, then is the convex hull of where is a discrete subgroup of . Thus is an invariant of . Now the double (defined at the start of Subsection 2.1) has the form , where is a Kleinian group containing . Since is hyperbolic with finite volume, is an algebraic number field. Hence the subfield is also an algebraic number field. We compute this by combining Orb with a modified version of Oliver Goodman’s program Snap ([17]).
Snap begins with generators and relations for , and a numerical approximation to provided by Orb. It first refines this using Newton’s method to obtain a high precision numerical approximation to , and then tries to find exact descriptions of matrix entries and their traces as algebraic numbers using the LLL-algorithm. Finally Snap verifies that we have an exact representation of by checking that the relations for are satisfied using exact calculations in a number field, and computes the invariant trace field and associated algebraic invariants. (See [8] for a detailed description of Snap.)
3. Complexity theory
A theory of complexity for 3-orbifolds, mimicking Matveev’s theory for manifolds [32], was developed in [41]. Removing all references to edge orders and their contributions to the complexity, one deduces a theory of complexity for 3-valent graphs embedded in closed orientable -manifolds. In this paragraph we will summarize the main features of this theory. The main ideas of this theory are as follows:
-
•
Triangulations are the best way to manipulate 3-dimensional topological objects by computer.
-
•
Therefore, the minimal number of tetrahedra required to triangulate an object gives a very natural measure of the complexity of the object.
-
•
However, there exists another definition of complexity, based on the notion of simple spine. A triangulation, via a certain “duality,” gives rise to a simple spine, therefore complexity defined via spines is not greater than complexity defined via triangulations.
-
•
Simple spines are more flexible than triangulations. In particular, there are more general non-minimality criteria for simple spines than for triangulations. More specifically, there are instances where a triangulation may appear to be minimal (as a triangulation) whereas the dual spine is obviously not minimal (as a simple spine).
-
•
A theorem ensures that for a hyperbolic object a minimal simple spine is always dual to a triangulation.
-
•
As a conclusion, if one wants to carry out a census of hyperbolic objects in order of increasing complexity, one deals by computer with triangulations, but one discards triangulations to which, via duality, the stronger non-minimality criteria for spines apply. This is because, thanks to the theorem, such a triangulation encodes either a non-hyperbolic object or a hyperbolic object that has been met earlier in the census.
We will now turn to a more detailed discussion.
3.1. Simple spines and complexity
To proceed with the key notions and results we recall a definition given in the Introduction. We call simple111In [32] such a polyhedron was originally called almost simple, while the term simple was employed for almost special polyhedra, see Subsection 3.2. a compact polyhedron (in the PL sense [44]) such that the link of each point is a subset of the 1-skeleton of the tetrahedron. We denote by the set of points of having the whole 1-skeleton of the tetrahedron as a link, and we note that is a finite set.
Definition 3.1.
A simple spine of a trivalent graph is a simple polyhedron embedded in in such a way that:
-
(1)
intersects transversely. (In particular, consists of a finite number of points that are not vertices of ).
-
(2)
Removing an open regular neighbourhood of from gives a finite collection of balls, each of which intersects in either
-
•
the empty set, or
-
•
a single unknotted arc of , or
-
•
a vertex of with unknotted strands leaving the vertex and reaching the boundary of the ball. (See Figure 1.)
-
•
It is very easy to see (and it will follow from the duality with triangulations in Proposition 3.2) that each admits simple spines. Therefore the complexity of , that we define as
is a finite number.
3.2. Special spines and duality
To illustrate the relation between spines and triangulations, we need to introduce two subsequent refinements of the notion of simple polyhedron. We will say that is almost-special if it is a compact polyhedron and each of its points has one of the following sets as a link:
-
(1)
The -skeleton of the tetrahedron with two open opposite edges removed (a circle);
-
(2)
The -skeleton of the tetrahedron with one open edge removed (a circle with a diameter);
-
(3)
The -skeleton of the tetrahedron (a circle with three radii).
The corresponding local structure of an almost-special polyhedron is shown in Figure 6.

Besides the set of vertices already introduced above for simple polyhedra, we can define for an almost-special the singular set, given by the non-surface points and denoted by . We remark that is a 4-valent graph with vertex set . Note also that if is an almost-special spine of , by the transversality assumption, intersects away from .
An almost-special polyhedron is called special if is a union of open discs and is a union of open segments. A special spine of a graph is a simple spine which, in addition, is a special polyhedron.
The following result, which refers to the case of manifolds without graphs embedded in them, has been known for a long time. We point out that we use the term triangulation for a (closed, connected, orientable) -manifold in a generalized (not strictly PL [44]) sense. Namely, we mean a realization of as a simplicial pairing between the faces of a finite union of tetrahedra, i.e., we allow multiple and self-adjacencies between tetrahedra.
Proposition 3.2.
Given a -manifold , for each triangulation of define as the -skeleton of the cell decomposition dual to , see Figure 7.

Then defines a bijection between the set of (isotopy classes of) triangulations of and the set of (isotopy classes of) special spines of .
3.3. (Efficient) triangulations of graphs
We now turn to graphs , and we define a triangulation of to be a (generalized) triangulation of which contains as a subset of its 1-skeleton. We will further say that is efficient if it has precisely one vertex at each vertex of , one on each knot component of , and no other vertices.
The following easy result shows that under suitable conditions Proposition 3.2 has a refinement to graphs:
Proposition 3.3.
For a simple spine of a graph the following conditions are equivalent:
-
•
is dual to a triangulation of ;
-
•
is special, intersects transversely away from , and each component of intersects at most once.
3.4. Minimal spines
A simple spine of a graph is called minimal if it has vertices and no subset of is also a spine of . The success of the strategy based on complexity theory (as outlined at the beginning of this section) for the enumeration of hyperbolic graphs depends on the next three results. They require the concept of -irreducibility defined in the introduction. The first one is part of Theorem 2.4, the next two easily follow from [41, Theorem 2.6].
Proposition 3.4.
If is hyperbolic with parabolic meridians then is -irreducible.
Proposition 3.5.
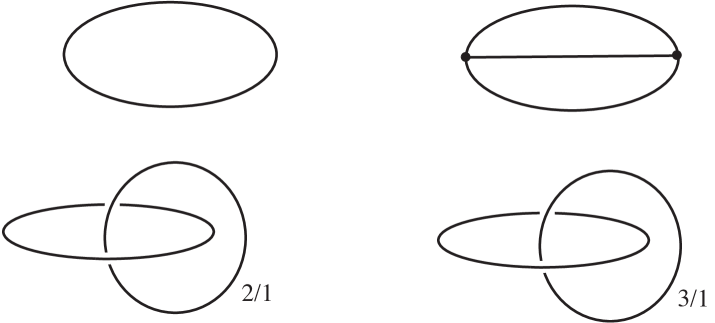
The -irreducible graphs with are those described as follows and illustrated in Figure 8:
-
•
is either , or , or , and is either empty or the core of a Heegaard solid torus of ;
-
•
is and is the trivially embedded -graph.
Theorem 3.6.
Let be a graph with . Then the following are equivalent:
-
•
is -irreducible;
-
•
admits a special minimal spine;
-
•
Every minimal spine of is special and dual to it there is an efficient triangulation of .
3.5. Non-minimality criteria
The following result was used for the enumeration of candidate triangulations of -irreducible graphs, as explained in more detail in the next section:
Proposition 3.7.
Let be a triangulation of a graph , and let be the special spine dual to . Suppose that in there is an edge not lying in and incident to distinct tetrahedra, with . Then is not minimal.
Proof.
We will show that we can perform a move on leading to a simple spine of with fewer vertices than .
For we do not even need to use spines, the move exists already at the level of triangulations: it is the famous Matveev-Piergallini move [33, 42] illustrated in Figure 9. We only need to note that after the move we still have a triangulation of because the edge that disappears with the move does not lie in .
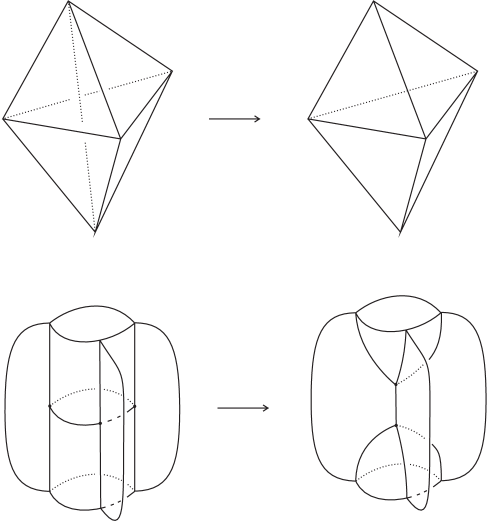
For we do need to use spines. The moves we apply (a and a move) are illustrated in Figure 10. Both moves involve the removal of the component of dual to the edge of the statement, and the result of the move is still a spine of because does not meet . We note that the move leads to an almost-special polyhedron, but it can create a spine with an annular non-singular component, in which case the spine is not dual to a triangulation. The move gives a spine which is not almost-special. ∎
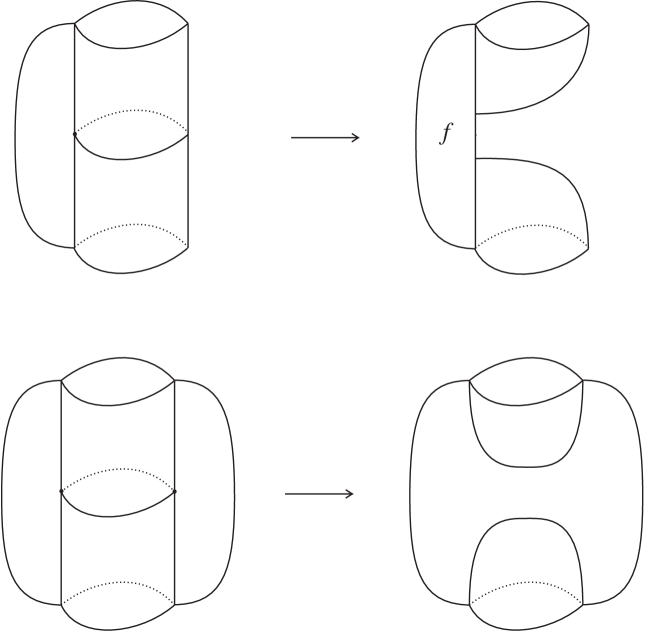
Remark 3.8.
Sometimes the non-minimality criteria of the previous proposition do not apply directly, but only after a modification of the triangulation. For instance, a triangulation with tetrahedra may be transformed into one with tetrahedra via a move: if contains an edge incident to or distinct tetrahedra, the dual spine can be transformed into a simple spine with at most vertices by applying one of the moves in Figure 10. Therefore the original triangulation is not minimal.
3.6. Complexity of the complement
Matveev’s complexity [32] is defined for every compact -manifold, with or without boundary. The complement of an open regular neighbourhood of a graph in a closed -manifold therefore has a complexity, which is related to as follows.
Proposition 3.9.
For any graph we have
If is -irreducible with and , then
Proof.
If is a minimal simple spine of then the graph intersects in a finite number of points. Removing from open regular neighbourhoods of these points gives a simple polyhedron which is a spine of with the same vertices as . Therefore .
If is -irreducible, and , then Theorem 3.6 shows that a minimal simple spine of is special and consists of some points belonging to the interior of distinct disc components of . Removing these discs we get a simple spine of with strictly fewer vertices than . ∎
Remark 3.10.
A compact -manifold which admits a complete hyperbolic metric with geodesic boundary and finite volume (after removing the tori from its boundary) has complexity at least , see [32, 2, 11]. This explains why the first hyperbolic knots have (see Tables 1 and 2). Analogously, the first graphs whose complement is hyperbolic with geodesic boundary must have . (In fact they have complexity , see Subsection 5.4.)
4. Computer programs and obstructions to hyperbolicity
In this section we describe the Haskell code we have written to enumerate triangulations, and the computer program Orb we have used to investigate hyperbolic structures. We also describe how non-hyperbolic graphs were identified (see also Section 6 below).
4.1. Enumeration of marked triangulations
Thanks to Theorem 3.6 and the other results stated in the previous section, the enumeration of -irreducible graphs of complexity can be performed by listing all efficient triangulations with tetrahedra satisfying some minimality criteria. This was done via a separate program, written in Haskell [18], which suitably adapts the strategy already used in similar censuses (e.g. [30, 35]).
A triangulation of a graph can be encoded as a triangulation of with some marked edges. A triangulation here is just a gluing of tetrahedra, which can be described via a connected -valent graph (the incidence graph of the gluing) having a label on each edge encoding how the corresponding triangular faces are identified (there are possibilities).
A first count gives triangulations to check, where is the number of -valent graphs with vertices (and edges), shown in Table 3. On each triangulation there are distinct markings of edges, where is the number of edges and is the number of vertices in the triangulation of . Since there are at least triangles in the link of each vertex, , and . There are therefore up to marked triangulations to check. This number is already too big for , so in order to simplify the problem we used some tricks.
We are only interested in orientable manifolds . We can therefore orient each tetrahedron and require the identifications of faces to be orientation-reversing. This reduces the number of possible labels on edges from to , and the number of triangulations to , where is the number of -valent graphs with “oriented” vertices: each vertex has a fixed parity of orderings of the incident edges. For a fixed -valent graph with vertices, the vertices can be oriented in different ways, but up to the symmetries of the number of distinct orientations typically turns out to be very small. This explains why is actually much less than , as shown in the table.
We selected from the resulting list of triangulations only those yielding closed manifolds. Finally, on each triangulation we a priori had distinct markings on edges to analyze. Proposition 3.7 was used to discard many of these: in a triangulation dual to a minimal spine an edge incident to at most distinct tetrahedra is necessarily marked. It remained then to check which markings give rise to efficient triangulations.
4.2. “Orb”
Hyperbolic structures were computed using the program Orb written by Damian Heard [20, 19]. This program builds on ideas of Thurston, Weeks, Casson and others to find hyperbolic structures and associated geometric invariants for a large class of 3-dimensional manifolds and orbifolds. The program begins with a triangulation of the space with the singular locus or graph contained in the 1-skeleton and tries to find shapes of generalized hyperbolic tetrahedra (with vertices inside, on, or outside the sphere at infinity) which fit together to give a hyperbolic structure.
The generalized hyperbolic tetrahedra are described by using one parameter for each edge in the triangulation. For a general tetrahedron a lift to Minkowski space is chosen, then the parameters are Minkowski inner products of the vertex positions. For compact tetrahedra, each parameter is just the hyperbolic cosine of the edge length. For each ideal vertex the lift to Minkowski space determines a horosphere centred at the vertex; for each hyperideal vertex a geodesic plane orthogonal to the incident faces is determined. Then the edge parameters are simple functions of the hyperbolic distances between these surfaces.
Given the edge parameters, all dihedral angles of the tetrahedra are determined. Moreover the parameters give a global hyperbolic structure if and only if the sum of the dihedral angles around each edge is (or the desired cone angle, in the orbifold case). This gives a system of equations that Orb solves numerically using Newton’s method, starting with suitable regular generalized tetrahedra as the initial guess.
Once a hyperbolic structure is found, Orb can compute many geometric invariants including volumes, the Kojima canonical decompositions, and symmetry groups. This uses methods based on ideas of Weeks [52], Ushijima [50] and Frigerio-Petronio [12], too complicated to be reproduced here.
After computing hyperbolic structures numerically using Orb, we checked the correctness of the results by using Jeff Weeks’ program SnapPea [51] to calculate complete hyperbolic structures on the manifolds with torus cusps obtained by doubling along all 3-punctured sphere boundary components.
Finally, we verified the results by using Oliver Goodman’s program Snap [17, 8] to find exact hyperbolic structures. This provides a proof that the hyperbolic structures are correct and allows us to compute associated arithmetic invariants (including invariant trace fields), as already mentioned in Subsection 2.6 above.
4.3. Non-hyperbolic knots and links
Many knots and links in the census turned out to be torus links in lens spaces, see Subsection 6.1 below. From , we then decided to rule out the non-hyperbolic knots and links from our census (except for those in at ); this helped a lot in simplifying the classification. Many non-hyperbolic knots and links were easily identified by the following criterion:
Remark 4.1.
The remaining knots and links were shown to be non-hyperbolic by examining their fundamental groups with the help of the following observations.
Lemma 4.2.
Let be an orientable finite volume hyperbolic -manifold, and let . Then
-
(i)
if for some integers then ,
-
(ii)
if and then .
Proof.
The results are clear if or is the identity, so we may assume that and correspond to loxodromic or parabolic isometries of .
In part (i), the elements must have the same axis or fixed point at . Since the same is true for and , so and commute.
In part (ii), and have the same fixed point set on the sphere at infinity, and takes to itself. Since is not elliptic, it must fix each point of . Thus has the same axis or fixed point at as and , so it commutes with them.∎
Lemma 4.3.
Let be an orientable finite volume hyperbolic -manifold. Then cannot have a presentation of the form
-
(i)
where are integers with , or
-
(ii)
.
Proof.
(i) If , then by part (i) of Lemma 4.2. Hence and , again by part (i) of Lemma 4.2. So the group would be abelian, which is impossible.
(ii) The group has a presentation
We can rewrite this as
Hence by part (ii) of Lemma 4.2 and . So the group would be abelian, which is again impossible. ∎
Among the knots and links up to complexity 4 for which Orb did not find a hyperbolic structure, all but one of the complements had a fundamental group with presentation of the form , or . These all correspond to non-hyperbolic links by the Lemmas above. The one remaining knot had a presentation as in part (ii) of Lemma 4.3, so is also non-hyperbolic.
4.4. Non-hyperbolic graphs
For graphs with at least one vertex, we first eliminated all triangulations whose dual spines had non-minimal complexity hence were either reducible or occurred earlier in our list. This left a handful of examples for which Orb failed to find a hyperbolic structure. These were first examined using Jeff Weeks’ program SnapPea, by constructing triangulations of the manifolds with torus cusps obtained by doubling along the 3-punctured sphere boundary components. We used SnapPea’s “splitting” function to look for incompressible Klein bottles and tori in the doubles. This suggested that incompressible Klein bottles were present in the original graph complements. We then verified this and showed that these examples were indeed non-hyperbolic by theoretical means, as explained below in Section 6.
5. Hyperbolic census details
In this section we will expand on the information given in Table 1, providing details of all the 123 hyperbolic graphs up to complexity 5. Pictures of the hyperbolic graphs up to complexity 4 will be shown in Section 7.
5.1. Name conventions
For future reference, we have chosen a name for each of the graphs we have found. The name has the form
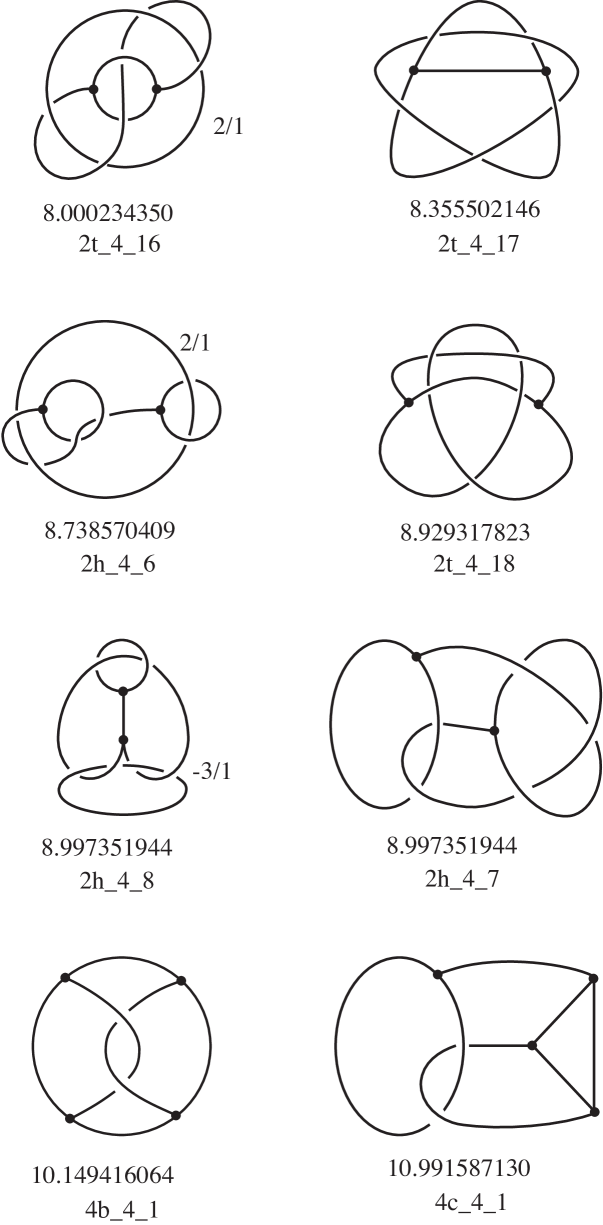
where is the number of vertices of the graph, is a string describing the abstract graph type, is the complexity, and is an index (starting from for any given ). We have found in our hyperbolic census only 6 graph types, described above in Figure 2, so a string of one letter only (or the empty string, for knots) was sufficient to identify them. For graphs with 2 vertices, the letters and were suggested by the common names “-graph” and “handcuffs”. The choice of letters was arbitrary for graphs with vertices.
5.2. Organization of tables
We will give separate tables for -graphs, handcuffs, -vertex graphs, and knots. Within each table, graphs are always arranged in increasing order of their hyperbolic volumes. For graphs having vertices, the columns of the tables respectively contain:
-
(1)
The name of the graph .
-
(2)
The volume of the hyperbolic structure with parabolic meridians on .
-
(3)
A description of the cells of the Kojima canonical decomposition for this structure. When all these cells are tetrahedra we simply indicate their number, otherwise we add an asterisk in the table and provide additional information separately.
-
(4)
The symmetry group of , with denoting the dihedral group with elements.
-
(5)
Whether is chiral (c) or amphichiral (a).
-
(6)
The name of the underlying space . This is almost always a lens space; otherwise it is a Seifert fibred space which we describe in the usual way (as in [34, p. 406]).
-
(7)-(9)
The degree, signature and discriminant of the invariant trace field. Details of minimal polynomials for the fields are available on the web at www.ms.unimelb.edu.au/˜snap/knotted_graphs.html.
-
(10)
Whether all traces of group elements are algebraic integers.
-
(11)
Whether the group is arithmetic (after doubling to obtain a finite covolume group).
| name | volume | (K) | sym | a/c | space | deg | sig | disc | int | ar |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.333489567 | 3 | c | 2 | 0, 1 | 7 | Y | Y | |||
| 5.333489567 | 3 | c | (3,1) | 2 | 0, 1 | 7 | Y | Y | ||
| 6.354586557 | 4 | c | 3 | 1, 1 | 44 | Y | N | |||
| 6.354586557 | 4 | c | (4,1) | 3 | 1, 1 | 44 | Y | N | ||
| 6.551743288 | 7 | c | 3 | 1, 1 | 107 | Y | N | |||
| 6.551743288 | 7 | c | (5,2) | 3 | 1, 1 | 107 | Y | N | ||
| 6.755194816 | 5 | c | (3,1) | 4 | 0, 2 | 2917 | Y | N | ||
| 6.755194816 | 5 | c | (5,1) | 4 | 0, 2 | 2917 | Y | N | ||
| 6.927377112 | 11 | c | 4 | 0, 2 | 1929 | Y | N | |||
| 6.927377112 | 11 | c | (7,3) | 4 | 0, 2 | 1929 | Y | N | ||
| 6.952347978 | 6 | c | (4,1) | 5 | 1, 2 | 7684 | Y | N | ||
| 6.952347978 | 6 | c | (6,1) | 5 | 1, 2 | 7684 | Y | N | ||
| 6.987763199 | 7 | c | (3,1) | 5 | 1, 2 | 77041 | Y | N | ||
| 6.987763199 | 7 | c | (7,2) | 5 | 1, 2 | 77041 | Y | N | ||
| 7.035521457 | 8 | c | 5 | 1, 2 | 5584 | Y | N | |||
| 7.035521457 | 8 | c | (8,3) | 5 | 1, 2 | 5584 | Y | N | ||
| 7.084790037 | 15 | c | 5 | 1, 2 | 49697 | Y | N | |||
| 7.084790037 | 15 | c | (9,2) | 5 | 1, 2 | 49697 | Y | N | ||
| 7.142157274 | 9 | c | (5,2) | 7 | 1, 3 | 123782683 | Y | N | ||
| 7.142157274 | 9 | c | (9,2) | 7 | 1, 3 | 123782683 | Y | N | ||
| 7.157517365 | 8 | c | (4,1) | 7 | 1, 3 | 2369276 | Y | N | ||
| 7.157517365 | 8 | c | (10,3) | 7 | 1, 3 | 2369276 | Y | N | ||
| 7.175425922 | 9 | c | (3,1) | 7 | 1, 3 | 88148831 | Y | N | ||
| 7.175425922 | 9 | c | (11,3) | 7 | 1, 3 | 88148831 | Y | N | ||
| 7.192635929 | 11 | c | (5,2) | 8 | 0, 4 | 5442461517 | Y | N | ||
| 7.192635929 | 11 | c | (11,3) | 8 | 0, 4 | 5442461517 | Y | N | ||
| 7.193764490 | 12 | c | 7 | 1, 3 | 1523968 | Y | N | |||
| 7.193764490 | 12 | c | (12,5) | 7 | 1, 3 | 1523968 | Y | N | ||
| 7.216515907 | 11 | c | (3,1) | 8 | 0, 4 | 3679703653 | Y | N | ||
| 7.216515907 | 11 | c | (13,5) | 8 | 0, 4 | 3679703653 | Y | N | ||
| 7.327724753 | 4 | a | 2 | 0, 1 | 4 | Y | Y | |||
| 7.517689896 | 6 | c | (3,1) | 3 | 1, 1 | -104 | Y | N | ||
| 7.706911803 | 5 | c | 3 | 1, 1 | 59 | Y | N | |||
| 7.706911803 | 5 | c | (5,1) | 3 | 1, 1 | 59 | Y | N | ||
| 7.867901276 | 7 | c | (7,2) | 5 | 3, 1 | -112919 | Y | N | ||
| 7.940579248 | 9 | c | (8,3) | 3 | 1, 1 | -76 | Y | N | ||
| 7.940579248 | 9 | c | 3 | 1, 1 | -76 | Y | N | |||
| 8.000234350 | 4 | c | 2 | 0, 1 | 7 | Y | Y | |||
| 8.087973789 | 5 | c | 4 | 2, 1 | 6724 | Y | N | |||
| 8.195703083 | 7 | c | (5,2) | 5 | 1, 2 | 65516 | Y | N | ||
| 8.233665208 | 6 | c | (6,1) | 6 | 2, 2 | 1738384 | Y | N | ||
| 8.338374585 | 8 | c | (9,2) | 6 | 2, 2 | 2463644 | Y | N | ||
| 8.355502146 | 8 | c | 4 | 0, 2 | 3173 | Y | N | |||
| 8.355502146 | 6 | c | 4 | 0, 2 | 3173 | Y | N | |||
| 8.372209945 | 8 | c | (10,3) | 7 | 3, 2 | 87357184 | Y | N | ||
| 8.388819035 | 10 | c | (4,1) | 5 | 1, 2 | 26084 | Y | N |
| name | volume | (K) | sym | a/c | space | deg | sig | disc | int | ar |
|---|---|---|---|---|---|---|---|---|---|---|
| 8.403864479 | 10 | c | (11,3) | 7 | 3, 2 | 186794473 | Y | N | ||
| 8.487060022 | 8 | c | (9,2) | 8 | 4, 2 | 17112324248 | Y | N | ||
| 8.527312899 | 10 | c | (11,3) | 9 | 5, 2 | 5328053407637 | Y | N | ||
| 8.546347793 | 11 | c | (12,5) | 8 | 4, 2 | 2498992192 | Y | N | ||
| 8.565387019 | 12 | c | (13,5) | 9 | 5, 2 | 1944699708173 | Y | N | ||
| 8.612415201 | 1* | c | (4,1) | 4 | 2, 1 | 400 | Y | N | ||
| 8.778658803 | 9 | c | 5 | 1, 2 | 15856 | Y | N | |||
| 8.778658803 | 9 | c | 5 | 1, 2 | 15856 | Y | N | |||
| 8.793345604 | 7 | c | 4 | 0, 2 | 257 | Y | N | |||
| 8.806310033 | 8 | c | (8,3) | 4 | 2, 1 | 1968 | Y | N | ||
| 8.908747390 | 11 | c | (3,1) | 5 | 1, 2 | 31048 | Y | N | ||
| 8.929317823 | 6 | c | 3 | 1, 1 | 116 | Y | N | |||
| 8.967360849 | 7 | c | 4 | 0, 2 | 697 | Y | N | |||
| 8.967360849 | 7 | c | (7,2) | 4 | 0, 2 | 697 | Y | N | ||
| 9.045557688 | 5 | c | (3,1) | 5 | 1, 2 | 73532 | Y | N | ||
| 9.272866192 | 7 | c | 6 | 0, 3 | 4319731 | Y | N | |||
| 9.353881135 | 7 | c | (3,1) | 6 | 0, 3 | 2944468 | Y | N | ||
| 9.437583617 | 9 | c | 4 | 0, 2 | 2312 | Y | N | |||
| 9.491889687 | 5 | c | 4 | 0, 2 | 257 | Y | N | |||
| 9.491889687 | 5 | c | (3,1) | 4 | 0, 2 | 257 | Y | N | ||
| 9.503403931 | 9 | c | 4 | 0, 2 | 788 | N | N | |||
| 10.149416064 | 1* | c | 2 | 0, 1 | 3 | Y | Y | |||
| 10.396867321 | 6* | c | 3 | 1, 1 | 139 | Y | N | |||
| 10.666979134 | 6 | a | 2 | 0, 1 | -7 | Y | Y | |||
| 10.666979134 | 6 | c | 2 | 0, 1 | 7 | N | N | |||
| 10.666979134 | 5 | c | (3,1) | 2 | 0, 1 | -7 | Y | Y | ||
| 10.666979134 | 5 | c | (3,1) | 2 | 0, 1 | -7 | Y | Y |
| name | volume | (K) | sym | a/c | space | deg | sig | disc | int | ar |
|---|---|---|---|---|---|---|---|---|---|---|
| _ 1_ 1 | 3.663862377 | 1 | a | 2 | 0, 1 | -4 | Y | Y | ||
| _ 2_ 1 | 5.074708032 | 2 | a | 2 | 0, 1 | 3 | Y | Y | ||
| _ 3_ 1 | 5.875918083 | 3 | c | 3,1) | 4 | 0, 2 | 656 | Y | N | |
| _ 3_ 2 | 6.138138789 | 5 | c | 4 | 0, 2 | 320 | Y | N | ||
| _ 4_ 1 | 6.354586557 | 4 | c | 4,1) | 3 | 1, 1 | -44 | Y | N | |
| _ 4_ 2 | 6.559335883 | 5 | c | 3,1) | 6 | 0, 3 | 382208 | Y | N | |
| _ 5_ 1 | 6.647203159 | 5 | c | 5,1) | 6 | 0, 3 | 242752 | Y | N | |
| _ 4_ 3 | 6.784755787 | 9 | c | 6 | 0, 3 | 108544 | Y | N | ||
| _ 4_ 4 | 6.831770496 | 6 | c | 4 | 0, 2 | 892 | Y | N | ||
| _ 5_ 2 | 6.854770090 | 7 | c | 5,2) | 8 | 0, 4 | 502248448 | Y | N | |
| _ 5_ 3 | 6.952347978 | 6 | c | 4,1) | 5 | 1, 2 | 7684 | Y | N | |
| _ 5_ 4 | 6.969842840 | 5 | a | 5,2) | 6 | 0, 3 | 179776 | Y | N | |
| _ 5_ 5 | 7.008125009 | 9 | c | 5,2) | 10 | 0, 5 | 1192884600832 | Y | N | |
| _ 5_ 6 | 7.020614792 | 13 | c | 8 | 0, 4 | 89276416 | Y | N | ||
| _ 5_ 7 | 7.056979121 | 7 | c | 3,1) | 10 | 0, 5 | 586177642496 | Y | N | |
| _ 5_ 8 | 7.136868364 | 10 | c | 6 | 0, 3 | 682736 | Y | N | ||
| _ 5_ 9 | 7.146107337 | 9 | c | 3,1) | 12 | 0, 6 | 8746362208256 | Y | N | |
| _ 3_ 3 | 7.327724753 | 4 | a | 2 | 0, 1 | 4 | Y | Y | ||
| _ 4_ 5 | 7.327724753 | 4 | a | 2 | 0, 1 | 4 | Y | Y | ||
| _ 5_ 10 | 7.731874058 | 5 | c | 4,1) | 6 | 0, 3 | 96512 | Y | N | |
| _ 5_ 11 | 8.140719221 | 6 | c | 6 | 0, 3 | 382208 | Y | N | ||
| _ 5_ 12 | 8.140719221 | 5 | c | 6 | 0, 3 | 382208 | Y | N | ||
| _ 4_ 6 | 8.738570409 | 4 | a | 4 | 0, 2 | 144 | Y | N | ||
| _ 5_ 13 | 8.997351944 | 3* | c | 4 | 0, 2 | 784 | Y | N | ||
| _ 4_ 7 | 8.997351944 | 4 | c | 4 | 0, 2 | 784 | Y | N | ||
| _ 4_ 8 | 8.997351944 | 4 | c | 3,1) | 4 | 0, 2 | 784 | Y | N | |
| _ 5_ 14 | 9.539780459 | 5 | c | 3,1) | 4 | 0, 2 | 656 | Y | N | |
| _ 5_ 15 | 9.539780459 | 5 | c | 4 | 0, 2 | 656 | Y | N | ||
| _ 5_ 16 | 9.592627932 | 6 | c | 4 | 0, 2 | 1436 | Y | N | ||
| _ 5_ 17 | 9.802001166 | 5 | c | 4 | 0, 2 | 320 | N | N | ||
| _ 5_ 18 | 9.876829057 | 5 | c | 6 | 0, 3 | 239168 | Y | N | ||
| _ 5_ 19 | 10.018448934 | 5 | c | 6 | 0, 3 | 30976 | N | N | ||
| _ 5_ 20 | 10.018448934 | 5 | c | 4,1) | 6 | 0, 3 | 30976 | Y | N | |
| _ 5_ 21 | 10.018448934 | 5 | c | 4,1) | 6 | 0, 3 | 30976 | Y | N | |
| _ 5_ 22 | 10.069070958 | 7 | c | 4 | 0, 2 | 1384 | Y | N | ||
| _ 5_ 23 | 10.149416064 | 4* | c | 2 | 0, 1 | 3 | Y | Y | ||
| _ 5_ 24 | 10.215605665 | 5 | c | 6 | 0, 3 | 732736 | N | N | ||
| _ 5_ 25 | 10.215605665 | 5 | c | 5,2) | 6 | 0, 3 | 732736 | Y | N | |
| _ 5_ 26 | 10.215605665 | 5 | c | 5,2) | 6 | 0, 3 | 732736 | Y | N | |
| _ 5_ 27 | 10.408197599 | 5 | c | 4 | 0, 2 | 441 | N | N |
| name | volume | (K) | sym | a/c | space | deg | sig | disc | int | ar |
| _ 2_ 1 | 7.327724753 | 2 | a | 2 | 0, 1 | 4 | Y | Y | ||
| _ 5_ 1 | 11.751836165 | 6 | c | 4 | 0, 2 | 656 | Y | N | ||
| _ 5_ 2 | 12.661214320 | 5 | c | 4 | 0, 2 | 784 | Y | N | ||
| _ 4_ 1 | 10.149416064 | 4 | a | 2 | 0, 1 | -3 | Y | Y | ||
| _ 4_ 1 | 10.991587130 | 4 | a | 2 | 0, 1 | -4 | Y | Y |
5.3. Table of knots
As already mentioned, we have classified hyperbolic knots only up to complexity 4, finding 5 of them. The table containing their description differs from the previous ones only in that the third column gives the number of cells in the Epstein-Penner [9] canonical decomposition (the Kojima decomposition is not defined). We also provide an additional table showing the name of each knot complement in the SnapPea census [2], and either the name of the knot in [43] (for the knots in ) or the surgery coefficients on one of the components of the Whitehead link ( in [43]) yielding the knot.
As shown in the introduction and in Section 6 below, there are many -irreducible knots in complexity up to , and most of them are not hyperbolic: this phenomenon can be understood using spines, see Proposition 3.9.
| name | volume | (EP) | sym | a/c | space | deg | sig | disc | int | ar |
|---|---|---|---|---|---|---|---|---|---|---|
| 0_ 3_ 1 | 2.029883213 | 2 | a | 2 | 0,1 | 3 | Y | Y | ||
| 0_ 4_ 1 | 2.029883213 | 2 | c | 2 | 0,1 | 3 | Y | Y | ||
| 0_ 4_ 2 | 2.568970601 | 4 | c | 3 | 1,1 | 59 | Y | N | ||
| 0_ 4_ 3 | 2.666744783 | 3 | c | 2 | 0,1 | 7 | Y | Y | ||
| 0_ 4_ 4 | 2.828122088 | 4 | c | 3 | 1,1 | 59 | Y | N |
5.4. Compact totally geodesic boundary
The 3 graphs referred to in Proposition 1.1 are , and in Table 5; these are shown in Figure 3. (In particular, Thurston’s knotted [46, pp. 133-137] is .) Their hyperbolic structures were constructed using Orb. They all have the lowest possible volume () for hyperbolic -manifolds with genus 2 boundary (see [26]), but they can be distinguished by their Kojima decompositions or symmetry groups. All the other graphs were shown not to have such a structure by studying spines for their complements constructed as in the proof of Proposition 3.9. In all but two cases, this produced a spine for the complement of complexity having less than vertices, hence the complement has no hyperbolic structure with geodesic boundary by Remark 3.10. For the two remaining cases, we found a spine having 2 vertices but not dual to a triangulation. It again follows that these manifolds are not hyperbolic with geodesic boundary, because a minimal simple spine of a hyperbolic manifold is always dual to a triangulation [34].
6. Irreducible non-hyperbolic graphs
This section is devoted to the description of the -irreducible but non-hyperbolic graphs we have found in our census, including the proof that indeed they have these properties.
6.1. Knots and links
As already stated in the introduction, we have shown that if a graph with is -irreducible but non-hyperbolic then has no vertices. More precisely, is either empty, or a knot, or a two-component link. Since this paper is chiefly devoted to the understanding of graphs with vertices, we will only very briefly describe our discoveries for the case without vertices. In particular, we will not refer to the case of empty (i.e., to the case of manifolds), addressing the reader to [34], and we will describe the following non-hyperbolic knots and links:
-
•
up to complexity , in general manifolds;
-
•
in complexity , in .
To proceed we will introduce some general machinery.
6.2. Torus knots in lens spaces
Consider the solid torus and the basis of given by a longitude and a meridian . These elements are characterized up to symmetries of by the property that the restriction to of the map is surjective, while is the kernel of this map.
For coprime we will denote by a simple closed curve on (unique up to isotopy) representing in . For we will also denote by the union of parallel copies of .
We will assume from now on that the lens space is obtained from by Dehn filling along . Therefore any can be viewed as a torus knot on the Heegaard torus in . An easy application of the Seifert-Van Kampen theorem implies the following:
Proposition 6.1.
For coprime integers, with and .
Remark 6.2.
The curves and coincide as knots in . For instance and are equivalent trefoil knots in . This is of course consistent with the computation of the fundamental group.
Proposition 6.3.
If then is a -irreducible pair except in the following cases:
-
•
or , and (i.e., );
-
•
and (i.e., ).
Proof.
If or then bounds a meridian disc of either or the complementary solid torus attached to . Therefore is the unknot, and the pair is not -irreducible when . If , the knot intersects the sphere in points. Therefore if the pair is not -irreducible.
Conversely, let us assume that there exists an essential sphere in meeting transversely in points. Suppose first that . If and are non-zero, the complement of in has a Seifert fibration over the disc with two singular fibers of orders and : such a manifold is irreducible, so cannot be essential, a contradiction. So either or , which implies that is the unknot in one of the solid tori and is the boundary of a ball containing . Since is essential it follows that , namely . (This argument shows in particular that when (i.e., ), the pair is 0-reducible only for .)
Suppose now and assume, after an isotopy, that is transverse to the Heegaard torus . Considering this transverse intersection on we see that there must be at least two innermost discs. Moreover any innermost disc belongs to one of the following types:
-
(I)
Its boundary is inessential on and disjoint from ;
-
(II)
Its boundary is inessential on and meets transversely in two points;
-
(III)
It is a meridian disc of either or of the complementary solid torus.
Discs of type (I) can be removed by an isotopy. If there is a disc of type (II) then doing surgery close to it we can replace by an essential sphere disjoint from , so we are led back to the case . Therefore we can assume all the discs are of type (III). If or , we can again reduce to the case . So we can assume that all the innermost discs meet , which easily implies that there are only two of them, either sharing their boundary or separated by an annulus. In the first case we see that (i.e., ) and . In the second case we deduce that is actually inessential, which is absurd. This concludes the proof. ∎
6.3. Layered triangulations
A layered triangulation (see [22]) of a lens space is constructed as follows. We start with a solid torus triangulated using one tetrahedron as in Figure 11. The boundary torus is triangulated by 2 triangles, 3 edges and 1 vertex. A change of the triangulation on the boundary by a diagonal exchange move (“flip”) can be realized by adding one tetrahedron. After a series of these moves, the resulting triangulation can be closed up by adding another 1-tetrahedron triangulation of a solid torus to produce a lens space.

Such a layered triangulation of with one vertex and one marked edge always gives rise to some torus knot . Using the Farey tessellation of hyperbolic plane we will now show the converse, namely for every torus knot we will construct a layered triangulation.
Recall that the Farey tessellation of is constructed in the half-plane model by joining with a geodesic every pair of rational ideal points in where are integers with . After fixing some basis for , every slope (i.e., unoriented essential simple closed curve) on a torus is represented by a rational number , and two such numbers are connected by an edge of the tessellation when they have geometric intersection number .
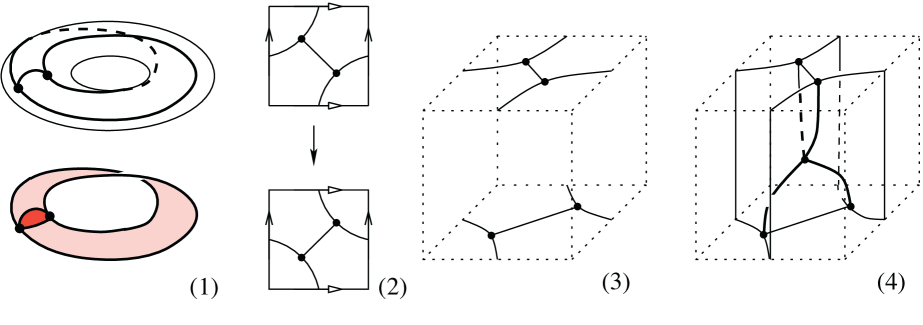
Every triangle of the tessellation represents three slopes with pairwise intersection , and hence a -vertex triangulation of . Dually, they represent a -graph in as in Figure 12-(1-top). Moreover, every edge of the tessellation represents a flip relating the -graphs of corresponding to the adjacent triangles as in Figure 12-(2,3).
A layered triangulation of a lens space is easily encoded via a path of triangles of the tessellation connecting the rational numbers and , i.e., a sequence of triangles such that and share an edge for , the vertex of disjoint from is , and the vertex of disjoint from is . The path need not to be injective, i.e., there may be repetitions. Such a path is similar to the one defined in [22, 31] for layered solid tori. It determines a layered triangulation of with tetrahedra, edges and vertex, as described in Fig 12.
The edges of the layered triangulation become torus knots, and they correspond to all the slopes contained in some except and . (There are different such slopes, but the two in different from give isotopic links in , and in fact the same edge in the layered triangulation, and similarly for the two slopes in different from , whence the number ). See Figure 13 for some examples.
Let then be the length of the shortest path of triangles from to which contains . By what just said, we have:
It was conjectured in [32] that every with has a minimal triangulation which is layered, namely that , where is the length of the shortest path of triangles from to . We now propose the following extension:
Conjecture 6.4.
The complexity of a -irreducible torus knot in a lens space is
As the census in Table 10 shows, the conjecture holds for complexity up to .
6.4. Non-hyperbolic knots and links
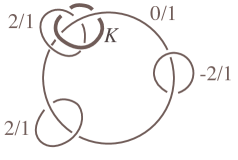
The non-hyperbolic knots and links up to complexity 2, and those having complexity 3 contained in , are described in Table 10. They are all torus links in lens spaces, except for a knot in the elliptic Seifert space , whose exterior is the twisted interval bundle over the Klein bottle. This pair is pictured in Figure 14.
Note that is the only lens space in the table not admitting a symmetry switching the two cores of the Heegaard solid tori, and that both these cores appear in the list.
| type | space | description of knot or link | |
|---|---|---|---|
| 0 | knot | unknot | |
| 0 | knot | core of Heegaard torus | |
| 0 | knot | core of Heegaard torus | |
| 1 | knot | trefoil | |
| 1 | link | Hopf link | |
| 1 | knot | core of Heegaard torus | |
| 1 | knot | core of Heegaard torus | |
| 2 | knot | [43] | |
| 2 | knot | core of Heegaard torus | |
| 2 | knot | core of one Heegaard torus | |
| 2 | knot | core of other Heegaard torus | |
| 2 | knot | core of Heegaard torus | |
| 2 | knot | ||
| 2 | knot | ||
| 2 | knot | ||
| 2 | knot | ||
| 2 | knot | ||
| 2 | knot | ||
| 2 | link | union of cores of Heegaard tori | |
| 2 | knot | singular fibre of | |
| 3 | knot | [43] | |
| 3 | knot | [43] | |
| 3 | knot | [43] | |
| 3 | link | [43] |
6.5. -graphs with Klein bottles
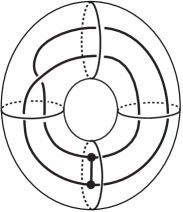
In complexity 5 we have only investigated pairs where is non-empty and all its components have vertices. As mentioned above, we have found here 5 very interesting pairs, where is a -graph and the pair is -irreducible, but non-hyperbolic since contains an embedded Klein bottle, so it is not atoroidal.
Proposition 6.5.
There are five -irreducible non-hyperbolic pairs such that and has no knot component. They are described as follows:
-
(i)
Let be the twisted interval bundle over the Klein bottle.
-
(ii)
Let be the solid torus with the embedded -graph shown in Figure 15.
-
(iii)
Then is obtained by gluing to so that is one of the manifolds , , , , or .
This result was proved as follows. We first analyzed the triangulations of the pairs produced by our Haskell code on which Orb failed to construct a hyperbolic structure. This allowed us to show that the pairs are those described in points (i)-(iii) of the statement, whence to see that they are not hyperbolic. We then proved that they are indeed (0,1,2)-irreducible by classical topological techniques, the key point being that a compressing disc of must intersect in at least two points.
Here are the details of the argument. Suppose there is a sphere intersecting transversely in at most points, and isotope to minimize its intersection with . Now consider an innermost disc on bounded by a simple closed curve in . Since there is no compressing disc in , such a disc must be a compressing disc in , so it must intersect at least twice. But if then there are at least two innermost discs on , whence contains at least 4 points, which is impossible. This shows that is disjoint from , so it is contained either in or in . However is irreducible, and is -irreducible (in fact, it is easy to see that it is hyperbolic with parabolic meridians). Therefore must bound a trivial ball in .
7. Figures
This section contains pictures of the hyperbolic graphs up to complexity 4, given in the form of a surgery description when the underlying space is not . For each graph, we give the name and the volume of the hyperbolic structure with parabolic meridians.
The figures were produced using Orb [19] and the census of knotted graphs in [5]. Most of the graphs in occurred in [5]; the graphs not in generally arose as Dehn surgeries on knot components of disconnected graphs in [5]. There were a couple of remaining examples which were constructed by hand. In all cases, we used Orb to identify the graphs by matching triangulations.

References
- [1] M. Boileau, B. Leeb, J. Porti, Geometrization of -dimensional orbifolds, Ann. of Math. 162 (2005), 195-290.
- [2] P. J. Callahan, M. V. Hildebrand, J. R. Weeks, A census of cusped hyperbolic -manifolds, Math. Comp. 68 (1999), 321-332.
- [3] C. Cao, G. Meyerhoff, The orientable cusped hyperbolic -manifolds of minimum volume, Invent. Math. 146 (2001), 451-478.
- [4] A. Casson, “Geo”, A computer program for geometrizing -manifolds, available from computop.org.
- [5] M. Chiodo, D. Heard, C. Hodgson, J. Saunderson, N. Sheridan, Enumeration and classification of knotted graphs in , in preparation.
- [6] J. Conway, An enumeration of knots and links, and some of their algebraic properties, in: Computational Problems in Abstract Algebra (Proc. Conf., Oxford, 1967), 329-358, Pergamon, Oxford, 1970.
- [7] D. Cooper, C. Hodgson, S. Kerckhoff, “Three-Dimensional Orbifolds and Cone Manifolds”, Mathematical Society of Japan Memoirs, Vol. 5, Tokyo, 2000.
- [8] D. Coulson, O. Goodman, C. Hodgson, W. Neumann, Computing arithmetic invariants of -manifolds, Experiment. Math. 9 (2000), 127-152.
- [9] D. B. A. Epstein, R. C. Penner, Euclidean decompositions of noncompact hyperbolic manifolds, J. Differential Geom. 27 (1988), 67-80.
- [10] E. Flapan, “When Topology Meets Chemistry. A topological look at molecular chirality”, Cambridge University Press, Cambridge, 2000.
- [11] R. Frigerio, B. Martelli, C. Petronio, Small hyperbolic -manifolds with geodesic boundary, Experiment. Math. 13 (2004), 171-184.
- [12] R. Frigerio, C. Petronio, Construction and recognition of hyperbolic -manifolds with geodesic boundary, Trans. Amer. Math. Soc. 356 (2004), 3243-3282.
- [13] M. Fujii, Hyperbolic -manifolds with totally geodesic boundary which are decomposed into hyperbolic truncated tetrahedra, Tokyo J. Math. 13 (1990), 353-373.
- [14] D. Gabai, R. Meyerhoff, P. Milley, Mom technology and volumes of hyperbolic -manifolds, arXiv:math.GT/0606072.
- [15] by same author, Minimum volume cusped hyperbolic three-manifolds, arXiv:math.GT/0705.4325.
- [16] F. W. Gehring, G. J. Martin, Minimal co-volume hyperbolic lattices I: the spherical points of a Kleinian group, Ann. of Math., to appear.
- [17] O. Goodman, “Snap”, A computer program for studying arithmetic invariants of hyperbolic -manifolds, available from www.ms.unimelb.edu.au/˜snap and sourceforge.net/projects/snap-pari.
- [18] “Haskell”, An advanced purely functional programming language, available from www.haskell.org.
- [19] D. Heard, “Orb”, The computer program for finding hyperbolic structures on hyperbolic 3-orbifolds and -manifolds, available from www.ms.unimelb.edu.au/˜snap/orb.html.
- [20] by same author, Computation of hyperbolic structures on -dimensional orbifolds, PhD thesis, University of Melbourne, 2005, www.ms.unimelb.edu.au/˜snap/DHeard-PhD.pdf.
- [21] J. Hoste, M. Thistlethwaite, J. Weeks, The first 1,701,936 knots. Math. Intelligencer 20 (1998), no. 4, 33-48.
- [22] W. Jaco, J. H. Rubinstein, Layered triangulations of -manifolds, arXiv:math.GT/0603601 .
- [23] M. Kapovich, “Hyperbolic Manifolds and Discrete Groups”, Progress in Mathematics, Vol. 183, Birkhäuser Inc., Boston, MA, 2001.
- [24] S. Kojima, Polyhedral decomposition of hyperbolic manifolds with boundary, Proc. Work. Pure Math. 10 (1990), 37-57.
- [25] by same author, Polyhedral decomposition of hyperbolic -manifolds with totally geodesic boundary, In: “Aspects of low-dimensional manifolds”, Adv. Stud. Pure Math. Vol. 20, Kinokuniya, Tokyo, 1992, pp. 93-112.
- [26] S. Kojima, Y. Miyamoto, The smallest hyperbolic -manifolds with totally geodesic boundary, J. Differential Geom. 34 (1991), 175-192.
- [27] R. Litherland, A table of all prime theta-curves in up to crossings, letter, 1989.
- [28] C. Maclachlan, A. Reid, “The Arithmetic of Hyperbolic 3-Manifolds”, Springer-Verlag, New York, 2003.
- [29] T. H. Marshall, G. J. Martin, Minimal co-volume hyperbolic lattices, II: simple torsion in Kleinian groups, preprint.
- [30] B. Martelli, C. Petronio, -manifolds having complexity at most , Experiment. Math. 10 (2001), 207-237.
- [31] by same author, Complexity of geometric -manifolds, Geom. Dedicata 108 (2004), 15-69.
- [32] S. V. Matveev, Complexity theory of three-dimensional manifolds, Acta Appl. Math. 19 (1990), 101-130.
- [33] by same author, Transformations of special spines, and the Zeeman conjecture (Russian), Izv. Akad. Nauk SSSR Ser. Mat. 51 (1987), 1104-1116, 1119. (English translation: Math. USSR-Izv. 31 (1988), 423-434.)
- [34] by same author, “Algorithmic Topology and Classification of 3-Manifolds”, Algorithms and Computation in Mathematics, Vol. 9, Springer-Verlag, Berlin, 2003.
- [35] by same author, Tabulation of three-dimensional manifolds, Russ. Math. Surv. 60 (2005), 673-698.
- [36] Y. Miyamoto, Volumes of hyperbolic manifolds with geodesic boundary, Topology 33 (1994), 613-629.
- [37] J. Morgan, On Thurston’s uniformization theorem for three-dimensional manifolds, In: “The Smith Conjecture” (New York, 1979), Pure Appl. Math. Vol. 112, Academic Press, Orlando, FL, 1984, pp. 37-125.
- [38] H. Moriuchi, An enumeration of theta-curves with up to seven crossings, In: Proceedings of the East Asian School of Knots, Links, and Related topics, 2004, Seoul, Korea, pp. 171-185, knot.kaist.ac.kr/2004/proceedings/MORIUCHI.pdf.
- [39] by same author, A table of handcuff graphs with up to seven crossings, OCAMI Studies Vol. 1, Knot Theory for Scientific Objects (2007), www.omup.jp/modules/papers/knot/chap15.pdf.
- [40] C. Petronio, Spherical splitting of -orbifolds, Math. Proc. Cambridge Philos. Soc. 142 (2007), 269-287.
- [41] by same author, Complexity of -orbifolds, Topology Appl. 153 (2006), 1658-1681.
- [42] R. Piergallini, Standard moves for standard polyhedra and spines, Rend. Circ. Mat. Palermo (2) Suppl. 18 (1988), 391-414.
- [43] D. Rolfsen, “Knots and Links”, Publish or Perish, Berkeley, California, 1976.
- [44] C. Rourke, B. Sanderson, “Introduction to Piecewise Linear Topology”, Ergebn. der Math. Vol. 69, Springer-Verlag, New York-Heidelberg, 1972.
- [45] J. Simon, A topological approach to the stereochemistry of nonrigid molecules, Graph theory and topology in chemistry (Athens, Ga., 1987), 43–75, Stud. Phys. Theoret. Chem., 51, Elsevier, Amsterdam, 1987.
- [46] W. P. Thurston, “Geometry and Topology of 3-Manifolds”, mimeographed notes, Princeton University, 1979, available from msri.org/publications/books/gt3m/.
- [47] by same author, Hyperbolic geometry and -manifolds, In: “Low-Dimensional Topology” (Bangor, 1979), London Math. Soc. Lecture Note Ser. Vol. 48, Cambridge University Press, Cambridge, New York, 1982, pp. 9-25.
- [48] by same author, “Three-dimensional geometry and topology”, Vol. 1, Princeton University Press, 1997.
- [49] J. L. Tollefson, Involutions of sufficiently large -manifolds, Topology 20 (1981), 323-352.
- [50] A. Ushijima, The tilt formula for generalized simplices in hyperbolic space, Discrete Comput. Geom. 28 (2002), 19-27.
- [51] J. R. Weeks, “SnapPea”, The hyperbolic structures computer program, available from www.geometrygames.org.
- [52] by same author, Convex hulls and isometries of cusped hyperbolic -manifolds, Topology Appl. 52 (1993), 127-149.