Hyperspherical Loss-Aware Ternary Quantization
Abstract
Most of the existing works use projection functions for ternary quantization in discrete space. Scaling factors and thresholds are used in some cases to improve the model accuracy. However, the gradients used for optimization are inaccurate and result in a notable accuracy gap between the full precision and ternary models. To get more accurate gradients, some works gradually increase the discrete portion of the full precision weights in the forward propagation pass, e.g., using temperature-based Sigmoid function. Instead of directly performing ternary quantization in discrete space, we push full precision weights close to ternary ones through regularization term prior to ternary quantization. In addition, inspired by the temperature-based method, we introduce a re-scaling factor to obtain more accurate gradients by simulating the derivatives of Sigmoid function. The experimental results show that our method can significantly improve the accuracy of ternary quantization in both image classification and object detection tasks.
Introduction
Most deep neural network (DNN) models have a huge amount of parameters, making it impractical to deploy them on edge devices. When deploying DNN models with latency, memory, and power restrictions, the inference efficiency and model size are the main obstacles. There are many studies on how to use quantization and pruning to reduce model size and computation footprint.
DNN model compression has always been an important area of research. For instance, quantization and pruning are frequently used because they can minimize model size and resource requirements. Pruning can retain higher accuracy at the expense of a longer inference time, while quantization can accelerate and compress the model at the expense of accuracy. The purpose of model quantization is to get a DNN model with maximum accuracy and minimum bit width. Low-bit quantization has the advantage of quick inference, but accuracy is often reduced by inaccurate gradients (yin2019understanding) that are estimated using discrete weights (gholami2021survey). Compared to the low-bit method, weight sharing quantization (stock2019killthebits; martinez_2020_pqf; cho2021dkm) has less model accuracy drop, while inference time is longer because the actual weight values used are remain full precision.
The discrepancy between the quantized weights in the forward pass and the full precision weights in the backward pass can be reduced by gradually discretizing the weights (louizos2018relaxed; jang2016categorical; chung2016hierarchical). However, it only works well with 4-bit (or higher) precision, as the ultra-low bit (binary or ternary) quantizer may drastically affect the weight magnitude and lead to unstable weights (gholami2021survey). Recent research indicates that the essential semantics in feature maps are preserved by direction information (liu2016large; liu2017deephyperspherical; liu2017sphereface; TimRDavidson2018HypersphericalVA; deng2019arcface; SungWooPark2019SphereGA; BeidiChen2020AngularVH).
In this work, inspired by the hyperspherical learning (liu2017deephyperspherical), we rely on the direction information of weight values to perform ternary quantization. Before performaing quantization, we use a regularization term to reduce the cosine similarity between the full precision weight values and their ternary masks under hyperspherical settings (liu2017deephyperspherical). Then we use the proposed gradient scaling method with the straight-through estimator (STE) (bengio2013estimating) to fulfill the ternary quantizaiton. The following is a summary of our contributions:
-
•
We propose a loss-aware ternary quantization method which uses loss regularization terms to reduce the cosine distance between full precision weight values and their ternary counterparts. Once the training is done, the weight values will be separated into three clusters, aloowing for a more accurate quantization.
-
•
We propose a learned quantization threshold to improve the weight sparsity and the quantization performance. We use a re-scaling method during backpropagation to simulate the temperature-based method to obtain more accurate gradients.
Related Work
To reduce model size and accelerate inference, a notable amount of research has been devoted to model quantization methods, such as binary quantization (courbariaux2015binaryconnect; rastegari2016xnor) and ternary quantization (hwang2014fixed; li2016twn; zhu2016ttq). In ternary models training, optimization is difficult because the discrete weight values hinder efficient local-search. Gradient projection method such as straight-through estimator (STE) is usually used to overcome this difficulty:
| (1) |
is the projection operator and projects to a discrete . The optimization of is equivalent to:
| (2) |
where is the scaling factor (bai2018proxquant; parikh2014proximal; li2016twn). A fixed threshold is often introduced by previous works (li2016twn; zhu2016ttq) to determine the quantization intervals of (Eq. (1)). Therefore, ternary quantization can be divided into estimation and optimization-based methods depending on how we obtain and .
Estimation-Based Ternary Quantization
The estimation-based methods, such as (li2016twn), use the approximated form and as optimizing and are time consuming. (wang2018two_27) uses an alternating greedy approximation method to improve and . Given the has a closed form optimal solution (li2016twn; zhu2016ttq). However, direct or alternating estimation is a very rough approximation for . The best optimization result of Eq. (1) cannot be guaranteed.
Optimization-Based Ternary Quantization
The optimization-based method TTQ (zhu2016ttq) uses a fixed and two SGD-optimized scaling factors to improve the quantization results. The intuition is straightforward: since is an unstable approximation, we can use SGD to optimize the scaling factor . The following works (yang2019quantization_22; dbouk2020dbq_20; li2020rtn_23) add more complicated scaling factors and provide corresponding optimization schemes.
There is another subclass in the optimization-based methods, which aims to manipulate the gradient and filter out the less salient weight values by adding regularization terms to the loss function. For example, (hou2018loss_31) uses second-order information to rescale the gradient to find out the weight values that are not sensitive to the ternarization, i.e. the less salient weight values. (zhou2018explicit_26.5) adds a regularization term to refine the gradient through the L1 distance. If is close to , the regularization should be small, otherwise the regularization should be large. The intuition is simple: if and are close to each other, they should not change frequently. However, the discrete ternary values are always involved in this kind of optimization-based methods, so the gradient is not accurate, which affects the optimization results. More advanced methods (dbouk2020dbq_20; yang2019quantization_22) introduce a temperature-based Sigmoid function after ternary projection in order to gradually discretize . Since part of the optimization process is in continuous space, more accurate and can be obtained after the weights are fully discretized. One advantage of using the Sigmoid function is that the gradient is rescaled during backpropagation, i.e., as approaches , the gradient approaches 0, and as approaches , the gradient gets larger. However, this Sigmoid-based method is very time-consuming as it performs layer-wise training and quantization. It is infeasible for very deep neural networks.
Unlike the above methods, our proposed method optimizes the distance between and in continuous space to overcome inaccurate gradients before the conventional ternary quantization. Our method has similar advantages as the Sigmoid-based methods: the use of full-precision weights to optimize the distance. Compared with their time-consuming layer-wise training strategy, our method works globally and requires much less training epoch. In addition, we propose a novel way to re-scale gradients during backpropagation.
Preliminary and Notations
Hyperspherical Networks
A hyperspherical neural network layer (liu2017deephyperspherical) is defined as:
| (3) |
where is the weight matrix, is the input vector to the layer, represents a nonlinear activation function, and is the output feature vector. The input vector and each column vector of subject to for all , and .
Ternary Quantization
To adapt to the hyperspherical settings, the ternary quantizer is defined as:
| (4) |
| (5) |
where is a quantization threshold, denotes the number of non-zero values in , and . The ternary hyperspherical layer has the following property: where .
Loss-Aware Ternary Quantization
The magnitude and direction information of weight vectors change dramatically during ternary quantization. Hyperspherical neural networks can work without taking the magnitude change into account. Combining ternary quantization with hyperspherical learning may offer stable features beneficial for quantization performance.
In this section, to relieve the magnitude and direction deviation in the subsequent quantization procedure, we first introduce a regularization term to push full precision weights toward their ternary counterparts. Then, a re-scaling factor is applied during the quantization stage to obtain more accurate gradients. We also propose a learned threshold to facilitate the quantization process.

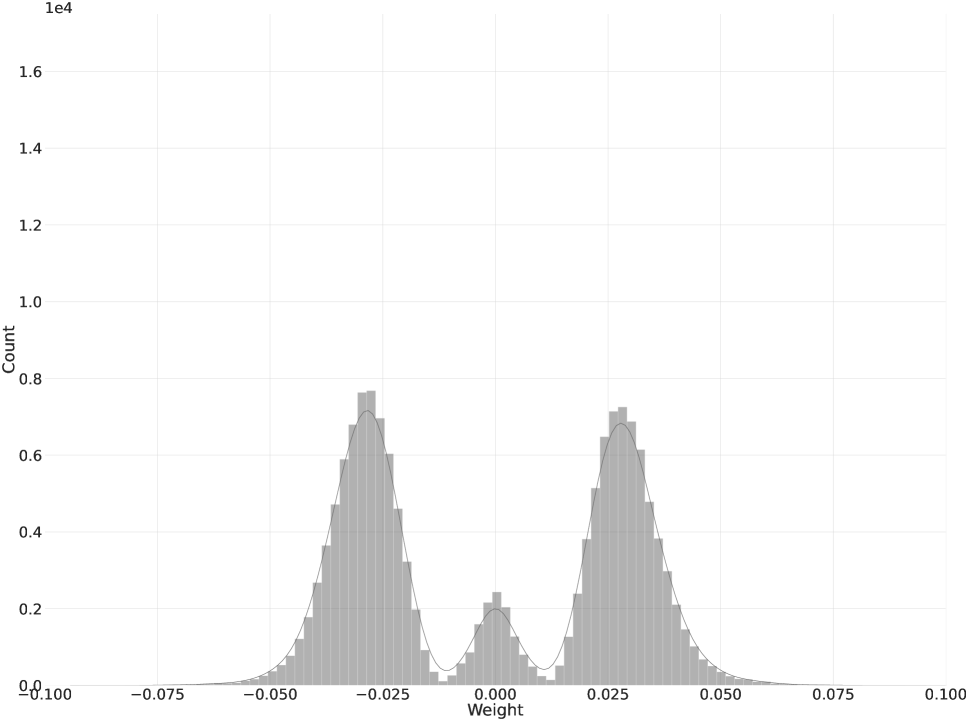


Pushing close to before Quantization
Given a regular objective function , we formulate the optimization process as:
| (6) |
The regularization term is defined as:
| (7) |
where is the identity matrix, and returns the diagonal elements of a matrix. The threshold is:
| (8) |
where controls the sparsity, i.e., percentage of zero values, of (Figure 1), and returns a value of at the index idx. During training, based on the work of (liu2018rethinking), we initially assign , namely, removing values by their magnitude in as the potential ternary references , then is gradually increased to , i.e., 70% of is zero. We use the quadratic term to keep and at the same scale. Since consists of two parts and is optimized in continuous space, the distance between and will gradually decrease without much change in model accuracy. In practice, we observe that applying barely reduces the model accuracy.
Since we are training with hyperspherical settings, i.e., , the diagonal elements of in Eq. (7) denotes the cosine similarities between and . Minimizing is equivalent to pushing close to , namely, making part of the magnitude of weight values close to (Eq. (4)) while the rest close to zero (Figure 1). In addition, the gradient of can adjust , which is similar to the works of (hou2018loss_31; yang2019quantization_22; zhou2018explicit_26.5; dbouk2020dbq_20).
Rescaling the Gradient During Quantization

With getting close to before the ternary quantization, we still need to convert the full precision weight to ternary values. We change the to a learnable threshold and empirically initialize via Eq. (8). The Eq. (6) becomes:
| (9) |
We introduce a gradient scaling factor and adopt STE (bengio2013estimating) to bypass the non-differentiable problem of :
Forward:
| (10) | ||||
Backward:
| (11) |
where is defined as:
| (12) |
and denotes the element-wise multiplication. Inspired by the work of (yang2019quantization_22), is used to re-scale the gradient of as it shares similarities with the derivative of (Figure 2). is intuitive and easy to calculate. The gradient of should be smaller when it gets farther away from . This intuition is the same as the works of (hou2018loss_31; zhou2018explicit_26.5; dbouk2020dbq_20).
We simply apply the averaged gradients of to update the quantization threshold :
| (13) |
Figure 1 shows that we can initialize with a smaller value and then gradually increase it until the near-zero portion is converted to zero during quantization. We should increase the threshold rapidly when the error is very large. As the training error becomes smaller, such increase should slow down.
Implementation Details
Training Algorithm
The proposed method is in Algorithm 1. We gradually increase the from to based on (liu2018rethinking). gives 70% sparsity (Eq. (8)). The overall process can be summarized as: i) Fine-tuning from pre-trained model weights with hyperspherical learning architecture (liu2017deephyperspherical); ii) Initialize to convert near-zero weight values to zero; iii) Ternary quantization, updating the weights and through STE. Note that is a global magnitude threshold (blalock2020state) and is initialized globally and updated by SGD in layer-wise manner.
Training Time
When training the ResNet-18 model with 8V100 and mixed-precision (16-bit), each epoch takes about 6 minutes. It takes about 100 epochs to obtain a hyperspherical ready-to-quantize model. The inner SGD loop (Line 7-11 in Algorithm 1) takes about 10 epochs. The ternary quantization loop (Line 16-21 in Algorithm 1) takes about 200 epochs.
Discussion
Our work shows that the model’s angular information, i.e., the cosine similarity, connects sparsity and quantization on the hypersphere. We demonstrate how gradually adjusting the sparsity constraints can facilitate ternary quantization.
Most ternary quantization works try to directly project full precision models into ternary ones. However, the discrepancy between the full precision and ternary values before quantization is more or less ignored. Only a few approaches (ding2017three_40; hu2019cluster_24) attempt to minimize the discrepancy prior to quantization. Intuitively, the gradients during ternary quantization are inaccurate; therefore, it is inapproriate to use such gradients for distance optimization. Accurate gradients, which are produced by full precision weights, are better than estimated gradients in terms of reducing discrepancy. Our work shows that by making the full precision weights close to the ternary in the initial steps, we can improve the performance of ternary quantization.
In mainstream ternary quantization works, such as TWN (li2016twn) and TTQ (zhu2016ttq), due to the non-differentiable thresholds and unstable weight magnitudes, fixed thresholds and learned scaling factors are used to optimize ternary boundaries to determine which values should be zero. In our work, the clustered weight values with hyperspherical learning allows us to use the average gradient to update the quantization threshold directly, as the thresholding only needs a tiny increment to push the less important weights to zero.
Compared to temperature-based works (yang2019quantization_22) using Sigmoid function for projection and layer-wise training, our proposed method is simple yet effective: by combining a bell-shaped gradient re-scaling factor with ternary quantization, we achieve a better efficiency-accuracy trade-off. In addition, our method does not need too many hyperparameters and sophisticated learned variables (li2020rtn_23; yang2019quantization_22). Compared to other loss-aware ternary quantization works (zhou2018explicit_26.5; hou2018loss_31) using estimated gradients to optimize the loss penalty term, our method minimizes the loss function by using full precision weights before quantization, which is more accurate and efficient.
Experiments
Our method is evaluated on image classification and object detection tasks with the ImageNet dataset (ILSVRC15). The ResNet-18/50 (he2016deep) and MobileNetV2 (sandler2018mobilenetv2) architectures are for image classification. The Mask R-CNN (he2017mask) with ResNet-50 FPN (wu2019detectron2) is for object detection. The object detection tasks are performed on the MS COCO (lin2014mscoco) dataset. The pre-trained weights are provided by the PyTorch zoo and Detectron2 (wu2019detectron2).
Experiment Setup
For image classification, the batch size is 256. The weight decay is 0.0001, and the momentum of stochastic gradient descent (SGD) is 0.9. We use the cosine annealing schedule with restarts (loshchilov2016sgdr) to adjust the learning rates. The initial learning rate is 0.01. All of the experiments use 16-bit Automatic Mixed Precision (AMP) from PyTorch to accelerate the training process. The first convolutional layer and last fully-connected layer are skipped when quantizing ResNet models. For the MobileNetV2, and Mask R-CNN, we only skip the first convolutional layer.