decays with a magnetic dipole term
Abstract
Using the massive helicity formalism we calculate the five-body average square amplitude of the decays within the Standard Model (SM), we then introduce a dimension-five effective vertex in order to determine the feasibility of imposing limits on the tau anomalous magnetic dipole moment () via the current or future experimental measurements of the branching ratio for the decay .
Keywords: tau lepton, magnetic dipole moment, 5-body tau decay, helicity formalism
PACS: 13.35.Dx, 13.40.Em, 12.38.Bx
pacs:
Valid PACS appear hereI Introduction
We found that the SM five body decays whose branching ratios, at the tree level, have been calculated by Dicus and Vega Dicus , Volobouev of the CLEO Collaboration CLEO and more recently by López Castro et. al. Roig . However Dicus and Roig differ from the predictions of CLEO whose various branching ratios are higher. The CLEO II experiment has searched for the decay, whose measured value is PDG :
| (1) |
The statistical, systematic and background uncertainties are but forthcoming BELLE measurements are expected to improve to and on the statistical and systematic uncertainties junya , respectively. The importance of our independent calculation is that it is useful to overcome this discrepancy. Furthermore, we analyze the possibility of limiting the value by using current and future experimental measurements by BELLE or other future collaborations.
Leptons offer some of the cleanest signals that can be obtained in collider physics experiments and might also provide new insight into physics beyond the standard model (SM). In particular, with the yet unsolved origin of the discrepancy between the experimental and theoretical SM prediction of the muon anomalous magnetic dipole moment . Although much work has already been devoted to , the has recently become the source of theoretical and experimental interest, which is why in the present work we suggest a tau decay as a means to obtain further insight into . The current lower and upper bounds on , with 95 C.L. DELPHI , were obtained via the process by the DELPHI collaboration. These bounds differ from the theoretical value predicted by the SM by one order of magnitude: SMMomMagTAU . Measurements of the electron and muon Anomalous Magnetic Dipole Moments (AMDM) were obtained by means of spin precession experiments, however, in the case of the tau lepton this class of measurements are troublesome due to its short lifetime, . Even though there is a plethora of tau decays, only a few of them are viable candidates to constrain . Whereas two- and three-body decays do not involve the coupling, the decay, as suggested in Ref. tauTOfourbodies , is constrained by the tau lifetime and is only sensitive to large values of . The use of tau decays to constrain is particularly relevant because the Belle-II experiment is expected to produce about tau leptons annually, which greatly exceeds the previous CLEO-II experiment, in which there were produced tau leptons.
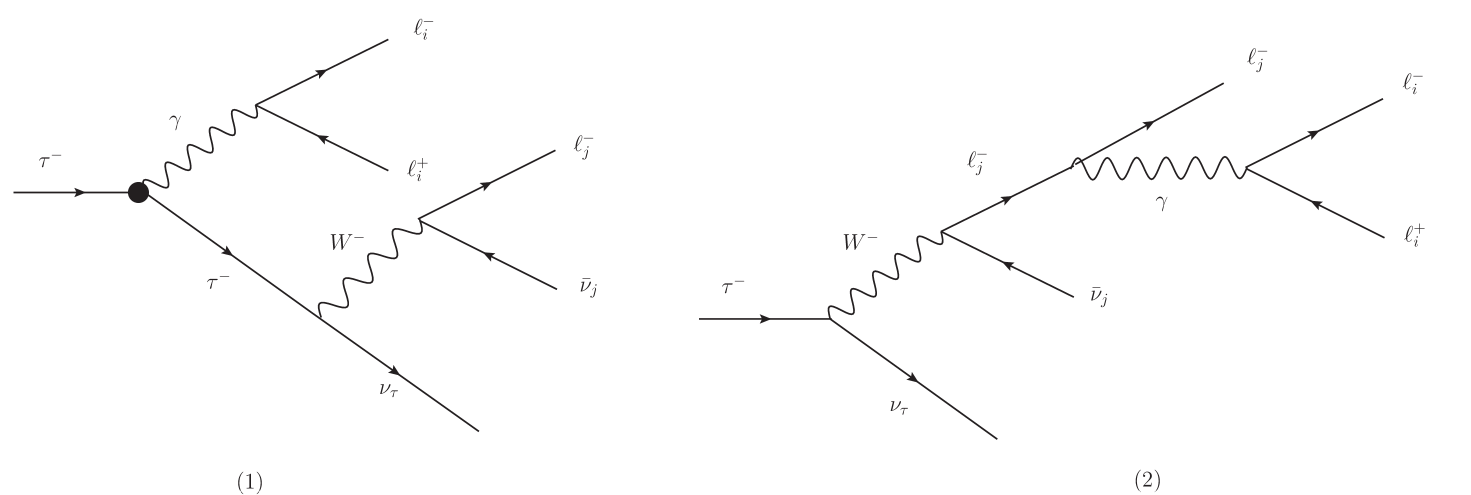
The dominant Feynman diagrams for this decay within the SM are shown in Fig. 1, where the dot represents the QED contribution along with an extra contribution from the tau AMDM. All other tree-level diagrams give a negligible contribution.
In this work we will consider this branching ratio to obtain a bound on . To this aim we will consider the following effective vertex of the photon to a charged lepton pair respecting Lorentz invariance:
| (2) |
where is the photon transferred four-momentum. Here is the tau electric charge form factor ( at the tree level), whereas the five-dimensional -conserving and -violating terms correspond to the static anomalous magnetic dipole moment and the electric dipole moment , which are given by:
| (3) | |||||
| (4) |
We will assume invariance and take =0.
The rest of this presentation is organized as follows. In Section II we will present the unpolarized square amplitude for the decay via the massive helicity formalism dittmaier , which considerably simplifies the calculation. The numerical integration of the decay width and the resulting bound on the are presented in Sec. III, whereas Sec. IV is devoted to the conclusions and outlook. Details of the calculation are presented in Appendix A.
II Unpolarized square amplitude
We will calculate the average square amplitude of the decay using the massive helicity formalism for which usual treatments, such as dixon or elvang , only deal with the massless case. Here we need to take into account the mass of the tau lepton, so must go further. In particular, in dittmaier the two main ways to deal with massive helicity amplitudes are presented, although with a somewhat old-fashioned notation. We use here the approach that consists in performing a light-cone decomposition to write the four-momentum of a massive particle as a linear combination of two light-like momenta. For a detail account we refer the interested reader to Ref. proceedings , where this formalism is presented in a self-contained manner (with opposite metric signature convention). We will present a brief outline here for convenience.
Let be the four-momentum of a massive particle of mass , which can always be written in terms of two light-like ones and as
| (5) |
where satisfies but is otherwise arbitrary, and is defined through (5). The positive frequency momentum space Dirac equation has two linearly independent solutions, which we label with the subindices and . It is easily checked that they are given (maybe up to a phase) by
| (6) |
while for the negative frequency we have
| (7) |
Here and are 2-component Weyl spinors linked to the light-like momenta and proceedings . We will use these solutions to calculate the helicity amplitudes for the decay, where is the helicity of the particle with four-momentum , and the subindex labels each Feynman diagram of Fig. 1: it runs from 1 to 4 in the case that the charged leptons and are identical, such as in the decay, but it only runs from from 1 to 2 if and are distinguishable.
To determine the individual non-zero helicity amplitudes we will neglect the mass of the outgoing charged leptons, which is a good approximation as their mass is negligible as compared to the tau mass. In this limit, each amplitude will vanish unless the helicities of particles 4, 5 and 6 have certain fixed signs because of its spinor index structure. After doing that, we present the sum of the squared modulus of the helicity amplitudes and then all of the interferences.
In the unitary gauge, the amplitude for the first Feynman diagram of Fig. 1, dubbed (1), is
| (8) | |||||
where we use the short-hand notation and the four-momenta are the ones of the virtual particles of this diagram. Note that we are using the effective interaction (2) for the vertex but in our calculation below we will use the tree-level value . In addition
| (9) |
with . The helicity structure of the amplitude fixes , , and . We then write
| (10) |
We now choose and define
| (11) | |||
| (12) |
thus the individual helicity amplitudes are given by
| (13) |
| (14) |
| (15) |
and
| (16) |
To obtain the helicity amplitudes of the the third Feynman diagram, obtained from the first one after the exchange of identical particles, we simply exchange the momenta and helicities of particles 2 and 4, both in the helicity amplitudes and in the definitions of and , leading to new coefficients that we denote as and , respectively.
By an analogous procedure, we obtain for the Feynman diagram (2) of Fig. 1
| (17) | |||
| (18) | |||
| (19) | |||
| (20) |
where
| (21) |
We straightforwardly obtain the corresponding amplitudes for the fourth diagram after the exchange of the momenta and helicities of particles 2 and 4.
We now factor all the dependence on the form factors and by defining the following coefficients:
| (22) | |||
| (23) | |||
| (24) |
from which we obtain the sum of the squared helicity amplitudes of the first diagram:
| (25) |
where is defined in Appendix A. For the second diagram we get
| (26) |
The corresponding expression for the fourth diagram is attained by exchanging and .
On the other hand, the non-zero interferences are given by
| (27) |
| (28) |
| (29) |
and
| (30) |
where stands for the interference between the amplitudes of diagrams and . Explicit expressions for the functions are given in Appendix A.
The full unpolarized squared amplitude for the decay is given by
| (31) |
It is worth noting that this method is straightforward and yields compact results easy to handle in the numerical integration.
III Numerical results
We now turn to compute the branching ratio of the tau five-body decay . The decay width is given by the usual formula
| (32) |
After dividing by the tau total width we obtain the corresponding branching ratio
| (33) |
According to Ref.EspFase the four-momenta of the involved particles in a five-body decay can be related to eight independent Lorentz invariant parameters through the relations:
| (34) |
| (35) |
| (36) |
The phase-space integral (32) was numerically computed over these kinematic variables via Monte-Carlo integration by using the VEGAS routines Lepage . A cross-check of our results was done by implementing the electromagnetic vertex in the CalcHEP package Belyaev:2012qa , which performs all the numerical calculation.
We first consider that the impact of the magnetic form factor is negligible, i.e. we use and make a comparison of our numerical results for the widths of the allowed decays with those obtained in previous studies. The results are shown in Table 1. The uncertainties arise from the numerical integration. Our results are in good agreement with these predictions, though are closer to those of Ref. Roig , which could be attributed to the fact that we used the same values of the tau mass and mean lifetime. Additionally, for completeness, we computed the for which we obtain .
| Branching ratio | RefDicus | Ref. CLEO | Ref. Roig | Our results |
|---|---|---|---|---|
III.1 Effect of on the decay
We will now analyze the impact of the dipole term on the branching ratio of the tau five-body decay. The behavior of as a function of is shown in Fig. 2. The horizontal red lines corresponds to the 95% C.L. interval obtained from the experimental measurement of PDG , and the horizontal black line corresponds to our calculation for the tree-level SM prediction, i.e. . The purple curve corresponds to our prediction for the branching ratio as a function of . Assuming that there are no extra contribution rather than that due to we can conclude that the points of the purple curve falling above the upper experimental bound on would be excluded, thereby yielding the bound . This allow us to gain an improvement over the current upper bound by DELPHI: . Since there is a slight dependence of on , this method is not useful to set a lower bound on it with current measurements.
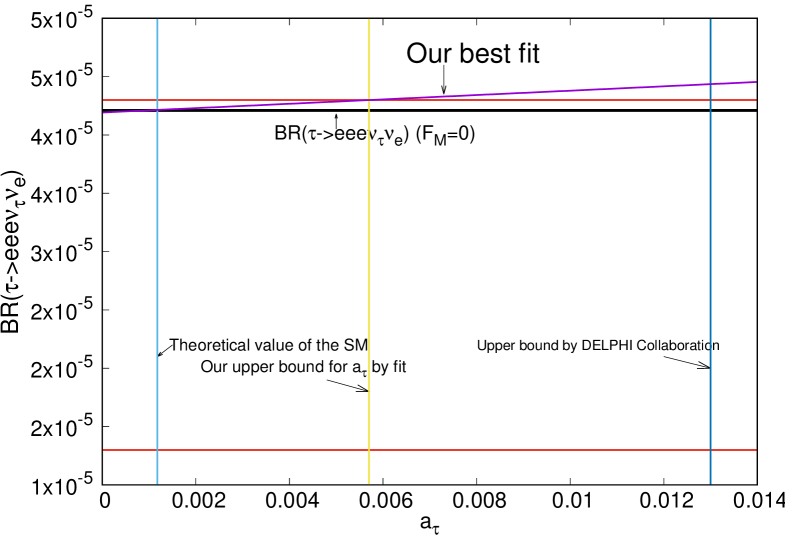
Forthcoming measurements might reach a statistical uncertainty of and a systematic uncertainty of . Which we found is not good enough so that we may obtain improved bounds, since our lower bound would only improve to a level of -0.02. But new runs at BELLE II or future experiments we hope might offer more precise measurements, which is why we optimistically assume that if the statistical and systematic uncertainty is improved to the 2% level, we expect to find that the bound of would fall in the range of , see Fig. 3.
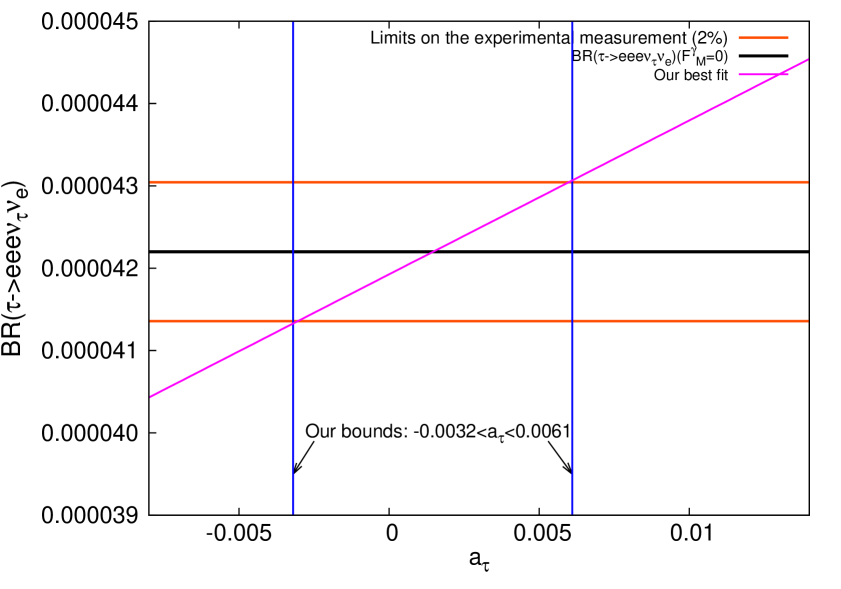
Other approaches similarly yield stringent bounds on through electroweak precision data (EWPD) and the experimental data for the : Escribano , Springberg and more recently Epifanov . While on the theoretical side, other model extensions predict values for of the order of MoyTav -MSSM , which could be useful in the case of a discrepancy between the experimental measurement and the SM prediction.
IV Conclusions
In this work we present the results of a numerical calculation for the predictions of the branching ratio of the allowed decays, which are consistent with previous results reported by Dicus and Vega and López Castro et. al. In addition, we use the current experimental measurement on the branching ratio of the decay to obtain an upper limit on the tau anomalous magnetic dipole moment by using an effective electromagnetic vertex including a dipole term. We find that the effect of the magnetic dipole form factor on the reported value by CLEO II colaboration for the branching ratio of the decay allows to extract an upper bound of , which is below the current upper bound by the DELPHI collaboration. With the next measurements by BELLE II results are expected with and of statistical and systematic uncertainties. Under this scenario, we find that the effect of on the is such that the lower bound is given by but it is not possible to extract a good upper bound. Finally, assuming an accurate measurement of the of statistical and systematic uncertainties, it is found that our best bounds are .
Acknowledgements.
We acknowledge support from CONACYT (México).Appendix A Conventions for the massive helicity formalism and interference terms for the unpolarized square amplitude.
We use the abbreviated notation
| (37) |
(where stands for the real part of the complex number ), with even. It is easy to show that
| (38) |
It is well known that, for even, the trace of the product of gamma matrices is proportional (the proportionality constant being ) to terms, each of which is the product of metric tensors. In the particular case of only two indices we write as an abbreviation of even when the momenta and are not null. When there are more indices the individual momenta must be light-like.
Several properties can be obtained immediately. For instance, cyclicity of the trace translates into cyclicity of indices:
| (39) |
Using the definition (37) we see that a multi-index with two equal adjacent indices vanishes because
| (40) |
On the other hand, using we obtain the following general “index-commuting formula”:
| (41) |
In a scattering (or decay) process with external legs, we have distinct four-momenta. If we calculate a squared amplitude and get a with more than indices, we use the (40) and (41) properties to write everything in terms of only ’s with at most indices, i.e. is an upper bound for the number of indices in an particle tree level process. In our case there are six external legs, therefore ’s with more than six indices shall not appear.
For the interferences we use the following expressions:
| (42) | ||||
| (43) |
| (44) | ||||
| (45) |
| (46) | ||||
| (47) | ||||
| (48) | ||||
| (49) | ||||
| (50) |
| (51) |
| (52) |
| (53) |
| (54) | ||||
| (55) |
| (56) | ||||
| (57) |
| (58) | ||||
| (59) | ||||
| (60) | ||||
| (61) |
| (62) | ||||
| (63) |
| (64) |
| (65) |
| (66) | ||||
| (67) | ||||
| (68) |
where the can be written in terms of the by means of the following recursion formulas
| (69) | ||||
| (70) |
Furthermore, the subindex is determined by
| (71) | ||||
| (72) |
References
- (1) D. A. Dicus and R. Vega, Phys. Lett. B 338, 341 (1994) doi:10.1016/0370-2693(94)91389-7 [hep-ph/9402262].
- (2) M. S. Alam et al. [CLEO Collaboration], Phys. Rev. Lett. 76, 2637 (1996). doi:10.1103/PhysRevLett.76.2637
- (3) A. Flores-Tlalpa, G. López Castro and P. Roig, JHEP 1604, 185 (2016) doi:10.1007/JHEP04(2016)185 [arXiv:1508.01822 [hep-ph]].
- (4) C. Patrignani et al. [Particle Data Group], Chin. Phys. C 40, no. 10, 100001 (2016). doi:10.1088/1674-1137/40/10/100001
- (5) Junya Sasaki, Hiroaki Aihara, Denis Epifanov, Kiyoshi Hayasaka, Nobuhiro Shimizu, Yifan Jin, and Belle Collaboration The international workshop on future potential of high intensity accelerators for particle and nuclear physics (HINT2016).
- (6) J. Abdallah et al. [DELPHI Collaboration], Eur. Phys. J. C 35, 159 (2004) doi:10.1140/epjc/s2004-01852-y [hep-ex/0406010].
- (7) S. Eidelman and M. Passera, Mod. Phys. Lett. A 22, 159 (2007) doi:10.1142/S0217732307022694 [hep-ph/0701260].
- (8) M. L. Laursen, M. A. Samuel and A. Sen, Phys. Rev. D 29, 2652 (1984) Erratum: [Phys. Rev. D 56, 3155 (1997)]. doi:10.1103/PhysRevD.29.2652, 10.1103/PhysRevD.56.3155.
- (9) L. J. Dixon, doi:10.5170/CERN-2014-008.31 arXiv:1310.5353 [hep-ph].
- (10) H. Elvang and Y. Huang, Scattering Amplitudes in Gauge Theory and Gravity, Cambridge University Press (2015).
- (11) S. Dittmaier, Phys. Rev. D 59, 016007 (1998) doi:10.1103/PhysRevD.59.016007 [hep-ph/9805445].
- (12) J. L. Diaz-Cruz, B. O. Larios and O. Meza-Aldama, J. Phys. Conf. Ser. 761, no. 1, 012012 (2016) doi:10.1088/1742-6596/761/1/012012 [arXiv:1608.04129 [hep-ph]].
- (13) R. Kumar, Phys. Rev. 185, 1865 (1969). doi:10.1103/PhysRev.185.1865.
- (14) G. P. Lepage, J. Comput. Phys. 27 (1978) 192.
- (15) A. Belyaev, N. D. Christensen and A. Pukhov, Comput. Phys. Commun. 184, 1729 (2013) doi:10.1016/j.cpc.2013.01.014 [arXiv:1207.6082 [hep-ph]].
- (16) R. Escribano and E. Masso, Phys. Lett. B 395, 369 (1997) doi:10.1016/S0370-2693(97)00059-2 [hep-ph/9609423].
- (17) G. A. Gonzalez-Sprinberg, A. Santamaria and J. Vidal, Nucl. Phys. B 582, 3 (2000) doi:10.1016/S0550-3213(00)00275-3 [hep-ph/0002203].
- (18) S. Eidelman, D. Epifanov, M. Fael, L. Mercolli and M. Passera, JHEP 1603, 140 (2016) doi:10.1007/JHEP03(2016)140 [arXiv:1601.07987 [hep-ph]].
- (19) A. Moyotl and G. Tavares-Velasco, Phys. Rev. D 86, 013014 (2012) doi:10.1103/PhysRevD.86.013014 [arXiv:1210.1994 [hep-ph]].
- (20) A. Bolaños, A. Moyotl and G. Tavares-Velasco, Phys. Rev. D 89, no. 5, 055025 (2014) doi:10.1103/PhysRevD.89.055025 [arXiv:1312.6860 [hep-ph]].
- (21) M. Arroyo-Ureña and E. Díaz, J. Phys. G 43, no. 4, 045002 (2016) doi:10.1088/0954-3899/43/4/045002 [arXiv:1508.05382 [hep-ph]].
- (22) M. A. Arroyo-Ureña, G. Hernández-Tomé and G. Tavares-Velasco, Eur. Phys. J. C 77, no. 4, 227 (2017) doi:10.1140/epjc/s10052-017-4803-z [arXiv:1612.09537 [hep-ph]].
- (23) T. Ibrahim and P. Nath, Phys. Rev. D 78, 075013 (2008) doi:10.1103/PhysRevD.78.075013 [arXiv:0806.3880 [hep-ph]].