Improve Variational AutoEncoder with
Auxiliary SOFTMAX MultiClassifier

Modeling the joint distribution of the latent variable ${\mathbf{z}}$ and the observed variable ${\mathbf{x}}$, VAE calculates the margin distribution of ${\mathbf{x}}$. Consider the sample data set ${\bm{X}}=\{{\bm{x}}^{(i)}\}_{i=1}^{N}$ consisting of $N$ i.i.d. samples. Introduce the latent variable ${\mathbf{z}}$, the joint distribution of ${\mathbf{x}}$ and ${\mathbf{z}}$ is $p_{\theta}({\mathbf{x}},{\mathbf{z}})$. The true distribution of ${\mathbf{x}}$ can be obtained by computing the margin distribution $p_{\theta}({\mathbf{x}})=\int p_{\theta}({\mathbf{x}}\mid{\mathbf{z}})p_{\theta}({\mathbf{z}})\text{d}{\mathbf{z}}$. However, this integral is often intractable, so VAE uses the approximate distribution $q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})$ to solve the problem by variational inference.

The margin likelihood function can be written as the sum of the likelihood function for each sample point, $\text{log}p_{\theta}({\bm{x}}^{(1)},\cdots,{\bm{x}}^{(N)})=\sum_{i=1}^{N}\text{log }p_{\theta}({\bm{x}}^{(i)})$. Combin with Jensen Inequality, for each sample ${\bm{x}}^{(i)}$,

	$\displaystyle\text{log}p_{\theta}({\bm{x}}^{(i)})$	$\displaystyle=\text{log}\int p_{\theta}({\bm{x}}^{(i)},{\mathbf{z}})\text{d}{\mathbf{z}}=\text{log}\mathbb{E}_{q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})}\left[\frac{p_{\theta}({\bm{x}}^{(i)},{\mathbf{z}})}{q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})}\right]$
		$\displaystyle\geq\mathbb{E}_{q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})}\left[\text{log}p_{\theta}({\bm{x}}^{(i)},{\mathbf{z}})-\text{log}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})\right]=\mathcal{L}_{ELBO}(\theta,\phi;{\bm{x}}^{(i)})$		(1)

where, joint distribution is $p_{\theta}({\mathbf{x}},{\mathbf{z}})=p_{\theta}({\mathbf{x}}\mid{\mathbf{z}})p_{\theta}({\mathbf{z}})$, the evidence lower bound can be written as

$\displaystyle\mathcal{L}_{ELBO}(\theta,\phi;{\bm{X}})$

$\displaystyle=\sum_{i=1}^{N}\left[\mathbb{E}_{q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})}\left[\text{log}p_{\theta}({\bm{x}}^{(i)}\mid{\mathbf{z}})\right]-D_{KL}\left[q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})\ ||\ p_{\theta}({\mathbf{z}})\right]\right]$

(2)

It can be seen from the equation 2 that the loss function of VAE consists of two parts. One part of the loss is the observation ${\bm{x}}^{(i)}$ reconstruction error, and the other part is the difference between the posterior distribution $q_{\phi}({\mathbf{z}}|{\mathbf{x}})$ and the prior distribution $p_{\theta}({\mathbf{z}})$.

The prior distribution of the latent variable ${\mathbf{z}}$ chosen by VAE is denoted as $p_{\theta}({\mathbf{z}})$, General assumption is a multidimensional standard normal distribution $\mathcal{N}({\mathbf{z}};\bm{0},{\bm{I}})$ to facilitate sampling of the model. The complete calculation of VAE includes two processes of encoding and decoding. During the encoding process, the encoder training fit a conditional posterior distribution of ${\mathbf{z}}$ after ${\mathbf{x}}$ is observed, noted as $q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})$. We use KL-Divergence $D_{KL}(q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})\ ||\ p_{\theta}({\mathbf{z}}))$ to evaluate the similarity of a prior and conditional posterior distributions of latent variable. That is, the posterior distribution generated by the encoder is required to be as close as possible to a standard normal distribution. The decoding process is to sample ${\bm{z}}\sim p_{\theta}({\mathbf{z}})$ from the prior distribution, then use the decoder $p_{\theta}({\mathbf{x}}|{\bm{z}})$ to generate a ${\bm{x}}$ refactoring $\hat{{\bm{x}}}$. Compare the difference between ${\bm{x}}$ and $\hat{{\bm{x}}}$ as a loss function, calculating the gradient to update parameters $\theta,\phi$.

The calculation of $\text{log }p_{\theta}({\bm{x}}^{(i)},{\mathbf{z}})$ in VAE depends on sampling. Specifically, for each sample ${\bm{x}}^{(i)}$, VAE encoder fits the variables $\mu({\bm{x}}^{(i)})$ and $\sigma({\bm{x}}^{(i)})$, it is used to define the posterior distribution $q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})=\mathcal{N}({\mathbf{z}};\mu({\bm{x}}^{(i)}),\sigma({\bm{x}}^{(i)}))$ of the latent variable ${\mathbf{z}}$. Then VAE completes $L$ samples and calculates

$$\tilde{\mathcal{L}}(\theta,\phi;{\bm{X}})\simeq\frac{1}{N}\sum_{i=1}^{N}\left[\frac{1}{L}\sum_{l=1}^{L}\left(\text{log}p_{\theta}({\bm{x}}^{(i)}\mid{\bm{z}}^{(l)})\right)-D_{KL}\left[q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})\ ||\ p_{\theta}({\mathbf{z}})\right]\right]$$

In order to ensure the continuity of the loss calculation, enable the inverse gradient descent training process. VAE uses the technique of reparameterization during the sampling process. First sample the random variable $\varepsilon^{(l)}$ from $\mathcal{N}(0,1)$, then let ${\bm{z}}^{(l)}=\mu({\bm{x}}^{(i)})+\sigma({\bm{x}}^{(i)})\odot\varepsilon^{(l)}$.

For VAE, the latent variable space needs to have sufficient feature coding ability to express complex real distributions. The sample space is often discrete, but the encoder needs to smooth and fill the missing parts between discrete samples to generate new pictures or text. At the same time, the coding space must be conducive to sampling and likelihood calculations, which requires that the prior distribution $p_{\theta}({\mathbf{z}})$ is simple.

The VAE encoder encodes each discrete sample ${\bm{x}}^{(i)}$ of ${\bm{X}}$ into a continuous latent random variable ${\mathbf{z}}$. It can be seen that ${\bm{x}}^{(i)}$ is mapped to a continuous area of distribution defined by $q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})=\mathcal{N}(z;\mu({\bm{x}}^{(i)}),\sigma({\bm{x}}^{(i)}))$. Intuitively, in the calculation of the equation equation 2, VAE hopes that the difference between the distribution of ${\mathbf{z}}$ generated by each ${\bm{x}}^{(i)}$ encoding is large to reduce the error of reconstruction. But minimizing the KL-Divergence term pushes $q_{\phi}({\mathbf{z}}|{\bm{x}}^{(i)})$ to a uniform standard normal distribution. These two optimization directions are contradictory, When VAE tries to reduce the reconstruction error, it is bound to increase the difference of the code distribution $q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})$, then KL-Divergence will increase. When the reduced reconstruction error is smaller than the increased KL-Divergence, VAE directly reduces the KL-Divergence without the error reduction.

Design an experiment, when feeding a completely random set of images to VAE for learning, we will find that the KL-Divergence will soon tend to $0$. Because the image does not contain any rules, the VAE reconstruction error is optimized so small that it does not start at all.

There are two cases of coding collapse. One is that in the early stage of model training, because the parameters optimization of the decoder have not been completed or because the randomness of the training samples is too strong, strong KL-Divergence constraints will result in a high optimization constraint threshold, models are easier to optimize only KL-Divergence. In a more general view, the text (He et al., 2019) rewrites the ELBO to

$$\mathcal{L}_{ELBO}(\theta,\phi;{\bm{X}})=\sum_{i=1}^{N}\left[\text{log }p_{\theta}({\bm{x}}^{(i)})-D_{KL}\left[q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})\ ||\ p_{\theta}({\mathbf{z}}\mid{\bm{x}}^{(i)})\right]\right]$$

The first term in R.H.S can be seen as the maximum log likelihood of the decoder’s distribution. The KL-Divergence of the second term characterizes the degree of similarity between $p_{\theta}({\mathbf{z}}\mid{\mathbf{x}})$ and $q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})$. When the VAE is trained in the beginning, the encoder is not perfect, the correlation between ${\mathbf{z}}$ and ${\mathbf{x}}$ is not strong and can be regarded as an independent variable. When $p_{\theta}({\mathbf{z}})$ is simple, minimizing the KL-Divergence requires $q_{\phi}({\mathbf{z}}|{\mathbf{x}})$ to be directly locked to $p_{\theta}({\mathbf{z}})$, which is, ${\mathbf{z}}$ is independent with ${\mathbf{x}}$, $q_{\phi}({\mathbf{z}}_{d}\mid{\bm{x}}^{(i)})=q_{\phi}({\mathbf{z}}_{d})\sim\mathcal{N}({\mathbf{z}}_{d};0,1)$, similarly $p_{\theta}({\mathbf{z}}_{d}\mid{\bm{x}}^{(i)})=p_{\theta}({\mathbf{z}}_{d})\sim\mathcal{N}({\mathbf{z}}_{d};0,1)$, $D_{KL}$ item disappears on this element.

Another type of collapse is due to the lack of correlation in the model encoding, or the need of correlation for reconstruction is small, it also causes the fact that the feature space dimension exceeds the active number of latent variable. Image and language coding often have autocorrelation, such as the value of a pixel in an image and the value of surrounding pixels. In the case of a strong decoder, using the autocorrelation information, ${\mathbf{x}}$ can be recovered without ${\mathbf{z}}$, As can be seen from the Table 1, with the increase of layers of Decoder network, the decoding ability of decoder is continuously enhanced. Encoder $q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})$ constructs $\mu({\bm{x}})$ according to ${\bm{x}}$, The number of dimensions with larger variances of $\mu({\bm{x}})$ continues to decline. This shows that the higher the complexity of the Decoder, then the less information is used in the information contained in ${\mathbf{z}}$.

From the above, in order to prevent the posterior collapse, we need to increase the correlation between ${\mathbf{z}}$ and ${\mathbf{x}}$ in the joint distribution to prevent independent of ${\mathbf{z}}$ and ${\mathbf{x}}$. The correlation in the joint distribution is mainly controlled by mutual information. The problem of blurred images is also related to mutual information. Mentioned in the article (Zhao et al., 2017b), the optimal solution to reconstruction loss of decoder for a given $q_{\phi}$ is $\mathbb{E}_{q_{\phi}({\mathbf{x}}\mid{\bm{z}})}\left[{\mathbf{x}}\right]$. That is to say, the reconstructed image of VAE is the expectation of a set of images, which is related to the smoothness of the latent variable distribution. The mutual information is directly related to the entropy of $q_{\phi}({\mathbf{x}}|{\bm{z}})$. We prefer to think the blurry as a trade-off rather than a problem. In the article (Shwartz-Ziv & Tishby, 2017; Alemi et al., 2016) on information bottlenecks, the neuron network will have a decrease in mutual information $I_{q_{\phi}}(Z,X)$ in the later stage of optimization training. It is actually an optimization that reduces overfitting. when the mutual information is reduced, the smoothness of the model is higher, and the anti-noise and fitting between samples is better. As the mutual information increases, the error of model reconstruction will be smaller, but the generalization performance of the model will be worse. Therefore, for mutual information, what we need more is to better control according to the model task, rather than simply increasing or decreasing.

According to (Hoffman & Johnson, 2016; Dieng et al., 2018), the KL-Divergence term in the ELBO of the VAE can be expressed as (See the appendix for details).

$$\frac{1}{N}\sum_{i=1}^{N}D_{KL}(q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})||p_{\theta}({\mathbf{z}}))=\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})+D_{KL}(q_{\phi}({\mathbf{z}})||p_{\theta}({\mathbf{z}}))$$

where $\mathcal{I}_{q_{\phi}}$ is the mutual information between ${\mathbf{x}}$ and ${\mathbf{z}}$, measure the correlation between ${\mathbf{x}}$ and ${\mathbf{z}}$. And $D_{KL}(q_{\phi}({\mathbf{z}})||p_{\theta}({\mathbf{z}}))$ is the KL-Divergence between code marginal distribution $q_{\phi}({\mathbf{z}})$ and prior distribution $p_{\theta}({\mathbf{z}})$.

In order to control the mutual information and the marginal KL-Divergence more precisely, rewrite the ELBO:

$\displaystyle\hat{\mathcal{L}}(\theta,\phi;{\bm{X}})$

$\displaystyle\simeq\frac{1}{N}\sum_{i=1}^{N}\left[\frac{1}{L}\sum_{l=1}^{L}\left(\text{log}p_{\theta}({\bm{x}}^{(i)}\mid{\bm{z}}^{(l)})\right)\right]-\alpha\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})-\beta D_{KL}\left[q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}})\right]$

(3)

Where $\alpha$ and $\beta$ are Lagrange multiplier, By adjusting $\alpha$, $\beta$, we can adjust the performance of VAE-AS to meet different optimization requirements.

The calculation of mutual information and marginal KL-Divergence involves solving the margin distributions of $q_{\phi}({\mathbf{z}})$. For research objects such as images and texts, the dimensions are often large and the probability of the samples are both small. Select sample each time, the distribution of the sample $\{{\bm{x}}^{(1)},\cdots,{\bm{x}}^{(N)}\}$ can be considered as a discrete Categorical distribution $Cat(c^{(1)},\cdots,c^{(N)})$, where $c^{(1)}=\cdots=c^{(N)}=\frac{1}{N}$. We note this category distribution as $q_{\phi}({\mathbf{x}})$. Since $q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)})=\frac{1}{N}$, the empirical distribution can be derived as $q_{\phi}({\mathbf{z}})=\sum_{i=1}^{N}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)})=\frac{1}{N}\sum_{i=1}^{N}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})$. $q_{\phi}({\mathbf{z}})$ is called aggregated posterior distribution (Makhzani et al., 2015), which is difficult to obtain analytical solutions. Sampling to calculate the estimate of mutual information and marginal KL-Divergence is generally (Hoffman & Johnson, 2016; Dieng et al., 2018).

We explore mutual information $\mathcal{I}_{q_{\phi}}$ from the perspective of empirical distribution. According to the definition of mutual information, the mutual information $\mathcal{I}_{q_{\phi}}$ can be rewritten as:

$\displaystyle\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})=\mathbb{E}_{q_{\phi}({\mathbf{x}})}\left[\int q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})\text{log }\frac{q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})}{q_{\phi}({\mathbf{z}})}\text{d}{\mathbf{z}}\right]$

(4)

For the integral term in the form equation 4, since $q_{\phi}({\mathbf{z}})=\frac{1}{N}\sum_{i=1}^{N}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})$. we can select $M$ sample to approximate in each training batch, $q_{\phi}({\mathbf{z}})\simeq\frac{1}{M}\sum_{i=1}^{M}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})$. But unfortunately, this method of estimation is biased, we will use another method to calculate mutual information.

From Theorem 3.1, MINE (Belghazi et al., 2018) has been proposed as a method for estimating mutual information using a neural network. If $p({\bm{x}}),q({\bm{x}})$ are the density functions of $\mathbb{P},\mathbb{Q}$ respectively, given any subclass $\mathcal{F}$ of such functions, then have

$$\mathcal{I}({\mathbf{x}},{\mathbf{z}})\geq\sup_{T\in\mathcal{F}}\big{\{}\mathbb{E}_{p({\mathbf{x}},{\mathbf{z}})}[T({\mathbf{x}},{\mathbf{z}})]-\text{log }\big{(}\mathbb{E}_{p({\mathbf{x}})p({\mathbf{z}})}\big{[}\text{exp }\big{(}T({\mathbf{x}},{\mathbf{z}})\big{)}\big{]}\big{)}\big{\}}$$

(6)

where $T\in\mathcal{F}$ can be fitted with a neuron network $T_{\psi}$ parameterized $\psi\in\Psi$. The expectations in the above lower-bound can then be estimated by Monte-carlo sampling. After sampling, we can get

$$\hat{\psi}=\arg\sup_{\psi\in\Psi}\big{\{}\mathbb{E}_{q({\mathbf{x}},{\mathbf{z}})}[T_{\psi}({\mathbf{x}},{\mathbf{z}})]-\text{log }\big{(}\mathbb{E}_{q({\mathbf{x}})q({\mathbf{z}})}\big{[}\text{exp }\big{(}T_{\psi}({\mathbf{x}},{\mathbf{z}})\big{)}\big{]}\big{)}\big{\}}$$

(7)

then we obtain the Mutual Information Neural Estimator (MINE):

$$\hat{\mathcal{I}}({\mathbf{x}},{\mathbf{z}})=\mathbb{E}_{q({\mathbf{x}},{\mathbf{z}})}[T_{\hat{\psi}}({\mathbf{x}},{\mathbf{z}})]-\text{log }\big{(}\mathbb{E}_{q({\mathbf{x}})q({\mathbf{z}})}\big{[}\text{exp }\big{(}T_{\hat{\psi}}({\mathbf{x}},{\mathbf{z}})\big{)}\big{]}\big{)}$$

(8)

In this paper, we add an auxiliary softmax multi-classifier based on VAE to solve the mutual information $\mathcal{I}_{q_{\phi}}$, which is called VAE-AS. For mutual information, we can write

$\displaystyle\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})=\text{log }N-\mathbb{E}_{q_{\phi}({\mathbf{z}})}\left[\mathcal{H}\left(q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})\right)\right]$

(9)

In order to calculate the mutual information, we need to solve $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$ and the entropy of $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$. According to Bayes’ theorem, $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})=\frac{q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})q_{\phi}({\mathbf{x}})}{q_{\phi}({\mathbf{z}})}$, and $q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)})=\frac{1}{N}$, $q_{\phi}({\mathbf{z}})=\frac{1}{N}\sum_{i=1}^{N}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})$, we know,

$\displaystyle q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)}\mid{\mathbf{z}})=\frac{q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})}{\sum_{j=1}^{N}q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(j)})}$

(10)

As can be seen from the discussion in the previous section, it is still difficult to directly calculate equation 10. We use the auxiliary softmax multi-classifier to fit $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$. First number each sample, let $\{{\bm{x}}^{(1)},\ldots,{\bm{x}}^{(N)}\}\mapsto\{1,\cdots,N\}$. Equivalent to determining a label ${\bm{e}}^{(i)}$ for each sample ${\bm{x}}^{(i)}$, Where ${\bm{e}}^{(i)}$ is the one-hot variable $[0,\dots,0,1,0,\dots,0]$ with a 1 at position $i$. i.e.

$${\mathbf{e}}_{j}^{(i)}=\left\{\begin{aligned} &1\quad if\ j=i\\ &0\quad if\ j\neq i\end{aligned}\right.$$

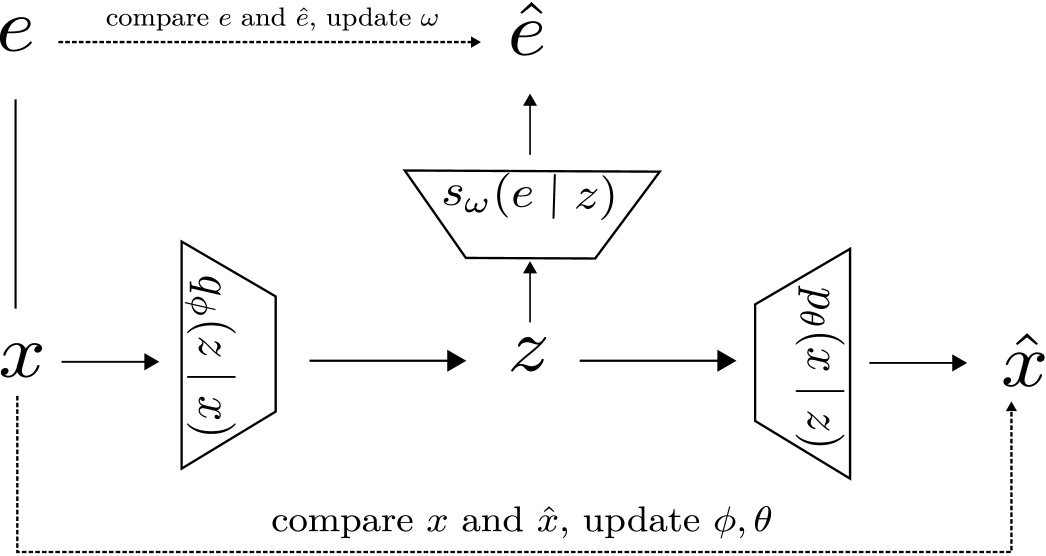
Based on the structure of VAE, we add a multi layer neural network $s_{\omega}(\hat{{\mathbf{e}}}\mid{\mathbf{z}})$ to fit the distribution $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$ . The network $s_{\omega}(\hat{{\mathbf{e}}}\mid{\mathbf{z}})$ is trained in a supervised manner, we use the one-hot variable ${\bm{e}}$ as label, the activation function of the network $s_{\omega}(\hat{{\mathbf{e}}}\mid{\mathbf{z}})$ is the softmax function.

For each sampled ${\bm{z}}^{(l)}$, after a multi-layered neuron network transformation, let ${\bm{h}}^{(l)}_{0}={\bm{z}}^{(l)}$, ${\bm{h}}^{(l)}_{t}=g(\omega_{t-1}^{T}{\bm{h}}^{(l)}_{t-1})$, where $g(\cdot)$ is activation function, such as $tanh$ or $ReLU$. The output ${\bm{h}}^{(l)}_{o}=\omega_{t}^{T}{\bm{h}}^{(l)}_{t}$, where ${\bm{h}}^{(l)}_{o}$ is $N$ dimensions vector, The element $i$ of ${\bm{h}}^{(l)}_{o}$ is ${\bm{h}}^{(l)}_{o,i}$. The auxiliary softmax multi-classifier can be written as:

$\displaystyle s_{\omega}(\hat{{\mathbf{e}}}_{i}=1\mid{\bm{z}}^{(l)})=\frac{\text{exp }({\bm{h}}^{(l)}_{o,i})}{\sum_{j=1}^{N}\text{exp }({\bm{h}}^{(l)}_{o,j})}$

(11)

Since the serial number can be seen as a random tag ${\bm{e}}^{(i)}$ allocated for each sample ${\bm{x}}^{(i)}$, The loss function is the cross entropy of the softmax function, i.e.

$\displaystyle loss_{s}=-\frac{1}{L}\sum_{l=1}^{L}\sum_{j=1}^{N}{\bm{e}}_{j}^{(i)}\text{log }s_{\omega}(\hat{{\mathbf{e}}}_{j}=1\mid{\bm{z}}^{(l)})$

(12)

Minimizing the cross entropy loss function, We hope $s_{\omega}(\hat{{\mathbf{e}}}\mid{\mathbf{z}})$ will gradually converge to $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$. After completing the fitting of the distribution $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$, we can calculate the entropy $\mathcal{H}\left(q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})\right)$ .

$\displaystyle\mathcal{H}\left(q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})\right)=-\sum_{i=1}^{N}q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)}\mid{\mathbf{z}})\text{log }q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)}\mid{\mathbf{z}})$

(13)

then we can calculate the mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ with equation 9.

For Calculating $D_{KL}\left(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}})\right)$, we need calculate $q_{\phi}({\mathbf{z}})$, and then estimate with Monte Carlo Sampling. After using the auxiliary softmax to estimate $q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)}\mid{\mathbf{z}})$, we can estimate $q_{\phi}({\mathbf{z}})$ by Bayesian formula.

$\displaystyle q_{\phi}({\mathbf{z}})=\frac{q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})}{Nq_{\phi}({\mathbf{x}}={\bm{x}}^{(i)}\mid{\mathbf{z}})}$

(14)

After estimating the mutual information and the marginal divergence we can calculate ELBO as equation 3.

Calculating mutual information by the formula equation 13 requires traversal of all samples, which is computationally burdensome. The following proposition will give an approximate estimate.

Intuitively, Theorem prop-1 simplifies the entropy calculation in a Multinomial distribution by using the part of the error probability as a whole. Therefore, a bias of $\mathbb{P}_{e}\text{log }N$ will be generated. With optimization, the predicted error rate $\mathbb{P}_{e}$ will gradually decrease, The gap between $\hat{\mathcal{I}}({\mathbf{z}},{\mathbf{x}})$ and $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ will be gradually reduced to $0$.

When the sample size is large, the cost of softmax multi-classification calculation is large. $q_{\phi}({\mathbf{z}})$ needs to calculate the sum of all categories probability, i.e. the normalized part of the denominator of the softmax function. To reduce the computational load of the softmax function, similar to the Huffman tree method used in (Morin & Bengio, 2005), we uses bianry tree.

For each ${\bm{x}}^{(i)}$ we define tags ${\bm{e}}^{(i)}$, ${\bm{e}}$ is one-hot random vector, w.r.t. sampling ${\bm{z}}^{(l)}$, the output vector of classifier network $s_{\omega}$ is ${\bm{h}}^{(l)}$. Construct a $V$ layers binary tree, each leaf node, representing a component of the one-hot vector, every two child node has one parent node, finally shrink to the root node. Each layer before the leaf node is noted as ${\bm{t}}^{(1)},\dots,{\bm{t}}^{(V)}$, let ${\bm{t}}^{(l,v)}=\omega^{(v)}{\bm{h}}^{(l)}$, where $\omega^{(v)}$ is parameter matrix. The vector length is increased layer by layer, with up to $2^{v}$ nodes per layer. It can be seen that for $N$ samples, $V>=\text{log}_{2}\frac{N}{2}$. Except for leaf nodes, each node component $t^{(v)}_{j}$ has one left and one right child nodes (edge nodes maybe has one child). The path from the parent node to the child node is denoted as $d_{j}^{(v)}$, and when $d_{j}^{(v)}=1$, the node $t_{j}^{(v)}$ select the path to left child, select right child when $d_{j}^{(v)}=0$.

using the sigmoid activation function $\sigma(\cdot)$ to calculate the probability of two paths.

$$\mathbb{P}(d^{(v)}_{j}=1\mid{\bm{z}}^{(l)})=\sigma(t^{(l,v)}_{j})$$

correspondingly we know $\mathbb{P}(d_{j}^{(v)}=0\mid{\bm{z}}^{(l)})=1-\sigma(t^{(l,v)}_{j})$. For an one-hot vector ${\bm{e}}^{(i)}$, there is a unique path on the binary tree pointing to its corresponding leaf node. The node through which the path passes is $t_{j_{1}}^{(l,1)},\dots,t_{j_{V}}^{(l,V)}$, The path of the selected child node for each node $t_{j_{v}}^{(l,v)}$ is $d_{j_{v}}^{(l,v)}$. Then the fit probability of the classifier is

$$s_{\omega}(\hat{{\bm{e}}}={\bm{e}}^{(i)}\mid{\bm{z}}^{(l)})=\prod_{v=1}^{V}\mathbb{P}(d_{j_{v}}^{(l,v)}\mid{\bm{z}}^{(l)})$$

where $d_{j_{v}}^{(l,v)}$ is $0$ or $1$. Compare $\hat{{\bm{e}}}$ and ${\bm{e}}$ to construct the loss function, the parameters $\omega$ in the binary tree are optimized to fit the softmax function.

Using the softmax function approximation, the computational complexity is $O(hN)$, where $h$ is the classifier output feature number. Based on multidimensional binary labels, the computational complexity is optimized to $O(h\text{ log}_{2}N)$.

In the structure of VAE, when the distributions mapped by one sample ${\bm{x}}^{(i)}$ and another sample ${\bm{x}}^{(j)}$ are far away in the latent variable space, i.e. ${\bm{x}}^{(i)}$ and ${\bm{x}}^{(j)}$ are quite different, Even if the identity of the two is same, it will not affect the system’s fit of $q_{\phi}({\mathbf{x}}\mid{\mathbf{z}})$. In other words, the number of label categories we randomly select for the sample can be smaller than the actual number of samples. If we select the number of tag categories as $V$, refer to the entropy $\mathcal{H}(q_{\phi}({\mathbf{x}}\mid{\mathbf{z}}))$ for equation 13, The maximum entropy of the fitted distribution is $\text{log }V$, which is the case where the fitting distribution is completely indistinguishable from the uniform probability value of ${\mathbf{x}}$. From $0<\mathcal{I}_{q_{\phi}({\mathbf{z}},{\mathbf{x}})}<\text{log }N$ (see Appendix for details), The maximum value of the mutual information $\mathcal{I}_{q_{\phi}}$ and the maximum value of $\mathbb{E}_{q_{\phi}({\mathbf{z}})}\mathcal{H}(q_{\phi}({\mathbf{x}}|{\mathbf{z}}))$ is same, i.e. $\text{log }N$. The maximum mutual information that we can provide by using the $V$ tag category through the auxiliary softmax multi-classifier is $\text{log }V$. Since the log function grows very slowly, selecting $V$ categories smaller than $N$ will not affect the VAE-AS’s mutual information so much.

To test the actual effect of VAE-AS, we selected two reference data sets of image, MNIST (LeCun et al., 1998) and Omniglot (Lake et al., 2013; Burda et al., 2015). The MNIST data set includes 70,000 binary black and white handwritten digital images, for MNIST, 55,000 for training and 10,000 for testing. The Omniglot data set contains $1623$ different handwritten characters from 50 different alphabets. The training set has $24345$ samples, and test set has $8069$ samples. Each characters was drawn online by $20$ different people. The image size of both data sets is $28\times 28$

Firstly, we use of VAE-AS to estimate mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ and marginal divergence $D_{KL}(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}}))$. For the dataset MNIST (LeCun et al., 1998), Construct encoders, decoders and classifiers using MLP, the number of layers is $2$, $3$, $2$, the number of hidden layers is chosen to be $500$, the dimension of ${\mathbf{z}}$ is set to $40$, the mini-batches is set to $100$ and the iteration epochs is set to $120$.

From the model, for each sample ${\bm{x}}^{(i)}$, $\mu({\bm{x}}^{(i)})$ and $\sigma({\bm{x}}^{(i)})$ is generated, Using Monte Carlo method to estimate $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ and $D_{KL}(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}}))$, the method is same as  (Hoffman & Johnson, 2016). Set sample number of Monte Carlo to $S$, sampling $55000,10000,5000,1000,500,100$ to estimate mutual information and marginal divergence.

Set the number of softmax labels to the full sample size of training set of MNIST $55000$, using VAE-AS to estimate mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ and marginal divergence $D_{KL}(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}}))$. The test is notted as $\text{VAE-AS}_{55000}$. To compare the results, we set the number of softmax labels to $10000$, performe a comparision test $\text{VAE-AS}_{10000}$. The test results are shown in Figure 2:

From the Figure 2 we can see, for the Monte Carlo method, as the number of samples drops, whether the mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ or marginal divergence $D_{KL}(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}}))$, will produce large bias. And in the case of a small sample, there are a lot of fluctuations in the curve, which shows that Monte Carlo method will introduce a large variance due to sampling. Generally limited by computing resources, we can’t choose too much for mini-batch size during training. Using VAE-AS to fit $q_{\phi}({\mathbf{x}}={\bm{x}}^{(i)}\mid{\mathbf{z}})$, then estimate mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ and marginal divergence $D_{KL}(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}}))$. The estimated results are close to the large sample size Monte Carlo method. Since VAE-AS only needs a large vocabulary, the dimension of the classification label is small, the demand for computation space can generally be satisfied.

The third figure depicts the sum of mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$ and marginal divergence $D_{KL}(q_{\phi}({\mathbf{z}})\ ||\ p_{\theta}({\mathbf{z}}))$, compare with KL-Divergence $D_{KL}(q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})\ ||\ p_{\theta}({\mathbf{z}}))$. It can be seen that the sum of mutual information and marginal divergence has a good convergence to the mean of KL-Divergence, where SC is softmax cross-entropy.

We tested the results of different parameters $\alpha$ and $\beta$ on VAE-AS optimization. The encoder inference network $q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})$ , the decoder generation network $p_{\theta}({\mathbf{x}}\mid{\mathbf{z}})$ and the classifier network $s_{\omega}({\mathbf{e}}\mid{\mathbf{x}})$ are both constructed using multiple hidden layer neural networks MLP, the number of layers is $2$, $5$, $2$. The number of hidden layers is chosen to be $500$. the dimension of ${\mathbf{z}}$ is set to $40$, the mini-batches is set to $128$ and iteration epochs is set to $300$. No other regular constraints are set.

In the test metrics, NLL_test is a non-negative likelihood based on the test set evaluation. Using the method described in  (Burda et al., 2015), the number of samples is $4096$. KL_test is the KL-Divergence $D_{KL}\left[q_{\phi}({\mathbf{z}}\mid{\bm{x}}^{(i)})\ ||\ p_{\theta}({\mathbf{z}})\right]$ based on the test set. AU is the number of active units of the latent variable ${\mathbf{z}}$, for this indicator we use the definition in  (Burda et al., 2015):

$$AU=\sum_{d=1}^{D}\mathbb{I}\{\text{Cov}_{p({\mathbf{x}})}\left(\mathbb{E}_{q_{\phi}({\mathbf{z}}\mid{\mathbf{x}})}[{\mathbf{z}}_{d}]\right)\geq\varepsilon\}$$

Where $\mathbb{I}(\cdot)$ is the indicator function, $D$ is the dimension of the latent variable ${\mathbf{z}}$, ${\mathbf{z}}_{d}$ is the element $d$ of ${\mathbf{z}}$, $\varepsilon$ is the judgment threshold and is set to $0.01$. NNL_train, KL_train is the reconstruction error and KL-Divergence based on the training set. MI is mutual information $\mathcal{I}_{q_{\phi}}({\mathbf{z}},{\mathbf{x}})$, MD is marginal divergence $D_{KL}(q_{\phi}({\mathbf{z}})||p_{\theta}({\mathbf{z}}))$, estimated by VAE-AS during training. SC is softmax cross-entropy.