MuLan Collaboration
Improved Measurement of the Positive Muon Lifetime and
Determination of the Fermi Constant
Abstract
The mean life of the positive muon has been measured to a precision of 11 ppm using a low-energy, pulsed muon beam stopped in a ferromagnetic target, which was surrounded by a scintillator detector array. The result, s, is in excellent agreement with the previous world average. The new world average s determines the Fermi constant GeV-2 (5 ppm). Additionally, the precision measurement of the positive muon lifetime is needed to determine the nucleon pseudoscalar coupling .
pacs:
14.60.Ef, 13.35.-r, 13.35.BvThe predictive power of the standard model relies on precision measurements of its input parameters. Impressive examples include the fine-structure constant gerry , the mass ewwg , and the Fermi constant vanRitbergen:All , having relative precisions of 0.0007, 23, and 9 ppm, respectively.
The Fermi constant is related vanRitbergen:All to the electroweak gauge coupling by
| (1) |
where represents the weak-boson-mediated tree-level and radiative corrections, which have been computed to second order Awramik:TwoLoopMuonLifetime . Comparison of the Fermi constant extracted from various measurements stringently tests the universality of the weak interaction’s strength fermiconstants .
The most precise determination of is based on the mean life of the positive muon, . It has long been known that in the Fermi theory, the QED radiative corrections are finite to first order in and to all orders in the electromagnetic coupling constant, BermanSirlin . This provides a framework vanRitbergen:All for extracting from ,
| (2) |
where is the sum of phase space and both QED and hadronic radiative corrections, which have been known in lowest-order since the 1950s oldQED . Relation 2 does not depend on the specifics of the underlying electroweak model.
Until recently, the uncertainty on extracting from was limited by the uncertainty in higher-order QED corrections, rather than by measurement. In 1999, van Ritbergen and Stuart’s calculation of the second-order QED corrections vanRitbergen:All reduced the relative theoretical uncertainty in the determination of to less than 0.3 ppm. The dominant uncertainty is currently from , which motivates this work. While the final goal of our experiment is a 1 ppm uncertainty on , we report here a result having a precision of 11 ppm—2.5 times better than any previous measurement lifetimes —based on data obtained in 2004, the commissioning run period.
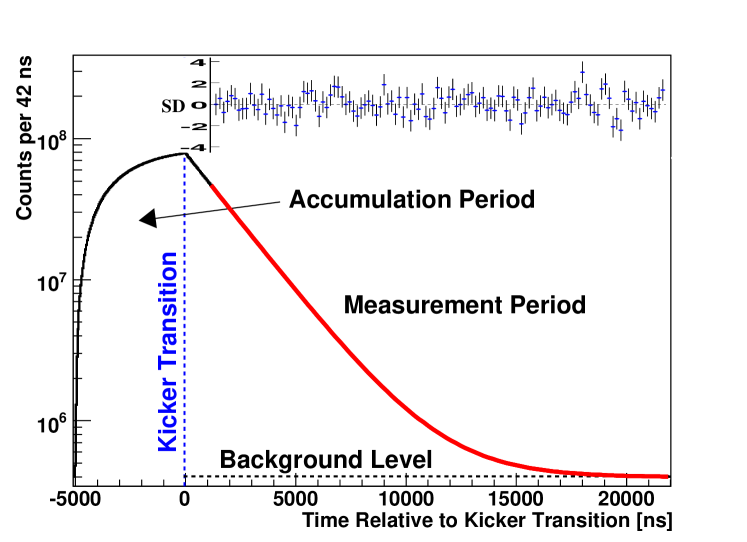
The experimental design is conceptually simple. Longitudinally polarized muons from the E3 beamline at the Paul Scherrer Institute are stopped in a thin ferromagnetic target. A fast-switching kicker imposes a cycle on the continuous beam, consisting of a s “beam-on” period of stopped-muon accumulation, , followed by a s “beam-off” measurement period, . The muon decay positrons are detected in a scintillator array which surrounds the target. A decay time spectrum for a subset of the detectors is shown in Fig. 1. The background level is indicative of the “extinction” of the beam during , caused by the kicker.
The beamline is tuned to transport 28.8 MeV/ muons from pions that decay at rest near the surface of the production target. Two opposing bends raise the beam from ground level to the experimental area, where it is directed parallel to the optic axis through an velocity separator that removes the contamination. The muons continue undeflected through the (uncharged) kicker and are focused on a 1.2-cm tall by 6.5-cm wide aperture. The activated (charged) kicker induces a 36 mrad vertical deflection, which causes the beam to be blocked at the aperture. In 2004, the average unkicked muon rate was limited to MHz; approximately 10 muons were accumulated per cycle, of which 4 remained undecayed when began.
The kicker is described in detail in Ref. kicker . Briefly, it consists of two pairs of electrode plates biased to produce a potential difference of up to kV, with a virtual ground at the midplane. Modulators, using series-connected MOSFETs operating in push-pull mode, charge or discharge the plates. In 2004, a partial system achieved an average beam extinction of with a 60 ns switching time kickernow . During , changed by less than 0.25 V. A time dependence of at this level, together with a voltage dependent extinction, gives rise to a 3.5 ppm systematic error on the muon lifetime.
The parity-violating correlation between the muon’s spin orientation and the emission direction of its decay positron can lead to a systematic shift in the extracted lifetime, for the following reasons: Suppose detector at position counts positrons at the rate , where is the polarization of the stopped muons. If varies with time because of relaxation or spin rotation caused by magnetic fields, so will . A temporal variation that is long compared to will manifest itself as an unobserved distortion to the fitted lifetime of the detector. The spin-related systematic uncertainty in is minimized through both detector symmetry and target choice: the positron detectors are arranged as a symmetric ball covering a large solid angle, and every detector at position is mirrored by another detector, at . To the extent that the detector pairs have the same geometrical acceptance and efficiency is independent of the value of , and therefore also its time variation. Finally, a target possessing a high internal magnetic field is used so that the muon spin precession period is .
As depicted in Fig. 2, the muon beam exits its vacuum pipe through a 9.3-cm diameter, 76-m-thick Mylar window, then passes through a thin, high-rate multiwire entrance muon chamber (EMC), which records the time and position of muons entering the detector. Roughly 1 in muons stop in the EMC. Their spins precess in the field of a permanent magnet array, which has a mean transverse field of 11 mT at the EMC center. The field orientation was regularly reversed throughout data taking. The region between the exit of the EMC and the target is spanned by a helium-filled balloon (instead of air) to minimize muon stops and scattering.
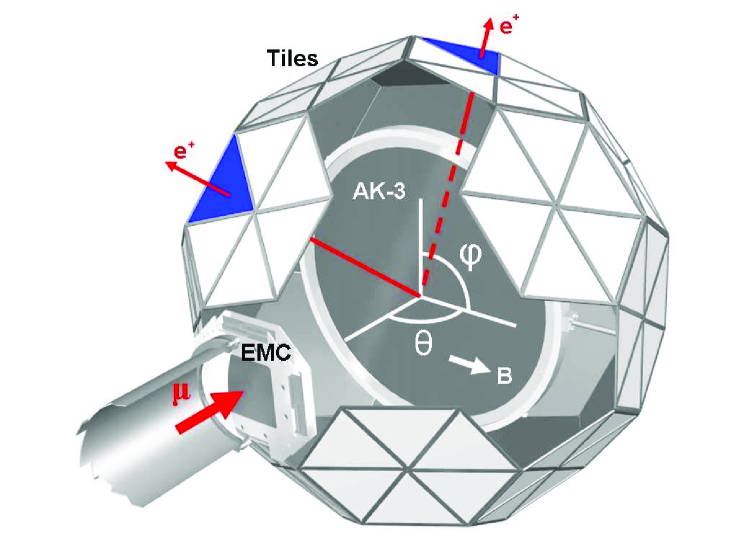
The stopping target is a 0.5-mm thick, 50-cm diameter disk of ArnokromeTM III (AK-3) arnokrome , having an internal magnetic field of approximately 0.4 T, oriented transverse to the muon spin axis. The field direction was reversed at regular intervals. Dedicated SR measurements morenzoni on an AK-3 sample show an 18-ns oscillation period with a large initial asymmetry that relaxes with a time constant of 14 ns. These times are considerably shorter than the accumulation period, . Using the difference spectrum of counts from mirrored detectors versus time; e.g., , the longer-term components are shown to be negligible.
The decay positrons are recorded by 170 detector elements, each consisting of an inner and outer layer of 3-mm-thick, BC-404 plastic scintillator. Each triangle-shaped scintillator is read edge-on using a lightguide mounted at , which is coupled to a 29-mm photomultiplier tube (PMT). The 170 elements are organized in groups of six and five to form the 20 hexagon and 10 pentagon faces of a truncated icosahedron (two pentagons are omitted for the beam entry and symmetric exit). The distance from target center to an inner scintillator is 40.5 cm. The total acceptance is , taking into account the reduction in the geometrical coverage of from positron range and annihilation in the target and detector materials.
A clip line reshapes the natural PMT pulse width to a full-width at maximum of 9 ns. These signals are routed to leading-edge discriminators that have 10 ns output widths. On average, a throughgoing positron gives a signal of 70 photoelectrons, producing a 400-mV pulse height. The data taking was split almost evenly between periods of 80-mV and 200-mV discriminator thresholds. The arrival time of a positron is measured with respect to the kicker transition by a CAEN V767 128-channel, multihit TDC. An Agilent E4400B frequency synthesizer, operating at approximately 190.2 MHz, serves as the master clock. Its absolute frequency is accurate to and its central value did not change at this level over the course of the run. A clock step-down and distribution system provides a 23.75 MHz square wave as the input clock for each TDC.
The master clock frequency was given a concealed offset within ppm from 190.2 MHz. The analyzers added a fitting offset to when reporting intermediate results. Only after the analysis was complete was the exact oscillator frequency revealed, and the fitting offset removed, to obtain the lifetime.
The raw data consist of individual scintillator hit times for each cycle. The kicker transition defines a common (global) , using the 1.32 ns resolution provided by the 32 subdivisions of the TDC input oscillator period. To avoid problems with differential nonlinearities in the TDC clock period division circuit, coincidence windows, artificial deadtimes, and decay histogram bin widths were always set at integer multiples of the undivided input clock period (42 ns).
Events are missed if a positron passes through a detector during the electronic or software-imposed deadtime following a recorded event in the same detector. With peak rates in individual detectors of 7 kHz, the “pileup” probability for a 42-ns deadtime is . If unaccounted for, this leads to a 67 ppm shift in the fitted . Pileup can be accommodated by including an term in the fit function, but this doubles the uncertainty on the fitted . Instead, an artificial pileup spectrum, constructed from secondary hits occurring in a fixed-width time window that is offset from a primary hit, is added back to the raw spectrum, thus restoring, on average, the missing hits. The procedure is repeated using a wide range of artificial deadtime periods and offsets, and the corrected spectra all give consistent lifetimes. The systematic uncertainty from this procedure is 2 ppm.
Preliminary fits to the decay time spectra using the function showed a common structure in the residuals at early times, independent of experimental condition or detector. The structure is caused by an intrinsic flaw in the TDC, which does not lose events but can shift them in time by ps. This behavior was characterized in extensive laboratory tests using white-noise and fixed-frequency sources, together with signals that simulate the kicker transitions. For a fit start time of s, the TDC response settles into a simple pattern that can be described well by a modification of the decay time spectrum by a factor
| (3) |
where , and with typical values of , ns, and ns. A spectrum of white-noise events was fit to a constant function, modified by , achieving a good and structureless residuals.
The function used to fit the decay time spectra is
| (4) |
Because the clock frequency was blinded during the analysis, and in could not be fixed in the fits. With the clock frequency revealed, these parameters are found to be consistent with the laboratory values. In an important test of the appropriateness of Eq. 4, the fitted is found to be independent of the fit start time beyond the minimal s. The systematic uncertainty for the TDC response is 1 ppm.
Subsequent to the 2004 run, waveform digitizers (WFDs) replaced the discriminator and TDC timing system. The WFDs establish the stability of the PMT gain versus time during . A gain change, together with a fixed discriminator threshold (as in 2004), will appear as a time-dependent efficiency. The analysis of the PMT gain stability over a range of instantaneous rates indicates a systematic effect of less than 1.8 ppm on .
A powerful consistency test is performed by grouping data from detectors having a common azimuthal angle (see Fig. 2), fitting each group independently, and sorting the lifetime results by , where is the polar angle. For the AK-3 data, the lifetime distribution is flat over (). For data taken with a 20-cm diameter sulfur target, surrounded by a permanent magnet array, the same distribution is not flat (). The cause in the latter case is a higher fraction of muons that miss the target and stop downstream along inner detector walls. The SRIM program sims finds that of the muons miss the smaller sulfur target, while only miss the AK-3 target. In both cases, suffer large-angle scatters in the EMC or backscatter from the target, stopping in upstream detector walls. Simulated decay spectra for all “errant” muons—using the muon stopping distribution predicted by SRIM and including detector element acceptance, initial muon polarization, and relaxation—were used to determine the expected distortion to the lifetime. The procedure was tested against a special data set in which all incoming muons were stopped in a plastic plate placed midway between the EMC and the target. The distribution of lifetimes with was successfully reproduced. For the AK-3 target, a distortion as large as 1 ppm could be expected. However, a negative shift in the range of ppm is implied for sulfur, principally owing to the times larger fraction of downstream muon stops. The uncertainty on a correction of this magnitude could be as large as , exceeding the 15 ppm statistical precision of the sulfur data sample. Therefore, we chose not to use the sulfur data in our reported results—a decision made prior to unblinding the clock frequency—even though such a correction would bring the fitted sulfur lifetime into excellent agreement with that found for AK-3. We conservatively assign a 2 ppm systematic uncertainty to this procedure for the AK-3 data set.
Other small systematic uncertainties are listed in Table 1. Data integrity checks indicate a small fraction of hits () that may be duplicates of earlier hits. When the duplicates are removed, shifts upwards by 2 ppm. Since the status of these hits is uncertain, a correction of +1 ppm is applied to with a systematic uncertainty of 1 ppm. A systematic error from queuing losses in the TDC single-channel buffer is calculated to be less than 0.7 ppm. The systematic error from timing shifts induced by previous hits in a channel during the measurement period is less than 0.8 ppm.
The final result is based on a fit using Eq. 4 to the events in the summed AK-3 spectra, giving
with a . The first error is statistical and the second is the quadrature sum of the systematic uncertainties in Table 1. Figure 1 indicates the range of the fitted region and the inset displays the residuals divided by their uncertainty in units of standard deviations from the fit. The consistency of was checked against experimental conditions, including detector, threshold, target and magnet orientation, extinction factor, kicker voltage, and run number. Only a sub-group of runs at the beginning of the production period exhibited an anomalous lifetime compared to the sum. When all runs, in groups of 10, are fit to a constant, a is obtained, suggestive that the sub-group fluctuation was statistical.
Our fitted lifetime is in excellent agreement with the world average, s, which is based on four previous measurements lifetimes . The improved world average is
Assuming the standard model value of the Michel parameter , and light neutrinos, determines the Fermi constant
In a companion Letter MuCap , a new determination of the induced pseudoscalar coupling is reported. It depends mainly on a comparison of negative and positive muon lifetimes, the latter quantity being reported here.
We acknowledge the generous support from PSI and the assistance of its accelerator and detector groups. We thank W. Bertl, J. Blackburn, K. Gabathuler, K. Dieters, J. Doornbos, J. Egger, W.J. Marciano, D. Renker, U. Rohrer, R. Scheuermann, R.G. Stuart and E. Thorsland for discussions and assistance. This work was supported in part by the U.S. Department of Energy, the U.S. National Science Foundation, and the John Simon Guggenheim Foundation (DWH).
| Source | Size (ppm) |
|---|---|
| Extinction stability | 3.5 |
| Deadtime correction | 2.0 |
| TDC response | 1.0 |
| Gain stability | 1.8 |
| Errant muon stops | 2.0 |
| Duplicate words (+1 ppm shift) | 1.0 |
| Queuing loss | 0.7 |
| Multiple hit timing shifts | 0.8 |
| Total | 5.2 |
References
- (1) G. Gabrielse, D. Hanneke, T. Kinoshita, M. Nio, and B. Odom, Phys. Rev. Lett. 97, 030802 (2006).
- (2) S. Schael et al., Phys. Rept. 427, 257 (2006).
- (3) T. van Ritbergen and R. G. Stuart, Nucl. Phys. B564, 343 (2000); T. van Ritbergen and R. G. Stuart, Phys. Lett. B437, 201 (1998); T. van Ritbergen and R. G. Stuart, Phys. Rev. Lett. 82, 488 (1999).
- (4) M. Awramik, M. Czakon, A. Freitas, and G. Weiglein, Phys. Rev. D69, 053006 (2004).
- (5) W.J. Marciano, Phys. Rev. D60, 093006 (1999).
- (6) S.M. Berman and A. Sirlin, Ann. Phys. 20, 20 (1962).
- (7) S.M. Berman, Phys. Rev. 112, 267 (1958); T. Kinoshita and A. Sirlin, Phys. Rev. 113, 1652 (1959).
- (8) G. Bardin et al., Phys. Lett. B137, 135 (1984); K. Giovanetti et al., Phys. Rev. D29, 343 (1984); M.P. Balandin et al., Sov. Phys. JETP 40, 811 (1974); and J. Duclos et al., Phys. Lett. B47, 491 (1973).
- (9) M.J. Barnes and G.D. Wait, IEEE Trans. Plasma Sci. 32, 1932 (2004); R.B. Armenta, M.J. Barnes, G.D. Wait, Proc. of 15th IEEE Int. Pulsed Power Conf., June 13-17 2005, Monterey, USA.
- (10) Using the full system (four modulators instead of two), is achieved with a 45 ns switching time.
- (11) ArnokromeTM III (AK-3) is an alloy of Cr, Co and Fe. Arnold Engineering Co., Alnico Products Division, 300 N. West Street, Marengo, IL 60152.
- (12) E. Morenzoni and H. Luetkens, private communication.
- (13) J.F. Ziegler, J.P. Biersack and U. Littmark, The Stopping and Range of Ions in Matter, Pergamon Press, New York, (2003).
- (14) MuCap Collaboration: V.A. Andreev et al., This volume.