Improved Vocal Effort Transfer Vector Estimation for Vocal Effort-Robust Speaker Verification
Abstract
Despite the maturity of modern speaker verification technology, its performance still significantly degrades when facing non-neutrally-phonated (e.g., shouted and whispered) speech. To address this issue, in this paper, we propose a new speaker embedding compensation method based on a minimum mean square error (MMSE) estimator. This method models the joint distribution of the vocal effort transfer vector and non-neutrally-phonated embedding spaces and operates in a principal component analysis domain to cope with non-neutrally-phonated speech data scarcity. Experiments are carried out using a cutting-edge speaker verification system integrating a powerful self-supervised pre-trained model for speech representation. In comparison with a state-of-the-art embedding compensation method, the proposed MMSE estimator yields superior and competitive equal error rate results when tackling shouted and whispered speech, respectively.
Index Terms— Speaker verification, vocal effort, embedding compensation, shouted speech, whispered speech
1 Introduction
State-of-the-art speaker verification technology achieves impressive performance when dealing with neutrally-phonated (i.e., normal) speech [1, 2, 3]. However, because normal speech data are mostly used —due to obvious reasons— to train speaker verification systems, their performance tends to dramatically drop in the presence of non-neutrally-phonated (e.g., shouted and whispered) speech [4, 5]. To mitigate this issue, previous work [4, 5] explored a series of minimum mean square error (MMSE) techniques estimating normal speaker embeddings from non-neutrally-phonated ones. Among all of these techniques, multi-environment model-based linear normalization (MEMLIN) [6] —modeling both the normal and non-neutrally-phonated embedding spaces by Gaussian mixtures— provided the best performance in terms of equal error rate (EER) when dealing with both shouted and whispered speech [5].
Under Gaussian mixture modeling assumption, it is well known that the MMSE estimator can be expressed as a weighted sum of a set of partial estimates [7]. A shortcoming of MEMLIN is that the set of partial estimates is pre-computed (during an offline training stage) and fixed [6]. Therefore, these partial estimates do not account for the specificities of the non-neutrally-phonated embeddings observed at test time. In this paper, we propose an alternative MMSE estimator that overcomes this MEMLIN’s limitation by modeling the joint distribution of the vocal effort transfer vector111As explained in Section 2, the vocal effort transfer vector relates equivalent normal and non-neutrally-phonated speaker embeddings according to an additive model. and non-neutrally-phonated embedding spaces. Furthermore, to circumvent non-neutrally-phonated speech data scarcity, we also propose to carry out the estimation in a principal component analysis (PCA) domain. In fact, this data scarcity prevents us from leveraging deep learning for embedding compensation.
We conduct experiments employing a state-of-the-art speaker verification system consisting of the concatenation of a powerful self-supervised pre-trained model for speech representation so-called WavLM [3] and an ECAPA-TDNN [1] back-end for speaker embedding extraction. In comparison with MEMLIN, the proposal at hand shows superior and competitive EER performance when dealing with shouted and whispered speech, respectively.
The remainder of this manuscript is organized as follows. Our normal speaker embedding estimation methodology is developed in Section 2. Section 3 provides the reader with an overview of the whole vocal effort-robust speaker verification system. Section 4 is devoted to discuss the experimental results. Finally, Section 5 wraps up this work.
2 Normal Speaker Embedding Estimation
2.1 Problem Statement
Given a particular speaker, let be a -dimensional speaker embedding extracted from an utterance with normal vocal effort. Furthermore, let be a non-neutrally-phonated counterpart of . Then, we assume the following additive model:
| (1) |
where represents a vocal effort transfer vector between the normal and non-neutrally-phonated modes.
For vocal effort-robust speaker verification purposes, previous work [4, 5] proposed to estimate from an estimate of the vocal effort transfer vector, , by following the additive model of Eq. (1):
| (2) |
Several MMSE compensation techniques where studied in [4, 5] to realize Eq. (2), and, among them, MEMLIN [6] showed to be the best performing one. Assuming that the non-neutrally-phonated embedding domain is modeled by a -component Gaussian mixture model (GMM), MEMLIN —which also models the normal embedding space by another -component GMM— approximates from a weighted combination of partial estimates :
| (3) |
where are the combination weights.
As introduced in Section 1, a limitation of MEMLIN is that, unlike the combination weights, the set of partial estimates is independent of the observed non-neutrally-phonated embedding , which constrains the potentials of the Bayesian estimation framework222In MEMLIN, the set of partial estimates is pre-computed during an offline training stage [6].. In the next subsection, we propose a different MMSE compensation approach where also the partial estimates exploit , which yields significant speaker verification performance improvements in Section 4.
2.2 Estimation Methodology
Inspired by classical noise-robust speech recognition methods such as front-end joint uncertainty decoding (FE-Joint) [8] and stereo-based stochastic mapping (SSM) [9], we explore jointly modeling the vocal effort transfer vector and non-neutrally-phonated embedding domains by means of a -component GMM . However, estimating requires the computation of covariance matrices that are ill-conditioned under our non-neutrally-phonated speech data scarcity scenario (see Subsection 3.1). To deal with this issue, we propose to use PCA as detailed below.
Let be a PCA transform matrix calculated from normal and non-neutrally-phonated embeddings. This matrix is comprised, column-wise, of principal eigenvectors, where . We can express and in the PCA domain as
| (4) |
Then, the joint variable , , is modeled by a -component GMM:
| (5) |
In Eq. (5), is the set of prior probabilities, whereas the mean vector and covariance matrix of the -th Gaussian density can be partitioned as
| (6) |
where all , and are diagonal matrices.
Given Eq. (5), the MMSE estimate of , , is calculated as follows:
| (7) |
where denotes the expectation operator. On the one hand, the combination weights in Eq. (7) are obtained, by means of the Bayes’ rule, according to
| (8) |
where . On the other hand, given that the joint density is Gaussian, the conditional density is also Gaussian, and, therefore, , i.e., the partial estimates in Eq. (7), can be expressed, , as [10]
| (9) |
Finally, an estimate of the normal embedding is achieved by means of Eq. (2) along with the application of the inverse PCA transform to the result of Eq. (7), namely,
| (10) |
Note that, in order to apply this method in Section 4, both the PCA transform matrix and the GMM are calculated from a training set comprising paired normal and non-neutrally-phonated embeddings (see Subsection 3.1).
For the sake of reproducibility, a Python implementation of this speaker embedding compensation methodology has been made publicly available333https://ilopezes.files.wordpress.com/2023/06/mmsev.zip.
3 System Overview
Figure 1 depicts a block diagram of the proposed vocal effort-robust speaker verification system. First, the powerful self-supervised pre-trained model WavLM [3] is used to compute a high-level representation of the input speech signal. Based on a Transformer structure, WavLM extends HuBERT [11] to masked speech prediction and de-noising to allow the pre-trained model to perform well in a variety of speech processing tasks including speaker verification. Second, an ECAPA-TDNN [1] back-end extracts a speaker embedding from the representation outputted by WavLM. Then, the speaker embedding compensation methodology of Section 2 is applied only in the case that the embedding comes from non-neutrally-phonated speech. To detect this case, a simple, yet virtually flawless logistic regression-based detector [4, 5] can be used. That being said, note that the results reported in Section 4 are obtained by oracle non-neutrally-phonated speech detection for the sake of simplicity. Finally, the resulting embedding is compared with a reference embedding by cosine similarity to produce a score .
3.1 Shouted and Whispered Speech Corpora
For experimental purposes, we consider the vocal effort modes shouted and whispered in addition to normal. To this end, we employ two different (i.e., disjoint) corpora: the speech corpus informed in [12], which comprises paired shouted-normal speech utterances in Finnish from 22 speakers, and CHAINS (CHAracterizing INdividual Speakers) [13], which contains paired whispered-normal speech utterances in English from 36 speakers. Due to speech data scarcity, all the embedding compensation experiments in Section 4 are performed —as in [5]— by following a leave-one-speaker-out cross-validation strategy, which serves to split the corpora into training and test sets.
We consider the following 4 test conditions (trial lists) under the shouted-normal scenario: A-A (all shouted and normal utterances vs. all shouted and normal utterances; 557,040 trials), N-N (normal utterances vs. normal utterances; 139,128 trials), S-S (shouted utterances vs. shouted utterances; 139,128 trials) and N-S (normal utterances vs. shouted utterances; 278,784 trials). Furthermore, we similarly examine 4 equivalent test conditions under the whispered-normal scenario, namely, A-A (2,821,498 trials), N-N (705,078 trials), W-W (704,950 trials) and N-W (1,411,344 trials).
| Condition | E-T+MFCC | E-T+WavLM | MEMLIN | MEMLIN+PCA | MMSE | MMSE |
|---|---|---|---|---|---|---|
| A-A | 19.96 | 17.11 | 15.62 | 31.50 | 28.72 | 15.22 |
| N-N | 9.73 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 |
| S-S | 11.58 | 9.94 | 10.44 | 27.46 | 25.53 | 5.91 |
| N-S | 25.28 | 21.76 | 20.74 | 41.00 | 35.56 | 17.74 |
| Condition | E-T+MFCC | E-T+WavLM | MEMLIN | MEMLIN+PCA | MMSE | MMSE |
|---|---|---|---|---|---|---|
| A-A | 16.54 | 11.24 | 8.25 | 31.87 | 23.95 | 8.27 |
| N-N | 1.21 | 0.62 | 0.62 | 0.62 | 0.62 | 0.62 |
| W-W | 4.38 | 5.26 | 4.00 | 19.31 | 19.77 | 2.87 |
| N-W | 12.81 | 9.81 | 11.47 | 44.38 | 30.59 | 8.86 |
3.2 System Implementation Details
The used ECAPA-TDNN back-end was trained, employing the additive angular margin (AAM) loss [14], on an augmented version of the VoxCeleb2 [15] dataset to extract -dimensional speaker embeddings. Considering an AAM loss margin of 0.2, first, WavLM —which was pre-trained on 94k hours of unlabeled speech data— was fixed and the ECAPA-TDNN parameters were trained for a total of 20 epochs. Second, WavLM and the ECAPA-TDNN back-end were jointly fine tuned for 5 epochs. Finally, by following the large margin fine-tuning strategy reported in [16], WavLM and the ECAPA-TDNN back-end were jointly trained for 2 more epochs by considering an AAM loss margin of 0.4. Notice that, for the sake of reproducibility, the model corresponding to this speaker verification system is publicly available444https://github.com/microsoft/unilm/tree/master/wavlm. The reader is referred to [3] for further information on this speaker verification system.
4 Experimental Results
In this section, EER is chosen as the speaker verification performance metric. Besides, as in previous work [4, 5], all the embedding compensation techniques evaluated make use of -component GMMs.
4.1 WavLM Performance
Tables 1 and 2 show speaker verification results in terms of EER under the shouted-normal and whispered-normal scenarios, respectively. The left part of these tables compare, when no embedding compensation is considered, the use of WavLM speech representations (as in Section 3), E-T+WavLM, with the use of traditional speech features, E-T+MFCC (note that E-T stands for ECAPA-TDNN). Specifically, the speaker verification system E-T+MFCC, which is publicly available555https://huggingface.co/speechbrain/spkrec-ecapa-voxceleb, employs 80-dimensional Mel-frequency cepstral coefficients [17]. In line with [3], we can see from these tables that E-T+WavLM generally outperforms E-T+MFCC. That being said, we can also observe that there is still a large room for improvement in the presence of vocal effort mismatch (all conditions except N-N and N-N) that will be addressed by embedding compensation in the next subsections. Bear in mind that all the embedding compensation experiments in this section are carried out by employing E-T+WavLM as the baseline system.
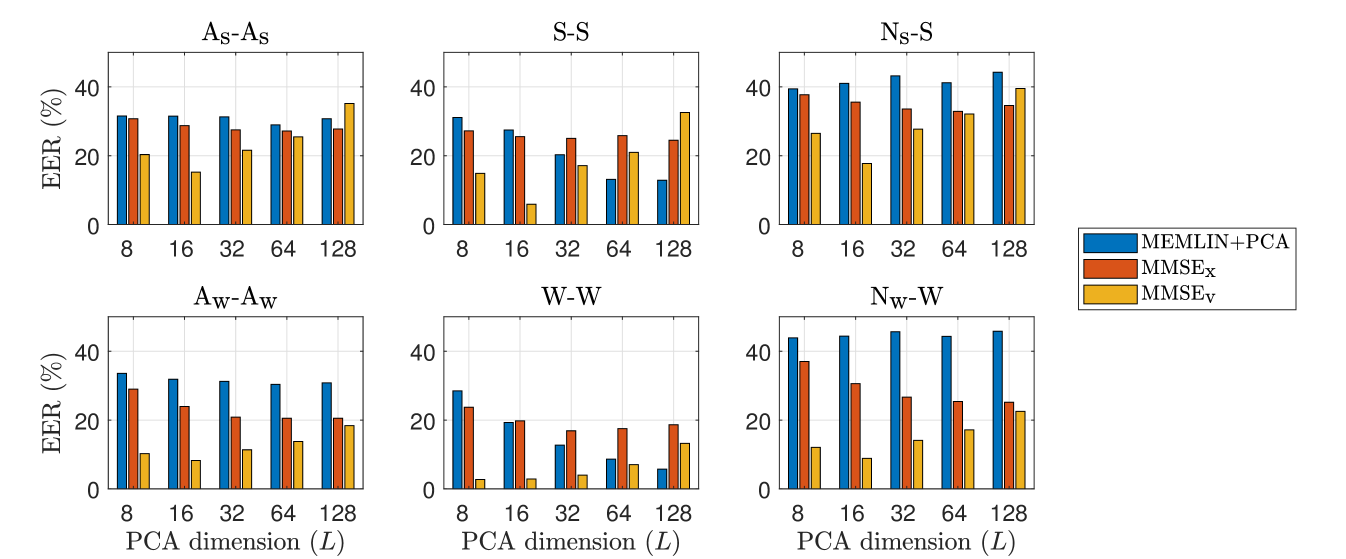
4.2 Effect of PCA Dimension
Figure 2 plots the EER performance of the estimation methodology proposed in Section 2, MMSE, as a function of the PCA dimension . For comparison, these bar plots also show results from MEMLIN (applied in the PCA domain) as well as from an MMSE estimator equivalent to that of Section 2 that directly estimates the normal embedding from , MMSE. From this figure, we can see that MEMLIN’s performance tends to drop when decreasing as a result of the information loss caused by PCA compression, which can be particularly harmful when the estimation relies on a small set of pre-computed and fixed partial estimates.
On the other hand, MMSE involves the computation of covariance matrices, , under a data scarcity scenario. Given our small sample size, reducing helps to achieve better-conditioned covariance matrices to be used in Eqs. (8) and (9). This, together with the fact that MMSE exploits the observed non-neutrally-phonated embedding for partial estimate calculation, can explain why EER decreases up to for MMSE (see Figure 2). Keeping decreasing beyond this point harms speaker verification performance due to the information loss entailed by PCA compression.
In relation to MMSE, an internal analysis revealed that estimating the normal embedding from yields target and non-target score probability masses that are poorly separated as a result of compensated embeddings where the specific-speaker information is significantly distorted. Interestingly, we also observed that the vocal effort transfer vector has a weak speaker-dependence. Therefore, estimating as according to MMSE better preserves the specific-speaker information contained in , which, in turn, leads to better-separated target and non-target score probability masses.
4.3 Embedding Compensation Performance Summary
The right part of Tables 1 and 2 compare standard MEMLIN (i.e., without PCA) with MMSE, MMSE and MEMLIN applied in the PCA domain (MEMLIN+PCA). Note that, in these tables, the three latter techniques process, after PCA application, -dimensional embeddings. Under the shouted-normal scenario (Table 1), MMSE outperforms MEMLIN in the presence of vocal effort mismatch (i.e., in A-A, S-S and N-S). Furthermore, while MEMLIN is on par with MMSE in A-A under the whispered-normal scenario (Table 2), MMSE achieves in N-W a 22.7% EER relative improvement with respect to MEMLIN which actually worsens the baseline system E-T+WavLM (as in the S-S condition).
5 Concluding Remarks
In this work, we have shown that embedding compensation can significantly mitigate the speaker verification performance drop caused by vocal effort mismatch when a state-of-the-art speaker verification system integrating a cutting-edge self-supervised pre-trained model for speech representation is used. With the aim of improving a reference embedding compensation method —i.e., MEMLIN—, we have proposed an MMSE estimator of the vocal effort transfer vector that, unlike MEMLIN, exploits the non-neutrally-phonated embeddings observed at test time for partial estimate calculation and performs in a PCA domain to cope with non-neutrally-phonated speech data scarcity. Compared with MEMLIN, the proposed MMSE estimator has shown superior and competitive EER performance when processing shouted and whispered speech, respectively.
References
- [1] Brecht Desplanques, Jenthe Thienpondt, and Kris Demuynck, “ECAPA-TDNN: Emphasized channel attention, propagation and aggregation in TDNN based speaker verification,” in Proceedings of INTERSPEECH 2020 – 21st Annual Conference of the International Speech Communication Association, October 25-29, Shanghai, China, 2020, pp. 3830–3834.
- [2] Zhengyang Chen, Sanyuan Chen, Yu Wu, Yao Qian, Chengyi Wang, Shujie Liu, Yanmin Qian, and Michael Zeng, “Large-scale self-supervised speech representation learning for automatic speaker verification,” in Proceedings of ICASSP 2022 – 47th International Conference on Acoustics, Speech, and Signal Processing, May 23-27, Singapore, 2022, pp. 6147–6151.
- [3] Sanyuan Chen, Chengyi Wang, Zhengyang Chen, Yu Wu, Shujie Liu, Zhuo Chen, Jinyu Li, Naoyuki Kanda, Takuya Yoshioka, Xiong Xiao, Jian Wu, Long Zhou, Shuo Ren, Yanmin Qian, Yao Qian, Jian Wu, Michael Zeng, Xiangzhan Yu, and Furu Wei, “WavLM: Large-scale self-supervised pre-training for full stack speech processing,” IEEE Journal of Selected Topics in Signal Processing, vol. 16, pp. 1505–1518, 2022.
- [4] Santi Prieto, Alfonso Ortega, Iván López-Espejo, and Eduardo Lleida, “Shouted speech compensation for speaker verification robust to vocal effort conditions,” in Proceedings of INTERSPEECH 2020 – 21st Annual Conference of the International Speech Communication Association, October 25-29, Shanghai, China, 2020, pp. 1511–1515.
- [5] Santi Prieto, Alfonso Ortega, Iván López-Espejo, and Eduardo Lleida, “Shouted and whispered speech compensation for speaker verification systems,” Digital Signal Processing, vol. 127, 2022.
- [6] Luis Buera, Eduardo Lleida, Antonio Miguel, Alfonso Ortega, and Oscar Saz, “Cepstral vector normalization based on stereo data for robust speech recognition,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 15, pp. 1098–1113, 2007.
- [7] José A. González López, Reconocimiento robusto de voz con datos perdidos o inciertos, Ph.D. thesis, University of Granada, 2013.
- [8] H. Liao and M.J.F. Gales, “Issues with uncertainty decoding for noise robust automatic speech recognition,” Speech Communication, vol. 50, pp. 265–277, 2008.
- [9] Mohamed Afify, Xiaodong Cui, and Yuqing Gao, “Stereo-based stochastic mapping for robust speech recognition,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 17, pp. 1325–1334, 2009.
- [10] Athanasios Papoulis and S. Unnikrishna Pillai, Probability, Random Variables and Stochastic Processes (4th Edition), McGraw-Hill Europe, 2002.
- [11] Wei-Ning Hsu, Benjamin Bolte, Yao-Hung Hubert Tsai, Kushal Lakhotia, Ruslan Salakhutdinov, and Abdelrahman Mohamed, “HuBERT: Self-supervised speech representation learning by masked prediction of hidden units,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 29, pp. 3451–3460, 2021.
- [12] Cemal Hanilçi, Tomi Kinnunen, Rahim Saeidi, Jouni Pohjalainen, Paavo Alku, and Figen Ertaş, “Speaker identification from shouted speech: Analysis and compensation,” in Proceedings of ICASSP 2013 – 38th International Conference on Acoustics, Speech, and Signal Processing, May 26-31, Vancouver, Canada, 2013, pp. 8027–8031.
- [13] Fred Cummins, Marco Grimaldi, Thomas Leonard, and Juraj Simko, “The CHAINS corpus: CHAracterizing INdividual Speakers,” in Proceedings of SPECOM, 2006, pp. 431–435.
- [14] Jiankang Deng, Jia Guo, Niannan Xue, and Stefanos Zafeiriou, “ArcFace: Additive angular margin loss for deep face recognition,” in Proceedings of CVPR 2019 – IEEE/CVF Conference on Computer Vision and Pattern Recognition, June 15-20, Long Beach, USA, 2019, pp. 4685–4694.
- [15] Joon Son Chung, Arsha Nagrani, and Andrew Zisserman, “VoxCeleb2: Deep speaker recognition,” in Proceedings of INTERSPEECH 2018 – 19th Annual Conference of the International Speech Communication Association, September 2-6, Hyderabad, India, 2018, pp. 1086–1090.
- [16] Jenthe Thienpondt, Brecht Desplanques, and Kris Demuynck, “The Idlab Voxsrc-20 submission: Large margin fine-tuning and quality-aware score calibration in DNN based speaker verification,” in Proceedings of ICASSP 2021 – 46th International Conference on Acoustics, Speech, and Signal Processing, June 6-11, Toronto, Canada, 2021, pp. 5814–5818.
- [17] S. Davis and P. Mermelstein, “Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 28, pp. 357–366, 1980.