PHENIX Collaboration
Improving constraints on gluon spin-momentum correlations in transversely polarized protons via midrapidity open-heavy-flavor electrons in collisions at GeV
Abstract
Polarized proton-proton collisions provide leading-order access to gluons, presenting an opportunity to constrain gluon spin-momentum correlations within transversely polarized protons and enhance our understanding of the three-dimensional structure of the proton. Midrapidity open-heavy-flavor production at GeV is dominated by gluon-gluon fusion, providing heightened sensitivity to gluon dynamics relative to other production channels. Transverse single-spin asymmetries of positrons and electrons from heavy-flavor hadron decays are measured at midrapidity using the PHENIX detector at the Relativistic Heavy Ion Collider. These charge-separated measurements are sensitive to gluon correlators that can in principle be related to gluon orbital angular momentum via model calculations. Explicit constraints on gluon correlators are extracted for two separate models, one of which had not been constrained previously.
I Introduction
Polarized proton-proton collisions provide a unique opportunity to improve our understanding of gluon contributions to the spin structure of the proton, because they are accessible at leading order, which is not true for lepton-hadron scattering. The complex spin structure of the proton leads to emergent properties such as spin-momentum and spin-spin correlations analogous to the fine and hyperfine structure of atoms. These correlations in protons are experimentally accessible through observables known as transverse single-spin asymmetries (TSSAs). TSSAs quantify azimuthal modulations of particle production in collisions of transversely polarized nucleons with unpolarized particles, and have been measured to reach magnitudes up to 40% in hadron-hadron collisions [1, 2, 3, 4]. Perturbative quantum chromodynamics (pQCD) calculations had predicted TSSAs of % from purely perturbative contributions [5]; recent calculations suggest small additional perturbative contributions [6].
Two complementary theoretical frameworks exist for describing large TSSAs in which contributions arise from nonperturbative elements of the factorized cross section — transverse-momentum-dependent (TMD) factorization [7, 8, 9], and twist-3 factorization [10, 11] (see Ref. [12] for a recent review). The two frameworks are related, and phenomenological arguments indicate TSSAs in various reactions share a common origin in multiparton correlations [13]. The TMD framework has explicit dependence on transverse momentum of partons within hadrons in addition to the longitudinal momentum fraction . In this approach, standard collinear parton distribution functions (PDFs) and fragmentation functions (FFs) are replaced with TMD functions. The twist-3 approach considers power-suppressed terms with respect to the hard-scattering energy scale in the factorization expansion. Constraining TMD functions experimentally requires access to both a hard scale and soft scale sensitive to partonic transverse momentum in the proton or the process of hadronization, with , while the higher-twist formalism only requires access to a hard scale that is represented by the transverse momentum of the produced particle (). Twist-3 correlation functions can be written in terms of moments of corresponding TMDs [14]. Both frameworks have demonstrated success in modeling TSSAs in complementary regions of [14, 15, 16], and are relevant for constraining orbital angular momentum of quarks and gluons in protons [17, 18, 19]. At twist-3, quantum interference between standard QCD processes and some processes involving an extra gluon must be considered, introducing additional terms to cross-section calculations depending on the number of colliding or produced hadrons. These terms encode quantum interference in twist-3 correlation functions convoluted with standard collinear PDFs and FFs. TSSAs are defined in Eq. (6), leading to the following proportionality at twist-3 [20, 21]:
| (1) |
Each term with a superscript corresponds to a twist-3 correlation function; the rest are at leading twist (twist-2), where represents a convolution in longitudinal momentum fractions () of partons in parent protons and collinear momentum fractions () of produced hadrons with respect to their originating partons [21]. The primed variables originate from the unpolarized proton in the initial state, and the numbered variables appear in twist-3 correlators, where multiparton correlations must be considered. The and denote PDFs and FFs respectively, where the lowercase subscripts represent the parton type, and the uppercase subscripts represent the parent hadron. The term is the transversity distribution, a spin-spin correlation of transversely polarized quarks in transversely polarized hadrons [22]. Twist-3 correlators have more intuitive physical meaning through their relation to corresponding TMDs [14, 7, 8, 9].
In collisions at GeV, open-heavy-flavor (OHF) production at midrapidity is dominated by gluon-gluon fusion, receiving only a small contribution from quark-antiquark annihilation [23]. In gluon-gluon fusion events, only the first term in Eq. (1) is relevant (as the gluon does not have a transversity distribution in spin nucleons), providing sensitivity to the trigluon correlation functions in polarized protons. The relevant twist-3 correlators for quark-antiquark annihilation and gluon-gluon fusion are the Efremov-Teryaev-Qiu-Sterman () correlator [10, 24], and the trigluon () correlators [25, 26, 27, 28, 29] respectively. Note that the trigluon correlators were introduced in Ref. [25], and were subsequently clarified to be two independent functions [26, 27, 28, 29]. The correlator has been experimentally constrained from global fits, discussed in Ref. [13], while the correlators have received less attention, with few measurements capable of providing indirect constraints [30, 31, 32, 33, 34, 35] or direct constraints [36, 37].
The TSSA for open-charm production in collisions at GeV was calculated in Refs. [38] and [39] within the twist-3 framework. The trigluon correlation functions are defined in Ref. [38] as (antisymmetric) and (symmetric), where the and superscripts represent three gluon-field color indices contracting with antisymmetric or symmetric structure tensors. Lack of direct information on the trigluon correlators has led to simple phenomenological models with normalization parameters to the unpolarized gluon PDF. In Ref. [38] (following from Ref. [20]) parameters and are introduced:
| (2) |
The trigluon correlation functions in Ref. [39] are instead defined as (antisymmetric), and (symmetric), with four independent contributions to TSSAs, . As shown in Ref. [39], at GeV the asymmetries depend on effective trigluon correlators and , which are directly related to and in Ref. [28]. Reference [39] introduces parameters and with the assumptions:
| (3) | ||||
| (4) | ||||
| (5) |
Note that the assumptions on the trigluon correlators in Eqs. 2, 4, and 5 (e.g., the functional dependence on and the proportionality to the unpolarized gluon PDF) are oversimplified. For this reason, it is advantageous to compare to different models with various dependencies. The results presented in this paper place direct constraints on and .
Open-charm production at the Relativistic Heavy Ion Collider (RHIC) has also been investigated with the TMD factorization approach as a means of constraining the gluon Sivers PDF (see Refs. [40, 41, 42]). The measurements presented here will be useful in providing constraints to the gluon Sivers TMD PDF through constraining the twist-3 trigluon correlators, which are related to moments of the gluon Sivers PDF [14].
II Data Analysis
The asymmetry measurements presented here utilize data recorded in 2015 by the PHENIX experiment at RHIC with collisions of transversely polarized protons on transversely polarized protons at GeV, and approximately 23 pb-1 of integrated luminosity. The polarization of each beam at RHIC in 2015 is measured to be for the clockwise beam and for the counterclockwise beam, with transverse polarization direction aligned vertically to the accelerator plane [43]. The polarization direction is varied from bunch to bunch (a) to reduce systematics related to detector coverage and performance, and (b) to allow for the polarization of a single beam to be considered at a time by averaging over the polarization directions of the opposing beam. This yields two independent data sets from which the transverse single-spin asymmetries are extracted, validated for consistency, and averaged to obtain the final result.
The PHENIX detector is described in detail in Ref. [44]. Detector subsystems used for midrapidity charged-particle detection comprise two central-arm spectrometers oriented to the left and right of the beam axis, each with acceptance and , and a silicon vertex detector (VTX) [45, 46] with acceptance of and per arm. The central arms contain drift and pad chambers for tracking [47], electromagnetic calorimeters (EMCal) to measure energy deposition of charged particles and photons [48], and a ring-imaging Čerenkov (RICH) detector for particle identification with separation up to GeV/ [49].
Curating the electron candidate sample follows the same procedure as in Ref. [50]. The electron candidate sample is composed of tracks reconstructed from hits in the drift and pad chambers of the central arm spectrometers coincident with hits in the silicon vertex detector. Tracks within (GeV/c) that fire at least one photomultiplier (PMT) tube in the RICH detector, and that have a maximum displacement of 5 cm between the track projection and center of the ring of Čerenkov light as measured by the PMTs in the RICH are considered. In order to increase the electron purity, track energy deposited in the EMCal and track momentum should have a ratio near unity, as electrons deposit most of their energy in the EMCal while charged hadrons do not. The distribution for electron candidates in Run-15 was fit with an exponential + Gaussian, where the mean and width of the Gaussian portion were extracted and used to impose the following condition . Spatial displacements and of track projections and corresponding electromagnetic showers in the EMCal are required to be separated by no more than 3 standard deviations of the corresponding and distributions, and the probability that an EMCal cluster originates from an electromagnetic shower (as calculated by the shower shape) is required to be above 0.01. Tracks reconstructed in the central arms are projected to the VTX detector and fit to coincidental VTX hits via the iterative algorithm described in Ref. [51] — the fit is required to satisfy . A hit is required in both of the inner two layers of the VTX to veto conversion electrons created by photons interacting with detector material, and an additional hit is required in either of the outer layers of the VTX. The narrow opening angle between from photonic conversions is exploited to further reduce background from conversions in the beam pipe or inner two layers of the VTX; more details for this and the VTX detector can be found in Ref. [50]. An additional requirement was placed on the number of live trigger counts per bunch crossing because the asymmetry analysis is performed bunch-by-bunch.
TSSAs can be calculated as amplitudes of sinusoidal modulations of azimuthal particle production:
| (6) |
where correspond to transversely polarized cross sections for different spin orientations. Due to the nature of the azimuthal angular acceptance of the PHENIX spectrometer arms, the measurements of midrapidity TSSAs are integrated in for one arm at a time. This necessitates division by an azimuthal correction factor . Equation (6) must also be corrected for the polarization . All of these corrections are applied as seen in the “relative luminosity formula”, a well-established PHENIX method used in Refs. [37, 34, 36, 52, 53] to extract TSSAs:
| (7) |
In Eq. (7), are the spin-dependent yields for collisions with polarized bunch crossings respectively, and is the relative luminosity, defined as the ratio of luminosities for collisions with oppositely oriented bunch crossing polarization. The azimuthal correction factor is calculated in each transverse momentum () bin for the electron candidate sample to account for detector efficiency effects. To serve as a cross check to Eq. (7), the asymmetries are also calculated with the “square root formula,” as shown in Eq. (8). The difference in asymmetries calculated with the separate methods is taken as a systematic uncertainty .
| (8) |
The subscripts represent the left and right spectrometer arm with respect to the polarized proton-going direction. The square root formula cannot be used independently on each spectrometer arm, leading to only two independent data sets for cross validation and averaging corresponding to the two beams, rather than four independent data sets as is the case for the relative luminosity formula, corresponding to the two beams and two spectrometer arms. As an additional cross check, was calculated as shown in Eq. 6, via sinusoidal fits, with 3 bins per spectrometer arm, yielding consistent results with that of Eqs. 7 and 8.
Once is calculated for the electron candidate sample, background corrections allow for extraction of the asymmetry for OHF decay electrons. The relevant background sources are electrons from other parent particles (, direct photons ) and charged hadrons misidentified as electrons (primarily ). To calculate the background-corrected asymmetry, the fraction of each background source present in the data sample needs to be calculated and the background asymmetries need to be measured. Equation (9) shows the formula for extracting the asymmetry from the electron-candidate-sample asymmetry,
| (9) |
where represent the background fractions, is the asymmetry calculated on the electron candidate sample, and are the background asymmetries. The procedure to calculate the background fractions and a more detailed description of background sources can be found in Ref. [50]. This procedure is repeated in this analysis with the relevant bins, and uncertainties on calculated background fractions are propagated through Eq. (9) to obtain systematic uncertainties . Figure 1 shows the resulting background fractions for electrons and positrons combined. The Ke3 background source, which consists of Dalitz decays of and , is heavily suppressed over the measured range. The transverse single-spin asymmetries for or have not been measured in GeV collisions. However, given that the Ke3 background fraction is on the order of , and is the smallest contributor, it is safely neglected in the background correction procedure. The relevant background fractions are calculated separately for positrons and electrons as shown in Table 1, with resulting background fractions shown in Figures 5 and 5.

| range (GeV/c) | (GeV/c) | ||||||
|---|---|---|---|---|---|---|---|
| 1.0 – 1.3 | 1.161 | 0.458 | 0.0738 | 0.00274 | 0.00916 | 0.0140 | |
| 1.3 – 1.5 | 1.398 | 0.318 | 0.0592 | 0.00336 | 0.0195 | 0.00924 | |
| 1.5 – 1.8 | 1.639 | 0.264 | 0.0582 | 0.00339 | 0.0344 | 0.0120 | |
| 1.8 – 2.1 | 1.936 | 0.215 | 0.0458 | 0.00399 | 0.0520 | 0.0134 | |
| 2.1 – 2.7 | 2.349 | 0.173 | 0.0394 | 0.00481 | 0.0823 | 0.0179 | |
| 2.7 – 5.0 | 3.290 | 0.111 | 0.0297 | 0.00480 | 0.122 | 0.0300 | |
| 1.0 – 1.3 | 1.161 | 0.439 | 0.0704 | 0.00335 | 0.00900 | 0.0261 | |
| 1.3 – 1.5 | 1.398 | 0.347 | 0.0692 | 0.00364 | 0.0206 | 0.0198 | |
| 1.5 – 1.8 | 1.639 | 0.299 | 0.0665 | 0.00394 | 0.0375 | 0.0230 | |
| 1.8 – 2.1 | 1.936 | 0.252 | 0.0478 | 0.00535 | 0.0577 | 0.0205 | |
| 2.1 – 2.7 | 2.349 | 0.208 | 0.0429 | 0.00490 | 0.0872 | 0.0245 | |
| 2.7 – 5.0 | 3.290 | 0.143 | 0.0296 | 0.00572 | 0.127 | 0.0279 |
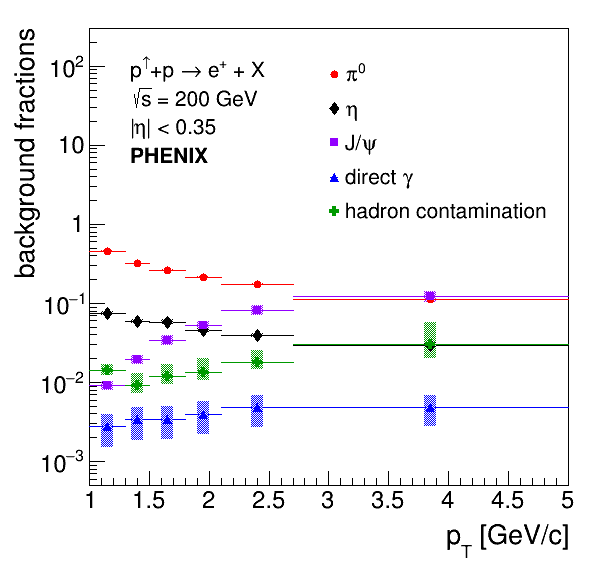
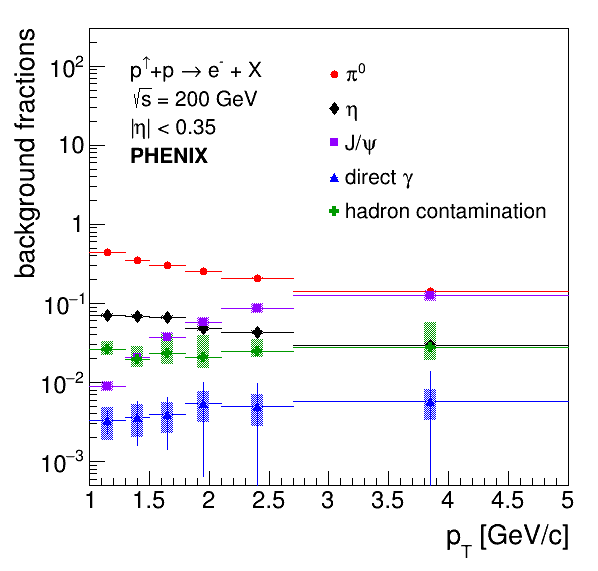
TSSAs for each background source have been measured at PHENIX at midrapidity in collisions at GeV. The asymmetries for photonic background sources , and were all measured by PHENIX to be consistent with zero using the same dataset as this measurement [34, 37]. They are therefore set to zero in Eq. (9), with a systematic uncertainty assigned for setting and based on propagating uncertainties from the measurements, while the uncertainty associated with setting the direct photon TSSA is negligible because is on the order of (see Table 1). The TSSAs for [52] and charged hadrons [53] were measured with previous PHENIX data sets. The TSSA for has a large statistical uncertainty [52], and contributes significantly to the statistical uncertainty of this measurement, especially at high . This is due to the azimuthal angle of the decay lepton becoming more strongly correlated with the azimuthal angle of the at higher . Additionally, the statistical precision of could not be improved upon in the Run-15 data given the high degree of photonic electron background. The TSSA for midrapidity production measured in Ref. [52] was recalculated as a function of decay lepton using pythia [54] decay simulations for the channel to apply Eq. (9).
Due to the large contribution of statistical uncertainty coming from propagating the previously measured from Ref. [52] through the background correction formula (Eq. 9), we report nonphotonic electron and positron asymmetries in addition to the open-heavy-flavor-decay electron and positron asymmetries. This allows the statistical precision of the open-heavy-flavor result to be improved upon given a more statistically precise measurement of . Figures 5 and 5 do not show the nonphotonic electron asymmetries because they are not the focus of this paper. However, these asymmetries are shown and discussed below. The formula for extracting the nonphotonic electron () asymmetry from the electron candidate sample asymmetry is
| (10) |
Note that Eq. 10 only differs from Eq. 9 by the omission of the terms including background fractions and asymmetries.
The TSSAs for midrapidity open charm production () predicted in Refs. [38] and [39] were also recalculated as a function of decay lepton for all possible semileptonic decay channels, with decay kinematics simulated in pythia [54] to obtain correlations between and of the decay lepton and meson. The distribution was then weighted in accordance with in each bin and then fit with to extract the decay lepton asymmetry. and production was considered for comparisons to results from Refs. [38] and [39], while and production was additionally considered when comparing to results of Ref. [39]. OHF production is dominated by open charm at the relevant kinematics, for which , and cover a significant fraction. The effect of including and in comparing to Ref. [39] makes very little difference as supported by our simulations, implying that comparing to and for Ref. [38] is sufficient. A scan over parameter space and independent scans over and were performed to generate a set of theory curves for comparison, allowing for best-fit parameters and confidence intervals to be determined from data.
| range | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (GeV/) | (GeV/) | |||||||||
| 1.0–1.3 | 1.161 | -0.00256 | 0.0212 | 0.00193 | 0.000855 | 0.00264 | 0.000435 | 0.00330 | 0.00281 | |
| 1.3–1.5 | 1.398 | 0.0105 | 0.0178 | 0.00142 | 0.00108 | 0.00143 | 0.000621 | 0.00211 | 0.00189 | |
| 1.5–1.8 | 1.639 | 0.00571 | 0.0159 | 0.000468 | 0.000401 | 0.00118 | 0.000432 | 0.00134 | 0.00132 | |
| 1.8–2.1 | 1.936 | 0.0126 | 0.0192 | 0.00101 | 0.000856 | 0.000889 | 0.00697 | 0.00710 | 0.00708 | |
| 2.1–2.7 | 2.349 | 0.00208 | 0.0210 | 0.00140 | 0.00109 | 0.000719 | 0.00446 | 0.00473 | 0.00465 | |
| 2.7–5.0 | 3.290 | 0.0357 | 0.0287 | 0.00595 | 0.00364 | 0.000474 | 0.00342 | 0.00688 | 0.00501 | |
| 1.0–1.3 | 1.161 | -0.0113 | 0.0186 | 0.00404 | 0.00237 | 0.00247 | 0.000120 | 0.00474 | 0.00343 | |
| 1.3–1.5 | 1.398 | -0.0297 | 0.0181 | 0.00466 | 0.00335 | 0.00174 | 0.000672 | 0.00502 | 0.00384 | |
| 1.5–1.8 | 1.639 | 0.0139 | 0.0167 | 0.00117 | 0.000789 | 0.00147 | 0.000917 | 0.00209 | 0.00191 | |
| 1.8–2.1 | 1.936 | 0.0105 | 0.0207 | 0.00136 | 0.000990 | 0.00109 | 0.000234 | 0.00176 | 0.00149 | |
| 2.1–2.7 | 2.349 | -0.0267 | 0.0227 | 0.000104 | 0.000152 | 0.000899 | 0.00253 | 0.00269 | 0.00269 | |
| 2.7–5.0 | 3.290 | 0.0237 | 0.0305 | 0.00509 | 0.00313 | 0.000589 | 0.00174 | 0.00541 | 0.00363 |
| range | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (GeV/) | (GeV/) | |||||||||
| 1.0– 1.3 | 1.161 | -0.00202 | 0.0207 | 0.00115 | 0.000531 | 0.00259 | 0.000435 | 0.00286 | 0.00268 | |
| 1.3– 1.5 | 1.398 | 0.0103 | 0.0172 | 0.00128 | 0.000996 | 0.00138 | 0.000621 | 0.00198 | 0.00181 | |
| 1.5– 1.8 | 1.639 | 0.00379 | 0.0148 | 0.000119 | 8.15e-05 | 0.00112 | 0.000432 | 0.00120 | 0.00120 | |
| 1.8– 2.1 | 1.936 | 0.00836 | 0.0170 | 0.000222 | 0.000144 | 0.000825 | 0.00697 | 0.00702 | 0.00702 | |
| 2.1– 2.7 | 2.349 | -0.00371 | 0.0163 | 0.000239 | 7.51e-05 | 0.000642 | 0.00446 | 0.00452 | 0.00451 | |
| 2.7– 5.0 | 3.290 | 0.0220 | 0.0201 | 0.00205 | 0.000814 | 0.000404 | 0.00342 | 0.00401 | 0.00354 | |
| 1.0–1.3 | 1.161 | -0.0106 | 0.0182 | 0.00338 | 0.00203 | 0.00242 | 0.000120 | 0.00416 | 0.00316 | |
| 1.3–1.5 | 1.398 | -0.0284 | 0.0174 | 0.00386 | 0.00284 | 0.00168 | 0.000672 | 0.00426 | 0.00337 | |
| 1.5–1.8 | 1.639 | 0.0111 | 0.0153 | 0.000538 | 0.000288 | 0.00138 | 0.000917 | 0.00174 | 0.00168 | |
| 1.8–2.1 | 1.936 | 0.00565 | 0.0178 | 0.000282 | 0.000131 | 0.000996 | 0.000234 | 0.00106 | 0.00103 | |
| 2.1–2.7 | 2.349 | -0.0297 | 0.0171 | 0.000446 | 0.000351 | 0.000790 | 0.00253 | 0.00269 | 0.00268 | |
| 2.7–5.0 | 3.290 | 0.0108 | 0.0207 | 0.00134 | 0.000466 | 0.000495 | 0.00174 | 0.00225 | 0.00187 |
III Results
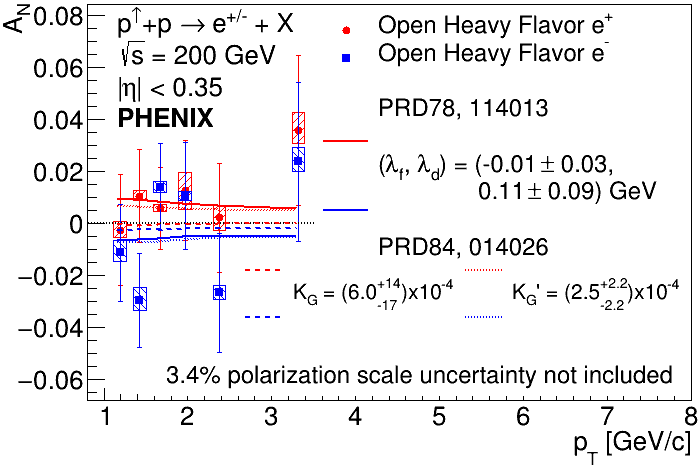
The TSSAs are plotted in Fig. 5 alongside theoretical predictions of from Ref. [38] in (red/blue) solid lines, and from Ref. [39] in (red/blue) dashed and dotted lines, with , , and chosen to best fit the data for the separate charges simultaneously. The measurements are consistent with zero, and are statistically more precise than previous heavy-flavor measurements. The total systematic uncertainties come from combining those associated with the background fractions, background asymmetries, and the difference in calculating with Eqs. (7) and (8); there is no dominant source of systematic uncertainty across charges and bins. The systematic uncertainty reaches at most 37% of the corresponding statistical uncertainty (see Table 3), while it is typically suppressed by an order of magnitude or more. The placement of the theoretical curves in Fig. 5 differs for vs due to the contribution of the symmetric trigluon correlator having opposing signs in charm vs anticharm production, leading to constructive vs destructive interference with the antisymmetric trigluon correlator contribution for the separate charges. This allows for constraining power on all parameters. Summaries for final asymmetries with statistical and systematic uncertainties are given in Table 3 for OHF positrons and electrons and in Table 3 for nonphotonic (NP) positrons and electrons .
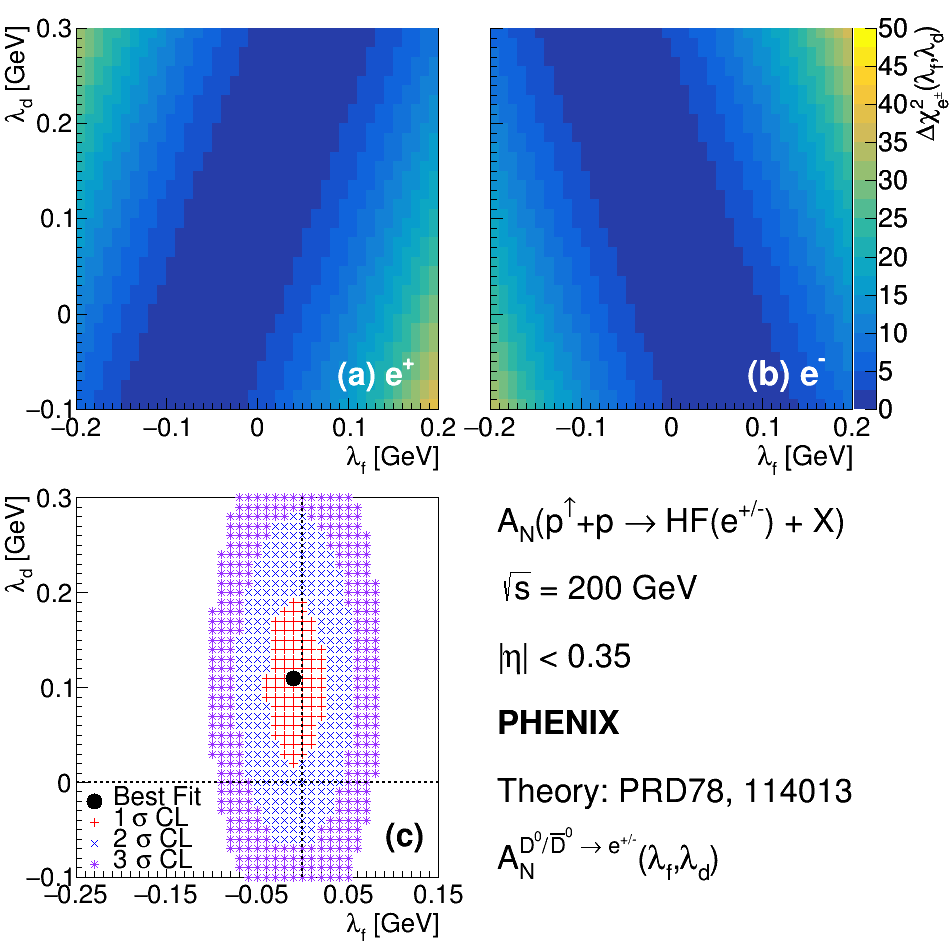
To determine theoretical parameters that fit the data best, , , and were calculated for the separate charges and summed to extract minimum values. The results along with confidence intervals are GeV and GeV for parameters introduced Ref. [38], and , and for parameters introduced in Ref. [39]. This corresponds to the first constraints on , and is in agreement with previous constraints on and derived in Ref. [39]. Figure 5 summarizes the results of the statistical analysis performed to extract best-fit parameters and , where the theoretical asymmetries depend on both parameters. Nicely illustrated are the constraining power of the individual charges and the necessity of combining the charges in the statistical analysis. Both charges predict that contributions from trigluon correlations are small, indicating that and values that result in cancellation of their contributions to the asymmetry calculation are preferred.
IV Summary
In summary, the PHENIX experiment has measured the transverse single-spin asymmetry of midrapidity open-heavy-flavor decay electrons and positrons as a function of in collisions at GeV. Open-heavy-flavor production at RHIC is an ideal channel for probing trigluon correlations in polarized protons because initial-state correlations in the proton and final-state twist-3 correlations in hadronization contribute negligibly. This measurement provides constraints for the antisymmetric and symmetric trigluon correlation functions in transversely polarized protons, including the first constraints on and as GeV and GeV — a necessary step forward in our understanding of proton structure through correlations between proton spin and gluon momentum.
Acknowledgements.
We thank the staff of the Collider-Accelerator and Physics Departments at Brookhaven National Laboratory and the staff of the other PHENIX participating institutions for their vital contributions. We also thank Z. Kang and S. Yoshida for providing calculations corresponding to the models introduced in Refs. [38] and [39]. We acknowledge support from the Office of Nuclear Physics in the Office of Science of the Department of Energy, the National Science Foundation, Abilene Christian University Research Council, Research Foundation of SUNY, and Dean of the College of Arts and Sciences, Vanderbilt University (U.S.A), Ministry of Education, Culture, Sports, Science, and Technology and the Japan Society for the Promotion of Science (Japan), Natural Science Foundation of China (People’s Republic of China), Croatian Science Foundation and Ministry of Science and Education (Croatia), Ministry of Education, Youth and Sports (Czech Republic), Centre National de la Recherche Scientifique, Commissariat à l’Énergie Atomique, and Institut National de Physique Nucléaire et de Physique des Particules (France), J. Bolyai Research Scholarship, EFOP, the New National Excellence Program (ÚNKP), NKFIH, and OTKA (Hungary), Department of Atomic Energy and Department of Science and Technology (India), Israel Science Foundation (Israel), Basic Science Research and SRC(CENuM) Programs through NRF funded by the Ministry of Education and the Ministry of Science and ICT (Korea). Ministry of Education and Science, Russian Academy of Sciences, Federal Agency of Atomic Energy (Russia), VR and Wallenberg Foundation (Sweden), University of Zambia, the Government of the Republic of Zambia (Zambia), the U.S. Civilian Research and Development Foundation for the Independent States of the Former Soviet Union, the Hungarian American Enterprise Scholarship Fund, the US-Hungarian Fulbright Foundation, and the US-Israel Binational Science Foundation.References
- Klem et al. [1976] R. D. Klem, J. E. Bowers, H. W. Courant, H. Kagan, M. L. Marshak, E. A. Peterson, K. Ruddick, W. H. Dragoset, and J. B. Roberts, Measurement of Asymmetries of Inclusive Pion Production in Proton Proton Interactions at 6 GeV/ and 11.8 GeV/, Phys. Rev. Lett. 36, 929 (1976).
- Adams et al. [1991] D. L. Adams et al. (FNAL-E704 Collaboration), Analyzing power in inclusive and production at high with a 200-GeV polarized proton beam, Phys. Lett. B 264, 462 (1991).
- Allgower et al. [2002] C. E. Allgower et al., Measurement of analyzing powers of and produced on a hydrogen and a carbon target with a 22-GeV/ incident polarized proton beam, Phys. Rev. D 65, 092008 (2002).
- Arsene et al. [2008] I. Arsene et al. (BRAHMS Collaboration), Single Transverse Spin Asymmetries of Identified Charged Hadrons in Polarized Collisions at = 62.4 GeV, Phys. Rev. Lett. 101, 042001 (2008).
- Kane et al. [1978] G. L. Kane, J. Pumplin, and W. Repko, Transverse Quark Polarization in Large- Reactions, Jets, and Leptoproduction: A Test of Quantum Chromodynamics, Phys. Rev. Lett. 41, 1689 (1978).
- Benic et al. [2019] S. Benic, Y. Hatta, H.-n. Li, and D.-J. Yang, Single-spin asymmetries at two loops, Phys. Rev. D 100, 094027 (2019).
- Sivers [1990] D. Sivers, Single-spin production asymmetries from the hard scattering of pointlike constituents, Phys. Rev. D 41, 83 (1990).
- Boer and Mulders [1998] D. Boer and P. J. Mulders, Time-reversal odd distribution functions in leptoproduction, Phys. Rev. D 57, 5780 (1998).
- Collins [1993] J. Collins, Fragmentation of transversely polarized quarks probed in transverse momentum distributions, Nucl. Phys. B 396, 161 (1993).
- Efremov and Teryaev [1985] A. V. Efremov and O. V. Teryaev, QCD Asymmetry and Polarized Hadron Structure Functions, Phys. Lett. B 150, 383 (1985).
- Qiu and Sterman [1991] J.-W. Qiu and G. Sterman, Single transverse spin asymmetries, Phys. Rev. Lett. 67, 2264 (1991).
- Anselmino et al. [2020] M. Anselmino, A. Mukherjee, and A. Vossen, Transverse spin effects in hard semi-inclusive collisions, Prog. Part. Nucl. Phys. 114, 103806 (2020).
- Cammarota et al. [2020] J. Cammarota, L. Gamberg, Z.-B. Kang, J. A. Miller, D. Pitonyak, A. Prokudin, T. C. Rogers, and N. Sato (Jefferson Lab Angular Momentum Collaboration), Origin of single transverse-spin asymmetries in high-energy collisions, Phys. Rev. D 102, 054002 (2020).
- Ji et al. [2006] X. Ji, J.-W. Qiu, W. Vogelsang, and F. Yuan, A Unified picture for single transverse-spin asymmetries in hard processes, Phys. Rev. Lett. 97, 082002 (2006).
- Koike et al. [2008] Y. Koike, W. Vogelsang, and F. Yuan, On the relation between mechanisms for single-transverse-spin asymmetries, Phys. Lett. B 659, 878 (2008).
- Yuan and Zhou [2009] F. Yuan and J. Zhou, Collins function and the single transverse spin asymmetry, Phys. Rev. Lett. 103, 052001 (2009).
- Ji et al. [2003] X.-d. Ji, J.-P. Ma, and F. Yuan, Three quark light cone amplitudes of the proton and quark orbital motion dependent observables, Nucl. Phys. B 652, 383 (2003).
- [18] Y. Hatta, K. Tanaka, and S. Yoshida, Twist-three relations of gluonic correlators for the transversely polarized nucleon, J. High Energy Phys. 02 04 (2013) 003.
- Hatta and Yao [2019] Y. Hatta and X. Yao, QCD evolution of the orbital angular momentum of quarks and gluons: Genuine twist-three part, Phys. Lett. B 798, 134941 (2019).
- Qiu and Sterman [1999] J.-w. Qiu and G. F. Sterman, Single transverse spin asymmetries in hadronic pion production, Phys. Rev. D 59, 014004 (1999).
- Kouvaris et al. [2006] C. Kouvaris, J.-W. Qiu, W. Vogelsang, and F. Yuan, Single transverse-spin asymmetry in high transverse momentum pion production in pp collisions, Phys. Rev. D 74, 114013 (2006).
- Ralston and Soper [1979] J. P. Ralston and D. E. Soper, Production of dimuons from high-energy polarized proton-proton collisions, Nucl. Phys. B 152, 109 (1979).
- Norrbin and Sjostrand [2000] E. Norrbin and T. Sjostrand, Production and hadronization of heavy quarks, Eur. Phys. J. C 17, 137 (2000).
- Qiu and Sterman [1992] J.-W. Qiu and G. F. Sterman, Single transverse spin asymmetries in direct photon production, Nucl. Phys. B 378, 52 (1992).
- Ji [1992] X. Ji, Gluon correlations in the transversely polarized nucleon, Phys. Lett. B 289, 137 (1992).
- Belitsky et al. [2001] A. V. Belitsky, X. Ji, W. Lu, and J. Osborne, Singlet structure function in the next-to-leading order, Phys. Rev. D 63, 094012 (2001).
- Braun et al. [2009] V. M. Braun, A. N. Manashov, and B. Pirnay, Scale dependence of twist-three contributions to single spin asymmetries, Phys. Rev. D 80, 114002 (2009).
- Beppu et al. [2010] H. Beppu, Y. Koike, K. Tanaka, and S. Yoshida, Contribution of twist-3 multigluon correlation functions to single spin asymmetry in semi-inclusive deep inelastic scattering, Phys. Rev. D 82, 054005 (2010).
- Kang and Qiu [2008] Z.-B. Kang and J.-W. Qiu, Single transverse-spin asymmetry for -meson production in semi-inclusive deep inelastic scattering, Phys. Rev. D 78, 034005 (2008).
- Adamczyk et al. [2012] L. Adamczyk et al. (STAR Collaboration), Longitudinal and transverse spin asymmetries for inclusive jet production at mid-rapidity in polarized collisions at gev, Phys. Rev. D 86, 032006 (2012).
- Bland et al. [2015] L. C. Bland et al. (AnDY Collaboration), Cross Sections and Transverse Single-Spin Asymmetries in Forward Jet Production from Proton Collisions at GeV, Phys. Lett. B 750, 660 (2015).
- Adolph et al. [2017] C. Adolph et al. (COMPASS Collaboration), First measurement of the Sivers asymmetry for gluons using SIDIS data, Phys. Lett. B 772, 854 (2017).
- Adamczyk et al. [2018] L. Adamczyk et al. (STAR Collaboration), Azimuthal transverse single-spin asymmetries of inclusive jets and charged pions within jets from polarized-proton collisions at GeV, Phys. Rev. D 97, 032004 (2018).
- Acharya et al. [2021a] U. Acharya et al. (PHENIX Collaboration), Transverse single-spin asymmetries of midrapidity and mesons in polarized collisions at GeV, Phys. Rev. D 103, 052009 (2021a).
- Abdallah et al. [2022] M. Abdallah et al. (STAR), Azimuthal transverse single-spin asymmetries of inclusive jets and identified hadrons within jets from polarized collisions at = 200 GeV, Phys. Rev. D 106, 072010 (2022).
- Aidala et al. [2017] C. Aidala et al. (PHENIX Collaboration), Cross section and transverse single-spin asymmetry of muons from open heavy-flavor decays in polarized + collisions at GeV, Phys. Rev. D 95, 112001 (2017).
- Acharya et al. [2021b] U. Acharya et al. (PHENIX Collaboration), Probing Gluon Spin-Momentum Correlations in Transversely Polarized Protons through Midrapidity Isolated Direct Photons in Collisions at GeV, Phys. Rev. Lett. 127, 162001 (2021b).
- Kang et al. [2008] Z.-B. Kang, J.-W. Qiu, W. Vogelsang, and F. Yuan, Accessing tri-gluon correlations in the nucleon via the single spin asymmetry in open charm production, Phys. Rev. D 78, 114013 (2008).
- Koike and Yoshida [2011] Y. Koike and S. Yoshida, Probing the three-gluon correlation functions by the single spin asymmetry in , Phys. Rev. D 84, 014026 (2011).
- Anselmino et al. [2004] M. Anselmino, M. Boglione, U. D’Alesio, E. Leader, and F. Murgia, Accessing Sivers gluon distribution via transverse single-spin asymmetries in processes at BNL RHIC, Phys. Rev. D 70, 074025 (2004).
- D’Alesio et al. [2017] U. D’Alesio, F. Murgia, C. Pisano, and P. Taels, Probing the gluon Sivers function in and , Phys. Rev. D 96, 036011 (2017).
- D’Alesio et al. [2019] U. D’Alesio, C. Flore, F. Murgia, C. Pisano, and P. Taels, Unraveling the Gluon Sivers Function in Hadronic Collisions at RHIC, Phys. Rev. D 99, 036013 (2019).
- Schmidke et al. [2018] W. B. Schmidke et al. (The RHIC Polarimetry Group), RHIC polarization for Runs 9–17 (2018), https://technotes.bnl.gov/Home/ViewTechNote/209057.
- Adcox et al. [2003a] K. Adcox et al. (PHENIX Collaboration), PHENIX detector overview, Nucl. Instrum. Methods Phys. Res., Sec. A 499, 469 (2003a).
- Nouicer et al. [2008] R. Nouicer et al. (PHENIX Collaboration), Silicon Vertex Tracker for PHENIX Upgrade at RICH: Capabilities and Detector Technology, Proc. Sci. Vertex 2007, 042 (2008).
- Nouicer et al. [2009] R. Nouicer et al. (PHENIX Collaboration), Status and Performance of New Silicon Stripixel Detector for the PHENIX Experiment at RHIC: Beta Source, Cosmic-rays and Proton Beam at 120 GeV, J. Instrum. 4 (04), P04011.
- Adcox et al. [2003b] K. Adcox et al. (PHENIX Collaboration), PHENIX central arm tracking detectors, Nucl. Instrum. Methods Phys. Res., Sec. A 499, 489 (2003b).
- Aphecetche et al. [2003] L. Aphecetche et al. (PHENIX Collaboration), PHENIX calorimeter, Nucl. Instrum. Methods Phys. Res., Sec. A 499, 521 (2003).
- Aizawa et al. [2003] M. Aizawa et al. (PHENIX Collaboration), PHENIX central arm particle ID detectors, Nucl. Instrum. Methods Phys. Res., Sec. A 499, 508 (2003).
- Aidala et al. [2019] C. Aidala et al. (PHENIX Collaboration), Measurement of charm and bottom production from semileptonic hadron decays in collisions at GeV, Phys. Rev. D 99, 092003 (2019).
- Adare et al. [2016] A. Adare et al. (PHENIX Collaboration), Single electron yields from semileptonic charm and bottom hadron decays in AuAu collisions at GeV, Phys. Rev. C 93, 034904 (2016).
- Adare et al. [2010] A. Adare et al. (PHENIX Collaboration), Measurement of Transverse Single-Spin Asymmetries for Production in Polarized Collisions at GeV, Phys. Rev. D 82, 112008 (2010), [Phys. Rev. D 86, 099904(E) (2012)].
- Adler et al. [2005] S. S. Adler et al. (PHENIX Collaboration), Measurement of transverse single-spin asymmetries for mid-rapidity production of neutral pions and charged hadrons in polarized p+p collisions at GeV, Phys. Rev. Lett. 95, 202001 (2005).
- Sjöstrand et al. [2001] T. Sjöstrand, P. Eden, C. Friberg, L. Lönnblad, G. Miu, S. Mrenna, and E. Norrbin, High-energy physics event generation with PYTHIA 6.1, Comput. Phys. Commun. 135, 238 (2001).