Improving results by improving densities: Density-corrected density functional theory
I. Introduction
Density functional calculations have become ubiquitous in modern chemistry and materials science since the award of the 1998 Nobel prize in chemistry.[1] There are now many computer codes available for performing such calculations.[2, 3, 4, 5, 6, 7] It is a straightforward matter to choose a basis set and an approximate functional, and calculate an interesting property, such as a reaction barrier, bond length, or dipole moment. But it requires judgment and experience to choose wisely.[8] Ensuring the quantity is converged with respect to basis is relatively simple. Given hundreds of possible DFT approximations available in a code, the choice can be difficult.[9]
There are myriad approaches to constructing exchange-correlation (XC) approximations, varying from appeals to general principles of quantum mechanics to fits to large databases.[10, 11, 12, 13] Modern approximations include generalized gradient approximations (GGA), hybrids, range-separated functionals, the random phase approximation and variants thereof, dispersion corrections of at least three distinct flavors, double-hybrids, and many, many more.[11, 14, 15, 16] All over the world, theorists of many different backgrounds work at improving (or at least, expanding) on our current choices, either with improved accuracy, lower computational cost, or greater reliability.[17]
In each of the countless DFT calculations performed worldwide each year, the Kohn-Sham (KS) equations[18] are iterated to a self-consistent (SC) electronic density and orbitals, and the total energy of the system is reconstructed with these final quantities. By definition, this process finds the unique[19] density that minimizes the approximate energy. All components of that energy are exactly determined, apart from the notorious XC energy. It is that piece which is approximated in DFT and whose derivative appears in the KS equations as the XC potential.
Thus, whatever choice of XC is made, it is actually used twice in the calculation. Once in finding the density and a second time in finding the energy, so that neither is quite correct. As the foundation of DFT is to consider the energy as a functional of the density[19], we may write the error in any self-consistent KS calculation as:
| (1) |
where is the exact density and is the exact functional, while tildes denote approximate quantities. In most practical calculations, modern XC approximations yield excellent approximate densities[20], so that the energy error would barely change if the approximation were evaluated on the exact density.
It is certainly extremely convenient to use the self-consistent solution density. It is easily computed from the KS equations. By being self-consistent, many important properties, especially those depending on derivatives of the energy, are much simpler and many additional terms need not be calculated. This is so convenient that essentially all modern codes use the self-consistent density in almost all circumstances. However, this was not always so. In the earliest days, the Hartree-Fock (HF) density was often used instead.[24, 25, 26, 27, 28] Mostly, it was used as a matter of convenience, so as to avoid needing to do a self-consistent calculation, in the belief that it mattered little. Later, the HF density was used as a matter of principle, to compare functionals against each other without having to worry about changes in the density.[26, 27, 28] It was even presciently noted that, in some cases, it really did seem to matter, and in those cases, it was often better to use HF densities.[29, 30, 31]
This article shows that, in fact, it really does matter, both theoretically and very practically. Until about 10 years ago, no careful, systematic analysis had been performed on this question. In fact, every single KS-DFT calculation ever run can be analyzed, to separate its functional error (energy error made on exact density) from its density-driven error (the remainder). Surprisingly large classes of calculation, such as typical reaction barriers, contain significant density-driven errors with standard functionals, such as B3LYP. One of the major reasons for this is the over-delocalization of charges and spins due to semilocal XC approximation.[32, 33] These errors are typically substantially reduced by using the HF density instead of the self-consistent density. Even highly accurate (and expensive) DFT approximations such as double-hybrids can be improved by separating out these two error sources in their design.
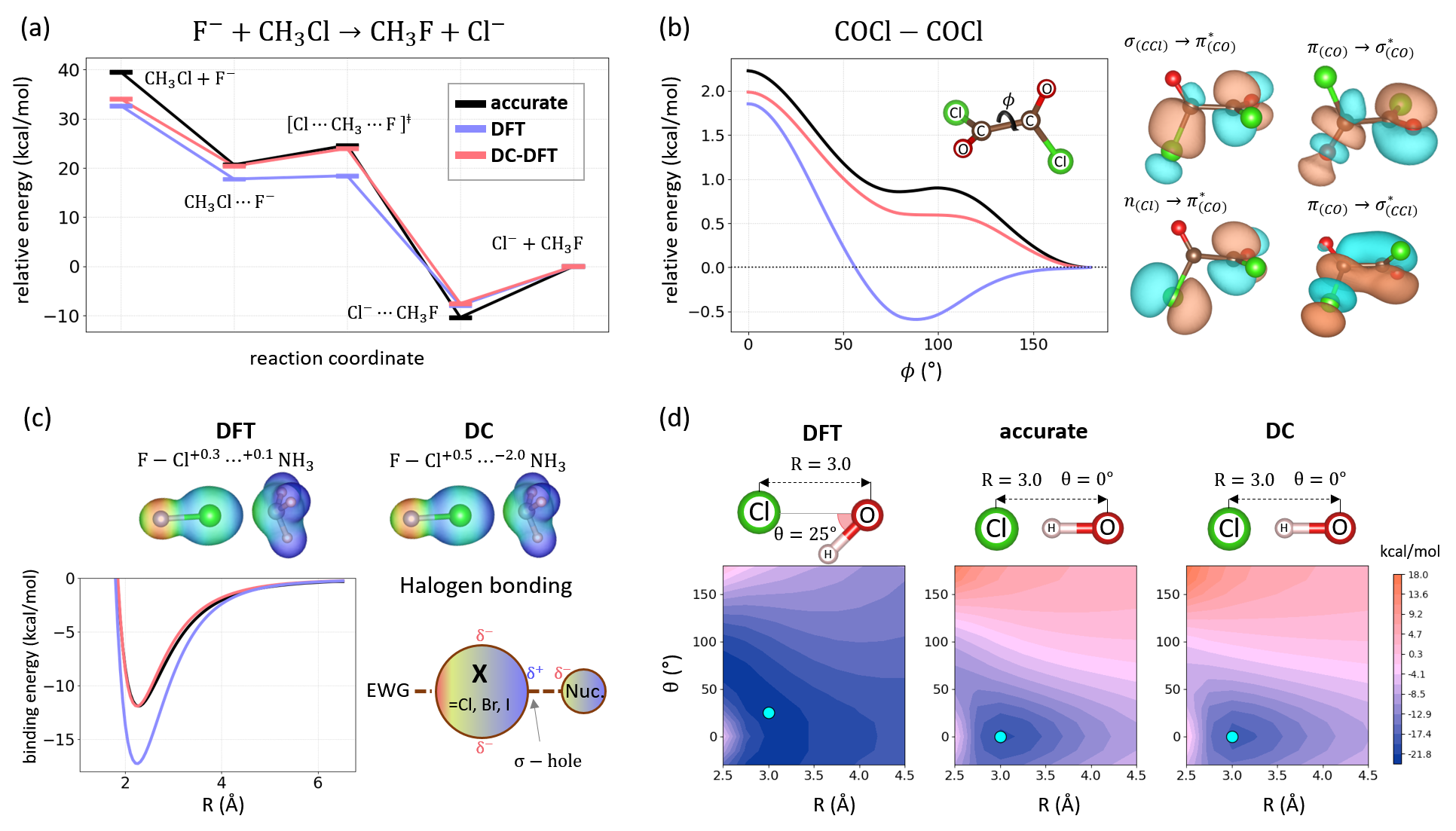
Figure 1 is a panoply of calculations where the density really matters. In every case, when self-consistent densities are replaced by HF densities, the energy errors drop by a substantial margin. In panel (a), we show an energy diagram for a textbook SN2 reaction. Starting from either reactants or products, negatively charged complexes are formed barrierlessly, while the interconversion between the two involves a barrier of 35 kcal/mol in the backward and 5 kcal/mol in the forward directions. Standard DFT provides reasonable reaction energies, but fails badly for barrier heights in both directions for the complex interconversion. DFT underestimates the backward barrier height by about 10 kcal/mol, implying a reaction many orders of magnitude faster than reality. The barrier height is indeed smaller in the forward direction, but standard DFT yields no barrier at all. A long time ago it has been demonstrated that the use of HF densities fixes failures of DFT for barrier heights, and so does here.[31, 34] For the backward barrier, density-corrected DFT (DC-DFT) reduces the error of DFT by about 6 kcal/mol, whereas the DC-DFT forward barrier height matches the reference.
Panel (b) demonstrates the power of using DC-DFT to fix the failures of DFT for difficult torsional barrier heights, whose accurate predictions play a crucial role in describing a range of chemical processes (e.g., selectivity, protein folding, molecular electronics, etc.).[21] Most torsional barriers are very accurate with standard DFT (errors below 1 kJ/mol), but barriers of a single bond participating in -conjugation are particularly problematic for DFT.[12, 35] For the oxalyl chloride shown, the standard DFT energy diagram is qualitatively wrong, incorrectly predicting that the perpendicular conformation is more stable () than the trans conformation (), where is the torsional angle depicted in panel (b). DFT also finds that there is no barrier upon conversion from trans to perpendicular. Using DC-DFT with HF densities, these barriers become far more accurate as shown.
For some weak interactions, such as halogen bonds, DC-DFT greatly improves over its self-consistent counterpart. The binding energy curve for one halogen bonded complex is shown in panel (c).[22] Standard DFT overbinds the complex by about 50 at equilibrium, whereas the DC-DFT binding curve is almost indistinguishable from the reference. In contrast to DC-DFT, dispersion corrections (such as the commonly used D3[36]) cannot fix bad DFT densities, and their addition has almost no effect on the DFT binding curve in panel (c). Despite these large improvements in energetics when HF densities are used in place of self-consistent densities, their electrostatic potentials are almost identical, as shown. From the DC-DFT perspective, there is no need to stare at density or electrostatic potential plots to decide which density is better. DC-DFT measures the accuracy of densities directly in terms of their impact on the energy, the quantity that really matters. Even the tiny differences visible in the electrostatic potentials can be measured.
Finally, panel (d) reminds us of one of the earliest successes of DC-DFT – the description of odd-electron radical complexes, which play important roles in atmospheric and environmental chemistry, cell biology, etc.[23] In panel (d), we compare potential energy surface for the HOCl- complex by varying the distance and angle, as shown. Self-consistent DFT fails badly in simulating the potential energy surface: (i) it finds that the equilibrium structure is bent instead of linear ( instead of ), (ii) gives contour of the wrong shape leading to wrong forces, and (iii) gives too blue (too negative) potential energy surface. DC-DFT again saves its self-consistent counterpart by not only yielding the correct linear structure of HOCl- as the most stable, but also producing a far more accurate potential energy surface and equilibrium structure. In this way, we see that DC-DFT not only improves DFT energetics, but also gives more accurate geometries and force fields. For applications of the principles of DC-DFT to geometry optimization of any electronic structure method, see Ref. [37, 38], which contains many surprising results about functional performance for geometry.
For the cognoscenti, in Figure 1, all DFT calculations are with PBE, except in (a) which uses B3LYP, and all accurate reference calculations are DLPNO-CCSD(T)-F12, except in (d), which is simple CCSD(T). The rest of this article is about why the basic ideas of DFT do not imply always choosing the self-consistent density. This is followed by a discussion of practical DC-DFT, with many examples illustrating crucial aspects of density-sensitive systems and calculations. We next explore some of the finer points of theory, ending with a surprise: Although Diels-Alder reactions are not density sensitive, functionals (double-hybrids) designed to take advantage of DC-DFT perform better. We end with many challenges and potential of DC-DFT.
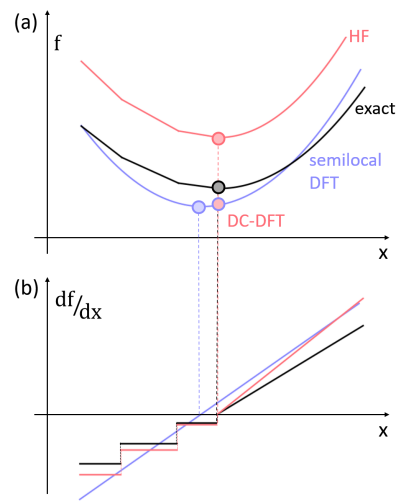
First we ask, why is this a question at all? Surely the self-consistent density is ‘best’ because it minimizes the (approximate) energy functional? It does, but because the functional is approximate, its minimum might well be below the true ground-state energy. Moreover, all useful properties are actually energy differences, and the difference between two minima does not obey a variational property. One of the most well-documented failings of most density functional approximations is that they are too smooth, especially as particle numbers pass through integer values.[39, 40] You might object that, in reality, all molecules have integer numbers of electrons. But as a bond is stretched, the exact functional develops sharp cusps that force integer numbers of electrons onto each fragment, while typical DFT approximations are smooth.[41] Figure 2 is a cartoon showing how function with a cusp can be well-approximated by a smooth one everywhere, but whose derivative is very wrong in the vicinity of that cusp. Semilocal XC approximations yield curves that are smooth everywhere, which causes the overdelocalization of charges when bonds are stretched.[42] The HF energy functional depends explicitly on only occupied orbitals, making it often even sharper than the exact functional. Relative to HF, correlation includes infinite sums over orbitals, which typically dampen the cusp as the particle number changes.
Basic separation into functional and density-driven errors: Having established that the self-consistent density need not yield the most accurate energy, how then should we decide when we might want to avoid it? We simply decompose the energy error into two well-defined pieces.[20] The functional error is simply the error in the energy if we had evaluated it on the true density, not the self-consistent one. Many would consider this the ‘true’ DFT error, as this is an apples-to-apples comparison. Moreover, the beauty of the KS scheme is that only the XC contribution to the energy is approximated. Thus, in any KS calculation, the functional error is entirely due to the XC approximation:
| (2) |
The remainder of the energy error is called the density-driven error,
| (3) |
and is given by the difference in the approximate functional on the exact and self-consistent densities. This is always negative for any given energy calculation.
Universality of energy decomposition: Thus, no matter what XC approximation you use or can afford, no matter what molecule or solid you study, and no matter which property you extract from your KS-DFT calculation, you will have some error, and that error is the sum . In the vast majority of routine calculations, the self-consistent DFT densities are incredibly accurate, so that the density-driven term has negligible effect, and DC-DFT will not help (). But, with certain classes of approximation, certain classes of molecules, and certain properties, it has been found that the density-driven error is large enough to substantially contribute or even distort calculations.[43, 44, 45] Moreover, in such cases, using a better density has led to much better energetics.[46]
With some thought, these statements would appear paradoxical. If the functional is working well for the system you are calculating, how could its density be wrong? Well, this happens because its derivative, the XC potential, is sufficiently inaccurate as to produce a sufficiently flawed density as to mess up your energy evaluation. Return to Figure 2 to see a good approximation to a function whose derivative is lousy. Doesn’t a better functional automatically imply a better XC potential? No, it does not. Almost all modern XC approximations have very poor-looking XC potentials, often shifted by very large amounts relative to the exact XC potential.[47] Yet they still usually yield highly accurate densities in the regions where it matters. GGA approximations to XC often have worse looking potentials than their LDA counterparts, but nonetheless have much better energetics.[48, 49]
In the original work[20], the term ’abnormal’ was used to designate those KS-DFT calculations whose results were contaminated by density-driven errors, and this is a characteristic of the approximate functional, the property of interest, and the given system. By contaminated, one means that the error in the energy being calculated changes substantially if the exact density is used instead. There a small KS HOMO-LUMO gap in self-consistent DFT was identified as a signal of abnormality. But the use of the gap as the abnormality indicator is not ideal, as some calculations (e.g., those involving stretching of homonuclear bonds) have small HOMO-LUMO gaps without density-driven errors. More appropriate indicators of abnormality have been built and are detailed below.
II. Practical DC-DFT
In practice, much of the above is just so much theorizing, as, if we need to do a DFT calculation, we surely cannot afford to calculate the exact (or highly accurate) density. Fortunately, we show below that, in the cases where there is a significant density-driven error with a standard DFT calculation, very often using the HF density significantly reduces the density-driven error. This is presumably because HF, although yielding woefully inadequate energetics, suffers from the reverse of the errors of most density functional approximations. Essentially, DFT approximations almost always include some variety of semi-local density functional (i.e., depending on the density, its gradient, and/or its laplacian or kinetic energy density). These approximations tend to delocalize the density relative to the exact one, whereas the HF density is typically overlocalized. This is not to say that HF densities are somehow ’better’ than approximate self-consistent DFT densities. As discussed above, there is no well-defined meaning to being better. All this means is exactly what is stated: In cases where the self-consistent approximate DFT density is unusually poor, the HF density is often more accurate in the very precise and limited sense of yielding more accurate energetics.
Problems with indiscriminant use of HF densities: So, why not use HF densities in all DFT calculations? The first problem is that self-consistency simplifies tremendously many practical aspects of modern DFT calculations, such as finding forces, vibration frequencies, polarizabilities and hyper-polarizabilities, etc. Anything that can be written as a derivative of the energy with respect to some parameter becomes much more complicated when the calculation is not self-consistent. The second is that, in general, if a calculation is not ’abnormal’, we have no reason to think the HF density (or even the exact density) would yield a more accurate energy than the self-consistent density. Thus, we may actually reduce accuracy overall if we blindly use HF densities everywhere.[52] Thirdly, for some difficult systems, where the HF calculation is substantially spin contaminated i.e., the HF <> is significantly different from the exact value, (resulting from an artificial mixing of spin-states[53]) or which are multi-determinantal in character (systems whose physics is poorly described by a single-configuration)[54], the HF density is likely to worsen the energy substantially. Imagine, for example, a database of 100 reaction energies of some kind. Suppose, with a given approximate XC, that 5 are abnormal. And further suppose that using HF densities reduces the abnormal errors by 5 kcal/mol, on average. If the HF densities worsen the normal cases by just 0.26 kcal/mol on average, HF-DFT (always using HF densities) worsens the overall results on the database, and misses the large improvements on the abnormal cases.
How to spot when a calculation is density sensitive: Thus it is crucial to have a procedure or recipe that automatically determines if a calculation is abnormal. The original criterion, that the gap is unusually small, is merely qualitative.[20] How small is small? After many variations were tried, we settled on a simple heuristic, which was called the density sensitivity.[43] It is defined as the change in the energy being calculated when going from the HF density to the LDA density, where LDA denotes local density approximation[18] (often used in the SVWN form).[55]
| (4) |
This is easily computable in standard molecular codes at DFT cost. LDA is likely to suffer more from delocalization than any more modern functional, and so acts as a canary in a coal mine for density-driven errors. If is significant, we declare the calculation likely to be abnormal and only then do we use the HF density in place of the self-consistent density. We found that a cutoff of 2 kcal/mol worked well for most small chemically bonded molecules, but of course this value must be adjusted for the circumstances. It must become larger for larger molecules,[56] and become smaller for smaller energy differences, such as in non-covalent interactions[22] and intramolecular torsional barriers[21]. DC-DFT is the formal name of the analysis that leads to these conclusions,[20, 23] and DC(HF)-DFT is the application of HF-DFT only to those cases that are density sensitive. Thus, in the 100 reaction energy set, HF-DFT may worsen the overall statistics, but DC(HF)-DFT will improve them by a small amount, but will produce significant quantitative improvement on the density-sensitive set. The theory behind DC-DFT leads to many useful concepts for understanding errors in functionals and differences between approximate functionals.[44]
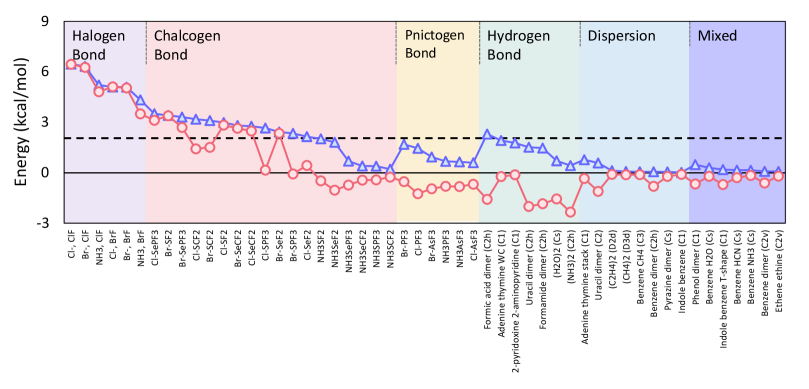
Importance of DC-DFT for non-covalent interactions: To illustrate the utility of density sensitivity, consider Figure 3. Along the -axis, we have listed 52 non-covalently bonded molecules and complexes. The right-hand-side contains the members of the well-established S22[12, 51] dataset, sorted into three categories, depending on whether they are hydrogen-bonded, weak dispersion bonds, or mixed. Within each category, they are arranged in order of PBE density-sensitivity, with highest on the left. The PBE sensitivity is the absolute difference between the PBE energy on the HF and LDA densities, Eq. 4. While it increases from right to left, it only barely reaches 2 kcal/mol for the most sensitive H bonds. Thus such weakly bonded compounds are density insensitive, and DC(HF)-DFT will not improve their energetics. But now look on the left-hand side. The B30 set contains unusual weakly-bound molecules in three distinct categories: Pnictogen, chalcogen, and halogen bonds.[50] Overall, their density sensitivities grow from right to left, and most of the chalcogens and all the halogen cases are density sensitive. Thus those molecules should have better energetics when HF densities are used. The red line shows how much the energy error changes when going from the self-consistent to the HF densities. It is the difference between the absolute value of the SC error and the absolute value of the error with HF density. Where it is positive, the SC error is larger than the HF error. Its magnitude tracks the blue line very well, showing that large changes occur where the density sensitivity is largest. On the left, the density sensitivity essentially tracks this error difference, which is positive, and dominated by the self-consistent error. On the right, the curves are almost anticorrelated, and the error difference is usually negative, showing SC yields better energetics than HF densities. For chalcogens, the mean absolute error of SC-DFT is 1.9 kcal/mol, while DC(HF)-DFT is 0.5 kcal/mol.[22] Note that improvements in energetics for halogen bonds hugely outweigh those due to dispersion corrections, as shown in panel (c) of Figure 1. Thus unwitting inclusion of such cases into databases for fitting dispersion corrections, without DC(HF)-DFT, worsens such corrections instead of improving them.[46]
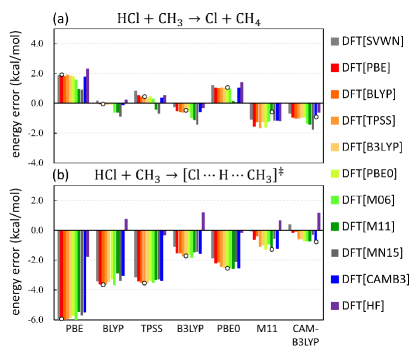
Reducing the spread of DFT results for density-sensitive problems: Next consider Figure 4, which shows many different functionals evaluated on each other’s densities for a simple reaction. Each collection of bars is the energy of a given functional, using all the different densities, color coded. The leftmost bar is gray (LDA density) and the rightmost is purple (HF density). The density sensitivity for that functional is the difference between those two. In panel (a), the numbers are plotted for the reaction energy. For any of the functionals chosen, there is little difference between the gray and purple bars. This reaction energy is density insensitive.
But consider panel (b), where the results for forward barrier heights are plotted. Most functionals give about the same answer, except when the HF density is used. Now the differences between gray and purple are huge. Moreover, the answer often changes sign (i.e., goes from no barrier in SC-DFT to having a small one in HF-DFT). Also, the spread in the different self-consistent answers (shown by open circles) is now far greater than the variation in the purple bars. This is a pattern we often see: If a problem is density sensitive, often a standard bag of functionals which usually agree with one another show a wide disparity of results, when evaluated self-consistently. But on the HF density, their spread is smaller than usual.
Improved calculations of spin gaps: The accurate calculation of spin gaps in transition metal complexes is notoriously difficult. Many methods have very different errors for high- and low-spin states, so calculating their difference accurately is very difficult.[57, 58, 59] It is well-known that many commonly used density functionals produce a large spread of answers, much more divergent than they usually give, especially when mixing HF exchange.[60] Measures of how sensitive the results are on the amount of HF exchange in a DFT functional has been recently used by Kulik and co-workers to improve predictions of properties of transition-metal compounds. [61, 62, 63]. In extreme cases, even knowing which state is the ground state of a transition-metal complex is difficult. Ab initio quantum chemistry also has difficulty in these cases. Standard CCSD(T) methods can be converged with very large basis sets, but the usual indicators suggest a strong multi-reference character, making its reliability questionable. On the other hand, multireference methods are difficult to converge with respect to the size of the active space and the size of ones computer budget. An alternative approach is to use quantum Monte Carlo (QMC), a method available for both molecules and solids[64], but using totally different technology to that of ab initio quantum chemistry.
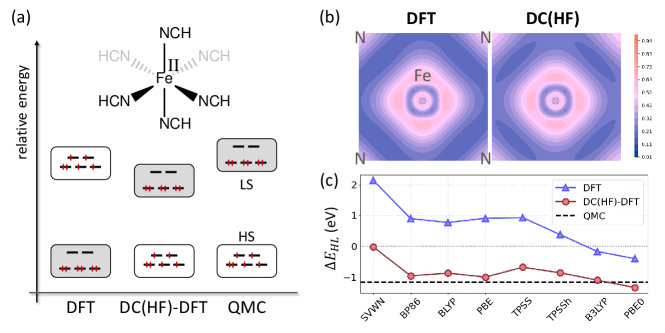
Several years ago, a study was performed on pseudo octahedral Fe(II) complexes with various ligands.[65] All were wide spin gap cases, of order 1 eV (about 20 kcal/mol) but even so, different functionals yielded wildly different gaps. The spread in their results dropped by about a factor of 2 when HF densities were used instead. The average results differed significantly from those of CCSD or CCSD(T), but agreed (within error bars) with some very expensive, state-of-the-art QMC calculations. Since then, many authors have tackled these systems with many variations on many methods, so the jury is still out on whether or not DFT on HF densities yields accurate spin gaps here.[59, 66, 67]
Figure 5 illustrates some results for the Fe[(NCH)6]2+ complex. Panel (a) shows energy differences between high- and low-spin states. A metaGGA called TPSS[68], when applied self-consistently, incorrectly yields the low-spin state as lower than the high-spin state, contradicting the QMC result. This is true of many semi-local functionals. Inclusion of a moderate fraction of exact exchange may bring the high-spin state slightly lower, but not enough (see blue curve in (c)). On the other hand, almost all functionals have the correct ordering when evaluated on HF densities, and most yield quite accurate spin gaps (red curve in (c)). Just as in the rainbow plot of Figure 4, there is a characteristic reduction in the spread of predictions when the HF density is used in a density-sensitive system. Finally, panel (b) shows the localized orbital locator (LOL)[69] for both calculations. One can see small differences in the bonding regions using LOL, because it is specifically designed to make such differences visible, but it is impossible to tell by visual inspection of densities or their differences which one is better and why.
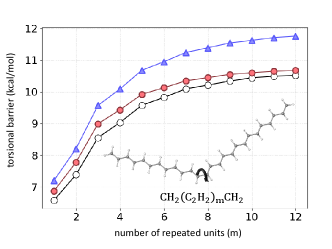
When torsional barrier errors get large: We return now to the torsional barriers in Figure 1(b). In Ref. [21], the density-sensitivity cutoff was set to 2 kJ/mol instead of 2 kcal/mol, for the obvious reason that all energetic differences were much smaller than for stronger chemical interactions. Nonetheless, the consequences of errors in self-consistent DFT torsional barriers can be much larger. Consider Figure 6, which shows the torsional barrier height of conjugated polymer chains at different lengths using the ever-popular B3LYP functional. The overestimate of the barrier height grows with the chain length, reaching almost 2 kcal/mol when , the number of repeated units. On the other hand, DC(HF)-B3LYP becomes almost perfect in this limit.
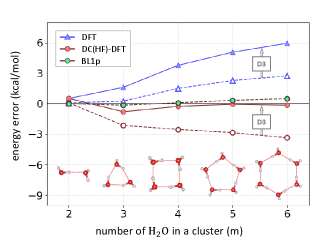
Great success of DC-DFT for water clusters: To end this tour, we consider binding energies of water clusters. DFT has been very successful in describing properties of water,[70, 71] and a recent paper has shown that DC-DFT can achieve near CCSD(T) accuracy for describing a range of water properties, using the SCAN functional on HF densities.[72] In Figure 7, we show errors in PBE binding energies for small water clusters from self-consistent DFT and DC(HF)-DFT, with and without the D3 correction. In contrast to the earlier complex shown in Figure 1(c) where D3 was not affecting the DFT results, here it has a large effect on the DFT errors. When added to self-consistent DFT, D3 substantially worsens the results, suggesting an issue inherent to D3.[73] But in fact D3 greatly reduces the errors when added to DC(HF)-DFT (in Ref. [46], we discuss in more detail how large density errors can contaminate and obscure D3 effects). BL1p, a double-hybrid which was designed using principles of DC-DFT[46] (see next section), is also highly accurate for water complexes.
III. Theoretical considerations
In principle, DC-DFT is a much more general concept than those that appear in the literature: self-interaction, strong-correlation, delocalization, straight-line behavior of the energy as a functional of non-integer particle number, etc. It is based on a two-line decomposition of the error in any DFT calculation. Thus it can be applied to every functional approximation ever suggested and every DFT calculation ever performed, including the first ever Thomas-Fermi atomic calculations.[74, 75] Our focus here has been on KS calculations based on semi-local approximations, where the HF density typically works to cure significant density-driven errors, but DC-DFT can be applied much more broadly. DC-DFT analysis will usually provide different insights to these traditional analysis tools and may be less useful. But more importantly, DC-DFT can unite aspects of these other characterization tools.
Using DC-DFT to quantify errors in densities: A recent application of DC-DFT involves answering an apparently very simple question: How do you measure the accuracy of a density?[43] A popular publication claimed that some of the most recent empirical density functionals were producing worse densities than earlier functionals, suggesting that DFT development was ‘straying from the path’ toward the exact functional.[76, 77] However, closer examination of the methodology used showed that the results found were due to the choices made by the authors. Many papers commented on the original claims[78, 79, 80], some referring to DC-DFT.
With the tools provided by DC-DFT, it is straightforward to address this question from a pragmatic viewpoint. The first and foremost point is that, despite its name, the primary purpose of (ground-state) DFT is to produce ground-state energies for different molecular configurations, not densities. Few users ever output or examine the density closely, precisely because it is not what matters to their results. Thus the success of DFT in predicting those energies does not depend on how accurately approximations reproduce the density. Nevertheless, when the density or a property computed from it (e.g., electrostatic potential, partial atomic charges, etc.) is of interest to a user, it is usually better to use HF densities than SC ones provided that a calculation is density sensitive. This is illustrated later in Figure 9, where we compare HF and DFT atomic charges as we stretch NaCl.
Of course, the exact functional reproduces both the exact energy and the exact density but, as we have seen, a functional which yields usefully accurate energies need not yield accurate densities. This leads directly to a second important point. No matter how one might choose to measure density errors (and there are infinitely many choices, including infinitely many reasonable ones), there must be some sense of scale. If density differences are miniscule, why should anybody care, as they will have essentially no impact on predicted energies? Thus DC-DFT is the perfect tool for answering this question, as it measures the accuracy of densities directly in terms of their impact on the energy.
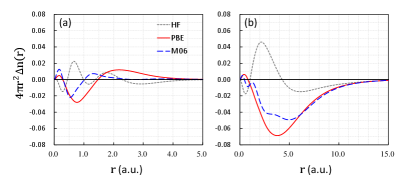
Figure 8 shows density errors for two very different two electron systems. The first is the He atom which is density-insensitive. Errors in these densities have little effect on energies. Furthermore, given the error profiles, which approximation has the ‘best’ density? The ranking depends entirely on one’s choice of measure. On the right, we have the same errors for H-. This is a case of extreme density sensitivity, and was used as the prototype[20] for understanding density sensitivity. These are among the ‘largest’ density errors found in self-consistent DFT calculations, yet they are comparable in magnitude to those in He. But the observant will notice that the approximate functionals (PBE and M06 here) have errors that do not integrate to zero! How can this be? In fact, a correct self-consistent calculation[20] has about 0.3 electrons escape entirely from the system (and a HOMO of exactly zero).
There are two lessons here. First, in almost all interesting cases and all those discussed in this article, the density errors are small and subtle. We have never been able to understand energetics from studying these small differences directly. The relationship between densities and approximate XC is just far too complicated. On the other hand, we never need to do this, as our measures are all based on calculable energies, which speak for themselves.
The second lesson concerns electron affinities, and is more subtle. A popular method for calculating anions with self-consistent semi-local functionals is to use a basis set similar to that used for the neutral, and find electron affinities by subtraction. This method works surprising well, often yielding errors smaller than those of ionization potentials. But a sure sign that the anionic calculation is unconverged is the existence of a positive HOMO.[81, 82, 83] The basis-set is artificially binding the last electron. The fully converged calculation is like that of H- shown, with a fraction of the last electron lost to the void. The beauty of the DC-DFT treatment is that it produces a well-bound density for the anion without a positive HOMO, and yields accuracies comparable to the artificial methods in common practice. In fact, it was studies of this issue[84, 85, 86], mostly couched in the language of self-interaction, that ultimately led to the more general concepts of DC-DFT[20].
Using DC-DFT to avoid altering the fraction of exact exchange: Becke introduced the idea of a (global) hybrid functional, replacing a fraction of GGA exchange with HF.[87, 88] It has since become common to vary the fraction of HF exchange in DFT calculations, both for molecules and materials.[89, 90, 91] In the molecular case, different functionals are designed with different amounts. The original global hybrids had about 20-25 % exchange, for reasons that could at least be understood, but more recent (and often more accurate) functionals might have ’2X’, or about 50 % mixing,[92] and many double-hybrid functionals have even more.[93, 94] But at least the amount is fixed once and for all. In materials calculations, it has become increasingly popular to vary the amount of mixing, in order to position the single-particle levels at some desirable location, such as putting defect levels correctly in a gap. Adjusting the amount for each different system actually leaves the realm of DFT, as your functional has picked up an illegal dependence on the external potential. Of course, the adjustment may well be describing good physics, but the road to (formal) hell is paved with good (physical) intuition. DC-DFT is much less sensitive to the exchange portion than its self-consistent counterpart providing reliable energies without adjusting the fraction of exact exchange. In Figure 4, the purple bars differ by about 3 kcal/mol for different functionals, but the white dots differ by twice that amount. This strongly suggest that such adjustments are simply trading density-driven errors for functional errors, obscuring the underlying physics. Practical DC-DFT never suffers from this problem because it always uses the same HF density. Very often, high accuracy is achieved with the moderate exchange fraction used in popular hybrids such as B3LYP and PBE0.
The ease of performing DC-DFT calculations: As a practical matter, for molecular calculations, it is trivial to evaluate a density functional on the HF density (and orbitals, if needed). One simply converges a HF calculation and then use its solution as the initial guess in a DFT calculation, while setting the number of iterations to zero. The computer will evaluate the DFT energy on those orbitals without updating them. Scripts for performing this operation are available from the website.[95]
In fact, this is not quite the same as evaluating on the HF density, as the HF kinetic energy is not quite the same as the KS kinetic energy.[96] However, this difference has been found to be much smaller than the improvement typically provided by using HF densities in cases where density-driven errors are large.[45] (See also Figure 11 below). In other words, HF densities do far more good than harm for density-sensitive calculations. Moreover, to the extent practical with finite basis sets, the differences with using the exact density have been found to also be very small, i.e., use of HF-DFT yields almost all the benefits that the exact density would confer.
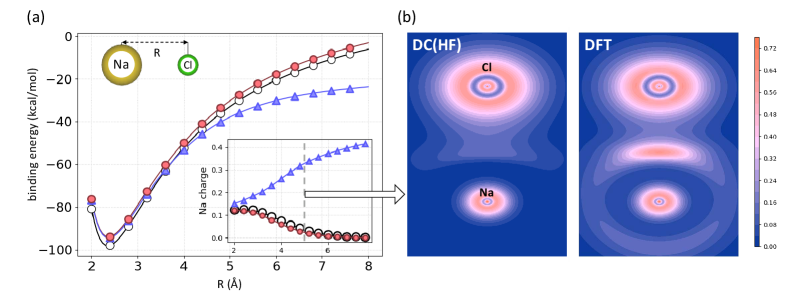
DC-DFT fixes problems with heteronuclear stretched bonds: A major problem with semi-local DFT is failures in binding energy curves. Typically, as bonds are stretched substantially beyond equilibrium values, some qualitatively incorrect behavior appears. For stretched heteronuclear diatomics, because semi-local functionals are smooth, they allow an incorrect fractional charge to be transferred, while the exact functional localizes integer numbers of electrons on each sight. The classic prototype is NaCl(gas), which dissociated into neutral atoms, unlike NaCl(aq) which dissociates into ions. In the stretched limit, semi-local DFT tends to unphysically transfer 0.4 electrons to the Cl ion. This additional fraction of an electron (and missing fraction from Na) causes the SC-DFT binding energy curve to be almost 1 eV too low at large bond distances, as shown in Figure 9. Because HF localizes charges (more or less correctly, see inset), HF-DFT yields a much more accurate curve. This correct localization in DC(HF)-DFT can be seen clearly on the right, where the LOL has been plotted in a plane including the bond axis.
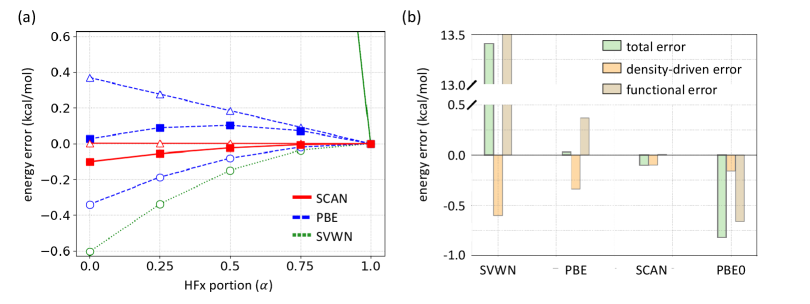
DC-DFT and functional development: One way to illustrate the relevance of DC-DFT is to study the evolution of non-empirical functionals and their global hybrids on the total energy (or ionization energy) of the simplest possible system, a single H atom.[16, 44, 97] In Figure 10, we consider LDA (SVWN), PBE, and SCAN, and study their behavior under interpolation toward the exact functional, in this case HF, i.e., . For , we have the original functional, but for , we have pure HF. For , we have (almost) PBE0 (except correlation has been reduced by 25 %).
The functional error of LDA is enormous on this scale, but the density-driven contribution is very small, illustrating the normalcy of this system and the high typical accuracy of even LDA densities. But note the accuracy of the total energy of PBE, i.e., at . That this is accidental can be seen both by the increased deviation as grows, but more relevant is that the total error is small because the functional and density-driven errors are both much larger in magnitude, but mostly cancel. In fact, this cancellation is greatest at and is less effective as more of the exact answer is added. Technically, this makes the H atom density sensitive for PBE, but this is entirely due to the accidental accuracy at self-consistency.
Finally, we see that SC-SCAN has a larger energy error than SC-PBE for the H atom, but in fact this is all density-driven. The SCAN functional error is zero for the H atom, by construction, but its error is non-zero when performed self-consistently. It can be perfectly possible for an approximate functional to be designed to be self-interaction error free for exponential densities, and yet produce a finite density-driven error for the H atom, because it’s XC potential will be incorrect. Ironically, SCAN is less accurate for the H atom than PBE is, despite SCAN using the H atom as an appropriate norm.
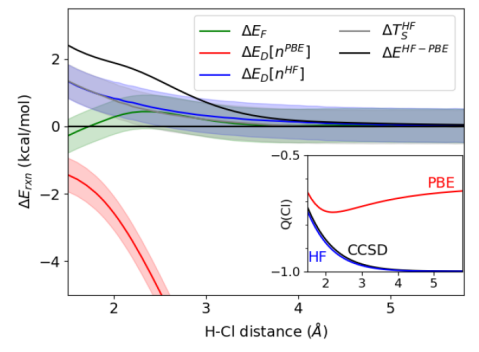
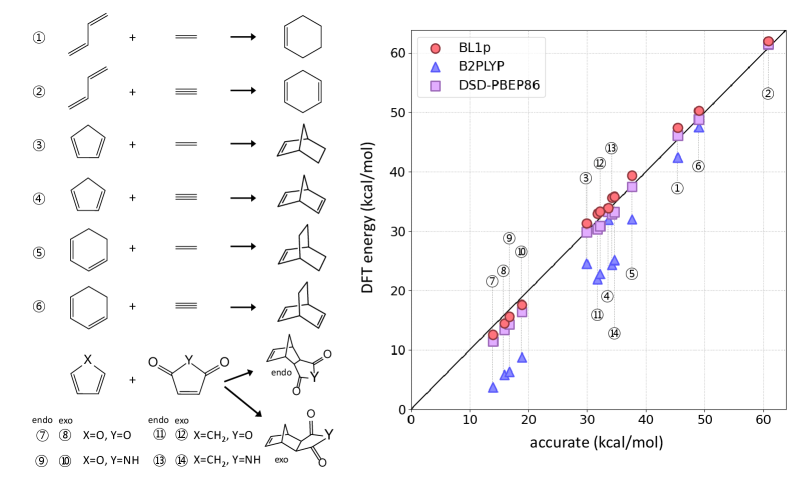
Figure 1(d) showed the PES of self-consistent and DC PBE calculations of OHCl-. Figure 11 shows what is happening as OHCl- dissociates, breaking down the PBE errors into their density-driven and functional-driven components, i.e., it is like Figure 10, but looking here at differences. The shaded regions indicate uncertainties due to the limitations of KS inversion methods with atomic basis sets, which we use to reverse-engineer the ’exact’ density and KS orbitals from a correlated wavefunction.[45] The density-driven component is sufficiently large as to be off-scale beyond about 2.5 Å. Also plotted are the errors of HF-PBE and the small error due to using the HF kinetic energy instead of the KS kinetic energy.
How DC-DFT can improve density-insensitive calculations: Our last point in the theoretical section concerns functional development. Double-hybrid functionals, those including fractions of both HF exchange and MP2 (or other) correlation energy, have been developed and yield extremely high accuracy, albeit at computational costs greater than traditional DFT calculations. In many cases, their densities are so good that one cannot imagine them suffering from a significant density-driven error.
But, you might be surprised. The parameters in such functionals are chosen by minimizing errors on large curated databases, such as the GMTKN55 collection of 55 databases.[12] This process matches the calculated energetic errors relative the exact energies, not the functional errors. Moreover, the densities used in the calculation are typically not quite self-consistent, as it is more involved[99, 100] to optimize a functional involving MP2 (which depends on orbital energies). Thus the finding of the best parameters has (very small) inefficiencies. Because these functionals are so accurate, it only requires a very little density-driven error to make them suboptimal.
We recently used this insight to demonstrate such issues, creating our own 1-parameter double-hybrid, BL1p, but optimized to minimize functional errors rather than total energy errors.[46] For standard semilocal density functionals, DC-DFT tells us to use HF densities in density-sensitive cases. But because of the inclusion of approximate ab initio correlation in double-hybrids, the fraction of exact exchange is typically much higher, and it is fine to always use HF density as long as training is done with that density. The crucial step is to train on the functional error alone, i.e., subtracting the density-driven contribution from energy errors. Thus BL1p fixes the failures of standard double-hybrids for typical density sensitive calculations (e.g., dissociation of NaCl)[46, 52], but also provides improvements for density insensitive cases as will be illustrated below.
In Figure 12, we show results for the DARC database of Diels-Alder reactions. These reactions are long known as cases where standard functionals like B3LYP fail badly, and even double-hybrids. The figure shows B2PLYP, perhaps the most popular current double-hybrid, along with the more recent DSD-PBEP86.[101] On the other hand, BL1p uses the exact same ingredients, contains only one empirically determined parameter and uses the HF density. Furthermore, BL1p is trained on atomization energies of ony 6 molecules, while DSD-PBEP86 is trained on many more datapoints. The improvement of BL1p over B2PLYP is remarkable, further reinforcing the need to account for DC-DFT even with the latest, greatest approximations. We have recently shown that DFT calculations for DARC reactions are density insensitive making their errors almost entirely functional-driven.[46] Nevertheless, our BL1p still gives improvement for the DARC dataset because it is designed by the minimization of functional errors, while density-driven errors are taken care already by its construction.
IV. Challenges
As we have seen, the concept of density-driven errors is becoming widespread in the chemical literature and to a lesser extent, in the materials world.[102, 103, 104] Moreover, increasing numbers of authors are finding that the selective use of HF densities does indeed significantly reduce density-driven errors. In this section, we list some of the more obvious limitations of the current theory and also where it might be expanded.
Stretched H2 and H: Our first stop is the iconic prototypes of self-interaction error and strong correlation in chemistry. These are the binding energy curves of H and H2, respectively. The H curve is a pure example of unbalanced self-interaction error. Because it is a one-electron system, HF densities and energies are exact. But essentially any semi-local approximation has an unbalanced error in going from the equilibrium situation to the stretched bond, where half an electron localizes on each proton. The self-interaction error changes greatly, leading to a very unfortunate binding energy curve. The other example is stretched H2, where the problem is 1/2 an electron of each spin being localized on each proton.[32, 105] A restricted KS calculation with a semi-local approximation will dissociate to incorrect fragments with the wrong energetics (namely, spin-unpolarized H atoms).
In its current form, DC-DFT has nothing to say about how semi-local DFT can be improved for these systems, as they do not appear to be density sensitive. The errors made by the semi-local approximations on the stretched bonds are not much different if one uses exact densities or approximate restricted densities. And evaluation of the approximate functionals on the exact densities still produces the large errors. Thus these are functional errors by our current classification scheme.
But did we not say that a success of DC-DFT was to improve the dissociation limit of many molecules? Yes we did, but these are heteronuclear molecules whose stretched limit is not symmetric, and whose HF density is much more accurate in that limit, because of charge localization. We suspect that some generalization of DC-DFT ought to be able to include both stretched H and H2 but we have not yet found it.
Energy-density consistency: A second challenge is to restore self-consistency. While there are firm theoretical justifications for building DFT approximations to be applied to HF densities,[106, 107, 108, 109] we have already mentioned the many practical advantages of using self-consistent densities. In fact, in principle, restoring self-consistency is always straightforward with any approximation for the energy. If we consider as the DC(HF)-DFT energy for any given problem, characterized by external potential and electrons, then the corresponding density is just its functional derivative with respect to , which can always be calculated by making small changes, pointwise in space. Thus one can imagine performing such a calculation on the DC(HF)-DFT energy. This would produce a density that differs from both the HF and the self-consistent (of the original XC approximation) densities. While easy in principle, in practice it may not be, and one could use a basis set to represent this density to avoid doing the calculation pointwise. It would be very interesting to see in what way such a density differed from its progenitors, and if it looked more like the exact density.
Of course, a much more satisfactory approach is to construct functionals that yield both good energetics and good densities when performed self-consistently.[110] Perhaps the foremost approach is that of Yang and co-workers in this direction.[33] Their approach is designed to reduce delocalization errors (both functional- and density-driven components) by explicitly imposing the well-known linearity condition with respect to particle number.[111] Many failures in DFT are attributed to deviations from this condition.[112] Cohen and co-workers have recently constructed DeepMind 21, a functional where machine learning has been used to address deviations from linearity condition.[113] This and other machine-learning approaches[114, 115] are also very promising when it comes to building functionals that give both good energetics and self-consistent densities.
Using DC-DFT to analyse orbital-free DFT errors: A major use would be to apply it to orbital-free DFT (OF-DFT). The few cases we have considered suggest that many orbital-free approximations yield errors that are dominated by their density-driven component. When the KS kinetic energy is approximated, even if very accurately, even small imperfections in the derivative will yield large errors in the density.[44] Thus DC-DFT allows one to balance improvements in the approximate potential (and therefore the density) relative to those of the KS kinetic energy functional itself, such as whether exact conditions on the potential are relevant to the energies.[116] This is an area with great potential applications. In the light of DC-DFT, another way to view the genius of KS is that it (usually) reduces density-driven errors to negligible amounts.
Complications with transition metal chemistry: There are many more applications of DC-DFT in main group than in transition metal chemistry. But transition metal applications are slowly catching up. We illustrated Fe(II) spin gaps earlier. Also, Martín-Fernández and Harvey applied their normalized sensitivity metrics to classify Fe and FeMo clusters by their density sensitivity.[56] In general, more tests are needed to see whether HF densities improve density-sensitive calculations of transition metal compounds to the extent they do for main group molecules. In these cases, it is less clear that the HF density is sufficiently close to the exact density to guarantee improvement of energetics.
Applications to bulk materials and their surfaces: Another neglected area of application is in materials and surface science. Almost all our own work has involved molecular calculations. In molecular cases, the HF density is easy to calculate, and is often a good proxy for the exact density in density-sensitive cases. The need for DC-DFT analysis may well be even greater in materials calculations than in molecular calculations. Do we really know if and when calculations in materials and surface science suffer from substantial density-driven errors? There are a few cases described in the literature, where the results of semi-local calculations have been analyzed by DC-DFT. In some instances (e.g., the adsorption of CO on metallic surfaces), better results were obtained by the use of presumably more accurate densities.[102] In other cases, such as the challenging barrier height for attaching O2 to the Al(111) surface, semi-local calculations appear to benefit little from more accurate densities.[103] Nevertheless, there are still too few cases of applying DC-DFT in materials and surface science to draw general conclusions about when and how these fields can benefit from DC-DFT. Furthermore, HF calculations can be formally and computationally problematic in periodic systems. Janesko overcomes this difficulty by applying DC-DFT without HF exchange.[16]
Forces and geometry optimization with DC-DFT: From Figure 1(d), we saw that DC-DFT also improves standard DFT forces and geometries in density-sensitive calculations. While there are a few codes that can be used to run geometry optimizations by using DC-DFT[34], these are not yet widely available. A more widespread implementation of DC-DFT forces and reactive potentials would facilitate molecular dynamics based on DC-DFT (to be used in e.g., atmospheric chemistry for odd-electron radical complexes).[23] Such implementations would make it possible to study DC-DFT’s performance for geometries as well as energies.[37]
Excited states in DC-DFT: We are often asked about applying the concepts of DC-DFT to excited states, such as from the predictions of TDDFT in linear response.[117, 118] However, excited-states do not have their own Hohenberg-Kohn theorem[119] and so the variational principle upon which so much of DC-DFT is built does not apply here. On the other hand, there has been a resurgence of interest in ensemble DFT to extract excited-state energies.[120, 121, 122] Ensemble DFT is based on a variational principle using the density, and so the analysis methods of DC-DFT can be applied.[122, 123]
We conclude by simply noting that DC-DFT is based on a simple one-line decomposition
of DFT errors, based on the variational principle. In the past, many aspects of this
decomposition had been noticed and mused over in understanding DFT results, but DC-DFT
is a formal analysis that puts all these disparate pieces (and disparate sources of
error) together. The concepts of DC-DFT are appearing more and more frequently in the
chemistry and materials literature, and calculations using DC-DFT are being reported.
As long as researchers continue to use KS-DFT as a standard tool for scientific discovery,
DC-DFT will play an ever-expanding role in analyzing the inevitable errors.
Acknowledgment
ES and SS are grateful for support from the National Research Foundation of Korea (NRF-2020R1A2C2007468 and NRF-2020R1A4A1017737). KB acknowledges funding from NSF (CHEM 1856165). SV acknowledges funding from the Marie Sklodowska-Curie grant 101033630 (EU’s Horizon 2020 programme). ES and SS thank Prof. Soo Hyuk Choi for useful comments on the illustrations.
References
- [1] Walter Kohn. Nobel Lecture: Electronic structure of matter—wave functions and density functionals. Reviews of Modern Physics, 71(5):1253, 1999.
- [2] TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- [3] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox. Gaussian16 Revision B.01, 2016. Gaussian Inc. Wallingford CT.
- [4] Evgeny Epifanovsky, Andrew TB Gilbert, Xintian Feng, Joonho Lee, Yuezhi Mao, Narbe Mardirossian, Pavel Pokhilko, Alec F White, Marc P Coons, Adrian L Dempwolff, et al. Software for the frontiers of quantum chemistry: An overview of developments in the q-chem 5 package. The Journal of Chemical Physics, 155(8):084801, 2021.
- [5] Georg Kresse and Jürgen Furthmüller. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B, 54(16):11169, 1996.
- [6] Qiming Sun, Timothy C. Berkelbach, Nick S. Blunt, George H. Booth, Sheng Guo, Zhendong Li, Junzi Liu, James D. McClain, Elvira R. Sayfutyarova, Sandeep Sharma, Sebastian Wouters, and Garnet Kin-Lic Chan. Pyscf: the python-based simulations of chemistry framework. WIREs Computational Molecular Science, 8(1):e1340, 2018.
- [7] Frank Neese, Frank Wennmohs, Ute Becker, and Christoph Riplinger. The orca quantum chemistry program package. The Journal of Chemical Physics, 152(22):224108, 2020.
- [8] Kieron Burke. Perspective on density functional theory. The Journal of Chemical Physics, 136(15):150901, 2012.
- [9] Dmitrij Rappoport, Nathan R. M. Crawford, Filipp Furche, and Kieron Burke. Approximate Density Functionals: Which Should I Choose? John Wiley & Sons, Ltd, 2011.
- [10] Aurora Pribram-Jones, David A. Gross, and Kieron Burke. Dft: A theory full of holes? Annual Review of Physical Chemistry, 66(1):283–304, 2015.
- [11] Narbe Mardirossian and Martin Head-Gordon. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Molecular Physics, 115(19):2315–2372, 2017.
- [12] Lars Goerigk, Andreas Hansen, Christoph Bauer, Stephan Ehrlich, Asim Najibi, and Stefan Grimme. A look at the density functional theory zoo with the advanced gmtkn55 database for general main group thermochemistry, kinetics and noncovalent interactions. Physical Chemistry Chemical Physics, 19(48):32184–32215, 2017.
- [13] Pragya Verma and Donald G Truhlar. Status and challenges of density functional theory. Trends in Chemistry, 2(4):302–318, 2020.
- [14] Jan ML Martin and Golokesh Santra. Empirical Double-Hybrid Density Functional Theory: A ‘Third Way’in Between WFT and DFT. Israel Journal of Chemistry, 60:1–19, 2019.
- [15] Benjamin G. Janesko. Replacing hybrid density functional theory: motivation and recent advances. Chemical Society Reviews, 50:8470–8495, 2021.
- [16] Benjamin G Janesko. Reducing density-driven error without exact exchange. Physical Chemistry Chemical Physics, 19(6):4793–4801, 2017.
- [17] Frank Neese, Mihail Atanasov, Giovanni Bistoni, Dimitrios Maganas, and Shengfa Ye. Chemistry and quantum mechanics in 2019: give us insight and numbers. Journal of the American Chemical Society, 141(7):2814–2824, 2019.
- [18] Walter Kohn and Lu Jeu Sham. Self-consistent equations including exchange and correlation effects. Physical Review, 140(4A):A1133, 1965.
- [19] P. Hohenberg and W. Kohn. Inhomogeneous electron gas. Physical Review, 136(3B):B864–B871, Nov 1964.
- [20] Min-Cheol Kim, Eunji Sim, and Kieron Burke. Understanding and reducing errors in density functional calculations. Physical Review Letters, 111(7):073003, 2013.
- [21] Seungsoo Nam, Eunbyol Cho, Eunji Sim, and Kieron Burke. Explaining and fixing dft failures for torsional barriers. The Journal of Physical Chemistry Letters, 12(11):2796–2804, 2021.
- [22] Yeil Kim, Suhwan Song, Eunji Sim, and Kieron Burke. Halogen and chalcogen binding dominated by density-driven errors. The Journal of Physical Chemistry Letters, 10(2):295–301, 2018.
- [23] Min-Cheol Kim, Eunji Sim, and Kieron Burke. Ions in solution: Density corrected density functional theory (dc-dft). The Journal of Chemical Physics, 140(18):18A528, 2014.
- [24] George C Lie and Enrico Clementi. Study of the electronic structure of molecules. xxi. correlation energy corrections as a functional of the hartree-fock density and its application to the hydrides of the second row atoms. The Journal of Chemical Physics, 60(4):1275–1287, 1974.
- [25] Renato Colle and Oriano Salvetti. Approximate calculation of the correlation energy for the closed shells. Theoretica Chimica Acta, 37(4):329–334, 1975.
- [26] Peter MW Gill, Benny G Johnson, John A Pople, and Michael J Frisch. An investigation of the performance of a hybrid of hartree-fock and density functional theory. International Journal of Quantum Chemistry, 44(S26):319–331, 1992.
- [27] Peter MW Gill, Benny G Johnson, John A Pople, and Michael J Frisch. The performance of the Becke—Lee—Yang—Parr (B—LYP) density functional theory with various basis sets. Chemical Physics Letters, 197(4-5):499–505, 1992.
- [28] Benny G Johnson, Peter MW Gill, and John A Pople. Preliminary results on the performance of a family of density functional methods. The Journal of Chemical Physics, 97(10):7846–7848, 1992.
- [29] Jerzy Cioslowski and Asiri Nanayakkara. Electron correlation contributions to one-electron properties from functionals of the hartree–fock electron density. The Journal of Chemical Physics, 99(7):5163–5166, 1993.
- [30] Nevin Oliphant and Rodney J Bartlett. A systematic comparison of molecular properties obtained using hartree–fock, a hybrid hartree–fock density-functional-theory, and coupled-cluster methods. The Journal of Chemical Physics, 100(9):6550–6561, 1994.
- [31] Benjamin G Janesko and Gustavo E Scuseria. Hartree–fock orbitals significantly improve the reaction barrier heights predicted by semilocal density functionals. The Journal of Chemical Physics, 128(24):244112, 2008.
- [32] Aron J. Cohen, Paula Mori-Sánchez, and Weitao Yang. Insights into current limitations of density functional theory. Science, 321(5890):792–794, 2008.
- [33] Chen Li, Xiao Zheng, Neil Qiang Su, and Weitao Yang. Localized orbital scaling correction for systematic elimination of delocalization error in density functional approximations. National Science Review, 5(2):203–215, 2017.
- [34] Prakash Verma, Ajith Perera, and Rodney J. Bartlett. Increasing the applicability of dft i: Non-variational correlation corrections from hartree-fock dft for predicting transition states. Chemical Physics Letters, 524:10 – 15, 2012.
- [35] Alfred Karpfen, Cheol Ho Choi, and Miklos Kertesz. Single-bond torsional potentials in conjugated systems: a comparison of ab initio and density functional results. The Journal of Physical Chemistry A, 101(40):7426–7433, 1997.
- [36] Stefan Grimme, Jens Antony, Stephan Ehrlich, and Helge Krieg. A consistent and accurate ab initio parametrization of density functional dispersion correction (dft-d) for the 94 elements h-pu. The Journal of Chemical Physics, 132(15):154104, 2010.
- [37] Stefan Vuckovic and Kieron Burke. Quantifying and understanding errors in molecular geometries. The Journal of Physical Chemistry Letters, 11(22):9957–9964, November 2020.
- [38] Stefan Vuckovic. Quantification of geometric errors made simple: Application to main-group molecular structures. The Journal of Physical Chemistry A, 126(7):1300–1311, 2022.
- [39] John P. Perdew. What do the Kohn-Sham orbitals mean? How do atoms dissociate?, page 265. Plenum, NY, 1985.
- [40] Robert G Parr and Weitao Yang. Density Functional Theory of Atoms and Molecules. Oxford University Press, 1989.
- [41] Min-Cheol Kim, Hansol Park, Suyeon Son, Eunji Sim, and Kieron Burke. Improved dft potential energy surfaces via improved densities. The Journal of Physical Chemistry Letters, 6(19):3802–3807, 2015.
- [42] Chen Li, Xiao Zheng, Aron J Cohen, Paula Mori-Sánchez, and Weitao Yang. Local scaling correction for reducing delocalization error in density functional approximations. Physical Review Letters, 114(5):053001, 2015.
- [43] Eunji Sim, Suhwan Song, and Kieron Burke. Quantifying density errors in dft. The Journal of Physical Chemistry Letters, 9(22):6385–6392, 2018.
- [44] Stefan Vuckovic, Suhwan Song, John Kozlowski, Eunji Sim, and Kieron Burke. Density functional analysis: The theory of density-corrected dft. Journal of Chemical Theory and Computation, 15(12):6636–6646, 2019.
- [45] Seungsoo Nam, Suhwan Song, Eunji Sim, and Kieron Burke. Measuring density-driven errors using kohn–sham inversion. Journal of Chemical Theory and Computation, 16(8):5014–5023, July 2020.
- [46] Suhwan Song, Stefan Vuckovic, Eunji Sim, and Kieron Burke. Density sensitivity of empirical functionals. The Journal of Physical Chemistry Letters, 12(2):800–807, 2021.
- [47] Cyrus J Umrigar and Xavier Gonze. Accurate exchange-correlation potentials and total-energy components for the helium isoelectronic series. Physical Review A, 50(5):3827, 1994.
- [48] Kin-Chung Lam, Federico G. Cruz, and Kieron Burke. Virial exchange-correlation energy density in hooke’s atom. International Journal of Quantum Chemistry, 69(4):533–540, 1998.
- [49] Kieron Burke, Federico G. Cruz, and Kin-Chung Lam. Unambiguous exchange-correlation energy density. J. Chem. Phys., 109(19):8161–8167, 1998.
- [50] Antonio Bauza, Ibon Alkorta, Antonio Frontera, and Jose Elguero. On the reliability of pure and hybrid dft methods for the evaluation of halogen, chalcogen, and pnicogen bonds involving anionic and neutral electron donors. Journal of Chemical Theory and Computation, 9(11):5201–5210, 2013.
- [51] Petr Jurečka, Jiří Šponer, Jiří Černỳ, and Pavel Hobza. Benchmark database of accurate (mp2 and ccsd (t) complete basis set limit) interaction energies of small model complexes, dna base pairs, and amino acid pairs. Physical Chemistry Chemical Physics, 8(17):1985–1993, 2006.
- [52] Suhwan Song, Stefan Vuckovic, Eunji Sim, and Kieron Burke. Density-corrected dft explained: Questions and answers. Journal of Chemical Theory and Computation, 18(2):817–827, 2022.
- [53] Jason L. Sonnenberg, H. Bernhard Schlegel, and Hrant P. Hratchian. Spin Contamination in Inorganic Chemistry Calculations. John Wiley & Sons, Ltd, 2011.
- [54] James B Foresman, Martin Head-Gordon, John A Pople, and Michael J Frisch. Toward a systematic molecular orbital theory for excited states. The Journal of Physical Chemistry, 96(1):135–149, 1992.
- [55] Seymour H Vosko, Leslie Wilk, and Marwan Nusair. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Canadian Journal of Physics, 58(8):1200–1211, 1980.
- [56] Carlos Martín Fernández and Jeremy N. Harvey. On the use of normalized metrics for density sensitivity analysis in dft. The Journal of Physical Chemistry A, 125(21):4639–4652, 2021. PMID: 34018759.
- [57] Shengfa Ye and Frank Neese. Accurate modeling of spin-state energetics in spin-crossover systems with modern density functional theory. Inorganic Chemistry, 49(3):772–774, 2010.
- [58] Kasper P Kepp. Consistent descriptions of metal–ligand bonds and spin-crossover in inorganic chemistry. Coordination Chemistry Reviews, 257(1):196–209, 2013.
- [59] Benedikt M Floser, Yang Guo, Christoph Riplinger, Felix Tuczek, and Frank Neese. Detailed pair natural orbital-based coupled cluster studies of spin crossover energetics. Journal of Chemical Theory and Computation, 16(4):2224–2235, 2020.
- [60] Andrew Mahler, Benjamin G Janesko, Salvador Moncho, and Edward N Brothers. When hartree-fock exchange admixture lowers dft-predicted barrier heights: Natural bond orbital analyses and implications for catalysis. The Journal of chemical physics, 148(24):244106, 2018.
- [61] Jon Paul Janet and Heather J Kulik. Predicting electronic structure properties of transition metal complexes with neural networks. Chemical Science, 8(7):5137–5152, 2017.
- [62] Terry ZH Gani and Heather J Kulik. Unifying exchange sensitivity in transition-metal spin-state ordering and catalysis through bond valence metrics. Journal of Chemical Theory and Computation, 13(11):5443–5457, 2017.
- [63] Vyshnavi Vennelakanti, Aditya Nandy, and Heather J Kulik. The effect of hartree-fock exchange on scaling relations and reaction energetics for c–h activation catalysts. Topics in Catalysis, 65(1):296–311, 2022.
- [64] Anouar Benali, Kevin Gasperich, Kenneth D Jordan, Thomas Applencourt, Ye Luo, M Chandler Bennett, Jaron T Krogel, Luke Shulenburger, Paul RC Kent, Pierre-Francois Loos, et al. Toward a systematic improvement of the fixed-node approximation in diffusion Monte Carlo for solids—A case study in diamond. The Journal of Chemical Physics, 153(18):184111, 2020.
- [65] Suhwan Song, Min-Cheol Kim, Eunji Sim, Anouar Benali, Olle Heinonen, and Kieron Burke. Benchmarks and reliable dft results for spin gaps of small ligand fe (ii) complexes. Journal of Chemical Theory and Computation, 14(5):2304–2311, 2018.
- [66] Mariusz Radoń. Benchmarking quantum chemistry methods for spin-state energetics of iron complexes against quantitative experimental data. Physical Chemistry Chemical Physics, 21(9):4854–4870, 2019.
- [67] Lorenzo A Mariano, Bess Vlaisavljevich, and Roberta Poloni. Biased spin-state energetics of fe (ii) molecular complexes within density-functional theory and the linear-response hubbard u correction. Journal of Chemical Theory and Computation, 16(11):6755–6762, 2020.
- [68] Jianmin Tao, John P Perdew, Viktor N Staroverov, and Gustavo E Scuseria. Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids. Physical Review Letters, 91(14):146401, 2003.
- [69] HL Schmider and AD Becke. Chemical content of the kinetic energy density. Journal of Molecular Structure: THEOCHEM, 527(1-3):51–61, 2000.
- [70] Michael J Gillan, Dario Alfe, and Angelos Michaelides. Perspective: How good is dft for water? The Journal of chemical physics, 144(13):130901, 2016.
- [71] Eleftherios Lambros, Jie Hu, and Francesco Paesani. Assessing the accuracy of the scan functional for water through a many-body analysis of the adiabatic connection formula. Journal of Chemical Theory and Computation, 17(6):3739–3749, 2021.
- [72] Saswata Dasgupta, Eleftherios Lambros, John P Perdew, and Francesco Paesani. Elevating density functional theory to chemical accuracy for water simulations through a density-corrected many-body formalism. Nature communications, 12(1):1–12, 2021.
- [73] Alastair JA Price, Kyle R Bryenton, and Erin R Johnson. Requirements for an accurate dispersion-corrected density functional. The Journal of Chemical Physics, 154(23):230902, 2021.
- [74] L. H. Thomas. The calculation of atomic fields. Math. Proc. Camb. Phil. Soc., 23(05):542–548, 1927.
- [75] E. Fermi. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente (a statistical method for the determination of some atomic properties and the application of this method to the theory of the periodic system of elements). Zeitschrift für Physik A Hadrons and Nuclei, 48:73–79, 1928.
- [76] Michael G Medvedev, Ivan S Bushmarinov, Jianwei Sun, John P Perdew, and Konstantin A Lyssenko. Density functional theory is straying from the path toward the exact functional. Science, 355(6320):49–52, 2017.
- [77] Michael G Medvedev, Ivan S Bushmarinov, Jianwei Sun, John P Perdew, and Konstantin A Lyssenko. Response to Comment on “Density functional theory is straying from the path toward the exact functional”. Science, 356(6337):496–496, 2017.
- [78] Sharon Hammes-Schiffer. A conundrum for density functional theory. Science, 355(6320):28–29, 2017.
- [79] Kasper P Kepp. Comment on ‘’density functional theory is straying from the path toward the exact functional”. Science, 356(6337):496–496, 2017.
- [80] Tim Gould. What makes a density functional approximation good? insights from the left fukui function. Journal of Chemical Theory and Computation, 13(6):2373–2377, 2017.
- [81] Notker Rosch and SB Trickey. Concerning the applicability of density-functional methods to atomic and molecular negative-ions-comment. Journal of Chemical Physics, 106(21):8940–8941, 1997.
- [82] Notker Rösch and SB Trickey. Comment on “Concerning the applicability of density functional methods to atomic and molecular negative ions”[J. Chem. Phys. 105, 862 (1996)]. The Journal of Chemical Physics, 106(21):8940–8941, 1997.
- [83] Andrzej A Jaręcki and Ernest R Davidson. Density functional theory calculations for f-. Chemical Physics Letters, 300(1-2):44–52, 1999.
- [84] Donghyung Lee and Kieron Burke. Finding electron affinities with approximate density functionals. Molecular Physics, 108(19-20):2687–2701, 2010.
- [85] Donghyung Lee, Filipp Furche, and Kieron Burke. Accuracy of electron affinities of atoms in approximate density functional theory. The Journal of Physical Chemistry Letters, 1(14):2124–2129, 2010.
- [86] Min-Cheol Kim, Eunji Sim, and Kieron Burke. Communication: Avoiding unbound anions in density functional calculations. The Journal of Chemical Physics, 134(17):171103, 2011.
- [87] Axel D Becke. Density-functional thermochemistry. iii. the role of exact exchange. The Journal of Chemical Physics, 98(7):5648–5652, 1993.
- [88] Axel D Becke. A new mixing of hartree–fock and local density-functional theories. The Journal of Chemical Physics, 98(2):1372–1377, 1993.
- [89] P. J. Stephens, F. J. Devlin, C. F. Chabalowski, and M. J. Frisch. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. The Journal of Physical Chemistry, 98(45):11623–11627, 1994.
- [90] Jochen Heyd, Gustavo E Scuseria, and Matthias Ernzerhof. Hybrid functionals based on a screened coulomb potential. The Journal of Chemical Physics, 118(18):8207–8215, 2003.
- [91] Takeshi Yanai, David P Tew, and Nicholas C Handy. A new hybrid exchange–correlation functional using the coulomb-attenuating method (cam-b3lyp). Chemical Physics Letters, 393(1-3):51–57, 2004.
- [92] Yan Zhao and Donald G Truhlar. The m06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four m06-class functionals and 12 other functionals. Theoretical Chemistry Accounts, 120(1):215–241, 2008.
- [93] Ying Zhang, Xin Xu, and William A Goddard. Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proceedings of the National Academy of Sciences, 106(13):4963–4968, 2009.
- [94] Sebastian Kozuch and Jan ML Martin. Spin-component-scaled double hybrids: an extensive search for the best fifth-rung functionals blending dft and perturbation theory. Journal of Computational Chemistry, 34(27):2327–2344, 2013.
- [95] Yonsei University Theoretical and Computational Chemistry Laboratory. Density corrected-density functional theory. http://tccl.yonsei.ac.kr/mediawiki/index.php/DC-DFT. visited on 2022-03-14.
- [96] Andreas Görling and Matthias Ernzerhof. Energy differences between kohn-sham and hartree-fock wave functions yielding the same electron density. Physical Review A, 51(6):4501, 1995.
- [97] Hugh G. A. Burton, Clotilde Marut, Timothy J. Daas, Paola Gori-Giorgi, and Pierre-Francois Loos. Variations of the Hartree–Fock fractional-spin error for one electron. The Journal of Chemical Physics, 155(5):054107, 2021.
- [98] Erin R Johnson, Paula Mori-Sánchez, Aron J Cohen, and Weitao Yang. Delocalization errors in density functionals and implications for main-group thermochemistry. The Journal of Chemical Physics, 129(20):204112, 2008.
- [99] Szymon Śmiga, Odile Franck, Bastien Mussard, Adam Buksztel, Ireneusz Grabowski, Eleonora Luppi, and Julien Toulouse. Self-consistent double-hybrid density-functional theory using the optimized-effective-potential method. The Journal of Chemical Physics, 145(14):144102, 2016.
- [100] Eduardo Fabiano, Szymon Śmiga, Sara Giarrusso, Timothy J Daas, Fabio Della Sala, Ireneusz Grabowski, and Paola Gori-Giorgi. Investigation of the exchange-correlation potentials of functionals based on the adiabatic connection interpolation. Journal of Chemical Theory and Computation, 15(2):1006–1015, 2019.
- [101] Sebastian Kozuch and Jan ML Martin. Dsd-pbep86: in search of the best double-hybrid dft with spin-component scaled mp2 and dispersion corrections. Physical Chemistry Chemical Physics, 13(45):20104–20107, 2011.
- [102] Abhirup Patra, Haowei Peng, Jianwei Sun, and John P Perdew. Rethinking co adsorption on transition-metal surfaces: Effect of density-driven self-interaction errors. Physical Review B, 100(3):035442, 2019.
- [103] Nick Gerrits, Egidius W. F. Smeets, Stefan Vuckovic, Andrew D. Powell, Katharina Doblhoff-Dier, and Geert-Jan Kroes. Density functional theory for molecule–metal surface reactions: When does the generalized gradient approximation get it right, and what to do if it does not. The Journal of Physical Chemistry Letters, 11(24):10552–10560, December 2020.
- [104] Jonathan M. Skelton, David S. D. Gunn, Sebastian Metz, and Stephen C. Parker. Accuracy of hybrid functionals with non-self-consistent kohn–sham orbitals for predicting the properties of semiconductors. Journal of Chemical Theory and Computation, 16(6):3543–3557, May 2020.
- [105] Stefan Vuckovic, Lucas O Wagner, André Mirtschink, and Paola Gori-Giorgi. Hydrogen molecule dissociation curve with functionals based on the strictly correlated regime. Journal of Chemical Theory and Computation, 11(7):3153–3162, 2015.
- [106] A. Görling and M. Levy. Exact kohn-sham scheme based on perturbation theory. Physical Review A, 50:196, 1994.
- [107] Timothy J Daas, Juri Grossi, Stefan Vuckovic, Ziad H Musslimani, Derk P Kooi, Michael Seidl, Klaas JH Giesbertz, and Paola Gori-Giorgi. Large coupling-strength expansion of the møller–plesset adiabatic connection: From paradigmatic cases to variational expressions for the leading terms. The Journal of Chemical Physics, 153(21):214112, 2020.
- [108] Michael Seidl, Sara Giarrusso, Stefan Vuckovic, Eduardo Fabiano, and Paola Gori-Giorgi. Communication: Strong-interaction limit of an adiabatic connection in hartree-fock theory. The Journal of chemical physics, 149(24):241101, 2018.
- [109] Timothy J Daas, Eduardo Fabiano, Fabio Della Sala, Paola Gori-Giorgi, and Stefan Vuckovic. Noncovalent interactions from models for the møller–plesset adiabatic connection. The journal of physical chemistry letters, 12:4867–4875, 2021.
- [110] Kushantha PK Withanage, Sharmin Akter, Chandra Shahi, Rajendra P Joshi, Carlos Diaz, Yoh Yamamoto, Rajendra Zope, Tunna Baruah, John P Perdew, Juan E Peralta, et al. Self-interaction-free electric dipole polarizabilities for atoms and their ions using the fermi-löwdin self-interaction correction. Physical Review A, 100(1):012505, 2019.
- [111] John P. Perdew, Robert G. Parr, Mel Levy, and Jose L. Balduz. Density-functional theory for fractional particle number: Derivative discontinuities of the energy. Physical Review Letters, 49:1691–1694, Dec 1982.
- [112] Leeor Kronik and Stephan Kümmel. Piecewise linearity, freedom from self-interaction, and a coulomb asymptotic potential: three related yet inequivalent properties of the exact density functional. Physical Chemistry Chemical Physics, 22(29):16467–16481, 2020.
- [113] James Kirkpatrick, Brendan McMorrow, David HP Turban, Alexander L Gaunt, James S Spencer, Alexander GDG Matthews, Annette Obika, Louis Thiry, Meire Fortunato, David Pfau, et al. Pushing the frontiers of density functionals by solving the fractional electron problem. Science, 374(6573):1385–1389, 2021.
- [114] Ryo Nagai, Ryosuke Akashi, and Osamu Sugino. Completing density functional theory by machine learning hidden messages from molecules. npj Computational Materials, 6(1):1–8, 2020.
- [115] Li Li, Stephan Hoyer, Ryan Pederson, Ruoxi Sun, Ekin D. Cubuk, Patrick Riley, and Kieron Burke. Kohn-sham equations as regularizer: Building prior knowledge into machine-learned physics. Physical Review Letters, 126:036401, Jan 2021.
- [116] Jeremy J Redd and Antonio C Cancio. Analysis of atomic pauli potentials and their large-z limit. The Journal of Chemical Physics, 155(13):134112, 2021.
- [117] Erich Runge and E. K. U. Gross. Density-functional theory for time-dependent systems. Phys. Rev. Lett., 52(12):997, Mar 1984.
- [118] Neepa T Maitra. Perspective: Fundamental aspects of time-dependent density functional theory. The Journal of Chemical Physics, 144(22):220901, 2016.
- [119] P. Bokes and R. W. Godby. Conductance and polarization in quantum junctions. Phys. Rev. B, 69:245420, 2004.
- [120] Eberhardt KU Gross, Luiz N Oliveira, and Walter Kohn. Density-functional theory for ensembles of fractionally occupied states. i. basic formalism. Physical Review A, 37(8):2809, 1988.
- [121] Zeng-hui Yang, Aurora Pribram-Jones, Kieron Burke, and Carsten A. Ullrich. Direct extraction of excitation energies from ensemble density-functional theory. Phys. Rev. Lett., 119:033003, Jul 2017.
- [122] Tim Gould and Stefano Pittalis. Density-driven correlations in many-electron ensembles: Theory and application for excited states. Physical Review Letters, 123(1):016401, 2019.
- [123] Tim Gould. Approximately self-consistent ensemble density functional theory: toward inclusion of all correlations. The Journal of Physical Chemistry Letters, 11(22):9907–9912, 2020.