Improving the scalability of parallel N-body applications with an event driven constraint based execution model

Chirag Dekate^1,2, Matthew Anderson², Maciej Brodowicz², Hartmut Kaiser^1,2,Bryce Adelstein-Lelbach²,Thomas Sterling^1,2 ¹Department of Computer Science, Louisiana State University, Baton Rouge, LA 70803,
²Center for Computation and Technology, Louisiana State University, Baton Rouge, LA 70803

(September 28, 2025)

Abstract

The scalability and efficiency of graph applications are significantly constrained by conventional systems and their supporting programming models. Technology trends like multicore, manycore, and heterogeneous system architectures are introducing further challenges and possibilities for emerging application domains such as graph applications. This paper explores the space of effective parallel execution of ephemeral graphs that are dynamically generated using the Barnes-Hut algorithm to exemplify dynamic workloads. The workloads are expressed using the semantics of an Exascale computing execution model called ParalleX. For comparison, results using conventional execution model semantics are also presented. We find improved load balancing during runtime and automatic parallelism discovery improving efficiency using the advanced semantics for Exascale computing.

I Introduction

A large class of problems in physics and molecular biology can be represented using a particle interaction method commonly known as N-Body and computational techniques based on these discretization methods. The science domains utilizing the particle interaction discretization model are limited by the number of particles that can be simulated and the time it takes to execute the computational techniques. Conventional practices have significantly advanced particle interaction based methodologies. However, the combined ecosystem of emerging multicore based system architectures and conventional programming models are imposing grave challenges to the continued effectiveness of these methods. This research identifies and addresses these challenges through the hypothesis that emerging system architectures and extreme scale oriented runtime systems can dramatically improve the end science.

Applications based on graphs and tree data structures rely on more dynamic, adaptive, and irregular computations. This work explores an exemplar dynamic tree based application embodied by an N-Body simulation. Systems comprising many particles (N-Body problem) interacting through long-range forces have considerable computational science interest. N-Body systems comprising three or more particles do not have a closed form solution; consequently, iterative methods are used to approximate solutions for the N-Body problem. The N-Body problem simulates the evolution of $n$ particles under the influence of mutual pairwise interactions through forces such as gravitational pull or electrostatic forces. This work focuses on gravitational forces operating on the N-Body system and the Barnes-Hut approximation of the N-Body solution.

While several approaches to simulating N-Body systems exist, the Barnes-Hut algorithm barneshut is widely used in astrophysical simulations mainly due to its logarithmic computational complexity while generating results that are within acceptable bounds of accuracy. In the Barnes-Hut algorithm the particles are grouped by a hierarchy of cube structures using a recursive algorithm which subdivides the cubes until there is one particle per sub-cube. It then uses the adaptive octree data structure to compute center of mass and force on each of the cubes. The data structure organization is key to the resultant $O(N\log{N})$ computational complexity of the algorithm.

During the simulation the position of the particles change as a result of interaction with other particles, consequently the representative Barnes-Hut tree changes dynamically during the computation. The dynamic tree based evolution of the system is not as common to conventional computational applications, which are dominated by simulations where the fundamental data structures are arrays/matrices that can exploit data locality for performance, through techniques such as row/column striping striping . Graph/Tree data structures have non uniform data access patterns which prevent tree based applications from taking advantage of data locality and fully utilizing the parallelism offered by the underlying system. The emergence of multicore processor architecture, while providing capabilities for significant intra-node parallelism, poses new challenges. When used in isolation, traditional programming techniques fail to expose the underlying parallelism to the high performance computing applications since they cannot address the intra-node parallelism provided by multicore processor architecture. Conventional clusters comprise multicore nodes interconnected by a low latency high bandwidth network such as InfiniBand and are usually programmed using MPI MPISpec . When conventional techniques such as message passing are used in isolation the intra-node parallelism offered by each of the multicore nodes is under utilized, primarily due to limitations of the implementations of MPI. Performance and scalability of graph applications are further affected by high performance computing system architectures that are more suitable for computations with static, predictable data access patterns. Systems architectures such as clusters and massively parallel processors (MPPs) have co-evolved with programming models and applications that provide high data locality to computations.

The fundamental challenges to improving performance and scalability of parallel N-Body simulations using the Barnes-Hut algorithm in a system context are:

•

Dynamic Load Balancing The Barnes-Hut algorithm generates a new unique tree for each iteration which is different than the tree used in the previous iteration; consequently, conventional load balancing techniques such as striping are ineffective and result in poor load balancing.
•

Variable Workload In addition to the varying Barnes-Hut tree, a fundamental resource management problem encountered while simulating these systems is the variable workload per particle. That is, each particle in the system will interact with a constantly varying number of particles in the system. Consequently, predicting workload per particle in N-Body simulations is difficult.
•

Data Driven Computation The Barnes-Hut tree algorithm, like other graph computations, is data driven. The computations performed by the Barnes-Hut algorithm are dictated by the vertex and edge structure of the tree rather than by directly expressing computations in code. This results in irregular communication patterns and irregular data access patterns limiting ability to parallelize using conventional techniques.
•

Data Locality The irregular and unstructured computations in dynamic graphs result in poor data locality resulting in degraded performance on conventional systems which rely on exploitation of data locality for their performance.

This paper compares the Barnes-Hut tree algorithm using the conventional execution model semantics of OpenMP openmp1 ; openmp2 with the dynamic data-driven semantics and execution techniques of the ParalleX scaling_impaired_apps ; tabbal execution model. In section II, an overview of the ParalleX execution model will be given along with the key characteristics that distinguish it from the communicating sequential processes execution model typified by MPI MPISpec . In section III, the Barnes-Hut algorithm will be recast into dynamic data-driven semantics for use in an Exascale execution model. Section IV will present the experimental set-up and tests performed while section V will present the results of the experiments. Our conclusions are found in section VI.

II ParalleX

As technologies advance towards enabling Exascale computing, major challenges of scalability, efficiency, power and programmability will need to be addressed. New models of computation will be needed to provide the governing principles for co-design and operation of the cooperating system layers from programming models through system software to process or architectures.

The ParalleX execution model scaling_impaired_apps ; tabbal is derived with the goal of specifying the next execution paradigm essential to exploitation of future technology advances and architectures in the near term as well as to guide co-design of architecture and programming models in conjunction with supporting system software in the long term. ParalleX is intended to catalyze innovation in system structure, operation, and application to realize practical Exascale processing capability by the end of this decade and beyond.

The four principal properties exhibited by ParalleX to this end are:

1.

Exposure of intrinsic parallelism, especially from meta-data, to meet the concurrency needs of scalability by systems in the next decade,
2.

Intrinsic system-wide latency hiding for superior time and power efficiency,
3.

Dynamic adaptive resource management for greater efficiency by exploiting runtime information, and
4.

Global name space to reduce the semantic gap between application requirements and system functionality both to enhance programmability and to improve overall system utilization and efficiency.

ParalleX provides an experimental conceptual framework to explore these goals and their realization through the concepts identified above to inform the community development of a future shared execution model. The evolution of ParalleX has been, in part, motivated and driven by the needs of the emerging class of applications based on dynamic directed graphs. Such applications include scientific algorithms like adaptive mesh refinement, particle mesh methods, multi-scale finite element models and informatics related applications such as graph explorations. They also include knowledge-oriented applications for future web search engines, declarative user interfaces, and machine intelligence. The strategy of ParalleX is to replace the conventional static Communicating Sequential Processes model csp of computation with one based on a dynamic multiple-threaded work-queue processing model discussed above. ParalleX also incorporates message-driven computation through Parcels, an advanced form of active messages.

ParalleX can be viewed as a combination of ParalleX Elements and ParalleX Semantic Mechanisms. ParalleX Elements are the fundamental building blocks of the execution model comprising ParalleX Threads, ParalleX Parcels, Localities and ParalleX Processes. ParalleX mechanisms are complex interactions enabled by the structure, semantics of the ParalleX elements, and the dynamics involved in the execution model (see Table 1).

Table 1: ParalleX Concepts Summary

ParalleX Elements	ParalleX Mechanisms	Emergent Properties
ParalleX Threads	Multi-Threaded Work Queue	Percolation
Parcels	Message Driven	Security
Local Control Objects	Synchronization	Adaptive Scheduling
ParalleX Processes	Active Global Address Space	Self Aware
Localities	Overlap Computation and Communication	Split-Phase Transactions

ParalleX Elements are the fundamental building blocks managed by the mechanisms. The elements comprise: ParalleX Threads, Parcels, Processes, LCOs, and Localities. Each of the elements will be discussed below. More discussion of ParalleX mechanisms and emergent properties, including message-driven computation, the Active Global Address Space, percolation, and split-phase transactions, is found in chiragsthesis .

II.1 ParalleX Threads

The fundamental element that accomplishes computational work is, as is referred to in many programming models, the “thread”. Like more conventional threads in other models, ParalleX confines the execution of a thread to a single localized physical domain, conventionally referred to as a “node” and here as “locality” in ParalleX terminology (see section II.5). A thread is a place of local control and data for execution of a set of instructions.

Unlike traditional threading models such as Pthreads pthreads , in ParalleX threads are highly ephemeral. A ParalleX thread may contain a continuation continuations , which specifies an action to be taken once the current thread terminates.

ParalleX threading is also heterogeneous. ParalleX threads of many different forms (code) can be instantiated at the same time without restrictions. Both these properties distinguish ParalleX threads from those of UPC upc1 ; upc2 .

A particularly important distinguishing aspect of ParalleX threads is that they are first class objects; they are named as is any other variable or object and may be manipulated within the limitations of their type class from any part of the allocated system. ParalleX threads may be as short as a atomic memory operation on a given data structure element or as long as a conventional process that lasts the entire duration of the user program. The intended mode of operation, however, is for short lived threads that operate exclusively on private or local data within a single locality and then pass on the flow of control to a remote locality (by instantiating a new thread there), where the execution continues based on data placement.

A ParalleX thread which is unable to proceed in its execution due to incomplete control state transitions (e.g., a required intermediate value is still pending) is “suspended” (it has no more work it can do) and is transformed in to a new kind of object with the same name. This is one of a general class of lightweight objects that includes control state referred to in ParalleX vocabulary as a “Local Control Object” or “LCO” described in section II.4. In doing so the ParalleX thread saves its requisite private state and relinquishes the physical resources for other active threads in the locality. A ParalleX thread differs in one last way from more conventional threads in that typically a thread is assumed to be sequential in its instruction issue. ParalleX incorporates a possible intra-thread parallelism based on a data flow control schema for intermediate values not unlike static dataflow dennisdataflow . This eliminates anti-dependencies at least for intermediate (intra-thread) values allowing generalized application to a diverse set of processor core instruction set architectures, thus facilitating the use of heterogeneous computing systems. Overall, ParalleX threads support parallelism at two levels: concurrent threads and operation level parallelism within a thread through the data flow control.

II.2 ParalleX Parcels

ParalleX embodies a powerful, general, and dynamic method of message-driven computation called Parcels that allows the invocation of threads on remote localities through a class of messages that carry information about an action to be performed as well as some data that may be involved in the remote computation. Parcels (PARallel Control ELements) are a form of active message activemessages that extend the semantics of parallel execution to the (highly asynchronous) inter-locality domain for scalability and efficiency. The parcel supports message-driven computation allowing work to be moved to the data rather than the data always gathered to the localized site of the work. Parcels reduce both bandwidth requirement and hide latency for greater efficiency and scalability. Parcels extend the effectiveness of the work-queue model to operate across localities, not just within a single locality, as would be the case without them.

II.3 Processes

Conventionally, a process is a form of a task or action comprising many specified steps or instructions. A process generally runs on a processor core and perhaps communicates with other processes via messages in the system I/O distributed name space. ParalleX views processes as contexts containing named entities including data constants and variables, concurrent threads both active and suspended, local control objects, and other child processes. Processes also enable “symmetry” of semantics that allow a user to perform remotely the same activities that an application would perform locally. The important property of a ParalleX process that distinguishes it from conventional process oriented models is that it can occupy many localities (i.e. system nodes) at the same time using the combined resources of the collection of assigned localities to perform the process’ active threads and to store the process data. Like threads, processes are ephemeral. A process is instantiated from a combination of a procedure specification, a set of operand values, and allocated physical localities at any point in time of the execution of a parent process.

The ParalleX semantic mechanism associated with processes is the Active Global Address Space (AGAS). ParalleX supports a shared memory model that distinguishes it from the conventional distributed memory MPP and cluster system architectures, but is also different from the cache-coherent shared memory systems such as symmetric multiprocessors (SMPs). It incorporates a strategy among the class of “Global Address Space” models sometimes referred to as put-get models. AGAS differs from the more widely employed model called Partitioned Global Address Space (PGAS gasnet ; UPCSpec ; Charles:2005:XOA:1103845.1094852 ) in one specific and important way. With PGAS a virtual object has a restricted scope of allocation within the confines of a particular partition. ParalleX, at the risk of additional overhead, relaxes this constraint. It permits virtual objects to be moved across the system between localities while retaining their original virtual addresses. This is the “active” aspect of AGAS versus the passive or static nature of the “partitioned” aspect of PGAS. This property is critical for dynamic directed graphs and for load balancing as well as system reconfiguration.

II.4 Local Control Objects

One of the most powerful aspects of the ParalleX model is the way it represents and manages global flow control. Typically, distributed applications employ the construct of the global barrier to manage phased execution in what is referred to as the Bulk Synchronous Protocol or BSP model bsp . Simply, BSP uses a compute-synchronize-communicate phased management approach where the exchange of data via messages only occurs after all processes have finished their respective work for the current cycle. A global barrier is a synchronization object that ensures the strictness of this ordering requiring all processes to check in to the barrier upon completion of their work and to not proceed with their communication phase until notified to do so by the barrier (which makes certain that all processes have finished). For many applications and systems this has proven an effective approach. But this coarse grained parallelism precludes the more fine grained and adaptive parallelism required for extended scalability.

Local Control Objects (LCOs) are event driven conditional structures that, upon satisfying specific criteria, will cause a thread or some other action to be instantiated. Events are either direct accesses by threads within the same locality and process, or through parcel messages outside these restricted domains. Local Control Objects improve efficiency by avoiding barriers and permitting highly dynamic flow control.

Among the simplest form of an LCO is a mutex mutex . But the more interesting forms include the dataflow template and the futures futures2 construct. A future is a promise of a returned value, which may be any first class object. If the value itself is not required, such as manipulating the metadata surrounding it, then computation may proceed. Further computation will be blocked only when the actual value is required and not just its placeholder. But futures are far more powerful. They can coordinate anonymous producer-consumer computation such as histogramming and can also coordinate access to a shared structure such as a vertex of a graph.

II.5 Localities

Like many models dealing with distributed concurrent computing, ParalleX recognizes a contiguous local physical domain. In the case of ParalleX, a locality is the locus of resources that can be guaranteed to operate synchronously and for which hardware can guarantee compound atomic operation on local data elements. Within a locality, all functionality is bounded in space and time permitting scheduling strategies to be applied and structures that prevent race conditions to be built. The locality also manages intra-locality latencies and exposes diverse temporal locality attributes. A locality in ParalleX is a first-class object, meaning that each locality in a ParalleX system has a globally unique identifier associated with it and can be addressed throughout the user global address space. The locality comprises heterogeneous processing units including, for example, a combination of homogeneous multicore processing elements and GPGPU accelerators.

Table 2: Overview of ParalleX mechanisms that enable dynamic directed graph processing.

Dynamic Directed Graph Requirements	ParalleX Enablers
Data-driven computing	Parcels carry data, target address, action, continuation.
	Allows work to be moved to data.
	Enables migration of flow control.
	Supports asynchronous event driven execution.
Support for fine-grained parallelism	Work queue model enables split phase transactions,
	i.e., overlapping computation with communication.
	Threads support dataflow on transient values.
Dynamic thread support	Multithreaded light weight entities;
	first class objects;
	may be created and addressed in suspended state;
	may be compiled to different types of processors.
Global memory access	PX communication using AGAS and Parcels;
	non cache-coherent global memory space;
	supports copy semantics and affinity relationships.

The ParalleX mechanisms that enable the dynamic directed graph processing needed for the Barnes-Hut algorithm are summarized in Table 2. The next section describes in detail the Barnes-Hut algorithm as implemented in ParalleX.

III Barnes-Hut Algorithm in ParalleX

The Barnes-Hut algorithm barneshut is widely used in the astrophysics community as it is the simplest hierarchical N-Body algorithm. The N-Body algorithm exploits the same idea used by all tree codes where the forces on a body from a remote cluster of bodies can be approximated by treating the remote cluster as a single body. The accuracy of these approximations (see Figure 1) depends on the distance (D) of the cluster from the body and the radius (r) of the cluster of particles. Remote clusters of bodies are treated as a single body only if D is greater than $r/\theta$ , consequently the parameter $\theta$ controls the error of the approximation.

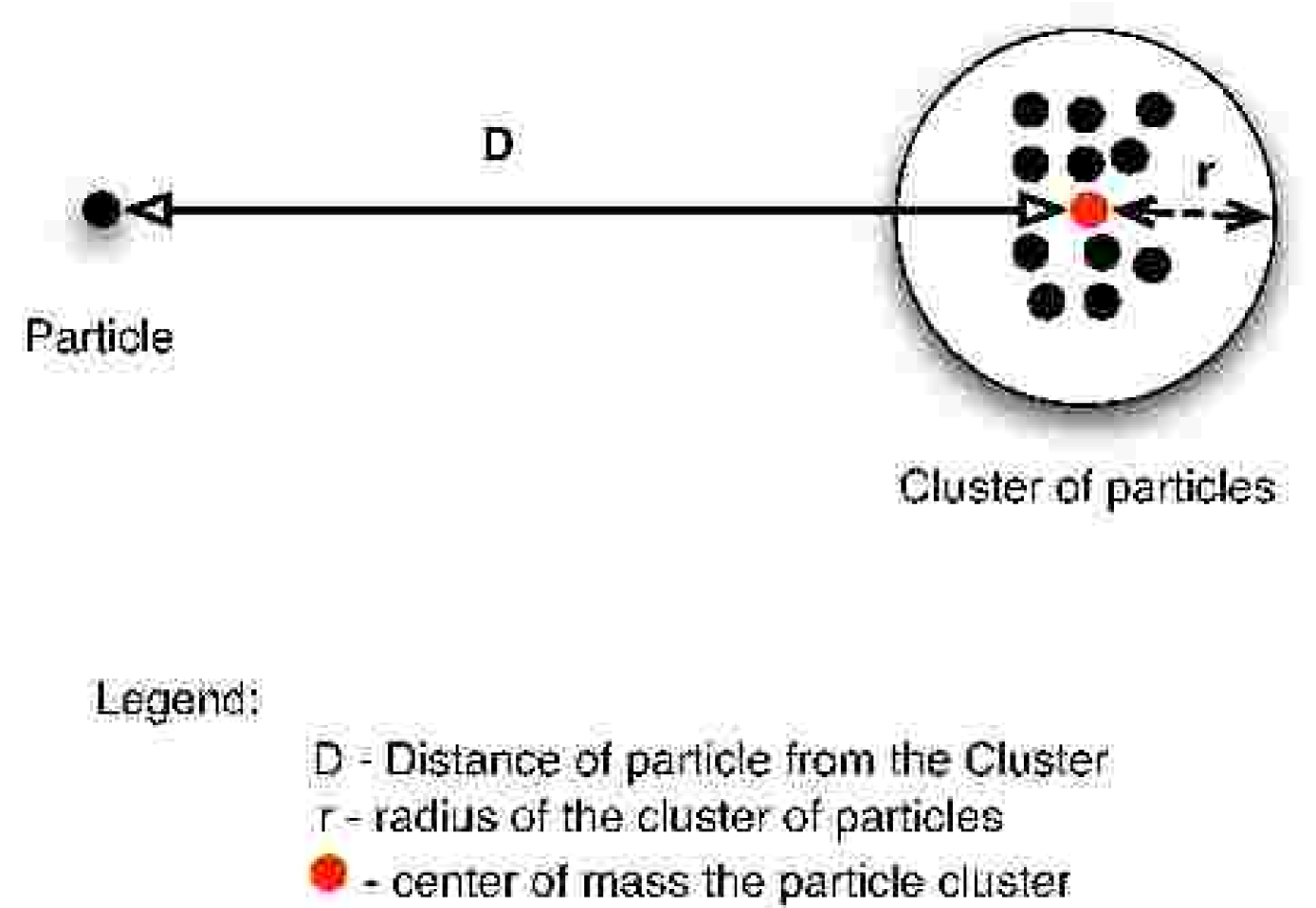
Refer to caption — Figure 1: Barnes-Hut Approximation Criteria

The Barnes-Hut algorithm has been successfully parallelized using several techniques warren ; salmon_thesis ; liu ; psingh ; dubinski ; makino . The key challenges in parallelizing the Barnes-Hut algorithm include domain decomposition of the Barnes-Hut tree across the allocated memory resources and load balancing the workloads across the allocated processors.

The ParalleX version of the Barnes-Hut algorithm explored here is implemented using the HPX runtime system scaling_impaired_apps , the reference C++ implementation of ParalleX. The ParalleX Barnes-Hut implementation has the following goals:

•

Parallelizing force calculation step using HPX
•

Creating interaction list and co-locating related work to provide data locality
•

Utilizing futures based asynchrony and work queue based computation for force calculations to provide balanced loads to the processors.
•

Providing support for controlling the granularity of each HPX Thread to determine the best workload characteristics for fast, scalable processing of the algorithm.

Inherent in the Barnes-Hut algorithm is a global barrier at the tree construction stage of every iteration, where the algorithm requires positional information of all particles in the system. The research implementation explores opportunities to exploit parallelism within each iteration. The computationally intensive force calculation is the key focus for parallelization using the HPX runtime system. The main challenges in parallelizing the force computation are:

•

exposing fine grained control and parallelism at the particle interaction level and devising methodology to express each interaction as a work unit
•

the number of interactions for each particle varies across iterations; consequently, new ways of providing dynamic load balancing are required to manage efficient execution of the fine grained computations.

The technical approach in addressing the above challenges involves exploiting a dataflow based framework for executing the Barnes-Hut N-Body simulation. The dataflow approach allows for representation of each of the interactions as a work unit and helps take advantage of a proven approach to providing scalability for scaling constrained applications. Inherent in the HPX based dataflow approach is the use of futures for resolving data dependencies. This provides asynchronous access to data required for computing forces acting on each particle. Two modes of granularity support are enabled: workload based HPX thread allocation, which allows for managing the size of HPX threads and increasing the number of threads based on the workload; or, alternatively, workload based on a fixed number of threads and the variable workload size adapted to match the resource allocations. These methodologies provide a path for implementing dynamic workload management and load balancing.

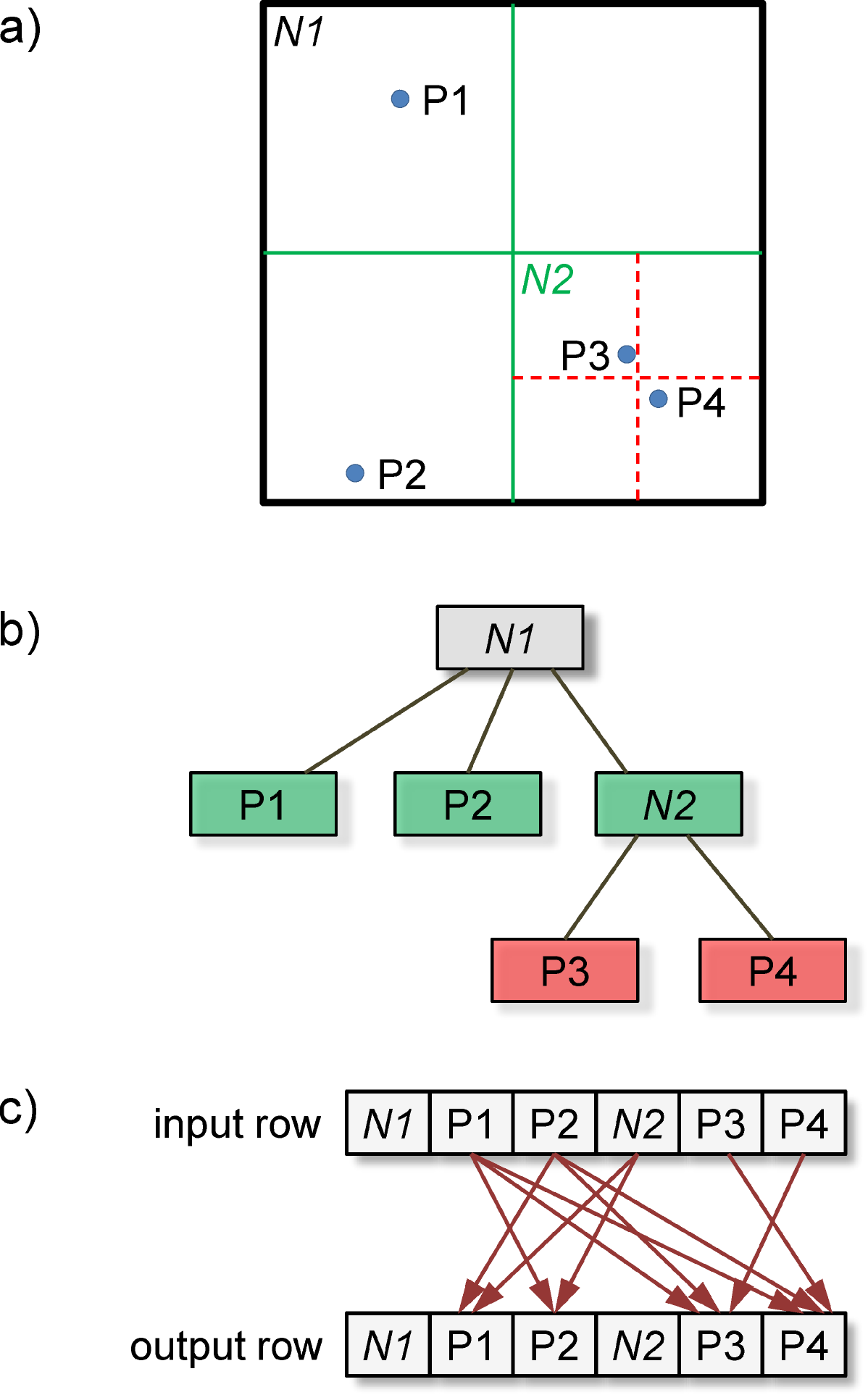
The most computationally intensive part of the Barnes-Hut algorithm is the force computation stage. The HPX parallelization efforts and the research implementation focuses on parallelizing the force computation stage of the Barnes-Hut algorithm. This is done by representing the computations as a work flow based on repeatable arrangement of rows of dataflow elements. The fully populated Barnes-Hut tree is flattened into an input row of dataflow elements, comprising all the tree nodes including the particles and the intermediate tree nodes (see Figure 2). A complementary output row of dataflow elements representing the result buffer is created to store the results from the force calculation stage. Each dataflow element in both the input and output rows has a unique Global IDentifier (GID) associated with it. Each element in the input row maps to a corresponding element in the output row. Additionally, for each element in the output row that is of particle type, connections are made to the input rows. The connections are made on the basis of the Barnes-Hut approximation criteria of $D/r<\theta$ . In this context, making a connection implies that each output row element holds a vector of GIDs which identifies the input row elements which provide the necessary data for computing the force on the particle in the output row.

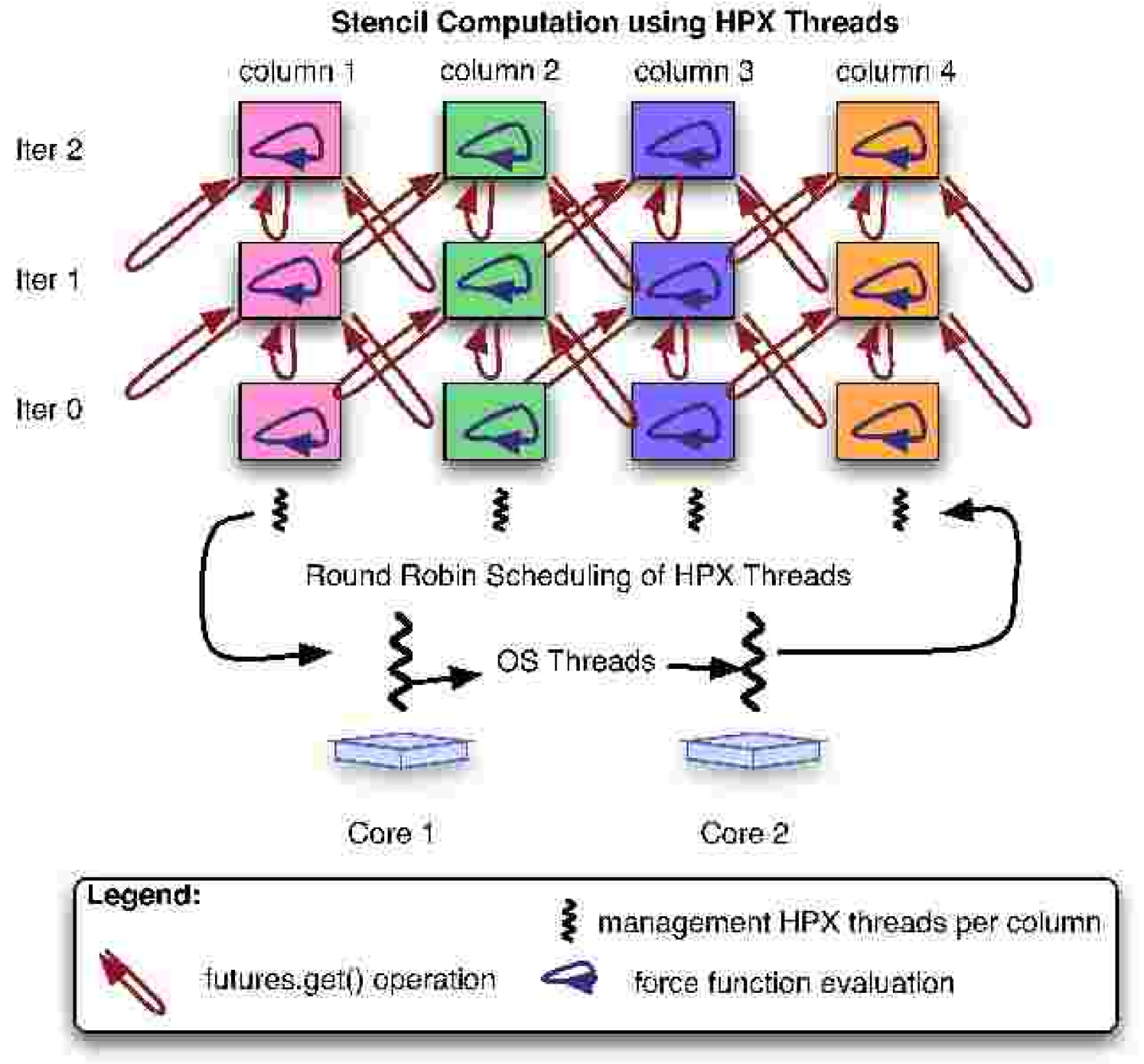
Each column in this connected network of rows has an HPX thread for managing the internal force computations. This network is depicted in the Figure 3. When executed in parallel a global pool of these management threads are created and made available to the allocated resources. HPX user level threads are allocated from the global pool in a round-robin manner and scheduled on top of the operating system threads running on each of the cores in the parallel system. The user may also specify the mapping of the HPX threads to preferred local queues in the HPX system.

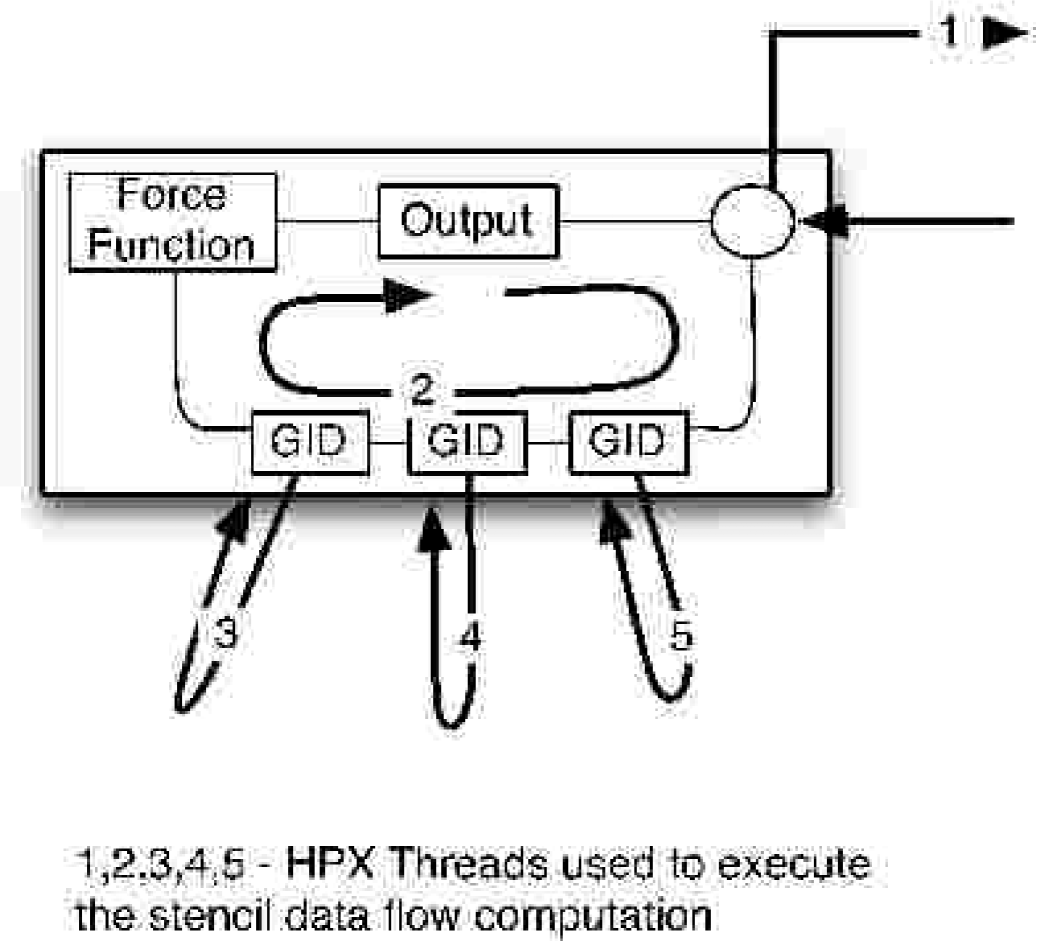
Each HPX thread managing a column triggers the dataflow for every element allocated. This work flow is depicted in the Figure 4. The management thread is depicted as the arrow numbered 1 in the diagram. When the computation flow in each dataflow element is triggered, a new HPX thread for that element is created. This thread is identified as Thread 2 in the diagram. This element-specific HPX thread performs a futures.get() operation on each of the GIDs for the input elements that the particle interacts with. For each futures.get() operation a new HPX thread is created to manage the asynchronous data accesses (3,4,5). For each input datum that is available, the local management thread (2) computes the force function and stores the intermediate result in a result buffer. For each element evaluation a total of $(2+n)$ threads are required (1 column manager thread + 1 local computation thread + n futures.get() created threads). Once the current element is completely evaluated, the next one is loaded and the same workflow is repeated. The average overhead for creation of a lightweight thread in HPX is about 3-5 $\mu$ s.

The futures based asynchrony in representing the interconnections provides rich semantics for exploiting the parallelism available within each iteration. HPX semantics and the implementation also allow specifying granularity, or quantum of work, of each execution block, thus allowing for co-locating related computations to provide implicit data locality and amortize thread overhead.

The key algorithmic difference between the ParalleX version of Barnes-Hut and the OpenMP version is that the ParalleX version includes the creation of a tagged tree data structure which is flattened to produce an interaction list. This interaction list is then used to set up the dataflow LCO used for the force computation.

IV Experimental set-up

All experiments have been executed on a 32 core shared memory multiprocessor system. The system has 8 processor sockets, each attached to a local memory bank. The processors use HyperTransport interconnect to access memory across the system. Sockets are populated with quad-core 2.7 GHz AMD Opteron processors (family 8384) with 512 KB L2 cache per core and 6 MB of shared L3 cache. Each socket in the system is also equipped with 8 GB dual channel DDR2 DRAM. The system has therefore an aggregate memory of 64 GB that can be addressed by each of the 32 cores in the system, albeit not with a uniform latency (NUMA). The OS used is 64 bit Linux kernel version 2.6.18.

All programs used in the experiment have been compiled using the standard GNU g++ compilers version 4.4.2. The HPX runtime system is currently under active development. For the purposes of this experimentation, HPX version 3 is used. The OpenMP linking is done through the version of OpenMP primitives available in the GNU g++ compilers version 4.4.2. The OpenMP comparison code is characterized in chiragsthesis . The OpenMP, HPX, and serial version of the N-Body codes are available upon request nbody_download .

The input data used in the problem size variation studies have been generated using the standard Plummer model plummer which is used to model globular clusters. The program used to generate the input data was obtained from the online computational course created by Piet Hut directnb .

In the experiments conducted here, the problem sizes are varied between 10,000 and 100,000 particles. For each of the problem sizes, the number of operating system threads are varied and the grain sizes are varied to determine the correlation of the parallelism to the workload granularity. For each of the combinations the time taken to execute the force calculation loop is measured.

V Results

In this section, results from the HPX dataflow approach to Barnes-Hut and an OpenMP Barnes-Hut implementation are presented. Parallelism in the HPX Barnes-Hut code was controlled using two main parameters: the number of operating systems threads and the workload grain size (which directly impacts the number of HPX threads used). As the grain size of the workloads decreases (the work per thread is made more fine-grained) the number of HPX threads increase and the work done by each of the HPX threads decreases. The number of operating system threads controls the explicit parallelism such that each of the threads gets the activities to be performed from the pool of HPX threads created. The maximum number of the operating system threads used in scaling tests to support the execution of HPX threads was limited to 28 (vs. 32 cores available in testbed) to allow sufficient hardware resources for OS activity and certain runtime system functions (such as asynchronous I/O) that also require OS threads.

In Figures 5, 6, and 7 the trade-off between fine-grained parallelism and overhead is explored for cases with various numbers of particles and iterations. In each example, as the grain size is decreased, the Barnes-Hut N-Body problem is better load balanced at a cost of the higher overhead which results from the addition HPX threads required. The optimal grain size for each problem is found experimentally and generally differs for different problem sizes and, occasionally, different numbers of OS threads.

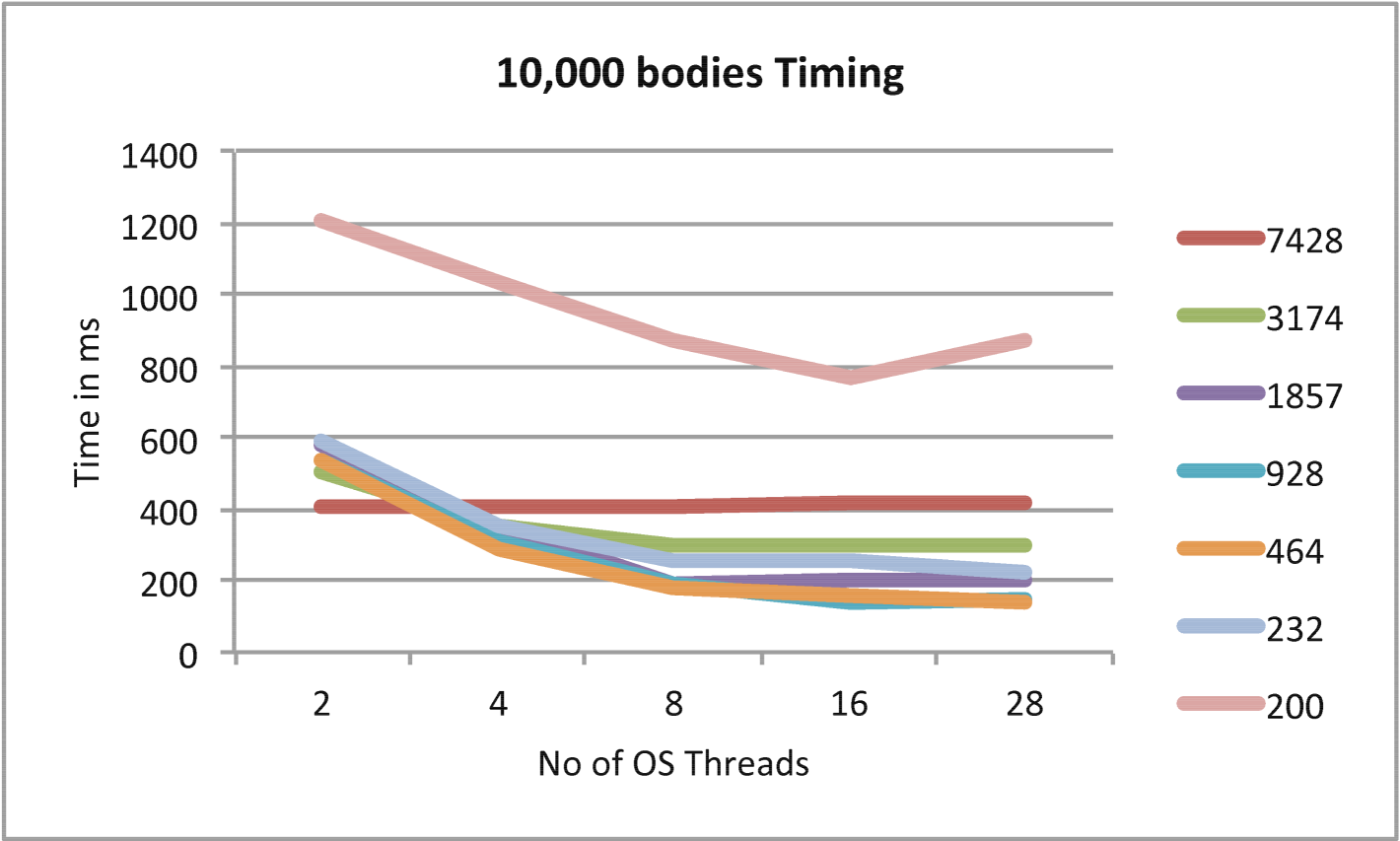
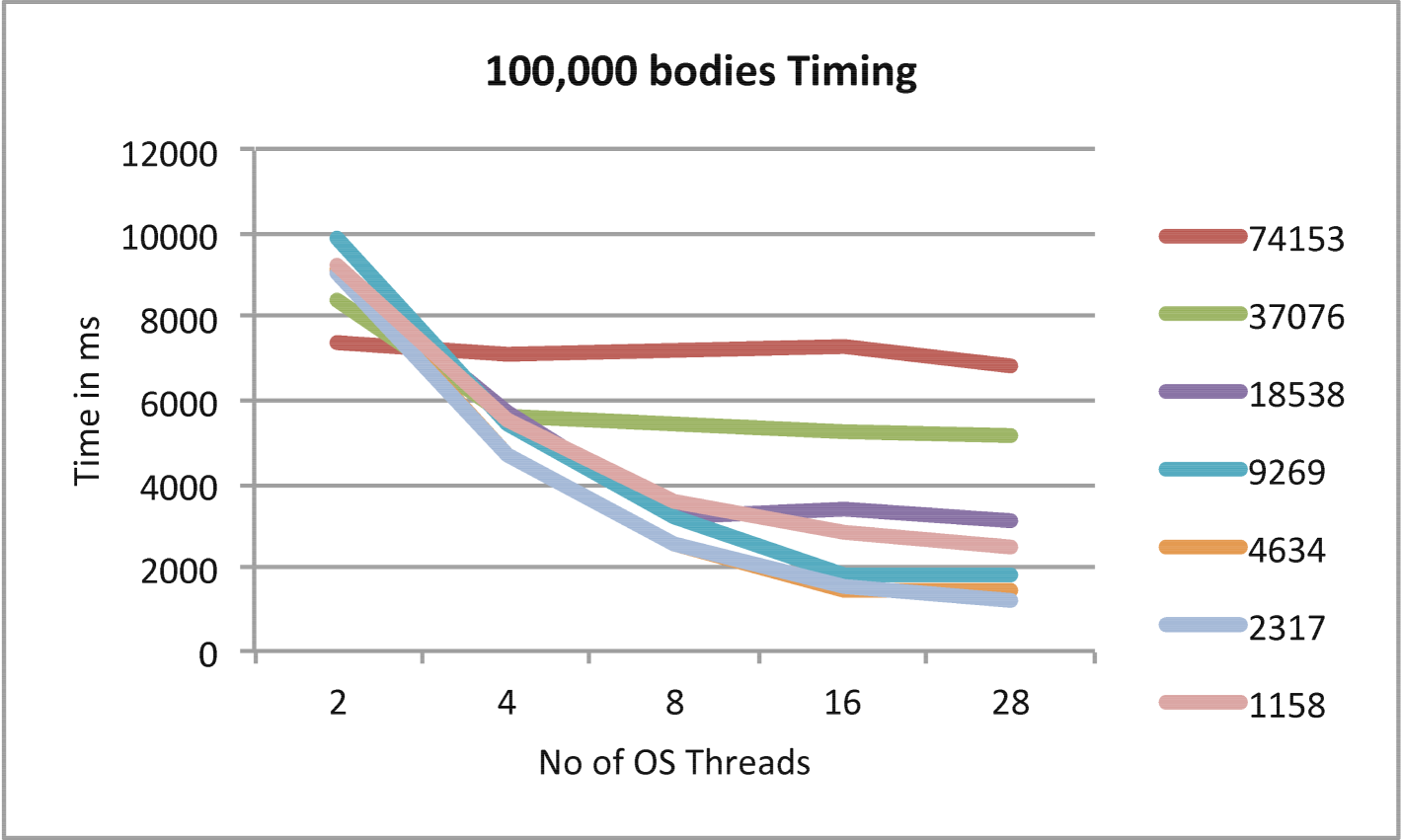
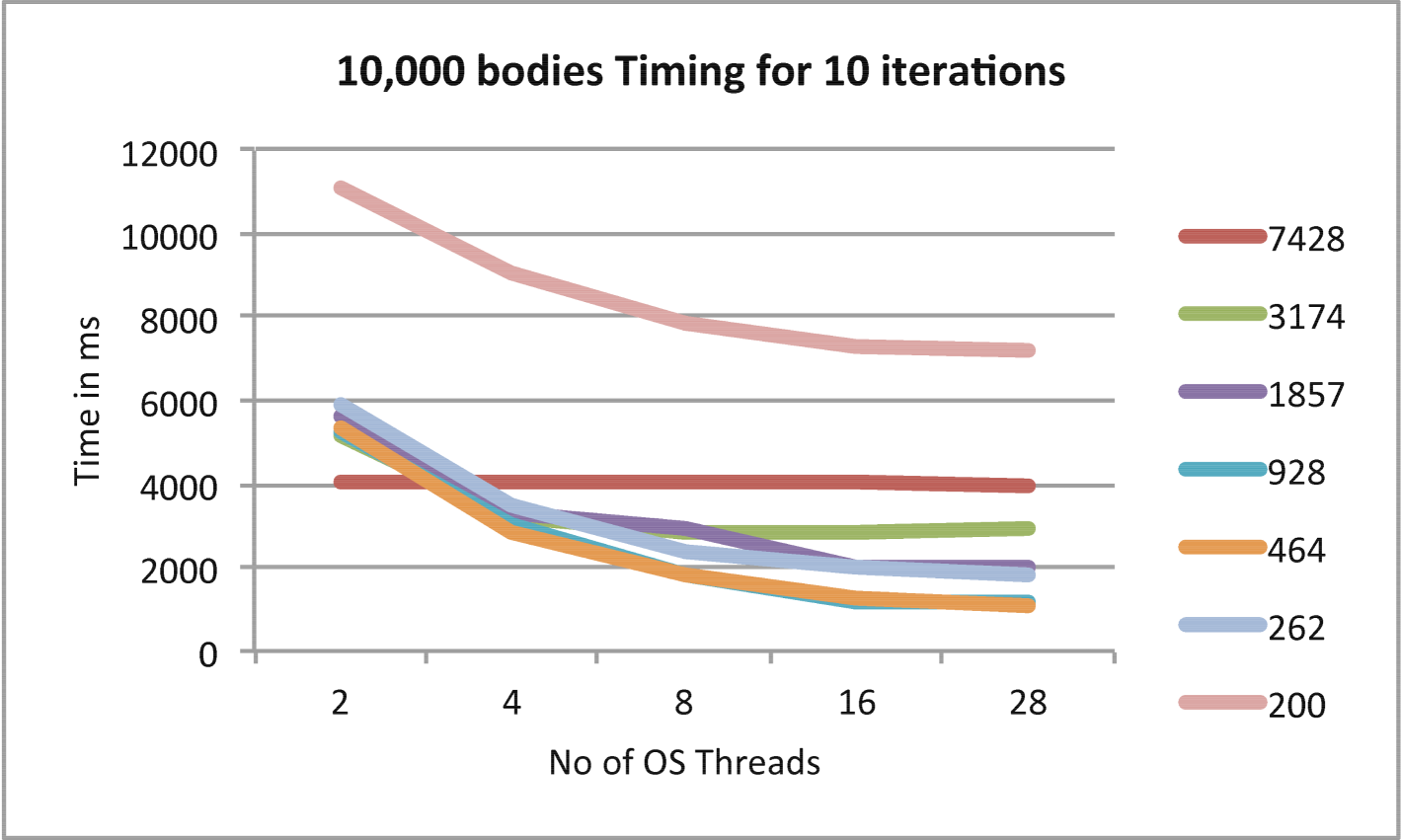
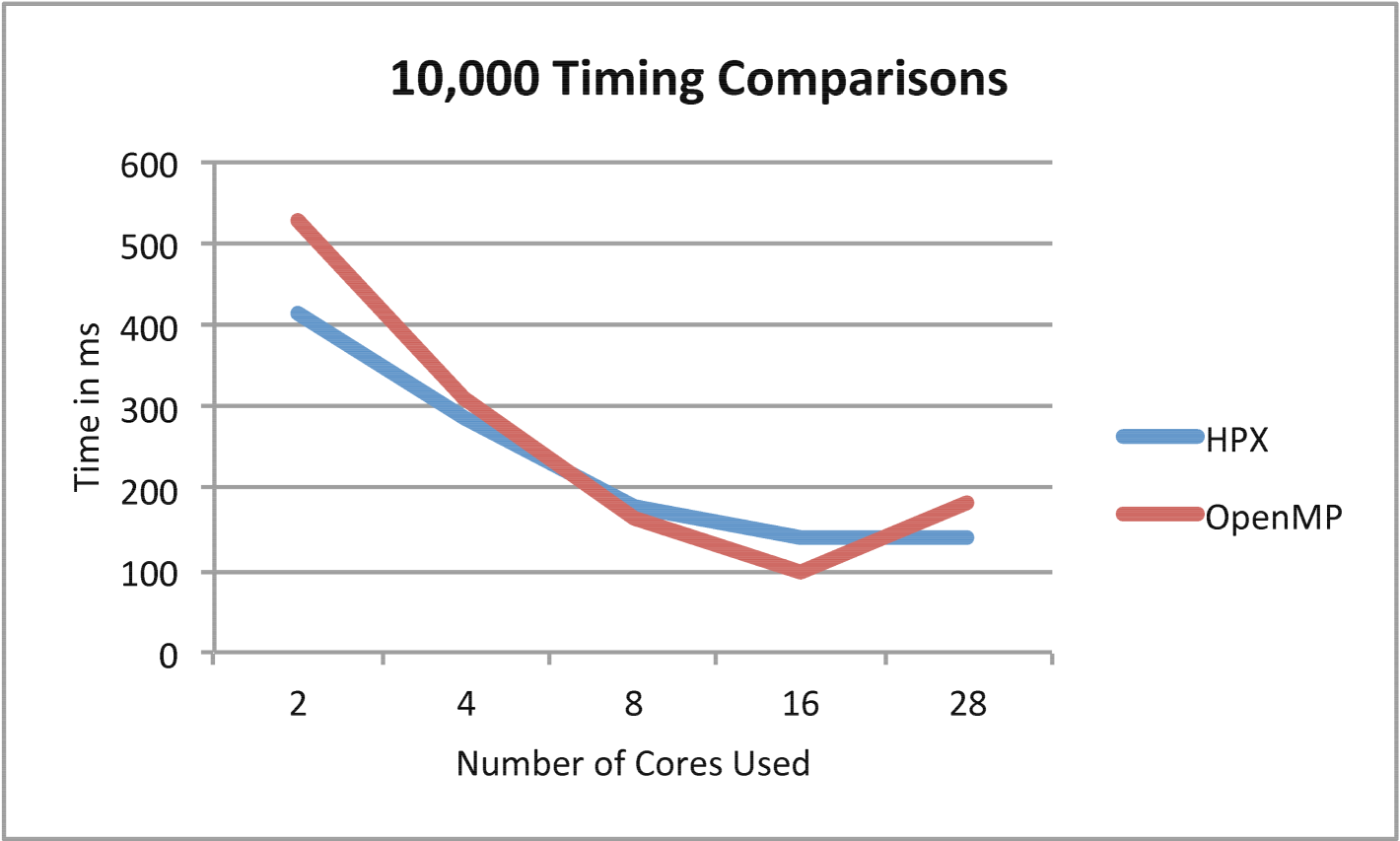
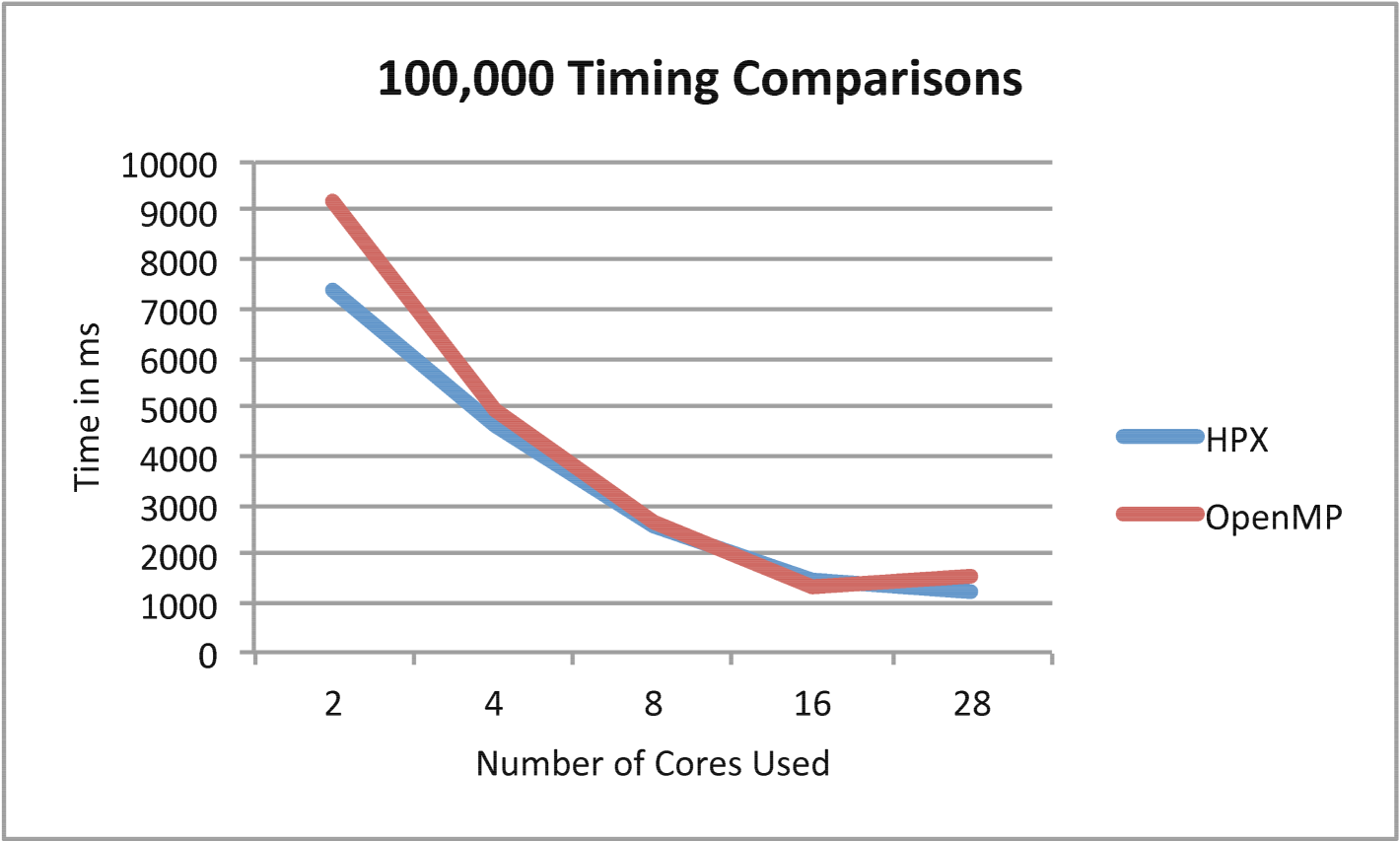
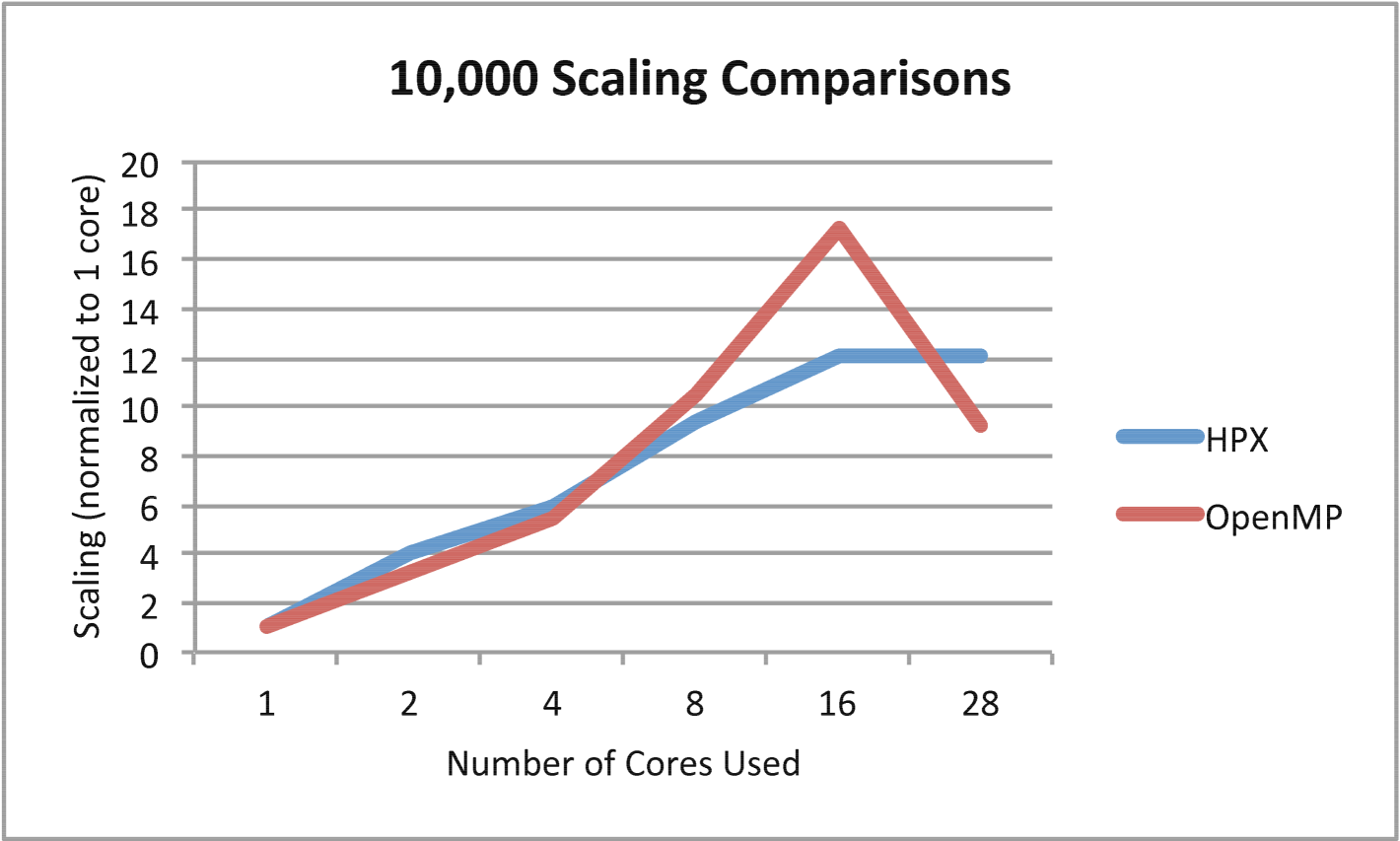
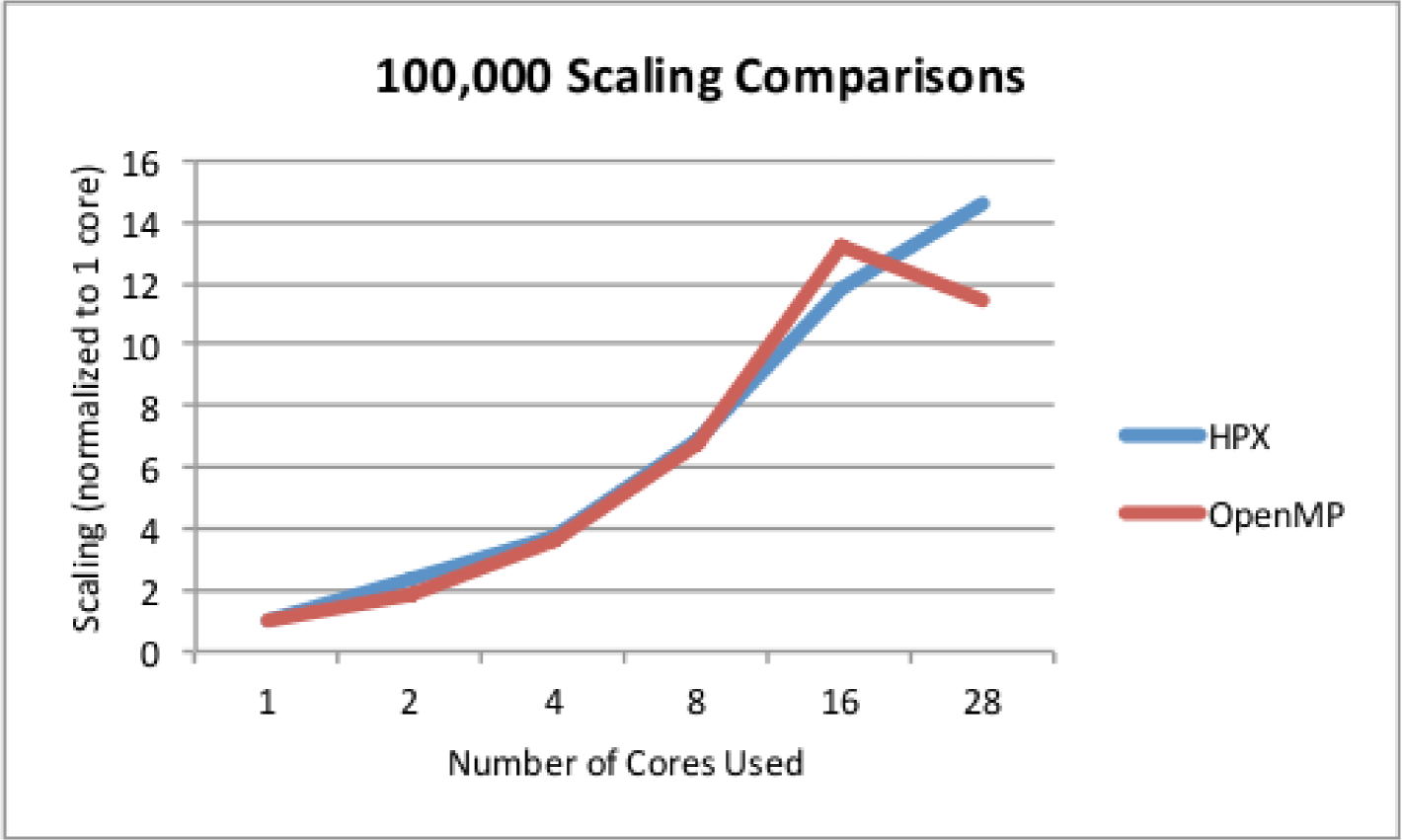
In Figures 8 and 10 the timing comparison and scaling comparison between the HPX and OpenMP versions of Barnes-Hut using multiple iterations are presented in the case of 10,000 particles. Figures 9 and 11 show similar information for the case of 100,000 particles. In the case of 100,000 particles, HPX both outscales and outperforms the OpenMP implementation. This is attributed to the improved load balancing resulting from the dataflow semantics and fine-grained parallelism provided by ParalleX. Also key to this result is the flexibility in ParalleX to control the thread grain size as evidenced in Figures 5, 6,and 7. The main caveat for fine grained load balancing is that the potential for overheads to dominate the computations is higher.

The results obtained from the ParalleX version of the Barnes-Hut algorithm are consistent irrespective of the number of iterations used or the problem size. The performance, scaling, and the consistent results validate the viability of ParalleX semantics for variable data structure problems such as the Barnes-Hut N-Body problem.

VI Conclusion

The HPX Barnes-Hut implementation presented here is the first implementation of a tree based scientific computation using the ParalleX model of execution. With the overall goal of providing extreme scalability to scaling-constrained applications, especially to those involving trees and graphs, this work provides a demonstration of techniques to exploit parallelism within each iteration of the Barnes-Hut algorithm. Direct comparisons were made with an OpenMP implementation of Barnes-Hut in order to provide a benchmark against which to compare the results. However, it is noted that HPX is not limited to shared memory machines.

The HPX Barnes-Hut implementation exploits futures based asynchrony and AGAS-based globally unique identifiers to facilitate on-demand data driven force computation. Conventional parallelism approaches rely on access to data through either system architectures such as shared memory where the data resident in shared memory can be accessed by all computing resources, or through message passing where, in many cases, the critical path of execution is blocked until remote data can be fetched. Future based data access in the HPX Barnes-Hut implementation allows for local force computations to continue executing operations on available data while some of the threads are suspended in the get() call. In the case of remote fetches which cannot be satisfied immediately, the executing HPX thread suspends operation allowing for another dataflow element to continue force calculation. This on-demand data access provides asynchrony without blocking the critical execution path, thereby allowing the application to fully exploit the underlying resources. It is expected that this feature will be especially useful in a distributed memory setting.

Future extensions of this work will include performance benchmarks on distributed memory machines benchmarked against an OpenMP–MPI hybrid Barnes-Hut implementation for comparison. The performance of current Barnes-Hut implementation in HPX can be further improved by applying alternative methods for computation of the approximation criterion $\theta$ and incorporating multipole moments while removing the global barrier so that multiple iterations can proceed simultaneously.

Acknowledgments: We would like to thank Steven Brandt and Dylan Stark for stimulating discussions. We acknowledge support comes from NSF grants 1048019 and 1029161 to Louisiana State University.

References

(1) S. J. Aarseth, M. Henon, and R. Wielen. A comparison of numerical methods for the study of star cluster dynamics. Astronomy and Astrophysics Journal, 37:183–187, December 1974.
(2) Robert A. Alfieri. An efficient kernel-based implementation of posix threads. In Proceedings of the USENIX Summer 1994 Technical Conference on USENIX Summer 1994 Technical Conference - Volume 1, USTC’94, pages 5–5, Berkeley, CA, USA, 1994. USENIX Association.
(3) A. W. Appel and T. Jim. Continuation-passing, closure-passing style. In POPL ’89: Proceedings of the 16th ACM SIGPLAN-SIGACT symposium on Principles of programming languages, pages 293–302, New York, NY, USA, 1989. ACM.
(4) Henry C. Baker, Jr. and Carl Hewitt. The incremental garbage collection of processes. In Proceedings of the 1977 symposium on Artificial intelligence and programming languages, pages 55–59, New York, NY, USA, 1977. ACM.
(5) Joshua Barnes and Piet Hit. A hierarchical O(N log N) force-calculation algorithm. Nature, 324:446–449, December 1986.
(6) Dan Bonachea. Gasnet specification, v1.1. Technical report, Berkeley, CA, USA, 2002.
(7) S. D. Brookes, C. A. R. Hoare, and A. W. Roscoe. A theory of communicating sequential processes. J. ACM, 31(3):560–599, 1984.
(8) Robit Chandra, Leonardo Dagum, Dave Kohr, Dror Maydan, Jeff McDonald, and Ramesh Menon. Parallel programming in OpenMP. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2001.
(9) Philippe Charles, Christian Grothoff, Vijay Saraswat, Christopher Donawa, Allan Kielstra, Kemal Ebcioglu, Christoph von Praun, and Vivek Sarkar. X10: an object-oriented approach to non-uniform cluster computing. SIGPLAN Not., 40:519–538, October 2005.
(10) P. J. Courtois, F. Heymans, and D. L. Parnas. Concurrent control with “readers” and “writers”. Commun. ACM, 14(10):667–668, 1971.
(11) Leonardo Dagum and Ramesh Menon. OpenMP: An industry-standard api for shared-memory programming. IEEE Computational Science and Engineering, 5(1):46–55, 1998.
(12) C Dekate, H Kaiser, M Anderson, B Lelbach, and T Sterling. N-body code svn repository. https://svn.cct.lsu.edu/repos/projects/parallex/ trunk/hpx/examples/history/nbody, 2011.
(13) Chirag Dekate. Extreme Scalel Parallel N-Body Algorithm With Event Driven Constraint Based Execution Model. PhD thesis, Baton Rouge, LA, USA, 2011.
(14) Juan Miguel del Rosario, Rajesh Bordawekar, and Alok Choudhary. Improved parallel I/O via a two-phase run-time access strategy. SIGARCH Comput. Archit. News, 21:31–38, December 1993.
(15) J. B. Dennis. Data flow supercomputers. Computer, 13(11):48–56, 1980.
(16) John Dubinski. A parallel tree code. New Astronomy, 1(2):133 – 147, 1996.
(17) T.v. Eicken, D.E. Culler, S.C. Goldstein, and K.E. Schauser. Active messages: A mechanism for integrated communication and computation. Computer Architecture, 1992. Proceedings., The 19th Annual International Symposium on, pages 256–266, 1992.
(18) Tarek El-Ghazawi, William Carlson, Thomas Sterling, and Katherine Yelick. UPC: Distributed Shared-Memory Programming. Wiley-Interscience, 2003.
(19) Tarek El-Ghazawi and Lauren Smith. Upc: unified parallel c. In SC ’06: Proceedings of the 2006 ACM/IEEE conference on Supercomputing, page 27, New York, NY, USA, 2006. ACM.
(20) Hartmut Kaiser, Maciej Brodowicz, and Thomas Sterling. ParalleX: An advanced parallel execution model for scaling-impaired applications. In Parallel Processing Workshops, pages 394–401, Los Alamitos, CA, USA, 2009. IEEE Computer Society.
(21) Pangfeng Liu and Sandeep N. Bhatt. Experiences with parallel n-body simulation. In Proceedings of the sixth annual ACM symposium on Parallel algorithms and architectures, SPAA ’94, pages 122–131, New York, NY, USA, 1994. ACM.
(22) Junichiro Makino, Kei Hiraki, and Mary Inaba. Grape-dr: 2-pflops massively-parallel computer with 512-core, 512-gflops processor chips for scientific computing. In SC, page 18, 2007.
(23) Message Passing Interface Forum. MPI: A Message-Passing Interface Standard, Version 2.2. High Performance Computing Center Stuttgart (HLRS), Stuttgart, Germany, September 2009.
(24) Jun Makino Piet Hut. Moving stars around. http://http://www.artcompsci.org//, 2010. [Online; accessed 19-Feb-2010].
(25) John K. Salmon. Parallel hierarchical N-body methods. PhD thesis, Pasadena, CA, USA, 1991.
(26) Jaswinder Pal Singh. Parallel hierarchical N-body methods and their implications for multiprocessors. PhD thesis, Stanford University, Stanford, CA, USA, 1993. UMI Order No. GAX93-17818.
(27) A. Tabbal, M. Anderson, M. Brodowics, and T. Kaiser, H. andSterling. Preliminary design examination of the ParalleX system from a software and hardware perspective. SIGMETRICS Performance Evaluation Review, 38:4, Mar 2011.
(28) UPC Consortium. UPC Language Specifications, v1.2. Tech Report LBNL-59208, Lawrence Berkeley National Lab, 2005.
(29) Leslie G. Valiant. A bridging model for parallel computation. Commun. ACM, 33(8):103–111, 1990.
(30) M. S. Warren and J. K. Salmon. A parallel hashed oct-tree n-body algorithm. In Proceedings of the 1993 ACM/IEEE conference on Supercomputing, Supercomputing ’93, pages 12–21, New York, NY, USA, 1993. ACM.