In-context Ranking Preference Optimization

Junda Wu¹, Rohan Surana^1∗, Zhouhang Xie¹, Yiran Shen¹, Yu Xia¹,
Tong Yu², Ryan Rossi², Prithviraj Ammanabrolu¹, Julian McAuley¹
¹UC San Diego ²Adobe Research
{juw069,rsurana,zhx022,jes038,yux078,prithvi,jmcauley}@ucsd.edu
{tyu,ryrossi}@adobe.com
These authors contributed equally to this work.

Abstract

Recent developments in Direct Preference Optimization (DPO) allow large language models (LLMs) to function as implicit ranking models by maximizing the margin between preferred and non-preferred responses. In practice, user feedback on such lists typically involves identifying a few relevant items in context rather than providing detailed pairwise comparisons for every possible item pair. Besides, many complex information retrieval tasks, such as conversational agents and summarization systems, critically depend on ranking the highest-quality outputs at the top, further emphasizing the need to support natural and flexible forms of user feedback. To address the challenge of limited and sparse pairwise feedback in the in-context setting, we propose an In-context Ranking Preference Optimization (IRPO) framework that directly optimizes LLMs based on ranking lists constructed during inference. To further capture the natural and flexible forms of feedback, IRPO extends the DPO objective by incorporating both the relevance of items and their positions in the list. Modeling these aspects jointly is non-trivial, as ranking metrics are inherently discrete and non-differentiable, making direct optimization challenging. To overcome this, IRPO introduces a differentiable objective based on positional aggregation of pairwise item preferences, enabling effective gradient-based optimization of discrete ranking metrics. We further provide theoretical insights showing that IRPO (i) automatically emphasizes items with greater disagreement between the model and the reference ranking, and (ii) shows its gradient’s linkage to an importance sampling estimator, resulting in an unbiased gradient estimator with reduced variance. Empirical evaluations demonstrate that IRPO outperforms standard DPO approaches in ranking performance, highlighting its effectiveness and efficiency in aligning LLMs with direct in-context ranking preferences.

1 Introduction

Recent advancements in Direct Preference Optimization (DPO) (Rafailov et al., 2023) allow large language models (LLMs) to compare and optimize the pairwise margin (Meng et al., 2024; Wu et al., 2024b) between positive and negative responses without explicit reward functions. However, in real-world applications (e.g., conversational recommendation (Huang et al., 2025a; b; Surana et al., 2025), generative retrieval (Li et al., 2025)), such feedback is typically collected by presenting users with an ordered in-context ranking list and asking them to select relevant items (He et al., 2023; Xie et al., 2024) rather than providing detailed pairwise comparisons, which highlights the need for frameworks that support natural and flexible feedback formats. Such in-context feedback on ranked lists yields sparse preference signals that are not directly comparable as explicit pairwise preferences. In addition, modeling natural and flexible ranking feedback effectively requires capturing both item relevance and positional importance, of which conventional DPO methods and their underlying preference models (e.g., (Rafailov et al., 2023; Chen et al., 2024; Liu et al., 2024b)) are limited in modeling directly. Existing works enable approximations of Plackett-Luce (PL) models for ranking feedback by averaging pairwise Bradley-Terry (BT) comparisons without directly modeling the PL distributions (Zhu et al., 2024; Chen et al., 2024; Liu et al., 2024b). Directly applying supervised fine-tuning (SFT) to LLMs is also insufficient for addressing this type of feedback, since ranked-list interactions inherently produce discrete and non-differentiable signals, making direct gradient-based optimization challenging.

To address these limitations of existing approaches, we propose an In-context Ranking Preference Optimization (IRPO) framework that integrates design choices across modeling and optimization to better align with real-world ranking feedback. IRPO first captures the natural form of user interactions, where users select relevant items from an in-context ranked list without providing exhaustive pairwise comparisons. To model such feedback, IRPO employs a PL-inspired positional preference model, which allows the framework to interpret sparse listwise signals by considering both item relevance and positional importance. While this formulation improves modeling fidelity, directly optimizing such objectives remains challenging due to the discrete and non-differentiable nature of common ranking metrics. To overcome this, IRPO introduces a differentiable objective based on the positional aggregation of pairwise item preferences, enabling effective gradient-based optimization.

To understand the optimization behavior of IRPO, we conduct gradient analysis and provide theoretical insights into its connection to importance sampling gradient estimation. Specifically, we show that IRPO acts as an adaptive mechanism that automatically prioritizes items with significant discrepancies between learned and reference policies, resulting in efficient and stable optimization. In addition, we derive an importance-weighted gradient estimator and show that it is unbiased with reduced variance. Empirically, we evaluate IRPO across diverse ranking tasks, including conversational recommendation, generative retrieval, and question-answering re-ranking, with various LLM backbones. Our results consistently show that IRPO significantly improves ranking performance. We summarize our contributions as follows:

•

We propose In-context Ranking Preference Optimization (IRPO), a novel framework extending Direct Preference Optimization (DPO) that directly optimizes sparse and in-context ranking feedback.
•

Specifically we incorporate both graded relevance and positional importance into preference optimization, addressing challenges posed by discrete ranking positions.
•

We provide theoretical insights linking IRPO’s optimization to gradient estimation techniques, demonstrating its computational and analytical advantages.
•

Extensive empirical evaluations across diverse ranking tasks demonstrate that IRPO achieves consistent performance improvement.

2 Related Work

2.1 Ranking Generation with LLMs

Recent work has leveraged LLMs for ranking across diverse applications—including sequential (Luo et al., 2024) and conversational (Yang & Chen, 2024) recommendation, document retrieval (Liu et al., 2024a), and pair-wise document relevance judgments (Zhuang et al., 2023). Most approaches exploit LLMs’ domain-agnostic strengths rather than improving their intrinsic ranking capabilities (Wu et al., 2024c; Pradeep et al., 2023), though fine-tuning has been recently explored (Luo et al., 2024). To our knowledge, we are the first to enhance LLM rankings through an alignment framework. Meanwhile, in contrast to prior works that focus on settings where candidate items are available (Chao et al., 2024), our framework is general and applies to cases where LLMs directly generate a list of responses from input.

2.2 Direct Preference Optimization for Ranking

Recent work aligns language models with human feedback via direct preference optimization (Rafailov et al., 2023; Meng et al., 2024; Wu et al., 2024b). Building on learning-to-rank methods (Valizadegan et al., 2009; Wu et al., 2024a; 2021), several approaches recast preference alignment as a ranking task (Xie et al., 2025; Zhang et al., 2024). For example, GDPO (Yao et al., 2024) handles feedback diversity through group-level preferences, and S-DPO (Chen et al., 2024) extends these ideas to recommendation systems using multiple negatives and partial rankings. However, these approaches generally assume fully supervised or explicitly labeled feedback and require multiple forward passes for optimization, limiting their applicability to more realistic scenarios with sparse and implicit feedback.

Several recent approaches, including Ordinal Preference Optimization (OPO) (Zhao et al., 2024), Direct Ranking Preference Optimization (DRPO) (Zhou et al., 2024), and Listwise Preference Optimization (LiPO) (Liu et al., 2024b), explicitly leverage differentiable surrogates of ranking metrics such as NDCG to guide optimization. OPO uses a NeuralNDCG surrogate built from differentiable sorting (e.g., NeuralSort with Sinkhorn scaling) to align gains with positional discounts, thereby encoding positional importance in a smooth objective. DRPO goes further by explicitly introducing differentiable sorting networks and a margin-based Adaptive Rank Policy Score, and then trains with a differentiable NDCG objective. In contrast, LiPO frames alignment as a listwise learning-to-rank problem and commonly employs lambda-weighted pairwise objectives (LiPO- $\lambda$ ) to approximate listwise metrics like NDCG while operating over all pairs in a list.

In contrast, IRPO addresses a fundamentally distinct and practically motivated framework that extends the DPO (Rafailov et al., 2023) objective by jointly modeling graded relevance and positional importance, and by directly optimizing margins within a single in-context ranking list. Unlike prior works, IRPO does not rely on sorting networks or differentiable sorting approximations, and is designed to eliminate multiple forward passes, enabling a single forward pass per ranked list and lower computational cost.

3 Preliminaries

3.1 Direct Preference Alignment

DPO (Rafailov et al., 2023) enable reinforcement learning from human feedback (RLHF) (Christiano et al., 2017; Stiennon et al., 2020; Ouyang et al., 2022) without explicit reward modeling. Suggested by the Bradley-Terry-Luce (BTL) model of human feedback (Bradley & Terry, 1952), a response $y_{1}$ with a reward of $r(x,y_{1})$ is preferred over a response $y_{2}$ with a reward of $r(x,y_{2})$ with the probability:

p^{*}(y_{1}\succ y_{2}\mid x)=\sigma\left(r(x,y_{1})-r(x,y_{2})\right),

(1)

where $\sigma(z)=1/(1+\exp[-z])$ is the sigmoid function. Suggested in (Rafailov et al., 2023), the optimal policy in the original RLHF maximization problem with a reference policy $\pi_{\text{ref}}(y\mid x)$ is given by

\pi_{\theta}(y\mid x)=\frac{1}{Z(x)}\,\pi_{\text{ref}}(y\mid x)\exp\!\left(\frac{1}{\beta}r(x,y)\right),Z(x)=\sum_{y}\pi_{\text{ref}}(y\mid x)\cdot\exp\left(\frac{1}{\beta}r(y,x)\right),

(2)

where the partition function $Z(x)$ serves as a normalizer (Rafailov et al., 2023). By rearranging equation 2, the implicit reward model can be derived and plugged into equation 1,

r(y,x)=\beta\,\log\frac{\pi^{*}(y\mid x)}{\pi_{\text{ref}}(y\mid x)}+\beta\,\log Z(x),

which formulates the maximum likelihood objective for the target policy $\pi_{\theta}$ as follows,

\mathcal{L}_{\text{DPO}}(\pi_{\theta};\pi_{\text{ref}})=-\mathbb{E}_{(x,y_{1},y_{2})\sim D}\left[\log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{1}\mid x)}{\pi_{\text{ref}}(y_{1}\mid x)}-\beta\log\frac{\pi_{\theta}(y_{2}\mid x)}{\pi_{\text{ref}}(y_{2}\mid x)}\right)\right],

where $Z(x)$ cancels out and thus directly optimizes the target policy without an explicit reward function.

3.2 Discounted Cumulative Gain

Discounted cumulative gain (DCG) has been widely used in various information retrieval and ranking tasks as a metric to capture the graded relevance of items in a ranked list while accounting for their positions (Jeunen et al., 2024; Agarwal et al., 2019). Consider a set of candidate items $\bm{e}=[e_{1},e_{2},\dots,e_{n}]$ in a ranking list, where these items represent the potential outputs or responses for a prompt $x$ . To rank these candidates, $\tau$ is a permutation over $\{1,2,\dots,n\}$ such that the item at rank $i$ is given by $e_{\tau(i)}$ . where the ranking vector is defined as $\bm{k}=[k_{1},k_{2},\dots,k_{n}],\>k_{i}=\tau(i)$ , so that $e_{k_{i}}=e_{\tau(i)}$ is the item placed at the $i$ -th position in the ranked list (Plackett, 1975).

For each item $e_{k_{i}}$ , users may assign a relevance label $y_{k_{i}}$ with explicit or implicit feedback (Järvelin & Kekäläinen, 2002), where its gain is scaled as $G(y_{k_{i}})=2^{y_{k_{i}}}-1$ . In addition, a positional discount factor $d(i)=1/\log_{2}(1+i)$ models the decreasing importance of items placed lower in the ranking list, which leads to a weighted gain at position $i$ given as follows,

w(i)=G(y_{k_{i}})\cdot d(i)=\frac{2^{y_{k_{i}}}-1}{\log_{2}(1+i)}.

(3)

The quality of a ranked list is measured using the Discounted Cumulative Gain (DCG):

\text{DCG}(\tau)=\sum_{i=1}^{n}w(i)=\sum_{i=1}^{n}\frac{2^{y_{\tau(i)}}-1}{\log_{2}(1+i)}

where $w(i)$ represents the gain at rank $i$ for the item with relevance $y_{\tau(i)}$ .

4 IRPO: In-context Ranking Preference Optimization

4.1 Preference Modeling

To capture listwise preferences within the DPO framework, for each position $i$ in a ranking list $\tau$ , we provide a positional preference model based on pairwise comparisons. Following the Plackett-Luce (PL) preference model (Plackett, 1975; Luce et al., 1959), for the item $e_{\tau(i)}$ at rank $i$ ,

p^{*}\Bigl{(}e_{\tau(i)}\succ\{e_{j}\}_{j\neq\tau(i)}\mid x\Bigr{)}=\sigma\!\Biggl{(}-\log\sum_{j=1}^{n}\exp\Bigl{(}s(e_{j}\mid x)-s(e_{\tau(i)}\mid x)\Bigr{)}\Biggr{)},

(4)

where $\sigma(z)=1/(1+\exp[-z])$ is the sigmoid function and $s(e\mid x)$ is a score function quantifying the quality of item $e$ given the prompt $x$ . In equation 4, we aggregate the in-context pairwise differences between the score of $e_{\tau(i)}$ and all candidate items $e_{j}$ .

To evaluate the entire ranked list, we further aggregate the individual positional preferences into an overall list preference model by weighting each position by its NDCG gain:

P^{*}(\tau\mid x)\propto\prod_{i=1}^{n}\Bigl{[}p^{*}\Bigl{(}e_{\tau(i)}\succ\{e_{j}\}_{j\neq\tau(i)}\mid x\Bigr{)}\Bigr{]}^{w(i)},

(5)

whose log-likelihood can be derived as follows,

\log P^{*}(\tau\mid x)=\sum_{i=1}^{n}w(i)\cdot\log\sigma\!\Biggl{(}-\log\sum_{j=1}^{n}\exp\!\Bigl{(}s(e_{j}\mid x)-s(e_{\tau(i)}\mid x)\Bigr{)}\Biggr{)},

(6)

which ensures that every rank contributes to the assessment of the entire ranking list.

4.2 Policy Optimization Objective

Following DPO (Rafailov et al., 2023) we plug the reward-based score from equation 2 into the positional NDCG preference model in equation 4, to derive our policy optimization objective for IRPO that incorporates graded relevance and the positional importance. Taking the expectation over the data distribution $(x,\bm{y})\sim D$ and summing over all ranks, the final IRPO objective is given by:

\displaystyle\mathcal{L}_{\text{IRPO}}(\pi_{\theta};\pi_{\text{ref}})=-\mathbb{E}_{(x,\bm{y})}\Biggl{[}\sum_{i=1}^{n}w(i)\cdot\log\sigma(z_{i})\Biggr{]},\quad w(i)=\frac{2^{y_{\tau(i)}}-1}{\log_{2}(1+i)},

(7)

where $w(i)$ is the NDCG gain at rank $i$ according to equation 3, while the individual rank’s preference $z_{i}$ is

z_{i}=-\log\sum_{j=1}^{n}\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}.

(8)

Our formulation naturally extends to other ranking metrics, including P@K, MAP, MRR, and eDCG (detailed derivations in Appendix B), by considering their corresponding positional importance, as a generalized framework for in-context ranking preference optimization.

4.3 Gradient Analysis and Theoretical Insights

We further analyze the gradient (detailed derivation in Appendix C) by optimizing over IRPO objective to the model parameters $\theta$ :

\displaystyle\nabla_{\theta}\mathcal{L}_{\text{IRPO}}(\pi_{\theta};\pi_{\text{ref}})=\beta\,\mathbb{E}_{(x,\bm{y})}\left[\sum_{i=1}^{n}w(i)(1-\sigma(z_{i}))\cdot\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}\right],

(9)

with the importance weights defined as

\rho_{ij}=\frac{\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}}{\sum_{k=1}^{n}\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{k}\mid x)}{\pi_{\text{ref}}(e_{k}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}}.

(10)

Following previous DPO methods (Rafailov et al., 2023; Chen et al., 2024), the gradient term $\nabla_{\theta}[\log\pi_{\theta}(e_{j}\mid x)-\log\pi_{\theta}(e_{\tau(i)}\mid x)]$ in equation 9 optimizes the model to further distinguish between the item at rank $i$ and the remaining items in the ranking list. Intuitively, since $\sum_{j}\rho_{ij}=1$ for each position $i$ , the weights $\rho_{ij}$ act automatically as an adaptive mechanism that assigns higher importance to items where the discrepancy between the model and the reference policy is larger. In practice, higher importance weights prioritize the gradient contribution from items ranked most wrongly relative to the target ranking.

Inspired by the importance weights $\rho_{ij}$ , we further link our gradient analysis to the potential gradient estimator,

\hat{g}(e_{j})=\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)},

(11)

where the random variable $e_{j}$ is subordinate to the distribution of importance weights $p(e_{j})=\rho_{ij}$ at rank $i$ . In practice, the gradient calculation could be approximated through importance sampling with the distribution of $p_{i,j}$ at rank $i$ . We further show the mean and variance properties of the gradient estimator $\hat{g}(e_{j})$ , which serves as an unbiased estimator of the original gradient term and is more efficient in optimization.

Lemma 4.1 (Mean Analysis)

The proposed gradient estimator $\hat{g}(e_{j})$ is an unbiased estimation of the gradient term (proof in Appendix D),

g=\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)},

(12)

in equation 9, which can be achieved by importance sampling with $p(e_{j})=\rho_{ij}$ at rank $i$ .

Lemma 4.2 (Variance Analysis)

We show that the expected absolute deviation of the proposed estimator is upper bounded as (proof in Appendix E)

\mathbb{E}[|\hat{g}(e_{j})-g|]\leq\sqrt{\frac{1}{n}\|\rho_{i,j}\|_{\infty}\cdot\mathbb{E}\left[\|\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}\|^{2}\right]}\leq L\sqrt{\frac{\|\rho_{i,j}\|_{\infty}}{n}},

where $L=\max_{j}{[\nabla_{\theta}\log\pi_{\theta}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\theta}(e_{\tau(i)}\mid x)]}$ and practically clipped to maintain numerical stability (Ouyang et al., 2022; Schulman et al., 2017).

5 Experiments

5.1 Experimental Setup

Tasks

To evaluate the effectiveness of IRPO on enhancing LLMs’ ranking capabilities, we adopt three tasks: conversational recommendation on Inspired (Hayati et al., 2020) and Redial (Li et al., 2018) dataset; generative (supporting evidence) retrieval on HotpotQA (Yang et al., 2018) and MuSiQue (Trivedi et al., 2022) dataset; and question-answering as re-ranking on ARC (Clark et al., 2018) and CommonsenseQA (Talmor et al., 2019) dataset. Each of the tasks requires LLM to generate a ranked list among a set of candidate answers. We provide additional detail for task sections in sections 5.2, 5.3 and 5.4.

Baselines

We compare IRPO against several alignment baselines: Supervised fine-tuning (SFT), which directly optimizes model outputs from explicit human annotations without preference modeling; DPO (Rafailov et al., 2023), which optimizes models from pairwise human preferences by maximizing margins between preferred and non-preferred responses; and S-DPO (Chen et al., 2024), an extension of DPO tailored for ranking tasks, which leverages multiple negative samples, inspired by the Plackett-Luce preference model to capture richer ranking signals. We included more implementation details in Appendix A.

5.2 Conversational Recommendation

		Redial						Inspired
Model	Method	NDCG			Recall			NDCG			Recall
Model	Method	@1	@5	@10	@1	@5	@10	@1	@5	@10	@1	@5	@10
Llama3	Base	32.5	38.2	46.3	13.0	42.6	61.2	33.8	40.8	48.7	19.8	47.7	68.1
	SFT	21.6	26.5	34.9	8.1	31.2	50.4	13.8	24.7	36.2	8.1	31.7	63.3
	DPO	37.6	42.5	50.1	14.9	46.5	64.0	37.5	44.0	51.2	21.9	50.2	69.2
	SDPO	42.0	46.1	53.5	17.3	49.6	66.6	53.1	57.6	62.3	30.5	63.3	75.5
	IRPO	74.8	73.6	79.3	27.9	78.1	91.3	45.3	55.2	62.3	22.4	68.8	87.2
Phi3	Base	21.1	27.4	36.8	8.7	32.1	54.0	21.1	27.4	36.8	8.7	32.1	54.0
	SFT	15.9	22.2	32.7	5.8	27.2	51.6	22.1	27.0	36.6	8.5	31.2	53.4
	DPO	22.5	28.9	38.2	9.2	33.5	55.1	27.5	34.7	42.1	14.8	41.0	60.2
	SDPO	21.9	23.2	28.2	8.9	23.8	32.9	32.5	36.6	44.8	19.6	41.2	63.3
	IRPO	35.0	39.3	51.1	12.7	45.6	72.4	42.2	46.3	54.6	17.2	54.4	76.0
Gemma2	Base	19.2	26.8	38.0	7.2	32.8	58.5	15.3	22.4	31.7	7.7	28.5	52.0
	SFT	25.6	30.2	39.3	9.6	34.4	55.6	15.0	25.9	35.5	7.5	32.9	57.9
	DPO	30.1	36.0	44.3	12.1	40.4	59.4	27.5	34.7	42.1	14.8	41.0	60.2
	SDPO	48.5	52.7	59.2	19.6	55.8	70.9	40.0	44.0	48.4	22.7	48.2	60.0
	IRPO	68.8	71.4	77.3	25.1	77.0	90.5	42.2	46.3	54.6	17.2	54.4	76.0

Table 1: Performance on Redial and Inspired of Conversational Recommendation, evaluated using NDCG and Recall for the top 1, 5, and 10 predictions out of 20 candidate items.

For conversational recommendation, we use two widely adopted datasets, Inspired (Hayati et al., 2020) and Redial (Li et al., 2018). Following (He et al., 2023; Xie et al., 2024; Carraro & Bridge, 2024; Jiang et al., 2024), LLMs generate ranked lists of $20$ candidate movies per dialogue context. To evaluate IRPO and baselines in generating ranked conversational recommendation lists, we follow (He et al., 2023) and construct candidate movie sets for each dialogue context (detailed in Appendix A). These candidate movies are then assigned relevance scores reflecting their importance in calculating the NDCG gain for IRPO in equation 7, where ground-truth movies receive a score of 2, GPT-generated movies a score of 1, and random movies a score of 0. Following (He et al., 2023; Xie et al., 2024; Carraro & Bridge, 2024; Jiang et al., 2024), we report the Recall and NDCG at top- $k$ positions.

Results in Table 1 show that supervised fine-tuning (SFT) can be harmful for most metrics and datasets compared with base model performance, due to strong popularity bias in conversational recommendation datasets, which is likely to cause model overfitting (Gao et al., 2025; Lin et al., 2022; Klimashevskaia et al., 2024). With multi-negative policy optimization (SDPO), such biasing effects could be alleviated, leading to relatively better performance compared to DPO and SFT. In addition, we show that IRPO achieves consistently better or comparable performance across datasets in conversational recommendation compared with baselines, by further considering positional importance for each item, weighted by NDCG weights based on the relevancy score feedback from users. With the complete ranking list optimized by pairwise comparative margins measured by DPO (Rafailov et al., 2023), IRPO acts automatically as an adaptive mechanism that assigns higher importance to items where the discrepancy between the model and the reference policy is larger.

		HotpotQA						MuSiQue
Model	Method	NDCG			Recall			NDCG			Recall
Model	Method	@1	@3	@5	@1	@3	@5	@1	@3	@5	@1	@3	@5
Llama3	Base	21.8	31.3	38.2	19.1	38.4	54.4	42.5	43.5	51.9	18.8	44.9	60.7
	SFT	35.3	41.4	48.3	29.5	46.3	62.1	36.9	39.1	48.0	16.6	40.7	57.6
	DPO	31.2	39.5	46.3	27.3	45.6	61.0	51.1	53.9	60.8	21.6	55.8	68.9
	SDPO	41.3	48.9	54.6	36.2	54.7	68.1	58.6	60.8	66.7	26.0	62.3	73.3
	IRPO	94.6	97.2	97.5	83.6	99.1	99.8	65.1	59.4	69.4	27.6	59.2	78.0
Phi3	Base	24.0	32.1	39.4	21.2	38.3	55.8	23.9	24.8	31.8	9.8	26.0	39.2
	SFT	26.0	34.1	41.1	23.2	40.2	56.3	33.0	32.2	41.3	14.1	33.4	50.5
	DPO	45.8	52.5	57.6	40.6	57.7	69.5	31.6	34.4	43.5	13.5	36.5	53.7
	SDPO	45.5	52.3	57.4	40.2	57.4	69.3	41.9	43.9	52.0	18.4	45.5	60.7
	IRPO	61.2	73.8	78.5	53.8	82.9	93.7	41.5	43.9	52.4	18.5	45.7	61.7
Gemma2	Base	32.5	39.6	45.4	28.5	45.1	58.4	40.9	42.8	51.1	17.9	44.3	59.9
	SFT	19.7	27.8	35.4	16.6	33.7	51.1	39.8	43.3	51.7	17.2	45.3	61.3
	DPO	69.1	72.6	75.5	61.5	75.3	81.9	40.9	43.1	51.1	18.1	44.9	59.8
	SDPO	53.3	59.0	63.2	47.7	62.9	72.5	40.6	42.3	50.6	17.9	43.7	59.4
	IRPO	94.5	96.8	97.4	83.5	98.5	99.8	55.4	51.0	61.1	23.8	51.6	70.6

Table 2: Performance on HotpotQA and MuSiQue for Generative Retrieval, evaluated using NDCG and Recall for the top 1, 3, and 5 predictions out of 10 candidate contexts.

5.3 Generative Retrieval

For generative retrieval, we evaluate IRPO using multi-hop question-answering datasets, HotpotQA (Yang et al., 2018) and MuSiQue (Trivedi et al., 2022) (detailed in Appendix A). Following prior work (Shen et al., 2024; Xia et al., 2025), we prompt LLMs to rank a set of candidate context paragraphs per question. We assign binary relevance scores, setting a score of 1 for supporting contexts and 0 for distractors.

Based on the comparative results in Table 2, SFT consistently reduces retrieval effectiveness relative to base models. This occurs because SFT tends to over-optimize policies, limiting their ability to generalize effectively to the nuanced retrieval challenges inherent in multi-hop queries. While SDPO, leveraging multi-negative sampling, occasionally achieves better top-1 performance compared with IRPO, IRPO attains substantial improvements in NDCG and Recall across the entire ranking list, demonstrating its effectiveness in explicitly modeling positional importance. By optimizing pairwise comparative margins comprehensively across entire ranking lists, IRPO adaptively prioritizes contexts with larger divergences between model predictions and preference feedback. Thus, IRPO offers robust generalizability and better retrieval accuracy for complex generative retrieval tasks.

5.4 Question-answering as Re-ranking

In the question-answering as re-ranking scenario, we assess the ability of LLMs to identify correct answers from multiple choices based on contextual relevance. We evaluate IRPO on two widely-used datasets, ARC (Clark et al., 2018) and CommonsenseQA (Talmor et al., 2019) (detailed in Appendix A). Each candidate is explicitly assigned binary relevance: the correct answer receives a score of 1, and incorrect answers a score of 0.

Comparative results summarized in Table 3 highlight IRPO’s robust improvements across models and datasets. While SFT achieves relatively better performance compared to its performance on other tasks, it still struggles to prioritize and disambiguate the correct answer among similar candidate answers. On the other hand, SDPO, benefiting from multi-negative optimization, typically yields better performance by distinguishing subtle semantic differences among distractors. IRPO further demonstrates superior effectiveness in this challenging ranking task, substantially outperforming all baseline approaches. Aligned with our theoretical insights into IRPO optimization in Section 4.3, IRPO boosts performance by adaptively focusing on candidates with greater discrepancies, enabling comprehensive comparisons that effectively resolve subtle semantic differences and yield substantial gains on challenging datasets like ARC and CommonsenseQA.

		ARC						CommonsenseQA
Model	Method	NDCG			Recall			NDCG			Recall
Model	Method	@1	@3	@5	@1	@3	@5	@1	@3	@5	@1	@3	@5
Llama3	Base	13.2	21.7	28.6	13.2	28.4	44.9	24.1	32.6	38.9	24.1	39.3	54.8
	SFT	13.5	21.4	28.4	13.5	27.7	44.6	22.8	31.6	38.7	22.8	38.6	56.1
	DPO	15.2	22.8	30.4	15.2	29.1	47.3	54.4	59.5	63.4	54.4	63.6	73.2
	SDPO	23.4	28.3	35.4	23.4	32.5	50.0	54.2	59.9	63.9	54.2	64.4	74.2
	IRPO	27.4	38.9	46.5	27.4	47.6	66.3	68.6	83.1	85.0	68.6	92.8	97.5
Phi3	Base	9.8	17.9	25.1	9.8	24.3	41.9	24.3	33.2	38.7	24.3	40.0	53.6
	SFT	8.8	17.7	25.7	8.8	24.7	44.3	24.4	32.6	39.6	24.4	39.0	56.3
	DPO	9.5	17.9	25.5	9.5	24.7	43.2	54.0	59.7	63.5	54.0	64.0	73.4
	SDPO	9.7	18.0	25.2	9.7	24.7	42.4	48.1	54.3	59.0	48.1	59.0	70.4
	IRPO	10.4	19.5	26.8	10.4	25.7	43.8	53.1	70.1	74.1	53.1	82.2	92.0
Gemma2	Base	27.4	35.6	42.1	27.4	42.6	58.4	27.2	35.4	41.4	27.2	42.0	56.7
	SFT	23.6	32.9	39.3	23.6	40.2	55.7	29.5	38.0	44.1	29.5	44.7	59.7
	DPO	27.0	34.4	40.7	27.0	40.5	56.1	29.4	37.9	43.7	29.4	44.7	59.1
	SDPO	28.7	36.5	42.6	28.7	43.0	58.0	57.0	62.4	66.2	57.0	66.5	75.8
	IRPO	27.0	45.5	53.3	27.0	59.8	78.7	66.3	79.2	81.7	66.3	88.3	94.5

Table 3: Performance on the ARC and CommonsenseQA QA datasets, evaluated using NDCG and Recall for the top 1, 3, and 5 predictions out of 10 answer choices.

6 Analysis

In this section, we analyze the optimization behavior and performance of IRPO in both online and offline settings. For on-policy optimization (in Section 6.1), we extend IRPO to its online variant Iterative IRPO. Additionally, we present offline learning curves for IRPO across multiple tasks and various backbone LLMs (Section 6.2) in Figure 2. We then conduct an ablation study to investigate the role of relevance and positional weighting in IRPO’s objective (Section 6.3), demonstrating the necessity of jointly modeling these factors for effective ranking alignment. Finally, we compare IRPO with recent learning-to-rank approaches, focusing on LiPO (Liu et al., 2024b) (Section 6.4).

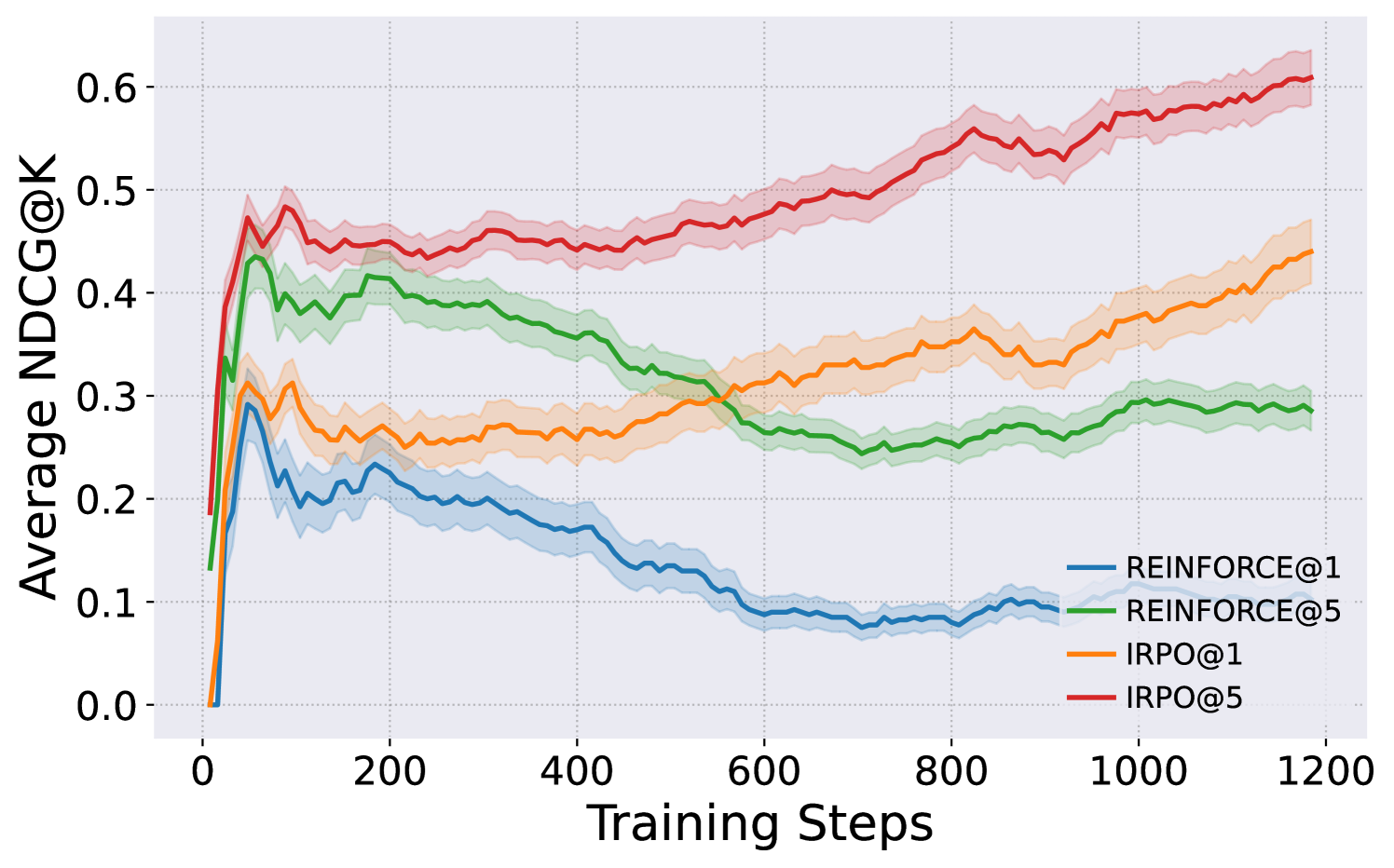
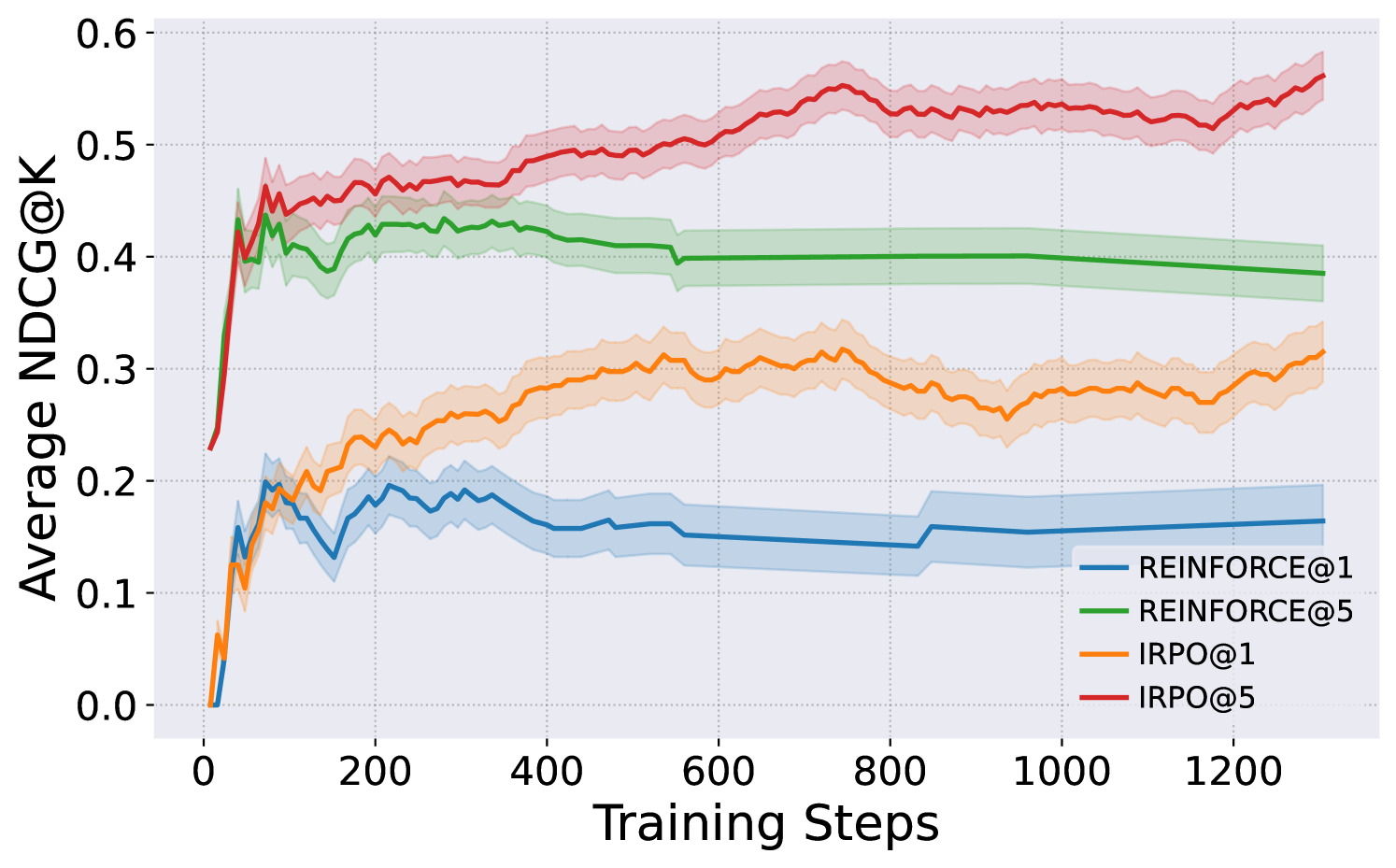
6.1 On-policy Online Optimization of Iterative IRPO

We explore an on-policy variant of IRPO, Iterative IRPO, which adapts to an online optimization setting Hu (2025); Wu et al. (2025); Shao et al. (2024). In this setting, models sample their responses based on queries, rather than relying on predefined ranking lists from the original datasets. These on-policy sampled responses are compared with ground-truth annotations, simulating a realistic human feedback loop. We conduct such on-policy online learning experiments on ARC and CommonsenseQA, compared to a standard policy-gradient baseline, REINFORCE (Sutton et al., 1999). In Figure 1, we show that the Iterative IRPO achieves constantly increasing NDCG scores, while REINFORCE fails to explore effective candidates, leading to insufficient feedback. Aligned with the design of IRPO, which prioritizes more relevant items while considering positional importance, Iterative IRPO could improve the general quality of the entire ranking list, which significantly benefits on-policy exploration performance. Supported by our theoretical insights (Section 4.3), we link IRPO’s optimization to an efficient importance sampling method, which inherently serves as an effective exploration mechanism when Iterative IRPO is enabled online. To further illustrate, we provide a qualitative comparison of outputs generated by the base model, Iterative IRPO, and REINFORCE in Section G.1.

6.2 Optimization Analysis of IRPO

We further evaluate IRPO’s offline optimization performance in the experimental results in Figure 2, showing that IRPO consistently achieves higher evaluation NDCG scores and exhibits stable optimization. across six diverse benchmarks (Inspired, HotpotQA, ARC, Redial, MuSiQue, and CommonsenseQA) using three different LLM backbones: Llama3, Gemma2, and Phi3. This robust performance improvement is attributable to IRPO’s adaptive importance weighting mechanism, which effectively prioritizes gradient updates toward ranking positions with higher relevance discrepancies. This mechanism allows IRPO to rapidly capture essential ranking signals from the feedback, leading to stable and consistent optimization behavior, a finding further supported by our theoretical analysis in Section 4.3.

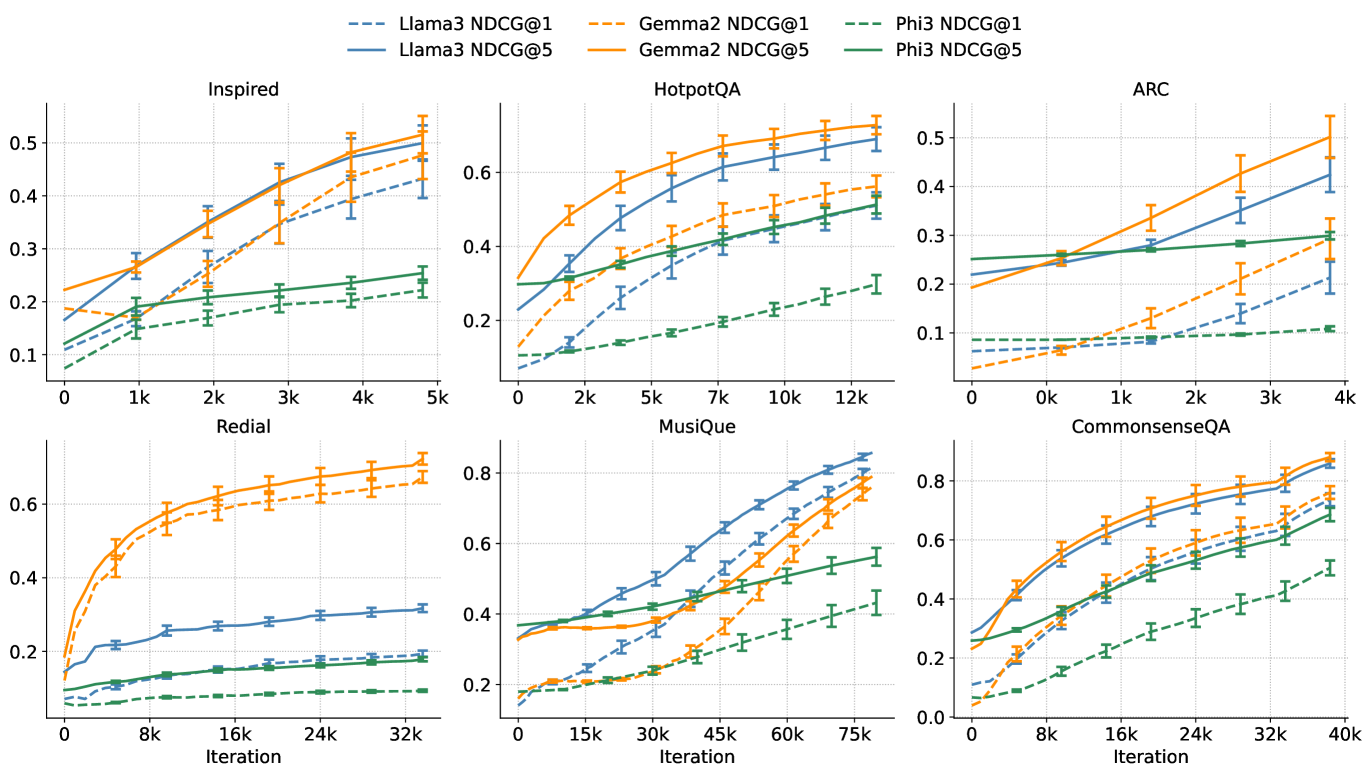
To highlight the strengths of IRPO over baseline methods, we include three representative qualitative examples in Section G.2. These showcase how IRPO more effectively ranks contextually relevant and coherent responses.

6.3 Ablation Study

IRPO inherently prioritizes relative comparisons over absolute weight magnitudes, making it less sensitive to specific weighting schemes. To validate this, we conduct an additional ablation study evaluating two alternative positional weighting methods: (1) abl1: $w(i)=\frac{1}{\log(1+i)}$ (positional weights without relevance) (2) abl2: $w(i)=\frac{2^{y_{i}}-1}{i}$ (alternative relevance scaling).

As shown in Appendix F, removing the relevance component (as in abl1) leads to significant degradation in ranking performance across all datasets. These results underscore the importance of modeling both item relevance and positional importance within IRPO’s objective.

6.4 Comparison with Learning-to-Rank (LiPO)

Although IRPO and LiPO (Liu et al., 2024b) address distinct feedback settings, we provide a comparative analysis here to clearly contextualize IRPO within recent learning-to-rank (LTR) paradigms. LiPO (Liu et al., 2024b) is a recent representative baseline explicitly extending direct preference optimization (DPO) by integrating general learning-to-rank principles. Unlike IRPO, LiPO is designed primarily for scenarios with fully supervised or extensively labeled listwise data, allowing straightforward integration into standard supervised ranking setups.

To meaningfully compare these distinct approaches, we adapt LiPO to align closely with our sparse, in-context feedback scenario and conduct comparative experiments on representative benchmarks (ARC and MuSiQue). Results summarized in Section F.2 indicate that IRPO consistently outperforms LiPO, underscoring the advantage of IRPO’s explicitly modeled positional relevance and sparse feedback setting.

7 Conclusion

In this work, we introduced IRPO, a novel alignment framework that directly optimizes LLMs for ranking tasks using sparse, in-context user feedback. By explicitly modeling both item relevance and positional importance within a differentiable ranking objective, IRPO effectively addresses the limitations of existing DPO methods. Our theoretical insights demonstrated IRPO’s adaptive prioritization mechanism and established its connection to importance sampling, providing unbiased gradient estimation with reduced variance. Extensive empirical evaluations across conversational recommendation, generative retrieval, and question-answering re-ranking tasks consistently showed IRPO’s superior ranking performance. Our findings highlight IRPO as an effective and efficient method for aligning LLMs with realistic user preferences, paving the way for broader integration into in-context action-space exploration and reinforcement learning in dynamic online settings.

References

Abdin et al. (2024) Marah Abdin, Jyoti Aneja, Hany Awadalla, Ahmed Awadallah, Ammar Ahmad Awan, Nguyen Bach, Amit Bahree, Arash Bakhtiari, Jianmin Bao, Harkirat Behl, et al. Phi-3 technical report: A highly capable language model locally on your phone. arXiv preprint arXiv:2404.14219, 2024.
Agarwal et al. (2019) Aman Agarwal, Kenta Takatsu, Ivan Zaitsev, and Thorsten Joachims. A general framework for counterfactual learning-to-rank, 2019. URL https://arxiv.org/abs/1805.00065.
Bradley & Terry (1952) Ralph Allan Bradley and Milton E. Terry. Rank analysis of incomplete block designs: I. the method of paired comparisons. Biometrika, 39(3/4):324–345, 1952. ISSN 00063444, 14643510. URL http://www.jstor.org/stable/2334029.
Carraro & Bridge (2024) Diego Carraro and Derek Bridge. Enhancing recommendation diversity by re-ranking with large language models. ACM Trans. Recomm. Syst., October 2024. doi: 10.1145/3700604. URL https://doi.org/10.1145/3700604. Just Accepted.
Chao et al. (2024) Wen-Shuo Chao, Zhi Zheng, Hengshu Zhu, and Hao Liu. Make large language model a better ranker. In Yaser Al-Onaizan, Mohit Bansal, and Yun-Nung Chen (eds.), Findings of the Association for Computational Linguistics: EMNLP 2024, pp. 918–929, Miami, Florida, USA, November 2024. Association for Computational Linguistics. doi: 10.18653/v1/2024.findings-emnlp.51. URL https://aclanthology.org/2024.findings-emnlp.51/.
Chen et al. (2024) Yuxin Chen, Junfei Tan, An Zhang, Zhengyi Yang, Leheng Sheng, Enzhi Zhang, Xiang Wang, and Tat-Seng Chua. On softmax direct preference optimization for recommendation. arXiv preprint arXiv:2406.09215, 2024.
Christiano et al. (2017) Paul F. Christiano, Jan Leike, Tom B. Brown, Miljan Martic, Shane Legg, and Dario Amodei. Deep reinforcement learning from human preferences. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, pp. 4302–4310, Red Hook, NY, USA, 2017. Curran Associates Inc. ISBN 9781510860964.
Clark et al. (2018) Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. Think you have solved question answering? try arc, the ai2 reasoning challenge, 2018. URL https://arxiv.org/abs/1803.05457.
Gao et al. (2025) Chongming Gao, Mengyao Gao, Chenxiao Fan, Shuai Yuan, Wentao Shi, and Xiangnan He. Process-supervised llm recommenders via flow-guided tuning, 2025. URL https://arxiv.org/abs/2503.07377.
Grattafiori et al. (2024) Aaron Grattafiori, Abhimanyu Dubey, Abhinav Jauhri, Abhinav Pandey, Abhishek Kadian, Ahmad Al-Dahle, Aiesha Letman, Akhil Mathur, Alan Schelten, Alex Vaughan, et al. The llama 3 herd of models. arXiv preprint arXiv:2407.21783, 2024.
Hayati et al. (2020) Shirley Anugrah Hayati, Dongyeop Kang, Qingxiaoyang Zhu, Weiyan Shi, and Zhou Yu. INSPIRED: Toward sociable recommendation dialog systems. In Bonnie Webber, Trevor Cohn, Yulan He, and Yang Liu (eds.), Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 8142–8152, Online, November 2020. Association for Computational Linguistics. doi: 10.18653/v1/2020.emnlp-main.654. URL https://aclanthology.org/2020.emnlp-main.654/.
He et al. (2023) Zhankui He, Zhouhang Xie, Rahul Jha, Harald Steck, Dawen Liang, Yesu Feng, Bodhisattwa Prasad Majumder, Nathan Kallus, and Julian Mcauley. Large language models as zero-shot conversational recommenders. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, CIKM ’23, pp. 720–730, New York, NY, USA, 2023. Association for Computing Machinery. ISBN 9798400701245. doi: 10.1145/3583780.3614949. URL https://doi.org/10.1145/3583780.3614949.
Hu (2025) Jian Hu. Reinforce++: A simple and efficient approach for aligning large language models. arXiv preprint arXiv:2501.03262, 2025.
Huang et al. (2025a) Chengkai Huang, Hongtao Huang, Tong Yu, Kaige Xie, Junda Wu, Shuai Zhang, Julian Mcauley, Dietmar Jannach, and Lina Yao. A survey of foundation model-powered recommender systems: From feature-based, generative to agentic paradigms. arXiv preprint arXiv:2504.16420, 2025a.
Huang et al. (2025b) Chengkai Huang, Junda Wu, Yu Xia, Zixu Yu, Ruhan Wang, Tong Yu, Ruiyi Zhang, Ryan A Rossi, Branislav Kveton, Dongruo Zhou, et al. Towards agentic recommender systems in the era of multimodal large language models. arXiv preprint arXiv:2503.16734, 2025b.
Järvelin & Kekäläinen (2002) Kalervo Järvelin and Jaana Kekäläinen. Cumulated gain-based evaluation of ir techniques. ACM Transactions on Information Systems (TOIS), 20(4):422–446, 2002.
Jeunen et al. (2024) Olivier Jeunen, Ivan Potapov, and Aleksei Ustimenko. On (normalised) discounted cumulative gain as an off-policy evaluation metric for top-n recommendation. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, KDD ’24, pp. 1222–1233, New York, NY, USA, 2024. Association for Computing Machinery. ISBN 9798400704901. doi: 10.1145/3637528.3671687. URL https://doi.org/10.1145/3637528.3671687.
Jiang et al. (2024) Chumeng Jiang, Jiayin Wang, Weizhi Ma, Charles L. A. Clarke, Shuai Wang, Chuhan Wu, and Min Zhang. Beyond utility: Evaluating llm as recommender, 2024. URL https://arxiv.org/abs/2411.00331.
Klimashevskaia et al. (2024) Anastasiia Klimashevskaia, Dietmar Jannach, Mehdi Elahi, and Christoph Trattner. A survey on popularity bias in recommender systems. User Modeling and User-Adapted Interaction, 34(5):1777–1834, July 2024. ISSN 0924-1868. doi: 10.1007/s11257-024-09406-0. URL https://doi.org/10.1007/s11257-024-09406-0.
Li et al. (2018) Raymond Li, Samira Kahou, Hannes Schulz, Vincent Michalski, Laurent Charlin, and Chris Pal. Towards deep conversational recommendations. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS’18, pp. 9748–9758, Red Hook, NY, USA, 2018. Curran Associates Inc.
Li et al. (2025) Xiaoxi Li, Jiajie Jin, Yujia Zhou, Yuyao Zhang, Peitian Zhang, Yutao Zhu, and Zhicheng Dou. From matching to generation: A survey on generative information retrieval, 2025. URL https://arxiv.org/abs/2404.14851.
Lin et al. (2022) Allen Lin, Jianling Wang, Ziwei Zhu, and James Caverlee. Quantifying and mitigating popularity bias in conversational recommender systems. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, CIKM ’22, pp. 1238–1247, New York, NY, USA, 2022. Association for Computing Machinery. ISBN 9781450392365. doi: 10.1145/3511808.3557423. URL https://doi.org/10.1145/3511808.3557423.
Liu et al. (2024a) Qi Liu, Bo Wang, Nan Wang, and Jiaxin Mao. Leveraging passage embeddings for efficient listwise reranking with large language models. In THE WEB CONFERENCE 2025, 2024a.
Liu et al. (2024b) Tianqi Liu, Zhen Qin, Junru Wu, Jiaming Shen, Misha Khalman, Rishabh Joshi, Yao Zhao, Mohammad Saleh, Simon Baumgartner, Jialu Liu, et al. Lipo: Listwise preference optimization through learning-to-rank. arXiv preprint arXiv:2402.01878, 2024b.
Luce et al. (1959) R Duncan Luce et al. Individual choice behavior, volume 4. Wiley New York, 1959.
Luo et al. (2024) Sichun Luo, Bowei He, Haohan Zhao, Wei Shao, Yanlin Qi, Yinya Huang, Aojun Zhou, Yuxuan Yao, Zongpeng Li, Yuanzhang Xiao, et al. Recranker: Instruction tuning large language model as ranker for top-k recommendation. ACM Transactions on Information Systems, 2024.
Meng et al. (2024) Yu Meng, Mengzhou Xia, and Danqi Chen. Simpo: Simple preference optimization with a reference-free reward. Advances in Neural Information Processing Systems, 37:124198–124235, 2024.
Ouyang et al. (2022) Long Ouyang, Jeffrey Wu, Xu Jiang, Diogo Almeida, Carroll Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, et al. Training language models to follow instructions with human feedback. Advances in neural information processing systems, 35:27730–27744, 2022.
Plackett (1975) Robin L Plackett. The analysis of permutations. Journal of the Royal Statistical Society Series C: Applied Statistics, 24(2):193–202, 1975.
Pradeep et al. (2023) Ronak Pradeep, Sahel Sharifymoghaddam, and Jimmy Lin. Rankvicuna: Zero-shot listwise document reranking with open-source large language models, 2023. URL https://arxiv.org/abs/2309.15088.
Rafailov et al. (2023) Rafael Rafailov, Archit Sharma, Eric Mitchell, Christopher D Manning, Stefano Ermon, and Chelsea Finn. Direct preference optimization: Your language model is secretly a reward model. Advances in Neural Information Processing Systems, 36:53728–53741, 2023.
Robert et al. (1999) Christian P Robert, George Casella, and George Casella. Monte Carlo statistical methods, volume 2. Springer, 1999.
Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.
Shao et al. (2024) Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Xiao Bi, Haowei Zhang, Mingchuan Zhang, YK Li, Yang Wu, et al. Deepseekmath: Pushing the limits of mathematical reasoning in open language models. arXiv preprint arXiv:2402.03300, 2024.
Shapiro (2003) Alexander Shapiro. Monte carlo sampling methods. Handbooks in operations research and management science, 10:353–425, 2003.
Shen et al. (2024) Tao Shen, Guodong Long, Xiubo Geng, Chongyang Tao, Yibin Lei, Tianyi Zhou, Michael Blumenstein, and Daxin Jiang. Retrieval-augmented retrieval: Large language models are strong zero-shot retriever. In Lun-Wei Ku, Andre Martins, and Vivek Srikumar (eds.), Findings of the Association for Computational Linguistics: ACL 2024, pp. 15933–15946, Bangkok, Thailand, August 2024. Association for Computational Linguistics. doi: 10.18653/v1/2024.findings-acl.943. URL https://aclanthology.org/2024.findings-acl.943/.
Stiennon et al. (2020) Nisan Stiennon, Long Ouyang, Jeff Wu, Daniel M. Ziegler, Ryan Lowe, Chelsea Voss, Alec Radford, Dario Amodei, and Paul Christiano. Learning to summarize from human feedback. In Proceedings of the 34th International Conference on Neural Information Processing Systems, NIPS ’20, Red Hook, NY, USA, 2020. Curran Associates Inc. ISBN 9781713829546.
Surana et al. (2025) Rohan Surana, Junda Wu, Zhouhang Xie, Yu Xia, Harald Steck, Dawen Liang, Nathan Kallus, and Julian McAuley. From reviews to dialogues: Active synthesis for zero-shot llm-based conversational recommender system. arXiv preprint arXiv:2504.15476, 2025.
Sutton et al. (1999) Richard S Sutton, David McAllester, Satinder Singh, and Yishay Mansour. Policy gradient methods for reinforcement learning with function approximation. Advances in neural information processing systems, 12, 1999.
Talmor et al. (2019) Alon Talmor, Jonathan Herzig, Nicholas Lourie, and Jonathan Berant. CommonsenseQA: A question answering challenge targeting commonsense knowledge. In Jill Burstein, Christy Doran, and Thamar Solorio (eds.), Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pp. 4149–4158, Minneapolis, Minnesota, June 2019. Association for Computational Linguistics. doi: 10.18653/v1/N19-1421. URL https://aclanthology.org/N19-1421/.
Team et al. (2024) Gemma Team, Morgane Riviere, Shreya Pathak, Pier Giuseppe Sessa, Cassidy Hardin, Surya Bhupatiraju, Léonard Hussenot, Thomas Mesnard, Bobak Shahriari, Alexandre Ramé, et al. Gemma 2: Improving open language models at a practical size. arXiv preprint arXiv:2408.00118, 2024.
Trivedi et al. (2022) Harsh Trivedi, Niranjan Balasubramanian, Tushar Khot, and Ashish Sabharwal. MuSiQue: Multihop questions via single-hop question composition. Transactions of the Association for Computational Linguistics, 10:539–554, 2022. doi: 10.1162/tacl˙a˙00475. URL https://aclanthology.org/2022.tacl-1.31/.
Valizadegan et al. (2009) Hamed Valizadegan, Rong Jin, Ruofei Zhang, and Jianchang Mao. Learning to rank by optimizing ndcg measure. Advances in neural information processing systems, 22, 2009.
Wu et al. (2021) Junda Wu, Canzhe Zhao, Tong Yu, Jingyang Li, and Shuai Li. Clustering of conversational bandits for user preference learning and elicitation. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, pp. 2129–2139, 2021.
Wu et al. (2024a) Junda Wu, Cheng-Chun Chang, Tong Yu, Zhankui He, Jianing Wang, Yupeng Hou, and Julian McAuley. Coral: collaborative retrieval-augmented large language models improve long-tail recommendation. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, pp. 3391–3401, 2024a.
Wu et al. (2025) Junda Wu, Yuxin Xiong, Xintong Li, Zhengmian Hu, Tong Yu, Rui Wang, Xiang Chen, Jingbo Shang, and Julian McAuley. Ctrls: Chain-of-thought reasoning via latent state-transition. arXiv preprint arXiv:2507.08182, 2025.
Wu et al. (2024b) Junkang Wu, Yuexiang Xie, Zhengyi Yang, Jiancan Wu, Jinyang Gao, Bolin Ding, Xiang Wang, and Xiangnan He. $\beta$ -dpo: Direct preference optimization with dynamic $\beta$ . Advances in Neural Information Processing Systems, 37:129944–129966, 2024b.
Wu et al. (2024c) Likang Wu, Zhi Zheng, Zhaopeng Qiu, Hao Wang, Hongchao Gu, Tingjia Shen, Chuan Qin, Chen Zhu, Hengshu Zhu, Qi Liu, Hui Xiong, and Enhong Chen. A survey on large language models for recommendation, 2024c. URL https://arxiv.org/abs/2305.19860.
Xia et al. (2025) Yu Xia, Junda Wu, Sungchul Kim, Tong Yu, Ryan A. Rossi, Haoliang Wang, and Julian McAuley. Knowledge-aware query expansion with large language models for textual and relational retrieval, 2025. URL https://arxiv.org/abs/2410.13765.
Xie et al. (2024) Zhouhang Xie, Junda Wu, Hyunsik Jeon, Zhankui He, Harald Steck, Rahul Jha, Dawen Liang, Nathan Kallus, and Julian Mcauley. Neighborhood-based collaborative filtering for conversational recommendation. In Proceedings of the 18th ACM Conference on Recommender Systems, RecSys ’24, pp. 1045–1050, New York, NY, USA, 2024. Association for Computing Machinery. ISBN 9798400705052. doi: 10.1145/3640457.3688191. URL https://doi.org/10.1145/3640457.3688191.
Xie et al. (2025) Zhouhang Xie, Junda Wu, Yiran Shen, Yu Xia, Xintong Li, Aaron Chang, Ryan Rossi, Sachin Kumar, Bodhisattwa Prasad Majumder, Jingbo Shang, et al. A survey on personalized and pluralistic preference alignment in large language models. arXiv preprint arXiv:2504.07070, 2025.
Yang & Chen (2024) Ting Yang and Li Chen. Unleashing the retrieval potential of large language models in conversational recommender systems. In Proceedings of the 18th ACM Conference on Recommender Systems, pp. 43–52, 2024.
Yang et al. (2018) Zhilin Yang, Peng Qi, Saizheng Zhang, Yoshua Bengio, William Cohen, Ruslan Salakhutdinov, and Christopher D. Manning. HotpotQA: A dataset for diverse, explainable multi-hop question answering. In Ellen Riloff, David Chiang, Julia Hockenmaier, and Jun’ichi Tsujii (eds.), Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pp. 2369–2380, Brussels, Belgium, October-November 2018. Association for Computational Linguistics. doi: 10.18653/v1/D18-1259. URL https://aclanthology.org/D18-1259/.
Yao et al. (2024) Binwei Yao, Zefan Cai, Yun-Shiuan Chuang, Shanglin Yang, Ming Jiang, Diyi Yang, and Junjie Hu. No preference left behind: Group distributional preference optimization. arXiv preprint arXiv:2412.20299, 2024.
Zhang et al. (2024) Zhehao Zhang, Ryan A Rossi, Branislav Kveton, Yijia Shao, Diyi Yang, Hamed Zamani, Franck Dernoncourt, Joe Barrow, Tong Yu, Sungchul Kim, et al. Personalization of large language models: A survey. arXiv preprint arXiv:2411.00027, 2024.
Zhao et al. (2024) Yang Zhao, Yixin Wang, and Mingzhang Yin. Ordinal preference optimization: Aligning human preferences via ndcg. arXiv preprint arXiv:2410.04346, 2024.
Zhou et al. (2024) Jiacong Zhou, Xianyun Wang, and Jun Yu. Optimizing preference alignment with differentiable ndcg ranking. arXiv preprint arXiv:2410.18127, 2024.
Zhu et al. (2024) Banghua Zhu, Michael I Jordan, and Jiantao Jiao. Iterative data smoothing: Mitigating reward overfitting and overoptimization in rlhf. arXiv preprint arXiv:2401.16335, 2024.
Zhuang et al. (2023) Honglei Zhuang, Zhen Qin, Kai Hui, Junru Wu, Le Yan, Xuanhui Wang, and Michael Bendersky. Beyond yes and no: Improving zero-shot llm rankers via scoring fine-grained relevance labels. arXiv preprint arXiv:2310.14122, 2023.

Appendix A Experimental Details

A.1 Implementation Details

We validate the effectiveness of IRPO against baseline methods using three popular pre-trained LLMs: Llama3.2-3B-Instruct (Grattafiori et al., 2024), a 3B-parameter model pretrained on 9 trillion tokens; Gemma2-2B-it (Team et al., 2024), a 2B-parameter model pre-trained on 2 trillion tokens; and Phi-3-mini-4k-instruct (Abdin et al., 2024), a 3.8 B-parameter model pre-trained on synthetic and publicly available data, featuring a 4K-token context length.

We used DPO’s codebase for implementing both our SFT and DPO baseline experiments. For S-DPO, we used the original codebase. For IRPO, we implemented our experiments using PyTorch and trained all models using NVIDIA A6000 GPUs. We set the KL penalty coefficient $\beta$ to 1.0.

A.2 Run-time Comparison

IRPO directly aligns LLMs to generate an entire ranked list in a single forward pass, whereas the other baselines require multiple forward passes to calculate pairwise margins. Consequently, IRPO significantly reduces inference time. To illustrate this advantage clearly, we report the average per-sample runtime measured under consistent evaluation settings. Table 4 summarizes these results.

Method	Run Time (per sample)
Base	0.1140 s
DPO	0.1145 s
SDPO	0.1144 s
LiPO	0.1154 s
IRPO	0.0313 s

Table 4: Run-time comparison of IRPO and baselines (average per-sample runtime).

Due to its single-pass architecture, IRPO achieves approximately a $4\times$ speedup in runtime per sample compared to other approaches.

A.3 Evaluation Details

Conversational Recommendation

Inspired (Hayati et al., 2020), containing 1,028 dialogues split into 730 training and 88 evaluation samples, and Redial (Li et al., 2018), which consists of 10,264 dialogues, divided into 8,945 training and 1,319 evaluation samples. 3 ground truth movies from logged human feedback ranked by popularity in the individual dataset; 5 GPT-generated movies produced by GPT-3.5 given the same context; and 12 randomly sampled movies sampled from a frequency-based distribution derived from the training corpus.

Generative Retrieval

HotpotQA contains approximately 23K challenging multi-hop questions, split into 15,661 for training and 7,405 for evaluation, while MuSiQue provides 22,355 questions, divided into 19,938 training and 2,417 evaluation samples. Each question is associated with supporting sentences labeled as relevant contexts and an additional set of 8 randomly sampled distractor sentences from the same document collection. This typically results in 10–12 candidate paragraphs per query. To ensure context fits within the LLM’s context window, we truncate each supporting paragraph to 50 tokens. Each question is associated with supporting sentences labeled as relevant contexts and an additional set of 8 randomly sampled distractor sentences from the same document collection.

Question-answering as Re-ranking

ARC (Clark et al., 2018), comprising 1,418 challenging science-based reasoning questions (1,119 for training and 299 for evaluation), and CommonsenseQA (Talmor et al., 2019), consisting of 10,962 commonsense reasoning questions (9,741 training and 1,221 evaluation). Originally, ARC presents four answer choices per question, while CommonsenseQA includes five. Specifically, we augment ARC questions with six additional distractors and CommonsenseQA questions with five. To evaluate LLMs re-ranking capabilities, we augment each dataset by introducing additional semantically similar but incorrect answers, increasing task complexity, resulting in a uniform set of $10$ candidates per question.

Appendix B Extending to Other Ranking Metrics

Our formulation naturally supports many other ranking metrics, such as P@K, MRR, MAP, and eDCG (from easiest to hardest in terms of optimization). P@K and MRR are simpler compared to the others due to their binary reciprocal structure, making them easier to optimize. MAP is more complex as it requires normalization, making optimization more difficult. NDCG and eDCG are the most complex as they have non-linear gradients due to their position-based and relevance-based weighting, leading to more complex updates.

Precision@k (P@k) is binary defined based on whether the item at rank $i$ is relevant within the top $k$ positions:

w(i)=\mathbb{I}(y_{\tau(i)}\geq 1),\quad\text{for}\ i\in\{1,2,\dots,k\},

where $\mathbb{I}(y_{\tau(i)}\geq 1)$ is an indicator function returning $1$ if relevant, and 0 otherwise.

Mean Average Precision (MAP) is the precision at each rank normalized by the total relevant items:

w(i)=\frac{2^{y_{\tau(i)}}-1}{\sum_{i=1}^{n}\mathbb{I}(y_{\tau(i)}\geq 1)}

Mean Reciprocal Rank (MRR) is based on the reciprocal rank of the first relevant item

w(i)=\frac{1}{\max(r_{\tau(i)},1)},\quad\text{for}\ y_{\tau(i)}\geq 1

The Exponential Discounted Cumulative Gain (eDCG) combines both relevance of an item and an exponential positional discount:

w(i)=\frac{2^{y_{\tau(i)}}-1}{\exp(\lambda\cdot i)}

where $\lambda$ controls exponential decay with regards to rank.

Appendix C Derivation of the gradient of IRPO

In this section, we provide a detailed derivation of the gradient of the IRPO objective with respect to the model parameters $\theta$ . Starting from the IRPO objective in Equation equation 7, we compute the gradient that forms the basis for our optimization process.

C.1 IRPO Objective

Recall that our IRPO objective is defined as:

	$\displaystyle\mathcal{L}_{\text{R-DPO}}(\pi_{\theta};\pi_{\text{ref}})$	$\displaystyle=-\mathbb{E}_{(x,\bm{y})}\Biggl{[}\sum_{i=1}^{n}w(i)\cdot\log\sigma(z_{i})\Biggr{]}$
	$\displaystyle w(i)$	$\displaystyle=\frac{2^{y_{\tau(i)}}-1}{\log_{2}(1+i)}$
	$\displaystyle z_{i}$	$\displaystyle=-\log\sum_{j=1}^{n}\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}$

C.2 Computing the Gradient

We compute the gradient of the IRPO objective with respect to the model parameters $\theta$ :

\displaystyle\nabla_{\theta}\mathcal{L}_{\text{R-DPO}}(\pi_{\theta};\pi_{\text{ref}})

\displaystyle=-\mathbb{E}_{(x,\bm{y})}\Biggl{[}\sum_{i=1}^{n}w(i)\cdot\nabla_{\theta}\log\sigma(z_{i})\Biggr{]}

Using the chain rule and properties of the sigmoid function, we can express the gradient of $\log\sigma(z_{i})$ as:

	$\displaystyle\nabla_{\theta}\log\sigma(z_{i})$	$\displaystyle=\frac{1}{\sigma(z_{i})}\cdot\nabla_{\theta}\sigma(z_{i})$
		$\displaystyle=\frac{1}{\sigma(z_{i})}\cdot\sigma(z_{i})\cdot(1-\sigma(z_{i}))\cdot\nabla_{\theta}z_{i}$
		$\displaystyle=(1-\sigma(z_{i}))\cdot\nabla_{\theta}z_{i}$

Since $1-\sigma(z_{i})=\sigma(-z_{i})$ , we have:

\displaystyle\nabla_{\theta}\log\sigma(z_{i})

\displaystyle=\sigma(-z_{i})\cdot\nabla_{\theta}z_{i}

C.3 Gradient of $z_{i}$

Next, we compute the gradient of $z_{i}$ :

	$\displaystyle\nabla_{\theta}z_{i}$	$\displaystyle=\nabla_{\theta}\left(-\log\sum_{j=1}^{n}\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}\right)$
		$\displaystyle=-\nabla_{\theta}\log\left(\sum_{j=1}^{n}\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}\right)$

Let us define:

	$\displaystyle\delta_{ij}$	$\displaystyle=\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}$
	$\displaystyle S_{i}$	$\displaystyle=\sum_{j=1}^{n}\exp(\beta\delta_{ij})$

Therefore, $z_{i}=-\log S_{i}$ and:

	$\displaystyle\nabla_{\theta}z_{i}$	$\displaystyle=-\nabla_{\theta}\log S_{i}$
		$\displaystyle=-\frac{1}{S_{i}}\nabla_{\theta}S_{i}$
		$\displaystyle=-\frac{1}{S_{i}}\nabla_{\theta}\left(\sum_{j=1}^{n}\exp(\beta\delta_{ij})\right)$
		$\displaystyle=-\frac{1}{S_{i}}\sum_{j=1}^{n}\nabla_{\theta}\exp(\beta\delta_{ij})$
		$\displaystyle=-\frac{1}{S_{i}}\sum_{j=1}^{n}\exp(\beta\delta_{ij})\cdot\beta\cdot\nabla_{\theta}\delta_{ij}$

C.4 Gradient of $\delta_{ij}$

Now we compute the gradient of $\delta_{ij}$ :

	$\displaystyle\nabla_{\theta}\delta_{ij}$	$\displaystyle=\nabla_{\theta}\left(\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\right)$
		$\displaystyle=\nabla_{\theta}\log\pi_{\theta}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\text{ref}}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\theta}(e_{\tau(i)}\mid x)+\nabla_{\theta}\log\pi_{\text{ref}}(e_{\tau(i)}\mid x)$

Since $\pi_{\text{ref}}$ does not depend on $\theta$ , $\nabla_{\theta}\log\pi_{\text{ref}}(e_{j}\mid x)=0$ and $\nabla_{\theta}\log\pi_{\text{ref}}(e_{\tau(i)}\mid x)=0$ . Therefore:

	$\displaystyle\nabla_{\theta}\delta_{ij}$	$\displaystyle=\nabla_{\theta}\log\pi_{\theta}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\theta}(e_{\tau(i)}\mid x)$
		$\displaystyle=\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}$

C.5 Importance Weights and Final Gradient

Substituting the gradient of $\delta_{ij}$ back into the gradient of $z_{i}$ :

\displaystyle\nabla_{\theta}z_{i}

\displaystyle=-\frac{1}{S_{i}}\sum_{j=1}^{n}\exp(\beta\delta_{ij})\cdot\beta\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}

Defining the importance weights $\rho_{ij}$ :

	$\displaystyle\rho_{ij}$	$\displaystyle=\frac{\exp(\beta\delta_{ij})}{S_{i}}$
		$\displaystyle=\frac{\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\text{ref}}(e_{j}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}}{\sum_{k=1}^{n}\exp\!\Bigl{(}\beta\Bigl{[}\log\frac{\pi_{\theta}(e_{k}\mid x)}{\pi_{\text{ref}}(e_{k}\mid x)}-\log\frac{\pi_{\theta}(e_{\tau(i)}\mid x)}{\pi_{\text{ref}}(e_{\tau(i)}\mid x)}\Bigr{]}\Bigr{)}}$

We can now express the gradient of $z_{i}$ as:

\displaystyle\nabla_{\theta}z_{i}

\displaystyle=-\beta\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}

Substituting this into the gradient of $\log\sigma(z_{i})$ :

	$\displaystyle\nabla_{\theta}\log\sigma(z_{i})$	$\displaystyle=\sigma(-z_{i})\cdot(-\beta)\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}$
		$\displaystyle=-\beta\sigma(-z_{i})\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}$

Finally, substituting into the gradient of the IRPO objective:

	$\displaystyle\nabla_{\theta}\mathcal{L}_{\text{R-DPO}}(\pi_{\theta};\pi_{\text{ref}})$	$\displaystyle=-\mathbb{E}_{(x,\bm{y})}\Biggl{[}\sum_{i=1}^{n}w(i)\cdot\nabla_{\theta}\log\sigma(z_{i})\Biggr{]}$
		$\displaystyle=-\mathbb{E}_{(x,\bm{y})}\Biggl{[}\sum_{i=1}^{n}w(i)\cdot\Bigl{(}-\beta\sigma(-z_{i})\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}\Bigr{)}\Biggr{]}$
		$\displaystyle=\beta\mathbb{E}_{(x,\bm{y})}\Biggl{[}\sum_{i=1}^{n}w(i)\sigma(-z_{i})\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}\Biggr{]}$

Appendix D Mean Analysis

Lemma 4.1

Let $\hat{g}(e_{j})$ be defined as in equation 11. Each $e_{j}$ is sampled from $e$ with the probability of $\rho_{i,j}=p(e_{j})$ , at position $i$ in the ranking list. Then $\mathbb{E}\left[\hat{g}(e_{j})\right]=g$ in equation 12.

Proof. Following , we derive the proof by a sequence of identities.

	$\displaystyle\mathbb{E}\Bigl{[}\hat{g}(e_{j})\Bigr{]}$	$\displaystyle=\mathbb{E}_{e_{j}\sim\bm{e}}\Bigl{[}\hat{g}(e_{j})\Bigr{]}$
		$\displaystyle=\mathbb{E}_{e_{j}\sim\bm{e}}\Bigl{[}\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}\Bigr{]}$
		$\displaystyle=\sum_{j=1}^{n}\rho_{ij}\cdot\nabla_{\theta}\log\frac{\pi_{\theta}(e_{j}\mid x)}{\pi_{\theta}(e_{\tau(i)}\mid x)}=g.$

Appendix E Variance Analysis

Lemma 4.2

With the assumption of $L=\max_{j}{[\nabla_{\theta}\log\pi_{\theta}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\theta}(e_{\tau(i)}\mid x)]}$ , we derive the expected absolute deviation of the gradient estimation $\mathbb{E}[|\hat{g}(e_{j})-g|]$ .

Proof. By Cauchy-Schwartz inequality , we have

\mathbb{E}[|\hat{g}(e_{j})-g|]\leq\sqrt{\mathbb{E}\Bigl{[}(\hat{g}(e_{j})-g)^{2}\Bigr{]}}.

Consider the variance of the estimator, $\operatorname{Var}\bigl{(}\hat{g}(e_{j})\bigr{)}=\mathbb{E}\Bigl{[}(\hat{g}(e_{j})-g)^{2}\Bigr{]}$ . We sample according to the importance weights $p(e_{j})=\rho_{ij}$ . Following standard importance sampling (Robert et al., 1999; Shapiro, 2003), we further obtain the estimation upper bound by a factor proportional to the maximum importance weight,

\operatorname{Var}\bigl{(}\hat{g}(e_{j})\bigr{)}\leq\frac{\|\rho_{i,j}\|_{\infty}}{n}\,\mathbb{E}\Bigl{[}\|z(e_{j})\|^{2}\Bigr{]},

where $z(e_{j})=\nabla_{\theta}\log\pi_{\theta}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\theta}(e_{\tau(i)}\mid x)$ , and the variance is reduced by the factor of $n$ independent samples. Substituting the variance bound into the expected absolute deviation, we have

\mathbb{E}[|\hat{g}(e_{j})-g|]\leq\sqrt{\frac{\|\rho_{i,j}\|_{\infty}}{n}\,\mathbb{E}\Bigl{[}\|z(e_{j})\|^{2}\Bigr{]}}.

With the assumption of bounded gradient difference $L=\max_{j}{[\nabla_{\theta}\log\pi_{\theta}(e_{j}\mid x)-\nabla_{\theta}\log\pi_{\theta}(e_{\tau(i)}\mid x)]}$ , which in practice is achieved by gradient clipping (Ouyang et al., 2022; Schulman et al., 2017), we achieve the final bound as

\mathbb{E}[|\hat{g}(e_{j})-g|]\leq\sqrt{\frac{\|\rho_{i,j}\|_{\infty}}{n}\,L^{2}}=L\sqrt{\frac{\|\rho_{i,j}\|_{\infty}}{n}}.

Appendix F Additional Results

F.1 Ablation Study Results

We compare these variants using the Llama3 backbone across three benchmarks, representing each task category: Inspired (conversational recommendation), MusiQue (generative retrieval), and ARC (question-answering re-ranking).

We provide detailed ablation results in Table 5–7, evaluating alternative positional weighting schemes across three benchmark tasks.

Method	N@1	N@5	N@10	R@1	R@5	R@10
IRPO	45.3	55.2	62.3	22.4	68.8	87.2
IRPO (abl1)	35.0	37.9	48.5	18.9	46.0	72.9
IRPO (abl2)	43.8	49.2	58.8	21.0	58.9	83.1

Table 5: Ablation results on the Inspired dataset.

Method	N@1	N@3	N@5	R@1	R@3	R@5
IRPO	65.1	59.4	69.4	27.6	59.2	78.0
IRPO (abl1)	50.9	54.0	65.8	21.0	56.9	78.9
IRPO (abl2)	68.3	62.8	72.7	29.0	62.9	81.5

Table 6: Ablation results on the MuSiQue dataset.

Method	N@1	N@3	N@5	R@1	R@3	R@5
IRPO	27.4	38.9	46.5	27.4	47.6	66.3
IRPO (abl1)	9.4	17.2	23.4	9.4	22.9	38.2
IRPO (abl2)	27.1	37.8	46.1	27.1	45.8	66.3

Table 7: Ablation results on the ARC dataset.

F.2 Comparision with LiPO (LTR)

We report detailed comparisons between IRPO and LiPO on the ARC and MuSiQue datasets. Tables 8 and 9 present results for both LLaMA3 and Gemma2 backbones, demonstrating IRPO’s consistent advantage.

Model	Method	N@1	N@3	N@5	R@1	R@3	R@5
LLaMA3	Base	13.2	21.7	28.6	13.2	28.4	44.9
	SFT	13.5	21.4	28.4	13.5	27.7	44.6
	SDPO	23.4	28.3	35.4	23.4	32.5	50.0
	LiPO	35.2	39.8	45.5	35.2	43.7	57.7
	IRPO	27.4	38.9	46.5	27.4	47.6	66.3
Gemma2	Base	27.4	35.6	42.1	27.4	42.6	58.4
	SFT	23.6	32.9	39.3	23.6	40.2	55.7
	SDPO	28.7	36.5	42.6	28.7	43.0	58.0
	LiPO	23.2	30.5	37.6	23.2	36.0	53.5
	IRPO	27.0	45.5	53.3	27.0	59.8	78.7

Table 8: Performance comparison on ARC.

Model	Method	N@1	N@3	N@5	R@1	R@3	R@5
LLaMA3	Base	42.5	43.5	51.9	18.8	44.9	60.7
	SFT	36.9	39.1	48.0	16.6	40.7	57.6
	SDPO	58.6	60.8	66.7	26.0	62.3	73.3
	LiPO	47.4	49.6	57.1	20.9	51.1	65.2
	IRPO	65.1	59.4	69.4	27.6	59.2	78.0
Gemma2	Base	40.9	42.8	51.1	17.9	44.3	59.9
	SFT	39.8	43.3	51.7	17.2	45.3	61.3
	SDPO	40.6	42.3	50.6	17.9	43.7	59.4
	LiPO	49.8	51.8	58.9	22.3	53.2	66.7
	IRPO	55.4	51.0	61.1	23.8	51.6	70.6

Table 9: Performance comparison on MuSiQue.