In-Field Critical Current of Type-II Superconductors Caused by Strain from Nanoscale Columnar Inclusions

Introduction. The ongoing development of thin films of superconducting YBa₂Cu₃O_7-δ (YBCO) for wire technology has resulted in world-record high critical currents.review In external magnetic field, the critical current is considerably enhanced by nano-rod inclusions that are aligned in parallel to the crystalline $c$ axis.bzo ^,goyal ^,bso_07 ^,mele08 The enhancement is strongest at orientations of the magnetic field parallel to the $c$ axis. Understanding the fundamental physics behind this effect remains a challenge. It is also unknown what drives the growth of nanorods in the first place in YBCO films.

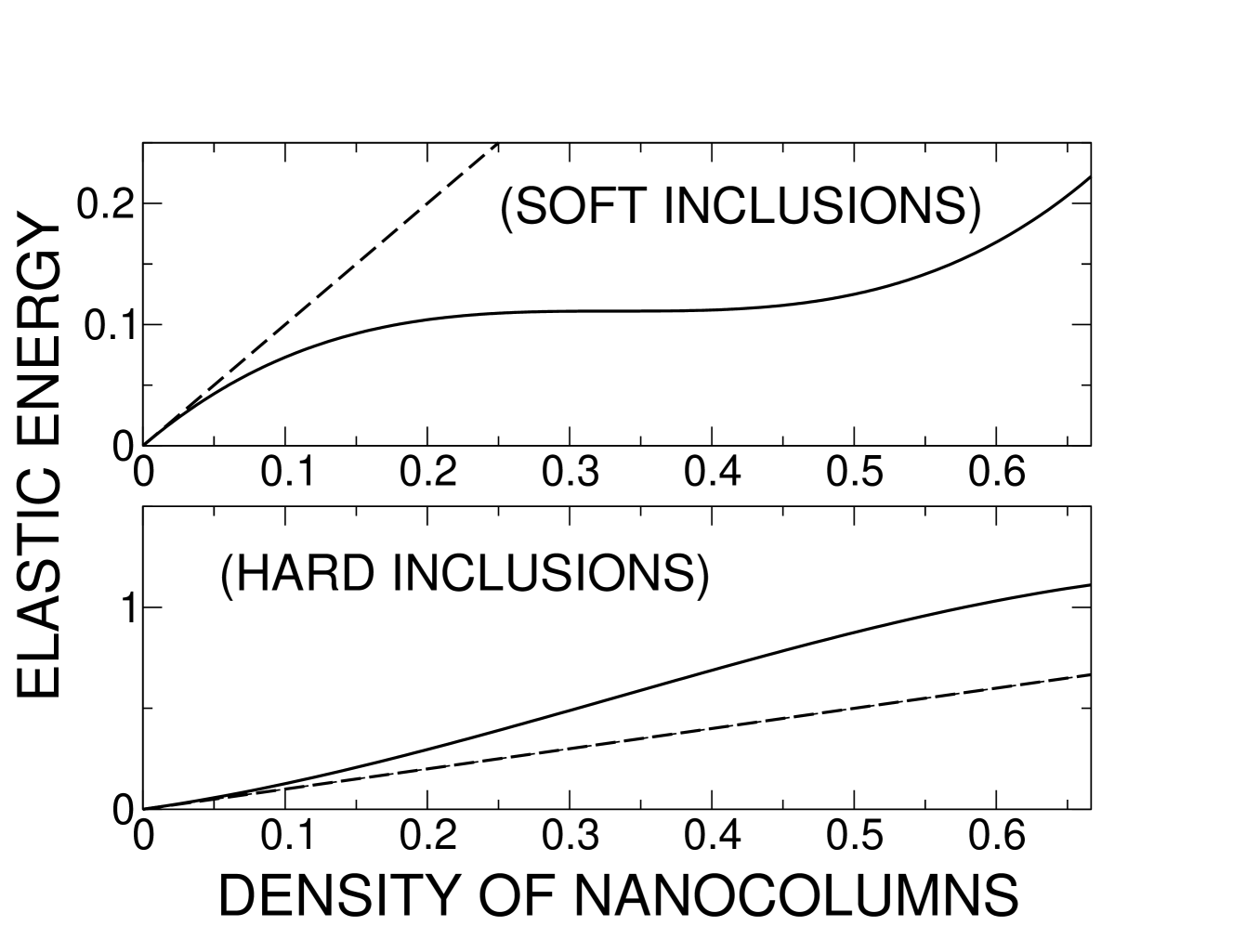
In this paper, we provide insight into both of these questions by computing the strain field due to nano-rod inclusions that thread a YBCO superconductor along the $c$ axis. The lattice constant of inclusions that optimize the critical current is typically 8% larger than that of the YBCO matrix in the $a$-$b$ plane. Assuming a coherent phase boundary between the inclusion and a given epitaxial layer of YBCO, a linear elasticity analysis yields that the nanocolumn is compressed axially, while the YBCO matrix is squeezed by pure shear about the nanocolumn. The critical temperature in optimally doped YBCO is known to couple strongly to pure shear in the $a$-$b$ plane.welp In applied magnetic field, we show theoretically how this experimental fact results in substantial collective pinning of the vortex lattice by the phase boundary separating the nano-column inclusion from the YBCO matrix.jpr-maley ^,jpr07 Also, the elastic energy shows weak metastability at a high density of nanocolumns when the nanocolumn is soft compared to the YBCO layer (see Fig. 1). We believe that this drives epitaxial growth of nano-rod inclusions in YBCO films.

Two-Dimensional Elasticity Theory. We shall determine first the elastic strain and the elastic energy cost due to a single nano-rod inclusion that threads a film of YBCO along the $c$ axis. Such nanorods are typically composed either of BaZrO₃ (BZO)bzo ^,goyal or of BaSnO₃ (BSO).bso_07 Both are cubic perovskites, with lattice constants ($a_{\rm in}$) that exceed that of the $a$-$b$ plane in YBCO, $a_{\rm out}=3.86\,{\rm\AA }$, by 9% and by 7% respectively.bzo ^,goyal ^,bso_07 Let us temporarily ignore the effect of the lattice mismatch along the $c$ axis by considering only epitaxial layers that are far from any possible partial misfit dislocation, and that therefore present a coherent phase boundary between the inclusion and the YBCO matrix. Such partial misfit dislocations are accompanied by stacking faults,book a topic which will be discussed later in the concluding section. The assumption of a coherent phase boundary is valid for a nano-rod inclusion of diameter less than the distance between possible misfit dislocations,book $a_{\rm Moire}=(a_{\rm out}^{-1}-a_{\rm in}^{-1})^{-1}$. BZO nanorods typically have a diameter ofgoyal $2{\rm-}3\,{\rm nm}$, which satisfies the bound $a_{\rm Moire}=5\,{\rm nm}$. BSO nanocolumns, on the other hand, typically have a diameter ofbso_07 $7{\rm-}8\,{\rm nm}$. It exceeds $a_{\rm Moire}=6\,{\rm nm}$, although not by much.

Consider then a cylindrical nano-column inclusion that presents a coherent phase boundary with a given epitaxial layer of the YBCO matrix. Unit cells match up one-to-one across the phase boundary in such case. The ideal axial symmetry, assumed here for simplicity, implies a radial displacement field, ${\bf u}({\bf r})=u(r){\bf\hat{r}}$. We then have the boundary condition

between the displacement fields of the nanocolumn (in) and of the YBCO layer (out) at the phase boundary. The in-plane lattice mismatch that it represents generates elastic strain in both the inclusion and in the YBCO matrix. The elastic energy due to a 2D strain field is given by the integralbook

over the corresponding area (prime), which is confined to $r<r_{\rm in}$ for the nanocolumn and to $r>r_{\rm out}$ for the YBCO matrix. Here, $c_{\parallel}$ and $c_{\perp}$ are the 2D bulk compression modulus and the 2D shear modulus, respectively. A useful identity for the pure shear component above reads

The strain tensor takes the form ${\boldmath\nabla}{\bf u}=(du/dr){\bf\hat{r}}\,{\bf\hat{r}}+(u/r){\boldmath\hat{\phi}}\,{\boldmath\hat{\phi}}$ in the present axially symmetric case. It combined with Eq. (3) results in the compact expression for the elastic energy, $E_{\rm 2D}=\int d^{2}r\{{1\over 2}c_{\parallel}[r^{-1}d(ru)/dr]^{2}+{1\over 2}c_{\perp}[r\,d(r^{-1}u)/dr]^{2}\}$. Calculus of variations then yields a nano-column inclusion squeezed by pure compression and a surrounding YBCO matrix squeezed by pure shear:

with corresponding strain tensors

The total elastic energy (2) generated by the nano-column inclusion is then $E_{\rm 2D}^{(1)}=2c_{\parallel}^{({\rm in})}\pi r_{\rm in}^{2}A_{0}^{2}+2c_{\perp}^{({\rm out})}\pi r_{\rm out}^{2}B_{0}^{2}$. Minimizing it with respect to the constants $A_{0}$ and $B_{0}$ while enforcing the boundary condition (1) yields optimal values $r_{\rm in}A_{0}=(\Delta r)c_{\perp}^{({\rm out})}/(c_{\parallel}^{({\rm in})}+c_{\perp}^{({\rm out})})$ and $r_{\rm out}B_{0}=(\Delta r)c_{\parallel}^{({\rm in})}/(c_{\parallel}^{({\rm in})}+c_{\perp}^{({\rm out})})$. Here $\Delta r=r_{\rm in}-r_{\rm out}$. These then yield an elastic energy cost

for the nano-column inclusion, which has an equilibrium radius $r_{\rm out}+u_{\rm out}(r_{\rm out})$ given by $r_{0}=(c_{\parallel}^{({\rm in})}r_{\rm in}+c_{\perp}^{({\rm out})}r_{\rm out})/(c_{\parallel}^{({\rm in})}+c_{\perp}^{({\rm out})})$.

Consider next a field of many cylindrical nano-column inclusions of radius $r_{0}$ centered at transverse locations $\{{\bf R}_{n}\}$. Suppose again that they all present a coherent phase boundary with a given epitaxial layer of the YBCO matrix. The displacement field is then a linear superposition of those generated by a single nano-column inclusion (4):

inside the $i^{\rm th}$ nanocolumn, and

inside the YBCO matrix. The pure shear terms that have been added to the pure compression inside of a nanocolumn (7) are required by the boundary condition (1). Observe now, by Eq. (5), that $\nabla^{2}{\bf u}_{\parallel}=0=\nabla^{2}{\bf u}_{\perp}$. Inspection of the elastic energy functional (2) combined with the identity (3) then yields that the above superpositions are stationary because ${\boldmath\nabla}\cdot{\bf u}_{\perp}$, ${\boldmath\nabla}\times{\bf u}_{\parallel}$ and ${\boldmath\nabla}\times{\bf u}_{\perp}$ all vanish. Indeed, the elastic energy cost reduces to a sum of surface integrals around the phase boundaries of the form $E_{\rm 2D}=\sum_{i}E_{\rm 2D}^{(1)}+\sum_{i}\sum_{j}^{\prime}[e_{i,j,i}({\rm out})+e_{i,i,j}({\rm out})]+\sum_{i}\sum_{j,k}^{\prime}[e_{i,j,k}({\rm in})+e_{i,j,k}({\rm out})]$, where the indices $j$ and $k$ refer to the terms in the superpositions (7) and (8), and where the index $i$ refers to the phase boundary. The prime notation over the summation symbols indicates that $i\neq j,k$. Each individual contribution $e_{i,j,k}$ is given by a surface integral around the circle $S_{i}$ of radius $r_{\rm out}$ that is centered at ${\bf R}_{i}$: $e_{i,j,k}(X)={\rm sgn}(X)\,c_{\perp}^{(X)}I_{i,j,k}$, with

Here, ${\rm sgn}({\rm in})=+1$ and ${\rm sgn}({\rm out})=-1$. Also, the measure $d{\bf a}$ on the circle $S_{i}$ points radially outward. Substituting in the strain fields (5) above yields ultimately that $e_{i,j,i}=0=e_{i,i,j}$, and that

for $i\neq j,k$. (See Appendix.) Here, ${\bf R}_{i,j}={\bf R}_{i}-{\bf R}_{j}$, and $\phi_{j,k}(i)$ denotes the angle between the vectors ${\bf R}_{i,j}$ and ${\bf R}_{i,k}$. The 2D elastic energy then is composed of a sum of 1-body , 2-body ($j=k$) and 3-body terms ($j\neq k$), $E_{\rm 2D}=\sum_{i}E_{\rm 2D}^{(1)}+\sum_{i}\sum_{j,k}^{\prime}V_{i,j,k}$, with the interaction energy given by

Notice that $V_{i,j,k}$ changes sign as a function of the relative rigidity between the nano-column inclusion and the YBCO matrix.

The elastic energy will now be obtained by computing subsequent self-energy corrections to the 2-body interaction and to the 1-body line tension. Let’s first fix the coordinate for the phase boundary above, ${\bf R}_{i}$, as well as one of the nanocolumn coordinates above, ${\bf R}_{j}$. Observe that the 3-body interaction (11) has zero angle average about the center ${\bf R}_{i}$ over the remaining nanocolumn coordinate ${\bf R}_{k}$. This is due simply to the fact that the contour integral $\oint dzz^{-1}(z-w)^{-2}$ around the unit circle, $z={\rm exp}[i\phi_{j,k}(i)]$, vanishes for complex $w$ inside of that circle. Let’s assume that each nanocolumn has a hard core of radius $r_{1}\sim r_{0}$. At $R_{i,j}\gg r_{1}$, we then obtain the estimate $\sum_{k}^{\prime}V_{i,j,k}=-\pi r_{1}^{2}\,n_{\phi}V_{i,j,j}$ for the correction to the 2-body interaction on average over the bulk of the system. Here, $n_{\phi}$ denotes the density of nanocolumns. The renormalized 2-body interaction that results is then $V_{i,j}^{(2)}=(1-\pi r_{1}^{2}\,n_{\phi})V_{i,j,j}$. Next, assume an effective hard-core of radius $r_{2}^{\prime}\sim r_{1}$ for the nanocolumn at the coordinate ${\bf R}_{j}$ that remains. We thereby obtain the estimate $\sum_{j,k}^{\prime}V_{i,j,k}=n_{\phi}\int^{\prime}d^{2}R_{i,j}V_{i,j}^{(2)}=-\pi r_{2}^{2}n_{\phi}(1-\pi r_{1}^{2}\,n_{\phi})E_{\rm 2D}^{(1)}$ for the net self-energy correction to the elastic energy of an isolated nano-column inclusion, with

This yields a total elastic energy density

as a function of the density of nanocolumns. The above third-order polynomial is depicted by Fig. 1. It notably predicts weakly metastable epitaxial growth for relatively soft nanorods within the YBCO matrix, such that $c_{\perp}^{({\rm in})}<c_{\perp}^{({\rm out})}$. This occurs at a density $n_{\phi}=(1+[1-(3r_{1}^{2}/r_{2}^{2})]^{1/2})/3\pi r_{1}^{2}$ of nano-rod inclusions, at large effective crossections $\pi r_{2}^{2}>3\pi r_{1}^{2}$. The equilibrium density of nano-rod inclusions therefore cannot be dilute. In particular, $3\pi r_{1}^{2}n_{\phi}$ must lie somewhere between $1$ and $2$. Inspection of Eq. (12) indicates that the former condition requires some degree of agglomeration among the nano-column inclusions: $r_{\rm out}<r_{2}^{\prime}<2r_{\rm out}$. This may, however, be an artifact of the previous estimate for the 2-body self-energy correction, which is not accurate at $R_{i,j}\sim r_{1}$. Last, the elastic energy cost per unit volume (13) at meta-stable equilibrium is $E_{\rm 2D}^{(1)}/9\pi r_{1}^{2}=(2/9)(\Delta r/r_{1})^{2}(c_{\parallel}^{({\rm in})-1}+c_{\perp}^{({\rm out})-1})^{-1}$ in the marginally stable limit at $r_{2}^{2}=3r_{1}^{2}$ (see Fig. 1). The strong dependence that it shows on the bulk compression modulus of the inclusion affects growth dynamics. This could be the root cause for the difference in length between BZO nanorods and BSO nanocolumns in YBCO.mele08

Critical Current by Two-Dimensional Collective Pinning. We shall now determine the critical current of a thin film of superconducting YBCO threaded by nano-rod inclusions along the crystalline $c$ axis and subject to external magnetic field aligned along the same axis. Recall that the critical temperature in an optimally doped YBCO superconductor is primarily sensitive to shear strain in the $a$-$b$ plane.welp That fact coupled with the shear strain generated by a nano-column inclusion (5) results in a potential-energy landscape for vortex lines that can collectively pin the vortex lattice. In particular, the contribution of the vortex core to the vortex line tension is approximated by the fundamental energy scale per unit length $\varepsilon_{0}=(\Phi_{0}/4\pi\lambda_{L})^{2}$, where $\lambda_{L}$ denotes the London penetration depth. The temperature dependence shown by the vortex line tension is therefore approximated by $\varepsilon_{0}(T)=\varepsilon_{0}(0)[1-(T/T_{c0})]$ near the mean-field critical temperature $T_{\rm c0}$. The potential-energy landscape experienced by a vortex line then has a contribution $\delta\varepsilon_{1}({\bf r})=\sum_{\alpha}\sum_{\beta}(\partial\varepsilon_{0}/\partial{T_{c}})(\partial{T_{c}}/\partial\epsilon_{\alpha,\beta})\epsilon_{\alpha,\beta}({\bf r})$, where $T_{c}$ is the true critical temperature, and where $\epsilon_{\alpha,\beta}$ is the symmetric strain tensor (5). It results in a $d$-wave potential-energy landscape about the nanocolumn for a vortex core,

with $\varepsilon_{\rm p}=\varepsilon_{0}(0)(T/T_{c0})T_{c}^{-1}[(\partial{T_{c}}/\partial\epsilon_{bb})-(\partial{T_{c}}/\partial\epsilon_{aa})]B_{0}$. Here the ratio between $T_{c0}$ and $T_{c}$ is assumed to be constant. A rigid vortex line therefore experiences a force field

due to the strain generated by a single nano-column inclusion, where $f_{\rm p}=2\varepsilon_{\rm p}/r_{\rm out}$ is the maximum force per unit length.

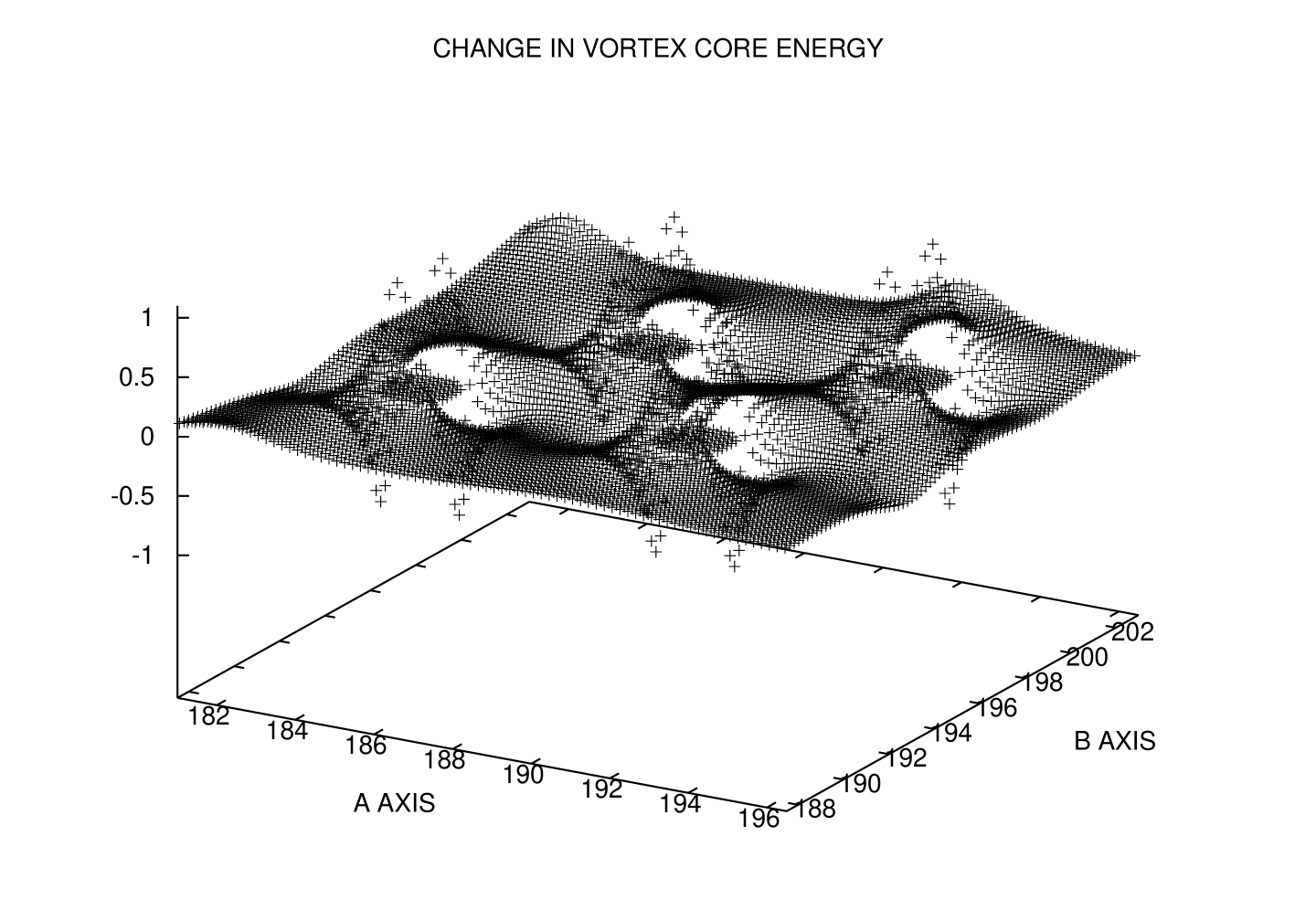
The above pinning/anti-pinning force (15) is long range. The presence of an extended field of nanocolumns can cut the range off, however. (See Fig. 2.) Such forces add within the present elastic approximation (8): ${\bf f}({\bf r})=\sum_{i}{\bf f}_{1}({\bf r}-{\bf R}_{i})$. The $d$-wave nature of each isolated force field (15) implies a null net force on average. A characteristic fluctuation of the force over the YBCO matrix remains: $\overline{f^{2}}=n_{\phi}\int^{\prime}d^{2}r|{\bf f}_{1}({\bf r})|^{2}={1\over 2}(\pi r_{\rm out}^{2}n_{\phi})f_{\rm p}^{2}$, where integration (prime) is restricted to the YBCO matrix. Matching $\overline{f^{2}}$ with $|{\bf f}_{1}({\bf r})|^{2}$ yields an effective range for each pinning/anti-pinning center $r_{\rm p}=(2/\pi n_{\phi})^{1/6}r_{\rm out}^{2/3}.$

The $d$-wave potential (14) that acts on rigid vortex lines in the vicinity of the phase boundaries between the nano-column inclusions and the YBCO matrix has zero angle average. It therefore cannot pin down a vortex line in isolation. Previous work by one of the authors and Maleyjpr-maley implies that many of them collectively pin the Abrikosov vortex lattice, however. A hexatic Bose glass state can exist at low temperature.jpr07 It is a vortex lattice threaded by isolated lines of edge dislocations in parallel to the relatively weak correlated pinning/anti-pinning centers. Plastic creep of the vortex lattice associated with glide by such edge dislocations limits the critical current,jpr-maley which is given by $j_{c}B/c\sim n_{\rm p}f^{2}_{\rm p}/c_{66}b$. Here $n_{\rm p}$ denotes the density of vortex lines pinned by the nanocolumns, $c_{66}=(\Phi_{0}/8\pi\lambda_{L})^{2}n_{B}$ is the elastic shear modulus of the pristine vortex lattice at a density $n_{B}$ of vortex lines,brandt77 and $b$ denotes the magnitude of the Burgers vector associated with the edge dislocations that thread the vortex lattice. The $d$-wave nature of the pinning/anti-pinning center (14) also implies that its occupation is purely random. The density of vortex lines that they collectively pin is then equal to $n_{\rm p}=(\sigma_{\rm p}n_{B})n_{\phi}$, where $\sigma_{\rm p}=\pi(r_{\rm p}^{2}-r_{\rm out}^{2})$ is the effective crossectional area of a pinning/anti-pinning center (see Fig. 2). The critical current density therefore obeys a pure inverse-square-root power law with magnetic field, $j_{c}\propto B^{-1/2}$. Taking values of $\partial{T_{c}}/\partial\epsilon_{aa}=230\,{\rm K}$ and $\partial{T_{c}}/\partial\epsilon_{bb}=-220\,{\rm K}$ for the strain derivatives of $T_{c}$ in optimally-doped YBCOwelp can result in a pinning efficiency, $|f_{p}|\xi/\varepsilon_{0}$, of 93% at liquid nitrogen temperature!

Discussion and Conclusions. We have found that the growth of nano-rod inclusions in YBCO films is very likely driven by weak metastability shown by the elastic energy of epitaxial layers. We also have pointed out how the sensitivity of the critical temperature in optimally-doped YBCO to pure shear strain inside of the $a$-$b$ planewelp results in an effective collective pinning center for the Abrikosov vortex lattice at the phase boundary between the nano-rod inclusion and the YBCO matrix.

The lattice mismatch along the $c$ axis between the nano-rod inclusion and YBCO has so far been neglected, however. YBCO has a unit cell that can be divided into a stack of three cubes along the $c$ axis, each with a lattice constant $c_{\rm out}/3=3.9\,{\rm\AA }$. The strain that results at the phase boundary with a BZO nanorod or with a BSO nanocolumn, both of which are cubic with lattice constants $a_{\rm in}=4.2\,{\rm\AA }$ and $4.1\,{\rm\AA }$, respectively, can be relieved by introducing partial misfit dislocations accompanied by stacking faults in the YBCO matrix.book The predicted spacing between such stacking faults, $c_{\rm Moire}=[(3/c_{\rm out})-a_{\rm in}^{-1}]^{-1}$, is then equal to $5\,{\rm nm}$ for BZO nanorods and to $8\,{\rm nm}$ for BSO nanocolumns (cf. ref. 5). Since their effect on the previous elasticity analysis can be accounted for by renormalized elastic moduli for the YBCO matrix, we believe that that our conclusions remain unchanged in their presence.

The authors thank George Levin for discussions. This work was supported in part by the US Air Force Office of Scientific Research under grant no. FA9550-06-1-0479.

*