In Square Circle: Geometric Knowledge of the Indus Civilization

The geometric principles expounded in the Sulbasutras (800-500 BCE) have often been considered to mark the beginning of mathematics in the Indian subcontinent Seidenberg75 ; Staal08 . This collection of sutras codify directions for constructing sacrificial fires, including rules for the complex configuration of ritual altars. The bird-shaped Agnicayan altar, consisting of five layers of two hundred bricks each, with the bricks being of square, rectangular or triangular shapes of various sizes, is considered by F. Staal to signal the beginning of geometry proper in South Asia Staal08 . It has been dated by him to about 1000 BCE as some of the mantras that are concerned with the consecration of bricks occur in the earliest Yajurveda Samhita, the Maitrayani. The absence of any recorded tradition of geometric knowledge predating these sutras have led some scholars to suggest a West Asian origin for the onset of mathematical thinking in India. However, the discovery of the archaeological remnants of the Indus Valley civilization in parts of Pakistan and northwestern India over the course of last century has revealed a culture having a sophisticated understanding of geometry which predated the Sulbasutras by more than a thousand years. It is difficult to ascertain whether there was any continuity between the geometry practised by the Indus civilization and that used by the later Vedic culture; however, it is not impossible that some of the earlier knowledge persisted among the local population and influenced the sulbakaras (authors of the Sulbasutras) of the first millennium BCE.

The Indus Valley civilization, also referred to as the Mature Harappan civilization (2500-1900 BCE), covered approximately a million square kilometres – geographically spread over what are now Pakistan and northwestern India Possehl02 . It was approximately contemporaneous with Old Kingdom Egypt, as well as, the Early Dynastic Period of the Sumerian Civilization and the Akkadian Empire in Mesopotamia. The Indus culture was characterized by extensive urbanization with large planned cities, as seen from the ruins of Harappa and Mohenjo-daro (among others). There is evidence for craft specialization and long-distance trade with Mesopotamia and Central Asia.

The well-laid out street plans of the Indus cities and their orientation along the cardinal directions have been long been taken as evidence that the Indus people had at least a working knowledge of geometry Amma79 ; Parpola94 . Earlier studies have suggested that not only did these people have a practical grasp of mensuration, but that they also had an understanding of the basic principles of geometry Kulkarni78 . The discovery of scales and instruments for measuring length in different Indus sites indicate that the culture knew how to make accurate spatial measurements Vij84 ; Balasubramaniam08 . For example, an ivory scale discovered at Lothal (in the western coast of India) has 27 uniformly spaced lines over 46 mm, indicating an unit of length corresponding to 1.70 mm Rao85 . The sophistication of the metrology practised by the Indus people is attested by the sets of regularly shaped artifacts of various sizes that have been identified as constituting a system of standardized weights. Indeed, there is a surprising degree of uniformity in the measurement units used at the widely dispersed centers of the civilization, indicating an attention towards achieving a standard system of units for measurement.

However, most of the literature available up till now on the subject of Indus geometry have been primarily concerned with patterns occurring at the macro-scale (such as building plans, street alignments, etc.). The smaller-scale geometric patterns that are often observed on seals or on the surface of pottery vessels have not been analysed in great detail. We believe that such designs provide evidence for a much more advanced understanding of geometry on the part of the Indus people than have hitherto been suggested in the literature.

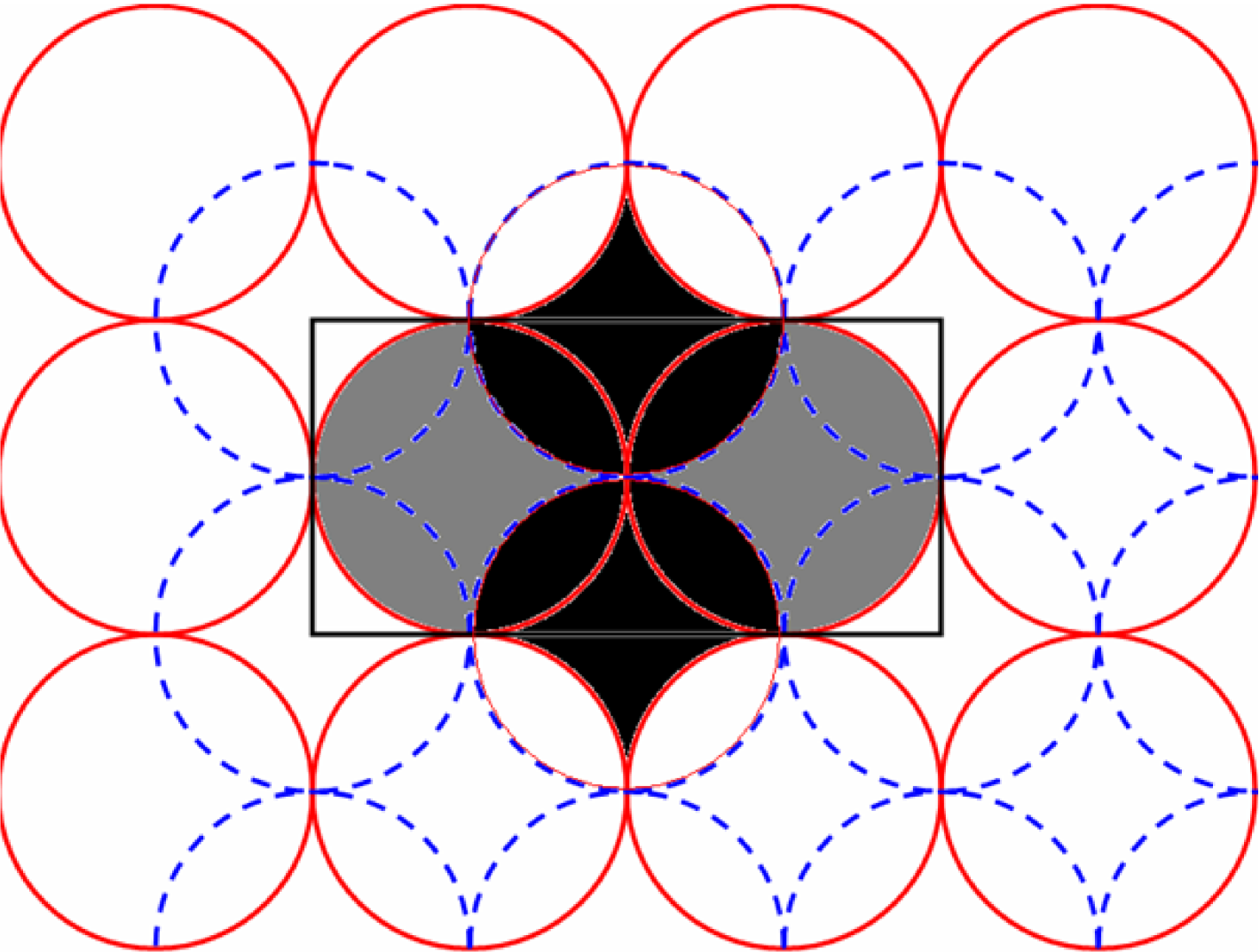
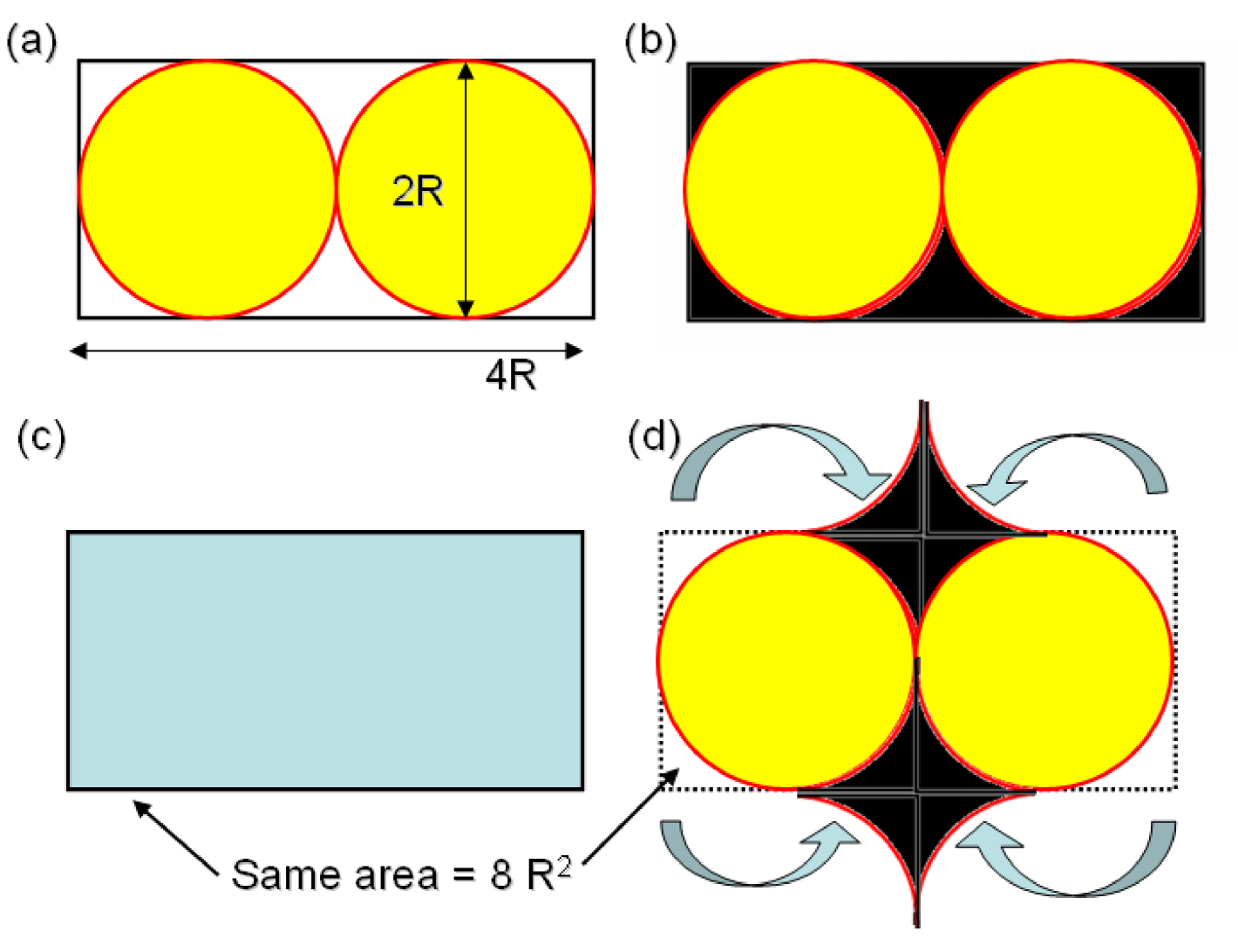
As an example, we direct the reader’s attention to the occurrence of a space-filling pattern on a seal, where a basic motif shaped like a Japanese fan has been used in different orientations to tile an approximately square domain (Fig. 1). The apparent simplicity of the design belies the geometric complexity underlying it. The actual repeating pattern is a fairly complicated shape that is composed of four of the basic fan-shaped motifs, each being rotated by 90 degrees (see the shaded object in Figure 2). The transformations that are required to construct this pattern from a rectangle whose length is twice its breadth is shown in Figure 3. Note that, despite the complex shape of the repeating pattern, its area is fairly simple to calculate. By construction, this area is equal to that of the rectangle. The construction also enables us to calculate the area of the fan-shaped basic motif as being $2R^{2}$ where $R$ is the length from its sharply pointed tip to the midpoint of its convex edge.

The set of operations that are required to generate the shapes described above suggest that the people of the Indus civilization were reasonably acquainted with the geometry of circular shapes and techniques of approximating their areas, especially as we know of several Indus artifacts which exhibit other designs that follow from these principles. In fact, we note that the Indus civilization paid special attention to the circle and its variants in the geometric designs that they made on various artifacts. It reminds us of the special place that the circular shape had in Greek geometry that is aptly summarised by the statement of the 5th century neo-Platonist Greek philosopher Proclus in his overview of Greek geometry: “The first and simplest and most perfect of the figures is the circle” Proclus .

The reason for the primacy of the circle in Indus geometry is probably not hard to understand if we focus on the technical means necessary to generate ideal geometric shapes. Unlike rectilinear shapes which are very difficult to draw exactly without the help of instruments that aid in drawing lines at right angles to each other, an almost perfect circle can be drawn by using a rope and a stick on soft clay. Indeed there is evidence for the use of compass-like devices for drawing circles in the Indus Valley civilization. E. J. H. Mackay, who excavated Mohenjo-daro between 1927-1932 expressed surprise on finding that “an instrument was actually used for this purpose [drawing circles] in the Indus Valley as early as 2500 BC” Mackay38 . In this context, it may be noted that later excavations at Lothal have unearthed thick, ring-like shell objects with four slits each in two margins that could have been used to measure angles on plane surfaces Rao85 .

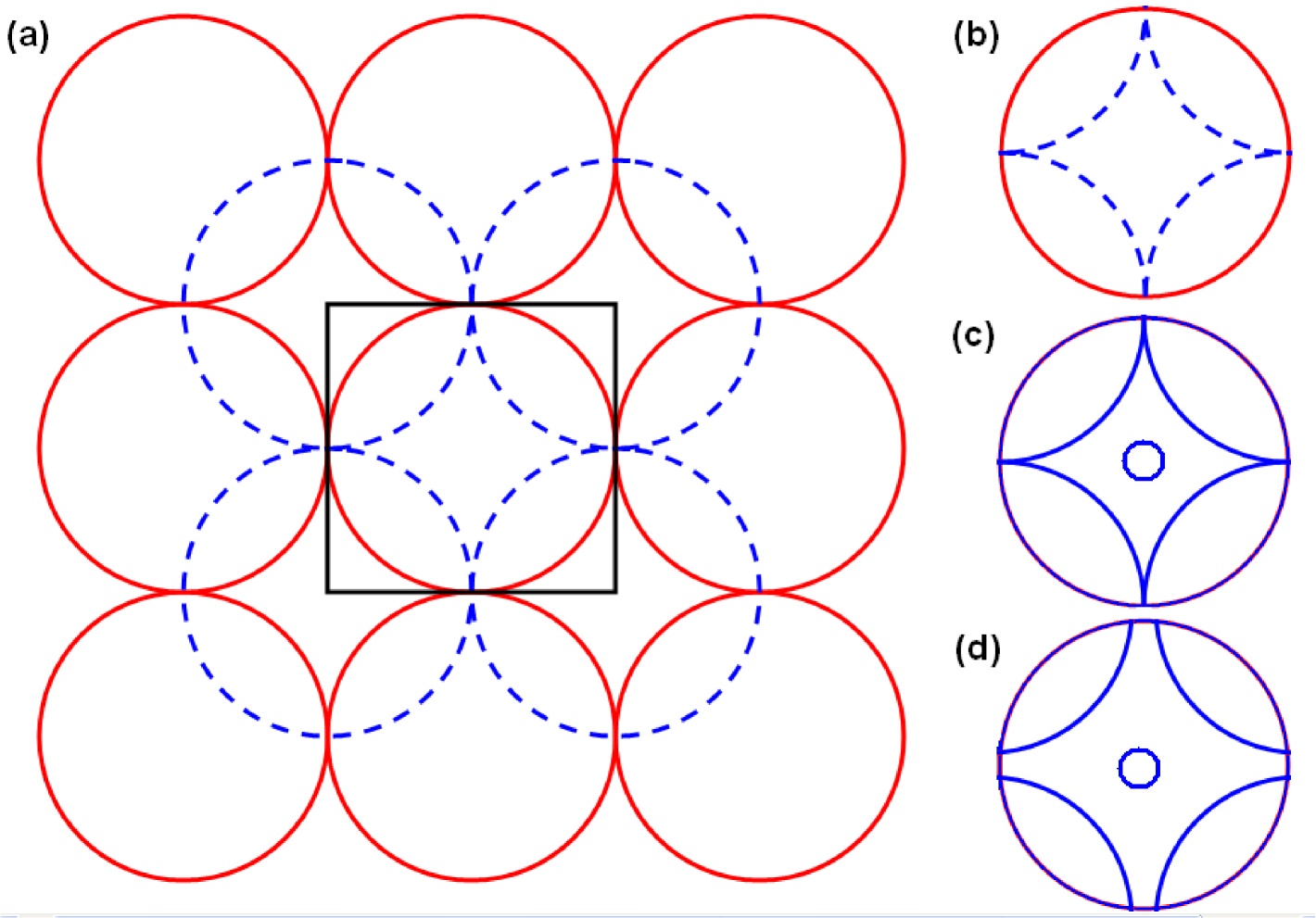
Let us return to the issue of how the sophisticated understanding of tiling the plane with shapes having circular edges may have emerged in the Indus civilization. A possible clue can be found from the construction given in Fig. 2, viz., the close-packing of circles on a plane in a four-fold symmetric arrangement. Such lattice patterns with the spatial period equal to the diameter of a circle, are easy to generate, for instance, by pressing an object with a circular outline on a wet clay surface repeatedly along rows and columns (Fig. 4 (a)). Indeed, certain Indus artifacts bear the impression of circular objects pressed on them to create a design. By exploring the variations of such a basic pattern, a variety of increasingly complicated design motifs can be generated which culminate in the complicated space-filling tiles shown in Figure 1.

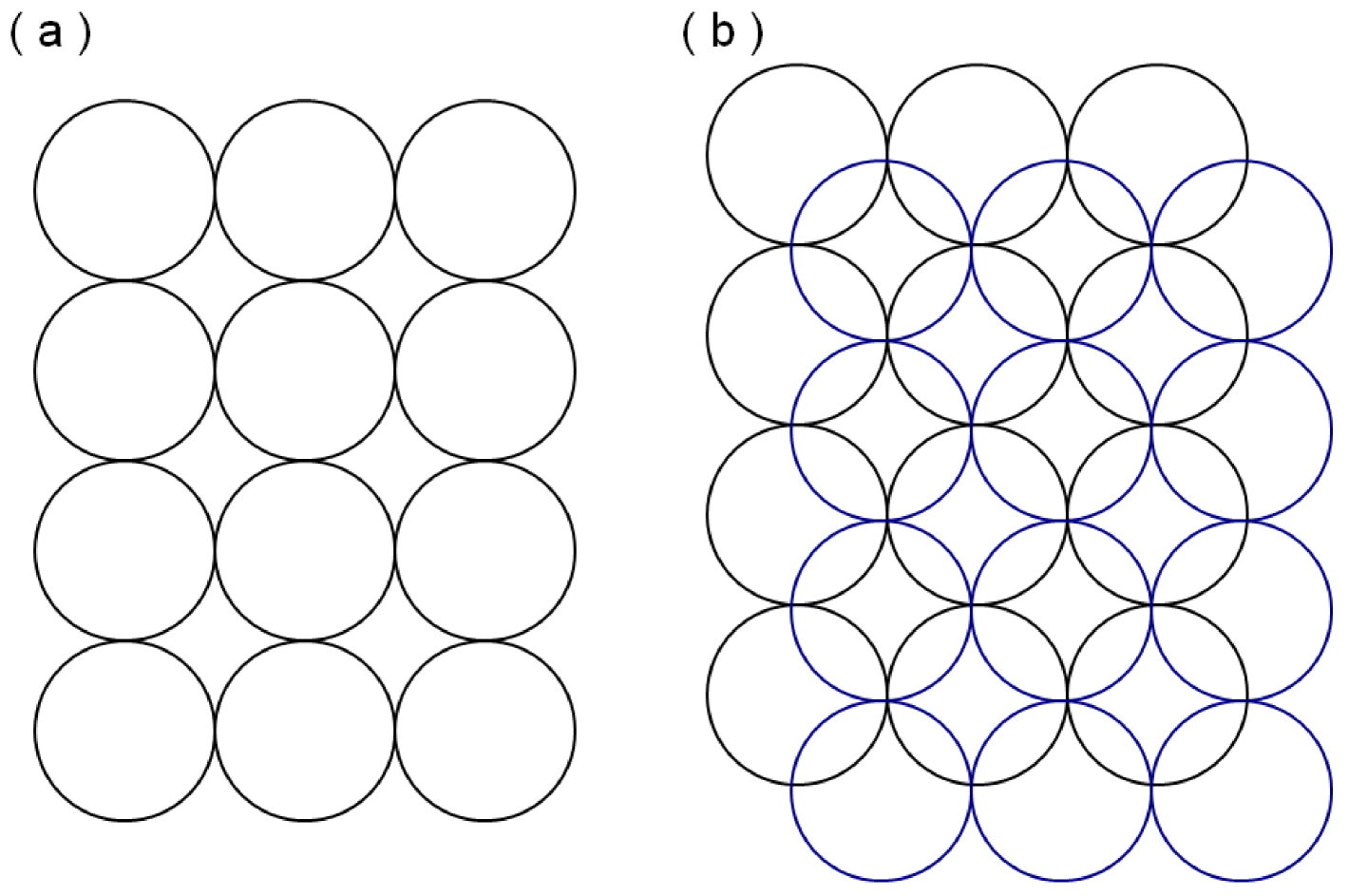
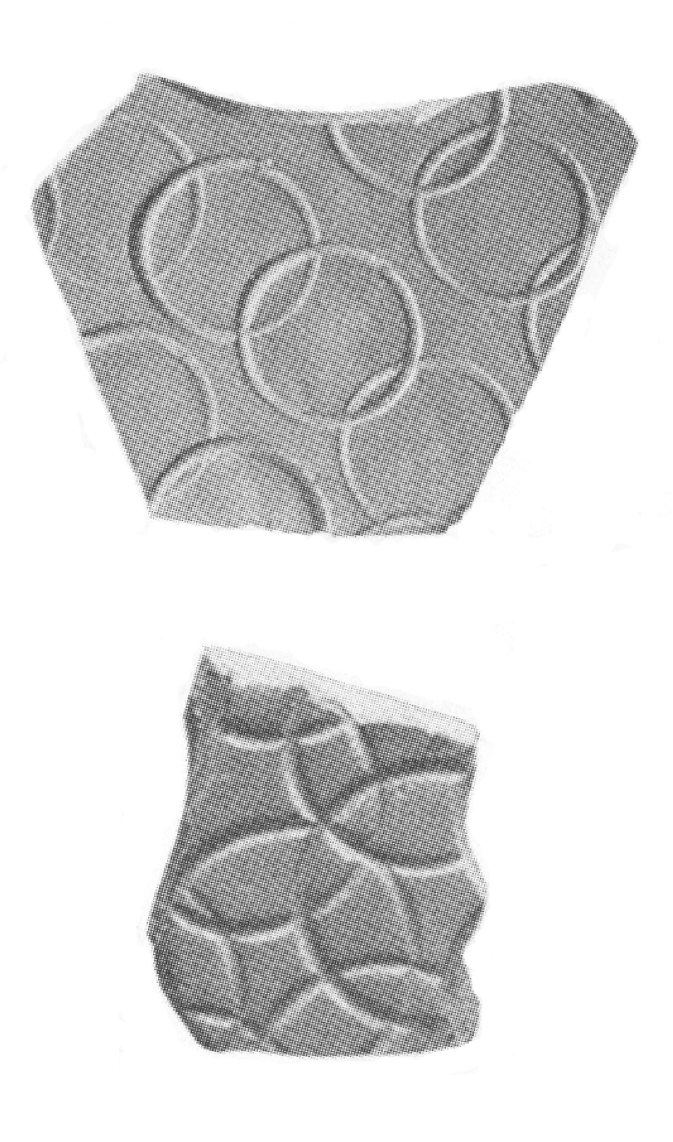
One of the simplest variations of the basic circular pattern is to have two layers of such close-packed lattices of circles, with one layer displaced by a length equal to the radius of a circle (i.e., half the lattice spacing) along both the horizontal and vertical directions (Fig. 4 (b)). The resulting intersecting circle lattice is a frequently occurring design motif in Indus artifacts. See Figure 5 for examples of this pattern, which occasionally occurs in a “decorated” variation (with points or lines used to fill the spaces within the circular shapes). In this context, one may mention that one of the signs that occur in frequently in the Indus seal inscriptions is in the form of two overlapping ellipses. Parpola has suggested as association of this sign with the Pleiades star system Parpola94 . It is a matter of conjecture whether the design of intersecting circles found in so many Indus artifacts has any astral significance.

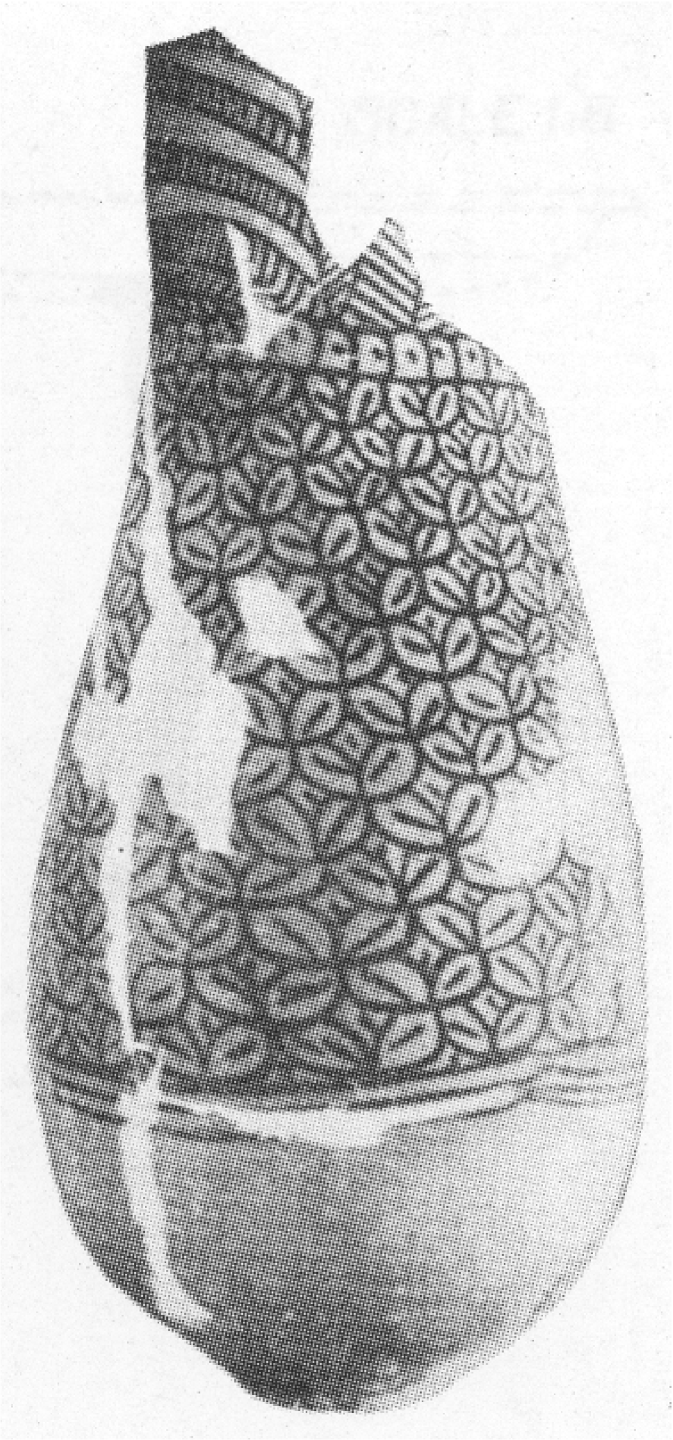
The next variation we discuss is the imbricate pattern having regularly arranged overlapping edges resembling fish scales. This pattern has also frequently appeared in artifacts of other cultures, including on the surface of West Asian Intercultural Style vessels Kohl78 . Figure 6 shows how the design is used for tiling the plane by having several rows of overlapping circles, each partially obscuring the layer beneath it. It is fairly easy to see that this is a variation of the intersecting circle lattice. One can envisage the design as being made up of multiple rows of circular tiles stacked one on top of the other with successive rows displaced by half a lattice spacing vertically and horizontally. The pattern can be seen frequently on the surface of Indus painted pottery, both in its original and “decorated” forms (Fig. 7) Starr41 .

Yet another possible variation obtained from the intersecting circle lattice is shown in Figure 8. If a square, the length of whose sides equal the diameter of each circle, is placed on the lattice so as to completely contain a circle inside it, one obtains a star-shaped motif by focusing exclusively within the region enclosed by the square (Fig. 8 (b)). A variant of this four-pointed star is obtained by relaxing the close-packed nature of the lattice so that the circles no longer touch each other. The resulting ‘cross’-shaped motif with a small circle added at the center (Fig. 8 (d)), sometimes referred to as the quincross sign, is found to occur very frequently in pre-Columbian iconography, especially in Mayan (‘Kan-cross’) and Zapotec (‘Glyph E’) designs Sugiyama05 . The meaning attached to this motif has been interpreted differently by various archaeologists, and in the context of the Maya, it has been claimed to be a representation of Venus. A possible astral significance of this sign in the context of Indus civilization is probably not far-fetched given its star-like shape. The motif, in both the exact four pointed star-like shape and in its cross-like variation, is found in many artifacts at both Harappa and Mohenjo-daro (Fig. 9).

The intersecting circle lattice is thus a fairly general mechanism for producing a variety of geometric patterns, ranging from quite simple ones that have been seen to occur across many different cultures to complicated tiling shapes that suggest a deeper understanding of the underlying geometry. This is especially the case for the complicated space-filling tile made from the four fan-shaped motifs shown in Fig. 3. It is clear from the construction procedure that the geometrical knowledge underlying the origin of this design is non-trivial and implies a sophisticated understanding of the principles of circular geometry.

To summarize, in this article we have argued that the origin of mathematics, and geometry in particular, in the Indian subcontinent may actually date back to the third millennium BCE and the Indus Valley civilization, rather than beginning with the Sulbasutras of the first millennium BCE as is conventionally thought. Although the well-planned cities, standardized system of measurements and evidence of long-range trade contacts with Mesopotamia and Central Asia attest to the high technological sophistication of this civilization, the unavailability of written records has up to now prevented us from acquiring a detailed understanding of the level of mathematical knowledge attained by the Indus people. By focusing on the geometry of design motifs observed commonly in the artifacts excavated from various sites belonging to this culture, we have shown that they suggest a deep understanding of the properties of circular shapes. In particular, designs which exhibit space-filling tiling with complicated shapes imply that the Indus culture may have been adept at accurately estimating the area of shapes enclosed by circular arcs. This speaks of a fairly sophisticated knowledge of geometry that may have persisted in the local population long after the decline of the urban centers associated with the civilization and it may well have influenced in some part the mathematical thinking of the later Vedic culture of the first millennium BCE.