Incorporating fat tails in financial models using entropic divergence measures
Abstract
In the existing financial literature, entropy based ideas have been proposed in portfolio optimization, in model calibration for options pricing as well as in ascertaining a pricing measure in incomplete markets. The abstracted problem corresponds to finding a probability measure that minimizes the relative entropy (also called -divergence) with respect to a known measure while it satisfies certain moment constraints on functions of underlying assets. In this paper, we show that under -divergence, the optimal solution may not exist when the underlying assets have fat tailed distributions, ubiquitous in financial practice. We note that this drawback may be corrected if ‘polynomial-divergence’ is used. This divergence can be seen to be equivalent to the well known (relative) Tsallis or (relative) Renyi entropy. We discuss existence and uniqueness issues related to this new optimization problem as well as the nature of the optimal solution under different objectives. We also identify the optimal solution structure under -divergence as well as polynomial-divergence when the associated constraints include those on marginal distribution of functions of underlying assets. These results are applied to a simple problem of model calibration to options prices as well as to portfolio modeling in Markowitz framework, where we note that a reasonable view that a particular portfolio of assets has heavy tailed losses may lead to fatter and more reasonable tail distributions of all assets.
1 Introduction
Entropy based ideas have found a number of popular applications in finance over the last two decades. A key application involves portfolio optimization where these are used (see, e.g., Meucci [33]) to arrive at a ‘posterior’ probability measure that is closest to the specified ‘prior’ probability measure and satisfies expert views modeled as constraints on certain moments associated with the posterior probability measure. Another important application involves calibrating the risk neutral probability measure used for pricing options (see, e.g., Buchen and Kelly [5], Stutzer [41], Avellaneda et al. [3]). Here entropy based ideas are used to arrive at a probability measure that correctly prices given liquid options while again being closest to a specified ‘prior’ probability measure.
In these works, relative entropy or -divergence is used as a measure of distance between two probability measures. One advantage of -divergence is that under mild conditions, the posterior probability measure exists and has an elegant representation when the underlying model corresponds to a distribution of light tailed random variables (that is, when the moment generating function exists in a neighborhood around zero). However, we note that this is no longer true when the underlying random variables may be fat-tailed, as is often the case in finance and insurance settings. One of our key contributions is to observe that when probability distance measures corresponding to ‘polynomial-divergence’ (defined later) are used in place of -divergence, under technical conditions, the posterior probability measure exists and has an elegant representation even when the underlying random variables may be fat-tailed. Thus, this provides a reasonable way to incorporate restrictions in the presence of fat tails. Our another main contribution is that we devise a methodology to arrive at a posterior probability measure when the constraints on this measure are of a general nature that include specification of marginal distributions of functions of underlying random variables. For instance, in portfolio optimization settings, an expert may have a view that certain index of stocks has a fat-tailed t-distribution and is looking for a posterior distribution that satisfies this requirement while being closest to a prior model that may, for instance, be based on historical data.
1.1 Literature Overview
The evolving literature on updating models for portfolio optimization builds upon the pioneering work of Black and Litterman [4] (BL). BL consider variants of Markowitz’s model where the subjective views of portfolio managers are used as constraints to update models of the market using ideas from Bayesian analysis. Their work focuses on Gaussian framework with views restricted to linear combinations of expectations of returns from different securities. Since then a number of variations and improvements have been suggested (see, e.g., [34], [35] and [37]). Recently, Meucci [33] proposed ‘entropy pooling’ where the original model can involve general distributions and views can be on any characteristic of the probability model. Specifically, he focuses on approximating the original distribution of asset returns by a discrete one generated via Monte-Carlo sampling (or from data). Then a convex programming problem is solved that adjusts weights to these samples so that they minimize the -divergence from the original sampled distribution while satisfying the view constraints. These samples with updated weights are then used for portfolio optimization. Earlier, Avellaneda et al. [3] used similar weighted Monte Carlo methodology to calibrate asset pricing models to market data (see also Glasserman and Yu [21]). Buchen and Kelly in [5] and Stutzer in [41] use the entropy approach to calibrate one-period asset pricing models by selecting a pricing measure that correctly prices a set of benchmark instruments while minimizing -divergence from a prior specified model, that may, for instance be estimated from historical data (see also the recent survey article [31]).
Zhou et.al in [43] consider a statistical learning framework for estimating default probabilities of private firms over a fixed horizon of time, given market data on various ‘explanatory variables’ like stock prices, financial ratios and other economic indicators. They use the entropy approach to calibrate the default probabilities (see also Friedman and Sandow [18]).
Another popular application of entropy based ideas to finance is in valuation of non-hedgeble payoffs in incomplete markets. In an incomplete market there may exist many probability measures equivalent to the physical probability measure under which discounted price processes of the underlying assets are martingales. Fritelli ([19]) proposes using a probability measure that minimizes the -divergence from the physical probability measure for pricing purposes (he calls this the minimal entropy martingale measure or MEMM). Here, the underlying financial model corresponds to a continuous time stochastic process. Cont and Tankov ([6]) consider, in addition, the problem of incorporating calibration constraints into MEMM for exponential Levy processes (see also Kallsen [28]). Jeanblanc et al. ([26]) propose using polynomial-divergence (they call it -divergence distance) instead of -divergence and obtain necessary and sufficient conditions for existence of an EMM with minimal polynomial-divergence from the physical measure for exponential Levy processes. They also characterize the form of density of the optimal measure. Goll and Ruschendorf ([22]) consider general -divergence in a general semi-martingale setting to single out an EMM which also satisfies calibration constraints.
A brief historical perspective on related entropy based literature may be in order: This concept was first introduced by Gibbs in the framework of classical theory of thermodynamics (see [20]) where entropy was defined as a measure of disorder in thermodynamical systems. Later, Shannon [39] (see also [30]) proposed that entropy could be interpreted as a measure of missing information of a random system. Jaynes [24], [25] further developed this idea in the framework of statistical inferences and gave the mathematical formulation of principle of maximum entropy (PME), which states that given partial information/views or constraints about an unknown probability distribution, among all the distributions that satisfy these restrictions, the distribution that maximizes the entropy is the one that is least prejudiced, in the sense of being minimally committal to missing information. When a prior probability distribution, say, is given, one can extend above principle to principle of minimum cross entropy (PMXE), which states that among all probability measures which satisfy a given set of constraints, the one with minimum relative entropy (or the -divergence) with respect to , is the one that is maximally committal to the prior . See [29] for numerous applications of PME and PMXE in diverse fields of science and engineering. See [12], [1], [14], [23] and [27] for axiomatic justifications for Renyi and Tsallis entropy. For information theoretic import of -divergence and its relation to utility maximization see Friedman et.al. [17], Slomczynski and Zastawniak [40].
1.2 Our Contributions
In this article, we restrict attention to examples related to portfolio optimization and model calibration and build upon ideas proposed by Avellaneda et al. [3], Buchen and Kelly [5], Meucci [33] and others. We first note the well known result that for views expressed as finite number of moment constraints, the optimal solution to the -divergence minimization can be characterized as a probability measure obtained by suitably exponentially twisting the original measure. This measure is known in literature as the Gibbs measure and our analysis is based on the well known ideas involved in Gibbs conditioning principle (see, for instance, [13]). As mentioned earlier, such a characterization may fail when the underlying distributions are fat-tailed in the sense that their moment generating function does not exist in some neighborhood of origin. We show that one reasonable way to get a good change of measure that incorporates views111In this article, we often use ‘views’ or ‘constraints’ interchangeably in this setting is by replacing -divergence by a suitable ‘polynomial-divergence’ as an objective in our optimization problem. We characterize the optimal solution in this setting, and prove its uniqueness under technical conditions. Our definition of polynomial-divergence is a special case of a more general concept of f-divergence introduced by Csiszar in [8], [9] and [10]. Importantly, polynomial-divergence is monotonically increasing function of the well known relative Tsallis Entropy [42] and relative Renyi Entropy [38], and moreover, under appropriate limit converges to -divergence.
As indicated earlier, we also consider the case where the expert views may specify marginal probability distribution of functions of random variables involved. We show that such views, in addition to views on moments of functions of underlying random variables are easily incorporated. In particular, under technical conditions, we characterize the optimal solution with these general constraints, when the objective may be -divergence or polynomial-divergence and show the uniqueness of the resulting optimal probability measure in each case.
As an illustration, we apply these results to portfolio modeling in Markowitz framework where the returns from a finite number of assets have a multivariate Gaussian distribution and expert view is that a certain portfolio of returns is fat-tailed. We show that in the resulting probability measure, under mild conditions, all assets are similarly fat-tailed. Thus, this becomes a reasonable way to incorporate realistic tail behavior in a portfolio of assets. Generally speaking, the proposed approach may be useful in better risk management by building conservative tail views in mathematical models.
Note that a key reason to propose polynomial-divergence is that it provides a tractable and elegant way to arrive at a reasonable updated distribution close to the given prior distribution while incorporating constraints and views even when fat-tailed distributions are involved. It is natural to try to understand the influence of the choice of objective function on the resultant optimal probability measure. We address this issue for a simple example where we compare the three reasonable objectives: the total variational distance, -divergence and polynomial-divergence. We discuss the differences in the resulting solutions. To shed further light on this, we also observe that when views are expressed as constraints on probability values of disjoint sets, the optimal solution is the same in all three cases. Furthermore, it has a simple representation. We also conduct numerical experiments on practical examples to validate the proposed methodology.
1.3 Organization
In Section 2, we outline the mathematical framework and characterize the optimal probability measure that minimizes the -divergence with respect to the original probability measure subject to views expressed as moment constraints of specified functions. In Section 3, we show through an example that -divergence may be inappropriate objective function in the presence of fat-tailed distributions. We then define polynomial-divergence and characterize the optimal probability measure that minimizes this divergence subject to constraints on moments. The uniqueness of the optimal measure, when it exists, is proved under technical assumptions. We also discuss existence of the solution in a simple setting. When under the proposed methodology a solution does not exist, we also propose a weighted least squares based modification that finds a reasonable perturbed solution to the problem. In Section 4, we extend the methodology to incorporate views on marginal distributions of some random variables, along with views on moments of functions of underlying random variables. We characterize the optimal probability measures that minimize -divergence and polynomial-divergence in this setting and prove the uniqueness of the optimal measure when it exists. In Section 5, we apply our results to the portfolio problem in the Markowitz framework and develop explicit expressions for the posterior probability measure. We also show how a view that a portfolio of assets has a ‘regularly varying’ fat-tailed distribution renders a similar fat-tailed marginal distribution to all assets correlated to this portfolio. Section 6 is devoted to comparing qualitative differences on a simple example in the resulting optimal probability measures when the objective function is -divergence, polynomial-divergence and total variational distance. In this section, we also note that when views are on probabilities of disjoint sets, all three objectives give identical results. We numerically test our proposed algorithms on practical examples in Section 7. Finally, we end in Section 8 with a brief conclusion. All but the simplest proofs are relegated to the Appendix.
We thank the anonymous referee for bringing Friedman et al [18] to our notice. This article also considers -divergence and in particular, polynomial-divergence (they refer to an equivalent quantity as -entropy) in the setting of univariate power-law distribution which includes Pareto and Skewed generalized -distribution. It motivates the use of polynomial-divergence through utility maximization considerations and develops practical and robust calibration technique for univariate asset return densities.
2 Incorporating Views using -Divergence
Some notation and basic concepts are needed to support our analysis. Let denote the underlying probability space. Let be the set of all probability measures on . For any the relative entropy of w.r.t or -divergence of w.r.t (equivalently, the Kullback-Leibler distance222though this is not a distance in the strict sense of a metric) is defined as
if is absolutely continuous with respect to and is integrable. otherwise. See, for instance [7], for concepts related to relative entropy.
Let be the set of all probability measures which are absolutely continuous w.r.t. , be a measurable function such that , and let
denote the logarithmic moment generating function of w.r.t . Then it is well known that
Furthermore, this supremum is attained at given by:
| (1) |
In our optimization problem we look for a probability measure that minimizes the -divergence w.r.t. . We restrict our search to probability measures that satisfy moment constraints and/or where each is a measurable function. For instance, views on probability of certain sets can be modeled by setting ’s as indicator functions of those sets. If our underlying space supports random variables under the probability measure , one may set so that the associated constraint is on the expectation of these functions.
Formally, our optimization problem is:
| (2) |
subject to the constraints:
| (3) |
for and
| (4) |
for . Here can take any value between 0 and .
The solution to this is characterized by the following assumption:
Assumption 1
The following theorem follows:
Theorem 1
Under Assumption 1, is an optimal solution to .
This theorem is well known and a proof using Lagrange multiplier method can be found in [7], [15], [5] and [2]. For completeness we sketch the proof below.
Proof of Theorem 1:
is equivalent to maximizing subject to the constraints (3)
and (4).
The Lagrangian for the above maximization problem is:
where . Then by (1) and the preceding discussion, it follows that maximizes . By Lagrangian duality, due to Assumption 1, also solves .
Note that to obtain the optimal distribution by formula (5), we must solve the constraint equations for the Lagrange multipliers . The constraint equations with its explicit dependence on ’s can be written as:
| (6) |
This is a set of nonlinear equations in unknowns , and typically would require numerical procedures for solution. It is easy to see that if the constraint equations are not consistent then no solution exists. For a sufficient condition for existence of a solution, see Theorem 3.3 of [11]. On the other hand, when a solution does exist, it is helpful for applying numerical procedures, to know if it is unique. It can be shown that the Jacobian matrix of the set of equation (6) is given by the variance-covariance matrix of under the measure given by (5). The last mentioned variance-covariance matrix is also equal to the Hessian of the following function
For details, see [5] or [2]. It is easily checked that (6) is same as
| (7) |
It follows that if no non-zero linear combination of has zero variance under the measure given by (5), then G is strictly convex and if a solution to (6) exists, it is unique. It also follows that instead of employing a root-search procedure to solve (6) for ’s, one may as well find a local minima (which is also global) of the function numerically. We end this section with a simple example.
Example 1
Suppose that under , random variables have a multivariate normal distribution , that is, with mean and variance covariance matrix . If constraints correspond to their mean vector being equal to , then this can be achieved by a new probability measure obtained by exponentially twisting by a vector such that
Then, under , is distributed.
3 Incorporating Views using Polynomial-Divergence
In this section, we first note through a simple example involving a fat-tailed distribution that optimal solution under -divergence may not exist in certain settings. In fact, in this simple setting, one can obtain a solution that is arbitrarily close to the original distribution in the sense of -divergence. However, the form of such solutions may be inelegant and not reasonable as a model in financial settings. This motivates the use of other notions of distance between probability measures as objectives such as -divergence (introduced by Csiszar [10]). We first define general -divergence and later concentrate on the case where has the form , . We refer to this as polynomial-divergence and note its relation with relative Tsallis entropy, relative Renyi entropy and -divergence. We then characterize the optimal solution under polynomial-divergence. To provide greater insight into nature of this solution, we explicitly solve a few examples in a simple setting involving a single random variable and a single moment constraint. We also note that in some settings under polynomial-divergence as well an optimal solution may not exist. With a view to arriving at a pragmatic remedy, we then describe a weighted least squares based methodology to arrive at a solution by perturbing certain parameters by a minimum amount.
3.1 Polynomial Divergence
Example 2
Suppose that under , non-negative random variable has a Pareto distribution with probability density function
The mean under this pdf equals . Suppose the view is that the mean should equal . It is well known and easily checked that
is an increasing function of that equals for . Hence, Assumption 1, does not hold for this example. Similar difficulty arises with other fat-tailed distributions such as log-normal and -distribution.
To shed further light on Example 2, for , consider a probability distribution
Where denote the indicator function of the set , that is, if and otherwise. Let denote the solution to
Proposition 1
The sequence and the the -divergence both converge to zero as .
Solutions such as above are typically not representative of many applications, motivating the need to have alternate methods to arrive at reasonable posterior measures that are close to and satisfy constraints such as (3) and (4) while not requiring that the optimal solution be obtained using exponential twisting.
We now address this issue using polynomial-divergence. We first define -divergence introduced by Csiszar (see [8], [9] and [10]).
Definition 1
Let be a strictly convex function. The -divergence of a probability measure w.r.t. another probability measure equals
if is absolutely continuous and is integrable w.r.t. . Otherwise we set .
Note that -divergence corresponds to the case . Other popular examples of include
In this section we consider and refer to the resulting -divergence as polynomial-divergence. That is, we focus on
It is easy to see using Jensen’s inequality that
is achieved by .
Our optimization problem may be stated as:
| (8) |
subject to (3) and (4). Minimizing polynomial-divergence can also be motivated through utility maximization considerations. See [17] for further details.
Remark 1
Relation with Relative Tsallis Entropy and Relative Renyi Entropy: Let and be a positive real numbers. The relative Tsallis entropy with index of w.r.t. equals
if is absolutely continuous w.r.t. and the integral is finite. Otherwise, . See, e.g., [42]. The relative Renyi entropy of order of w.r.t. equals
and
if is absolutely continuous w.r.t and the respective integrals are finite. Otherwise, (see, e.g, [38]).
It can be shown that as and as Also, following relations are immediate consequences of the above definitions:
and
Thus, polynomial-divergence is a strictly increasing function of both relative Tsallis entropy and relative Renyi entropy. Therefore minimizing polynomial-divergence is equivalent to minimizing relative Tsallis entropy or relative Renyi entropy.
In the following assumption we specify the form of solution to :
Assumption 2
Theorem 2
Under Assumption 2, is an optimal solution to .
Remark 2
In many cases the inequality (9) can be equivalently expressed as a finite number of linear constraints on ’s. For example, if each has as its range then clearly (9) is equivalent to for all . As another illustration, consider for and . Then (9) is equivalent to
Note that if each has -th moment finite, then (10) holds for .
Existence and Uniqueness of Lagrange multipliers: To obtain the optimal distribution by formula (11), we must solve the set of nonlinear equations given by:
| (12) |
for . In view of Assumption 2 we define the set
A solution to (12) is called feasible if lies in the set . A feasible solution is called strongly feasible if it further satisfies
| (13) |
Theorem 3 states sufficient conditions under which a strongly feasible solution to (12) is unique.
Theorem 3
Suppose that the variance-covariance matrix of under any measure is positive definite, or equivalently, that for any , for some constants and implies and for all . Then, if a strongly feasible solution to (12) exists, it is unique.
To solve (12) for one may resort to numerical root-search techniques. A wide variety of these techniques are available in practice (see, for example, [32] and [36]). In our numerical experiments, we used FindRoot routine from Mathematica which employs a variant of secant method.
Alternatively, one can use the dual approach of minimizing a convex function over the set . In the proof of Theorem 3 we have shown one convex function whose stationary point satisfies a set of equations which is equivalent and related to (12). Therefore, it is possible recover a strongly feasible solution to (12) if one exists. Note that, contrary to the case with -divergence where the dual convex optimization problem is unconstrained, here we have a minimization problem of a convex function subject to the constraints (9) and (13).
3.2 Single Random Variable, Single Constraint Setting
Proposition 2 below shows the existence of a solution to under a single random variable, single constraint settings. We then apply this to a few specific examples.
Note that for any random variable , a non-negative function and a positive integer , we always have , since random variables and are positively associated and hence have non-negative covariance.
Proposition 2
Consider a random variable with pdf , and a function such that for a positive integer . Further suppose that . Then the optimization problem:
subject to:
has a unique solution for , given by
where is a positive root of the polynomial
| (14) |
As we note in the proof in the Appendix, the uniqueness of the solution follows from Theorem 3. Standard methods like Newton’s, secant or bisection method can be applied to numerically solve (14) for .
Example 3
Suppose is log-normally distributed with parameters (that is, has normal distribution with mean and variance ). Then, its density function is
For the constraint
| (15) |
first consider the case . Then, the probability distribution minimizing the polynomial-divergence is given by:
From the constraint equation we have:
or
Since increases with and converges to as , it follows that our optimization problem has a solution if . Thus if and , Assumption 2 cannot hold. Further, it is easily checked that . Therefore, for , a solution always exists for .
Example 4
Suppose that rv has a Gamma distribution with density function
and as before, the constraint is given by (15). Then, it is easily seen that , so that a solution with exists for .
Example 5
Suppose has a Pareto distribution with probability density function:
and as before, the constraint is given by (15). Then, it is easily seen that
As in previous examples, we see that a probability distribution minimizing the polynomial-divergence with with exists when .
3.3 Weighted Least Squares Approach to find Perturbed Solutions
Note that an optimal solution to may not exist when Assumption 2 does not hold. For instance, in Proposition 2, it may not exist for . In that case, selecting and associated so that is very close to is a reasonable practical strategy.
We now discuss how such solutions may be achieved for general problems using a weighted least squares approach. Let denote and denote the measure defined by right hand side of (11). We write for and re-express the optimization problem as to explicitly show its dependence on . Define
Consider . Then, has no solution. In that case, from a practical viewpoint, it is reasonable to consider as a solution a measure corresponding to a such that this is in some sense closest to amongst all elements in . To concretize the notion of closeness between two points we define the metric
between any two points and in , where is a constant vector of weights expressing relative importance of the constraints : and .
Let , where is the closure of . Except in the simplest settings, is difficult to explicitly evaluate and so determining is also no-trivial.
The optimization problem below, call it , gives solutions such that the vector defined as
has -distance from arbitrarily close to when is sufficiently close to zero. From implementation viewpoint, the measure may serve as a reasonable surrogate for the optimal solution sought for . (Avelleneda et al. [3] implement a related least squares strategy to arrive at an updated probability measure in discrete settings).
| (16) |
subject to
| (17) |
This optimization problem penalizes each deviation from by adding appropriately weighted squared deviation term to the objective function. Let denote a solution to . This can be seen to exist under a mild condition that the optimal takes values within a compact set for any . Note that then .
Proposition 3
For any , the solutions to satisfy the relation
4 Incorporating Constraints on Marginal Distributions
Next we state and prove the analogue of Theorem 1 and 2 when there is a constraint on a marginal distribution of a few components of the given random vector. Later in Remark 3 we discuss how this generalizes to the case where the constraints involve moments and marginals of functions of the given random vector. Let and be two random vectors having a law which is given by a joint probability density function . Recall that is the set of all probability measures which are absolutely continuous w.r.t. . If then is also specified by a probability density function say, , such that whenever and . In view of this we may formulate our optimization problem in terms of probability density functions instead of measures. Let denote the collection of density functions that are absolutely continuous with respect to the density .
4.1 Incorporating Views on Marginal Using -Divergence
Formally, our optimization problem is:
subject to:
| (18) |
where is a given marginal density function of , and
| (19) |
for . For presentation convenience, in the remaining paper we only consider equality constraints on moments of functions (as in (19)), ignoring the inequality constraints. The latter constraints can be easily handled as in Assumptions (1) and (2) by introducing suitable non-negativity and complementary slackness conditions.
Some notation is needed to proceed further. Let and
Further, let denote the joint density function of , for all , and denote the expectation under .
For a mathematical claim that depends on x, say , we write for almost all to mean that , where is the measure induced by the density . That is, for all measurable subsets .
Assumption 3
There exists such that
for almost all w.r.t and the probability density function satisfies the constraints given by (19). That is, for all , we have
| (20) |
Theorem 4
Under Assumption 3, is an optimal solution to .
In Theorem 5, we develop conditions that ensure uniqueness of a solution to once it exists.
Theorem 5
Suppose that for almost all w.r.t. , conditional on , no non-zero linear combination of the random variables has zero variance w.r.t. the conditional density , or, equivalently, for almost all w.r.t. , almost surely () for some constants and implies and for all . Then, if a solution to the constraint equations (20) exists, it is unique.
Remark 3
Theorem 4, as stated, is applicable when the updated marginal distribution of a sub-vector of the given random vector is specified. More generally, by a routine change of variable technique, similar specification on a function of the given random vector can also be incorporated. We now illustrate this.
Let denote a random vector taking values in and having a (prior) density function . Suppose the constraints are as follows:
-
•
have a joint density function given by .
-
•
where and are some functions on .
If we define functions such that the function defined by has a nonsingular Jacobian a.e. That is,
where we are assuming that the functions allow such a construction.
Consider , where for and , where for Let denote the density function of . Then, by the change of variables formula for densities,
where denotes the local inverse function of , that is, if , then, .
The constraints can easily be expressed in terms of as
and
| (21) |
Setting , from Theorem (4) it follows that the optimal density function of as:
where ’s is chosen to satisfy (21).
Again by the change of variable formula, it follows that the optimal density of is given by:
4.2 Incorporating Constraints on Marginals Using Polynomial-Divergence
Extending Theorem 4 to the case of polynomial-divergence is straightforward. We state the details for completeness. As in the case of -divergence, the following notation will simplify our exposition. Let
If the marginal of is given by then the joint density is denoted by . denotes the expectation under .
Assumption 4
There exists such that
| (22) |
for almost all w.r.t. and
| (23) |
for almost all w.r.t. . Further, the probability density function satisfies the constraints given by (19). That is, for all , we have
| (24) |
Theorem 6
Under Assumption 4, is an optimal solution to .
Analogous to the discussion in Remark (3), by a suitable change of variable, we can adapt the above theorem to the case where the constraints involve marginal distribution and/or moments of functions of a given random vector.
We conclude this section with a brief discussion on uniqueness of the solution to . Any satisfying (22), (23) and (24) is called a feasible solution to . A feasible solution is called strongly feasible if it further satisfies
The following theorem can be proved using similar arguments as those used to prove Theorem 3. We omit the details.
Theorem 7
Suppose that for almost all w.r.t. , conditional on , no non-zero linear combination of has zero variance under any measures absolutely continuous w.r.t . Or equivalently, that for any measures absolutely continuous w.r.t almost everywhere , for some constants and , implies and for all . Then, if a strongly feasible solution to (24) exists, it is unique.
Note that when Assumptions 3 and 4 do not hold, the weighted least squares methodology developed in Section 3.3 can again be used to arrive at a reasonable perturbed solution that may be useful from implementation viewpoint.
5 Portfolio Modeling in Markowitz Framework
In this section we apply the methodology developed in Section 4.1 to the Markowitz framework: namely to the setting where there are assets whose returns under the ‘prior distribution’ are multivariate Gaussian. Here, we explicitly identify the posterior distribution that incorporates views/constraints on marginal distribution of some random variables and moment constraints on other random variables. As mentioned in the introduction, an important application of our approach is that if for a particular portfolio of assets, say an index, it is established that the return distribution is fat-tailed (specifically, the pdf is a regularly varying function), say with the density function , then by using that as a constraint, one can arrive at an updated posterior distribution for all the underlying assets. Furthermore, we show that if an underlying asset has a non-zero correlation with this portfolio under the prior distribution, then under the posterior distribution, this asset has a tail distribution similar to that given by .
Let have a dimensional multivariate Gaussian distribution with mean and the variance-covariance matrix
We consider a posterior distribution that satisfies the view that:
where is a given probability density function on with finite first moments along each component and is a given vector in . As we discussed in Remark 3 (see also Example 7 in Section 7), when the view is on marginal distributions of linear combinations of underlying assets, and/or on moments of linear functions of the underlying assets, the problem can be easily transformed to the above setting by a suitable change of variables.
To find the distribution of which incorporates the above views, we solve the minimization problem :
subject to the constraint:
and
| (25) |
where is the density of -variate normal distribution denoted by .
Proposition 4
Under the assumption that is invertible, the optimal solution to is given by
| (26) |
where is the probability density function of
where is the expectation of under the density function .
Tail behavior of the marginals of the posterior distribution: We now specialize to the case where (also denoted by ) is a single random variable so that , and Assumption 5 below is satisfied by pdf . Specifically, is distributed as with
where with
Assumption 5
The pdf is regularly varying, that is, there exists a constant ( is needed for to be integrable) such that
for all (see, for instance, [16]). In addition, for any and
| (27) |
for some non-negative function independent of (but possibly depending on and ) with the property that whenever has a Gaussian distribution.
Remark 4
Assumption 5 holds, for instance, when corresponds to -distribution with degrees of freedom, that is,
Clearly, is regularly varying with . To see (27), note that
Putting and we have
Now (27) readily follows from the fact that
for any two real numbers and . To verify the last inequality, note that if then and if then
Note that if or for any or then the last condition in Assumption 5 holds.
From Proposition (4), we note that the posterior distribution of is
where is the probability density function of
where is the expectation of under the density function . Let denote the marginal density of under the above posterior distribution. Theorem 8 states a key result of this section.
Theorem 8
Under Assumption 5, if , then
| (28) |
Note that (28) implies that
6 Comparing Different Objectives
Given that in many examples one can use -divergence as well as polynomial-divergence as an objective function for arriving at an updated probability measure, it is natural to compare the optimal solutions in these cases. Note that the total variation distance between two probability measures and defined on equals
This may also serve as an objective function in our search for a reasonable probability measure that incorporates expert views and is close to the original probability measure. This has an added advantage of being a metric (e.g., it satisfies the triangular inequality).
We now compare these three different types of objectives to get a qualitative flavor of the differences in the optimal solutions in two simple settings (a rigorous analysis in general settings may be a subject for future research). The first corresponds to the case of single random variable whose prior distribution is exponential. In the second setting, the views correspond to probability assignments to mutually exclusive and exhaustive set of events.
6.1 Exponential Prior Distribution
Suppose that the random variable is exponentially distributed with rate under . Then its pdf equals
Now suppose that our view is that under the updated measure with density function , .
-divergence: When the objective function is to minimize -divergence, the optimal solution is obtained as an exponentially twisted distribution that satisfies the desired constraint. It is easy to see that exponentially twisting an exponential distribution with rate by an amount leads to another exponential distribution with rate (assuming that ). Therefore, in our case
satisfies the given constraint and is the solution to this problem. Note here that the tail distribution function equals and is heavier than , the original tail distribution of .
Polynomial-divergence: Now consider the case where the objective corresponds to a polynomial-divergence with parameter equal to , i.e, it equals
Under this objective, the optimal pdf is
where is chosen so that the mean under equals .
While this may not have a closed form solution, it is clear that on a logarithmic scale, is asymptotically similar to as and hence has a lighter tail than the solution under the -divergence.
Total variation distance: Under total variation distance as an objective, we show that given any , we can find a new density function so that the mean under the new distribution equals while the total variation distance is less than . Thus the optimal value of the objective function is zero, although there may be no pdf that attains this value.
To see this, consider,
Then,
Thus, given any , if we select
we see that
We now show that total variation distance between and is less than . To see this, note that
for any set disjoint from , where the probability corresponds to the density . Furthermore, letting denote the Lebesgue measure of set ,
for any set . Thus, for any set
Therefore,
This also illustrates that it may be difficult to have an elegant characterization of solutions under the total variation distance, making the other two as more attractive measures from this viewpoint.
6.2 Views on Probability of Disjoint Sets
Here, we consider the case where the views correspond to probability assignments under posterior measure to mutually exclusive and exhaustive set of events and note that objective functions associated with -divergence, polynomial-divergence and total variation distance give identical results.
Suppose that our views correspond to:
For instance, if is a continuous random variable denoting loss amount from a portfolio and there is a view that value-at-risk at a certain amount equals . This may be modeled as and .
-divergence: Then, under the -divergence setting, for any event , the optimal
Select so that . Then it follows that the specified views hold and
| (29) |
Polynomial-divergence: The analysis remains identical when we use polynomial-divergence with parameter . Here, we see that optimal
Again, by setting , (29) holds.
Total variation distance: If the objective is the total variation distance, then clearly, the objective function is never less than . We now show that defined by (29) achieves this lower bound.
To see this, note that
7 Numerical Experiments
Three simple experiments are conducted. In the first, we consider a calibration problem, where the distribution of the underlying Black-Scholes model is updated through polynomial-divergence based optimization to match the observed options prices. We then consider a portfolio modeling problem in Markowitz framework, where VAR (value-at-risk) of a portfolio consisting of 6 global indices is evaluated. Here, the model parameters are estimated from historical data. We then use the proposed methodology to incorporate a view that return from one of the index has a distribution, along with views on the moments of returns of some linear combinations of the indices. In the third example, we empirically observe the parameter space where Assumption 2 holds, in a simple two random variable, two constraint setting.
Example 6
Consider a security whose current price equals . Its volatility is estimated to equal . Suppose that the interest rate is constant and equals . Consider two liquid European call options on this security with maturity year, strike prices , and market prices of and , respectively. It is easily checked that the Black Scholes price of these options at equals and , respectively. It can also be easily checked that there is no value of making two of the Black-Scholes prices match the observed market prices.
We apply polynomial-divergence methodology to arrive at a probability measure closest to the Black-Scholes measure while matching the observed market prices of the two liquid options. Note that under Black-Scholes
which is heavy-tailed in that the moment generating function does not exist in the neighborhood of the origin. Let denote the pdf for the above log-normal distribution. We apply Theorem 2 with to obtain the posterior distribution:
where and are solved from the constrained equations:
| (30) |
The solution comes out to be and (found using FindRoot of Mathematica). Note that and . Therefore these values are all feasible. Furthermore, since , they are strongly feasible as well. Plugging these values in we get the posterior density that can be used to price other options of the same maturity. The second row of Table 1 shows the resulting European call option prices for different values of strike prices under this posterior distribution.
| Strike | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
|---|---|---|---|---|---|---|---|
| BS | 5.2253 | 3.0200 | 1.62374 | 0.8198 | 0.3925 | 0.1798 | 0.0795 |
| Posterior I | 7.6978 | 5.0000 | 3.0000 | 1.6779 | 0.8851 | 0.4443 | 0.2139 |
| Posterior II | 8.0016 | 4.9698 | 3.0752 | 1.9447 | 1.15306 | 0.63341 | 0.3276 |
| Posterior III | 8.0000 | 4.9991 | 3.0201 | 1.8530 | 1.0757 | 0.5821 | 0.2977 |
| Posterior IV | 7.7854 | 4.8243 | 3.0584 | 1.9954 | 1.2092 | 0.6743 | 0.3525 |
Now suppose that the market prices of two more European options of same maturity with strike prices 50 and 65 are found to be 8.00 and 2.00, respectively. In the above posterior distribution these prices equal 7.6978 and 1.6779, respectively. To arrive at a density function that agrees with these prices as well, we solve the associated four constraint problem by adding the following constraint equations to (30):
| (31) |
where and .
With these added constraints, we observe that the optimization problem lacks any solution of the form (11). We then implement the proposed weighted least squares methodology to arrive at a perturbed solution. With weights and (so that each equals ), the new posterior is of the form (11) with -values given by and . The third row of Table 1 gives the option prices under this new posterior. The last two rows report the option prices under the posterior measure resulting from weight combinations and , respectively.
Example 7
We consider an equally weighted portfolio in six global indices: ASX (the SP/ASX200, Australian stock index), DAX (the German stock index), EEM (the MSCI emerging market index), FTSE (the FTSE100, London Stock Exchange), Nikkei (the Nikkei225, Tokyo Stock Exchange) and SP (the Standard and Poor 500). Let denote the weekly rate of returns333Using logarithmic rate of return gives almost identical results. from ASX, DAX, EEM, FTSE, Nikkei and SP, respectively. We take prior distribution of to be multivariate Gaussian with mean vector and variance-covariance matrix estimated from historical prices of these indices for the last two years (161 weeks, to be precise) obtained from Yahoo-finance. Assuming a notional amount of 1 million, the value-at-risk (VaR) for our portfolio for different confidence levels is shown in the second column of Table 3.
Next, suppose our view is that DAX will have an expected weekly return of and will have a -distribution with degrees of freedom. Further suppose that we expect all the indices to strengthen and give expected weekly rates of return as in Table 2. For example, the third row in that table expresses the view that the rate of return from emerging market will be higher than that of FTSE by . Expressed mathematically:
where is the expectation under the posterior probability. The other rows may be similarly interpreted.
We define new variables as , , , , and . Then our views are and has a standard -distribution with 3 degrees of freedom.
The third column in Table 3 reports VaRs at different confidence levels under the posterior distribution incorporating the only views on the expected returns (i.e, without the view that has a -distribution). We see that these do not differ much from those under the prior distribution. This is because the views on the expected returns have little effect on the tail: the posterior distribution is Gaussian and even though the mean has shifted (variance remains the same) the tail probability remains negligible. Contrast this with the effect of incorporating the view that has a -distribution. The VaRs (computed from samples) under this posterior distribution are reported in the last column.
| Index | average rate of return |
|---|---|
| ASX | 0.001 |
| DAX | 0.002 |
| EMM - FTSE | 0.002 |
| FTSE | 0.001 |
| Nikkei | 0.002 |
| SP | 0.001 |
| VaR at | Prior | Posterior 1 | Posterior 2 |
|---|---|---|---|
| 8500 | 8400 | 16000 | |
| 7200 | 7100 | 11200 | |
| 6000 | 5900 | 8200 |
Example 8
In this example we further refine the observation made in Proposition 2 and the following examples that typically the solution space where Assumption 2 holds increases with increasing . We note that even in simple cases, this need not always be true.
Specifically, consider random variables and such that
Then, and are log-normally distributed and their joint density function of is given by:
Consider the constraints
Our goal is to find values of and for which the associated optimization problem has a solution. The probability distribution minimizing the polynomial-divergence with is of the form:
Now from the constraint equations we have
and
Note that since and takes values in only and are feasible. Using ParametricPlot of Mathematica we plot the values of
for and in the range . Figure (1), depicts the range when respectively, for
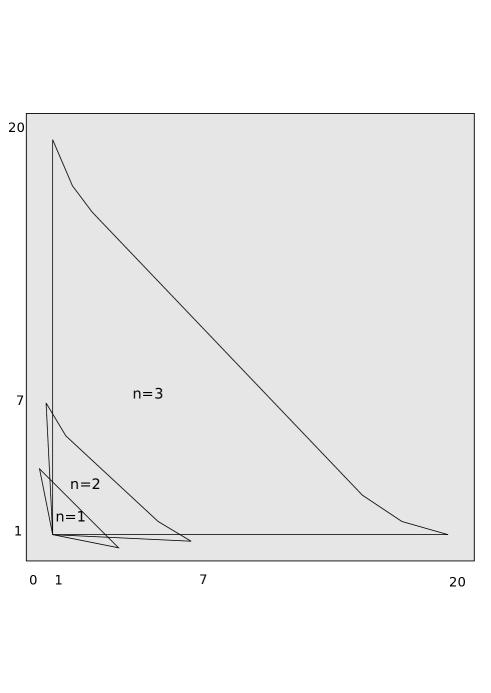
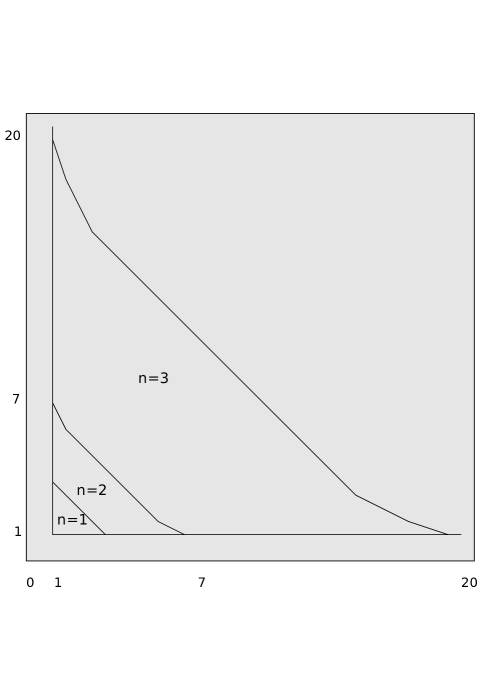
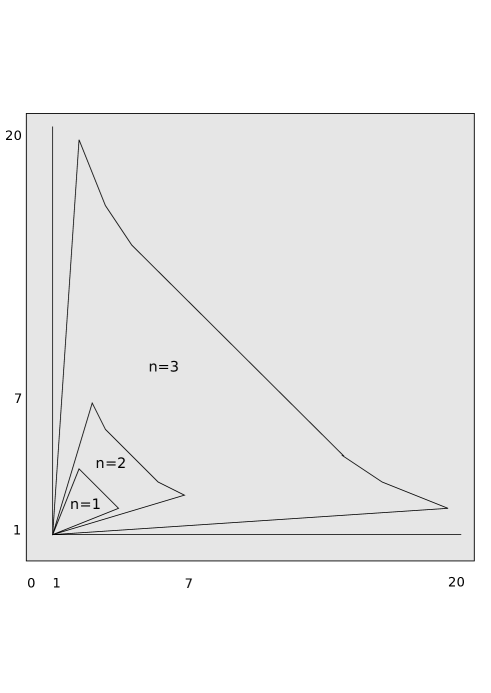
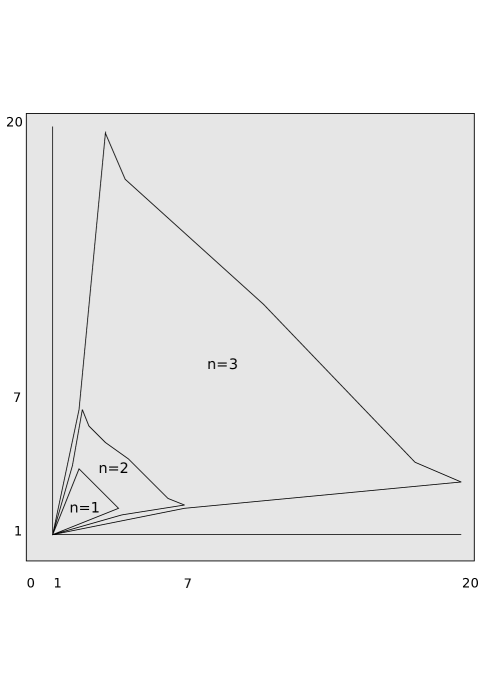
From the graph it appears that the solution space strictly increases with when . However, this is not true for .
8 Conclusion
In this article, we built upon existing methodologies that use relative entropy based ideas for incorporating mathematically specified views/constraints to a given financial model to arrive at a more accurate one, when the underlying random variables are light tailed. In the existing financial literature, these ideas have found many applications including in portfolio modeling, in model calibration and in ascertaining the pricing probability measure in incomplete markets. Our key contribution was to show that under technical conditions, using polynomial-divergence, such constraints may be uniquely incorporated even when the underlying random variables have fat tails. We also extended the proposed methodology to allow for constraints on marginal distributions of functions of underlying variables. This, in addition to the constraints on moments of functions of underlying random variables, traditionally considered for such problems. Here, we considered, both -divergence and polynomial-divergence as objective.
We also specialized our results to the Markowitz portfolio modeling framework where multivariate Gaussian distribution is used to model asset returns. Here, we developed close form solutions for the updated posterior distribution. In case when there is a constraint that a marginal of a single portfolio of assets has a fat-tailed distribution, we showed that under the posterior distribution, marginal of all assets with non-zero correlation with this portfolio have similar fat-tailed distribution. This may be a reasonable and a simple way to incorporate realistic tail behavior in a portfolio of assets.
We also qualitatively compared the solution to the optimization problem in a simple setting of exponentially distributed prior when the objective function was -divergence, polynomial-divergence and total variational distance. We found that in certain settings, -divergence may put more mass in tails compared to polynomial-divergence, which may penalize tail deviation more. Finally, we numerically tested the proposed methodology on some simple examples.
Acknowledgement: The authors would like to thank Paul Glasserman for many directional suggestions as well as specific inputs on the manuscript that greatly helped this effort. We would also like to thank the Associate Editor and the referees for feedbacks that substantially improved the article.
9 Appendix: Proofs
We first show that as . To this end, let
We have
where is the expectation operator w.r.t density function .
Also
Since satisfies , it follows that increasing leads to reduction in . That is, is a non-increasing function of .
Suppose that . Then for all . But since we have as , a contradiction. Hence, as .
Next, since
we see that
Hence, to prove that the LHS converges to zero as
, it suffices to show
that
or that
.
Note that the constraint equation can be re-expressed as:
or
| (32) |
Further, by integration by parts of the numerator, we observe that
From the above equation and (32), it follows that
| (33) |
Since , it suffices to show that
Suppose this is not true. Then, there exists an and a sequence such that . Equation (32) may be re-expressed as:
| (34) |
Given an arbitrary , one can find an (so that when ) such that, for
Re-expressing the LHS of (34) evaluated at as
we see that this is bounded from below by
For sufficiently large , this is greater than zero providing the desired contradiction to (34).
Proof of Theorem 2: Let . and . Consider the Lagrangian for defined as
| (35) |
We first argue that is a convex function of . Given that are linear in , it suffices to show that is a convex function of .
Note that for ,
equals
which in turn is dominated by
which equals
Therefore, the Lagrangian is a convex function of .
We now prove that is minimized at . For this, all we need to show is that we cannot improve by moving in any feasible direction away from . Since, satisfies all the constraints, the result then follows. We now show this.
Let denote and . Note that (35) may be re-expressed as
For any and consider the function
This in turn equals
We now argue that . Then from this and convexity of , the result follows.
To see this, note that equals
| (36) |
Due to the definition of and , it follows that the term inside the braces in the integrand in (36) is a constant. Since both and are probability measures, therefore and the result follows.
Proof of Theorem 3: Let denote the set of all strongly feasible solutions to (12). Consider the following set of equations:
| (37) |
We say that is a strongly feasible solution to (37) if it solves (37), and lies in the set:
Let denote the set of all strongly feasible solutions to (37).
Let and be the mappings defined by
and
It is easily checked that mapping is a bijection with inverse . Note that if , then . To see this, simply divide the numerator and the denominator in (12) by . Conversely, if , then . To see this, divide the numerator and the denominator in (37) by .
Therefore, its suffices to prove uniqueness of strongly feasible solutions to (37). To this end, consider the function :
Then,
| (38) |
and
We see that the last integral can be written as times a positive constant independent of and , where denotes expectation under the measure
Now from the identity
and the assumption on ’s it follows that the Hessian of the function is positive definite. Thus, is strictly convex in its domain of definition, that is in . Therefore if a solution to the equation
| (39) |
exists in , then it is unique. From (38) it follows that the set of equations given by (39) and (37) are equivalent.
Proof of Proposition 3: First assume that so that has no solution. Note that may not belong to so that may also not have a solution. Let denote the open ball centered at and radius with respect to the metric defined at Section 3.3. For arbitrary , let . Then has a solution, say and let denote the associated parameters. It follows that is feasible for for any . Since is a solution to , we have
or
But, by triangle inequality and definition of , it follows that
Therefore,
Since, we have
Since can be chosen arbitrarily small, we conclude that
| (40) |
Now, since , by definition of we have
Together with inequality (40), we have,
If then has a solution. Then the above analysis simplifies: and each can be taken to be equal to . We conclude that
or .
Proof of Theorem 4: In view of (18), we may fix the marginal distribution of to be and re-express the objective as
The second integral is a constant and can be dropped from the objective. The first integral may in turn be expressed as
Similarly the moment constraints can be re-expressed as
or
Then, the Lagrangian for this constraint problem is,
Note that by Theorem (1)
has the solution
where we write for . Now taking , it follows from Assumption 3 that is a solution to
Proof of Theorem 5: Let be a function defined as
Then,
Hence the set of equations given by (20) is equivalent to:
| (41) |
Since
we have
Where denote expectation with respect to the density function . By our assumption, it follows that the Hessian of is positive definite. Thus, the function is strictly convex in . Therefore if there exist a solution to (41), then it is unique. Since (41) is equivalent to (20), the theorem follows.
Proof of Theorem 6: Fixing the marginal of to be we express the objective as
This may in turn be expressed as
Similarly, the moment constraints can be re-expressed as
Then, the Lagrangian for this constraint problem is, up to the constant ,
By Theorem (2), the inner minimization has the solution . Now taking , it follows from Assumption (4) that is the solution to .
Proof of Proposition 2: In view of Assumption (2), we note that for all if . By Theorem (2), the probability distribution minimizing the polynomial-divergence (with ) w.r.t. is given by:
where
From the constraint equation we have
Since, , the -th degree term in (14) is strictly positive and the constant term is negative so there exists a positive that solves this equation. Uniqueness of the solution now follows from Theorem 3. .
Proof of Proposition 4: By Theorem 4:
where
Here the superscript corresponds to the transpose. Now is the -variate normal density with mean vector:
and the variance-covariance matrix:
Hence is the normal density with mean and variance-covariance matrix . Now the moment constraint equation (25) implies:
Therefore, to satisfy the moment constraint, we must take
Putting the above value of in we see that is the normal density with mean
and variance-covariance matrix
Suppose that the stated assumptions hold for . Under the optimal distribution, the marginal density of is
Now the limit in (28) is equal to:
The term in the exponent is:
where .
We make the following substitutions:
Assuming that , the inverse map
is given by:
The integrand becomes:
By assumption,
for some non-negative function such that when has a Gaussian distribution. We therefore have, by dominated convergence theorem
which, by our assumption on , in turn equals
References
- [1] S. Abe. Axioms and uniqueness theorem for tsallis entropy. Physics Letters A, 2000.
- [2] M. Avellaneda. Minimum entropy calibration of asset-pricing models. International Journal of Theoretical and Applied Finance., 1:447–472, 1998.
- [3] M. Avellaneda, R. Buff, C. Friedman, N. Grandchamp, L. Kruk, and J. Newman. Weighted monte carlo: A new technique for calibrating asset pricing models. International Journal of Theoretical and Applied Finance., 4(1):91–119, March 2001.
- [4] F. Black and R. Litterman. Asset allocation: combining investor views with market equilibrium. Goldman Sachs Fixed Income Research, 1990.
- [5] P. Buchen and M. Kelly. The maximum entropy distribution of an asset inferred from option prices. The Journal of Financial and Quantitative Analysis., 31(1):143–159, March 1996.
- [6] R. Cont and P. Tankov. Non-parametric calibration of jump-diffusion option pricing models. Journal of Computational Finance, 7(3):1–49, 2004.
- [7] T. Cover and J. Thomas. Elements of Information Theory. John Wiley and Sons, Wiley series in Telecommunications, 1999.
- [8] I. Csiszar. Information-type measures of difference of probability distributions and indirect observations. Studia Scientifica Mathematica Hungerica., 2:299–318, 1967.
- [9] I. Csiszar. On topology properties of -divergences. Studia Scientifica Mathematica Hungerica., 2:329–339, 1967.
- [10] I. Csiszar. A class of measure of informativity of observation channels. Periodica Mathematica Hungerica., 2(1-4):191–213, 1972.
- [11] I. Csiszar. I-divergence geometry of probability distribution and minimization problems. Annals of Probability, 3(1):146–158, 1975.
- [12] I. Csiszar. Axiomatic characterization of information measures. Entropy., 10:261–273, 2008.
- [13] A. Dembo and O. Zeitouni. Large Deviations Techniques and Applications. Springer, Application of mathematics-38, 1998.
- [14] R. J. V. dos Santos. Generalization of shannon’s theorem for tsallis entropy. Journal of Mathematical Physics, 21, 1997.
- [15] P. Dupuis and R. Ellis. A Weak Convergence Approach to the Theory of Large Deviations. Wiley, Wiley series in probability and statistics, 1986.
- [16] W. Feller. An Introduction to Probability Theory and its Applications,Vol-2. John Wiley and Sons Inc., New York, 1971.
- [17] C. Friedmann, J. Huang, and S. Sandow. A utility-based approach to some information measures. Entropy., 9(1):1–26, 2007.
- [18] C. Friedmann, Y. Zhang, and J. Huang. Estimating flexible, fat-tailed asset return distributions. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1626342,, 2010.
- [19] M. Fritelli. The minimal entropy martingale measures and the valuation problem in incomplete market. Mathematical Finance, 10:39–52, 2000.
- [20] J. Gibbs. Elementary Principles in Statistical Mechanics. New York: Scribner’s, 1902, Reprint-Ox Bow Press, 1981.
- [21] P. Glasserman and B. Yu. Large sample properties of weighted monte carlo estimators. Operation Research, 53(2):298–312, 2005.
- [22] T. Goll and L. Ruschendorf. Minimal distance martingale measure and optimal portfolios consistent with observed market prices. In Stochastic Monographs, volume 12, pages 141–154. Taylor and Francis, London, 2002.
- [23] L. Golshani, E. Pasha, and Y. Gholamhossein. Some properties of renyi entropy and renyi entropy rate. Information Sciences, 170:2426–2433, 2009.
- [24] E. Jaynes. Information theory and statistical mechanics. Physics Reviews., 106:620–630, 1957.
- [25] E. Jaynes. Probability Theory: The Logic of Science. Cambridge University Press, 2003.
- [26] M. Jeanblanc, S. Kloeppel, and Y. Miyahara. Minimal - martingale measures for exponential levy processes. Annals of Applied Probability, 17(5/6):1615–1638, 2007.
- [27] P. Jizba and T. Arimitsu. The world according to renyi:thermodynamics of multi fractal systems. Annals of Physics, 312:17–59, 2004.
- [28] M. Kallsen. Utility-based derivative pricing in incomplete markets. In Mathematical Finance - Bachelier Congress 2000, pages 313–338. Springer, Berlin, 2002.
- [29] J. Kapur. Maximum Entropy Models in Science and Engineering. New Age International Publishers, Wiley series in Telecommunications, 2009.
- [30] A. I. Khinchin. Mathematical foundation of information theory. Dover, New York, 1957.
- [31] Y. Kitamura and M. Stutzer. Entropy-based estimation methods. In Encyclopedia of Quantitative Finance, pages 567–571. Wiley, 2010.
- [32] D. Luenberger. Linear and Nonlinear Programming 2nd Edition. Springer, 2003.
- [33] A. Meucci. Fully flexible views: theory and practice. Risk, 21(10):97–102, 2008.
- [34] J. Mina and J. Xiao. Return to riskmetrics: the evolution of a standard. RiskMatrics publications, 2001.
- [35] J. Pazier. Global portfolio optimization revisited: a least discrimination alternative to black-litterman. ICMA Centre Discussion Papers in Finance, July 2007.
- [36] W. Press, S. Teukolsky, W. Vetterling, and B. Flannery. Numerical Recipes 3rd Edition: The Art of Scientific Computing. Cambridge University Press, 2007.
- [37] E. Qian and S. Gorman. Conditional distribution in portfolio theory. Financial analyst journal., 57(2):44–51, March-April 1993.
- [38] A. Renyi. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, pages 547–561, 1960.
- [39] C. Shannon. A mathematical theory of communication. The Bell System Technical Journal, 27:379–423,623–656, 1948.
- [40] W. Slomczynski and T. Zastawniak. Utility maximizing entropy and the second law of thermodynamics. The Annals of Probability., 32(3A):2261–2285, 2004.
- [41] M. Stutzer. A simple non-parametric approach to derivative security valuation. Journal of Finance, 101(5):1633–1652, 1997.
- [42] C. Tsallis. Possible generalization of boltzman gibbs statistics. Journal of Statistical Physics, 52:479, 1988.
- [43] X. Zhou, J. Huang, C. Friedmann, and S. Sandow. Private firm default probabilities via statistical learning theory and utility maximization. Journal of Credit Risk., 2(1):1–26, 2006.