Infinite Bar-Joint Frameworks, Crystals and Operator Theory
Abstract.
A theory of flexibility and rigidity is developed for general infinite bar-joint frameworks . Determinations of nondeformability through vanishing flexibility are obtained as well as sufficient conditions for deformability. Forms of infinitesimal flexibility are defined in terms of the operator theory of the associated infinite rigidity matrix . The matricial symbol function of an abstract crystal framework is introduced, being the matrix-valued function on the -torus representing as a Hilbert space operator. The symbol function is related to infinitesimal flexibility, deformability and isostaticity. Various generic abstract crystal frameworks which are in Maxwellian equilibrium, such as certain -regular planar frameworks, are proven to be square-summably infinitesimally rigid as well as smoothly deformable in infinitely many ways. The symbol function of a three-dimensional crystal framework determines the infinitesimal wave flexes in models for the low energy vibrational modes (RUMs) in material crystals. For crystal frameworks with inversion symmetry it is shown that the RUMS appear in surfaces, generalising a result of F. Wegner [32] for tetrahedral crystals.
1991 Mathematics Subject Classification:
52C75, 46T20.1. Introduction
Infinite bar-joint frameworks appear frequently as idealised models in the analysis of deformations and vibration modes of amorphous and crystalline materials. See [11], [18], [6], [14], [32] and [36] for example and the comments below. Despite these connections there has been no extended mathematical analysis of such models. Notions of rigidity, flexibility, deformability, constrainedness, independence and isostaticity, for example, are usually employed either in the sense of their usage for a finite approximating framework or in a manner drawn from experience and empirical fact in the light of the application at hand. It seems that a deeper understanding of the models is of considerable interest in its own right and that a mathematical development may prove useful in certain applications. In what follows we shall provide formal definitions of the terms above in quite a wide variety of forms and we examine some of their inter-relationships and manifestations.
Suppose that one starts with a flexible square bar-joint framework in two dimensions and that this is then extended periodically to create an infinite periodic bar-joint network. Is the resulting assemblage, with inextendible bars, continuously flexible in two dimensional space? A moment’s reflection reveals a proliferation of flexibility, such as sheering motions with one half of the network fixed.
However such movement is dramatically infinite and a natural second question is whether for periodic frameworks such as these there are flexes for which the total joint movement is finite. The less obvious negative answer in these cases offers some satisfaction in that it is consistent with so-called Maxwell counting in the case where the average number of degrees of freedom of the joints matches the average number of constraints per joint. (See Theorem 5.2 and Corollary 5.3.)
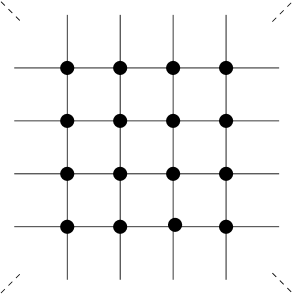
On the other hand if, for the grid example, one rigidifies alternate squares by adding diagonal bars, as shown, then the resulting structure of corner linked rigid squares remains properly flexible, although now uniquely so. In fact the unique flex has an affinely contracting character (See Definition 4.3) with alternating rotation of the squares.
More generally the flexibility of polytope networks in two and three dimensions continues to be of interest in the modeling of crystals and amorphous materials, especially with regard to their low frequency vibrational modes. Such modes appear, for example, in higher order symmetry phases of tetrahedral crystals and are referred to as rigid unit modes (RUMs). Indeed in the paper of Giddy et al [11] the alternating flex of the squares framework above has been associated with vibrational modes in perovskite. See also Hammond et al [18], Wegner [32], as well as Goodwin et al [14] for a useful overview. At the same time, in the modeling of amorphous materials, such as glasses, there is interest in understanding the critical probabilities that guarantee flexibility and rigidity for classes of randomly constructed frameworks. See, for example, Chubynsky and Thorpe [6] for the recent determination of such probabilities in simulation experiments.
Formally, a framework in (or bar-joint framework, or distance-constraint framework) is a pair where is a simple connected graph and is a framework vector made up of framework points in associated with the vertices of . The framework edges are the (closed) line segments associated with the edges of the graph . As the ellipsis suggest, we allow to be a countable graph. We shall also define a crystal framework as a framework with translational symmetry which is generated by a connected finite motif of edges and vertices. (See Definition 4.2.)
When is finite and the framework points are generically located in then a celebrated theorem of Laman [21], well-known in structural engineering and in the discrete mathematics of rigidity matroids [15], gives a simple combinatorial criterion for the minimal infinitesimal rigidity of the framework; the graph itself satisfies Maxwell’s counting rule , and subgraphs must comply with . This is a beautiful result since the rigidity here is the noncombinatorial requirement that the kernel of an associated rigidity matrix has the smallest dimension (namely three) for some (and hence all) generic framework. On the other hand frameworks with global symmetries, or even with ”symmetric elements” (such as parallel edges) are not generic, that is, algebraic dependencies do exist between the framework point coordinates. Such frameworks arise in classical crystallography on the one hand and in mathematical models in structural engineering and in materials science on the other. See, for example, Donev and Torquato [7], Hutchinson and Fleck [19], Guest and Hutchinson [16] and various papers in the conference proceedings [31].
The present paper develops two themes. The first concerns a mathematical theory of deformability and rigidity for general infinite frameworks, with frequent attention to the case of periodic frameworks. There is, unsurprisingly, a great diversity of infinite framework flexing phenomena and we introduce strict terminology and some methods from functional analysis to capture some of this. In the second theme we propose an operator theory perspective for the infinitesimal (first order) flexibility of infinite frameworks.
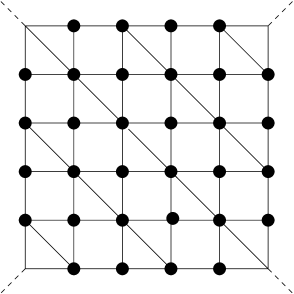
Particularly interesting classes of infinite frameworks, from the point of view of flexibility, are those in the plane whose graphs are -regular and those in three dimensions whose graphs are -regular. In this case the graphs are in Maxwell equilibrium, so to speak, and so in a generic framework realisation any flex must activate countably many vertices. This is also the case for various periodic realisations such as the kagome framework, , formed by corner-joined triangles in regular hexagonal arrangement, and frameworks in three dimensions formed by pairwise corner-joined tetrahedra. Despite being internally rigid in this way (Definition 2.18 (vi)) these frameworks admit diverse deformations. For example we note that the kagome framework admits uncountably many distinct deformations and in Theorem 4.4 we note that -periodic cell-generic grid frameworks in admit deformations associated with affine transformations.
A significant phenomenon in the infinite setting is the appearance of vanishing flexibility. This means, roughly speaking, that the framework is a union of finite flexible subframeworks but the extent of flexibility diminishes to zero as the size of these subframeworks increases, so that the infinite assemblage is inflexible. Elementary examples were indicated in [25] but we give more subtle examples here which are due to flex amplification at second order distances through concatenation effects. In particular there are bounded infinitesimal flexes in periodic frameworks that admit no continuous extensions and which do not arise as the derivative of a smooth deformation. We also note that there are -periodic crystal frameworks which are somewhat paradoxical, being indeformable despite the flexibility of all supercell subframeworks. On the other hand, in the positive direction, in Theorem 2.20 we give a general result which identifies a uniform principle for the existence of a deformation. The proof uses the Ascoli-Arzela theorem on the precompactness of equicontinuous families of local flexes. It remains an interesting open problem to determine necessary and sufficient conditions for the rigidity and bounded rigidity of periodic planar frameworks.
The operator theory perspective for frameworks was suggested in [25] as an approach to a wider understanding of infinitesimal flexibility and rigidity. In this consideration the rigidity matrix is infinite and determines operators between various normed sequence spaces associated with nodes and with edges. Also, in [27] we have given a direct proof of the Fowler-Guest formula [9] for symmetric finite frameworks which is based on the commutation properties of the rigidity matrix as a linear transformation and this adapts readily to the infinite case and the rigidity operators of crystal frameworks. Indeed, translational symmetry ensures that the rigidity matrix intertwines the coordinate shift operations. We consider square summable flexes and stresses and for distance regular locally finite frameworks is interpreted as a bounded operator between Hilbert spaces. Also, enlarging to complex Hilbert spaces the Fourier transform is identified as a multiplication operator
given by an matrix-valued function on the -torus. The function for is referred to as the matricial symbol function associated with the particular generating motif. The terminology and notation is borrowed from standard usage for Toeplitz operators and multiplication operators (see [3] for example). Many aspects of infinitesimal flexibility and isostaticity are expressible and analysable in terms of the matricial symbol function and its associated operator theory. For example a straightforward consequence of the operator theoretic approach is the square summable isostaticity of various nondegenerate regular frameworks that satisfy Maxwell counting, such as grid frameworks and the kagome framework.
An explicit motif-to-matrix function algorithm is given for the progression
Furthermore the identification of infinitesimal periodic-modulo-phase flexes and their multiplicities is determined by the degeneracies of as ranges on the -torus. In particular, the function
gives a determination of the mode multiplicity of periodic-modulo-phase infinitesimal flexes.
In the discussions below we are mainly concerned with properties of mathematical bar-joint frameworks. (The framework bars are indestructibly inextensible, the joints are located deterministically, they maintain perfect, frictionless fit and may even coincide.) Nevertheless, analysis of matricial symbol functions and their degeneracies are particularly relevant to the description and analysis of Rigid Unit Modes in material crystals. We show that for crystal frameworks with inversion symmetry the set of RUMS is a union of surfaces. This generalises and provides an alternative perspective for a recent result of Wegner [32] for tetrahedral crystals.
Operator theory methods have proven beneficial in many areas of mathematics and applications. This is evidently the case for multi-linear systems theory and in control theory for example. Infinite rigidity matrix analysis seems to possess some similitudes with these areas and it seems to us that here too the operator turn will be a useful one.
The development is as follows. Section 2 gives a self-contained account of continuous flexibility and rigidity, and vanishing flexibility and one-sided flexibility is proven for various periodic infinite frameworks. Forms of flexibility, such as bounded flexes, square summable flexes, summable flexes and vanishing flexes are defined and determined for some specific examples. Sufficient conditions are obtained for the existence of a smooth flex and a flex extension problem for generic finite frameworks is posed. A positive resolution of this problem would provide a natural extension of Laman’s theorem to infinite frameworks. In Section 3 we consider infinitesimal theory for general infinite frameworks and determine a number of rigidity operators and their flex and stress spaces. (The topic is taken up in more detail for crystal frameworks in Section 5.) In Section 4 we consider (abstract) crystal frameworks in two or three dimensions. These are generated by a motif and a discrete translation group. Various forms of deformations are considered, such as strict periodic flexibility, flow-periodic flexibility and flexes with reduced periodicity and symmetry. Also we indicate the flat torus model for crystal frameworks and recent results of Ross and Whiteley in this direction, including a periodic analogue of Laman’s theorem. In the final section we consider the matricial symbol function approach and various examples. In particular we determine the (unit cell) infinitesimal wave flex multiplicities for the kagome net framework by factoring the determinant of the matricial symbol function.
Acknowledgments. Some of the developments here have benefited from discussions and communications with Robert Connelley, Patrick Fowler, Simon Guest, Elissa Ross and Walter Whiteley during and following the Summer Research Workshop on ”Volume Inequalities and Rigidity”, organised by Károly Bezdek, Robert Connelly, Balázs Csikös and Tibor Jordán, at the Department of Geometry, Institute of Mathematics, Eotvos Lorand University in July 2009.
2. Infinite Bar-joint Frameworks
In this section we give a self-contained rigourous development of infinite frameworks and examine the nonlinear aspects of their flexibility by continuous deformations and their associated rigidity. In the next section we consider infinitesimal flexibility and rigidity in a variety of forms.
2.1. Continuous flexibility and rigidity
We first define continuous flexes and continuous rigidity. The latter means, roughly speaking, that the framework admits no proper deformations that preserve the edge lengths. The definition below gives straightforward generalisations of terms used for finite frameworks. In that case we note that a continuous flex is often referred to as a finite flex while in engineering models it is referred to as a finite mechanism.
Unless we specify otherwise we shall assume that the frameworks under consideration are proper in that the framework points do not lie on a hyperplane in the ambient space and that the framework edges have nonzero lengths .
Definition 2.1.
Let be an infinite framework in , with connected abstract graph , and .
(a) A base-fixed continuous
flex, or, simply, a flex of , is a function
from to with the following
properties;
(i) ,
(ii) each coordinate function is continuous,
(iii) for some base edge with , and for all ,
(iv) each edge distance is conserved; for all edges , and all , and
(v) for some .
(b) The framework is flexible, or more precisely, continuously flexible, if it possesses a base-fixed continuous flex.
(c) The framework is rigid, or continuously rigid, if it is not flexible.
Similarly one defines base-fixed continuous flexes and continuous rigidity for proper frameworks in by replacing a base edge by an appropriate set of framework points with maximal affine span.
The simplest kind of continuously rigid framework in the plane is one which is a union of continuously rigid finite frameworks. In particular the following theorem follows simply from the theorem of Laman indicated in the introduction.
Theorem 2.2.
Let be a connected graph which is the union of a sequence of finite Laman graphs. Then every generic realisation in the plane is continuously rigid.
By generic, or, more precisely, algebraically generic, we mean, as is usual, that the coordinates of any finite set of framework points is algebraically independent over the rational numbers. Unlike the case of finite frameworks it is possible to construct two generic frameworks with the same abstract graph one of which is flexible and one of which is rigid. Accordingly it seems appropriate to formulate the following definition to extend the usual usage.
Definition 2.3.
An infinite simple connected graph is said to be rigid, or generically rigid, for two dimensions, if every generic framework in the plane is rigid.
Note that if is rigid and if is a containing graph for with the same vertex set then every generic framework in the plane is rigid.
It seems likely that the converse to the theorem above holds. That is, if does not contain a sequentially Laman graph (in the sense below) with the same vertex set, then is not generically rigid. We comment more on this later in Section 2.6.
Rigidity and flexibility are properties of the entire framework and it is such entire features and their inter-relationships that are of primary interest in what follows. One would like to understand the relationship with small scale or local structure, such as local counting conditions and local connectivity. Additionally, as above, one would like to relate entire properties to sequential features that pertain to an exhausting chain of finite subframeworks and for this the following definition is helpful.
Definition 2.4.
If is a property for a class of finite, simple, connected graphs (resp. frameworks) then a graph (resp. framework ) is sequentially or - if is the union of graphs in some increasing sequence of vertex induced finite subgraphs and each graph (resp. framework ) has property .
For example, we may refer to an infinite graph as being -Laman, or -Laman and an infinite framework as being -rigid. To say that an infinite framework is -flexible, or sequentially flexible, is rather vacuous since it usually prevails for trivial reasons. (One can construct countably infinite edge complete frameworks that may fail to be so but all our examples are sequentially flexible.) The more interesting property is the failure of sequentially rigidity as in the following definition.
Definition 2.5.
A framework is said to have vanishing flexibility if it is continuously rigid but not -rigid.
An important topic in finite rigidity frameworks is that of global rigidity, also called unique rigidity. This holds, in the two dimensional setting, if there is, up to congruency, only one embedding of the framework in . This implies, for example, that these frameworks admit no foldings, and indeed have unique diagrams up to rotations and reflection. One can extend the term to infinite frameworks but we do not consider this issue here at all. One might be tempted to say that a rigid infinite framework, especially one with vanishing flexibility, is globally rigid, but we refrain from doing so because of conflict with this usage.
The term ”global” for global rigidity is natural since rigidity for finite frameworks is equivalent to the ”local” property that ”nearby equivalent frameworks are congruent”. That is, if there exists such that if is a finite framework with , for all , and if is equivalent to , in the sense that corresponding edges have the same length, then and are congruent. See, for example, Gluck [12] and Asimow and Roth [1].
An infinite simple graph is locally finite if for every vertex there are finitely many incident edges. Amongst such graphs are those for which there is an upper bound to the degree of the vertices, as in the case of the graphs of crystal frameworks. Within this class a graph is said to be -regular if every vertex has degree . We remark that the theory of tilings provides a wealth of examples of planar frameworks which are -regular.
Remark 2.6.
In what follows we consider only locally finite frameworks. Without this assumption it is possible to construct quite wildly flexing planar linkages. In fact, given a continuous function one can construct an infinite linkage, in the sense of the definition below, and a base-fixed flex with a motion for a particular vertex that is equal to . This includes the possibility of space filling curves. This is a consequence of a continuous analogue of a well known theorem of Kempe which asserts that any finite algebraic curve in the plane can be simulated by a finite linkage. For more details see Owen and Power [26].
2.2. Linkages
The removal of a framework edge from a rigid framework may result in flexibility which is, roughly speaking, of a one-dimensional nature. We reserve the term linkage for such a mathematical object, which we formally specify in the next definition. We remark that finite frameworks are also referred to as linkages, particularly when they are flexible, perhaps with several degrees of freedom, but this should not cause confusion.
A two-sided continuous flex of is defined as above but for the replacement of by . The following formal definition of an infinite linkage reflects the fact that the initial motion of a base-fixed linkage is uniquely determined by the angle change at any flexible joint.
Definition 2.7.
A linkage in is a finite or infinite connected framework in for which there exists a continuous two-sided base-fixed flex with framework edges such that the cosine angle function
is strictly increasing on , and such that is the unique two-sided flex of with , for .
Many interesting finite linkages were considered in the nineteenth century in connection with mechanical linkages. See, for example, Kempe [20]. Note however that the definition is liberal in allowing coincident joints and self-intersecting flexes. Also the definition refers to local deformation behaviour and this does not rule out the possibility of bifurcations occurring in a parameter extension of the given flex.
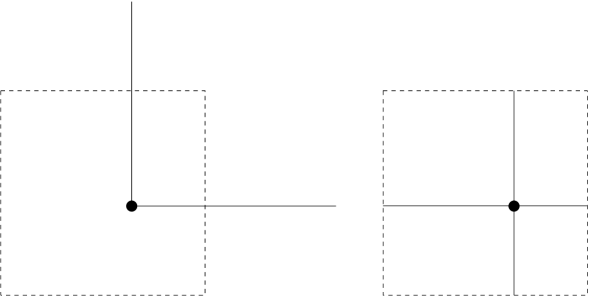
It is a simple matter to construct diverse infinite linkages by tower constructions or progressive assembly. (See, for example, the Cantor tree frameworks of [25].) However, some such constructions lead to frameworks with vanishing flexibility and so are not linkages in this case. An elementary illustration is given in Figure 4 wherein a two-way infinite rectangular strip linkage is augmented by adding flex-restricting cross braces in an alternating fashion. If the brace lengths tend to the diagonal length from above then the infinite framework is rigid. Evidently in this case the triangle inequality is playing a role in isolating one real solution to the solution set defined below. One can also construct examples in which this isolation is less evident, with all joint angles bounded away from zero and for example.
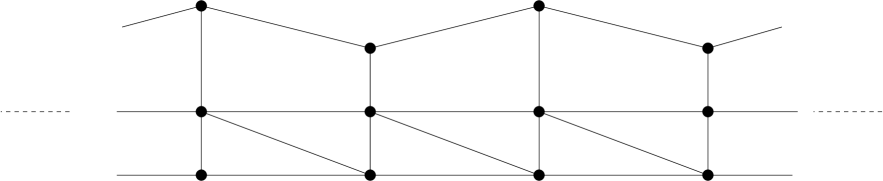
A more interesting and subtle form of vanishing flexibility is due to progressive flex amplification rather than local flex restrictions. Roughly speaking, if a small flex is initiated at a particular joint and the flex propagates in some amplifying manner, then the triangle inequality at some far remove may prohibit any further increase. If the framework is infinite then no local joint flex may be possible at all. The strip framework of concatenated levers in Figure 5 gives an example where the amplification is evident, while the rigidity of the strip framework in Figure 6 and the trapezium strip in Figure 7 is less evident. The lever framework has a natural infintesimal flex, in the sense of Section 3, which is unbounded. The corresponding flexes of Figures 6 and 7 however, are bounded with amplification unfolding as a second order effect. This is proven in the next subsection.


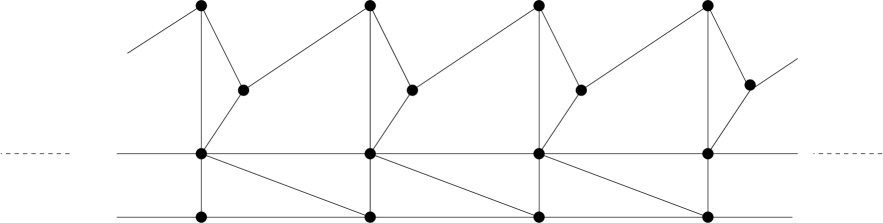


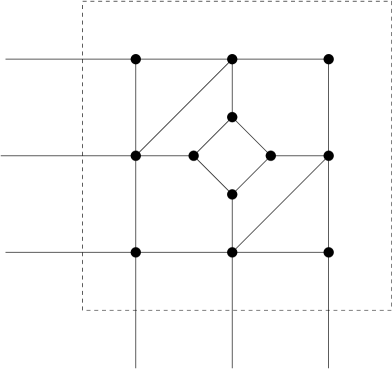
It is a straightforward matter to incorporate the vanishing flexibility of the strips above as subframeworks of a -periodic framework. This process is indicated in Figures 9, 10 and 11 below, where the infinite frameworks are determined as the periodic extensions of the given unit cell. Figure 9 shows a linkage formed as a ”fence lattice” composed of infinite horizontal and vertical -rigid bands. Figure 10 shows an analogue where the infinite bands have been replaced by rigid strip frameworks. Figure 11 is an elaboration of this in which cross braces have been introduced to remove the flexibility. (Only one edge is needed for this whereas the example given is periodic.) The additional degree 2 vertex in the cell ensures that the framework is not -rigid, while the infinite bands remain vanishingly rigid.
Let us note that for the framework in Figure 11, with its curious mixture of rigidity and flexibility, one can add any finite number of additional degree 2 vertices without changing the rigidity of the framework. In particular we have a construction that proves the following proposition.
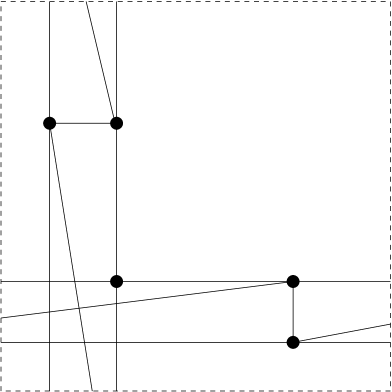
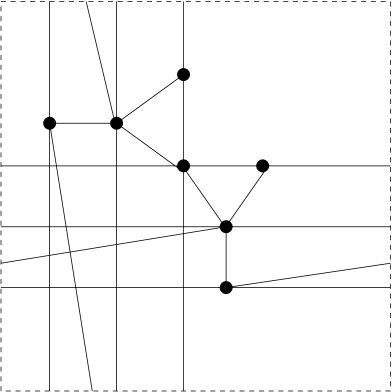
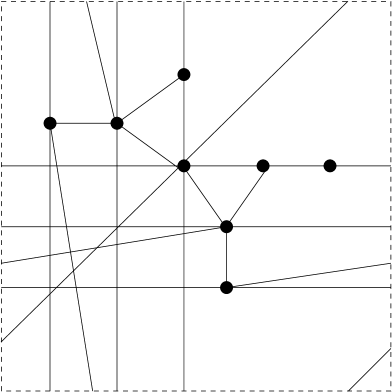
Proposition 2.8.
Let . Then there is a -periodic framework in which is rigid, which is not -rigid and for which the average vertex degree is less than .
One can readily extend this fanciful idea in various ways to obtain such structures in higher dimensions. For example, start with a one-dimensionally periodic -rigid girder in 3D and augment it with trapezium ”tents” of alternating height to creates vanishingly rigid girders. Also periodically interpolate any number of degree two vertices into the tent top edges without removing the vanishing flexibility. Join infinitely many such component girders periodically at appropriate tent-top edges to create a fence framework and add linear jointed cross braces to create, finally, a 2D periodic grid which is continuously rigid in 3D, which is not -rigid and which has average coordination number arbitrarily close to two.
2.3. Relative rigidity and the extension of flexes.
For a finite or infinite framework in define the function
This is the usual edge function of the framework and depends only on the abstract graph .
Definition 2.9.
The solution set, or configuration space, of a framework , denoted , is the set This is the set of all framework vectors for that satisfy the distance constraints equations
In general the solution set of an infinite framework need not be a real algebraic variety even when it is ”finitely parametrised”. In less wild situations it can be useful to relate to the algebraic variety associated with a finite subgraph of , or with an elementary subgraph such as a tree, or even a set of vertices.
Definition 2.10.
An infinite bar-joint framework in is rigid over a subframework if every continuous flex of which is constant valued on is constant. Similarly, if is a subgraph of a countable connected simple graph then is rigid over , or generically rigid over if, for every generic frameworks , every continuous flex of which is constant-valued on is constant.
We may also form the following associated notions.
Definition 2.11.
An infinite framework in is finitely determined if it is rigid over for some finite subgraph and is finitely flexible if it is flexible and finitely determined.
Finite flexibility in the sense above is a strong property in which paths from in the solution set are determined near by the finite algebraic variety . Note that the term ”infinitely flexible” is not appropriate to describe a flexible framework which is not finitely flexible since it is possible to construct linkages, in our formal sense, which are not finitely flexible. This is the case for the periodic framework in Figure 12 which is a linkage because of partial vanishing flexibility.
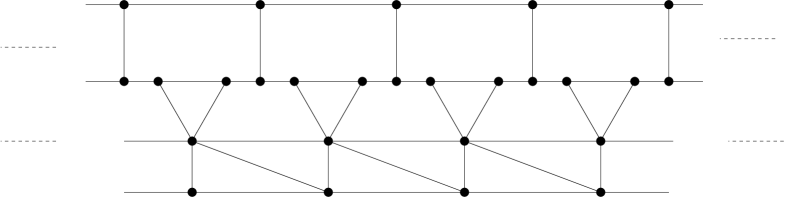
An important class of frameworks which appear in mathematical models are those that are distance regular.
Definition 2.12.
A framework in is distance-regular if there exist such that for all edges ,
For such a framework it is natural to consider the nearby frameworks with the same graphs but with slightly perturbed framework points (and therefore edge lengths). If a property holds for all such frameworks, for some perurbation distance then we call such a property a stable property for the the framework.
Formally, an -perturbation of a distance regular framework is a framework for which , for all corresponding framework points. Recall that a finite framework in is said to be -rigid if it is congruent to every equivalent -perturbation. Let us say that a general framework is perturbationally rigid if it is -rigid for some . It is a well-known fact that perturbational rigidity and rigidity are equivalent in the case of algebraically generic finite frameworks [1], [12]. However, it is straightforward to see that this equivalence thoroughly fails for general infinite frameworks (see [25]).
Definition 2.13.
Let be a distance-regular framework. Then is stably rigid (resp stably flexible) if it is rigid (resp. flexible) and for sufficiently small every -perturbation of is rigid (resp. flexible).
Likewise, if is any particular property of a distance-regular infinite framework then we may say that is stably if, for some , the property holds for all -perturbations.
Proposition 2.14.
The periodic trapezium strip frameworks, with alternating unequal heights , are rigid. In particular the rectangle strip linkage (of Figure 7) is not stably flexible.
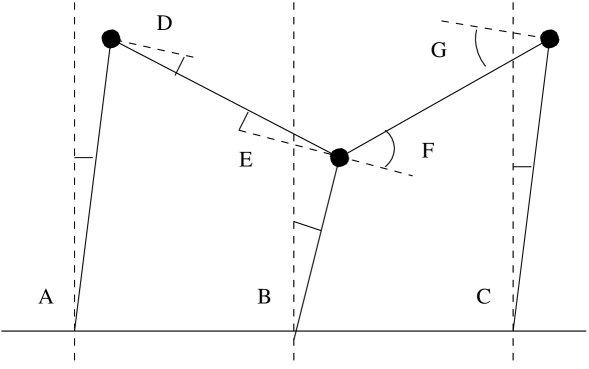
Proof.
Figure 13 shows the displacement of a double trapezium to the right. Let the three vertical bar lengths be and units with . The displaced position has angles at the base line and angles occurring relative to the trajectory tangents of the displaced vertices. For a subsequent incremental change , with resulting incremental changes we can see from simple geometry that to first order
Suppose now that is regarded as a specialisation of the input angle with resulting output angle , so that at we have . Then
Similarly, with angle regarded as the output angle for the angle transmission function , we have
and so
Note that since we have also , and since we have , from which it follows that both ratios above are less than one. Thus certainly for where is the first positive angle for which
It follows, from the mean value theorem, that the double trapezium angle transmission function is an increasing differentiable function with
It follows immediately that the right-semi-infinite trapezium strip is right flexible.
We let , which we refer to as the locking angle. Note the second trapezium of the double admits no increase of this angle. In view of the above we have .
Suppose now that is the two-way-infinite trapezium strip, with . Let be a flex and suppose that for a fixed framework edge with length the angle is greater than zero for some time and that is the first such time. Then certainly . Note that are the angles of the edges of length , counted off to the left. In view of the function dominance it follows that for some , which is a contradiction. ∎
The argument above also shows that the semi-infinite trapezium strip framework of Figure 7 has a continuous flex but no two-sided flex.
Remark 2.15.
It seems to be of interest to analyse strip frameworks in further detail. For example, a trapezium strip framework is not stably rigid, despite the apparent ”robustness” of the argument above. To see this use surgery in the following way. Remove one cross bar, then push the rightmost semifinite strip to the right, by an angle perturbation . Now insert a replacement bar of the required length. One can flex the resulting structure towards the left to restore the position of the right hand strip. Indeed, this is all the flexibility the framework has. The possible flex of an perturbation, such as the one described, seems to be of order and so there does seem to be ”approximate rigidity”.
Remark 2.16.
Consider a periodic trapezium grid framework obtained by perturbing by adding a fixed small positive value to the coordinate of the framework points for the odd values of and . It can be shown that this framework is rigid over any linear subframework. This contrasts with the grid framework itself which is freely flexible over its and axes in the following specific local sense: all sufficiently small flexes of the subframework extends to a flex of the whole framework. On the other hand note that Theorem 4.4 shows that is deformable.
2.4. Forms of flexibility
It seems to be a fundamental and interesting issue to determine the ways in which infinite bar-joint frameworks are rigid or continuously flexible. In this section we give some further definitions, we give sufficient conditions for the existence of a proper flex and we contemplate a plausible infinite framework version of Laman’s theorem.
Flexes are often infinitely differentiable or smooth in the sense of the following formal definition. This is the case for example, for the ”alternation” flexes of and .
Definition 2.17.
A continuous base-fixed two-sided flex of a framework in is a smooth flex if each coordinate function is infinitely differentiable.
The smoothness of a flex is a local requirement whereas the following terms impose various increasing forms of global constraint. In particular rotational flexes of infinite frameworks with unbounded diameter are not bounded flexes, while a translational flex of an infinite framework is a bounded flex but is not a vanishing flex. Adopting a term that has been used in applications [14] we refer to flexes which are not bounded as colossal flexes.
Definition 2.18.
A continuous flex of an infinite framework in is said to be
(i) a bounded flex if for some and every and ,
(ii) a colossal flex if it is not bounded,
(iii) a vanishing flex if is a bounded flex and if the maximal displacement
tends to zero as ,
(iv) a square-summable flex if
(v) a summable flex if
(vi) an internal flex if for all but finitely many the function is constant.
Also we say that has a deformation (resp. bounded or vanishing deformation) if it has a base-fixed flex (which is bounded or vanishing).
Definition 2.19.
A connected infinite locally finite proper framework in two or three dimensions is boundedly rigid (resp. summably rigid, square-summably rigid, smoothly rigid, internally rigid) if there is no deformation, that is, no base-fixed proper continuous flex, which is bounded (resp. summable, square-summable, smooth, internal).
2.5. Sufficient conditions for flexibility
There is a sense in which vanishing flexibility is almost the only obstacle to the existence of a flex of a framework all of whose finite subframeworks are flexible. More precisely, in the hypotheses of the next theorem we assume that there are two distinguished framework vertices, such that any finite subframework containing has a flex which properly separates this pair in the sense of condition (ii) below. The additional requirement needed is that there is a family of flexes of the finite subframeworks whose restrictions to any given subframework are uniformly smooth in the sense of condition (i). Note that the constant here depends only on and indeed the resulting flex may of necessity be a colossal flex.
Theorem 2.20.
Let be an infinite locally finite framework in with a connected graph, let
be subframeworks, determined by finite subgraphs with union equal to and let be vertices in . Suppose moreover that for each there is a base-fixed smooth flex of such that
(i) for each finite framework the set of restriction flexes
have uniformly bounded derivatives, that is, there are constants such that
(ii) the framework points are uniformly separated by each flex in the sense that
for some positive constant .
Then has a deformation.
Note that it is essential that the separated vertices of condition (ii) are the same for each subgraph. To see this note that the two-way infinite trapezium strip framework considered in Figure 7 has smooth deformations on each of its finite strip subframeworks, each of which ”separates” some two vertices (at the end of the strip) by a fixed positive distance. Nevertheless the infinite strip fails to have a deformation.
Proof.
For let be the space of continuous functions from to and note that the family , by the hypotheses, is an equicontinuous family in . Moreover with respect to the supremum norm is a bounded set. By the Ascoli-Arzela theorem (see [30] for example) is precompact and in particular for there is a subsequence such that the restrictions converge uniformly in their (finitely many) coordinates to a flex of . Relabel the sequence as . The restrictions of these flexes to similarly have a convergent subsequence, say , and so on. From this construction select the diagonal subsequence . This converges coordinatewise uniformly to a coordinatewise continuous function
Since the restriction of to every finite subframework is a flex, satisfies the requirements of a flex of , except possibly the properness requirement (v) of Definition 2.1. In view of (ii) however, and so is a continuous flex of . ∎
Remark 2.21.
Computer simulations provide evidence for the fact that small random perturbations of yield frameworks that are flexible. That is it seems that is stably flexible. It would be interesting if the theorem above could assist in a proof of this.
2.6. Flex extensions and generic rigidity
Let us recall a version of Laman’s theorem.
Theorem 2.22.
Let be an algebraically generic finite framework. Then is infinitesimally rigid if and only if the graph has a vertex induced subgraph , with , which is maximally independent in the sense that and for every subgraph of .
For convenience we refer to a maximally independent finite graph as a Laman graph. We remark that any Laman graph can be obtained from a triangle graph by a sequence of moves known as Henneberg moves. The first of these adds a new vertex with two connecting edges while the second breaks an edge into two at a new vertex which is then connected by a new edge to another point of the graph.
Now let be an infinite graph which contains a subgraph on all the vertices of and suppose that is -Laman. In view of Laman’s theorem every algebraically generic realisation of (and hence ) in the plane is -rigid and so continuously rigid. Is the converse true ? That is, if every generic realisation of an infinite graph is rigid does necessarily contain a -Laman subgraph with the same vertex set.
To see this one needs to show is that if is -(Laman-1) and not -Laman, then there exists a vertex generic realisation in the plane which has a continuous flex. That is, we want to build up a flex of the infinite structure by adding new vertices and edges, in the least handicapping way, to allow all, or most of the flex of an initial finite subgraph to be extended.
Alternatively, and more explicitly, suppose that one starts with a generic connected Laman-1 framework with vertices and an infinite sequence of Henneberg move ”instructions”. These instructions yield a unique infinite graph. Is it possible to choose associated framework points so judiciously that some (perhaps small) flex of extends fully to each successive finite extension framework (and hence the infinite framework) ?
3. Rigidity Operators and Infinitesimal Rigidity
In previous sections we have considered some variety in the nature of continuous flexes and how they might distinguished. A companion consideration is the analysis of various spaces of infinitesimal flexes. This gives insight into continuous flexes since the derivative of a differentiable flex is an infinitesimal flex.
Here we give an operator theory perspective for an infinitesimal theory of infinite frameworks in which the rigidity matrix is viewed as a linear transformation or linear operator between various spaces. The domain space contains a space of infinitesimal flexes, which lie in the kernel of the rigidity operator, while the range space contains a space of self-stress vectors namely those in the kernel of the transpose of .
3.1. Infinitesimal rigidity and the rigidity matrix.
Recall that for a finite framework in with an infinitesimal flex is a vector in the vector space such that the orthogonality relation holds for each edge . This condition ensures that if each is perturbed to , with small, then the edge length perturbations are of second order only as tends to zero. That is, for all edges,
If is a two-sided smooth flex of the finite framework then is an infinitesimal flex and for a generic finite framework every infinitesimal flex arises in this way. See Asimow and Roth [1] for example.
Associate with an infinite framework the product vector space
consisting of all sequences . Conceptually such a vector corresponds to a specification of instantaneous velocities, or to a perturbation sequence, applied to the framework joints. Define an infinitesimal flex of to be a vector in for which, as above, holds for each edge , and let denote the linear space of all these vectors. In the planar case contains the three-dimensional linear subspace (assuming has at least one edge) of the infinitesimal flexes that arise from the isometries of . Note that a nonzero rotation infinitesimal flex is an unbounded sequence if and only if is an unbounded framework. We denote the space of rigid body motion infinitesimal flexes as .
Definition 3.1.
An infinite framework is infinitesimally rigid if every infinitesimal flex is a rigid body motion infinitesimal flex.
If is infinite then contains properly the direct sum space consisting of vectors whose coordinates are finitely supported, in the sense of being finitely nonzero. The following definition is convenient and evocative.
Definition 3.2.
An infinite framework is internally infinitesimally rigid if every finitely supported infinitesimal flex is the zero flex.
We now give the usual direct definition of the rigidity matrix of a framework , allowing to be infinite. This matrix could also be introduced via the Jacobian of the equation system that defines since is the Jacobian evaluated at .
Write , , and denote the coordinate difference by . The rigidity matrix is an infinite matrix with rows indexed by edges and columns labeled by vertices but with multiplicity two, namely . Note that any matrix of this shape, with finitely many nonzero entries in each row, provides a linear transformation from to .
Definition 3.3.
The rigidity matrix of the infinite framework , with , is the matrix with entries occurring in the row with label with the respective column labels , and with zero entries elsewhere.
In particular a vector in is an infinitesimal flex if and only if .
Definition 3.4.
(i) A stress (or, more properly, a self-stress) of a finite or infinite framework is a vector in such that
(ii) A finite or infinite framework is isostatic, or absolutely isostatic, if it is infinitesimally rigid and has no nonzero self-stresses.
Since it is understood here that is a locally finite graph a rigidity matrix hase finitely many entries in each column and so its transpose corresponds to a linear transformations from to .
In the finite case a self-stress represents a finite linear dependence between the rows of the rigidity matrix, which one might abbreviate, with language abuse, by saying that the corresponding edges of the framework are linearly dependent. A self-stress vector can be simply related to a vector conceived of as a sequence of bar tension forces with a resolution, or balance, at each node. Indeed, for such a force vector the vector for which () is a stress vector. Thus there is a simple linear relationship between the space of internal stresses and the space of resolving bar tensions. We shall not consider here the more general stress vectors, important in engineering applications, that arise from an external loading vectors.
Let be the space of finitely supported vectors in . We say that an infinite framework is finitely isostatic if it is internally infinitesimally rigid and if the finite support stress space is equal to It is straightforward to see that the grid frameworks , in their ambient spaces, are finitely isostatic, as is the kagome framework.
Between the extremes of infinitesimal rigidity and internal rigidity there are other natural forms of rigidity such as those given in the following definition. Write , and to indicate the usual Banach sequence spaces for countable coordinates, and write for the corresponding subspaces of and .
Definition 3.5.
An infinite framework is
(i) square-summably infinitesimally rigid (or infinitesimally -rigid) if
(ii) boundedly infinitesimally rigid (or infinitesimally -rigid) if
(iii) vanishingly infinitesimally rigid (or infinitesially -rigid) if
(iv) square-summably isostatic (or -isostatic) if it is infinitesimally -rigid and
(v) boundedly isostatic if it is boundedly infinitesimally rigid and ,
(vi) vanishingly isostatic if it is vanishingly infinitesimally rigid and .
There is companion terminology for flexes and stresses. Thus we refer to vectors in as square summable infinitesimal flexes and so on.
Example 3.6.
Let us use the shorthand to denote a semi-infinite framework in whose abstract graph is a tree with a single branch, with edges and where . Then, writing and for the differences and , as before, the rigidity matrix with respect to the natural ordered bases takes the form
With respect to the coordinate decomposition we have
where , where and are the diagonal matrices
and
If we now identify the domain and range spaces in the natural way for these coordinates then we have where is the transpose of the forward unilateral shift operator on the linear space of real sequences.
The analogous framework has a similar matrix structure in all respects except that in place of the Toeplitz matrix one has the corresponding two-way infinite Laurent matrix where is the forward bilateral shift. In both cases, the two-dimensional subspace spanned by the translation flexes is evident, being spanned by the constant vectors in and . Evidently there are infinitely many finitely supported flexes and in fact it is possible to identify as a direct product space.
One can use operator formalism to examine the space of stresses. In the case of the simple framework note that and
where is the vector with every entry equal to . Since
it follows that a vector is a stress vector if and only if and . Thus for some constants we have , and so for all
This colinearity condition shows that the space of stresses is trivial unless the framework points , are colinear in which case is one dimensional. This includes the colinear cases in which is a bounded sequence and the framework lies in a finite line segment in .
Example 3.7.
With similar notational economy write , (resp. ) for frameworks associated with the grid graph with vertex set labeled by -tuples of integers (resp. positive integers) where the edges correspond to vertex pairs , where are the usual basis elements. The ambient space for the framework is either understood or revealed by the entries of the vector .
Again one can use operator formalism to analyse the space of stresses as a vector subspace of . In the special case of the regular grid framework in one can see that the vector subspace is a direct product vector space (like itself) whose product basis is indexed by (two-way infinite) linear subframeworks parallel to the coordinate axes. This is also true for a general orthogonal grid framework such as the bounded grid framework determined by the framework points
Note that we have defined an infinitesimal flex in a local way, being the verbatim counterpart of the usage for finite frameworks. In particular the notion takes no account of the possibility of (second order) amplification or vanishing flexibility.
Our examples above indicate the importance of shift operators and in the next section we see that the bilateral shift operators, in their Fourier transform realisation as multiplication operators, play a central role in the discussion of periodic frameworks.
Let us note here that approximate infinitesimal flexes are natural for infinite frameworks and the operator theoretic perspective.
Definition 3.8.
An approximate square-summable flex of an infinite framework is a sequence of finitely supported unit vectors in (or ) such that as .
Let be a distance regular framework. Then it is straightforward to show that the rigidity matrix determines a bounded Hilbert space operator . It is the metrical and geometric properties of the action of and its transpose that have relevance to rigidity theory rather than the spectral theory of . However we do have the almost vacuous statement that the existence of approximate (square-summable) flexes corresponds to the point belonging to the approximate point spectrum of . For if lies in the approximate point spectrum then (by definition) is a null sequence for some sequence of unit vectors , and approximation of these unit vectors by vectors with finite support yields, after normalisations, an approximate square-summable flex sequence .
It is implicit in the matricial function association below that the rigid unit modes of translationally periodic frameworks are tied to the existence of approximate flexes.
4. Crystal Frameworks and Flexibility
In previous sections we have constructed frameworks to illustrate various definitions and properties. It is perhaps of wider interest to understand, on the other hand, how extant infinite frameworks, such as those suggested by crystals or repetitive structures, may be flexible. Accordingly we now define crystal frameworks and investigate various forms of flexibility and rigidity.
4.1. Periodic and crystal frameworks.
We have already observed some properties of the basic examples of the grid framework , the squares framework and the kagome framework, . In we also have analogues, such as the cube framework , the octagon framework and the kagome net framework , which consist, respectively, of vertex-joined cubes, octahedra and tetrahedra, with no shared edges or faces, each in a natural periodic arrangement. The frameworks , and are polytope body-pin frameworks but we consider the polytope rigid units as bar-joint subframeworks formed by adding some, or perhaps all, internal edges. As such these frameworks are examples of crystal frameworks in the sense of the formal definition below. We first comment on a wider notion of periodicity.
Definition 4.1.
An affinely periodic framework in is a framework for which there exists a non-trivial discrete group of affine transformations , where each acts on framework points and framework edges.
For example, the two-way infinite dyadic cobweb framework of Figure 15 is affinely periodic for the dilation doubling map and the four-fold dihedral group .
For another example we may take the infinite -periodic framework in three dimensions for which Figure 16 forms a perspective view down a central axis, with framework vertices . Here the affine group is an isometry group isomorphic, as a group, to .
To illustrate the following definition observe in Figure 16 a template of six edges and three vertices which generates the kagome framework by the translations associated with the parallelogram unit cell. Borrowing crystallographic terminology we refer to such a template as a motif for the framework and the chosen translation group. The following formal definition gives a convenient way of specifying abstract crystal frameworks.
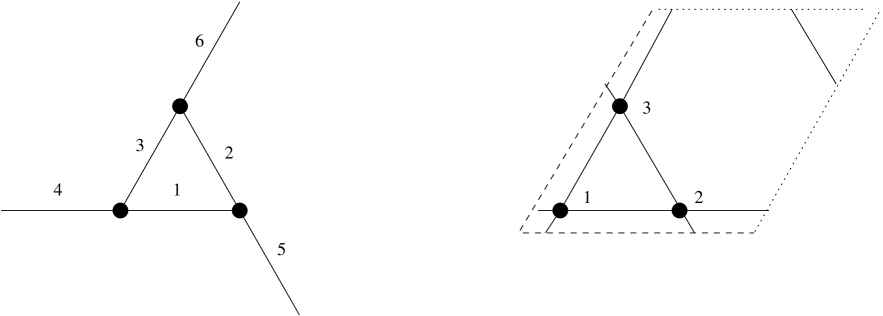
Definition 4.2.
A crystal framework in is a connected bar-joint framework for which there is a discrete group of translation isometries , a finite connected set of frameworks edges and a finite set of framework vertices (being a subset of the vertex set of ) such that
(i) the unions
coincide with the sets of framework edges and vertices, and
(ii) these unions are unions of disjoint sets.
We denote a crystal framework by the triple or by the triple in the case of integer translations. An associated unit cell for may be defined as a set which contains and no other framework points and for which the translates under the translation isometries are disjoint and partition the ambient space. For example in the case of we may take the semiopen set or the set as unit cells. Such parallelepiped unit cells are useful for us for torus models for crystal frameworks. Voronoi cells (Brillouin zones) also play a unit cell role in applications but we shall not need such geometric detail here.
In many applied settings the appropriate framework models have ”short” edges, spanning no more than two adjacent unit cells. Here we allow general edges which may span a chain of adjacent cells.
Recall from elementary crystallography that, modulo orthogonal transformations, there are 14 different forms (or symmetry types) in which a countable set of isolated points can be arranged with translational symmetry throughout three-dimensional space. These arrangements are called the Bravais lattices and the translation group above corresponds to such a lattice. Thus each point of the framework lies in the Bravais lattice generated by the orbit of its unique corresponding motif vertex under the translational group.
4.2. Deformability and flow flexibility.
Recall that a general (countable, locally finite, connected) framework is rigid if there is no base-fixed continuous flex and is boundedly rigid, or boundedly nondeformable, if there is no bounded base-fixed continuous flex . Recall, from Section 2, that bounded flexes are those for which there is an absolute constant such that for every vertex the time separation is bounded by for all and all .
We first describe a context for the standard ”alternation” flexes of and and certain periodic flexes of with reduced symmetry. For these nonbounded flexes translational periodicity is maintained but relative to an affine flow of the ambient space. By an affine flow we mean simply a path of affine transformations of which is pointwise continuous. The simplest such flow in two dimensions is a contracting flow such as , . The alternating flexes of and are associated with such a flow.
Definition 4.3.
Let , let be a flow of and let be a crystal framework for the translation group . A flow-periodic flex of , relative to the flow and the translation group , is a continuous flex such that for each the framework is - periodic, where .
Let us say simply that is affinely periodically deformable if there exists a non trivial flow-periodic flex.
A flow-periodic flex for can be defined for a given flow if and only if for each one can continuously solve the distance constraint equations for the vertex positions of the motif, with the periodicity constraint, in the -deformed unit cell. Equivalently, the motif and unit cell define a finite framework on a torus with the noninterior edges of the motif providing reentrant (”locally geodesic”) edges on the torus. For example consider the torus framework in Figure 17.
A horizontal affine contraction leads to a continuous flex of the torus framework and hence to a colossal flex of the associate crystal framework. The same is true for the vertical affine contraction and for the skew affine transformation
Note that this particular transformation preserves both the cyclic width and cyclic height of the torus.
For an illustration of the method we note the following affine deformation result for what might be termed periodic cell-generic grid frameworks in . For more general results of this nature see also Borcea and Streinu [2].
Theorem 4.4.
Let be a grid framework in which is -periodic and which is a -perturbation of in the sense that
for . Then is affinely periodically deformable.
Proof.
We sketch the proof in case with . For convenience re-scale the framework so that the large cell of becomes to the usual unit cell. Let be the motif representation of . Suppose first that and the motif has four noninterior edges (corresponding to the four reentrant edges on the associated torus). Let be with one vertical and one horizontal reentrant edge removed and let be the associated framework. (See Figure 17.) For taking positive values in some finite interval there are affine deformations of associated with each of the flows . Moreover there is an affine deformation associated with any composition , where the functions and are any continuous functions with , where takes values in some finite interval. Now note that we may chose so that the separation distance corresponding to the omitted horizontal edge is constant, and we may choose similarly for the omitted vertical edge. Note also the essential fact that does not change the cyclic width. In this way an affine deformation for is determined. (In the case of generic points, is determined uniquely on some finite interval).
The same principle operates for general . The subframework , with two deleted noninterior edges (one for each coordinate direction) once again has a flow periodic deformation associated with a composition , for in a sufficiently small interval. This follows from a simple induction argument. Once again the functions and are chosen to provide a deformation of in which the separations for the omitted edges is constant. In this way a flow periodic deformation of itself is determined. ∎
The deformations obtained in the last proposition are colossal deformations and this seems to be a necessary condition if some form of periodicity is to be maintained. It would be interesting to determine when such frameworks possess bounded ”unstructured” deformations.
One may also consider affine deformations relative to a subgroup of associated with a supercell. By a supercell we mean a finite union (or possibly an infinite union) of adjacent cells which tile the ambient space by translations from the subgroup. In this case the deformations maintain only a longer period of translational symmetry and for an infinite linear supercell one may even forgo translational symmetry in one direction.
To illustrate this let us note a class of interesting deformations of the kagome framework which have this form.
Start with an alternation flex which leaves fixed a particular vertex and leaves invariant a line of hexagon diameters. Note that this flex (which is not base-fixed) has bilateral symmetry with respect to the line (viewed as a mirror line) but that the inversion symmetry of about the fixed vertex is broken for . Perform identical surgeries on the frameworks as follows:
(i) cut the frameworks along the fixed line,
(ii) effect a reflection of one of the resulting half-planes frameworks in the orthogonal line through and rejoin the half-planes to create a new flex of .
We might view this flex as one with a symmetry transition line. The hexagons in this line maintain inversion symmetry while elsewhere the hexagons maintain bilateral symmetry.
One may perform such surgery on several parallel surgery lines simultaneously. Performing surgery on countably many lines leads to the following theorem. This shows, roughly speaking, that the kagome framework sits in its configuration space as an infinitely singular point in the sense that it is the starting point for uncountably many distinct flexes. (Here we use the term distinct in the sense of Definition 2.7.)
Theorem 4.5.
There are uncountably many distinct flow periodic flexes of the kagome framework.
4.3. Crystal frameworks and periodic infinitesimal flexibility.
Let be a crystal framework in the plane for the integer translation isometry group. A natural form of infinitesimal flex for is that of a -cell periodic flex in the following sense.
Definition 4.6.
A vector in the real vector space , or in the complex vector space , is a -cell-periodic infinitesimal flex for (or simply a periodic flex if there is no ambiguity) if and for all and .
Such an infinitesimal flex is a bounded sequence of vectors determined by periodic extension of what we may call the motif flex vector There is a one-to-one correspondence between these periodic flexes and the finite vectors that are in the kernel of the motif rigidity matrix which we may define as the natural ”periodic completion” of the submatrix of . This is the natural representing matrix for viewed as a linear transformation between the finite dimensional subspaces of -periodic vectors. If there are no reflexive edges in the motif then
Similarly we define periodic infinitesimal stresses as those which correspond to periodic extensions of vectors in the cokernel of the motif rigidity matrix.
The crystal framework , with given motif and discrete translation group indexed by , is said to be -cell-periodically isostatic (or simply periodically isostatic) if the only -cell periodic flexes are translation flexes and if there are no nontrivial -cell periodic stresses.
Once again it can be helpful to consider a flat torus model for such frameworks. Note for example that the generic periodic framework defined by Figure 17 is periodically rigid and indeed periodically isostatic.
The following interesting periodic variant of Laman’s theorem has been obtained recently by E. Ross [28]. Let us say that the planar periodic framework is topologically proper if is connected and for every torus subframework motif with there is an edge cycle from which properly wraps around the torus in the sense that the associated homotopy class is nonzero.
Theorem 4.7.
Let be an infinite framework in the plane which is periodic for the integer translation group and is topologically proper. Then following are equivalent.
(i) and for all edge induced submotifs we have .
(ii) is periodically isostatic in the sense that the periodic vectors in are spanned by the two translations (periodic rigidity) and the periodic vectors in are zero (periodic stress free).
As we have seen, a periodically infinitesimally rigid framework in the sense above may nevertheless correspond to a flat torus framework which can flex infinitesimally (and even deform) relative to contraction or expansion of the unit cell. Allowing such vertical and horizontal freedoms adds two further degrees of freedom to the constraint equations. It would be of interest to obtain a similar characterisation in this case as well as for the triply flexible affine torus.
5. The Matricial Symbol Function of a Crystal Framework
We now derive matrix function operators for general (abstract) crystal frameworks. Our approach is decidedly Hilbert space theoretic and allows for an extended conceptual framework for rigidity analysis. First we outline the standard identification of operators commuting with shift operators and multiplication operators in a Fourier transform space. We adopt complex scalars, replacing the spaces of Section 3 by their complex counterparts, and so forth.
5.1. Matrix function multiplication operators.
Let be a continuous complex-valued function on the unit circle . It defines a multiplication operator on the usual complex Hilbert space . Its representing matrix with respect to the standard orthonormal basis is the indexed matrix with entries
the Fourier coefficient of .
Similarly, let be a continuous matrix-valued function on the two or three dimensional torus taking values in the space of complex matrices. One can specify such a function in terms of a matrix of scalar functions . Given in this way defines a multiplication operator from to . Indeed, choose a basis for and an associated basis for the domain space. Similarly let be a basis for the codomain. Then the operator of multiplication by may be defined by specifying, for each continuous function on ,
and extending by linearity and continuity. Thus we can see that the representing matrix for with respect to these bases is determined by the Fourier coefficients of the matrix entries for :
Viewing an element of as a function taking values in (strictly speaking, taking values almost everywhere), and similarly for vectors in the codomain, one also considers as the function . This operator is usually denoted as .
Suppose now, starting afresh, we have orthonormal bases
for Hilbert spaces such as and respectively. Suppose also that we are given an operator from to by means of its representing matrix with respect to these bases and suppose moreover that this matrix has the translational symmetry above in the sense that the matrix entries
are independent of . Let be the Fourier transform and the Fourier transform for . These are simply the unitary operators determined by the natural bijection of basis elements, namely and , respectively. Thus, from the scalar matrix entries the functions are determined and hence the matrix function . In this way one identifies as the associated multiplication operator .
5.2. The rigidity matrix as a multiplication operator
Let us keep in view the special case of the -periodic grid framework determined by an algebraically generic quadrilateral in the unit cell.
Let be four framework vertices in the unit cell constituting the motif set of -periodic quadrilateral grid . Let , for , be the general framework points and let denote the eight edges which form the motif set given by
and let be a typical edge. Write the corresponding basis for the vector space as
Also, label the natural basis for as the set of vectors , where ranges from to and range through .
The rigidity matrix satisfies the following symmetry equations,
with respect to the translation shift operators on and on . By the discussion above the rigidity matrix for this framework gives rise to an matrix function on the torus in which is determined by the equations
together with a companion set of equations for the -labeled basis elements. Furthermore there is a simple algorithm for computing the symbol matrix function from the motif and the motif rigidity matrix.
For a general crystal frameworks in the plane we have the following recipe for identifying . There is an entirely similar identification of the matrix function of a crystal framework in higher dimensions.
Theorem 5.1.
Let be the matricial symbol function of the crystal framework . The entry of the rigidity matrix determined by the edge of and the column labeled (resp. ) provides the -th Fourier coefficient of (resp. ).
Note that for the motif for the periodic quadrilateral grid each edge has vertices with different index. This is rather typical and in such cases it follows that is either zero or has one nonzero Fourier coefficient. In the case of a ”reflexive” edge in , of the form there are entries in the columns for corresponding to where is the usual vector of coordinate differences appearing in the rigidity matrix for the edge . That is, .
Thus we may obtain the following identification where the direct construction of from is given above.
Theorem 5.2.
Let be a crystal framework with , and with rigidity operator from to .
(i) The motif determines a matrix-valued trigonometric function for which there is a unitary equivalence where is the multiplication operator
(ii) The framework is square-summably rigid (resp. square-summably stress-free) if the column rank (resp. row rank) of is maximal for almost every .
The following corollary shows that the existence of a square summable flex is a rather strong condition for a crystal framework and in fact ”typical” frameworks in Maxwell counting equilibrium have no such flexes. What is of particular significance for such frameworks however is the presence of approximate flexes, in the sense noted in Section 3, as these are related to the local rank degeneracies of and to periodic flexes.
Corollary 5.3.
The following are equivalent for a crystal framework with Maxwell counting equilibrium.
(i) has an nonzero internal (finitely supported) infinitesimal flex.
(ii) has an nonzero summable infinitesimal flex.
(iii) has an nonzero square-summable infinitesimal flex.
Proof.
Note that (i) implies (ii) and (ii) implies (iii) so it remains to show (iii) implies (i).
Suppose that the matrix has a square-summable vector in its kernel. Then for almost all points in the support of . Since is a mutivariable trigonometric polynomial it necessarily vanished identically, that is the polynomial is the zero polynomial.
Recall that for any square matrix over a ring we have
where is given by the usual formula
involving the cofactors .
In particular if is not zero and then for a nonzero column
vector of we have . Applying this to provides the desired polynomial (finitely supported) vector in this case.
If happens to be the zero matrix we make use of the minimal polynomial lemma below. To apply the lemma let be the minimum polynomial of so that . By the lemma we have and by minimality. Thus there is a nonzero vector in the range of and this provides the desired local flex. ∎
Lemma 5.4.
Let in be the minimal polynomial of an by matrix whose entries lie in an integral domain and suppose that . Then .
Proof.
Let be the characteristic polynomial . Recall from the Cayley-Hamilton theorem that . In the algebraic closure of the field of fractions of the linear factors of and agree. See Lange [22] for example. Thus
with for each . In particular for suitably large the polynomial is divisible by . Since it follows that and so . Since is in it is equal to zero and the proof is complete. ∎
5.3. From motifs to matrix functions.
We now consider some examples. Adjusting notation, write for the coordinates variables of so that a trigonometric polynomial takes the form a finite sum
Examining the recipe of Theorem 5.1 above in the case of the periodic quadrilateral grid we see that the internal edges of the motif provide four rows for whose entries are constant functions with constants corresponding to those of the rows for the rigidity matrix . The other edges provide rows according to the following simplified monomial rule. As we have intimated above, this rule applies generally when all the ”external” edges of the motif have vertices with distinct index:
the entries of the row of that appear in the columns for the external (non-motif) vertex are the corresponding entries for the motif rigidity matrix multiplied by the monomial , where is the shift index for the cell occupied by the external vertex.
Thus we obtain the matrix identification in the next proposition. We write , for . Note, for example, that the entry denotes the constant function corresponding to the entry of for row and column , while is the entry corresponding to the -coordinate of the external vertex of .
Proposition 5.5.
The matricial symbol function of the periodic quadrilateral grid framework for the four vertex motif is the matrix function on given by
Furthermore, if the four points in the unit cell have algebraically independent coordinates then is square-summably isostatic.
Proof.
The first four rows are linearly independent since the points have algebraically independent coordinates. It can be shown from elementary linear algebra for almost every the full matrix has rank . Thus Theorem 5.2 applies. ∎
As a special case we obtain the matrix symbol function for determined by the eight-edged motif, namely
The determinant in this case is
On the other hand for this symmetric quadrilateral framework the formalism above can be applied to a smaller unit cell with the simple two-edged motif of Figure 18.
Note that the index for the recipe takes the value only and both motif edges have vertices with the same index. It follows that the rigidity operator of associated with the motif is unitarily equivalent to the multiplication operator on the Hilbert space determined by the matricial symbol function
One can similarly verify the following.
Proposition 5.6.
(i) The matricial symbol function of the kagome framework determined by the six-edge motif is given by
(ii) The determinant of is a multiple of
(iii) The kagome framework is square-summably isostatic.
We remark that the function matrix association above has also arisen in engineering in the analysis of Hutchinson and Fleck [19] of the stresses and rigidity of the kagome repetitive truss framework. This is derived from the crystallographic perspective of wave periodic flexes and Bloch’s theorem.
5.4. Symmetry equations for infinite frameworks.
Let be a crystal framework in with complex Hilbert space rigidity operator . Also let be as before, let be the space of square-summable infinitesimal flexes, let be the space of square-summable infinitesimal stresses and let , be their complementary spaces.
As well as commuting with the coordinate shift operators the rigidity operator satisfies commutation relations for every isometric symmetry of . For example, let be an isometric (not necessarily linear) operator on which effects a symmetry of . There is an induced unitary operator on the complex Hilbert space and an analogous operator on which permute the standard basis elements. Write for the isometric (not necessarily linear) operator on where is also viewed as an isometric operator on . Then we have the fundamental symmetry equation . (See [27].)
Moreover, if is the symmetry group of arising from isometric transformations of and if and are the associated representations of on and then we have the symmetry equations
We have shown in [27] how such symmetry equations may be used to obtain a simple proof of a unitary equivalence which implies the Fowler-Guest formula [9] together with various generalisations. In the present setting we have the following analogue which also leads to counting conditions for isostatic and rigid frameworks.
Theorem 5.7.
Let be a crystal framework with isometry symmetry group and let
be the decompositions associated with the spaces of square-summable infinitesimal flexes and stresses. Then and are unitarily equivalent representations. In particular if is square summably isostatic then and are unitarily equivalent.
Proof.
In the square-summably isostatic case is a bounded operator with trivial kernel and trivial cokernel. The partially isometric part of the polar decomposition is therefore unitary and it is a standard verification that this unitary also intertwines the representations. In general the symmetry equations show that the space is reducing for and is reducing for and so the asserted direct sum decompositions do exist. Now the restriction of to maps to with trivial kernel and cokernel and so as before the restriction representations are unitarily equivalent. ∎
5.5. From matrix function to wave modes
For a crystal framework with a given motif let be the associated matricial symbol function.
Definition 5.8.
The mode multiplicity function of associated with the given motif and translation group is the function given by
For we also consider as being parametrised by coordinates in so that corresponds to . From the determinant calculations above we obtain the following.
Proposition 5.9.
(i) For the grid framework and the 8-edged motif the mode multiplicity function has values ,
if and are nonzero, and is zero otherwise.
(ii) For the kagome framework and the 6-edged motif the mode multiplicity function has values at the origin while if and and is zero otherwise.
Consider now the wave flexes of which we define as the infinitesimal flexes which are -cell-periodic modulo a phase factor.
Definition 5.10.
Let be a crystal framework in . An (infinitesimal) wave flex of is a complex infinitesimal flex which is wave periodic (or more precisely -cell wave periodic) in the sense that for some vector in
for each vertex in the motif set and each -tuple .
The values of the mode multiplicity function corresponds to the dimension of the spaces of wave flexes. To see this suppose that is the matricial symbol function for , that and that . Then for some nonzero complex motif vector . For the Dirac delta function on we have, informally, for all on the -torus where is the function . Thus, taking Fourier transforms it follows that the wave periodic vector in satisfies . This shows that the bounded (and non square-summable) vector
is a wave flex. The Dirac delta argument can be rigourised in the usual manner and so we obtain the following theorem.
Theorem 5.11.
Let be a crystal framework in with associated symbol function and suppose that has no internal (finitely supported) self-stresses and no internal (finitely supported) flexes. Then
(i) , the associated matricial symbol function on the -torus is square with full rank almost everywhere and is square-summably isostatic.
(ii) infinitesimal wave flexes (that are 1-cell periodic-modulo-phase) exist, with phase factor , if and only if . In this case the dimension of the corresponding space of wave flexes is .
It follows also from this that the zero set of the determinant of the matricial symbol function associated with the motif of an appropriate supercell coincides with the phases of supercell-periodic wave flexes.
Of particular computational and theoretical interest is what one might refer to as the wave flex acquisition when a crystal framework deforms under a colossal flex to a framework with higher symmetry. This phenomenon serves as a model for the appearance of so-called Rigid Unit Modes (RUMs) in higher symmetry phases of various material crystals.
The following theorem generalises an interesting result of Wegner [32] for tetrahedral crystals. It may be viewed as an expression of the simple principle that additional symmetry often entails additional flexibility. Our proof applies to arbitrary crystal frameworks and is quite direct, benefitting somewhat from the economy of operator theory formalism. We remark that there are also natural operator algebra perspectives that are relevant to symmetry considerations. The result shows in particular for that the RUM set is typically a union of surfaces, being the zero set of a single real-valued polynomial, rather than the intersection of the zero sets of the real and imaginary part of a complex polynomial.
For a given crystal framework and motif write for the subset of formed by the phases of the -cell periodic wave flexes. We also refer to this informally as the RUM set or the RUMs of .
Theorem 5.12.
Let be a crystal framework in with and suppose that possesses inversion symmetry. Then the set has the form
where is the zero set of a complex polynomial which is real-valued on .
Proof.
Let us denote the set of framework vertices and edges as
Effecting a translation, if necessary, we may assume that the inversion is , that the unit cell has inversion symmetry and . It may or may not be possible to re-choose the noninternal edges of so that that . Suppose first that this is the case. We show that itself is either real-valued or purely imaginary, from which the stated form for follows.
With the notation of Section 5.4 we have the symmetry equation
Recall that and are the isometric operators induced by the (isometric) symmetry element . Taking Fourier transforms this equation takes the form
where and are the unitary operators determined by their action on the distinguished orthonormal bases. In view of the assumption we have
(for certain induced permutations ) and
That is, these operators have the form
where is the inversion unitary operator on given by , and where and are scalar permutation matrices induced by . Substituting these forms we see that
It follows that
for some integer , since the determinant polynomial has real coefficients and so the determinant is either real or purely imaginary.
In the general case because of edges lying on inversion axes (lines through the origin) cannot be made to act freely on the motif edges. However for each motif edge index there is a monomial shift factor such that with the diagonal matrix function
we have
Now we see that for some multi-index . Write with the real-valued and with real. Equating real and imaginary parts it follows that either in which case and is real-valued, or . In all cases, for on the torus, if and only if and , as required. ∎
5.6. Honeycomb frameworks and the kagome net.
The explicit formulation of the matricial symbol function makes clear a simple additive principle which is useful for calculation : adding internal edges to a unit cell results in adding the same number of rows to the symbol function to form the new symbol function, and each of these rows has the standard form with constant entries.
Consider the following honeycomb frameworks based on regular
hexagons.
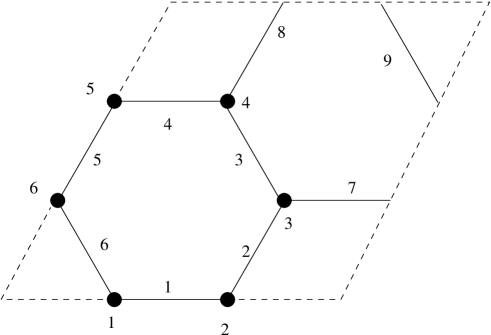
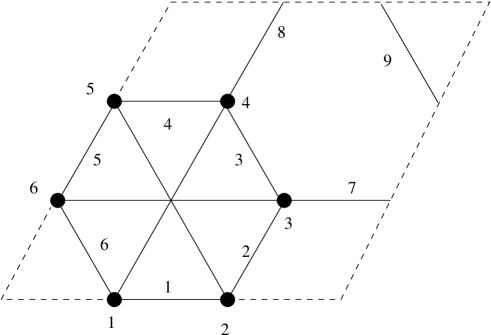
The -regular (symmetric) honeycomb framework has a by matricial symbol function. There are vectors in the kernel of the multiplication operator providing internal infinitesimal flexes and there are evident bounded infinitesimal flexes associated with ”parallel deformations”, for example.
A -regular framework may be constructed by rigidifying the hexagon internal to the unit cell, by adding three cross edges. The matricial symbol function is correspondingly enlarged by three scalar rows, appearing in rows to in the following matrix.
The cross-barred hexagon is continuously rigid but is infinitesimally flexible. We refer to this flex as the in-out flex. (See Whiteley [34] for related discussions.) It is straightforward to show that this flex extends periodically as a 1-cell-periodic infinitesimal flex of the framework.
The motif matrix function is obtained by evaluating at . This has rank reflecting the four independent -cell-periodic flexes corresponding to horizontal translation, to vertical translation, to local rotation of the cross-barred hexagon, and to the periodic ”in-out” flex.
We define the kagome net framework as the three dimensional crystal framework determined by the motif diagram in Figure 21. This figure shows a tetrahedron internal to a parallelepiped unit cell together with six additional non-internal edges, each of which extends a tetrahedron edge as indicated.
For the given motif the motif rigidity matrix takes the form of a by matrix valued function on the -torus. Different motifs, for the same translation group, give matrix functions that are related by permutations on columns and monomial multiplication on rows. It can be shown that the determinant of such a matrix function is equal to a scalar and monomial multiple of the polynomial
This is in complete analogy with the kagome framework and in the light of earlier discussions may draw the following conclusions.
Theorem 5.13.
(i) The kagome net is square-summably isostatic and possesses no internal infinitesimal flexes.
(ii) The mode multiplicity function of the kagome net framework has support equal to the intersection of with the six planes
5.7. Crystallography and Rigid Unit Modes.
Rigidity theory and a Hilbert space operator viewpoint have led us to determine, ab initio, the matricial symbol function of an abstract crystal framework and motif. The zeros of correspond to the phases of infinitesimal periodic-modulo-phase wave flexes and the mode multiplicity function of detects the multiplicities of independent wave flexes for . There are close connections between these mathematical observations and the Rigid Unit Modes (RUMs) that are observed in certain material crystals through diffraction experiments. This connection is part of the motivation for the formulation of the function . It seems to us that the explicit algorithm for the passage from crystal motif to matrix function will provide a useful computational and theoretical tool for identifying RUMs and their relationships.
Infinitesimal wave flexes for abstract crystal frameworks appear in the classical crystallography of Born von Karman theory. For example in the case of variants of quartz the low energy excitation modes result from rigid unit motions of molecular tetrahedra within a tetrahedral net. These modes are therefore modelled by the first order periodic-modulo-phase infinitesimal rigid motions of abstract tetrahedral net frameworks. For this connection see, for example, Chapter 3 of [35]. Comparisons of extensive simulations and experimental results have shown that the RUM modes of simulated crystals are closely correlated with observed RUMs. For this see the seminal paper of Giddy et al [11], and also, for example, Dove et al [8] and Goodwin et al [14].
An interesting advance has been obtained recently by Wegner [32] who has derived mathematically, rather than through simulation, the RUM sets for various idealised tetrahedral crystals that model the geometry of material crystals, including -cristobalite, HP tridymite, -quartz, -cristobalite and -quartz. These models are standard framework models that coincide with crystal bar-joint frameworks in our terminology and the results are obtained by determining vanishing determinants (zero sets of in our formalism) by means of computer algebra and symmetry reductions. In particular Wegner obtains an analytic derivation of some of the curious surfaces observed in experiments of Dove et al.
References
- [1] L. Asimow and B. Roth, The rigidity of graphs, Trans. Amer. Math. Soc., 245 (1978), 279-289.
- [2] C.S. Borcea and I. Streinu, Periodic frameworks and flexibility, Proc. R. Soc. A, doi:10.1098/rspa.2009.0676.
- [3] A. Böttcher, B. Silbermann, Analysis of Toeplitz operators, Springer-Verlag, Berlin, 1990.
- [4] R.Connelly, P.W.Fowler, S.D.Guest, B.Schulze, W.J.Whiteley, ”When is a pin-jointed framework isostatic?”, International Journal of Solids and Structures, 46 (2009), 762 - 773.
- [5] D. Cox, J. Little, D. O’Shea, Ideals, Varieties and Algorithms, Springer-Verlag, 1992.
- [6] M. V. Chubynsky and M. F. Thorpe, Algorithms for three-dimensional rigidity analysis and a first-order percolation transition, Physical Review E 76, 2007.
- [7] A. Donev and S. Torquato, Energy-efficient actuation in infinite lattice structures, J. Mech Phys. Solids, 51 (2003) 1459-1475.
- [8] M. T. Dove et al, Floppy Modes in Crystalline and Amorphous Silicates; in Rigidity Theory and Applications, Edited by M. F. Thorpe and P. M. Duxbury, Kluwer Academic/Plenum Publishers, New York (1999).
- [9] P.W. Fowler and S.D. Guest, A symmetry extension of Maxwell’s rule for rigidity of frames, International Journal of Solids and Structures 37 (2000) 1793 - 1804.
- [10] M. G. Frost and C. Storey, Equivalence of a matrix over with its Smith form, Int. J. Control, 28 (1978), 665-671.
- [11] A. P. Giddy, M.T. Dove, G.S. Pawley, V. Heine, The determination of rigid unit modes as potential soft modes for displacive phase transitions in framework crystal structures. Acta Crystallogr., A49 (1993), 697 - 703.
- [12] H. Gluck, Almost all simply connected closed surfaces are rigid, in Geometric Topology, Lecture Notes in Math., no. 438, Springer-Verlag, Berlin, 1975, pp. 225-239.
- [13] I. Gohberg, P. Lancaster, L. Rodman, Matrix Polynomials, Classics in Applied Mathematics, SIAM, 2009.
- [14] A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters, M. G. Tucker, Colossal Positive and Negative Thermal Expansion in the Framework Material Ag3[Co(CN)6], Science 8 February 2008: Vol. 319. no. 5864, pp. 794 - 797.
- [15] J. Graver, B. Servatius and H. Servatius, Combinatorial rigidity, Graduate Texts in Mathematics, vol 2, Amer. Math. Soc., 1993.
- [16] S. D. Guest and J. W. Hutchinson, On the determinacy of repetitive structures, Journal of the Mechanics and Physics of Solids, 51 (2003), 383 - 391.
- [17] B. Grunbaum, G.C. Shephard, Tilings and patterns, W.H. Freeman, New York, 1987.
- [18] K.D. Hammonds, M.T. Dove, A.P. Giddy, V. Heine, B. Winkler, Rigid-unit phonon modes and structural phase transitions in framework silicates, American Mineralogist, 81 (1996), 1057-1079.
- [19] R.G. Hutchinson and N.A. Fleck, The structural performance of the periodic truss, Journal of the Mechanics and Physics of Solids, 54 (2006) 756-782.
- [20] A. B. Kempe, On a general method of describing plane curves of the nth degree by linkwork, Proc. London Math. Soc., 7 (1876), 213-216.
- [21] G. Laman, On graphs and the rigidity of plane skeletal structures, J. Engineering Mathematics, 4 (1970), 331-340.
- [22] S. Lang, Algebra, Addison Wesley, 1993.
- [23] J.C. Maxwell, On the calculation of the equilibrium and stiffness of frames. Philosophical Magazine 27, (1864), 294 - 299.
- [24] J.C. Owen and S.C. Power, The non-solvability by radicals of generic 3-connected planar Laman graphs, Trans. Amer. Math. Soc., 359 (2007), 2269-2303.
- [25] J.C. Owen and S.C. Power, Infinite bar-joint frameworks, Proceedings of the Symposium in Applied Computing, (SAC 2009) March 8-12, 2009, Honolulu, Hawaii, U.S.A.
- [26] J.C. Owen and S.C. Power, Continuous curves from infinite Kempe linkages, Bull. London Math. Soc., 2009; doi: 10.1112/blms/bdp087
- [27] J.C. Owen and S.C. Power, Frameworks, symmetry and rigidity, to appear in the Inter. J. of Computational Geometry and Applications, arXiv:0812.3785.
- [28] E. Ross, private communication, July 2009.
- [29] B. Roth, Rigid and flexible frameworks, American Math. Monthly, Vol. 88 (1981), 6-21.
- [30] W. Rudin, Functional Analysis, McGraw and Hill, NY, 1991.
- [31] M. F. Thorpe and P. M. Duxbury, Rigidity Theory and Applications, Edited by Kluwer Academic/Plenum Publishers, New York (1999).
- [32] F. Wegner, Rigid-unit modes in tetrahedral crystals, Journal of Physics: Condensed Matter, Volume 19, Issue 40, (2007).
- [33] S.A. Wells, M. T. Dove, M. G. Tucker and K. Trachenko, Real-space rigid-unit-mode analysis of dynamic disorder in quartz, cristobalite and amorphous silica, J. Phys.: Condens. Matter 14 (2002), 4645 4657.
- [34] W. Whiteley, Matroids and rigid structures, in ”Matroid Applications” ed. N. White, Encyclodedia of Mathematics and its applications 40 (1992), 1-51.
- [35] B.T.M.Willis and A.W. Pryor, Thermal vibrations in crystallography, Cambridge University Press, 1975.
- [36] M. Wyart, Rigidity-based approach to the boson peak in amorphous solids: from sphere packing to amorphous silica, preprint 2008, arXiv:0806.4596v1.