Inside the Binary Reflected Gray Code:
Flip-Swap Languages in 2-Gray Code Order
Abstract
A flip-swap language is a set of binary strings of length such that is closed under two operations (when applicable): (1) Flip the leftmost ; and (2) Swap the leftmost with the bit to its right. Flip-swap languages model many combinatorial objects including necklaces, Lyndon words, prefix normal words, left factors of -ary Dyck words, and feasible solutions to - knapsack problems. We prove that any flip-swap language forms a cyclic -Gray code when listed in binary reflected Gray code (BRGC) order. Furthermore, a generic successor rule computes the next string when provided with a membership tester. The rule generates each string in the aforementioned flip-swap languages in -amortized per string, except for prefix normal words of length which require -amortized per string. Our work generalizes results on necklaces and Lyndon words by Vajnovski [Inf. Process. Lett. 106(3):9699, 2008].
1 Introduction
Combinatorial generation studies the efficient generation of each instance of a combinatorial object, such as the permutations of or the binary trees with nodes. The research area is fundamental to computer science and it has been covered by textbooks such as Combinatorial Algorithms for Computers and Calculators by Nijenhuis and Wilf [27], Concrete Mathematics: A Foundation for Computer Science by Graham, Knuth, and Patashnik [9], and The Art of Computer Programming, Volume 4A, Combinatorial Algorithms by Knuth [12]. In fact, Knuth’s section on Generating Basic Combinatorial Patterns is over 450 pages. The subject is important to every day programmers, and Arndt’s Matters Computational: Ideas, Algorithms, Source Code is an excellent practical resource [1]. A primary consideration is listing the instances of a combinatorial object so that consecutive instances differ by a specified closeness condition. Lists of this type are called Gray codes. This terminology is due to the eponymous binary reflected Gray code (BRGC) by Frank Gray, which orders the binary strings of length so that consecutive strings differ in one bit. The BRGC was patented for a pulse code communication system in 1953 [10]. For example, the order for is
| (1) | |||
Variations that reverse the entire order or the individual strings are also commonly used in practice and in the literature. We note that the order in (1) is cyclic because the last and first strings also differ by the closeness condition, and this property holds for all .
One challenge facing combinatorial generation is its relative surplus of breadth and lack of depth111This is not to say that combinatorial generation is always easy. For example, the ‘middle levels‘ conjecture was confirmed by Mütze [14] after 30 years and effort by hundreds of researchers.. For example, [1], [12], and [27] have separate subsections for different combinatorial objects, and the majority of the Gray codes are developed from first principles. Thus, it is important to encourage simple frameworks that can be applied to a variety of combinatorial objects. Previous work in this direction includes the following:
-
1.
the ECO framework developed by Bacchelli, Barcucci, Grazzini, and Pergola [2] that generates Gray codes for a variety of combinatorial objects such as Dyck words in constant amortized time per instance;
-
2.
the twisted lexico computation tree by Takaoka [22] that generates Gray codes for multiple combinatorial objects in constant amortized time per instance;
- 3.
-
4.
greedy algorithms observed by Williams [28] that provide a uniform understanding for many previous published results;
-
5.
the reflectable language framework by Li and Sawada [13] for generating Gray codes of -ary strings, restricted growth strings, and -ary trees with nodes;
-
6.
the bubble language framework developed by Ruskey, Sawada and Williams [17] that provides algorithms to generate shift Gray codes for fixed-weight necklaces and Lyndon words, -ary Dyck words, and representations of interval graphs;
-
7.
the permutation language framework developed by Hartung, Hoang, Mütze and Williams [11] that provides algorithms to generate Gray codes for a variety of combinatorial objects based on encoding them as permutations.
We focus on an approach that is arguably simpler than all of the above: Start with a known Gray code and then filter or induce the list based on a subset of interest. In other words, the subset is listed in the relative order given by a larger Gray code, and the resulting order is a sublist (Gray code) with respect to it. Historically, the first sublist Gray code appears to be the revolving door Gray code for combinations [26]. A combination is a length binary string with weight (i.e. number of ones) . The Gray code is created by filtering the BRGC, as shown below for and (cf. (1))
| (2) | |||
This order is a transposition Gray code as consecutive strings differ by transposing two bits222When each string is viewed as the incidence vector of a -subset of , then consecutive -subsets change via a “revolving door” (i.e. one value enters and one value exits).. It can be generated directly (i.e. without filtering) by an efficient algorithm [26]. Transposition Gray codes are a special case of 2-Gray codes where consecutive strings differ by flipping (i.e. complementing) at most two bits. Vajnovszki [23] proved that necklaces and Lyndon words form a cyclic -Gray code in BRGC order, and efficient algorithms can generate these sublist Gray codes directly [21]. Our goal is to expand upon the known languages that are 2-Gray codes in BRGC order, and which can be efficiently generated. To do this, we introduce a new class of languages.
A flip-swap language (with respect to 1) is a set of length binary strings such that is closed under two operations (when applicable): (1) Flip the leftmost ; and (2) Swap the leftmost with the bit to its right. A flip-swap language with respect to is defined similarly. Flip-swap languages encode a wide variety of combinatorial objects.
Theorem 1.1.
The following sets of length binary strings are flip-swap languages:
| Flip-Swap languages (with respect to ) i. all strings ii. strings with weight iii. strings iv. strings with inversions re: v. strings with transpositions re: vi. strings their reversal vii. strings their reversal (neckties) viii. strings their complemented reversal ix. strings their complemented reversal x. strings with forbidden xi. strings with forbidden prefix xii. -prefix normal words xiii. necklaces (smallest rotation) xiv. Lyndon words xv. prenecklaces (smallest rotation) xvi. pseudo-necklaces with respect to xvii. left factors of -ary Dyck words xviii. feasible solutions to 0-1 knapsack problems | Flip-Swap languages (with respect to ) all strings strings with weight strings strings with inversions re: strings with transpositions re: strings their reversal strings their reversal strings their complemented reversal strings their complemented reversal strings with forbidden strings with forbidden prefix -prefix normal words necklaces (largest rotation) aperiodic necklaces (largest rotation) prenecklaces (largest rotation) pseudo-necklaces with respect to |
Our second result is that every flip-swap language forms a cyclic -Gray code when listed in BRGC order. This generalizes the previous sublist BRGC results [21, 23].
Theorem 1.2.
When a flip-swap language is listed in BRGC order the resulting listing is a 2-Gray code. If includes then the listing is cyclic.
Our third result is a generic successor rule, which efficiently computes the next string in the -Gray code of a flip-swap language, so long as a fast membership test is given.
Theorem 1.3.
The languages in Theorem 1.1 can be generated in -amortized time per string, with the exception of prefix normal words which require -time.
In Section 2, we formally define our version of the BRGC. In Section 3, we prove Theorem 1.1, and define the flip-swap partially ordered set. In Section 4, we give our generic successor rule and prove Theorem 1.2. In Section 5, we present a generic generation algorithm that list out each string of a flip-swap language, and we prove Theorem 1.3.
2 The Binary Reflected Gray Code
Let denote the set of length binary strings. Let denote the listing of in BRGC order. Let denote the listing in reverse order. Then can be defined recursively as follows, where denotes the listing with the character appended to the end of each string:
For example, and , thus
.
This definition of BRGC order is the same as the one used by Vajnovzski [23]. When the strings are read from right-to-left, we obtain the classic definition of BRGC order [10]. For flip-swap languages with respect to 0, we interchange the roles of the 0s and 1s; however, for our discussions we will focus on flip-swap languages with respect to 1. Table 1 illustrates and six flip-swap languages listed in Theorem 1.1.
| all | necklaces | -PNW | neckties | |||
|---|---|---|---|---|---|---|
| BRGC | i. | xiii. | xii. | iii. | ii. | vii. |
| 0000 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 1000 | ✓ | ✓ | ✓ | |||
| 1100 | ✓ | ✓ | ||||
| 0100 | ✓ | ✓ | ✓ | |||
| 0110 | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 1110 | ✓ | |||||
| 1010 | ✓ | ✓ | ||||
| 0010 | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 0011 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 1011 | ✓ | ✓ | ||||
| 1111 | ✓ | ✓ | ✓ | |||
| 0111 | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 0101 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 1101 | ✓ | |||||
| 1001 | ✓ | ✓ | ✓ | ✓ | ||
| 0001 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| i. | xiii. | xii. | iii. | ii. | vii. |
|---|---|---|---|---|---|
|
|
|
|
|
|
|
3 Flip-swap languages
In this section, we formalize some of the non-obvious flip-swap languages stated in Theorem 1.1. Then we prove Theorem 1.1 for a subset of the listed languages including necklaces, prefix normal words, and feasible solutions to the 0-1 knapsack problems. The remainder of the languages are proved in the Appendix.
Consider a binary string . The weight of is the number of 1s it contains. An inversion in with respect to is an index pair such that and and . The number of transpositions of with respect to another binary string of length is the minimum number of adjacent transpositions required to transform to .
A necklace is the lexicographically smallest (largest) string in an equivalence class under rotation. An aperiodic necklace is a necklace that cannot be written in the form for some . A Lyndon word is an aperiodic necklace when using the lexicographically smallest string as the representative. A prenecklace is a prefix of a necklace. A block with respect to is a maximal substring of the form . A string is a pseudo-necklace with respect to if for all .
A -ary Dyck word is a binary string of length with copies of and copies of such that every prefix has at most copies of for every . The set of length prefixes of -ary Dyck words is called left factors of -ary Dyck words.
Let be the string obtained by complementing . Let be the string obtained by swapping and . When the context is clear we use and instead of and . Also, let denote the position of the leftmost of or if no such position exists. Similarly, let denote the position of the leftmost of or if no such position exists. We now prove that binary strings, necklaces, prefix normal words, and feasible solutions to the 0-1 knapsack problems are flip-swap languages with respect to 1.
Binary strings: Obviously the set satisfies the two closure properties of a flip-swap language and thus is a flip-swap language. In fact, the BRGC order induces a cyclic -Gray code for [12, 15].
Necklaces: Let be the set of necklaces of length and be a necklace in . By the definition of necklace, it is easy to see that and thus satisfies the flip-first property. For the swap-first operation, observe that if and , then the swap-first operation produces the same necklace. Otherwise if and , then the swap-first operation produces the string which is clearly a necklace. Thus, the set of necklaces is a flip-swap language.
Prefix normal words: A binary string is prefix normal with respect to (also known as -prefix normal word) if no substring of has more s than its prefix of the same length. For example, the string 001010010111011 is a -prefix normal word but the string 001010010011011 is not because it has a substring of length with four s while the prefix of length has only three s.
Observe that the set of -prefix normal words of length satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations either increases or maintain the number of s in its prefix. Thus, the set of -prefix normal words of length is a flip-swap language.
Feasible solutions to - knapsack problems: The input to a - knapsack problem is a knapsack capacity , and a set of items each of which has a non-negative weight and a value . A subset of items is feasible if the total weight of the items in the subset is less than or equal to the capacity . Typically, the goal of the problem is to find a feasible subset with the maximum value, or to decide if a feasible subset exists with value .
Given the input to a - knapsack problem, we reorder the items by non-decreasing weight. That is, for . Notice that the incidence vectors of feasible subsets are now a flip-swap language. More specifically, flipping any to causes the subset sum to decrease, and so does swapping any with the bit to its right. Hence, the language satisfies the flip-first and the swap-first closure properties and is a flip-swap language.
3.1 Flip-Swap poset
In this section we introduce a poset whose ideals correspond to a flip-swap language which includes the string .
Let be a length binary string. We define as follows:
| if , | ||||
| if and ( or ) (flip-first), | ||||
| otherwise (swap-first). |
Let denote the string that results from applying the operation times to . We define the binary relation on to be the transitive closure of the cover relation , that is if and for some . It is easy to see that the binary relation is irreflexive, anti-symmetric and transitive. Thus is a strict partial order. The relation on binary strings defines our flip-swap poset.
Definition 1.
The flip-swap poset is a strict poset with as the ground set and as the strict partial order.
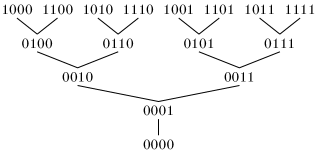
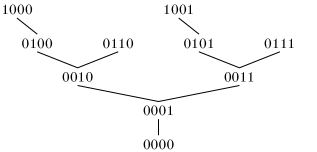
Figure 2 shows the Hasse diagram of with the ideal for binary strings of length that are lexicographically smaller or equal to in bold. Observe that is always a tree with as the unique minimum element, and that its ideals are the subtrees that contain this minimum.
Lemma 1.
A set over that includes is a flip-swap language if and only if is an ideal of .
Proof.
Let be a flip-swap language over and be a string in . Since is a flip-swap language, satisfies the flip-first and swap-first properties and thus is a string in . Therefore every string is in and hence is an ideal of . The other direction is similar. ∎
If S is a set of binary strings and is a binary string, then the quotient of S and is .
Lemma 2.
If and are flip-swap languages and is a binary string, then , and are flip-swap languages.
Proof.
Let and be two flip-swap languages and let be a binary string. The intersection and union of ideals of any poset are also ideals of that poset, so and are flip-swap languages. Now consider .
Suppose for some non-empty where . This means that . Consider three cases depending . If , then clearly . From Lemma 1, and thus . If , then and . Since is a flip-swap language . Again this implies that . If then and in this case. For each case we have shown that and thus is a flip-swap language by Lemma 1. ∎
Corollary 1.
Flip-swap languages are closed under union, intersection, and quotient.
Proof.
Let and be flip-swap languages and be a binary string. Since and can be represented by ideals of the flip-swap poset, possibly excluding , by Lemma 2 the sets , and are flip-swap languages. ∎
Lemma 3.
If is a binary string in a flip-swap language , then .
Proof.
This result follows from the flip-first property of flip-swap languages. ∎
4 A generic successor rule for flip-swap languages
Consider any flip-swap language that includes the string . Let denote the listing of in BRGC order. Given a string , we define a generic successor rule that computes the string following in the cyclic listing .
Let be a string in . Let be the leftmost position such that when , such a exists since satisfies the flip-first property and . Recall that is defined to be the position of the leftmost of (or if no such position exists). Notice that when since is a flip-swap language.
| Necklaces | Parity of | Successor | Case | ||
|---|---|---|---|---|---|
| 000000 | even | (4c) | |||
| 000011 | even | (4c) | |||
| 011011 | even | (4b) | |||
| 001011 | odd | (4e) | |||
| 001111 | even | (4c) | |||
| 111111 | even | (4b) | |||
| 011111 | odd | (4e) | |||
| 010111 | even | (4b) | |||
| 000111 | odd | (4e) | |||
| 000101 | even | (4b) | |||
| 010101 | odd | (4d) | |||
| 001101 | odd | (4e) | |||
| 001001 | even | (4b) | |||
| 000001 | odd | (4a) |
Let be the string obtained by complementing both and . When the context is clear we use instead of . Also, let denote the number of s of . We claim that the following function computes the next string in the cyclic ordering :
| if ; | (4a) | ||||
| if is even and ( or ); | (4b) | ||||
| if is even and ; | (4c) | ||||
| if is odd and ; | (4d) | ||||
| if is odd and . | (4e) |
Thus, successive applications of the function on a flip-swap language , starting with the string , list out each string in in BRGC order. As an illustration of the function , successive applications of this rule for the set of necklaces of length starting with the necklace produce the listing in Table 2.
Theorem 4.1 ().
If is a flip-swap language including the string and , then is the string immediately following the string in in the cyclic ordering .
We will provide a detailed proof of this theorem in the next subsection. Observe that each rule in complements at most two bits and thus successive strings in differ by at most two bit positions. Observe that when is excluded from , then is still a -Gray code (although not necessarily cyclic). This proves Theorem 1.2.
4.1 Proof of Theorem 4.1
This section proves Theorem 4.1. We begin with a lemma by Vajnovszki [23], and a remark that is due to the fact that is in a flip-swap language when .
Lemma 4.
Let and be length binary strings such that . Let be the rightmost position in which and differ. Then comes before in BRGC order (denoted by ) if and only if is even.
Remark 1.
A flip-swap language in BRGC order ends with when .
Let be the successor of in in BRGC order (i.e. the string after in the cyclic ordering ). Next we provide two lemmas, and then prove Theorem 4.1.
Lemma 5.
Let be a flip-swap language with and be a string in . Let be the leftmost position such that . If is even, then is the rightmost position in which and differ.
Proof.
By contradiction. Let and . Let be the rightmost position in which and differ with . If , then has the suffix since because . Thus by the flip-first property, and , a contradiction.
Lemma 6.
Let be a flip-swap language with and be a string in . If is odd, then is the rightmost position in which and differ.
Proof.
Since and is odd, . We now prove the lemma by contradiction. Let and . Let be the rightmost position in which and differ. If , then is odd but , a contradiction by Lemma 4. Otherwise if , then let . Clearly , and by the flip-first and swap-first properties, . Also, observe that is even because is odd, and thus by Lemma 4, . Further, has the suffix and is even because and is the rightmost position and differ, and thus also by Lemma 4, . Thus , a contradiction. Therefore . ∎
Proof of Theorem 4.1.
Let and . Let be the leftmost position such that . First we consider the case when . Recall that the first string in in BRGC order is [15] and is a string in by Lemma 3. Also, the last string in in BRGC order is by Remark 1 when . Thus the string that appears immediately after in the cyclic ordering is when . In the remainder of the proof, and we consider the following two cases.
- Case 1:
-
is even: If , then clearly . For the remainder of the proof, .
Since , has the prefix . We now consider the following two cases. If , then is the only string in that has as the rightmost position that differ with and has the prefix . Therefore, . Otherwise, and are the only strings in that have as the rightmost position that differ with and have the prefix . By Lemma 4, since is even. Thus, .
- Case 2:
Therefore, the string immediately after in the cyclic ordering is . ∎
5 Generation algorithm for flip-swap languages
In this section we present a generic algorithm to generate -Gray codes for flip-swap languages via the function .
A naïve approach to implement is to find by test flipping each bit in to see if the result is also in the set when is even; or test flipping the ()-th bit of to see if the result is also in the set when is odd. Since , we only need to examine the length prefix of to find . Such a test can be done in time, where is the time required to complete the membership test of the set under consideration. Pseudocode of the function is given in Algorithm 1.
To list out each string of a flip-swap language in BRGC order, we can repeatedly apply the function until it reaches the starting string. We also maintain and which can be easily maintained in time for each string generated. We also add a condition to avoid printing the string if is not a string in . Pseudocode for this algorithm, starting with the string , is given in Algorithm 2. The algorithm can easily be modified to generate the corresponding counterpart of with respect to .
A simple analysis shows that the algorithm generates in -time per string. A more thorough analysis improves this to -amortized time per string.
Theorem 5.1.
If is a flip-swap language, then the algorithm BRGC produces in -amortized time per string, where is the time required to complete the membership tester for .
Proof.
Let be a string in . Clearly can be computed in time when is odd. Otherwise when is even, the while loop in line 5 of Algorithm 1 performs a membership tester on each string in with and . Observe that each of these strings can only be examined by the membership tester once, or otherwise the while loop in line 5 of Algorithm 1 produces the same which results in a duplicated string, a contradiction. Thus, the total number of membership testers performed by the algorithm is bound by , and therefore runs in -amortized time per string. Finally, since the other part of the algorithm runs in time per string, the algorithm BRGC runs in -amortized time per string. ∎
The membership tests in this paper can be implemented in time and space; see [3, 7, 20] for necklaces, Lyndon words, prenecklaces and pseudo-necklaces of length . One exception is the test for prefix normal words of length , which requires time and space [5]. Together with the above theorem, this proves Theorem 1.3.
Visit the Combinatorial Object Server [6] for a C implmentation of our algorithms.
References
- [1] J. Arndt. Matters Computational: Ideas, Algorithms, Source Code. Springer, 2011.
- [2] S. Bacchelli, E. Barcucci, E. Grazzini, and E. Pergola. Exhaustive generation of combinatorial objects by ECO. Acta Informatica, 40(8):585–602, 2004.
- [3] K. S. Booth. Lexicographically least circular substrings. Inf. Process. Lett., 10(4/5):240–242, 1980.
- [4] B. Bultena and F. Ruskey. An Eades-McKay algorithm for well-formed parenthesis strings. Inf. Process. Lett., 68(5):255–259, 1998.
- [5] T. M. Chan and M. Lewenstein. Clustered integer 3SUM via additive combinatorics. In Proceedings of the Forty-seventh Annual ACM Symposium on Theory of Computing, STOC 15, pages 31–40, New York, NY, USA, 2015.
- [6] COS++. The Combinatorial Object Server. http://combos.org/brgc.
- [7] J. P. Duval. Factorizing words over an ordered alphabet. J. Algorithms, 4(4):363–381, 1983.
- [8] G. Ehrlich. Loopless algorithms for generating permutations, combinations, and other combinatorial configurations. J. ACM, 20(3):500–513, 1973.
- [9] R. Graham, D. Knuth, and O. Patashnik. Concrete Mathematics: A Foundation for Computer Science. Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA, 1994.
- [10] F. Gray. Pulse code communication, 1953. US Patent 2,632,058.
- [11] E. Hartung, H. P. Hoang, T. Mütze, and A. Williams. Combinatorial generation via permutation languages. In Proceedings of the Thirty-First Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’20, page 1214–1225, USA, 2020.
- [12] D. Knuth. The Art of Computer Programming. Volume 4, fascicule 2., Generating all tuples and permutations. The Art of Computer Programming. Addison-Wesley, Upper Saddle River (N.J.), 2005. Autre tirage : 2010.
- [13] Y. Li and J. Sawada. Gray codes for reflectable languages. Inf. Process. Lett., 109(5):296 – 300, 2009.
- [14] T. Mütze. Proof of the middle levels conjecture. Proceedings of the London Mathematical Society, 112:677––713, 2016.
- [15] F. Ruskey. Combinatorial Generation. Working version (1j-CSC 425/520) edition, 2003.
- [16] F. Ruskey and A. Proskurowski. Generating binary trees by transpositions. J. Algorithms, 11(1):68 – 84, 1990.
- [17] F. Ruskey, J. Sawada, and A. Williams. Binary bubble languages and cool-lex order. J. Comb. Theory Ser. A, 119(1):155 – 169, 2012.
- [18] F. Ruskey and A. Williams. Generating balanced parentheses and binary trees by prefix shifts. In Proceedings of the Fourteenth Symposium on Computing: The Australasian Theory - Volume 77, CATS ’08, pages 107–115, Darlinghurst, Australia, 2008.
- [19] C. Savage. A survey of combinatorial Gray codes. SIAM Rev., 39(4):605–629, 1997.
- [20] J. Sawada and A. Williams. A Gray code for fixed-density necklaces and Lyndon words in constant amortized time. Theor. Comput. Sci., 502:46 – 54, 2013.
- [21] J. Sawada, A. Williams, and D. Wong. Necklaces and Lyndon words in colexicographic and reflected Gray code order. J. Discrete Algorithms, 46-47:25–35, 2017.
- [22] T. Takaoka. An time algorithm for generating multiset permutations. In Algorithms and Computation, 10th International Symposium, ISAAC ’99, Chennai, India, December 16-18, 1999, Proceedings, volume 1741 of Lecture Notes in Computer Science, pages 237–246. Springer, 1999.
- [23] V. Vajnovszki. More restrictive Gray codes for necklaces and Lyndon words. Inf. Process. Lett., 106(3):96–99, 2008.
- [24] V. Vajnovszki and T. Walsh. A loop-free two-close Gray-code algorithm for listing -ary Dyck words. J. Discrete Algorithms, 4(4):633–648, 2006.
- [25] T. Walsh. Generating Gray codes in worst-case time per word. In Discrete Mathematics and Theoretical Computer Science, 4th International Conference, DMTCS 2003, Dijon, France, July 7-12, 2003. Proceedings, volume 2731 of LNCS, pages 73–88. Springer, 2003.
- [26] H. S. Wilf. A unified setting for sequencing, ranking, and selection algorithms for combinatorial objects. Adv. Math., 24:281–291, 1977.
- [27] H. S. Wilf and A. Nijenhuis. Combinatorial Algorithms: For Computers and Calculators. Academic Press, 2nd edition, 1978.
- [28] A. Williams. The greedy Gray code algorithm. In 13th International Symposium, WADS 2013, London, ON, Canada, August 12-14, 2013. Proceedings, pages 525–536, 2013.
Appendix: Proofs for flip-swap languages
This section provides the proofs for the remainder of the languages in Theorem 1.1. Unless otherwise stated, the discussion of flip-swap languages are with respect to 1.
Binary strings with weight
Recall the weight of a binary string is the number of 1s it contains. Let be the set of binary strings of length having weight less than or equal to some . Observe that satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations either decrease or maintain the weight. Thus, is a flip-swap language.
Binary strings
Let be the set of binary strings of length with each string lexicographically smaller or equal to some string . Observe that satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations either make the resulting string lexicographically smaller or produce the same string. Thus, is a flip-swap language.
Binary strings with inversions
Recall that an inversion with respect to in a binary string is any and such that . For example when , it has inversions: . Let be the set of binary strings of length with less than or equal to inversions with respect to . Observe that satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations either decrease or maintain the number of inversions. Thus, is a flip-swap language.
Binary strings with transpositions
Recall that the number of transpositions of a binary string with respect to is the minimum number of operations required to change into the form . For example, the number of transpositions of the string is . Let be the set of binary strings of length with less than or equal to transpositions with respect to . Observe that satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations either decrease or maintain the number of transpositions. Thus, is a flip-swap language.
Binary strings their reversal
Let be the set of binary strings of length with each string lexicographically smaller than their reversal. Observe that satisfies the swap-first property as the swap-first operation either produces the same string, or makes the resulting sting lexicographically smaller while its reversal lexicographically larger. Furthermore, satisfies the flip-first property as the flip-first operation complements the most significant bit of but the least significant bit of its reversal when ; or otherwise produces the string when . Thus, is a flip-swap language. The proof for the set of binary strings of length with each string lexicographically smaller than or equal to their reversal is similar to the proof for .
Equivalence class of strings under reversal has also been called neckties [19].
Binary strings their complemented reversal
Let be the set of binary strings of length with each string lexicographically smaller than (or equal to) its complemented reversal. Observe that satisfies the flip-first property as the flip-first operation makes the resulting string lexicographically smaller while its complemented reversal lexicographically larger. Furthermore, satisfies the swap-first property as the swap-first operation either produces the same string, or complements the most significant bit of and also a of its complemented reversal. Thus, the resulting string must also be less than its complemented reversal. Thus, is a flip-swap language.
Binary strings with forbidden
Let be the set of binary strings of length without the substring . Observe that satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations do not create the substring . Thus, is a flip-swap language.
Binary strings with forbidden prefix
Let be the set of binary strings of length without the prefix . Observe that satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations either create a string with the prefix or produce the same string. Thus, is a flip-swap language.
Lyndon words
Let denote the set of Lyndon words of length . Since is a flip-swap language and , it suffices to show that applying the flip-first or the swap-first operation on a Lyndon word either yields an aperiodic string or the string .
Clearly satisfies the two closure properties of a flip-swap language when . Thus in the remaining of the proof, . We first prove by contradiction that satisfies the flip-first closure property. Let be a string in . Suppose that does not satisfy the flip-first closure property and is periodic. Thus for some string and . Observe that which is clearly not a Lyndon word, a contradiction. Therefore satisfies the flip-first closure property.
Then similarly we prove by contradiction that satisfies the swap-first property. If , then applying the swap-first operation on produces the same Lyndon word. Thus in the remaining of the proof, . Suppose that does not satisfy the swap-first closure property such that but is periodic. Thus for some string and . Thus contains the prefix but also the substring in its suffix which is clearly not a Lyndon word, a contradiction. Thus, is a flip-swap language.
In [23], Vajnovszki proved that the BRGC order induces a cyclic -Gray code for the set of Lyndon words of length .
Prenecklaces
Recall that a string is a prenecklace if it is a prefix of some necklace. In Section 3 we prove that applying the flip-first or the swap-first operation on a necklace yields a necklace. Thus by the definition of prenecklace, applying the flip-first or the swap-first operation on a prenecklace also creates a string that is a prefix of a necklace. Thus, the set of prenecklaces of length is a flip-swap language.
Pseudo-necklaces
Recall that a block with respect to is a maximal substring of the form . Each block with respect to can be represented by two integers corresponding to the number of s and s respectively. For example, the string can be represented by . A block is said to be lexicographically smaller than a block (denoted by ) if or with .
A string is a pseudo-necklace with respect to if for all . Observe that the set of pseudo-necklaces of length satisfies the two closure properties of a flip-swap language as the flip-first and swap-first operations do not make the first block lexicographically larger, while the remaining blocks either remain the same or become lexicographically larger. Thus, the set of pseudo-necklaces of length is a flip-swap language.
In [21], the authors proved that the BRGC order induces a cyclic -Gray code for the set of pseudo-necklaces of length .
Left factors of -ary Dyck words
Recall that a -ary Dyck word is a binary string of length with copies of and copies of such that every prefix has at most copies of for every . It is well-known that -ary Dyck words are in one-to-one correspondence with -ary trees with internal nodes. When , Dyck words are counted by the Catalan numbers and are equivalent to balanced parentheses. As an example, is a -ary Dyck word and is also a balanced parentheses string while is not a -ary Dyck word nor a balanced parentheses because its prefix of length three contains more s than s. -ary Dyck words and balanced parentheses strings are well studied and have lots of applications including trees and stack-sortable permutations [4, 16, 18, 24].
The set of -ary Dyck words of length is not a flip-swap language with respect to since is a -ary Dyck word but is not. The set of length prefixes of -ary Dyck words is, however, a flip-swap language with respect to . This set is also called left factors of -ary Dyck words. Let be the set of left factors of -ary Dyck words. Observe that satisfies the two closure properties of a flip-swap language with respect to as the flip-first and swap-first operations do not increase the number s in the prefix. Thus, is a flip-swap language with respect to .