Intelligent metaphotonics empowered by machine learning

As demonstrated in the recent years, artificial intelligence (AI) is quickly becoming a ubiquitous concept in various physical sciences [1, 2, 3, 4, 5, 6]. Specifically, optics and photonics provide a variety of physical applications that can be studied and enhanced using these novel approaches. Merging AI with photonics is particularly advantageous as Maxwell’s equations fundamentally describe very precisely a wide range of experimentally observed phenomena. Thus they can be employed directly to generate vast amounts of training data required for implementing various AI algorithms. Also, by employing AI in optical physics, we may expect to create efficient photonic quantum machines that eventually may merge with much broader biological intelligence. Thus, a remarkably powerful AI methodology that complements many conventional analytical and numeric techniques find many important applications and demonstrations in photonics. In particular, such approaches are used for inverse design, optimization, big-data processing, underpinning the rapid development of precise photonic technologies.

Metaphotonics is a new and rapidly developing research direction in subwavelength photonics [7]. It is inspired by the physics of metamaterials where the electromagnetic response is associated with the magnetic dipole resonances and optical magnetism originating from the resonant dielectric nanostructures with high refractive index. The concept of all-dielectric resonant nanophotonics is driven by the idea to employ subwavelength dielectric Mie-resonant nanoparticles as “meta-atoms” for creating highly efficient optical metasurfaces and metadevices. These are defined as devices having unique functionalities derived from structuring of functional matter on the subwavelength scale [8], often termed as “meta-optics” for emphasizing the importance of optically-induced magnetic response of their artificial subwavelength-patterned structures. Because of the unique optical resonances and their various combinations for interference effects accompanied by strong localization of the electromagnetic fields, high-index nanoscale structures are expected to complement or even replace different plasmonic components in a range of potential applications. Moreover, many concepts which had been developed for plasmonic structures, but fell short of their potential due to strong losses of metals at optical frequencies, can now be realized based on low-loss dielectric structures.

High-index dielectric resonators can support both electric and magnetic Mie-type resonances which can be tailored by the nanoparticle geometry. Mie-resonant silicon nanoparticles have recently received considerable attention for applications in nanophotonics and metamaterials [9] including optical nanoantennas, wavefront-shaping metasurfaces, and nonlinear frequency generation. Importantly, the simultaneous excitation of strong electric and magnetic Mie-type dipole and multipole resonances can result in constructive or destructive interferences with unusual spatial scattering characteristics, and it may also lead to the resonant enhancement of magnetic fields in dielectric structures that could bring many novel effects in both linear and nonlinear regimes.

Here, we discuss the current progress in the recently emerged fields of machine learning and artificial intelligence focusing on their applications to metaphotonics driven by optically-induced electric and magnetic resonances. More specifically, we describe how these novel ideas can be applied to study optical nanoantennas and metasurfaces and improve their functionalities. We also present a summary of the basic concepts of machine learning with some specific examples developed and demonstrated for a variety of metasystems and metasurfaces.

This Perspective is organized as follows. In Sec. II we broadly discuss the basic concepts of machine learning irrespective of specific applications. We introduce the concepts of deep learning and machine learning and show how they are linked to artificial neutral networks and artificial intelligence concepts. Next, in Sec. III we summarize briefly the main ideas of metaphotonics and describe the main parameters and properties which are required usually for the optimisation. In Sec. IV we consider several examples of advanced nanoantennas and their optimisation with the help of machine learning. All Secs. V – VII discuss various aspects of functional and self-adaptive metasurfaces and their applications to sensing. Finally, Sec. VIII concludes the paper with perspectives and outlook.

In this Perspective article, we focus on phenomena and applications which can be reached via AI technologies, and we do not discuss particular methods in detail. Still, here we provide a brief description of machine learning (ML) algorithms in order to outline the general ideas of those methods suitable for applications.

While AI is a broad field closely connected with the development of systems mimicking intelligence, ML provides a set of data-driven algorithms for learning ability of AI [10]. The goal of ML algorithms is to find a sequence of programmatic transformations connecting the input and output data. This could constitute a mathematical model that connects physical parameters to an observed phenomena [11, 12, 13]. In another case it could be the use of a heuristic to classify labelled data. Considering an example from physics, this might be transformations which have to be applied to geometric parameters of a unit cell of a metagrating to obtain a corresponding reflection spectrum. Generally, provided a good source of data, the more input data the algorithm receives, the more accurate a result will be. It should be highlighted that ML algorithms can work with data itself and find correlations within it without any understanding of physical, mathematical, or other meaning. However, in some cases it is possible to provide physical intuition or to constrain models to obey physical models such as, for example, the Navier-Stokes equations [14, 15] or Maxwell’s equations [16]. Existing ML methods span a range of tasks, including but not limited to, classification, regression, clustering, anomaly detection and structured prediction. While ML has demonstrable efficacy for a number of tasks there remains significant overhead involved in the application of such techniques. This usually involves a number of tasks such as tuning and design of the models in question, with the largest task generally being the feature extraction process which often requires domain specific expertise.

Deep learning (DL) is a subclass of ML (see Fig. 1) solely based on layered structures referred to as artificial neural networks (ANNs). ANNs derive their name from the neural structures found in biological entities. This structure is emulated mathematically as a node, referred to as a neuron, which may contain many input and output connections with associated weightings. These neurons have a non-linear activation function which is a function that serves to map the inputs to an output and provide the switching behaviour seen in biological neurons [17]. These neurons are stacked into layers which are then connected to subsequent layers. The utility of this is to construct a sufficiently deep neural network such that any arbitrary function may be approximated [18]. ANNs thus may be considered as a mapping from some input space to some output space which can be arbitrarily defined. ANNs can also have complicated structures for different tasks. The inclusion of convolutional layers have demonstrated great success in image processing tasks [19] and auto-regressive models similarly with natural language processing [20] and sequentially organised data [21]. A key feature of these models and DL in general is that the design process does not require the same domain specific knowledge as other classical ML methods. Instead the features of a data set are learnt automatically to best facilitate the desired mapping from input to output. To perform a given task DL models must undergo a process known as training. Training a model requires the introduction of the so-called loss function, which provides feedback on the difference between the real output (or “truth”) and the output predicted by the network for the same given input data. Training the ANN aims to minimize the loss function by adjustment of the weight values at each layer. This tasks is generally achieved via some form of stochastic gradient descent which may be done efficiently over the network with backward propagation [22]. The training is termed complete when the model is capable of predicting the output with some desired accuracy.

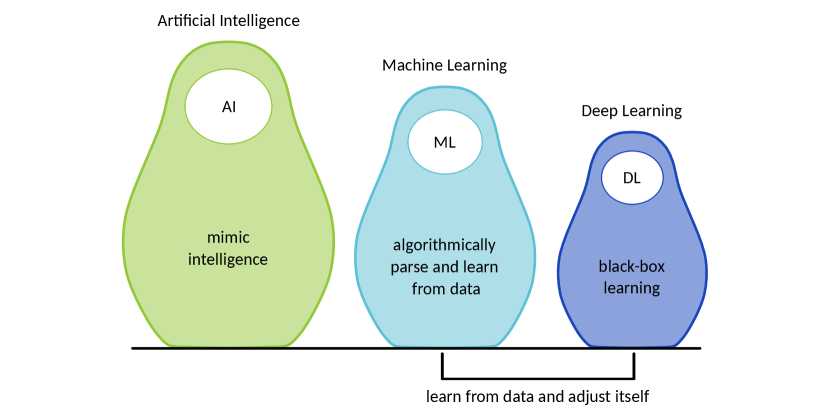
After the training, the ANN is able to accurately map the input to the desired output, implying that it has “learned” the necessary mapping from the given data. It should be noted that this mapping is not necessarily unique and differences in training procedure can cause a failure to converge. It is generally considered good practice to divide a dataset into training and validation sets. Due to the expressivity of high dimensional networks it is possible for over-fitting to occur which must be mitigated. Over-fitting can be monitored via the loss function applied to the validation set. Once the model is trained and over-fitting is mitigated the model can be said to be capable of generalising for an out of sample input. This of course assumes that the training data provided is representative of the problem that one is trying to learn. It is important to note that in general ML models are interpolative by construction, thus extrapolative intuition (not to be confused with generalisation) is still a difficult problem that is indeed difficult for human operators as well.

One of the major drawbacks of ML is the amount of data needed for the training procedure, which is typically dictated by the complexity of the problem. For DL increased training data also tends to mitigate over-fitting to a certain extent and thus can be even more important. The collection of the data as well as training may take an enormous time. Hence, the use of DL is usually justified when the same task has to be solved many times for slightly different set of parameters or the task of building a feature extractor is intractable.

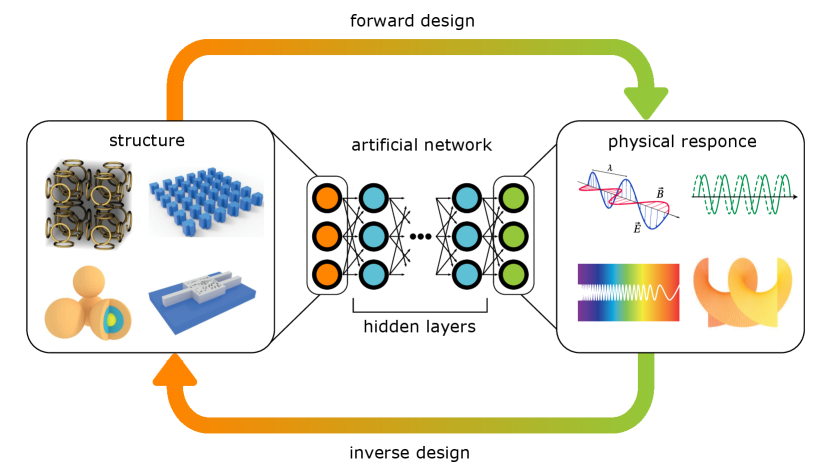
Concerning photonics, ML was so-far incorporated mainly as a tool for forward and inverse design procedures (see Fig. 2). Forward design is associated with prediction of a physical response (scattering spectra, polarization, etc.) for a given structure. This task can be solved via variety of different tools, such as T-matrix calculations, full-wave simulations and others, which are basically aimed to solve Maxwell’s equations in some form. Though ML may become an alternative method for the same purpose, possibly its greatest benefit is associated with inverse design problems — determination of structure parameters necessary to provide a given response. In this case DL can be used as a basis for the so-called surrogate modelling providing not a simulation but rather its data-driven approximation.

To illustrate the above ideas, we consider an example of a metaphotonic system which can be designed with the help of an ANN. Let the aim be to predict a scattering spectrum for a given radius of a uniform spherical particle. In this case the input is the radius, and the output is the value of a scattering cross-section (SCS) at some particular frequency. The training set consists of pairs [radius, SCS] and the network finds the mapping between these two values, meaning that it finds a sequence of mathematical transformations which converts a given radius to a known SCS value. In this case, the transformations are not constrained to have anything in common with any physical equation, theory, or model.

When the sequence is defined, the network can predict the unknown value of SCS for a radius which was not given during the training. Importantly, the reverse process is possible, and inputs can be swapped with outputs so the network will estimate parameters required for a given SCS value. No additional training procedures or any changes of the algorithm are needed — when the connections are determined they work in both ways. Therefore, the network can be trained with the data acquired by conventional solvers and then it is capable to solve the inverse task to find parameters for a desired physical response. However, it should be mentioned that for real-world tasks the procedure may be not that straightforward and to achieve high accuracy special architectures of ANNs and algorithms should be considered. Nevertheless, accuracy of the predictions may approach unity when provided enough data, with the speed of estimation suitable to many real-time tasks making DL a promising tool for design of photonic devices.

The same logic can be applied for other classes of problems, not necessary related to scattering. However, in this Perspective we describe not the algorithms themselves but some results which can be achieved with their help. Thus, below we refer to DL algorithms as black-boxes with unspecified structures and functional mappings between the physical parameters.

Electromagnetic metamaterials were suggested as artificial structures composed of subwavelength elements, and initially they were driven by curiosity such as negative refraction and super-lens. Some years later, metamaterials created a paradigm for engineering electromagnetic space with the help of transformation optics. More recently, research on metamaterials evolved into the study of metasystems and metasurfaces as basic components of the so-called metadevices defined as optical devices having unique and useful functionalities realized by structuring of functional matter on the subwavelength scale [8]. It is expected that future technologies will involve a high level of photonic integration achieved by embedding the data-processing and waveguiding functionalities at the material’s level. Thus, an important task is to study and optimize materials building blocks such as nanoantennas and metasurfaces.

Plasmonic and dielectric nanoantennas supporting resonances represent a novel type of building blocks of metamaterials for generating, manipulating, and modulating light [23, 7]. By combing both electric and magnetic modes, one can not only modify far-field radiation patterns but also localize the electromagnetic energy in open resonators by employing the physics of bound states in the continuum to achieve destructive interference of leaky modes [24].

Metasurfaces are created by artificial subwavelength elements with small thickness which provides novel capability to manipulate electromagnetic waves [25]. Well before the exploration of metasurfaces, tailoring the light scattering with planar optical structures has been majorly pursued with diffractive optical elements [26]. However, the concept of metasurfaces provides much broader and deeper insights and useful tools for complete control of light. Metasurfaces are characterized by reduced dimensionality, and usually they consist of arrays of optical resonators with spatially varying geometric parameters and subwavelength separation. In contrast to conventional optical components that achieve wavefront engineering by phase accumulation through light propagation in a medium, metasurface provides new degrees of freedom to control the phase, amplitude, and polarization of light waves with subwavelength resolution, as well as to accomplish wavefront shaping within a distance much less than the wavelength of light. The outstanding optical properties of dielectric metasurfaces drive the development of ultra-thin optical elements and devices, whether showing novel optical phenomena or new functionalities outperforming their traditional bulky counterparts [9, 27, 28]. Metasurfaces consist of carefully arranged “unit cells” or “meta-atoms” with subwavelength structures. The optical response (phase, amplitude, and polarisation) of the meta-atom changes with its geometry (height, width, material, etc). The meta-atoms are arranged into arrays to provide specific variations of parameters, depending on required functionalities. Meta-atoms can operate as subwavelength resonators supporting multipolar Mie resonances [9], or they can contribute to averaged parameters like metamaterials [27].

The concept of optical metasurfaces have been applied to demonstrate many exotic optical phenomena and various useful planar optical devices. Many of these metasurface-based applications are potentially very promising alternatives to replace conventional optical elements and devices, as they largely benefit from ultra-thin, lightweight, and ultracompact properties, provide the possibility of overcoming several limitations suffered by their traditional counterparts, and can demonstrate versatile novel functionalities. Metasurfaces were suggested for an efficient control of light-matter interaction with subwavelength resonant structures, and they have been explored widely in the recent years for creating transformational flat-optics devices.

Plasmonic metastructures suffer from significant losses and show low efficiency, but all-dielectric structures can readily combine electric and magnetic Mie resonances and control efficiently optical properties such as amplitude, phase, polarization, chirality, and anisotropy [7]. The control of all such parameters require a careful optimisation depending on the problems where the metasurfaces are used. Many such properties are driven by local electromagnetic resonances such as Mie-type scattering, bound states in the continuum, Fano resonances, and anapole resonances. The recent research frontiers in dielectric metasurfaces include wavefront-shaping, metalenses, multifunctional and computational approaches, with the main strategies to realize the dynamic tuning of dielectric metasurfaces.

Importantly, recent advances in nanofabrication technologies bring low-cost, large-area and mass productive approaches and capabilities for the development of various types of metasystems and metasurfaces, and the methods are gradually becoming mature. It is expected that flat-optics components based on dielectric metasurfaces will appear in our daily life very soon bringing complexity of optical components and novel functionalities [29].

One of the first illustrative examples for application of the ML techniques to metaphotonics is a design of nanoantennas as elementary units of metasystems meta-atoms. Engineering of a scattering response is often realized with core-shell structures via tuning of thickness and dielectric permittivity of the layers. In this case, a design of nanoantennas may be time consuming due to the overwhelming number of possible combinations of the nanoantenna parameters. Even accounting for manufacturing limitations, the number of possible materials and layer thicknesses can go far beyond thousands of values. Without advanced optimization techniques they should be iterated to fit a desired scattering spectrum, which implies a large number of calculations. In this case, the application of DL techniques can become very useful and productive.

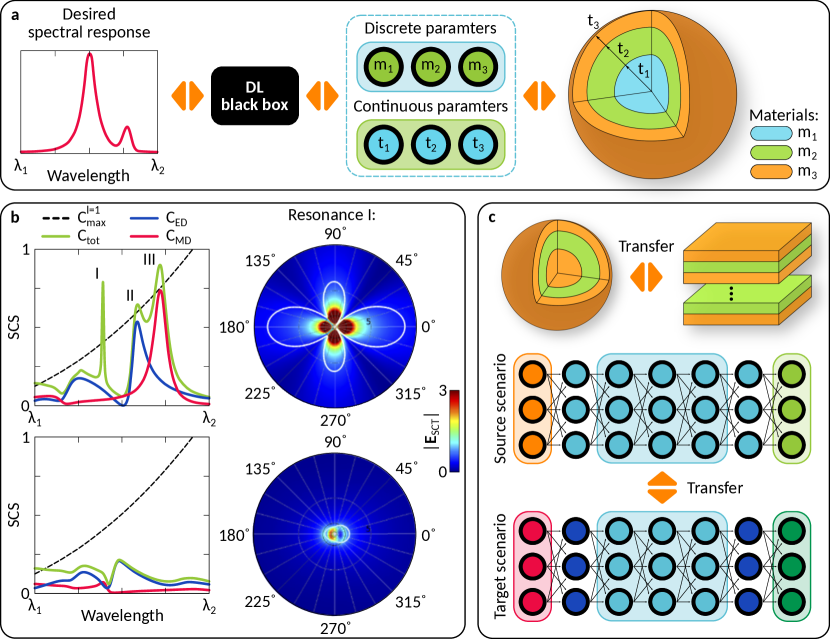
The general idea of a design procedure based on the DL approach is shown schematically in Fig. 3(a). One of the first results in this field was presented in Ref. [30] where the network was trained to determine a scattering spectrum of a layered spherical nanoparticle with fixed material parameters. The inputs of the network are the thicknesses of the layers ($30$ – $70$ nm) and the outputs are the scattering spectrum samples in the range of wavelengths between $400$ nm and $800$ nm. After the training, the network is able to generate a scattering spectrum for a given set of parameters within a second and with a high precision (mean relative error is below $1.5$%). Importantly, the re-trained network is used to provide an inverse design such that for a given spectra it gives a suitable set of thicknesses. Moreover, the network is used as a tool for optimizing the spectral features in narrow and broadband regions of the spectra. Similar tasks have also been considered in Refs. [31, 32], where more advanced DL techniques have been applied.

The DL procedure was further generalized to adjust not only thicknesses but also materials of a three-layered sphere via the application of neural network [33]. In this case, the inputs are electric and magnetic dipole responses while the output is the set of materials and thicknesses. To avoid arbitrary refractive indices which cannot be achieved in a real situation, the set of possible refractive indices is limited to $7$ values corresponding to typical materials used for nanofabrication (such as Si, SiO₂, Ag, etc.). On the one hand, such a strategy significantly limits the possible output parameters, but the computational problem actually become more complicated. In this case, two tasks have to be solved simultaneously: a regression problem, to estimate geometric parameters taking continuous values, and classification problem, to determine material properties. Additionally the network must also reconstruct the spectrum from the design parameters. The proposed solution is based on a purpose built hybrid architecture. Two networks are used here: one, to connect optical properties with parameters of the structure, and the other one, to map design parameters to optical responses. Importantly the training of both networks happens simultaneously with a combined loss function that imposes the networks learn forward and inverse design. The proposed DL architecture allows to find and tune electric and magnetic dipole resonances. For example, the algorithm is used to achieve the resonance spectral co-location. Simultaneous tuning of electric and magnetic dipole resonances also allow implementing the first Kerker condition and design even more complex media with negative index of refraction.

Implementation of ML-based numerical design techniques is not limited to spherical geometries and neural networks. Classical ML algorithm (the so-called Bayesian optimization) was applied for forward design of cylindrical metal-dielectric nanoantenna in order to achieve unidirectional scattering satisfying Kerker or anti-Kerker conditions [34]. Multipole engineering via DL techniques was also demonstrated, where an ANN was used to determine the far- and near-field response of arbitrary plasmonic and dielectric structures and the internal distribution of fields [35]. DL algorithms can be employed to study a variety of problems in metaphotonics including electric and magnetic dipole resonances, Kerker scattering, and destructive interferences leading to the anapole states.

Advantages of DL-based designs over FDTD simulations of core-shell nanoantennas have been discussed in Ref. [36]. In general, the speed of DL-based forward designs is $100$–$1000$ times faster in comparison with FDTD simulations. At the same time, accuracy of prediction reaches the values about $95\%$. Together with developing ML-supplemented methods for solving both forward and inverse scattering problems [37, 38, 39, 40], such studies suggest that AI technologies may constitute conventional numerical methods resulting in the development of novel computational tools. For instance, the recent results [41] suggests real-time web-based tools for designing far-fields of arbitrary-shaped structures.

Other examples of the scattering problems that can be tackled with DL algorithms include a design of invisible objects. In particular, $5$-layer particle (Ag and SiO₂ layers) was inversely designed to achieve extremely low scattering efficiency within an optical frequency spectrum [42]. Namely, the scattering efficiency was below $10^{-2}$ in the range from $400$ nm to $700$ nm, dropping below $10^{-4}$ between $510$ nm and $550$ nm. Another demonstration utilizes phase-change materials for realizing invisibility-to-superscattering switching [43]. Developed DL approach allowed to predict required materials and structural parameters to realize simultaneously satisfied conditions for super- and near-zero scattering for two phase states, see Fig. 3(b). The shape of a particle itself may also be a target of DL-based design procedure as for example in Ref. [44] where an all-dielectric shell was designed for optical cloaking.

Design of nanoantennas can also be used as a basis for solving other problems. As was mentioned above, to achieve reasonable accuracy, the application of DL methods requires a large amount of data. At the same time, ANNs are usually implemented for some specific systems, and a change of the system requires initiation of a new training process even if the general task remains the same. For example, a design of a scattering response of nanoparticles is completely different from the same procedure for metasurfaces though the outputs are quite similar (such as scattering spectra). This is reasonable, since these two systems are characterized by different sets of parameters, and hence there are different mappings between the input and output data. Nevertheless, it is possible to transfer knowledge gained by an ANN between completely different scenarios, referred to as transfer learning [45, 46]. This was demonstrated for the transmission of 8-layer films utilizing the results obtained for scattering from 8-layer nanoparticles [47]. The general idea is presented in Fig. 3(c), and the procedure requires merging two ANNs meaning that layers of one network (for the scattering problem) can be inserted into the other one (for the transmission problem). As a result, the learning error of the network for the multilayer films is reduced by almost $20\%$ (from $7.1\%$ to $5.7\%$). The proposed technique may be useful for insufficient data allowing to use ANNs already trained for other tasks. Similar idea was developed [48] to provide inverse design with finding simultaneous materials and continuous geometric parameters of core-shell particles and multilayer films.

Both shape and size of single-material nanoparticles may also be a target for the inverse design procedure. For instance, DL techniques were implemented to achieve a desired spectral emission [49] as well as far- and near-field properties [50, 51] of plasmonic nanoantennas. At the same time, a design of nanoparticles is required in many other fields apart from photonics, such as chemistry or biology. For instance, the DL-based inverse design can be implemented to realise specific interactions [52]. However, these topics are beyond the scope of the current paper.

Moving from isolated nanoantennas to their arrays, we wish to mention the results of the DL-based optimization of halide-perovskite thin solar cells combined with a layer of core-shell metallic nanoparticles [53]. This study employs the fact that core-shell nanoparticles may have two plasmon resonances located in different parts of spectra, and the resonances can be tuned by adjusting structural parameters. As a result, the efficiency of such solar cells can be improved by applying the ANN approach, e.g. by studying configurations of core-shell nanoparticles to maximize optical absorption. Similar ideas are applied to the design of metasurfaces with the optimization of structural parameters of single meta-atoms. Thus, it is natural to move from optimizing isolated nanoantennas to the use of DL approaches for advancing the field of metasurfaces.

The fundamental concepts and underlying optical physics of metasurfaces have been extensively explored with the field itself now exhibiting a comprehensive framework. Currently, more advanced engineering with optimization tools is required for moving this field to specific practical applications including bending of light, metalenses, and metaholograms. A rich variety of ML methods and DL approaches has already been explored for metasurfaces aiming to optimize their required functionalities. Below, we present only a few recent examples of such efforts concentrating on particular applications and specific optical devices and functionalities.

Inverse design of metasurfaces results in selecting particular shapes and materials of an isolated meta-atom as a specific element of metasurface supercell. In this case, representation of parameters plays an important role, often significantly affecting the result of the subsequent training procedure. Similar to the case of nanoantennas, the design procedure here may result in a set of geometric parameters of meta-atoms with fixed shapes. For example, such an approach was used for a metasurface with super-cells consisting of gold cross-shaped resonators (up to 25 resonators per supercell) [54]. Inputs to the DL algorithm were the corresponding sets of lengths, and the outputs were the absorption spectra. As a result, the algorithm allowed the design of narrow-band, broadband, and multiresonant absorbers. However, even with adjustment these constrained parameters may fail to provide a desired spectral response. As an alternative, a free-form design approach can be used. In this case, the DL algorithm process is based not on sets of parameters, but rather employs pixelated images of the unit cells [55]. Such techniques extend the expressivity of this approach, significantly extending the range of possible cell geometries. Conversely, the DL approach can also be used to restore a unit cell geometry from a given spectra [56]. The design procedure may also incorporate some transfer learning between meta-atoms of various shapes [57].

One of the critical tasks in the development of transformative metadevices is to engineer specific properties of the light-matter interaction. As a consequence, many studies are devoted to the design and optimization of specific absorptive, scattering, and diffracting properties [63, 64, 65, 66]. However, many studies focus more on design methods rather than specific applications. We would like to highlight several examples of particular devices benefiting from the AI approach.

Starting from absorbers, there are a variety of realised design procedures resulting in the development of perfect [67], multi-band [68], and ultrathin [69] absorbers. Such studies cover both plasmonic [70, 71] and dielectric [72] metastructures. DL also opens the route for the design of biology-inspired devices such as moth-eye structures [73] with the designed average absorption reaching $90\%$ in the range from $400$ nm to $1600$ nm. Scattering properties are a subject of many design procedures [74, 75, 76, 77, 56, 78], including those devoted to the development of anisotropic [79] and bianisotropic [80] metasurfaces, as well as switchable reflectors [59]. DL was also exploited for achieving electromagnetically-induced transparency [81, 82, 83]. Chiral metasurfaces are also among the typical applications of the DL design procedures [84, 85, 86, 87, 88, 60]. Phase-amplitude engineering supported by DL algorithms helps to overcome chromatism [89], achieve tunable beam-steering [62], and multiplex an aperture [90] of metasurfaces. AI-assisted design enables development and improvement of broadband achromatic [91, 92], bifocal [58], thermally tunable [93], and RGB (red, green, blue)  [94] metalenses.

Light-matter interaction plays an important role in our daily life providing such information about an object as its color. In general, coloration of objects may be achieved by using special pigments characterized by different absorption properties. Another approach is to employ structural colors generated via engineering of diffraction and reflection properties of an object. Apart from surface decoration, structural colors may be used for digital displays, sensing, storage of information, and many other applications [95]. Metasurfaces are able to absorb or scatter light selectively with particular wavelengths making them are promising candidates for structural color engineering [96]. Methods to design metasurfaces for this specific purpose also include the application of DL algorithms to plasmonic [97, 98] and, more extensively, for dielectric metastructures [99, 100, 101, 102, 103, 104].

Metasurfaces may also enhance the performance of solar cells. To further improve capabilities of metasystems, a novel design of silicon solar cell with an active nanopixel metasurface has been suggested [105]. The shape was optimized by using DL to solve the forward design problem, over which an optimisation search is performed using a genetic algorithm to find the maximum short circuit current. As a result, the optimized solar cell exhibited a $\leavevmode\nobreak\ 2.5$ times larger short circuit current than in any solar cell without metasurfaces, but with the same amount of crystalline silicon. It was demonstrated that the short circuit current was above $12$mA/cm² for all other polarizations and angles of incidence. Additionally, if the absorptive metasurfaces may be made of various materials, the design procedure can exploit transfer learning methods in order to account for the effect of different materials on the spectra [106].

One more application is laser imaging detection and ranging (LIDAR) systems [107] extensively used in many areas, such as biology, geology, atmosphere studies, astronomy, and many other fields. With the rise of augmented reality technologies and autonomous systems, such as self-driving vehicles, LIDAR systems entered a new stage of development as a tool for object recognition and 3D modeling of an environment. In Ref. [108], the authors suggested a device consisting of a metasurface covered by a layer of liquid crystals with high birefringence. The structure is sandwiched between two cover-slips with a transparent, patterned and conductive layer (ITO), serving as electrodes and connected to an field-programmable gate array (FPGA) control processor. The deflection is performed by the metasurface as well as a change of the surrounding media. Applied external voltage changes the orientation of liquid-crystal molecules resulting in a change of the refractive index enabling beam steering in the desired angle range. The metastructures consist of a patterned MoS₂ layer with thickness $30$ nm and refractive index $n=4.3+0.034i$. The ANN approach is employed to generate ensembles of topology-optimized metasurfaces for achieving the highest deflection efficiency for a desired deflection at the telecommunication wavelengths. The demonstrated deflection angles were $45^{\circ}$, $55^{\circ}$, and $65^{\circ}$ with an absolute efficiency of $\leavevmode\nobreak\ 0.7$ in all cases..

AI methods can also empower technologies such as near-eye displays, required for virtual and augmented reality systems as well as for vision correction. One of the promising platforms for realizing such displays is based on the application of metasurfaces [109, 110, 111, 112, 113] employing their ability to control wavefront, phase, amplitude, and polarization of light. Design of metasurfaces for such applications can be realized efficiently with the DL methods. The paper [114] provides an example of a design of a metasurface acting as a beam deflector. It consists of a stack of $L$-layer gratings made of TiO₂ with glass nanoridges where each grating layer is $300$ nm thick. The display system transfers a designated scene toward the human eye via grating-covered waveguide. The system consists of image projectors, in-coupling and out-coupling gratings, and a waveguide. Light propagates along the waveguide towards an eye, and the in-coupling grating is illuminated by single or multiple projectors. The aim of the DL-based metasurface design is to maximize the deflection efficiency for given operating wavelengths, here chosen to be $720$ nm (red), $540$ nm (green), and $432$ nm (blue). For the cases of integrated and separated RGB projectors, the achieved deflection efficiency was about $91\%$ and $95\%$ respectively, and the overall efficiency is about $80\%$. Also, the authors developed pupil expanded out-coupling grating consisting of three sections. For all of three designated diffraction efficiencies ($33\%$, $50\%$, and $100\%$), the design procedure led to the deflection efficiency above $85\%$.

A very interesting application of metasurfaces includes the development of the so-called light sails — structures for a spacecraft propulsion system relied on a force exerted due to the radiation pressure coming from the Sun or a strong laser beam [115]. Recent studies demonstrated that all-dielectric metasurfaces can maximize the acceleration combined with thermal management requirements and passive stabilization mechanisms [116, 117, 118], however, such designs require precise engineering of the structures. Along with some conventional techniques [119, 120], the DL algorithms were considered as candidates to solve this task [121]. Aiming to develop a meta-sail for ultralight spacecraft that can reach Proxima Centauri b in approximately 20 years, the authors of Ref. [121] designed free-form silicon metastructures to satisfy optical and weight constraints. They demonstrated that optimization algorithms converged to one-dimensional gratings which allow the acceleration distance $D=1.9\times 10^{9}$ m (distance required to reach target velocity $0.2$ of light speed) and mean reflectivity around $0.81$.

Some other practically important applications include thermal emitters [122], optical memory elements [123], smart windows [124], programmable switches [61], and transmission cloaking devices [125]. Below, we discuss the application of metasurfaces to biosensing where AI methods and DL tools may provide very beneficial outcomes.

Metasurfaces can be employed as a reliable and robust platform for various chemical and biological sensors [126, 127, 128]. Being one of the most promising and rapidly developing fields of modern photonics, biosensing has also utilised AI aided techniques  [129]. In this case, ML techniques may play two major roles. First, metasurfaces can be employed to optimize sensors [130, 131, 132, 133]. On the other hand, metasurfaces empowered by ML techniques provide a powerful tool for classification tasks, which can be exploited to analyze output data of a sensor [134, 135, 136, 137].

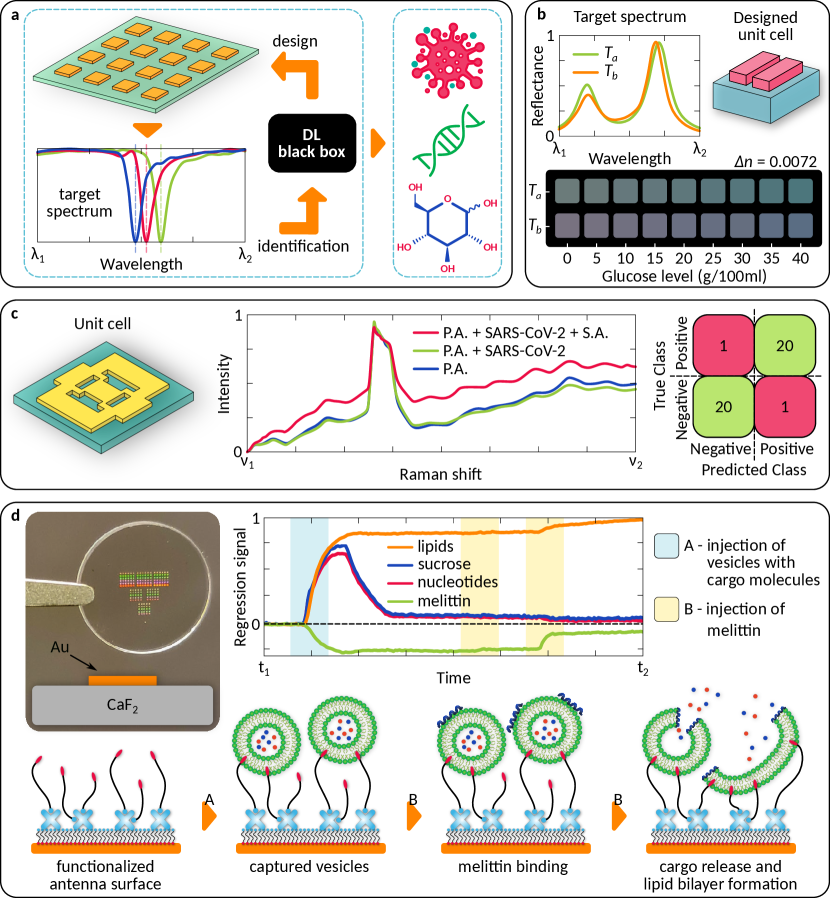
To demonstrate benefits of the ML-assisted metasensor design, we consider the example of a colorimetric sensor based on all-dielectric metasurfaces. Colorimetry techniques rely on detection of color variations associated with environmental change leading to a change of refractive index. Hence, optimization of colorimetric sensors implies maximization of color difference. In Ref. [132], the authors propose a metasurface consisting of double-bar elements. They demonstrated that a dual-resonant type of spectrum can achieve better color difference than a single resonance. Therefore, the design process aims to find target dual-resonance spectra with the highest sensitivity of color change with respect to minute spectral shifts. These spectra were used as inputs to a DL algorithm in order to find geometric parameters of the unit cell. This design procedure is shown in Fig. 5(a). The optimized structure was used to sense the concentration of a glucose solution. It was demonstrated that the sensing resolution was able to distinguish a change in refractive index of $\leavevmode\nobreak\ 0.0086$ with a mean square error within $0.005$.

Another demonstration of meta-sensor design includes the optimization of double-negative plasmonic metasurfaces for enhanced detection of DNA oligomers [133]. The overall device consisted of a layered structure comprised of a glass substrate, gold layer and negative-index effective medium. Immobilized and hybridized DNA oligonucleotides were placed on top of the metasurface and covered by a buffer ambience layer (distilled water). A standard multilayer perception was used to predict angular reflectance for a given thickness of the gold layer, effective permittivity and permeability. The obtained spectral characteristics were then clustered to ensure that resonance characteristics are appropriate for an efficient metasensor. The consequent application of DL and classical ML algorithms resulted in a sensitivity improvement of up to $13$ times, in comparison with conventional plasmonic sensors.

To illustrate how ML can be employed for classification of biomolecules, we mention the recently suggested platform for surface-enhanced infrared absorption spectroscopy empowered by DL algorithms [136]. In particular, they use nanoplasmonic metasurface supporting three resonances in a broad mid-IR spectrum ($1000$–$3000$ cm^-1) covering absorption bands of biomolecules. The sample consists of liposome nanoparticles loaded with sucrose and nucleotides. In addition, melittin is introduced to perforate the lipid membranes of the liposomes leading to dual cargo release and formation of supported lipid bilayer on the surface of the sensor. Real-time measurements of reflectance spectra are used to calculate absorbance which is analyzed via a DL technique. As a result, the algorithm able to distinguish between each analyte at each point of time [see Fig. 5(c)]. Therefore, the developed sensing platform enables simultaneous label-free monitoring of major biomolecule classes in water opening the route to study real-time biomolecular interactions, such as vesicle capture, perforation with dual cargo release, and partial transition to planar lipid bilayers.

Advances in metasensors have also been utilised to address global challenges such as COVID-19 pandemic. AI technologies were already exploited for diagnostics of coronavirus [138, 139] and recently they were proposed to be combined with meta-sensors. The SARS-CoV-2 saliva sensor [see Fig. 5(b)] proposed in Ref.[134] demonstrated sensitivity and specificity both reaching $95.2\%$ during clinical trials. The sensing platform is comprised of a plasmonic metasurface functionalized with thiol-modified primary DNA aptamers. Meta-atoms were optimized for maximization of the Raman cross-section using a genetic algorithm. Testing samples consisted of unprocessed saliva mixed with Cy5.5-modified fluorescent secondary DNA aptamers. After an allowed 15 minutes for binding, the solution was placed on the sensor to drain. The surface was then rinsed with double-distilled water and phosphate buffer saline. Identification of the virus was performed using an ML algorithm to process Raman shift spectra. Out of $69$ clinical samples only $1$ false positive and $1$ false negative result were obtained indicating a high potential worth further development. Moreover, the sensor was capable of variant detection among inactivated Alpha (B.1.1.7), Beta (B.1.351), and wild-type variants, with cumulative variance $99.7\%$.

We notice that classification of a metasensor output is not necessary done via DL algorithms. Classical ML methods, such as k nearest neighbours or principal component analysis with latent Dirichlet allocation, may provide no less good results. For instance, gaseous and liquid chemicals may be recognised using plasmonic mid-infrared spectral filters with a photodetector array [137] or plasmonic metasurfaces integrated with microfluidic channel [135].

We notice also that ML may be used not only to design and supplement metasensors, but also to sense the presence of metamaterials per se. As an example, a DL algorithm could process electromagnetic response signals obtained with THz-band time-domain spectroscopy in order to identify metamaterial in lactose mixtures [140]. The accuracy reached an astonishing value of $100\%$, while classical ML algorithm (support vector machine) allowed only $87.9\%$ and human’s ability to recognize the spectrum of a metamaterial was below $57\%$.

The examples described above, together with other achievements of AI-supplemented sensing, suggest the beginning of a revolutionary era of intelligent biosensors, extensively discussed in literature (see Refs. [129, 141, 142, 143, 144] for instance). Seemingly, metastructures and metasurfaces will play an important role in the development of those ideas. Apart from photonics, other sensing technologies have also experienced a rapid onset of AI resulting in the development of next-level intelligent systems based on principles of self-adjustment, which we discuss in the next section.

Progress in computer science enabled the development of such intriguing concepts as coding and digital (or programmable) metasurfaces [145, 146, 147, 148, 149, 150, 151, 152] that fill a gap between IT and electrodynamics. Though the ML concepts can also be used just for a straightforward design of such structures [153, 154, 155, 156, 157, 158, 159], they expose a range of additional possibilities. AI technologies which are capable of adjusting the response of a system to specific inputs are extremely useful for the development of self-adapting and re-programmable systems. In this case, ML can be used as a feedback mechanism, redefining programming sequences of a digital metasurface to adjust to environmental changes. In recent years, this concept has developed into a new branch of intelligent metasurfaces, which rapidly gained a lot of attention for wireless communications at radio frequencies, especially in 6G and internet-of-things technologies [160, 161, 162, 163, 164, 165, 166, 167]. Below we present only a few examples for illustrating those ideas.

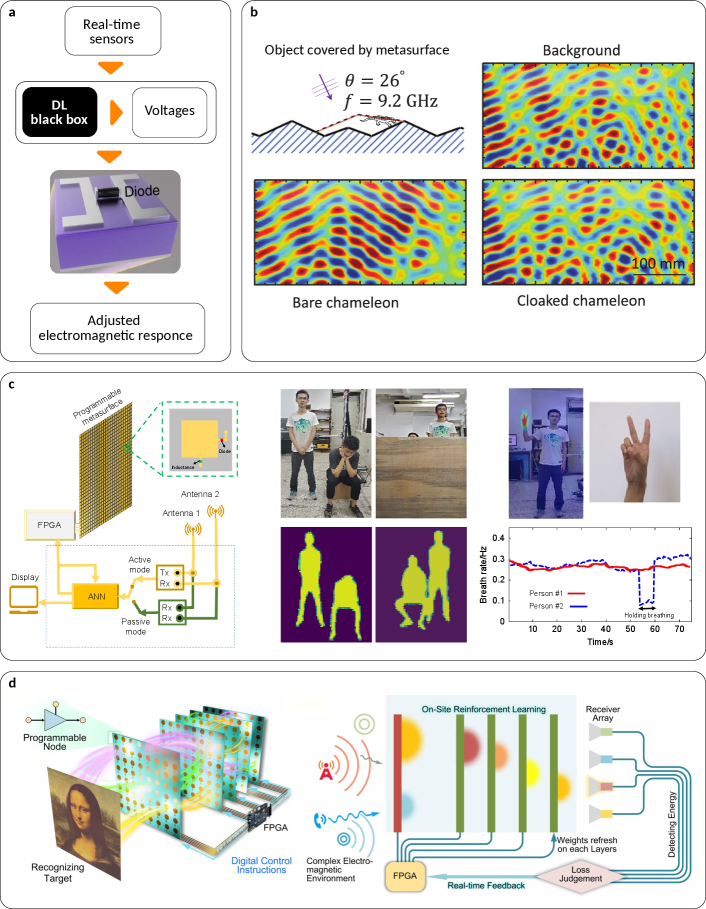
A self adapting approach was implemented to realize a real-time metasurface imager [171]. The proposed solution is based on $2$-bit coding metasurface — a structure made of independently controlled meta-atoms supporting four different digital responses, $00$, $01$, $10$ and $11$, which correspond to the physical phases $0$, $\pi/2$, $\pi$ and $3\pi/2$, respectively. Thus, an incident field with different coding sequences will produce different scattering patterns. The principle behind this imaging technique is based on the recognition of an object from the measured scattered fields. In the proposed design, the coding metasurface is controlled via a field programmable gate array. First, the ML algorithms are trained for the desired radiation patterns, and then coding patterns of the metasurface are determined from the obtained radiation patterns.

Another imager was developed in Ref. [169]. In this case, microwave data collected by a metasurface are used as an input for an ANN reconstructing the image of a human body. A second ANN is used to recognize a particular region within the recorded image, such as a hand or a head. Coding sequences needed for control of programmable metasurfaces are defined via the Gerchberg-Saxton algorithm. This sequence is implemented to focus radiation waves onto the desired regions of a human body to read the necessary data from the reflected echoes and was demonstrated experimentally. Further development of such systems may lead to next-level human-device interfaces used for smart environments, health monitoring, sign and speech recognition.

Metamaterial cloaks, or meta-cloaks, previously mentioned in the framework of inverse design, also may be supplemented by ML algorithms enabling self-adapting functions. The cloak presented in Ref. [168] is made of reconfigurable metasurface consisting of varactor diodes. Incoming waves sensed by detectors in real time are processed by a DL algorithm calculating voltages, which have to be applied across the diodes in order to adjust the scattering spectrum. As a result, the engineered scattered field will be similar to that in the case of bare surrounding without an intruding object. The use of DL allows fast determination of the necessary parameters of the metasurface in order to provide cloaking for a wide range of changing parameters, such as the angle and frequency of the incident wave and background variations. As discussed in the literature [172], AI technologies may become a key factor in the future development of meta-cloaks and even more fascinating devices.

Here, we also mention that a relation between AI and photonics is not one-sided. Photonic devices find broad applications for realizing optical ANNs [173, 174] due to their ability to provide parallel computing with the speed of light. Metasurfaces are among a variety of building blocks of such networks [175, 176]. Indeed, individual meta-atoms of digital metasurfaces may represent single artificial neurons, controlled via some predefined algorithms. Functionality of optical ANNs may be extended with the use of feedback mechanisms providing re-training of the meta-ANN. For instance, Ref. [170] demonstrates that coding sequences can be redefined with real-time field-programmable gate arrays. Feedback signals allowed to realize self-learning functions using data from the interaction with environment without prior knowledge. As a result, the authors of Ref. [170] developed wave-based intelligence machine able to perform such DL tasks as image recognition and feature detection as well as multi-channel coding and decoding tasks and dynamic multi-beam focusing. We believe that such systems can be developed further by adding a feedback mechanism with another ANN. More discussion on application of metasurfaces for optical neural networks is provided in Sec. VIII.

Moving away from metadevices, it should be mentioned that the AI tools become a part of establishing control systems for lasers [177]. In this case, ML algorithms are integrated into feedback mechanisms automatically adjusting position and orientation of laser elements, such as waveplates and polarizers. Emergence of similar intelligent systems may change the way how experimental characterization of metasystems and their manufacturing are performed. Below, we discuss briefly some other applications of the AI technologies to other related fields and also provide some perspective on how AI technologies may reshape the development and applications of metadevices.

Recent advancements in ML and AI methods are expected to reshape some major areas of metaphotonics where metastructures and metasurfaces play important roles. As we mentioned above, to develop metasurfaces with specific properties and functionalities, novel design strategies and approaches in advanced computational techniques are required. It is expected that ML and DL will be useful for developing sophisticated smartphones, robotic systems, and self-driving cars employing the concepts of flat optics. Importantly, ML can help to discover unconventional optical designs thus advancing imaging, sensing, and other functionalities of metaphotonic devices. Many recent studies are devoted to photonic design approaches and emerging material platforms showcasing ML-assisted optimization for intelligent metasurface designs.

Among emerging and future developments, we wish to mention a few examples of AI-supplemented systems, beyond the major scope of this paper but still closely related to metaphotonics.

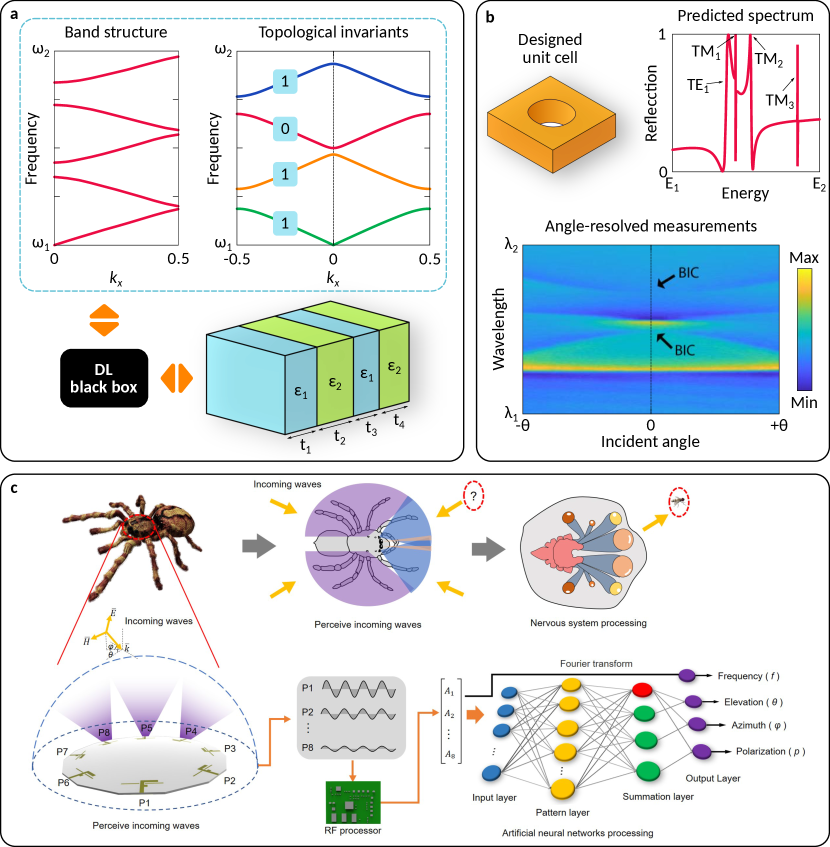
First, we wish to mention topological photonics being one of the most actively developing branches of photonics and physics in general. Realization of topological phases in physical systems opens a road towards novel robust structures protected from scattering losses and structural disorder [182, 183]. The current trends of AI-supplemented studies does not leave aside this important area of research. The first demonstrations of inverse design of photonic topological insulators include the DL-based estimation of geometric parameters of 1D photonic crystal to obtain protected edge states at target frequencies [184, 185, 178]. Later, this approach was also extended to 1D $\mathcal{PT}$-symmetric chains and cylindrical photonic crystal fibers [186]. In addition, ANN methods were used to predict topological transitions in photonic crystals [179]. Recent works successfully utilizing non-DL methods for inverse design of 2D topological insulators and waveguides [187, 188] indicates that ANNs soon may be applied to design topological structures beyond 1D geometry. At the same time, direction of modern research is turned towards reduction of size and realization of topological metadevices [189] meaning that AI technologies can find their applications in metaphotonics.

Metasurfaces supporting high-Q optical resonances are especially promising for applications in nanophotonics, including enhancement of light-matter interaction, high-harmonic generation, biosensing and nonlinear effects [190]. Realization of such opening opportunities require achievement of desired resonance properties. DL-based inverse design of photonic structures supporting BIC was presented in Refs. [191, 180]. In particular, in Ref. [180] authors consider suspended photonic crystal slab made of Si₃N₄ [see Fig. 7(b)]. Using DL, they find geometric parameters of the structure (radius and height of circular holes) for which symmetry-protected BIC may occur. Importantly, they support the results with experimental measurements demonstrating the presence of two BICs at $\Gamma$-point at wavelengths $700$ and $750$ nm. Widespread attention which BICs receive in the area of photonics [192, 193] suggests that more studies supported by AI-algorithms will appear in recent future.

While the previous sections of this review have discussed the application of DL techniques to photonics, here we briefly discuss an emerging field, namely that of photonic devices as platforms for physical neural networks. Recently there has been increasing interest in approaches termed neuromorphic computing with photonics providing a potentially viable platform [194, 195]. Neuromorphic computing aims to take an alternative approach to information processing by creating hardware structures that mimic that of nature’s analogue computing i.e. neural structures. This approach is a departure from standard computing models which rely on a centralized processing architecture, instead opting for a distributed model. This approach has several key advantages: firstly this model maps well to information tasks that are distributive, such as neural network models. This match between hardware and algorithm allows an energy efficient approach to information processing. Secondly, for photonics based systems the computation is inherently parallel due to the nature of the platform. Using photonics one can implement different types of neuron schemes with physical implementations having being demonstrated using Mach–Zehnder interferometers [196, 197], phase change materials [198] and diffractive elements [199]. Recently [200] increased the scope of such applications by proposing a physics aware training scheme that allows a wider class of systems to be trained for DL applications. As metaphotonics develops, it is likely that many of the mechanics and non-linearities possible with metaphotonics will be identified as potential candidates for DL platforms. A metaphotonic hybrid approach to computational sensors has already been demonstrated that operates similar to that of conventional convolutional neural networks [201].

Similar to neuromorphic structures there has been development of biology-inspired systems complimented with AI technologies. As an example, the spider-eye-like antenna demonstrated in Ref. [181] is supplemented by a generalised regression neural network [202] to analyze the incoming waves (see Fig. 7(a)). In particular, this algorithm predicts the direction of arrival and the polarization state, simulating a work of a spider’s neural system. Similar ideas were implemented for development of AI photonic synapse [203]. The structure is based on a filed-effect transistor with a floating gate of self-assembled perovskite nanocones embedded into a self-assembled block co-polymer. Arrays of such synapses imitate human retina with position-dependent photosynaptic performance defined by the spatial distribution of the nanocones. Such retina represents a single-layer neural network capable of image recognition with up to $90\%$ accuracy. We believe that intelligent metasurfaces may be integrated in such kind of systems to improve their performance and extend functionality, providing additional re-programmable functions or data processing with optical ANNs.

The use of DL methods is not limited to a design of nanoantennas and their optical response. It may become an extremely useful assisting tool for experimental measurements. The demonstrations in this field include characterization of orientation [204] or size [205] of metallic nanoparticles using measured spectral data. ML find its applications in a variety of microscopy and imaging techniques [206, 207] as well as for tracking [208], localization [209] and analysis of single molecules [210]. The proposed algorithms may become a basis for a fast automated retrieval of parameters of nanoantenna samples.

An additional application for DL methods lies within the realm of optimisation, specifically that of high dimensional systems. Global optimisation is a generally challenging endeavour with many problems becoming intractable with a growing number of parameters in the absence of prior knowledge of the parameter landscape. One approach that leverages the power of DL to generalise high dimensional systems is to perform an online optimisation. In this case an ML agent is put in a type of feedback loop with the agent providing predictions as to the best parameters, whilst updating its belief based on feedback from the system. This approach has been used to optimise the laser cooling sequences of cold atom traps with up to 63 individual controllable parameters [211, 212]. The use of DL allows one to consider optimisation problems with much higher dimensions compared to conventional approaches such as Gaussian process which are generally limited to smaller parameter spaces [213, 214]. Metaphotonics and metasurfaces in particular provide a range if different parameters and exhibit a rich range of phenomena owing to their subwavelength structuring. This provides an opportunity for direct optimisation both in a design setting and real-time capacity, such as that of programmable metasurfaces. Such approaches are indeed flexible as the objective function may be arbitrarily defined to suit any given purpose.

While metaphotonics structures have been intensively studied in the past decade, many challenges still exist for practical and end-specific utilization. Fabrication becomes a tricky issue for many accuracy-required structures, and it also becomes harder to modulate metasurfaces. With emerging materials, new physics, and advanced nanofabrication techniques, those challenges may be bypassed. We anticipate new insights being delivered by merging the concepts from several fields exploring interdisciplinary concepts of metaphotonics and creating new types of hybrid systems governed by the concepts of flat optics and metamaterial-inspired subwavelength engineering. We expect that the future research in intelligent metaphotonics will significantly broaden the horizons of photonics and offer new perspectives for novel applications beyond our current imagination.

The authors acknowledge useful comments and suggestions received from A. Chukhrov, A. Slobozhanyuk, I. Melchakova, and P. Belov. Y.K. acknowledges a support from the Strategic Fund of the Australian National University, The Australian Research Council (grants DP200101168 and DP210101292), the US Army International Office (grant FA5209-21-P0034), and the Russian Science Foundation (grant 21-72-30018). A.B. acknowledges a support from the Foundation for the Advancement of Theoretical Physics and Mathematics ”BASIS”. A.T. acknowledges a support from the Australian Research Council Grant No. CE170100012.