Interface phonon modes governing the ideal limit of thermal transport across diamond/cubic boron nitride interfaces
Abstract
Understanding the ideal limit of interfacial thermal conductance (ITC) across semiconductor heterointerfaces is crucial for optimizing heat dissipation in practical applications. By employing a highly accurate and efficient machine-learned potential trained herein, we perform extensive non-equilibrium molecular dynamics simulations to investigate the ITC of diamond/cubic boron nitride (BN) interfaces. The ideal diamond/BN interface exhibits an unprecedented ITC of 11.0 0.1 GW m-2 K-1, setting a new upper bound for heterostructure interfaces. This exceptional conductance originates from extended phonon modes due to acoustic matching and localized C-atom modes that propagate through B-C bonds. However, atomic diffusion across the ideal interface creates mixing layers that disrupt these characteristic phonon modes, substantially suppressing the thermal transport from its ideal limit. Our findings reveal how interface phonon modes govern thermal transport across diamond/BN interfaces, providing insights for thermal management in semiconductor devices.
I Introduction
The advancement of semiconductor materials has ushered in a new era of micro/nano electronic devices. However, as device dimensions continue to shrink following Moore’s law, efficient heat dissipation has emerged as a critical technological challenge, particularly under peak operating conditions Cheng et al. (2024). To optimize performance, modern microelectronic devices often integrate two or even more materials to leverage their complementary advantages, as seen in AlGaN/GaN high-electron mobility transistors Zhu et al. (2019), diamond-based semiconductor (e.g., Ga2O3, SiC) radiofrequency devices Zhao et al. (2024); Cheng et al. (2020); Ji et al. (2024), Al/GaN deep-ultraviolet photoelectric applications Tsao et al. (2018), and diamond/cubic boron nitride (cBN) electronic devices Bello et al. (2002). In these heterostructures, interfacial thermal conductance (ITC) plays a pivotal role in thermal management, as interfaces often serve as bottlenecks for thermal transport. Understanding the upper limit of ITC and underlying phonon transport mechanisms in heterostructures is thus crucial for optimizing semiconductor performance.
Among various heterointerfaces, diamond/cBN interfaces are particularly promising, as both crystalline diamond and cBN are superhard materials with exceptionally high thermal conductivity () Ralchenko et al. (2021); Chen et al. (2020). Furthermore, their minimal lattice mismatch enables the formation of an atomically flat interface, making them ideal candidates for maximizing ITC. Experimental fabrication of high-quality, flat diamond/cBN interfaces has been demonstrated Chen et al. (2015), providing an ideal model system for investigating the theoretical upper limit of ITC. Recent advancements in electron energy-loss spectroscopy (EELS) have enabled the probing of nanoscale interfacial phonon dispersions and phonon modes across the diamond/cBN interfaces Qi et al. (2021); Kikkawa et al. (2021), providing direct evidence for the existence of specific phonon modes Gordiz and Henry (2016). However, directly quantifying the contributions of interface phonon modes to thermal conductance in experiments remains challenging due to the nature of buried interfaces. Furthermore, roughness and atomic interdiffusion are prevalent in realistic interfaces Bello et al. (2005); Zhe et al. (2021), necessitating an understanding of how interface phonon modes evolve from smooth to rough interfaces and their effects on ITC for advanced semiconductor thermal management.
Besides experimental efforts, several computational approaches have attempted to predict ITC values for diamond/cBN interfaces. Molecular dynamics (MD) simulations Qi et al. (2021); Li et al. (2024) based on Tersoff potential Kınacı et al. (2012) have been conducted, yet this empirical potential lacks parametrization for diamond/cBN interfaces and fails to accurately capture interface phonon dispersions, severely limiting the reliability of ITC predictions. Alternatively, Monte Carlo simulations incorporates phonon properties from density functional theory (DFT) calculations Huang and Guo (2020) have been used to model steady-state thermal transport across the interface. However, these simulations rely on acoustic and diffusion mismatch models, which assume purely elastic phonon transport through ballistic or diffusive mechanisms, thereby neglecting the contributions of inelastic phonon transport—an essential factor in real interfaces with complex atomic configurations Chen et al. (2022); Li et al. (2022). To address these challenges, machine-learned potentials (MLPs) have emerged as a promising alternative Deringer et al. (2019); Dong et al. (2024); Ying et al. (2025). By being trained on energy, atomic forces, and virial data from first principles calculations such as DFT Behler and Parrinello (2007), MLPs enable MD simulations with near quantum mechanical accuracy while achieving computational speeds several orders of magnitude higher than ab initio molecular dynamics (AIMD). To date, MLP driven non-equilibrium molecular dynamics (NEMD) simulations have been applied to investigate the thermal conductance of semiconductor interfaces, including Ga2O3/diamond Sun et al. (2024), GaN/cubic boron arsenide Wu et al. (2024a) and Si/Ge Zhe et al. (2021), etc.
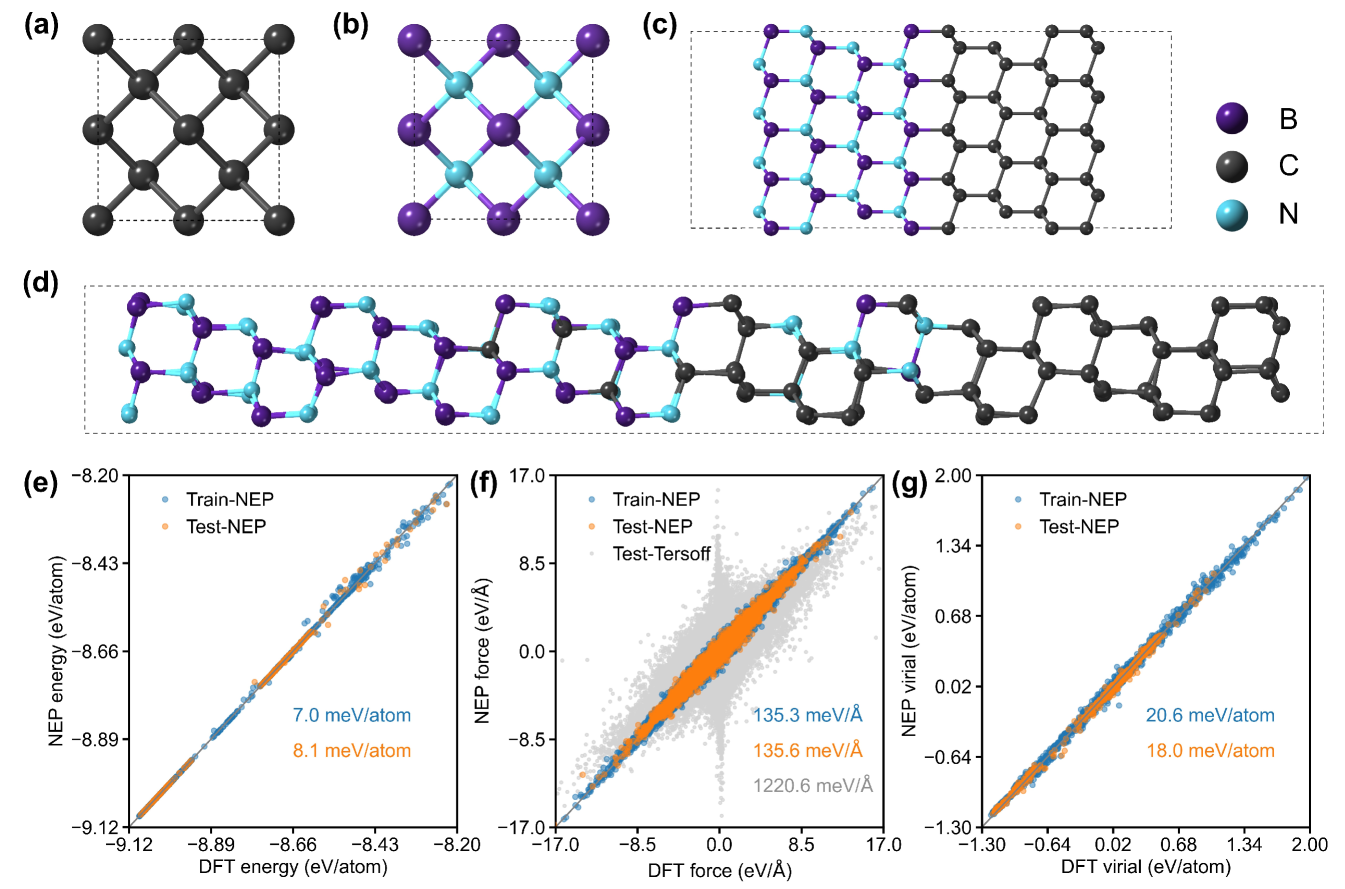
In this study, we develop a unified machine-learned neuroevolution potential (NEP) Fan et al. (2021, 2022) model for pure diamond and cBN, as well as diamond/cBN heterostructures (see Figure 1 (a-d)). We employ the NEP approach for its superior efficiency among existing MLP frameworks. After demonstrating its accuracy and reliability, we apply the developed NEP to perform extensive NEMD simulations to study the thermal transport across diamond/cBN interfaces. Our NEMD simulations predict an exceptionally high ITC for ideal flat diamond/cBN interfaces, which surpasses all existing heterointerface ITC results reported in both experimental measurements and theoretical predictions. This remarkably high ITC stems from interface phonon modes, particularly extended and localized modes, that facilitate efficient phonon transport. We also demonstrate the atomic diffusion at rough interfaces suppresses these modes, leading to a significant reduction in ITC.
II Results and discussions
II.1 Validation of the NEP model
To describe interatomic interactions across diamond/cBN interfaces, we employed the third generation of NEP frameworkFan et al. (2022) to train a unified machine-learned NEP for diamond, cBN, and their heterostructure (see Figure 1(a-d)). This is achieved by applying feedforward neural network (NN) together with separable natural evolution strategy (SNES) Schaul et al. (2011) to learn the energy, force, and virial of reference structures obtained from DFT calculations (see subsection IV.1 and subsection IV.2 for details). As shown in Figure 1(e-g), the developed NEP achieves high accuracy for both training and test datasets compared with DFT results, with root mean square error (RMSE) values of energy, force, and virial less than , , and , respectively. Notably, for the atomic forces in the test dataset, the RMSE of NEP is approximately an order of magnitude lower than that of the Tersoff potential, which was used to drive MD simulations for predicting the ITC of diamond/cBN interfaces in previous studies Qi et al. (2021); Li et al. (2024).
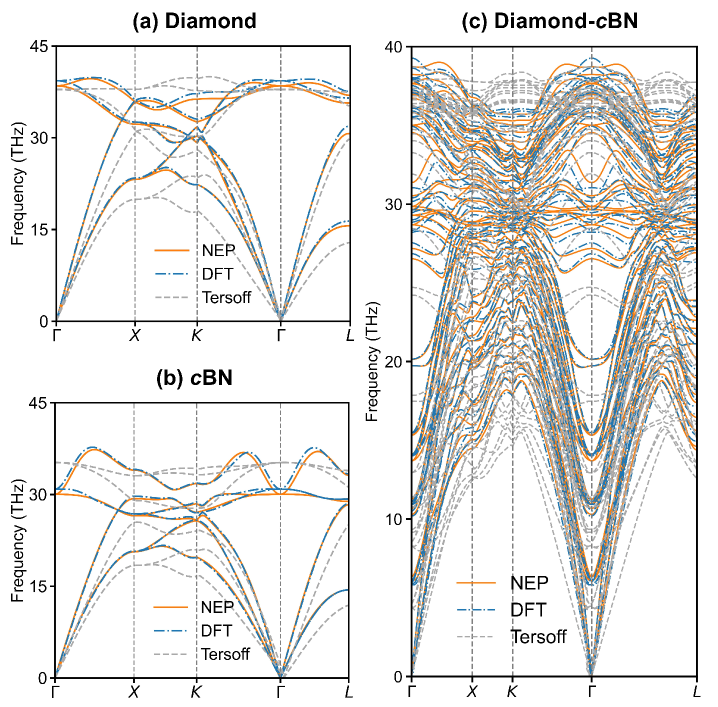
In Figure 2, we further validate the accuracy of the NEP model and the Tersoff potential in describing the phonon dispersions of diamond, cBN, and their ideal interface (see subsection IV.1 for details). The unified NEP accurately reproduces the phonon dispersion not only for bulk diamond and cBN (see Figure 2(a-b)) but also for their heterostructures (see Figure 2(c)). In contrast, the Tersoff potential exhibits apparent deviations, particularly showing a strong softening effect on the acoustic branches.
Before performing our ITC calculations for the diamond/cBN heterostructure, we first applied the developed NEP to conduct homogeneous non-equilibrium molecular dynamics (HNEMD) simulations and predict the of the bulk counterparts at (see Supporting Information (SI) section S1 for details). The predicted for diamond and cBN are and , respectively. In addition to the NEP-HNEMD approach, we also employed the Boltzmann transport equation (BTE) method to predict the for both diamond and cBN. And in the DFT-BTE approach, harmonic and thirdorder anharmonic force constants considered here were derived from DFT calculations performed at the same accuracy level as those used for NEP training (see subsection IV.1 for details). In LABEL:table:comparisons, we note that our NEP-MD prediction is lower than the DFT-BTE predictions, which can be potentially caused by the neglection of higher order phonon anharmonicity or phonon coherence effects in current BTE predictions.
We also compare our NEP and DFT-BTE predictions with reported measurement results, as well as previous MD predictions based on Tersoff potential in LABEL:table:comparisons. For experimental data, only the maximum Ralchenko et al. (2021); Chen et al. (2020) and minimum Slack (1973); morelli and Slack (2006); Slack (1973) reported values are listed to reflect variations due to sample quality, size and inevitable defects or impurities. In terms of the of two bulks, our NEP prediction falls within the range of corresponding experimental measurements. In contrast, the MD simulations based on Tersoff potential greatly underestimated the of two bulks, possibly due to their softening effect on phonon dispersions (see Figure 2). The good agreement between our NEP predictions and experimental measurements, combined with validations of atomic forces and interfacial phonon dispersions, confirms the reliability of NEP in modeling thermal transport across diamond/cBN interface.
| Method | Diamond | cBN |
| Our NEP-MD | 2215(70) | 1223(8) |
| Our DFT-BTE | 3362 | 1721 |
| Tersoff-MD | 1859Li et al. (2024) | 763Li et al. (2024) |
| Experiment | 2400(50),Ralchenko et al. (2021) 2000Slack (1973) | 1600(170),Chen et al. (2020) 760morelli and Slack (2006) |
II.2 Ideal limit of interfacial thermal conductance
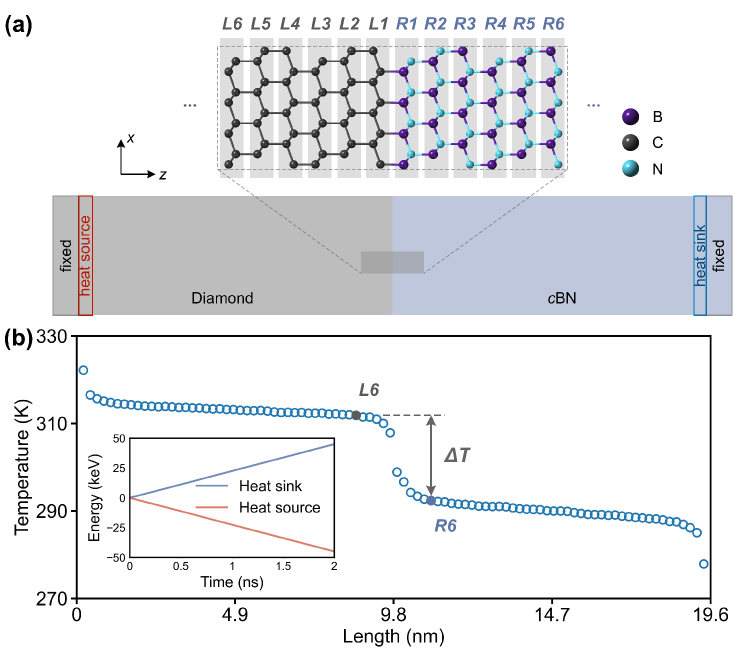
We then employ the trained NEP to perform NEMD simulations for diamond/cBN heterostructure (see subsection IV.3 for details). We first investigate the thermal transport across the ideal atomically flat interface of the diamond/cBN heterostructure. Figure 3(a) illustrates the model setup for NEMD simulations, where heat flux is transported from the left diamond side, across the central interface, to the right cBN side. To calculate the temperature profile (see Figure 3(b)), we divide the whole system into different groups along thermal transport direction, with each group representing a layer of diamond on the left side of the interface (labeled as , , , …) and a corresponding layer of cBN on the right (, , , …). The interface temperature difference used for predicting ITC in the NEMD simulations (see Equation 1) is consistently defined as the temperature difference between and , rather than and , in all cases. This definition of ensures a fair comparison between the ITC of the ideal interface and that of rough interfaces, where atomic diffusion is confined between and . A detailed discussion on rough interfaces is provided in subsection II.4. As shown in the inset of Figure 3(b), the equal absolute slopes of energy injection from heat source and extraction from heat sink confirm energy conservation and validate the steady-state regime. Within this steady-state window, temperature profile analysis reveals a distinct temperature discontinuity at the interface, attributable to interfacial thermal resistance.
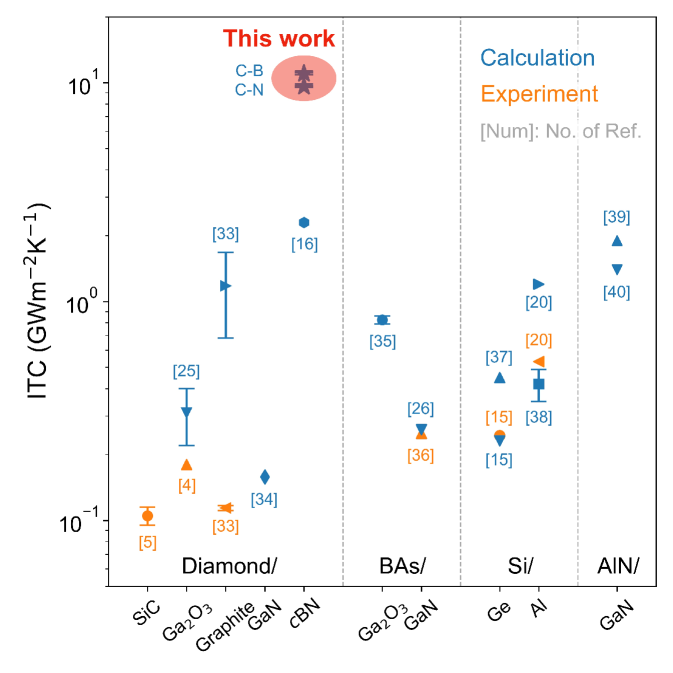
To form a heterostructure through ideal interfaces, diamond can establish covalent bonds with cBN through either C-B or C-N bonded pairs. Based on five independent NEMD simulations, we predict an ITC of for the C-B binding interface and for the C-N binding interface. As shown in Figure 4, the predicted ITC values for diamond/cBN are unprecedentedly high compared with existing theoretical and experimental results across various heterostructure interfaces. This significantly exceeds previous findings and appears to represent the ideal limit of ITC for solid heterointerfaces. As the ITC values for diamond/cBN with C-B and C-N bonded interfaces are very close, in the following discussion we focuse on the C-B bonded case, which exhibits the highest ITC observed, while the corresponding results for the C-N bonded interface are presented in SI Section S2.
II.3 Interface phonon modes
To understand the mechanism underlying the observed upper bound of ITC, we perform phonon analyses in this section. Specifically, we elucidate the role of interfacial phonon modes in governing phonon transport across the ideal diamond/cBN interface.
Based on the spectral heat current (SHC) analysis (see subsection IV.4 for details) Fan et al. (2017a), Figure 5(a) presents the phonon frequency dependent of bulk diamond and cBN from HNEMD simulations, and Figure 5(b) shows the ITC of their ideal interface as a function of phonon frequency from NEMD simulations. The ITC profile exhibits two prominent peaks at around the and (see Figure 5(b)), which identifies the dominant phonon modes contributing to interfacial thermal transport. While the peak corresponds to the maximum overlap of the spectrally decomposed of two bulk counterparts (see Figure 5(a)), the peak emerges without an apparent bulk contribution. This unexpected peak demonstrates that interfacial phonon transport cannot be explained solely by bulk phonon properties, suggesting the presence of additional phonon contributions originating from the interface. As shown in the phonon density of states (PDOS) distribution near the interface (see Figure 5(c)), a frequency shift is observed as the region approaches the interface, resulting in the emergence of the phonon mode (corresponding to approximately 140 meV). This observation of distinct interface phonon modes is consistent with previous EELS measurements (see Figure 5(d)) Qi et al. (2021).
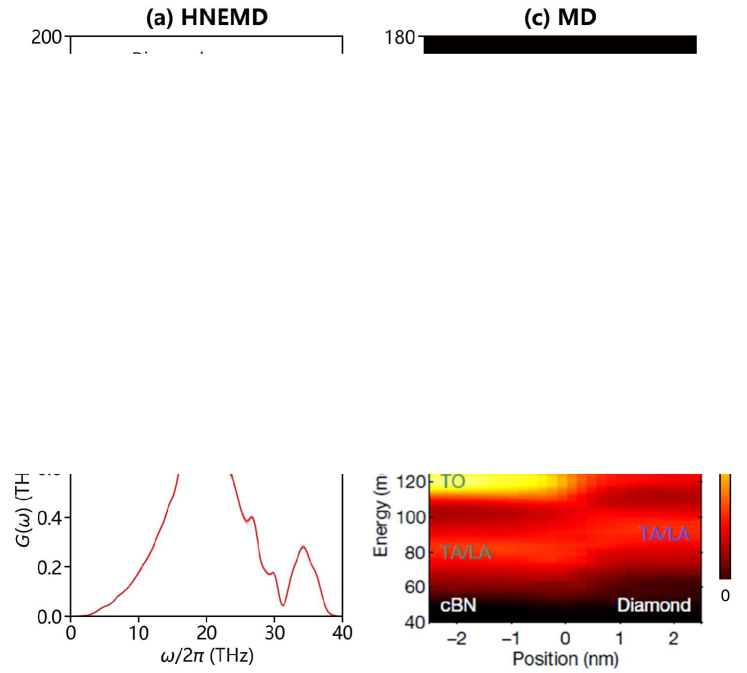
To reveal the formation mechanism of interface phonon modes, Figure 6(a) analyzes the local PDOS evolutions for representative atomic layers. The diamond layer adjacent to the interface ( group in Figure 3(a)) exhibits a distinctive spectral signature with a primary peak at approximately and a secondary peak at , corresponding to the B-C bond vibration detectable at via Fourier transforms infrared spectroscopyRomanos et al. (2013). Progressing to the group of diamond,a blue shift in the primary peak is observed, while the secondary peak vanishes entirely. From the group onward, the PDOS gradually stabilizes and becomes indistinguishable from layers farther from the interface (e.g., the group), indicating a transition to bulk phonon characteristics. Similar behavior is observed on the right cBN side. The layer-resolved PDOS analysis clearly demonstrates that interfacial phonon vibration modes differ substantially from those in the bulk regions.
For more comprehensive insight, we calculated the aggregate PDOS for multiple near-interface layers from left diamond to right cBN sides, as shown in Figure 6(b). As the interface region expands from the - region to - region, the relative contributions of phonon modes around and diminishes due to the incorporation of vibration modes from more distant layers, resulting in a blue shift of these peaks. Beyond approximately eight layers from the interface (-), the PDOS peak positions stabilize due to the predominance of bulk-like phonon modes. Notably, the peak at approximately remains consistently positioned across all regions, indicating its presence in both interface and bulk environments. The inset of Figure 6(b), we further visualizes the eigenmodes and analyzed atomic vibration amplitude eigenvectors of these three phonon modes (, , ) across eight layers in the interface region (-, spanning approximately ). The mode displays significant vibration amplitude throughout the entire interface region. The mode shows substantial amplitude exclusively at the immediate interface, and is confined primarily to two atomic layers. Similarly, the mode is localized at the interface but stems predominantly from B and N atomic vibrations at the boundary, which explains its negligible contribution to ITC (Figure 5(b)). Our findings provide conclusive evidence for the spatial evolution behavior of the interfacial localized phonon modes and their respective contributions to ITC, complementing the experimental observation Qi et al. (2021). These interfacial modes provide an additional pathway for phonon transport across the diamond/cBN heterointerface, and they are fundamentally distinct from those in the respective bulk materials.
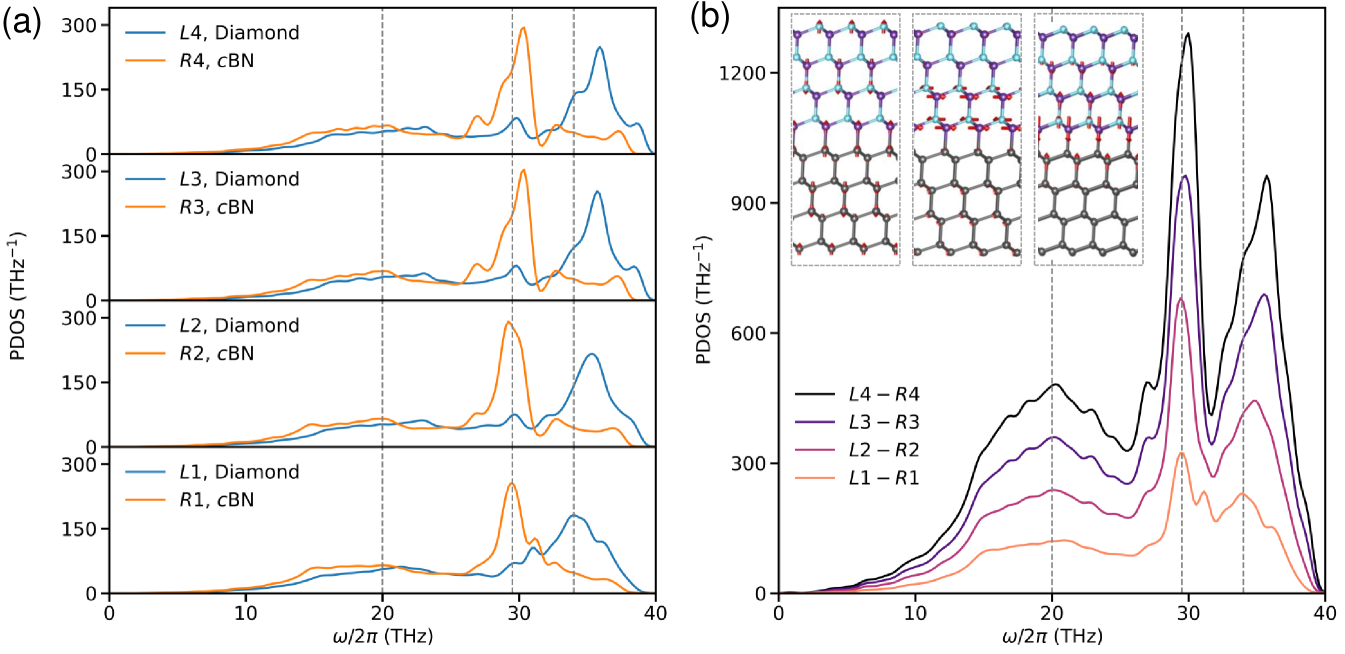
The different contribution of each representative phonon mode to ITC are derived from the different origins of their vibrations. Phonon modes around are highly localized at the interface, called the localized modes. These localized vibrational modes, primarily induced by interfacial C atoms (see Figure 6(a)), are stabilized by strong C-C bonds. Importantly, the presence of the C-B bonds enable the extension of these vibrational modes to B atoms on the cBN side. Further, the propagation direction of these phonons aligns with the thermal transport direction (see right inset in Figure 6(b)), thereby contributing significantly to ITC. Another notable peak, around , corresponds to acoustic phonon modes on both sides of the interface vibrating simultaneously (see left inset in Figure 6(b)). These are delocalized across the entire heterostructure and thus are known as the extended modes. In contrast, the phonon mode near involves horizontal vibrations at the interface that do not align with the effective heat transfer direction (see central inset in Figure 6(b)), resulting a negligible contribution to ITC. Therefore, both extended and localized modes play crucial roles to interfacial heat transport, with the former contributing more significantly. Together, these modes result in the highest known ITC for a semiconductor heterostructure, enabled by the ideally flat atomic interface formed through strong bonded pair and minimal mass mismatch.
II.4 Rough interface suppresses phonon transport
In this section, we further investigate the effect of interfacial atomic diffusion (i.e., roughness) on the ITC of diamond/cBN heterostructures. For this purpose, we performed a series of ITC calculations on diamond/cBN systems with rough interfaces. All systems involved use the same size as the ideal interfacial system, but randomly rearrange the atoms in the central region (2, 4, 6, and 10 layers, respectively) and achieve atomic mixing in different proportions (10% - 50%). Two cases are considered: (i) atomic diffusion confined within a fixed 10-layer region (from to ) with varying diffusion ratios (refer to the insert in Figure 7(a)), and (ii) atomic diffusion with a fixed 50% mixing ratio but confined within different numbers of diffusion layers (refer to the insert in Figure 7(c)). To ensure the accuracy of the ITC results, we performed three independent NEMD simulations using distinct random atomic configurations for each rough interface. For both cases, it can be found that the atomic diffusion results in significant suppression of ITC (see Figure 7(a) and (c)). Compared to the ideal interface, the maximum 50% atomic diffusion within in - region results in approximately a 71% reduction in ITC. It is worth noting that some previous studies have reported the opposite trend, where diffuse interfaces with appropriate atomic mixing, such as in Si/Ge Zhe et al. (2021), GaN/diamond Wu et al. (2024b), and Al/Si Rustam et al. (2022), can enhance ITC.
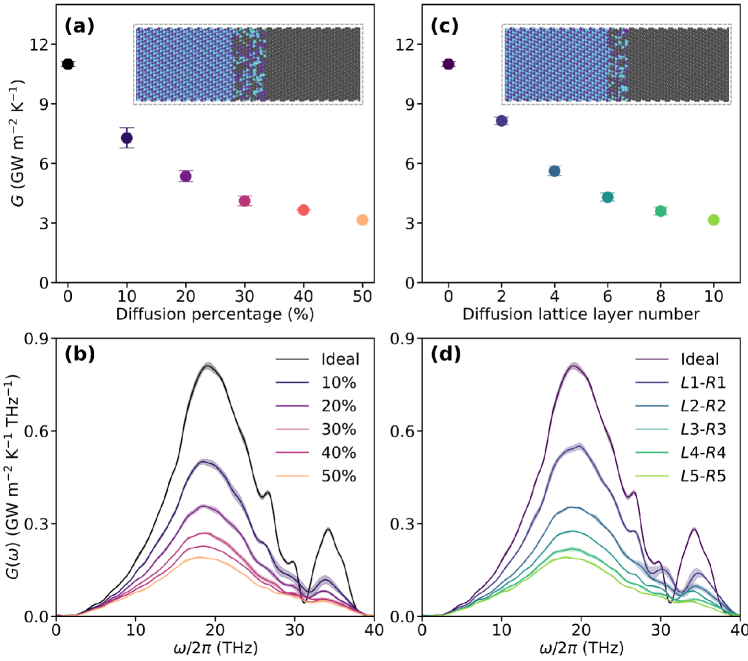
The main reason for this inconsistency lies in the role of diffuse layers at the interface. Generally, for interfaces where the phonon modes differ significantly between the two bulk sides, diffuse layers can serve as a bridge to smooth the mismatch and facilitate phonon transport. In contrast, for interfaces where the phonon modes are already well matched, the introduction of diffuse layers disrupts this alignment and hinders thermal transport. In other words, whether the diffuse transition layers enhance or suppress phonon transport at the interface depends on the similarity of phonon modes across the interface. In the ideal flat interface of diamond/cBN heterostructure, the enhanced ITC arises from the presence of well-matched phonon modes on both bulk sides of the interface. This can be attributed to two key factors: (i) the strong matching of acoustic phonon modes around facilitates the formation of extended modes that contribute significantly to ITC, and (ii) the alignment of high-frequency optical phonon modes around enables localized modes to also participate effectively in heat transfer. Given that diamond and cBN share similar lattice structure and exhibit very similar acoustic phonon properties, the presence of atomic diffusion at the interface can significantly disrupt the overall vibrational coherence. This disruption weakens the contribution of phonon modes across the interface. As a result, the contribution of extended modes to ITC is notably reduced, as evidenced by the spectral decomposition results shown in Figure 7(b) and (d). Furthermore, as the interface becomes increasingly rough, phonon mode matching becomes more difficult, and the distinct vibrational features that enable high interfacial thermal transport in the ideal interface gradually vanish (see SI section S3).
III Conclusions
To probe the ideal upper limit of ITC for semiconductor heterostructures, we developed a unified MLP for diamond, cBN, and their heterointerfaces. Based on extensive NEP-driven NEMD simulations at near first-principles accuracy, the room temperature ITC of the ideal diamond/cBN interface through C-B bonded pair is predicted to be , establishing a new upper bound among all existing theoretical predictions and experimental measurements. Our results demonstrate that the ITC is primarily governed by unique interface phonon modes, namely extended modes and localized modes, which are completely different from bulk-like phonon modes. Furthermore, when acoustic phonon mode matching between diamond and c-BN is disrupted by atomic diffusion, the contribution of extended modes to ITC is significantly diminished, and the presence of a diffuse interface severely impedes heat transfer. The highly localized modes with bridging effects also vanish under such disorder. Our work provides atomistic insights into the ideal limit of thermal transport across semiconductor interfaces, as well as the emergence and evolution of interfacial phonon modes that govern this limit, which may offer valuable guidance for related thermal management applications.
IV methods
IV.1 DFT calculations
All DFT calculations were performed using the Perdew-Burke-Ernzerhof functional within the generalized gradient approximation Blöchl (1994); Perdew et al. (1996), as implemented in the vasp package Kresse and Furthmüller (1996); Kresse and Joubert (1999). A plane-wave basis set with an energy cutoff of was employed, ensuring energy convergence within in the electronic self-consistent loop. The Brillouin zone was sampled using a -centered -point grid with a density of , and Gaussian smearing with a width of was applied.
To calculate the phonon dispersion of bulk diamond and cBN, as well as their ideal interface, the structural optimizations were first performed with an atomic force convergence threshold of . After that, the second-order interatomic force constants for optimized structures were calculated using density functional perturbation theory, as implemented in the phonopy package Togo and Tanaka (2015). For bulk diamond and cBN, \numproduct5x5x5 supercells were employed, whereas the diamond/cBN interface was constructed by combining \numproduct3x3x4 supercells of the primitive cells of both diamond and cBN, with C-B bonded pair at the interface.
In calculating the third-order interatomic force constants, the structures are generated by the random displacement method as implemented in the the Thirdorder script Li et al. (2014) and the \numproduct4x4x4 supercell is used for two bulk systems. To obtain accurate , we consider the interactions up to the seventh nearest neighbors. Based on second- and third-order interatomic force constants, the can be obtained by iteratively solving the linearized BTE using \numproduct5x5x5 supercells as implemented by ShengBTE package Li et al. (2014). The broadening factor was set to 0.1. A final q-points mesh of \numproduct31x31x31 was found to yield well-converged values.
IV.2 NEP training
Our reference structures include bulk diamond, cBN, and diamond/cBN heterostructures with both ideal flat and rough interfaces (see Figure 1 (a-d)), generated through AIMD sampling and perturbation. AIMD simulations were conducted at temperatures ranging from to over 10,000 steps, with a time step of . Perturbations were introduced by applying random cell deformations from -3% to 3% and atomic displacements within .
For bulk diamond and cBN, \numproduct4x4x4 supercells of the primitive cell, each containing 128 atoms, were constructed. We sampled 200 structures from AIMD and 50 structures from perturbation for both diamond and cBN, resulting in a total of 500 reference structures.
Mimicking the growth of cBN on diamond in the experiment, the diamond/cBN heterostructures with ideal interfaces along the interface was established. Compared with the direction, its interface binding energy is higher, ensuring enhanced thermodynamic stability Zhao et al. (2019). See Figure 1(c), we constructed a system composed of \numproduct3x3x4 supercells of both diamond and cBN primitive cells, containing a total of 144 atoms. We obtained 250 reference structures, including 200 from AIMD sampling and 50 from perturbation.
For diamond/cBN heterostructures with rough interfaces, the interface model containing mutual diffusion layers is mainly constructed by randomly shuffle atoms, where different diffusion ratios represent interfaces of different roughness Here, two configurations were considered to account for atomic diffusion effects: (i) we randomly replaced boron or nitrogen atoms with carbon atoms in \numproduct4x4x4 supercells of the primitive cell of cBN in increments of 10%; (ii) we constructed a 20-layer heterostructure comprising \numproduct2x2x10 supercells of the primitive cell for both diamond and cBN, containing 160 atoms in total, where in the central eight layers, carbon and boron or nitrogen atoms were randomly mixed, again in 10% incremental steps. All obtained structures, after atomic replacements or exchanges, were further subjected to perturbation. We generated 180 reference structures, with 90 structures for each configuration.
In total, we obtained 930 reference structures and performed single-point DFT calculations (see subsection IV.1 for details) on these structures to obtain the corresponding energy, forces, and virial data for subsequent NEP training. The complete reference dataset was randomly divided into a training set with 740 structures and a test set with 190 structures.
Using the obtained training and test datasets as input, we employed the NEP3 framework Fan et al. (2022), implemented in the gpumd package (verison v3.5) Fan et al. (2017b), to train a unified machine-learned NEP for diamond, cBN, and their heterostructures. NEP employs a feedforward NN to represent atomic site energy as a function of a descriptor vector containing radial and angular components, while SNES Schaul et al. (2011) optimizes the parameters to minimize the RMSEs of energy, forces, and virial against the training dataset. The cutoff radii for both radial and angular descriptor terms were set to . A feedforward NN with a hidden layer of 50 neurons was used. The separable natural evolution strategy algorithm was applied with a population size of 50, and a total number of generations was used to achieve convergence of the total loss function. The weights of energy, force, and virial RMSEs in the loss function were set to 1.0, 1.0, and 0.1, respectively. For more details of the NEP approach, we refer to the literature Fan et al. (2022).
IV.3 NEMD simulations
All MD simulations were performed using the gpumd package (version v3.5) Fan et al. (2017b). The NEMD approach was employed to investigate the thermal transport properties of diamond/cBN interfaces by establishing a non-equilibrium steady state with a constant heat flux using two local thermostats at different temperatures. A rectangular simulation box with dimensions of , containing 66,000 atoms, was used for all diamond/cBN heterostructures. This system size was tested and confirmed to be sufficiently large to obtain convergent ITC. Periodic boundary conditions were applied in all three spatial directions, and the heat flux direction was set from the diamond side to the cBN side (along the -direction in Figure 3(a)).
To ensure unidirectional thermal transport, atoms in the outermost five layers of both the diamond and cBN regions were fixed. Adjacent to these fixed layers, five-layer heat source and heat sink regions were introduced to generate the heat flux. The transport region, located between the heat source and sink, consisted of 90 atomic layers: 45 layers of diamond on the left and 45 layers of cBN on the right, with each layer containing 600 atoms. Moving outward from the center of the system, the layers on the left diamond side were labeled as , , , etc., while those on the right cBN side were labeled as , , , etc.
For the NEMD simulations, the diamond/cBN heterostructure was first relaxed for at using the Berendsen thermostat Berendsen et al. (1984) under the NVT ensemble. After relaxation, Langevin thermostats Bussi and Parrinello (2007) were applied to the heat source and sink regions, maintaining temperatures of and , respectively. The entire system reached a steady state within , after which temperature and energy profiles were sampled over the last .
The ITC is defined in terms of the temperature drop across an interface as:
| (1) |
where represents the average energy transfer rate along the temperature gradient direction, and is the cross-sectional area perpendicular to the transport direction. To fairly compare the ITC of ideal and rough interfaces, is calculated as the temperature difference between and , where atomic diffusion is confined between these two layers (see Figure 3(b)). For each case, three independent simulations were conducted to determine the average value as the predicted ITC, and the corresponding standard error was also calculated.
IV.4 Spectral heat current decomposition
To obtain the contribution of phonon modes with different frequencies, one can calculate spectrally decomposed thermal conductance in the NEMD approachFan et al. (2019):
| (2) |
where
| (3) |
Here, is the virial-velocity-time correlation function Gabourie et al. (2021) in the transport direction. The full vector of the virial-velocity correlation function is defined as
| (4) |
where is the virial tensor and is the velocity vector of atom .
Similar to thermal conductance, the can also be spectrally decomposed in the HNEMD approach:
| (5) |
| (6) |
where is the driving force parameters in the HNEMD method.
Acknowledgements.
The authors thank Mr. Ting Liang and Dr. Ke Xu for their help in validating the NEP model. This work was supported by the Key-Area Research and Development Program of Guangdong Province (Grant 2020B010169002), the Guangdong Special Support Program (Grant No.2021TQ06C953), and the Science and Technology Planning Project of Shenzhen Municipality (Grant No. GXWD20220811164433002). X. Wu is the JSPS Postdoctoral Fellow for Research in Japan (No. P24058). P. Ying is supported by the Israel Academy of Sciences and Humanities & Council for Higher Education Excellence Fellowship Program for International Postdoctoral Researchers.Conflict of Interest
The authors have no conflicts to disclose.
Data availability
The source code and documentation for gpumd are available at https://github.com/brucefan1983/GPUMD and https://gpumd.org, respectively. The inputs and outputs related to the NEP model training are freely available at the Gitlab repository https://gitlab.com/brucefan1983/nep-data.
References
- Cheng et al. (2024) Zhe Cheng, Zifeng Huang, Jinchi Sun, Jia Wang, Tianli Feng, Kazuki Ohnishi, Jianbo Liang, Hiroshi Amano, and Ru Huang, “(Ultra)wide bandgap semiconductor heterostructures for electronics cooling,” Applied Physics Reviews 11, 041324 (2024).
- Zhu et al. (2019) Jiyuan Zhu, Xingyu Zhou, Liang Jing, Qilin Hua, Weiguo Hu, and Zhong Lin Wang, “Piezotronic effect modulated flexible AlGaN/GaN high-electron-mobility transistors,” ACS Nano 13, 13161–13168 (2019).
- Zhao et al. (2024) Tiancheng Zhao, Xinxin Yu, Wenhui Xu, Yang He, Zhenyu Qu, Rui Shen, Ruize Wang, Huaixin Guo, Huarui Sun, Zhonghui Li, Min Zhou, Tiangui You, and Xin Ou, “First Demonstration of Wafer-Level Arrayed -Ga2O3 Thin Films and MOSFETs on Diamond by Transfer Printing Technology,” in 2024 IEEE International Electron Devices Meeting (IEDM) (2024) pp. 1–4.
- Cheng et al. (2020) Zhe Cheng, Virginia D. Wheeler, Tingyu Bai, Jingjing Shi, Marko J. Tadjer, Tatyana Feygelson, Karl D. Hobart, Mark S. Goorsky, and Samuel Graham, “Integration of polycrystalline Ga2O3 on diamond for thermal management,” Applied Physics Letters 116, 062105 (2020).
- Ji et al. (2024) Xiaoyang Ji, Zifeng Huang, Yutaka Ohno, Koji Inoue, Yasusyohi Nagai, Yoshiki Sakaida, Hiroki Uratani, Jinchi Sun, Naoteru Shigekawa, Jianbo Liang, and Zhe Cheng, “Interfacial Reaction Boosts Thermal Conductance of Room-Temperature Integrated Semiconductor Interfaces Stable up to ,” Advanced Electronic Materials , 2400387 (2024).
- Tsao et al. (2018) J. Y. Tsao, S. Chowdhury, M. A. Hollis, D. Jena, N. M. Johnson, K. A. Jones, R. J. Kaplar, S. Rajan, C. G. Van de Walle, E. Bellotti, C. L. Chua, R. Collazo, M. E. Coltrin, J. A. Cooper, K. R. Evans, S. Graham, T. A. Grotjohn, E. R. Heller, M. Higashiwaki, M. S. Islam, P. W. Juodawlkis, M. A. Khan, A. D. Koehler, J. H. Leach, U. K. Mishra, R. J. Nemanich, R. C. N. Pilawa-Podgurski, J. B. Shealy, Z. Sitar, M. J. Tadjer, A. F. Witulski, M. Wraback, and J. A. Simmons, “Ultrawide-bandgap semiconductors: Research opportunities and challenges,” Advanced Electronic Materials 4, 1600501 (2018).
- Bello et al. (2002) I. Bello, W.J. Zhang, K.M. Chan, C.Y. Chan, Y. Wu, F. Meng, C.W. Lam, J. Liu, and W.Y. Luk, “Diamond and cubic boron nitride: synthesis and electronic applications,” in The Fourth International Conference on Advanced Semiconductor Devices and Microsystem (2002) pp. 1–11.
- Ralchenko et al. (2021) V.G. Ralchenko, A.V. Inyushkin, Guoyang Shu, Bing Dai, I.A. Karateev, A.P. Bolshakov, A.A. Khomich, E.E. Ashkinazi, E.V. Zavedeev, Jiecai Han, and Jiaqi Zhu, “Thermal conductivity of diamond mosaic crystals grown by chemical vapor deposition: Thermal resistance of junctions,” Phys. Rev. Appl. 16, 014049 (2021).
- Chen et al. (2020) Ke Chen, Bai Song, Navaneetha K. Ravichandran, Qiye Zheng, Xi Chen, Hwijong Lee, Haoran Sun, Sheng Li, Geethal Amila Gamage Udalamatta Gamage, Fei Tian, Zhiwei Ding, Qichen Song, Akash Rai, Hanlin Wu, Pawan Koirala, Aaron J. Schmidt, Kenji Watanabe, Bing Lv, Zhifeng Ren, Li Shi, David G. Cahill, Takashi Taniguchi, David Broido, and Gang Chen, “Ultrahigh thermal conductivity in isotope-enriched cubic boron nitride,” Science 367, 555–559 (2020).
- Chen et al. (2015) Chunlin Chen, Zhongchang Wang, Takeharu Kato, Naoya Shibata, Takashi Taniguchi, and Yuichi Ikuhara, “Misfit accommodation mechanism at the heterointerface between diamond and cubic boron nitride,” Nature communications 6, 6327 (2015).
- Qi et al. (2021) Ruishi Qi, Ruochen Shi, Yuehui Li, Yuanwei Sun, and et al., “Measuring phonon dispersion at an interface,” Nature 599, 399–403 (2021).
- Kikkawa et al. (2021) Jun Kikkawa, Takashi Taniguchi, and Koji Kimoto, “Nanometric phonon spectroscopy for diamond and cubic boron nitride,” Phys. Rev. B 104, L201402 (2021).
- Gordiz and Henry (2016) Kiarash Gordiz and Asegun Henry, “Phonon transport at interfaces: Determining the correct modes of vibration,” Journal of Applied Physics 119, 015101 (2016).
- Bello et al. (2005) I. Bello, C.Y. Chan, W.J. Zhang, Y.M. Chong, K.M. Leung, S.T. Lee, and Y. Lifshitz, “Deposition of thick cubic boron nitride films: The route to practical applications,” Diamond and Related Materials 14, 1154–1162 (2005), proceedings of Diamond 2004, the 15th European Conference on Diamond, Diamond-Like Materials, Carbon Nanotubes, Nitrides and Silicon Carbide.
- Zhe et al. (2021) Cheng Zhe, Ruiyang Li, Xingxu Yan, Glenn Jernigan, Jingjing Shi, Michael E. Liao, Nicholas J. Hines, Chaitanya A. Gadre, Juan Carlos Idrobo, Eungkyu Lee, Karl D. Hobart, Mark S. Goorsky, Xiaoqing Pan, Tengfei Luo, and Samuel Graham, “Experimental observation of localized interfacial phonon modes,” Nature Communications 12, 6901 (2021).
- Li et al. (2024) Yangyang Li, Qiang Zhao, Yang Liu, Xiaoping Ouyang, et al., “Molecular dynamics study of thermal transport across diamond/cubic boron nitride interfaces,” Physica Scripta 99, 025944 (2024).
- Kınacı et al. (2012) Alper Kınacı, Justin B Haskins, Cem Sevik, and Tahir Çağın, “Thermal conductivity of BN-C nanostructures,” Physical Review B—Condensed Matter and Materials Physics 86, 115410 (2012).
- Huang and Guo (2020) Xu Huang and Zhixiong Guo, “High thermal conductance across c-BN/diamond interface,” Diamond and Related Materials 108, 107979 (2020).
- Chen et al. (2022) Jie Chen, Xiangfan Xu, Jun Zhou, and Baowen Li, “Interfacial thermal resistance: Past, present, and future,” Rev. Mod. Phys. 94, 025002 (2022).
- Li et al. (2022) Qinshu Li, Fang Liu, Song Hu, Houfu Song, Susu Yang, Hailing Jiang, Tao Wang, Yee Kan Koh, Changying Zhao, Feiyu Kang, et al., “Inelastic phonon transport across atomically sharp metal/semiconductor interfaces,” Nature communications 13, 4901 (2022).
- Deringer et al. (2019) Volker L. Deringer, Miguel A. Caro, and Gábor Csányi, “Machine learning interatomic potentials as emerging tools for materials science,” Advanced Materials 31, 1902765 (2019).
- Dong et al. (2024) Haikuan Dong, Yongbo Shi, Penghua Ying, Ke Xu, Ting Liang, Yanzhou Wang, Zezhu Zeng, Xin Wu, Wenjiang Zhou, Shiyun Xiong, Shunda Chen, and Zheyong Fan, “Molecular dynamics simulations of heat transport using machine-learned potentials: A mini-review and tutorial on gpumd with neuroevolution potentials,” Journal of Applied Physics 135, 161101 (2024).
- Ying et al. (2025) Penghua Ying, Cheng Qian, Rui Zhao, Yanzhou Wang, Ke Xu, Feng Ding, Shunda Chen, and Zheyong Fan, “Advances in modeling complex materials: The rise of neuroevolution potentials,” Chemical Physics Reviews 6, 011310 (2025).
- Behler and Parrinello (2007) Jörg Behler and Michele Parrinello, “Generalized neural-network representation of high-dimensional potential-energy surfaces,” Phys. Rev. Lett. 98, 146401 (2007).
- Sun et al. (2024) Zhanpeng Sun, Dongliang Zhang, Zijun Qi, Qijun Wang, Xiang Sun, Kang Liang, Fang Dong, Yuan Zhao, Diwei Zou, Lijie Li, et al., “Insight into Interfacial Heat Transfer of -Ga2O3/Diamond Heterostructures via the Machine Learning Potential,” ACS Applied Materials & Interfaces 16, 31666–31676 (2024).
- Wu et al. (2024a) Jing Wu, E Zhou, An Huang, Hongbin Zhang, Ming Hu, and Guangzhao Qin, “Deep-potential enabled multiscale simulation of gallium nitride devices on boron arsenide cooling substrates,” Nature Communications 15, 2540 (2024a).
- Fan et al. (2021) Zheyong Fan, Zezhu Zeng, Cunzhi Zhang, Yanzhou Wang, Keke Song, Haikuan Dong, Yue Chen, and Tapio Ala-Nissila, “Neuroevolution machine learning potentials: Combining high accuracy and low cost in atomistic simulations and application to heat transport,” Phys. Rev. B 104, 104309 (2021).
- Fan et al. (2022) Zheyong Fan, Yanzhou Wang, Penghua Ying, Keke Song, Junjie Wang, Yong Wang, Zezhu Zeng, Ke Xu, Eric Lindgren, J. Magnus Rahm, Alexander J. Gabourie, Jiahui Liu, Haikuan Dong, Jianyang Wu, Yue Chen, Zheng Zhong, Jian Sun, Paul Erhart, Yanjing Su, and Tapio Ala-Nissila, “GPUMD: A package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations,” The Journal of Chemical Physics 157, 114801 (2022).
- Schaul et al. (2011) Tom Schaul, Tobias Glasmachers, and Jürgen Schmidhuber, “High Dimensions and Heavy Tails for Natural Evolution Strategies,” in Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, GECCO ’11 (Association for Computing Machinery, New York, NY, USA, 2011) pp. 845–852.
- Slack (1973) G.A. Slack, “Nonmetallic crystals with high thermal conductivity,” Journal of Physics and Chemistry of Solids 34, 321–335 (1973).
- morelli and Slack (2006) Donald T. morelli and Glen A. Slack, “High lattice thermal conductivity solids,” in High Thermal Conductivity Materials, edited by Subhash L. Shindé and Jitendra S. Goela (Springer New York, New York, NY, 2006) pp. 37–68.
- Fan et al. (2017a) Zheyong Fan, Luiz Felipe C. Pereira, Petri Hirvonen, Mikko M. Ervasti, Ken R. Elder, Davide Donadio, Tapio Ala-Nissila, and Ari Harju, “Thermal conductivity decomposition in two-dimensional materials: Application to graphene,” Phys. Rev. B 95, 144309 (2017a).
- Qiu et al. (2025) Lin Qiu, Haimo Li, Xiaolu Yuan, Fengcheng Li, Yanhui Feng, Chengming Li, Jinlong Liu, and Xiaohua Zhang, “Ultra-Efficient Heat Transport Across a “2.5D” All-Carbon sp2/sp3 Hybrid Interface,” Angewandte Chemie International Edition 64, e202417902 (2025).
- Wu et al. (2024b) Kongping Wu, Guoqing Chang, Jiandong Ye, and Gang Zhang, “Significantly enhanced interfacial thermal conductance across GaN/Diamond interfaces utilizing AlxGa1–xN as a phonon bridge,” ACS Applied Materials & Interfaces 16, 58880–58890 (2024b), pMID: 39422442.
- Zhou et al. (2025) Wenjiang Zhou, Nianjie Liang, Wei Xiao, Zhaofei Tong, Fei Tian, and Bai Song, “Ultrahigh interfacial thermal conductance for cooling gallium oxide electronics using cubic boron arsenide,” (2025), arXiv:2501.11082 [cond-mat.mtrl-sci] .
- Kang et al. (2021) Joon Sang Kang, Man Li, Huan Wu, Huuduy Nguyen, Toshihiro Aoki, and Yongjie Hu, “Integration of boron arsenide cooling substrates into gallium nitride devices,” Nature Electronics 4, 416–423 (2021).
- Feng et al. (2019) Tianli Feng, Yang Zhong, Jingjing Shi, and Xiulin Ruan, “Unexpected high inelastic phonon transport across solid-solid interface: Modal nonequilibrium molecular dynamics simulations and landauer analysis,” Phys. Rev. B 99, 045301 (2019).
- Rustam et al. (2022) Sabiha Rustam, Malachi Schram, Zexi Lu, Anne M. Chaka, W. Steven Rosenthal, and Jim Pfaendtner, “Optimization of thermal conductance at interfaces using machine learning algorithms,” ACS Applied Materials Interfaces 14, 32590–32597 (2022).
- Xue et al. (2025) Juan Xue, Fengyi Li, Aoran Fan, Weigang Ma, and Xing Zhang, “Optimizing interfacial thermal resistance in GaN/AlN heterostructures: The impact of AlN layer thickness,” International Journal of Heat and Mass Transfer 239, 126629 (2025).
- Koh et al. (2009) Yee Kan Koh, Yu Cao, David G. Cahill, and Debdeep Jena, “Heat-transport mechanisms in superlattices,” Advanced Functional Materials 19, 610–615 (2009).
- Romanos et al. (2013) J. Romanos, M. Beckner, D. Stalla, A. Tekeei, G. Suppes, S. Jalisatgi, M. Lee, F. Hawthorne, J.D. Robertson, L. Firlej, B. Kuchta, C. Wexler, P. Yu, P. Pfeifer, and et al., “Infrared study of boron–carbon chemical bonds in boron-doped activated carbon,” Carbon 54, 208–214 (2013).
- Blöchl (1994) Peter E Blöchl, “Projector augmented-wave method,” Physical review B 50, 17953 (1994).
- Perdew et al. (1996) John P Perdew, Kieron Burke, and Matthias Ernzerhof, “Generalized gradient approximation made simple,” Physical review letters 77, 3865 (1996).
- Kresse and Furthmüller (1996) Georg Kresse and Jürgen Furthmüller, “Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set,” Physical Review B 54, 11169 (1996).
- Kresse and Joubert (1999) Georg Kresse and Daniel Joubert, “From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method,” Physical Review B 59, 1758 (1999).
- Togo and Tanaka (2015) Atsushi Togo and Isao Tanaka, “First principles phonon calculations in materials science,” Scripta Materialia 108, 1–5 (2015).
- Li et al. (2014) Wu Li, Jesús Carrete, Nebil A. Katcho, and Natalio Mingo, “ShengBTE: a solver of the Boltzmann transport equation for phonons,” Comp. Phys. Commun. 185, 1747–1758 (2014).
- Zhao et al. (2019) Dehe Zhao, Wei Gao, Yujing Li, Yuyuan Zhang, and Hong Yin, “The electronic properties and band-gap discontinuities at the cubic boron nitride/diamond hetero-interface,” RSC advances 9, 8435–8443 (2019).
- Fan et al. (2017b) Zheyong Fan, Wei Chen, Ville Vierimaa, and Ari Harju, “Efficient molecular dynamics simulations with many-body potentials on graphics processing units,” Computer Physics Communications 218, 10–16 (2017b).
- Berendsen et al. (1984) Herman JC Berendsen, JPM van Postma, Wilfred F Van Gunsteren, ARHJ DiNola, and Jan R Haak, “Molecular dynamics with coupling to an external bath,” The Journal of chemical physics 81, 3684–3690 (1984).
- Bussi and Parrinello (2007) Giovanni Bussi and Michele Parrinello, “Accurate sampling using langevin dynamics,” Physical Review E—Statistical, Nonlinear, and Soft Matter Physics 75, 056707 (2007).
- Fan et al. (2019) Zheyong Fan, Haikuan Dong, Ari Harju, and Tapio Ala-Nissila, “Homogeneous Nonequilibrium Molecular Dynamics Method for Heat Transport and Spectral Decomposition with Many-Body Potentials,” Physical Review B 99, 064308 (2019).
- Gabourie et al. (2021) Alexander J Gabourie, Zheyong Fan, Tapio Ala-Nissila, and Eric Pop, “Spectral decomposition of thermal conductivity: Comparing velocity decomposition methods in homogeneous molecular dynamics simulations,” Physical Review B 103, 205421 (2021).