Interval Posets and Polygon Dissections
Abstract
The Interval poset of a permutation is an effective way of capturing all the intervals of the permutation and the inclusions between them and was introduced recently by Tenner. Thi paper explores the geometric interpretation of interval posets of permutations. We present a bijection between tree interval posets and convex polygons with non-crossing diagonals, offering a novel geometric perspective on this purely combinatorial concept. Additionally, we provide an enumeration of interval posets using this bijection and demonstrate its application to block-wise simple permutations.
1 Introduction
In [5], Tenner defined the concept of an interval poset of a permutation. This is an effective way of capturing all the intervals of a permutation and the set of inclusions between them in one glance. Tenner dealt with structural aspects of the interval poset and characterized the posets that can be seen as interval posets of some permutations.
An interval poset might correspond to more than one permutation. For instance, all simple permutations of a given order share the same interval poset. Tener, in the aforementioned paper, enumerated binary interval posets and binary tree interval posets but left open the following question:
Question 1.1.
How many tree interval posets have minimal elements?
This question was answered by Bouvel, Cioni and Izart in [3]. They also noted that the number of tree interval posets is equal to the number of ways to place non-crossing diagonals in a convex -gon such that no quadrilaterals are created.
In this work we suggest a simple bijection between the set of tree interval posets and the set of -gons, satisfying the conditions listed above. We use this bijection also for enumerating the whole set of interval posets by using a broader set of polygons. In [3], the enumeration of the entire set of interval posets was done in an algebraic way, using generating functions, while our bijection grants a geometric view to the interval posets.
Another set of interval posets that can be enumerated by polygons is the one corresponding to block-wise simple permutations, a term that was introduced in a recent paper by the current authors [2].
2 Background
Definition 2.1.
Let the symmetric group on elements. Let . An interval (or block) of is a non-empty contiguous sequence of entries whose values also form a contiguous sequence of integers. For , denotes the interval of values that range from to . Clearly, is an interval, as well as for each . These are called trivial intervals. The other intervals are called proper.
For example, the permutation has as a proper interval as well as the following proper intervals: , .
A permutation is called simple if it does not have proper intervals. For example, the permutation is simple.
Following Tenner [5], we define an interval poset for each permutation as follows:
Definition 2.2.
In [5], the interval poset is embedded in the plane so that each node’s direct descendants are increasingly ordered according to the minimum of each interval from left to right. We note that in [3] another embedding of the same poset was presented.
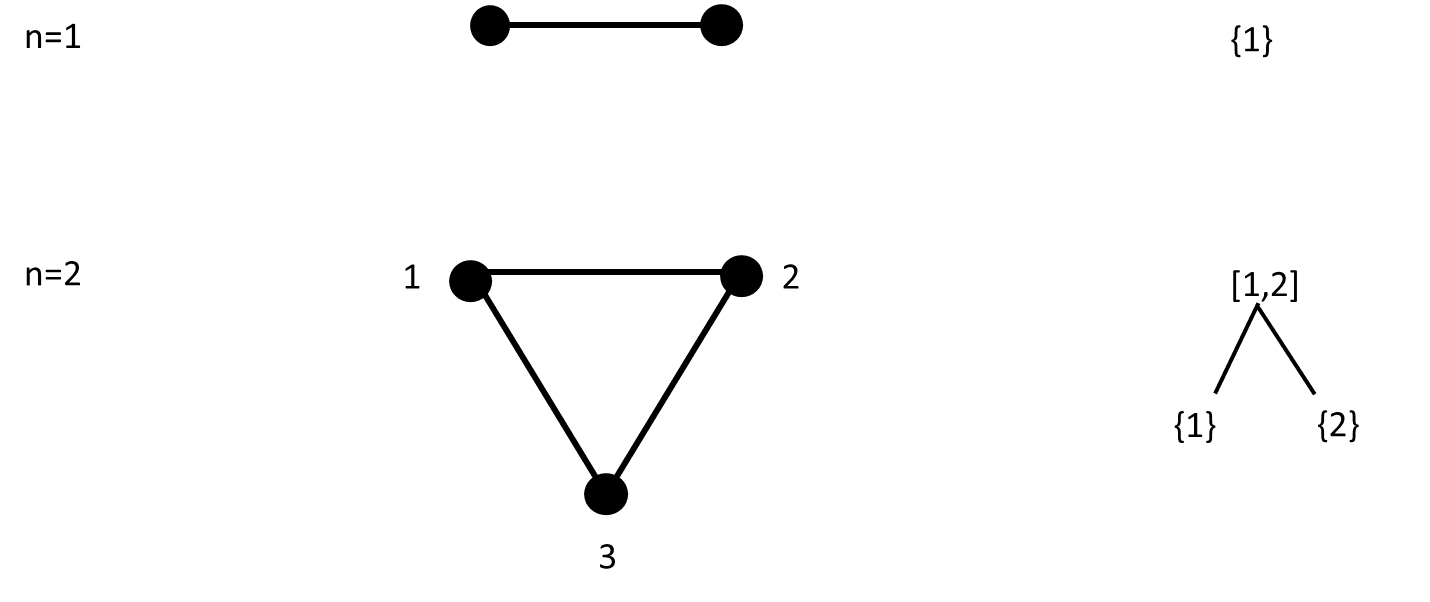
If is a simple permutation, the interval poset of comprises the entire interval with minimal elements as its only descendants. Hence, all simple permutations of a given order share the same interval poset (see for example Figure 2).
3 Geometrical view of interval posets
3.1 General interval posets
Bouvel, Cioni and Izart[3], provided a formula for the number of interval posets with minimal elements and added it to OEIS as sequence A348479 [4].
Here we provide a geometrical view to the interval posets by providing a bijection from the set of interval posets with minimal elements to a distinguished set of dissections of the convex gon, which we define below.
We identify a polygon with its set of vertices and denote a diagonal or an outer edge of the polygon from vertex to vertex by .
Definition 3.1.
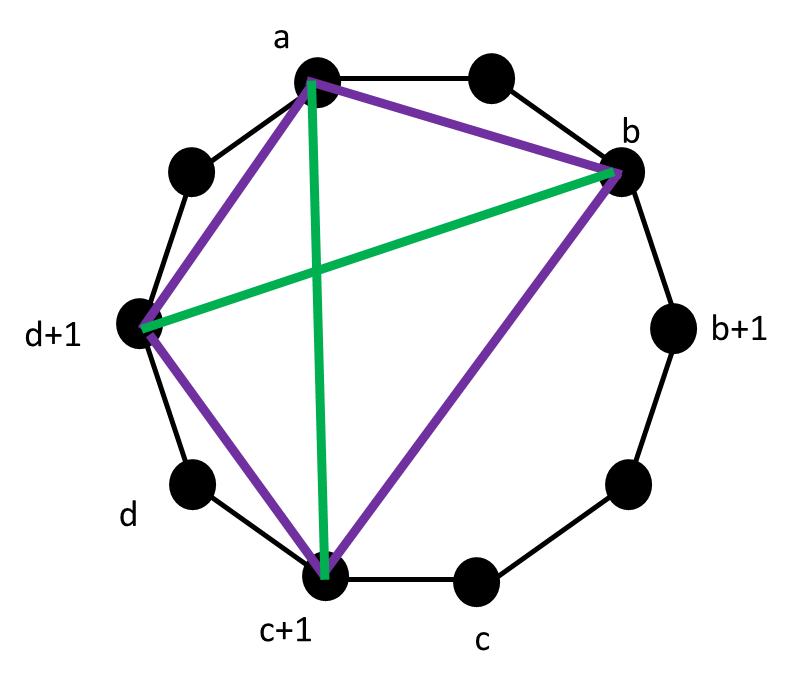
A dissection of an gon will be called diagonally framed if for each two crossing diagonals, their vertices are connected to each other. Explicitly, if and are two crossing diagonals, then the diagonals or outer edges must also exist. See Figure 5 for an example.
Before we proceed, we have to present two observations which provide some details on the structure of interval posets and will be used in the sequel.
Observation 3.2.
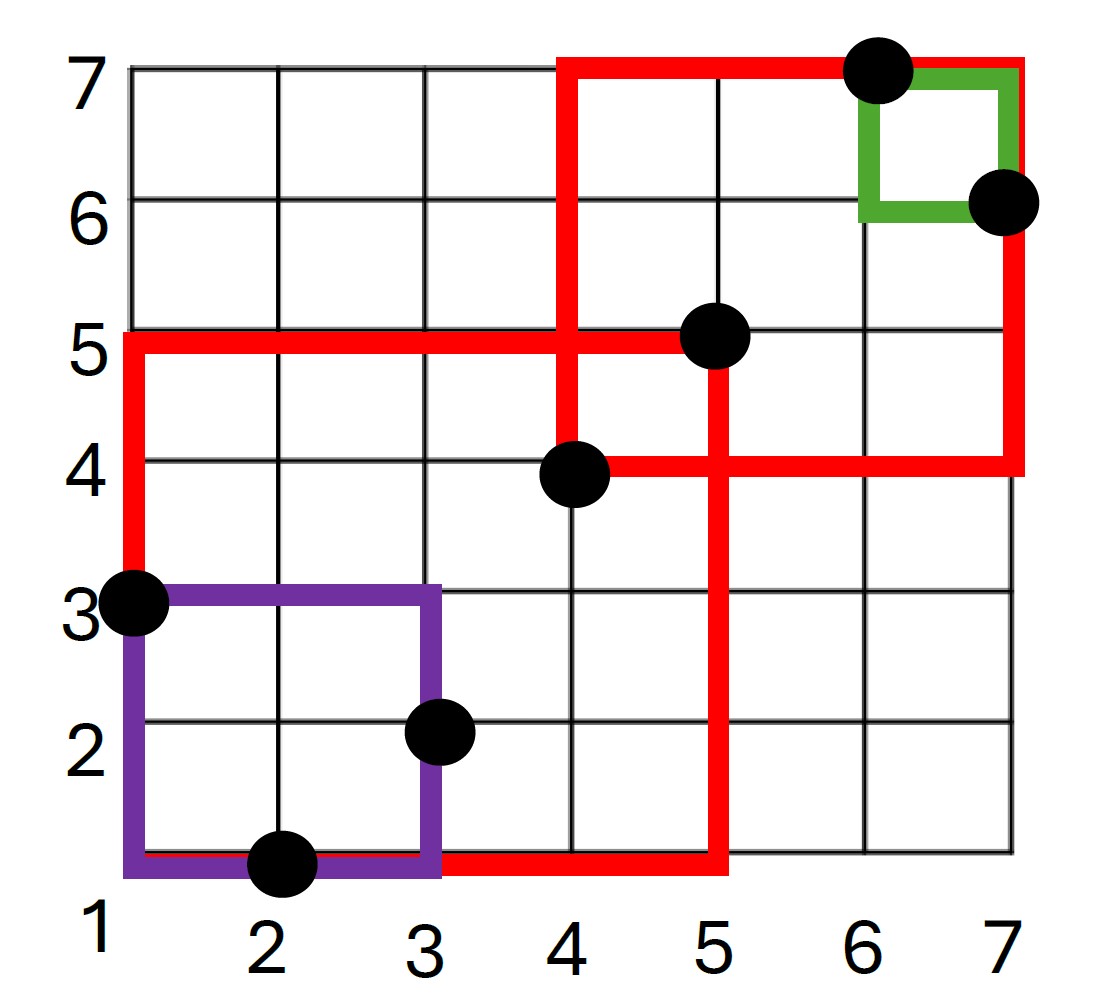
Let . If and are intervals of such that and and , then , , and are intervals of .
For example, take , then and are intersecting intervals of and thus are also intervals of , as can be seen in Figure 3 which depicts the permutation in the common graphical way.
Observation 3.3.
If is the interval poset of , then no element of has exactly direct descendants, since every permutation of order must contain a block of order .
We are ready now to present the main result of this subsection.
Theorem 3.4.
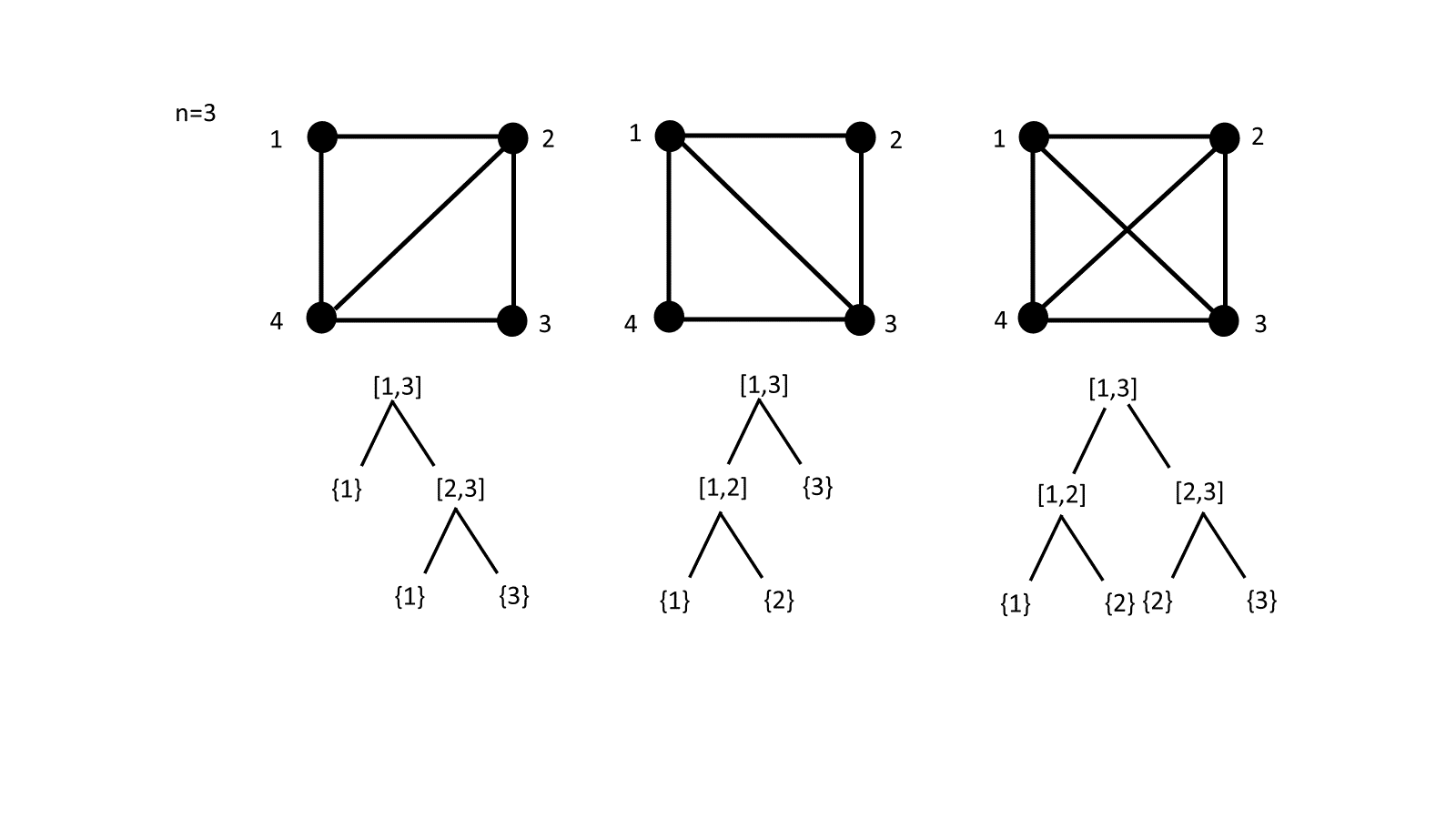
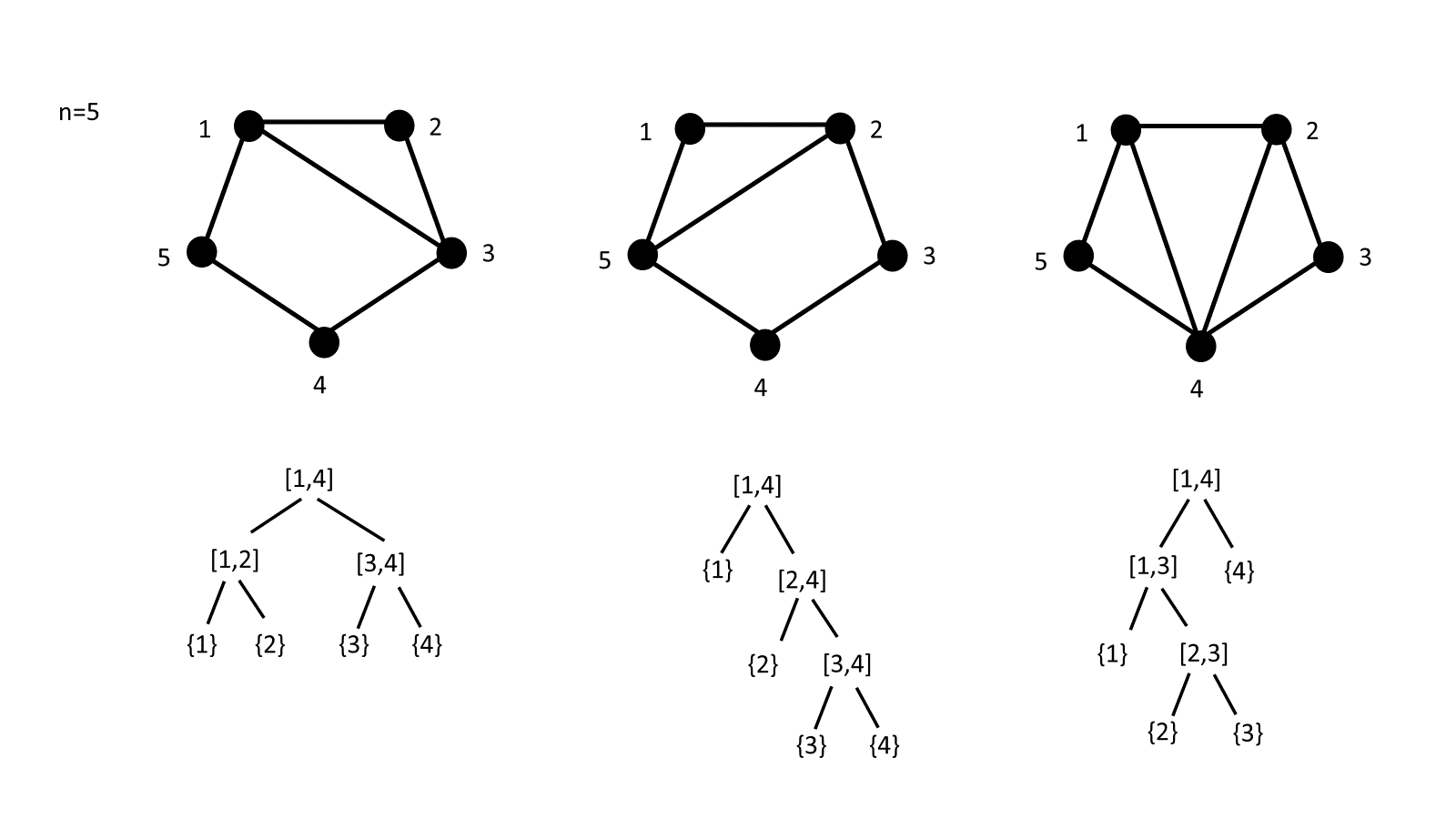
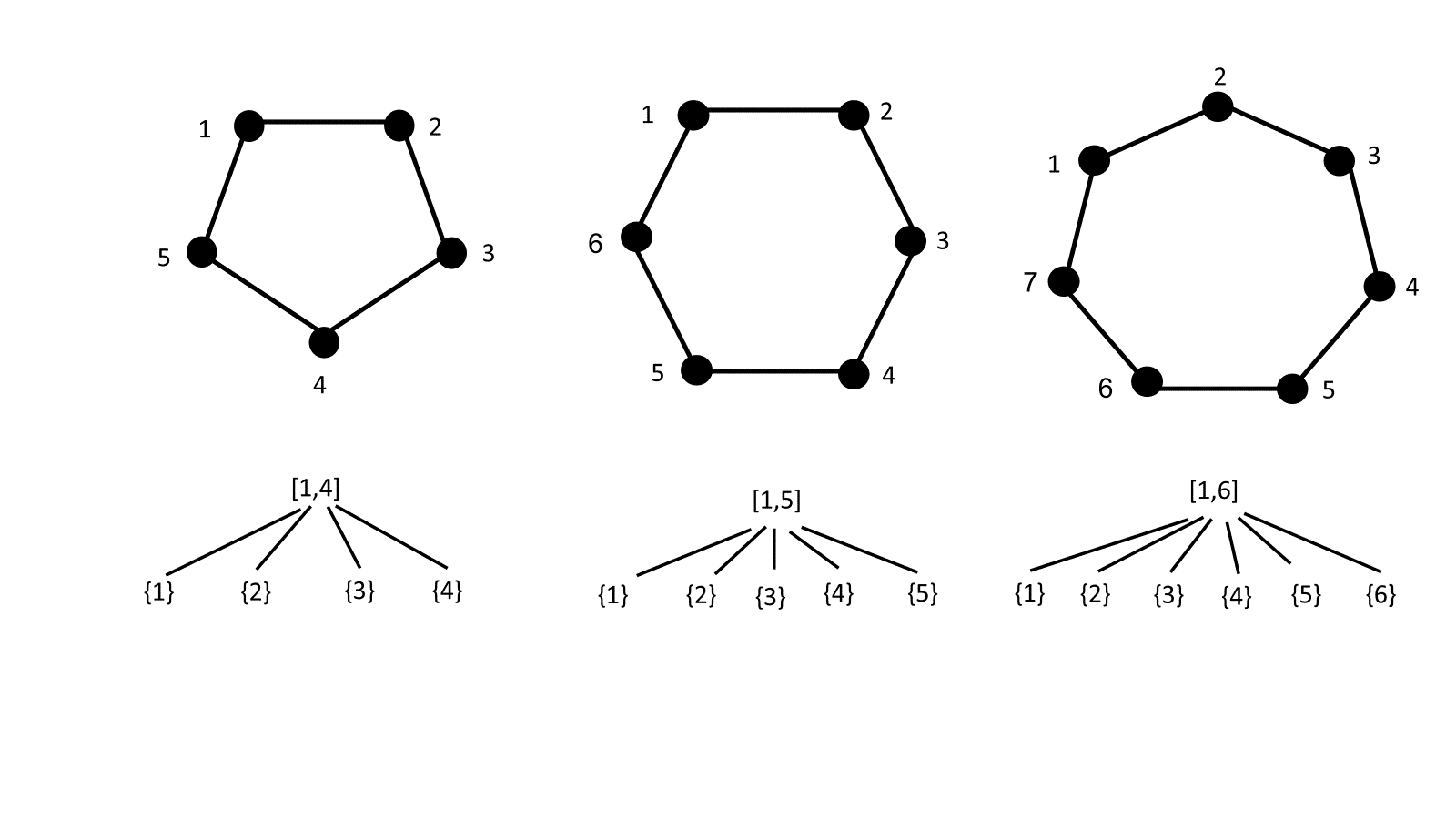
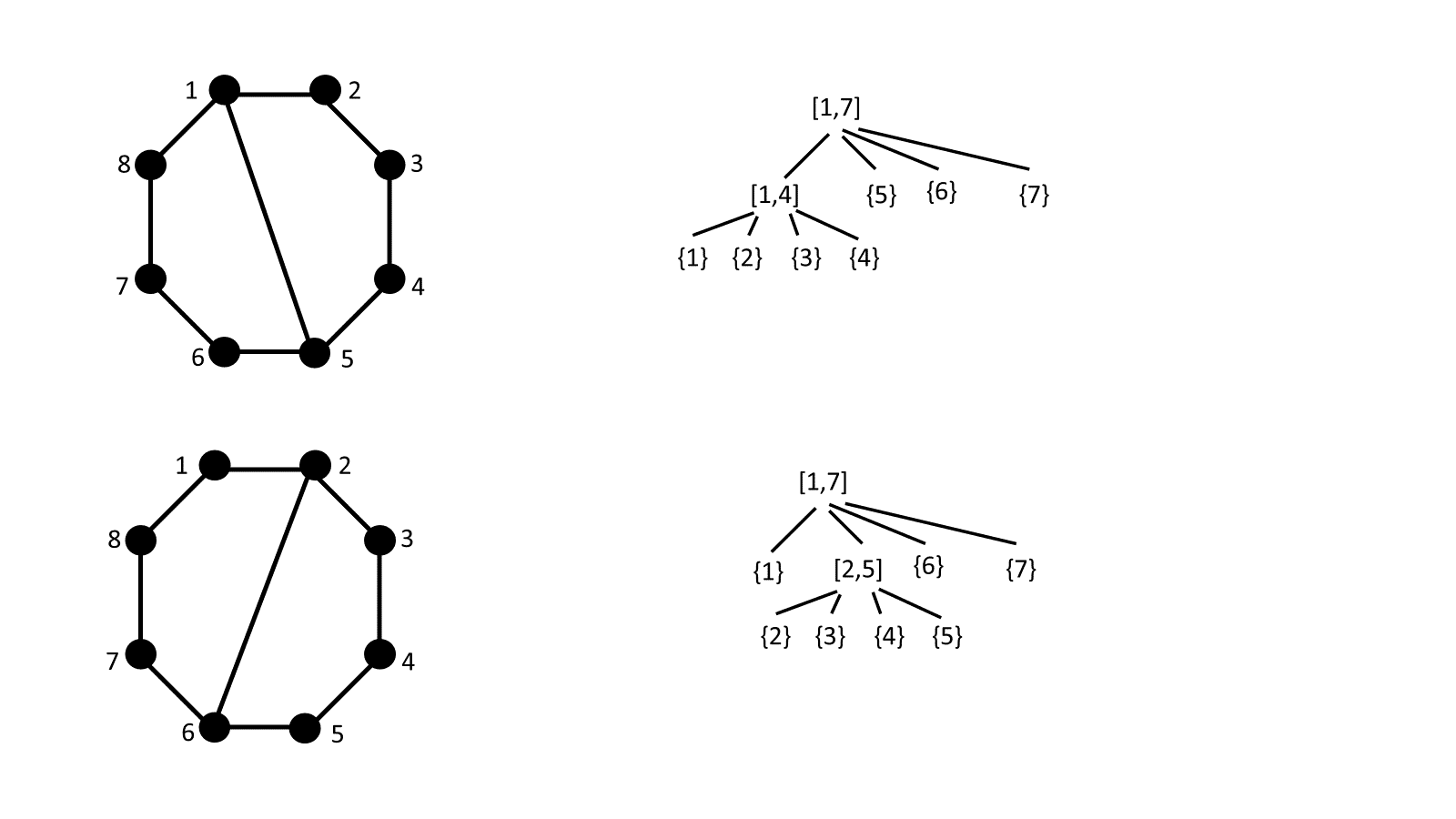
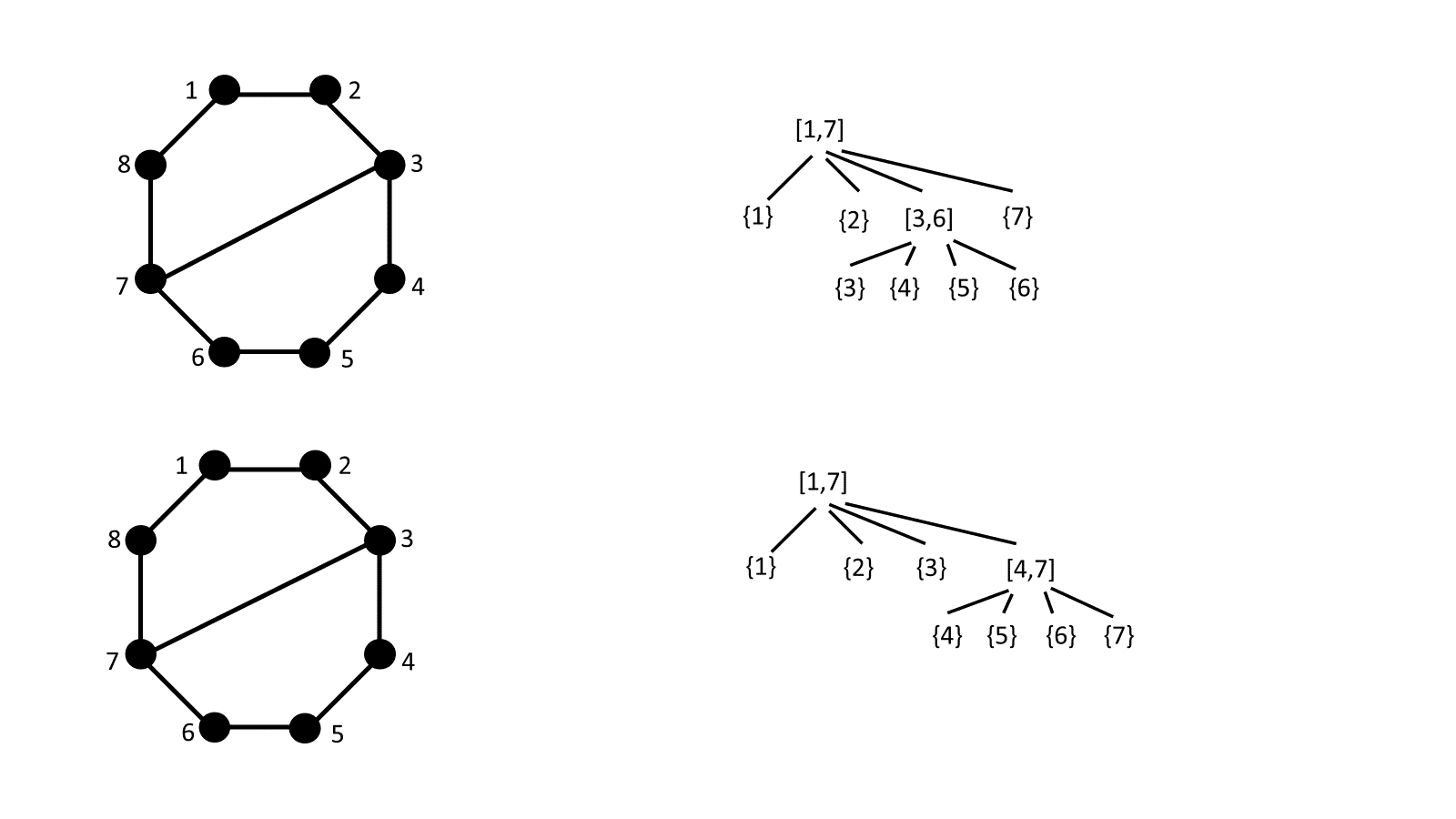
The number of interval posets with minimal elements is equal to the number of diagonally framed dissections of the convex ()-gon such that no quadrilaterals are present (see Figure 6 in the appendix for some examples of the bijection in small values of ).
Proof.
We define a bijection between the set of interval posets with minimal elements and the set of diagonally framed dissections of convex - gons without quadrilaterals as follows:
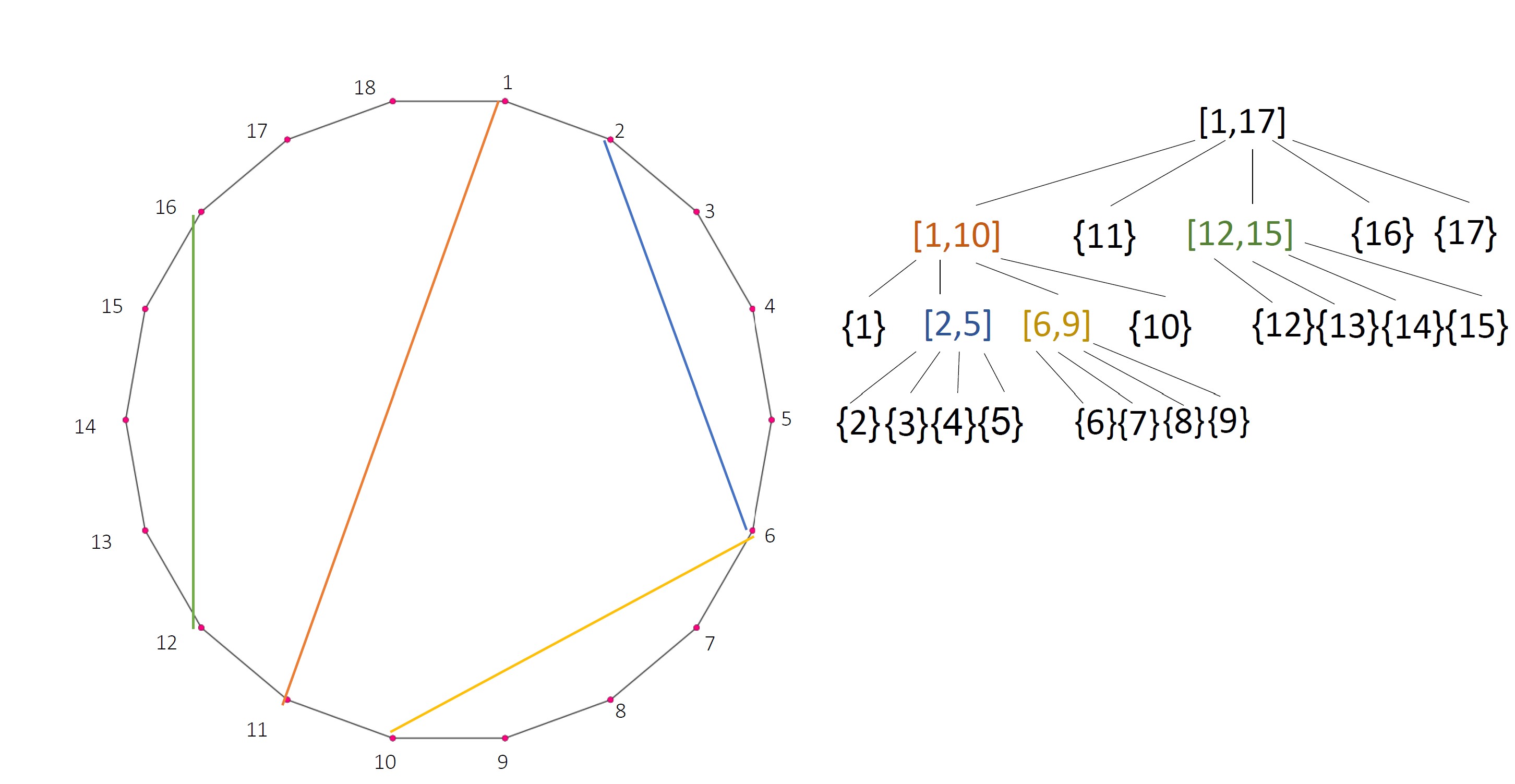
Let be the interval poset of some . We set to be the convex -gon whose set of diagonals is
i.e. to each interval of the form corresponds a diagonal in ; note that singletones intervals correspond to outer edges in the polygon (see Figure 4 for an example).
We claim now that must be a diagonally framed - gon. Indeed, if and are two crossing diagonals in , where , then and are intersecting intervals in and by Observation 3.2 we have that , , and are intervals in corresponding respectively to the diagonals and . (See Figure 5 for an illustration).
Moreover, must not contain any quadrilateral. Otherwise, if are such that is a quadrilateral (without any subdivision) then must contain the intervals and so we must have that the first three intervals are direct descendants of the fourth one and they are the only ones. By Observation 3.3, this is impossible. ∎
3.2 Tree interval posets
A tree poset is a poset whose Hasse diagram is a tree.
In [3], the authors calculated the generating function of the number of tree interval posets using generating functions and mentioned that this is equal to the number of ways to place non-crossing diagonals in a convex -gon such that no quadrilaterals are created (sequence A054515 from OEIS [4]).
Using the function defined above, one can easily produce a combinatorial proof of the following result.
Theorem 3.5.
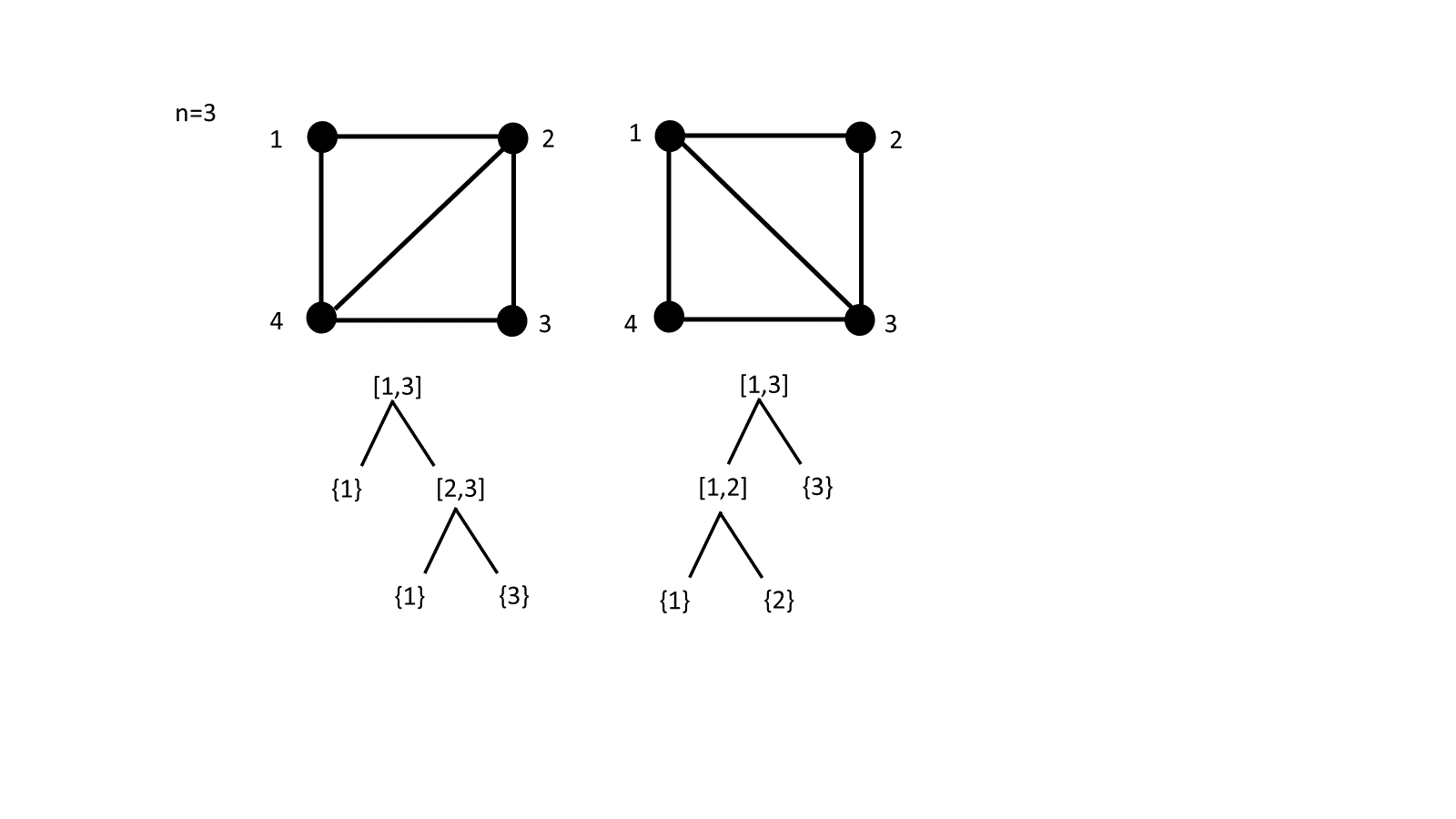
The number of tree interval posets with minimal elements is equal to the number of non crossing dissections of the convex gon such that no quadrilaterals are present (see Figure 7 in the appendix for some examples of the bijection).
Proof.
We use the same mapping which was applied in the proof of Theorem 3.4. It is now sufficient to prove that no crossing diagonals are obtained. This is implied by the fact that intersecting diagonals stem from intersecting intervals which can not exist in a tree since they cause a circle. (See Figure 1).
∎
3.3 Interval posets of block-wise simple permutations
In [2], the current authors introduced the notion of block-wise simple permutations. We cite here the definition:
Definition 3.6.
A permutation is called block-wise simple if it has no interval of the form or , where and stand for direct and skew sums of permutations respectively.
There are no block-wise simple permutations of orders and .
For , a permutation is block-wise simple, if and only if it is simple. One of the first nontrivial examples of block-wise simple permutations is .
In [2], the current authors enumerated the interval posets of block-wise permutations.
The first few values of the sequence of these numbers are . This is sequence A054514 from OEIS [4] which also counts the number of ways to place non-crossing diagonals in a convex -gon such that there are no triangles or quadrilaterals.
The geometrical interpretation of interval posets of block-wise permutations is as follows:
Theorem 3.7.
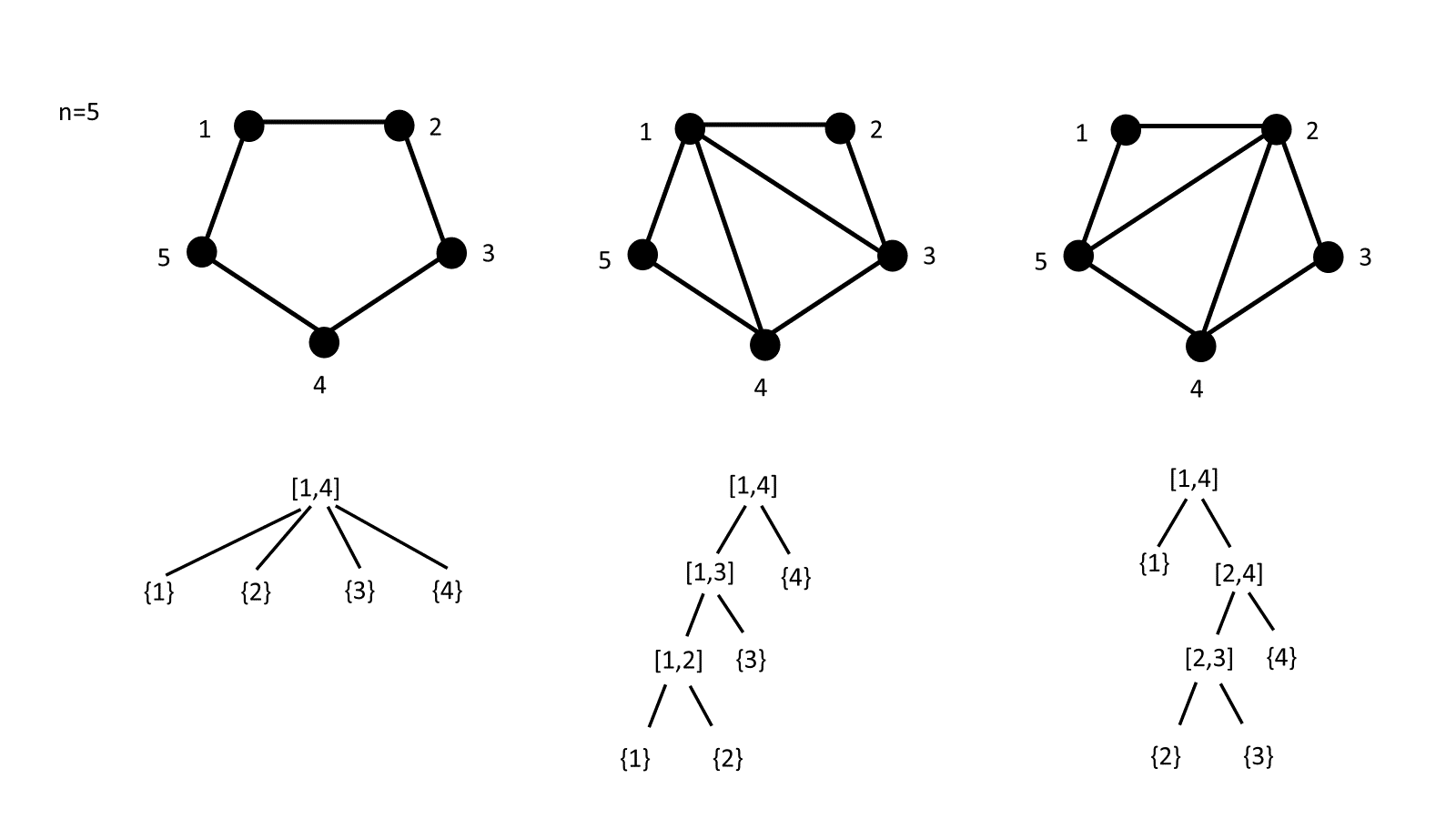
The number of interval posets that represent a block-wise simple permutation of order is equal to the number of ways to place non-crossing diagonals in a convex ()-gon such that no triangles or quadrilaterals are present (see Figure 8 in the appendix for some examples of the bijection).
Proof.
We use again the mapping , defined earlier. In [5] (Theorem 6.1), the author claimed that is a tree interval poset if and only if contains no interval of the form or . From here, and by Definition 3.6, it is obvious that an interval poset of a block-wise simple permutation is a tree. Hence it is sufficient to prove that for an interval poset of a block-wise permutation, has no triangles. This holds due to the fact that if contains a triangle with edges with then must contain the intervals and and thus is the direct parent of and which contradicts the definition of block-wise simple permutations. ∎
References
- [1]
- [2] E. Bagno, E. Eisenberg, S. Reches & M. Sigron (2023): Blockwise simple permutations. arXiv:https://arxiv.org/abs/2303.13115. Note.
- [3] M. Bouvel, L. Cionl & B. Izart (2021): The interval posets of permutations seen from the decomposition tree perspective. arXiv:https://arxiv.org/abs/2110.10000. Note.
- [4] OEIS Foundation Inc. (2022): The On-Line Encyclopedia of Integer Sequences. Available at http://oeis.org.
- [5] B.E. Tenner (2022): Interval Posets of Permutations. Orders, 10.1007/s11083-021-09576-1.
4 Appendix