Intrinsic Pulse Widths of FRB 20121102A and Calculation of Broadening from Propagation and Instrumental Effects
Abstract
The pulse widths of fast radio bursts are always broadened due to the scattering of the plasma medium through which the electromagnetic wave passes. The recorded pulse width will be further affected by the radio telescopes since the sampling time and the bandwidth cannot be infinitely small. In this study, we focus on the pulse widths of at least 3287 bursts detected from FRB 20121102A as of October 2023. Various effects such as the scattering broadening, the redshift-induced broadening and the instrumental broadening are examined. At a redshift of 0.193, the pulse width is broadened by a factor of approximately 0.16 due to cosmological time dilation. It is found that the instrumental broadening only contributes a fraction of – to the observed pulse width. The scattering broadening is even smaller, which constitutes a tiny fraction of – in the observed pulse width. After correcting for these broadenings, the intrinsic pulse width is derived for each burst. The maximum and minimum pulse widths at different frequencies are highlighted. The intrinsic widths of most bursts are in a narrow range of 1 – 10 ms, which leads to a quasi-linear correlation between the fluence and the peak flux. Besides, the mean value and the dispersion range of intrinsic pulse width are found to scale with the central frequency as and , respectively.
1 Introduction
Fast radio bursts (FRBs) are intense radio transients typically lasting for a few milliseconds, with an isotropic peak luminosity up to to erg s-1. Their brightness temperature is – K, indicating that coherent radiation mechanisms should be involved (Lorimer et al. 2007; Cordes & Chatterjee 2019; Petroff et al. 2019, 2022; Zhang 2023). The dispersion measure (DM) of FRBs, which is an integration of the column density of free electrons along the line of sight, is generally much larger than the value contributed by Galactic electrons predicted by the NE2001 model, implying an extra-galactic origin for them (Cordes & Lazio 2002; Thornton et al. 2013; Yao et al. 2017). There seem to be two classes of FRBs, i.e., repeaters and non-repeating ones (Thornton et al. 2013; Spitler et al. 2016; Zhang 2023). Currently, more than 800 FRB sources have been detected, among which there are only 60 FRBs verified to be repeaters and 40 are well-localized (Petroff et al. 2016, 2022; CHIME/FRB Collaboration et al. 2021; Chime/Frb Collaboration et al. 2022; Hu & Huang 2023; Xu et al. 2023; Zhang 2023). However, it is still unclear whether those one-off events are really non-repeating sources or are actually also repeaters whose repeated bursts simply were not recorded by us (Caleb et al. 2019). Among the repeaters, two sources are found to have long-term periodicity in their activity levels: a possible 160-day periodicity exists in the activities of FRB 20121102A, and a robust 16.35-day periodicity is found for FRB 20180916B, with an activity window of 5 days (Rajwade et al. 2020; CHIME/FRB Collaboration et al. 2020; Cruces et al. 2021). Statistically, repeating FRBs generally have a relatively larger width and narrower bandwidth (Andersen et al. 2019; Pleunis et al. 2021). They also have a complex time-frequency down-drifting behavior, generally referred to as the “sad-trombone” effect (Hessels et al. 2019; CHIME/FRB Collaboration et al. 2021; Pleunis et al. 2021).
The astrophysical origin of FRBs is still enigmatic. For repeating and one-off FRBs, many models have been proposed respectively. For example, possible models of repeating FRBs include: activities in the magnetosphere of magnetars (Beloborodov 2017, 2020; Margalit et al. 2019), giant pulses from young pulsars (Cordes & Wasserman 2016; Connor et al. 2016), or the fractional collapses of the crust of a strange star (Geng et al. 2021). On the other hand, models of non-repeating FRBs include: mergers of double neutron star systems (Totani 2013), or collapses of massive neutron stars to black holes (Falcke & Rezzolla 2014; Ravi & Lasky 2014; Zhang 2018).
FRB 20121102A was the first FRB source discovered to repeat, first observed with the 305 m Arecibo telescope (Spitler et al. 2014). It has been extensively monitored by many radio telescopes. More than three thousand FRBs have been observed from this source, which provides a valuable data set for us to study the nature of FRBs. Some key parameters are available for the bursts, such as their durations, fluences, and frequency ranges. However, note that when the radio emissions of FRBs propagate toward us, they will be affected by the plasma medium along the line of sight, which will lead to various effects such as the delay of lower frequency waves and the broadening of the pulse width. The plasma medium is inhomogeneous and includes many components, i.e. the interstellar medium (ISM) of the host galaxy, the intergalactic medium (IGM), and the ISM of our Milky Way (Rickett 1990; Petroff et al. 2019). When the radio waves travel through the medium, they will be scattered, leading to the delay and broadening of the FRB pulses (Rickett 1990; Xu & Zhang 2016). Additionally, the radio telescopes may also lead to some broadening of the observed widths of FRBs (Cordes & McLaughlin 2003), which is usually referred to as the instrumental effect. It has been argued that the broadening caused by scattering scales as a function of frequency as (Spitler et al. 2016; Michilli et al. 2018; Hessels et al. 2019; Snelders et al. 2023), but a detailed analysis on the exact amplitudes of the broadening is still lacking. In this study, we will investigate the various broadening effects on the at least 3287 bursts detected from FRB 20121102A by various instruments.
The structure of our article is organized as follows. The theory of radio wave scattering by plasma and the induced temporal broadening is introduced in Section 2, together with the introduction of the instrumental broadening. Our numerical results for 3287 bursts from FRB 20121102A are presented and analyzed in Section 3. Finally, our conclusions and some discussion are included in Section 4.
2 Temporal Broadening
When a pulse of radio waves travel through a plasma medium, it will be affected by electron scattering, leading to some chromatic behaviors (dispersion) and the broadening of the pulse duration. As a result, the recorded pulse width by an observer can be written as (Cordes & McLaughlin 2003; Lorimer & Kramer 2012; Zhang 2023)
| (1) |
where is the original intrinsic pulse width, is the redshift, and are the temporal broadenings caused by plasma scattering and instrumental effects, respectively.
2.1 Scattering broadening of the pulse width
The total scattering broadening is a combination of the scattering broadening caused by the ISM in the host galaxy and the Milky Way, and the IGM (Zhang 2023). For simplicity, we assume that each medium component itself is largely homogeneous and the intrinsic fluctuations are quasi-statistical (Barabanenkov et al. 1971). In this case, the scattering effect can be conveniently modelled by following the work of Rickett (1990).
In fact, the scattering broadening caused by IGM is negligible (Katz 2016). Following Rickett (1990), we denote the turbulence spectrum index as . The typical value of in case of IGM is 11/3 (i.e. the Kolmogorov turbulence spectrum). According to Xu & Zhang (2016), the outer length scale of the turbulence medium should be smaller than pc to cause a significant scattering broadening with this value. However, the outer scale of turbulence medium in the IGM is generally larger than pc (Luan & Goldreich 2014). Therefore, we will neglect the IGM contribution in this study.
For a homogeneous ISM in a galaxy (e.g. the Milky Way or the host galaxy of a FRB), Xu & Zhang (2016) argued that the density fluctuation is likely a short-wave-dominated spectrum (). We adopt that the diffractive length is smaller than the inner length scale of the turbulence and the scattering angle is much less than 1. Here we replace their with , where is the volume filling factor and is the root-mean-square of the electron density fluctuation (Xu & Zhang 2016). Therefore, we can derive the broadening timescale induced by the scattering of the galactic ISM as
| (2) |
where DM is the dispersion measure of the corresponding ISM (it can be either the ISM of the Milky Way or the ISM of the host galaxy), is the wavelength of the radio emission in the observer’s frame, and is correspondingly the electron number density. The density contrast in the host galaxy of FRB 20121102A is unknown. Here we take in our calculations, which is typical in the Milky Way (Xu & Zhang 2016). Equation (2) can then be further expressed as
| (3) |
by substituting the typical values of the parameters into it (Xu & Zhang 2016). In our calculations, we take and pc (Xu & Zhang 2016). We then can use this equation to conveniently calculate the contribution of scattering broadening from the ISM of the host galaxy and the Milky Way. For example, by substituting the redshift () and dispersion measure of the host galaxy (), and the observing frequency into Equation (3), we can obtain the scattering timescale due to the ISM of the host galaxy. We can also calculate the scattering timescale caused by the ISM of the Milky Way similarly.
However, cannot be directly measured through observations. Here we estimate it as follows. First, the total dispersion measure on the line of sight is a sum of several components (Thornton et al. 2013; Deng & Zhang 2014; Prochaska & Zheng 2019), i.e.
| (4) |
where are the contributions from the Milky Way, the Galactic halo and the IGM, respectively. Note that can be derived from FRB observations. Second, for our Galaxy, we have and in the direction of FRB 20121102A by referring to the NE2001 Galactic ISM model (Cordes & Lazio 2002; Zhang 2023). At the same time, the IGM contribution at can be calculated by using a linear formula of (Zhang 2018; Pol et al. 2019; Cordes et al. 2022)
| (5) |
where is the Hubble constant, is the energy density fraction of baryons, is the mass fraction of baryons in the IGM, and is the fraction of ionized electrons. So, from Equation (4), we can get an estimation of by subtracting other components from . In this way, of FRB 20121102A is estimated to be in a range of 200 – 220 . Consequently, the scattering broadening caused by the ISM of the host galaxy ranges from ms to ms, which is comparable to the ISM contribution of the Milky Way.
2.2 Instrumental broadening
The radio telescope can also have a complex effect on the observed pulse width. It depends on the DM of the source, the bandwidth of each frequency channel, and the sampling time. To be more specific, the instrumental broadening term of in Equation (1) can be written as (Cordes & McLaughlin 2003; Petroff et al. 2019)
| (6) |
Here, the first term, , is the frequency-dependent intra-channel dispersive smearing, which is further expressed as (Cordes & McLaughlin 2003)
| (7) |
where is the bandwidth of the channel (in units of MHz) and is its central frequency (in units of GHz).
The second term in Equation (6) originates from the deviations (i.e. ) between the true DM and the fiducial DM, which is chosen to de-disperse the channels coherently (Hessels et al. 2019). It can be expressed as (Cordes & McLaughlin 2003)
| (8) |
The third term in Equation (6) is the so-called bandwidth smearing (Bridle & Schwab 1999; Rioja et al. 2018), which can be approximately calculated as
| (9) |
Finally, the fourth term of in Equation (6) is simply the sampling time.
2.3 Redshift-induced broadening
The cosmological time dilation can also cause the broadening of pulse widths, namely, the redshift-induced broadening. It can be expressed as
| (10) |
Note that the intrinsic pulse width of in Equation (10) cannot be directly measured from observations, so this equation cannot be straightforwardly applied. Instead, we need to solve Equation (1) to derive first, which can be done by substituting the scattering broadening and instrumental broadening terms as described in Subsections 2.1 and 2.2 into Equation (1). Consequently, utilizing the derived intrinsic pulse widths of FRBs, we can calculate the redshift-induced broadening by using Equation (10). In the case of FRB 20121102A which resides at , since the scattering broadening and instrumental broadening are generally insignificant (see the section below), we find that the pulse width is broadened by a factor of approximately 0.16 due to cosmological time dilation.
3 Numerical Results for FRB 20121102A
As the first repeating FRB source, FRB 20121102A has been extensively monitored by many radio telescopes. The source is associated with a low-metallicity dwarf galaxy at a redshift of 0.193, located in the vicinity of a star-forming region (Cordes et al. 2006; Spitler et al. 2014, 2016; Lazarus et al. 2015; Chatterjee et al. 2017; Tendulkar et al. 2017; Marcote et al. 2017). The DM of FRB 20121102A was measured as 557.4 2.0 pc cm-3 on MJD 56233, and has increased to 565.8 0.9 pc cm-3 between MJD 58724 and MJD 58776, showing an increasing trend of 1 pc cm-3 year-1 (Spitler et al. 2014, 2016; Li et al. 2021). A linear polarization of nearly 100 percent was detected, with the polarization angle being almost constant (Michilli et al. 2018; Plavin et al. 2022; Hewitt et al. 2022). In the meantime, the rotation measure (RM) of FRB 20121102A has changed drastically from 1.46 105 rad m-2 to 7 104 rad m-2 over three years, which could point to the existence of an extreme magneto-ionic environment related to an accreting compact star, or a magnetized wind nebula around a magnetar (Spitler et al. 2016; Michilli et al. 2018). In addition, other environment models have been proposed, such as the binary interactions involving a neutron star (Wang et al. 2022). As of October 2023, at least 3287 bursts have been detected from FRB 20121102A by various telescopes (Li et al. 2021; Aggarwal et al. 2021; Hewitt et al. 2022; Jahns et al. 2023). We have collected the main observational parameters of these events from previous literature. An overview of our data set is presented in Table 1. In our study, we have directly taken the observed parameters from the corresponding references.
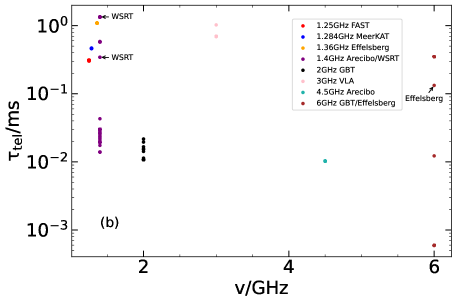
For the 3287 bursts from FRB 20121102A collected in our sample, we have comprehensively analyzed the broadening of their pulse widths caused by different factors by using the equations introduced in Section 2. For example, the scattering broadening can be calculated with Equation (3). It is found that the total scattering timescale caused by both the Milky Way and the host galaxy ranges from to ms. The effect of instrumental broadening at different observing frequencies is illustrated in Figure 1. We see that is generally between ms to 1 ms, which is about three magnitudes larger than the scattering broadening. This effect is significant for short FRBs, especially those lasting for less than 1 ms.
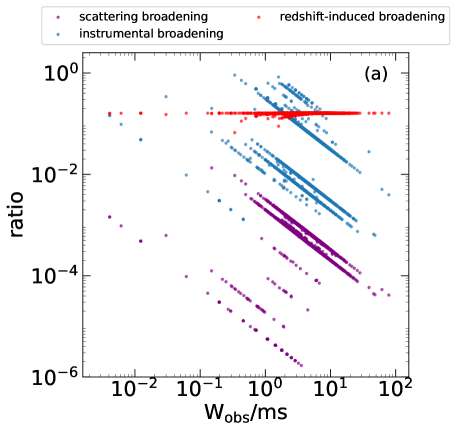
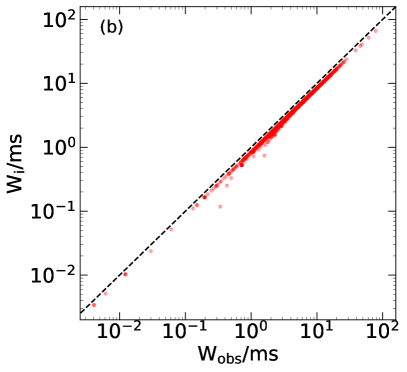
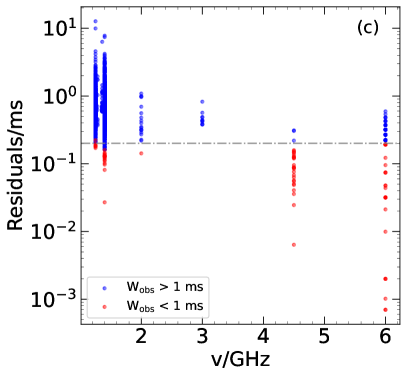
In Figure 2a, the fractions of pulse width broadening due to the redshift (), scattering () and instrumental () effects are shown for each pulse. The three effects are illustrated by different colors. Since FRB 20121102A is at a redshift of , we see that the redshift-induced broadening ratio is generally (the red dots). It leads to a broadening of – 1 ms for most FRBs. The ratio of instrumental broadening generally ranges between – 0.1. However, for some bursts, the ratio can be larger than 60%. They are mainly short events whose duration is less than 1 ms. In these cases, the sampling time could seriously affect the measured pulse width. Furthermore, we see that the ratio of scattering broadening generally ranges between – . It is much smaller than the instrumental broadening as a whole. After solving the effects of these factors, we can then easily correct them and derive the intrinsic pulse width, i.e. . Figure 2b plots versus the observed width. Here, the dashed line corresponds to . We see that most of the data points are very close to the dashed line, which means that the effects of all three broadening factors (i.e. redshift, scattering and instrumental effects) are unimportant for the majority of FRBs. The broadening is noticeable only for a very small portion of FRBs. They are typically short events that are more seriously subjected to the influence of the sampling time. Figure 2c plots the residuals between the observed and intrinsic pulse widths versus the central frequencies. Here the residual equals to . The gray dash-dotted line corresponds to a residual of 0.2 ms. We see that for the bursts with the width longer than 1 ms, the residual is generally larger than 0.2 ms, while for those shorter than 1 ms, the residual is generally less than 0.2 ms. At a particular frequency, the variation of the residual is mainly due to the difference of the observed width, i.e. .
Figures 1 – 2 present an overall analysis of all the pulses in our sample. Next, we will divide the 3287 bursts into subsamples according to the radio telescopes that detected them and analyze these subsamples separately. In our study, the curve-fit and scipy.stats codes111https://docs.scipy.org/doc/scipy/reference/index.html, which are based on the least square fitting method, are adopted to get a best-fit curve for the data points. Monte Carlo simulations are performed to obtain the corresponding confidence level of the fitting curve.
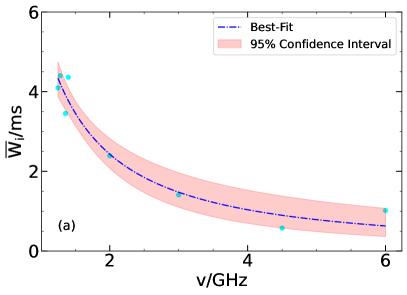
Our results based on subsample analysis of the intrinsic pulse width are illustrated in Figure 3. Figure 3a plots the mean intrinsic pulse width () versus the central frequency of the FRBs. We see that obviously has a decreasing tendency when the frequency increases, which has been observed by other groups as well (Gajjar et al. 2018; Chamma et al. 2023). It declines from ms at 1.3 GHz to ms at 6 GHz and generally follows a function of . In fact, the best-fit curve of the data points corresponds to
| (11) |
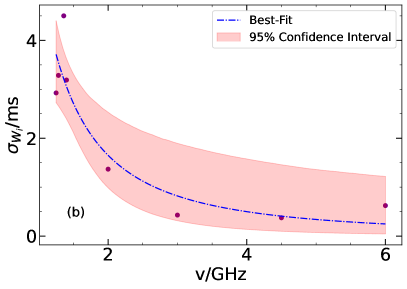
Figure 3b plots the dispersion range of the intrinsic pulse width () versus the central frequency. Interestingly, also has a decreasing tendency when the frequency increases. It declines from ms at 1.3 GHz to ms at 6 GHz, and scales as . The best-fit curve of the data points corresponds to
| (12) |
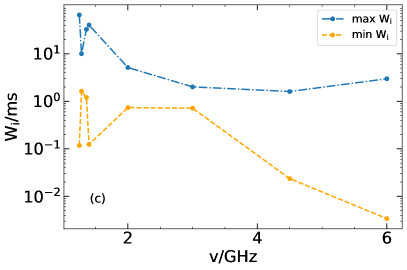
Figure 3c shows the maximum and minimum values of the intrinsic pulse width in each subsample. At a frequency of GHz, the minimum width is about 0.1 ms, while the maximum width can be up to ms. At 6 GHz, the minimum width is as short as ms and the maximum width is ms. The maximum and minimum widths can put stringent constraints on the trigger mechanism and radiation process of FRBs. A successful FRB model should be capable of explaining these extreme values (Beloborodov 2020; Zhang 2022).
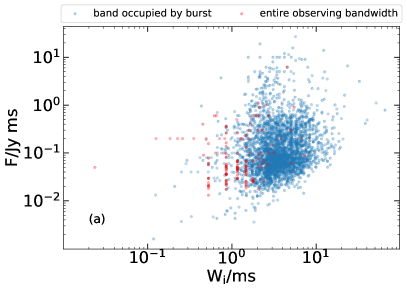
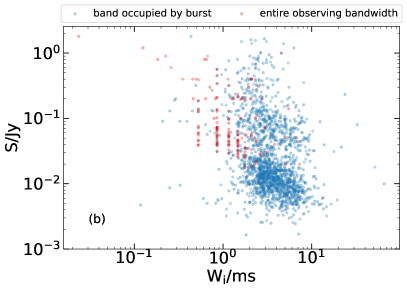
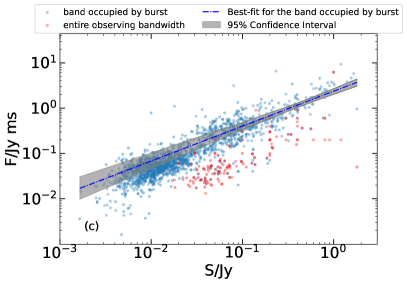
The peak flux (), fluence () and pulse width are three key parameters of FRBs. After acquiring the intrinsic pulse width, we can explore any possible connection between the parameters. Figure 4 shows the distribution of FRBs when one parameter is plotted versus another for the bursts with fluence and peak flux available. Note that the methods used to acquire the fluence are different by various groups so that there could exist a systematic discrepancy between different subsamples. Some authors calculated the fluence simply across the entire observing bandwidth, while others derived the fluence from the band occupied by the burst. To make a distinction, the data points corresponding the former cases are plotted in red (which only include 139 bursts) and the data in the latter cases are shown in blue (over 3000 bursts). From Figure 4a, we see that the distribution of the FRBs on the - plane is quite chaotic so that no correlation exists between these two parameters. Another feature is that the pulse widths of the majority of FRBs are distributed in a relatively narrow range ( – 10 ms). On the contrary, the distribution range of fluence is much wider, which spans over two magnitudes ( – 1 Jy ms). Figure 4b shows that there seems to exist a weak negative correlation between the peak flux and the intrinsic pulse width: a longer FRB tends to have a smaller peak flux. However, the correlation is generally too weak to draw any firm conclusion. Similarly, we notice that the peak flux also has a relatively large distribution range, which spans over two magnitudes (mainly in a range of – Jy). Figure 4c plots the fluence () versus the peak flux (). A clear positive correlation can be seen in the plot. Since the red points correspond to a minor portion of the data, we have analyzed the majoring blue points separately. A best fit of the blue data points gives
| (13) |
In fact, can be regarded as a product of the peak flux and the equivalent pulse width. The above positive correlation is a natural outcome giving the fact that the intrinsic pulse widths of FRBs are narrowly distributed in a small range.
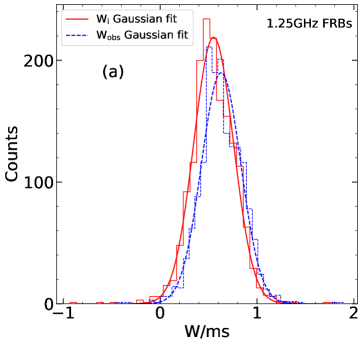
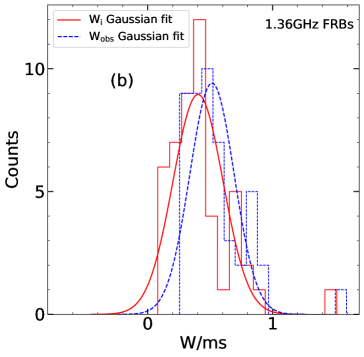
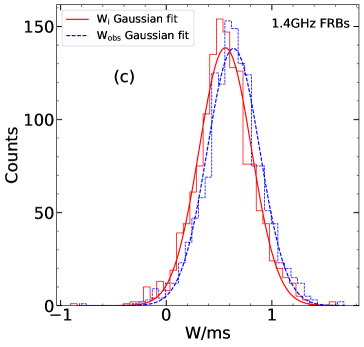
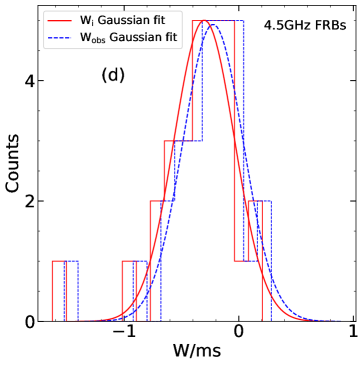
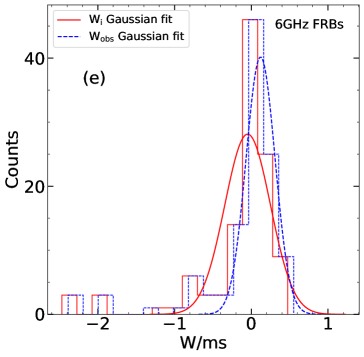
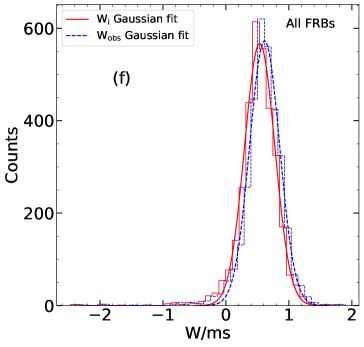
We have also divided the FRBs into several groups according to their central frequency (i.e. 1.25 GHz, 1.36 GHz, 1.4 GHz, 4.5 GHz and 6 GHz groups). The distribution of the observed/intrinsic pulse width is compared for each group to present a direct illustration of the broadening effects. Figure 5 plots the histogram distributions of the observed pulse width and the corrected intrinsic pulse width for each group. A Gaussian fit is performed for each distribution, which gives the most probable width () and the dispersion range () of the bursts at these frequencies. The derived parameters are listed in Table 2. The intrinsic pulse widths are slightly smaller than the observed width, but their distributions do not differ from each other significantly.
4 Conclusions and Discussion
With more and more FRB sources being detected, it is necessary to analyze the statistical features of their intrinsic parameters systematically. In this study, we have collected 3287 bursts and their parameters detected from FRB 20121102A as of October 2023. Various broadening effects on the pulse width, including the scattering broadening caused by turbulence and the instrumental broadening induced during observations, are considered and corrected. It is found that these broadening effects do not play a dominant role in the majority of bursts from FRB 20121102A. The instrumental broadening is mainly in a range of – 1 ms, which contributes a fraction of – to the observed pulse width. The scattering broadening is even smaller, which mainly ranges in – ms and only contributes a fraction of – to the observed pulse width. A quasi-linear correlation exists between the fluence and the peak flux, which is mainly due to the narrow distribution of the intrinsic pulse width for the majority of the bursts.
Interestingly, the mean intrinsic pulse width is found to decrease as the central frequency increases, i.e. . Some authors have also attempted to quantify the relationship between pulse width and frequency (Gajjar et al. 2018; Chamma et al. 2023). Especially, Chamma et al. (2023) pointed out that the observed width scales as , which is steeper than the power-law of the intrinsic width derived in this study. More strikingly, the dispersion range of the intrinsic pulse width also has a decreasing behavior, . We have normalized the dispersion of intrinsic pulse width by dividing it with the mean intrinsic pulse width to get the quantity of , which is a measure of the relative dispersion level. It is found that still has a decreasing trend with frequency in the range of 1.3 – 6 GHz, i.e. . In our sample, the duration of low-frequency bursts can be either long or short. For example, the widths of FAST bursts are in a wide range of 0.3 – 78.5 ms. However, the high-frequency bursts are all short ones. Therefore, at high-frequencies, the distribution of the observed pulse widths is more concentrated, leading to a lower value of correspondingly. The lack of long bursts at high-frequencies may reflect the intrinsic property of the central engine, but it could also be caused by observational selection effects since long bursts are relatively difficult to detect at high frequencies due to the sensitivity constraint.
The frequency-dependent behavior of and may place useful constraints on the triggering mechanism and radiation process of FRBs. It could be a natural outcome of the curvature radiation mechanism. For a particular observer, when the curvature radius of the magnetic field line is larger, the electron bunches will spend more time sweeping across the line of sight, which means the observed pulse width will be longer. Besides, the characteristic frequency of curvature radiation is inversely proportional to the curvature radius. It then naturally leads to the inverse correlation between pulse width and central frequency. However, note that other radiation mechanisms, such as the coherent Cherenkov radiation may also lead to a similar behavior. According to Liu et al. (2023), the characteristic frequency of coherent Cherenkov radiation scales as , where is the distance from the magnetar to the emission site. Again, a larger will correspond to a longer pulse width since the curvature radius is higher. More detailed analysis is necessary to further discriminate between various mechanisms, which is beyond the scope of this study.
It is worth noting that some bursts may have multiple components, i.e. sub-bursts. However, until now, there has been no consensus on how to distinguish between bursts and sub-bursts. For example, Jahns et al. 2023 distinguished bursts and sub-bursts by eyes. Li et al. 2021 argued that bursts with a complex time-frequency structure should be regarded as sub-bursts when there is a “bridge” emission between pulses. Hewitt et al. 2022 proposed a more stringent criterion. They suggested that a pulse could be identified as a distinct burst only when its Gaussian-like profile does not smear into other components but instead begins and ends at a baseline comparable to the noise. Otherwise, the components should be classified as sub-bursts. Obviously, the criterion of identifying sub-pulses will affect the study involving the pulse widths, which should be paid more attention in future researches.
Direct observational measurements of scintillation have been attempted in some previous studies (Spitler et al. 2016; Michilli et al. 2018; Gajjar et al. 2018; Hessels et al. 2019). Using the uncertainty relation of for a homogeneous medium or for a Kolmogorov medium, where is the scintillation bandwidth, the scattering timescale can also be derived from the scintillation bandwidth correspondingly (Cordes & Rickett 1998). For example, Spitler et al. 2016 reported that the scintillation bandwidth is 50 kHz at 1.5 GHz, which will lead to a scattering timescale of ms at this frequency. Hessels et al. 2019 reported the scintillation bandwidth as 58.1 kHz at 1.65 GHz, leading to a corresponding scattering timescale of ms. Michilli et al. 2018 argued that the scintillation bandwidth is 5 MHz at 4.5 GHz, corresponding to a scattering timescale of ms at that frequency. Gajjar et al. 2018 found that the scintillation bandwidth ranges from 7 to 87 MHz at 4.5 - 8 GHz, which corresponds to a scattering timescale of ms in that frequency range. The scattering timescales derived in our study ( – ms in 1.3 – 6 GHz) are consistent with all those previous results.
Although the scattering broadening seems to be insignificant in the case of FRB 20121102A, it may still play an important role in other FRB sources. In fact, from Equation (2), we see that the scattering broadening scales as . So, it sensitively depends on many parameters, such as the observing frequency, the total dispersion measure, the turbulence scale, and the density fluctuations. Especially, when the central frequency decreases to 300 MHz, the scattering broadening will be enlarged by a factor of . Note that the instrumental broadening may also be significantly amplified at low frequencies (see Equation (7)). As a result, these broadening effects should still be paid attention to in other FRB sources as long as the pulse width is involved.
Turbulence is also a complex factor that could seriously affect the two ISM parameters in Equation (2), i.e. and . Additionally, note that the spectrum index of turbulence () may also have some effects on the scattering broadening. In practice, when an FRB is detected by a radio telescope, the dynamical spectrum (or the so-called “waterfall” diagram) is usually available, which may contain rich information on the turbulence of the ISM. A detailed analysis of the dynamical spectrum may help determine these parameters. On the other hand, we have mainly considered the situation where the diffractive length of the ISM is smaller than . In realistic cases, the diffractive length could also be larger than . It may lead to some differences in the scattering broadening, which need to be addressed in the future.
acknowledgements
We would like to thank the anonymous referees for helpful suggestions that led to an overall improvement of this study. Our work was supported by the National Natural Science Foundation of China (Grant Nos. 12041306, 12233002, 12273113), by the National SKA Program of China Nos. 2020SKA0120300 and 2022SKA0120102, by the National Key R&D Program of China (2021YFA0718500, 2023YFE0102300), by the CAS “Light of West China” Program (No. 2021-XBQNXZ-005), by Xinjiang Tianshan Talent Program, and by the CAS Project for Young Scientists in Basic Research (Grant No. YSBR-063). YFH also acknowledges the support from the Xinjiang Tianchi Program.
References
- Aggarwal et al. (2021) Aggarwal, K., Agarwal, D., Lewis, E. F., et al. 2021, ApJ, 922, 115, doi: 10.3847/1538-4357/ac2577
- Andersen et al. (2019) Andersen, B., Bandura, K., Bhardwaj, M., et al. 2019, The Astrophysical Journal Letters, 885, L24
- Barabanenkov et al. (1971) Barabanenkov, Y. N., Kravtsov, Y. A., Rytov, S. M., & Tamarskiĭ, V. I. 1971, Soviet Physics Uspekhi, 13, 551, doi: 10.1070/PU1971v013n05ABEH004213
- Beloborodov (2017) Beloborodov, A. M. 2017, ApJ, 843, L26, doi: 10.3847/2041-8213/aa78f3
- Beloborodov (2020) —. 2020, ApJ, 896, 142, doi: 10.3847/1538-4357/ab83eb
- Bridle & Schwab (1999) Bridle, A. H., & Schwab, F. R. 1999, in Astronomical Society of the Pacific Conference Series, Vol. 180, Synthesis Imaging in Radio Astronomy II, ed. G. B. Taylor, C. L. Carilli, & R. A. Perley, 371
- Caleb et al. (2019) Caleb, M., Stappers, B., Rajwade, K., & Flynn, C. 2019, Monthly Notices of the Royal Astronomical Society, 484, 5500
- Caleb et al. (2020) Caleb, M., Stappers, B. W., Abbott, T. D., et al. 2020, MNRAS, 496, 4565, doi: 10.1093/mnras/staa1791
- Chamma et al. (2023) Chamma, M. A., Rajabi, F., Kumar, A., & Houde, M. 2023, MNRAS, 522, 3036, doi: 10.1093/mnras/stad1108
- Chatterjee et al. (2017) Chatterjee, S., Law, C. J., Wharton, R. S., et al. 2017, Nature, 541, 58, doi: 10.1038/nature20797
- CHIME/FRB Collaboration et al. (2020) CHIME/FRB Collaboration, Andersen, B. C., Bandura, K. M., et al. 2020, Nature, 587, 54, doi: 10.1038/s41586-020-2863-y
- CHIME/FRB Collaboration et al. (2021) CHIME/FRB Collaboration, Amiri, M., Andersen, B. C., et al. 2021, ApJS, 257, 59, doi: 10.3847/1538-4365/ac33ab
- Chime/Frb Collaboration et al. (2022) Chime/Frb Collaboration, Andersen, B. C., Bandura, K., Bhardwaj, M., et al. 2022, Nature, 607, 256, doi: 10.1038/s41586-022-04841-8
- Connor et al. (2016) Connor, L., Sievers, J., & Pen, U.-L. 2016, MNRAS, 458, L19, doi: 10.1093/mnrasl/slv124
- Cordes & Chatterjee (2019) Cordes, J. M., & Chatterjee, S. 2019, ARA&A, 57, 417, doi: 10.1146/annurev-astro-091918-104501
- Cordes & Lazio (2002) Cordes, J. M., & Lazio, T. J. W. 2002, arXiv e-prints, astro, doi: 10.48550/arXiv.astro-ph/0207156
- Cordes & McLaughlin (2003) Cordes, J. M., & McLaughlin, M. A. 2003, ApJ, 596, 1142, doi: 10.1086/378231
- Cordes et al. (2022) Cordes, J. M., Ocker, S. K., & Chatterjee, S. 2022, The Astrophysical Journal, 931, 88, doi: 10.3847/1538-4357/ac6873
- Cordes & Rickett (1998) Cordes, J. M., & Rickett, B. J. 1998, ApJ, 507, 846, doi: 10.1086/306358
- Cordes & Wasserman (2016) Cordes, J. M., & Wasserman, I. 2016, MNRAS, 457, 232, doi: 10.1093/mnras/stv2948
- Cordes et al. (2006) Cordes, J. M., Freire, P. C. C., Lorimer, D. R., et al. 2006, ApJ, 637, 446, doi: 10.1086/498335
- Cruces et al. (2021) Cruces, M., Spitler, L. G., Scholz, P., et al. 2021, MNRAS, 500, 448, doi: 10.1093/mnras/staa3223
- Deng & Zhang (2014) Deng, W., & Zhang, B. 2014, ApJ, 783, L35, doi: 10.1088/2041-8205/783/2/L35
- Falcke & Rezzolla (2014) Falcke, H., & Rezzolla, L. 2014, A&A, 562, A137, doi: 10.1051/0004-6361/201321996
- Gajjar et al. (2018) Gajjar, V., Siemion, A. P. V., Price, D. C., et al. 2018, ApJ, 863, 2, doi: 10.3847/1538-4357/aad005
- Geng et al. (2021) Geng, J., Li, B., & Huang, Y. 2021, The Innovation, 2, 100152, doi: https://doi.org/10.1016/j.xinn.2021.100152
- Gourdji et al. (2019) Gourdji, K., Michilli, D., Spitler, L. G., et al. 2019, ApJ, 877, L19, doi: 10.3847/2041-8213/ab1f8a
- Hardy et al. (2017) Hardy, L. K., Dhillon, V. S., Spitler, L. G., et al. 2017, MNRAS, 472, 2800, doi: 10.1093/mnras/stx2153
- Hessels et al. (2019) Hessels, J. W. T., Spitler, L. G., Seymour, A. D., et al. 2019, ApJ, 876, L23, doi: 10.3847/2041-8213/ab13ae
- Hewitt et al. (2022) Hewitt, D. M., Snelders, M. P., Hessels, J. W. T., et al. 2022, MNRAS, 515, 3577, doi: 10.1093/mnras/stac1960
- Hilmarsson et al. (2021) Hilmarsson, G. H., Michilli, D., Spitler, L. G., et al. 2021, ApJ, 908, L10, doi: 10.3847/2041-8213/abdec0
- Hu & Huang (2023) Hu, C.-R., & Huang, Y.-F. 2023, ApJS, 269, 17, doi: 10.3847/1538-4365/acf566
- Jahns et al. (2023) Jahns, J. N., Spitler, L. G., Nimmo, K., et al. 2023, MNRAS, 519, 666, doi: 10.1093/mnras/stac3446
- Katz (2016) Katz, J. I. 2016, ApJ, 818, 19, doi: 10.3847/0004-637X/818/1/19
- Law et al. (2017) Law, C. J., Abruzzo, M. W., Bassa, C. G., et al. 2017, ApJ, 850, 76, doi: 10.3847/1538-4357/aa9700
- Lazarus et al. (2015) Lazarus, P., Brazier, A., Hessels, J. W. T., et al. 2015, ApJ, 812, 81, doi: 10.1088/0004-637X/812/1/81
- Li et al. (2021) Li, D., Wang, P., Zhu, W. W., et al. 2021, Nature, 598, 267, doi: 10.1038/s41586-021-03878-5
- Liu et al. (2023) Liu, Z.-N., Geng, J.-J., Yang, Y.-P., Wang, W.-Y., & Dai, Z.-G. 2023, ApJ, 958, 35, doi: 10.3847/1538-4357/acf9a3
- Lorimer et al. (2007) Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., & Crawford, F. 2007, Science, 318, 777, doi: 10.1126/science.1147532
- Lorimer & Kramer (2012) Lorimer, D. R., & Kramer, M. 2012, Handbook of Pulsar Astronomy
- Luan & Goldreich (2014) Luan, J., & Goldreich, P. 2014, ApJ, 785, L26, doi: 10.1088/2041-8205/785/2/L26
- MAGIC Collaboration et al. (2018) MAGIC Collaboration, Acciari, V. A., Ansoldi, S., et al. 2018, MNRAS, 481, 2479, doi: 10.1093/mnras/sty2422
- Marcote et al. (2017) Marcote, B., Paragi, Z., Hessels, J. W. T., et al. 2017, ApJ, 834, L8, doi: 10.3847/2041-8213/834/2/L8
- Margalit et al. (2019) Margalit, B., Berger, E., & Metzger, B. D. 2019, ApJ, 886, 110, doi: 10.3847/1538-4357/ab4c31
- Michilli et al. (2018) Michilli, D., Seymour, A., Hessels, J. W. T., et al. 2018, Nature, 553, 182, doi: 10.1038/nature25149
- Oostrum et al. (2020) Oostrum, L. C., Maan, Y., van Leeuwen, J., et al. 2020, A&A, 635, A61, doi: 10.1051/0004-6361/201937422
- Petroff et al. (2019) Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2019, A&A Rev., 27, 4, doi: 10.1007/s00159-019-0116-6
- Petroff et al. (2022) —. 2022, A&A Rev., 30, 2, doi: 10.1007/s00159-022-00139-w
- Petroff et al. (2016) Petroff, E., Barr, E. D., Jameson, A., et al. 2016, PASA, 33, e045, doi: 10.1017/pasa.2016.35
- Plavin et al. (2022) Plavin, A., Paragi, Z., Marcote, B., et al. 2022, MNRAS, 511, 6033, doi: 10.1093/mnras/stac500
- Pleunis et al. (2021) Pleunis, Z., Good, D. C., Kaspi, V. M., et al. 2021, ApJ, 923, 1, doi: 10.3847/1538-4357/ac33ac
- Pol et al. (2019) Pol, N., Lam, M. T., McLaughlin, M. A., Lazio, T. J. W., & Cordes, J. M. 2019, ApJ, 886, 135, doi: 10.3847/1538-4357/ab4c2f
- Prochaska & Zheng (2019) Prochaska, J. X., & Zheng, Y. 2019, MNRAS, 485, 648, doi: 10.1093/mnras/stz261
- Rajwade et al. (2020) Rajwade, K. M., Mickaliger, M. B., Stappers, B. W., et al. 2020, MNRAS, 495, 3551, doi: 10.1093/mnras/staa1237
- Ravi & Lasky (2014) Ravi, V., & Lasky, P. D. 2014, MNRAS, 441, 2433, doi: 10.1093/mnras/stu720
- Rickett (1990) Rickett, B. J. 1990, ARA&A, 28, 561, doi: 10.1146/annurev.aa.28.090190.003021
- Rioja et al. (2018) Rioja, M. J., Dodson, R., & Franzen, T. M. O. 2018, MNRAS, 478, 2337, doi: 10.1093/mnras/sty1195
- Scholz et al. (2016) Scholz, P., Spitler, L. G., Hessels, J. W. T., et al. 2016, ApJ, 833, 177, doi: 10.3847/1538-4357/833/2/177
- Scholz et al. (2017) Scholz, P., Bogdanov, S., Hessels, J. W. T., et al. 2017, ApJ, 846, 80, doi: 10.3847/1538-4357/aa8456
- Snelders et al. (2023) Snelders, M. P., Nimmo, K., Hessels, J. W. T., et al. 2023, Nature Astronomy, 7, 1486, doi: 10.1038/s41550-023-02101-x
- Spitler et al. (2014) Spitler, L. G., Cordes, J. M., Hessels, J. W. T., et al. 2014, ApJ, 790, 101, doi: 10.1088/0004-637X/790/2/101
- Spitler et al. (2016) Spitler, L. G., Scholz, P., Hessels, J. W. T., et al. 2016, Nature, 531, 202, doi: 10.1038/nature17168
- Tendulkar et al. (2017) Tendulkar, S. P., Bassa, C. G., Cordes, J. M., et al. 2017, ApJ, 834, L7, doi: 10.3847/2041-8213/834/2/L7
- Thornton et al. (2013) Thornton, D., Stappers, B., Bailes, M., et al. 2013, Science, 341, 53, doi: 10.1126/science.1236789
- Totani (2013) Totani, T. 2013, PASJ, 65, L12, doi: 10.1093/pasj/65.5.L12
- Wang et al. (2022) Wang, F. Y., Zhang, G. Q., Dai, Z. G., & Cheng, K. S. 2022, Nature Communications, 13, 4382, doi: 10.1038/s41467-022-31923-y
- Xu et al. (2023) Xu, J., Feng, Y., Li, D., et al. 2023, Universe, 9, 330, doi: 10.3390/universe9070330
- Xu & Zhang (2016) Xu, S., & Zhang, B. 2016, ApJ, 832, 199, doi: 10.3847/0004-637X/832/2/199
- Yao et al. (2017) Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29, doi: 10.3847/1538-4357/835/1/29
- Zhang (2018) Zhang, B. 2018, ApJ, 854, L21, doi: 10.3847/2041-8213/aaadba
- Zhang (2022) —. 2022, ApJ, 925, 53, doi: 10.3847/1538-4357/ac3979
- Zhang (2023) —. 2023, Reviews of Modern Physics, 95, 035005, doi: 10.1103/RevModPhys.95.035005
- Zhang et al. (2018) Zhang, Y. G., Gajjar, V., Foster, G., et al. 2018, ApJ, 866, 149, doi: 10.3847/1538-4357/aadf31
| Telescope | Central Frequency/GHz | /ms | Burst Counts | Ref. | |
| FAST | 1.25 | 0.122 | 0.0983 | 1652 | (1) |
| Arecibo | 1.4 | 0.34/1.56 | 0.655/0.0102 | 11/1360 | (2),(3),(4),(5),(6),(7),(8) |
| 4.5 | 1.56 | 0.0102 | 29 | (9),(10) | |
| GBT | 2 | 1.56 | 0.0102 | 19 | (5),(6),(11) |
| 6 | 0.183/0.366/2.930 | 0.0102/0.35/0.000341 | 2/93/19 | (9),(12),(13) | |
| Effelsberg | 1.36 | 0.586 | 0.0546 | 49 | (14),(15) |
| 6 | 0.977 | 0.131 | 1 | (10) | |
| VLA | 3 | 0.25/4 | 1.024/5 | 2/9 | (10),(16) |
| WSRT | 1.4 | 0.781/0.195 | 0.00128/0.0819 | 29/1 | (17) |
| MeerKAT | 1.28 | 0.209 | 0.00479 | 11 | (18) |
-
•
Ref. (1) Li et al. 2021; (2) Spitler et al. 2016; (3) Hewitt et al. 2022; (4) Jahns et al. 2023; (5) Hessels et al. 2019; (6) Scholz et al. 2017; (7) Gourdji et al. 2019; (8) MAGIC Collaboration et al. 2018; (9) Michilli et al. 2018; (10) Hilmarsson et al. 2021; (11) Scholz et al. 2016; (12) Zhang et al. 2018; (13) Snelders et al. 2023; (14) Cruces et al. 2021; (15) Hardy et al. 2017; (16) Law et al. 2017; (17) Oostrum et al. 2020; (18) Caleb et al. 2020.
| Central Frequency/GHz | /ms | /ms | /ms | /ms |
|---|---|---|---|---|
| All | 3.47 | 1.74 | 4.07 | 1.74 |
| 1.25 | 3.55 | 1.58 | 4.27 | 1.58 |
| 1.36 | 2.51 | 1.58 | 3.24 | 1.51 |
| 1.4 | 3.63 | 1.78 | 4.37 | 1.78 |
| 4.5 | 0.50 | 1.82 | 0.60 | 1.82 |
| 6 | 0.89 | 2.00 | 1.32 | 1.55 |