Introducing 4D Geometric Shell Shaping for Mitigating Nonlinear Interference Noise
Abstract
Four dimensional geometric shell shaping (4D-GSS) is introduced as an approach for closing the nonlinearity-caused shaping gap. This format is designed at the spectral efficiency of 8 bit/4D-sym and is compared against polarization-multiplexed 16QAM (PM-16QAM) and probabilistically shaped PM-16QAM (PS-PM-16QAM) in a 400ZR-compatible transmission setup with high amount of nonlinearities. Reach increase and nonlinearity tolerance are evaluated in terms of achievable information rates and post-FEC bit-error rate. Numerical simulations for a single-span, single-channel show that 4D-GSS achieves increased nonlinear tolerance and reach increase against PM-16QAM and PS-PM-16QAM when optimized for bit-metric decoding (). In terms of , gains are small with a reach increase of 1.7% compared to PM-16QAM. When optimizing for mutual information, a larger reach increase of 3% is achieved compared to PM-16QAM. Moreover, the introduced GSS scheme provides a scalable framework for designing well-structured 4D modulation formats with low complexity.
Index Terms:
Constellation shaping, geometric shaping, four-dimensional constellations, probabilistic shaping, nonlinear fiber channel.I Introduction
In recent years, constellation shaping techniques such as probabilistic shaping (PS) [1, 2, 3, 4, 5, 6] and geometric shaping (GS) [7, 8, 9, 10, 11] have been widely investigated to cope with the exponentially increasing capacity demand of optical fiber communications. These techniques can be used to alter the properties of the transmitted constellation to increase the achievable information rates (AIRs) of a communication system. PS imposes a nonuniform probability distribution on the constellation points of a square constellation while GS changes the location of the constellation points and allows for nonequidistant spacing of the points. Combinations of PS and GS are also increasingly investigated in recent literature [12, 13]. This combination is called hybrid shaping. It has been shown that for the additive white Gaussian noise (AWGN) channel and a given (finite) constellation cardinality, PS outperforms GS [9, Fig. 2], [14, Figs. 2, 3] and also allows for very fine rate-adaptivity [1, Fig. 1]. This comes however at the cost of requiring additional steps in the digital signal processing (DSP) chain. For example, if the probabilistic amplitude shaping (PAS) architecture [1] is used, a shaper and a deshaper are required. GS has the advantage of not requiring extra DSP, but it does require changes to the mapper and demapper. It is well known that demapper complexity increases when increasing demapping dimensionality [15], however, it has been shown that careful design can achieve a good balance between performance and complexity for multidimensional soft demappers (see e.g., [16]). In [15], one method of reducing the complexity in the demapper is by exploiting quadrant symmetry in 2D constellations. This results in a reduction of the number of required Euclidean distance calculations by around a factor of four with minimal performance loss. This reduction factor is expected to scale exponentially with the number of dimensions.
Designing constellations via GS lifts restrictions previously in place from equally-spaced square quadrature amplitude modulation (QAM). Conventional shaped constellation design is done by targeting the AWGN channel, for which a Gaussian-like constellation shape is optimal [17, Chs. 8, 9]. The resulting increase in performance is called linear shaping gain. PS on square (2D) QAM achieves this by targeting the same Maxwell-Boltzmann (MB) distribution on every dimension, while GS places constellation points in the 2D I-Q plane allowing nonuniform distance between the constellation points. In the context of optical communications, AWGN-optimized constellations have been applied in nonlinear optical fiber communications [2, 9, 18, 19] by using polarization multiplexing. While this method of designing constellations is relatively simple and provides considerable performance improvements [3], the nonlinear nature of optical fibers results in an increasing mismatch between the assumed channel model and targeted optical link for increasing launch powers [20].
To further improve performance in fiber-optical systems, research has moved towards designing constellations with nonlinear tolerance in mind [20, 21]. It has been shown that multidimensional constellation design is able to provide tolerance against nonlinear fiber effects by reducing nonlinear interference noise (NLIN), effectively closing the nonlinearity-caused shaping gap, in addition to providing linear shaping gains [22, 10]. One explanation is that the set of multidimensional constellations that can be expressed as the Cartesian product of a lower-dimensional constellation with itself is a subset of all possible multidimensional constellations. Thus, optimizing the multidimensional constellation, instead of a lower-dimensional constellation, results in larger potential gains [23, Fig. 3(c)], [24, Fig. 1], [25].
Multiple forms of multidimensional modulation exist in the literature. Extending the constellation design to utilize both polarizations jointly in a single time instance is well known (e.g., [10]). This is called 4D modulation throughout this paper. Instead of employing polarization multiplexing, 4D modulation focuses on the design of constellations that are not a Cartesian product of lower-dimensionality constellations. Other methods include extending the number of dimensions over multiple time-slots [26, 27] or multiple (sub)-carriers [28]. While the above-mentioned methods are based on GS, short-blocklength PS, which can be considered a form of multidimensional modulation over multiple time-slots, also provides tolerance to nonlinearities [4, 29].
The challenge in designing constellations with more than two dimensions is the exponential increase in degrees of freedom (DOFs) that is generally associated with increasing the number of dimensions while maintaining equal spectral efficiency (SE) per real dimension. While simple unconstrained optimizations provide the best theoretical possible performance, they are time consuming, might not lead to a global optimum, and generally provide unstructured results. From a practical point of view, well-structured constellations are always preferred since they allow for more efficient demapping strategies (e.g., by utilizing separability and symmetry of the constellations) [30, 31].
Designing an optimal constellation generally requires some form of iterative optimization for evaluating performance after each iteration. A channel model of the target communication link is thus required. The most straightforward method is using the computationally expensive but very accurate split-step Fourier method (SSFM) method. It is however desirable to reduce complexity of the optimization procedure to a more manageable level by using a simplified model or a simplified optimization objective. For simplified models, closed-form models which approximate the NLIN are available, like the EGN model [32], or its recently introduced extension to dual-polarization [33]. Model-aided optimization is used, for example, in [20] and [34], where the EGN model, or derivations thereof, are used to simplify the evaluation of the optical channel during the optimization stage.
Currently, 4D geometrically shaped constellations optimized under an AWGN channel assumption providing reach increase for optical communications exist up to 10 bits/4D-sym [21, Fig. 2]. Similar constellations designed under an optical channel assumption also exist up to 10 bits/4D-sym [21, Fig. 3] and 12 bits/4D-sym [35], which employ machine learning to cope with the optimization complexity.
Another way of simplifying the design is reducing the DOFs within the optimization problem. This reduction in DOFs is generally achieved by imposing constraints which exploit existing regularities (e.g., symmetries), as used in [36, 11]. However, these works target the AWGN channel for constellation design, which potentially impacts performance negatively when applied to a nonlinear fiber communication system.
In this paper, a novel framework is introduced for geometrically optimizing 4D constellations for the nonlinear fiber channel by using shell constraints together with symmetry constraints. This framework is applied to both symbol-metric decoding (SMD) and bit-metric decoding (BMD) systems [3]. This approach, denoted as 4D geometric shell shaping (GSS), provides well-structured constellations, reduces optimization complexity, and leads to negligible performance degradation, all while providing increased nonlinear tolerance associated with multidimensional GS optimization. 4D-GSS is studied for a SE of 8 bits/4D-sym such that the proposed format can find application to the 400ZR system [37] (or the 800ZR system under preparation), which uses PM-16QAM for transmission. To the best of our knowledge, 4D geometrically-shaped constellations with the same SE as PM-16QAM specifically designed for nonlinear fiber transmission and using BMD do not exist in the literature. This is most likely because PM-16QAM with the binary reflected Gray code (BRGC) is very competitive already in terms of AIRs with BMD. Nevertheless, our optimized format demonstrate increased nonlinear tolerance, and in this challenging scenario, small reach increases against PM-16QAM and probabilistically shaped PM-16QAM are also reported.
II 4D Geometric Shell Shaping
II-A Notation Convention
Calligraphic letters represent sets. Blackboard bold letters denote matrices in which are row vectors denoting the row. Conditional probability density functions (PDFs) are denoted by , where and denote random (4D) vectors and and denote their realizations. Probability mass functions (PMFs) are denoted by , expectations are denoted by and denotes binary negation. The squared Euclidean norm of a matrix is denoted by , where . The indicator function is denoted by , which is 1 when its argument is true and 0 otherwise, and and denote the set of all real and natural numbers, respectively, with denoting the set of all positive real numbers.
Throughout this paper, we consider a constellation with real dimensions denoted by the real-valued matrix , where is the constellation cardinality, is a vector denoting the -th constellation point of with for . The 2D coordinates of the x- and y-polarization are represented by and , respectively, and the rows of are labeled using a fixed binary labeling. In other words, the -th symbol is associated with a unique binary label .
II-B Achievable Information Rates
A number of metrics exist for evaluating the performance of a fiber optical system. For systems based on SMD, the mutual information (MI) is often used. Using Monte-Carlo simulations, the MI can be approximated as
| (1) |
where is the probability of the symbol , is the number of transmitted symbols and is the auxiliary channel, which is an approximation of the actual channel law from which the samples are taken from. We use mismatched decoding [38] in this paper for which in (1) is considered to be the AWGN channel, i.e.,
| (2) |
where is the total noise variance of the 4D AWGN channel. The expression in (1) is a modified version of [39, Eq. (30)] that takes probabilities into account (for PS).
For bit-interleaved coded modulation (BICM) systems with BMD and probabilistic shaping, an AIR is the [40, eq. (1)],[3, eq. (6)]. When bit levels are independent, which is the case for conventional uniform signaling, the BMD rate reduces to the well known generalized MI [41, Thm. 4.11, Coroll. 4.12],[42].
We approximate the BMD rate via Monte-Carlo simulations as [3, Eq. (8)]
| (3) | ||||
| (4) |
where is the random variable representing the transmitted bit at bit position , is the bit-wise MI between and output , are the transmitted coded bits and are the log-likelihood ratios (LLRs) defined as
| (5) |
where is the set of constellation point indices with at bit position .
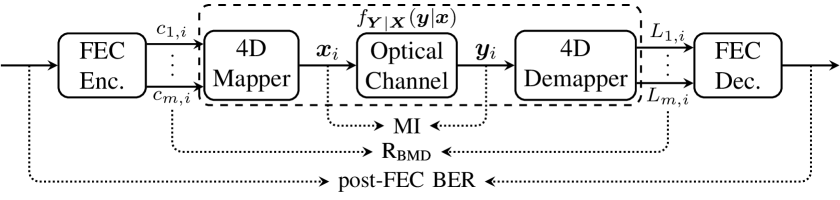
To evaluate the performance predictions made by the above-mentioned AIRs, post-forward error correction (FEC) bit error rates (BERs) will also be calculated. The system model is shown in Fig. 1 indicating the performance metrics which are considered in this paper.
II-C Optimizing Geometric Shaping in 4D
The constellation is typically designed to maximize a certain performance metric [9]. In this paper, is the chosen metric and the optimal constellation is denoted by . The resulting optimization problem is defined as
| (6) |
where is given by 4 and 5, and is the set containing all real-valued matrices satisfying a variance (power) constraint, i.e.,
| (7) |
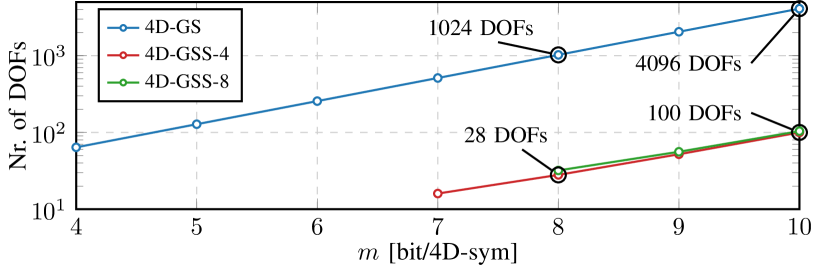
The optimization problem in 6 has four DOFs per constellation point, one for each dimension, resulting in DOFs. We call this the unconstrained optimization and denote it by 4D-GS. The DOFs are directly related to the dimensionality and the constellation cardinality . From this we see that for increasing constellation sizes, the DOFs grow exponentially and the optimization becomes challenging.
In this paper, instead of solving the unconstrained optimization in (6), we define a set of constraints which reduce the DOFs, while minimizing the potential loss in performance. The optimization under these constraints is defined as
| (8) |
where the optimization space is constrained to . As we will show below, the imposed constraints make the optimization problem in (8) to only have DOFs instead of DOFs for the chosen system .
In this paper we propose to impose three constraints on the constellation, which we call (i) “uniform -shell division”, (ii) “X-Y symmetry”, and (iii) “orthant111An orthant is a generalization in -dimensional Euclidean space of what a quadrant is in the 2D plane. symmetry”. We call the optimization under these constraints 4D-GSS. In what follows, we explain these three constraints and how they lead to DOFs for . As we will show in Sec. IV-B, the loss in performance by introducing these three constraints is minimal.
II-D GSS Constraints
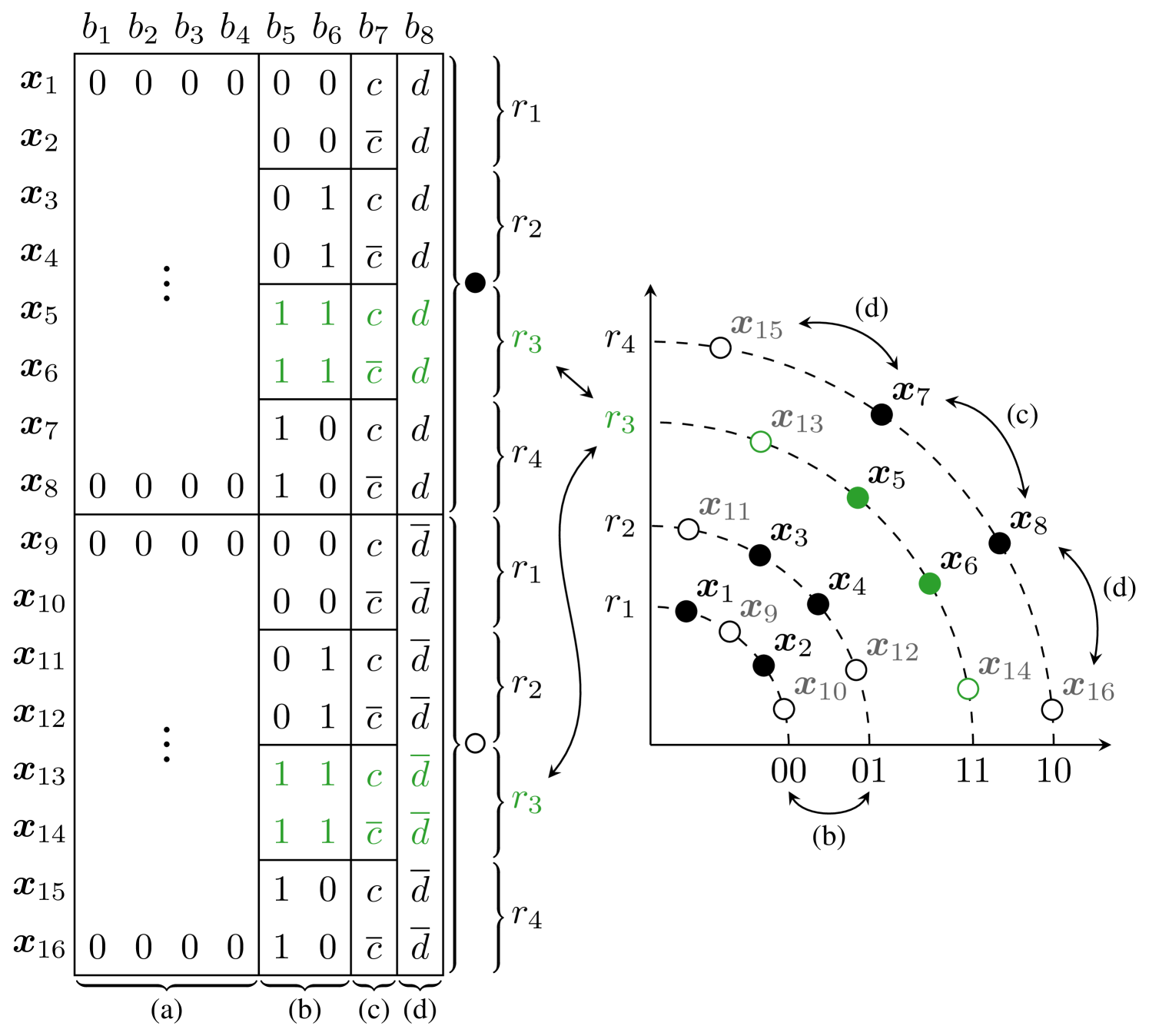
Each of the three constraints mentioned in Sec. II-C is associated with a part of the binary labeling, which is considered to be fixed. Fig. 2 provides an example of how the bit allocation is predefined under the considered constraints in a 4D constellation with bits and shells. The left side of Fig. 2 shows 16 constellation points belonging to a single orthant with their corresponding binary labels. The binary labels are grouped into sets of bits referred to by (a) through (d). The four bits in (a) define an orthant. In Fig. 2 only the first orthant is shown and thus, all have the same binary label (all zeros) for (a). The two bits in (b) determine the shell, with each shell having the same amount of points ( in this case). The bits in (c) select between two points on a shell, and (d) selects between two X-Y symmetric points.
The three GSS constraints described above reduce the number of 4D constellation points to be optimized from to only (filled circles in Fig. 2) with a reduction in DOFs from to . In what follows, we formally describe the set together with two symmetry operations that make up these three GSS constraints.
Definition 1 (Uniformly divided t-shell constraint)
| (9a) | ||||
| (9b) | ||||
| (9c) | ||||
where
| (10) |
and is the radius of the 4D shell out of a total of 4D shells.
The shell constraint forces constellation points to be equally divided on the concentric 4D shells in the all positive space (first orthant). This uniformly divided part of this constraint is provided by 9b. The upper limit for is given by (see (10)), which is equivalent to having a dedicated shell for each constellation point. In the case of , this constraint turns into a constant modulus constraint, effectively creating a generalization of the format proposed in [10]. By forcing each point to be on top of a certain shell, we take away one additional DOF per constellation point, such that DOFs per constellation point remain. However, extra DOFs are added due to the number of the shells. This results in DOFs. The advantage of having an integer power of two () shells is that out of bits can be used to select the shell. In Fig. 2, . This offers the possibility of achieving rate-adaptivity by adding PS on top of GSS using the PAS architecture [1], which is called hybrid shaping. In this case, only the bits which select the shell are shaped. The remaining uniform bits select the specific constellation points on a shell.
In the remainder of this section we will assume an identical setup to the one in the example in Fig. 2. As a result and the constellation points are labeled by .
Operation 1 (X-Y symmetry)
An X-Y symmetry operation applied to 8 points with results in 16 points and binary labels
| (11) |
X-Y symmetry mirrors the points in the set over its two polarizations. A single bit added to the labeling end is used to distinguish between the two X-Y symmetric points. The X-Y symmetry also ensures identical average transmit power over the two polarizations. In Fig. 2, this mirroring causes for example to become and the extra bit added to the binary labels is and , resp. After applying the X-Y symmetry operation to , we must apply the orthant symmetry operation, defined as follows.
Operation 2 (Orthant symmetry)
The orthant symmetry operation applied to 16 points with gives
| (12) |
for , and where is the mirroring matrix of the -th orthant
| (13) |
where is the binary representation of , i.e., with .
The mirroring matrices transform each of the 16 points in to all orthants with corresponding binary labels , resulting in a total of 256 constellation points and label combinations, given by
| (14) |
The first orthant in Example 1 only considers 4D symbols with all their components to be positive. Orthant symmetry is achieved by mirroring the constellation points (after applying the X-Y symmetry operation) with respect to the origin along the axes of the dimensions and by changing the bits (see 12), where each of these bits is associated with the sign of one real dimension. An advantage of assigning bits in this manner is that it ensures the orthants themselves are Gray-labeled (adjacent orthants differ only in one bit), which provides higher AIRs compared to other labeling strategies when used in BICM systems [43]. In the context of optical communications, the mirroring procedure was first used in [11, Sec. II-B].
constellations with .
| Name | DOFs | 4D shells |
|---|---|---|
| PM-16QAM | - | 9 |
| PM-2D-16-GS | 64 | 136 |
| 4D-256-GS | 1024 | 256 |
| 4D-256-GSS-4 | 28 | 4 |
| 4D-256-GSS-8 | 32 | 8 |
Example 1 (Application to 400ZR)
The described constraints are applied to 4D constellations targeting the same SE as uniform PM-16QAM, therefore . The number of shells is chosen to be . First, the uniformly divided -shell constraint is applied to the constellation points within the first orthant. This results in the set with DOFs. Since , two bits are used to index the shell. Applying the X-Y symmetry operation to increases the number of constellation points in the first orthant by a factor 2 to . When applying the orthant symmetry operation, four bits are assigned to select the orthant with groups of two bits assigned to the quadrants in the X and Y polarization respectively, which together define the orthant. This increases the number of constellation points by a factor , which results in the desired total amount of 4D constellation points.
By using the three constraints described above, the DOFs are reduced from an unconstrained to . Fig. 3 compares the DOFs when using 4D-GSS compared to the unconstrained case of 4D-GS for increasing constellation sizes. Table I shows the DOFs and the number of 4D shells for a number of different constellation types at a fixed SE of . This table also shows the amount of discrete 4D energy levels. One of the properties of GSS constellations is the ability to directly and efficiently control the energy of symbols in 4D (due to indexing a power of two shells), which is much more difficult in conventional QAM and GS constellations.
III System Setup and Optimization

III-A Link specification
For designing constellations with high nonlinear tolerance in mind, a suitable transmission scenario needs to be chosen which is expected to have high NLIN. For this reason an unamplified 400ZR link is chosen [37], for which the transmitted constellation is PM-16QAM, which matches the desired cardinality of the considered 4D-GSS constellation.
The considered system transmits a dual-polarized, single channel waveform of symbols with a fixed random seed over a single span of standard single-mode fiber (SSMF). This setup uses the Manakov equation as the fiber model [44, Sec. IV] and is simulated via the split-step Fourier method (SSFM) with 1000 steps per span using uniform step size and fiber parameters dB/km, ps2/km and (Wkm-1). Increasing the number of steps per span above 1000 has been verified to provide identical results for the highest launch powers and distances considered in this paper. The symbol rate is matched to the 400ZR specification at 59.84 Gbaud. At the transmitter, the generated symbol sequences are upsampled to 4 samples per symbol and pulse shaped using a root-raised-cosine filter with a roll-off of 1%. At the receiver, the waveforms are ideally compensated for chromatic dispersion, matched filtered, downsampled to 1 sample per symbol and corrected for phase rotation by utilizing cross-correlation between the input and output symbol sequences. Demapping is done in 4D using 5 to calculate the LLRs.
Since an unamplified link is used, noise sources due to transmitter and receiver impairments are emulated instead of simulating optical erbium-doped fiber amplifier (EDFA) amplification. For this, worst-case design parameters from the 400ZR specification will be used as a guideline.
III-B Transceiver impairments
At the transmitter side, the 400ZR specification requires the in-band optical signal-to-noise ratio (OSNR) to have a minimum value of 34 dB/0.1nm. At the receiver side, the concatenated FEC scheme in the 400ZR standard is specified to operate error-free (post-FEC BER = ) when a pre-FEC BER of or lower is achieved. The receiver sensitivity requires least dBm of power to be present at the input of the receiver. These previous two conditions combined with the minimum of 34 dB OSNR at the transmitter guarantee error-free operation.
In simulations, the transmitter is emulated by adding AWGN to the transmitted waveform such that the OSNR value is equal to the in-band OSNR limit. For the receiver it is possible to calculate the necessary AWGN addition using [45, Eq. (18)]
| (15) |
where is the targeted BER, is the Q-function and is the accompanying SNR per bit under a Gray-coded -QAM assumption in an AWGN channel. For 16QAM and a BER of , 15 provides an of 7.53 dB, which translates to a signal-to-noise ratio (SNR) of 13.5 dB. Assuming that an input power of dBm is present at the receiver in a back-to-back scenario, the amount of noise power added in the receiver is equal to dBm. This is added as AWGN after simulating the optical fiber.
III-C Forward Error Correction
400ZR uses a concatenated FEC scheme as defined in [37, Sec. 10] consisting of an outer staircase code (SCC) with hard-decision (HD) decoding of rate , and an inner Hamming code with soft-decision (SD) decoding of rate , resulting in a total overhead of . The SCC in 400ZR is defined to be taken from [46, Annex A], which describes a SCC with blocks of size and a Bose-Chaudhuri-Hocquenghem (BCH) code as the component code. The FEC code is a double-extended Hamming code using a parity-check matrix as described in [37, Sec. 10.5].
Instead of implementing the full concatenated FEC as described above, in this paper we only implemented the Hamming code and a SD decoder based on a Chase-I decoder [47]. A post-FEC BER after the Hamming decoder of is targeted, which is the required pre-FEC BER for the SCC to achieve a BER of at the output. The scrambling and interleaving steps are approximated by using a bit-wise fixed random permutation after FEC encoding and the inverse operation before FEC decoding. The full system diagram is shown in Fig. 4.
III-D Optimization
In 17, the optimization problem for determining was defined. If the constraints from Sec. II are applied, the optimization only needs to be performed for the 28 resulting DOFs. To enforce the shell constraints, each point out of the 8 points in is now represented in spherical coordinates , where and . The optimization problem can now be defined as
| (16) |
where the parameters are constrained such that the corresponding points are in .
Since there are no existing constellations which strictly adhere to the chosen constraints, selecting an initialization for the optimization procedure is not straightforward. It was determined on a trial-and-error basis that there were no clear differences in resulting performance after optimization between randomly initialized constellations and constellations which were initialized with a distinct structure. For that reason it was chosen to initialize all parameters at the halfway point between the upper and lower bounds, which are shown in 16.
Optimization over the system in Fig. 4 is performed using a patternsearch optimizer [48], which is a derivative-free multidimensional optimization algorithm. Patternsearch automatically finds the optimal way to spread out the constellation. During optimization, the number of transmitted symbols is lowered to using a different random seed compared to the results generation. The number of steps per span for the SSFM is kept at 1000. To enhance stability during the optimization procedure, fixed random seeds are used for the sequence generation and AWGN noise additions.
IV Results

IV-A Baselines
Conventional PM-16QAM, as used in the 400ZR standard, is considered as a baseline. Next to that, PS is applied on top of PM-16QAM by shaping each real dimension with an ideal amplitude shaper, where amplitudes are randomly drawn from a predefined distribution, which is identical over all dimensions. The distribution is optimized for each pair of launch power and transmission distance. This optimization is performed using the same patternsearch optimizer as Sec. III-D. Since PM-16QAM only has two amplitude values per dimension, the optimization effectively only has a single DOF. The proposed 4D-GSS-4 constellations are also optimized and evaluated for each pair of launch power and distance. Lastly, a 4D sphere packed constellation is also considered, specifically the 256 point Welti constellation (w4-256) [49]. Sphere packed constellations are optimal for the AWGN channel for a given SE and will provide insight into the maximum expected performance in the linear region later in this paper. For evaluation, w4-256 uses the optimized binary labeling from [50].
It is well known that symbol-level interleaving, as described in one of the DSP steps in the 400ZR standard [37, Sec. 11.1], has a negative impact on the performance of PS constellations implemented with a finite blocklength amplitude shaper [51]. This is due to symbol-level interleaving breaking time-domain structures of probabilistically shaped symbol sequences and can be mitigated by employing extra pre- and post-interleaving steps in the DSP chain [52]. In this paper, the coded bits of all considered constellations are independent. PM-16QAM-PS uses an ideal amplitude shaper, which does not implement an actual shaping algorithm, resulting in independent bits. 4D-GSS and the two other baselines all use uniform signaling and are thus also not affected by such dependencies. Since all considered constellations are not affected by symbol-level interleaving, only a bit-wise permutation as discussed in Sec. III-C was implemented.
IV-B optimized constellations
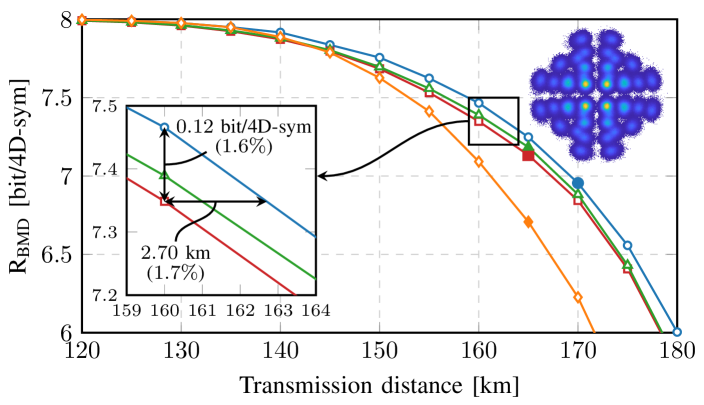
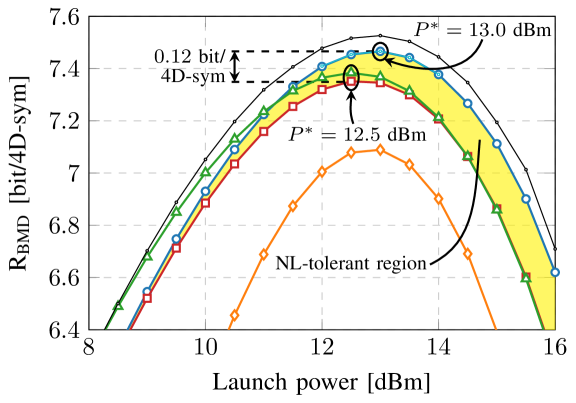
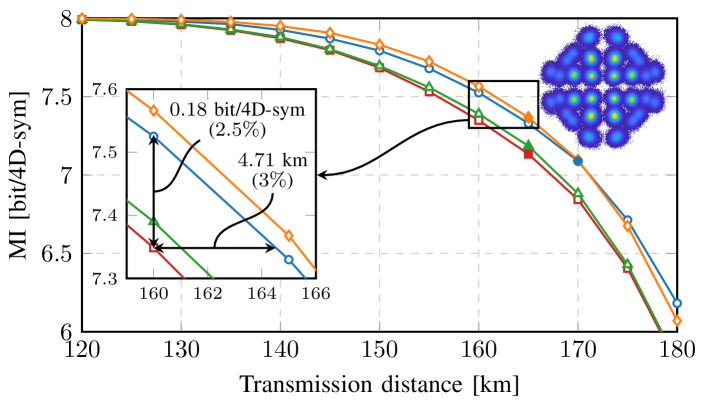
Fig. 5(a) shows results for a distance sweep between 120 and 180 km. In the inset of Fig. 5(a), 4D-GSS-4 achieves gain in and gain in distance compared to PM-16QAM around 160km. These gains represent the increase in data rate and distance as a result of the shaping gain. Since in this specific scenario, the 400ZR link is loss-limited, results are shown at optimal launch power until the distance is too large to satisfy the received power requirement of at least dBm. The point after which this occurs is indicated by solid markers. Beyond these markers, the constellations are pushed to launch powers above the optimal value to satisfy the received power requirement. In Fig. 5(a), it is shown that the distance for which 4D-GSS-4 can operate at optimal launch power is approximately km larger than the other considered constellations. This increase in maximum optimal launch power is also reflected in Fig. 5(b) where 4D-GSS-4 has dB higher optimal launch power () compared to the baselines and hence, the highest nonlinear tolerance among the considered schemes. The region where NL tolerance is observed is indicated in yellow. In the linear domain, 4D-GSS-4 has similar performance to PM-16QAM and loses in performance compared to PM-16QAM-PS. Even though an optimized binary labeling is used for the w4-256 constellation, since it is not designed to maximize , it performs poorly.
To evaluate the performance losses induced by the GSS constraints, optimized 4D constellations which have only orthant symmetry as the constraint (denoted with 4D-OS) are evaluated around the optimal launch power. It is shown in Fig. 5(b) that removing the shell constraints and X-Y constraint from 4D-GSS-4 has a negligible impact on performance. Furthermore, it has been shown in [11, Fig. 6] that lifting the orthant symmetry constraint has a marginal impact on performance. All this indicates that the proposed symmetry constraints as used in 4D-GSS-4 have very little impact on total performance, but do reduce the optimization complexity significantly. Fig. 5(b) also includes MI results for 4D-GSS-4 (denoted by 4D-GSS-4 MI). This indicates the theoretical upper limit for the where it is clear that quite a large gap still exists between the and the MI for 4D-GSS-4.
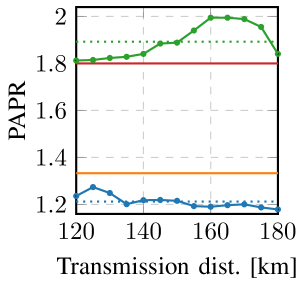
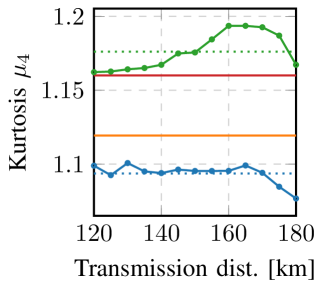
Possible explanations of the increased nonlinear tolerance of 4D-GSS-4 can be observed from Fig. 6, which shows the peak-to-average power rating (PAPR) (in linear units) and the fourth order standardized moment (i.e. the kurtosis222The kurtosis of a distribution depends on the dimensionality [53, Sec. III], where maximum kurtosis is achieved for a Gaussian distribution. Maximum kurtosis values for 2D and 4D constellations are and respectively. In this paper, only 4D kurtosis values are shown. It is also common practice to compare the kurtosis of an -D distribution to that of an -D univariate normal distribution. This is typically done by defining ‘excess kurtosis’, which is the kurtosis of the distribution minus the kurtosis of the Gaussian distribution, then comparing it to zero.) of the considered constellations. PAPR is a rough indicator for evaluating nonlinear tolerance [11, Sec. II-D] and also influences the amount of distortion resulting from limited equipment dynamic range and linearity, especially in orthogonal frequency division multiplexing transmission [54, Sec. V-A]. Kurtosis is considered to be more directly related to nonlinearities, where channel input distributions with high kurtosis lead to higher NLIN power [3, Sec. III-B]. Fig. 6(a) shows that PM-16QAM has a PAPR of 1.8, while 4D-GSS-4 constellations have a PAPR of 1.25 on average over the considered distances, which is a reduction of compared to PM-16QAM. Similarly, Fig. 6(b) shows a decrease in the kurtosis from 1.16 for PM-16QAM to 1.10 for 4D-GSS-4, which is a reduction of .

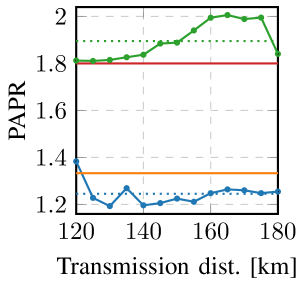
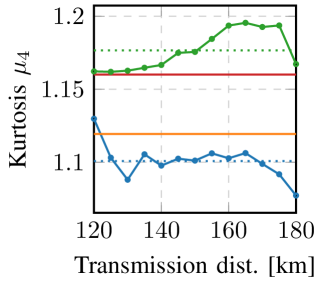
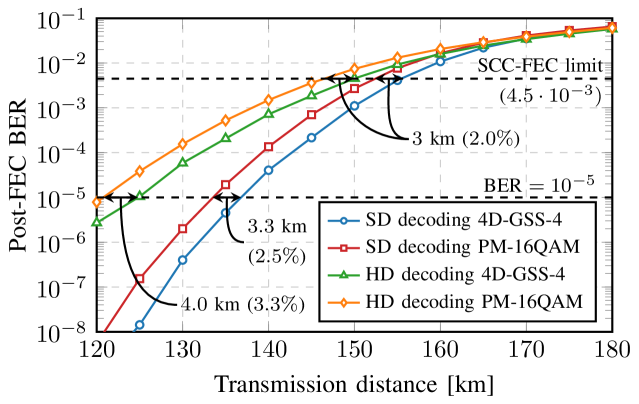
Fig. 7 shows the post-FEC BER of 4D-GSS-4 compared to PM-16QAM when the inner Hamming code is SD-decoded as described in Sec. III-C, together with HD decoding of the same code. The outer SCC has a FEC limit of , which is used as the minimum required BER after the Hamming code for error-free operation. A gain of in transmission distance between 4D-GSS-4 and PM-16QAM is achieved at the SCC-FEC limit, which is very close to the observed gain in . The HD-decoded Hamming code shows similar gains between the two constellation types but cannot satisfy the SCC-FEC limit over similar distances. When only the Hamming codes are considered without the outer SCC, gains increase to in-between and depending on the specific distance and code, as indicated by the BER line.
IV-C MI optimized constellations


It was observed in Fig. 5(b) that the for the optimized 4D-GSS-4 constellations was consistently lower than the MI by about bits/4D-sym. This could indicate an issue with the binary labeling since PM-16QAM(-PS) did not show such a gap. To find the potential upper performance limit of 4D-GSS-4, the optimization procedure was repeated using the MI as the performance metric using 1 for evaluating the MI. This results in the following optimization problem
| (17) |
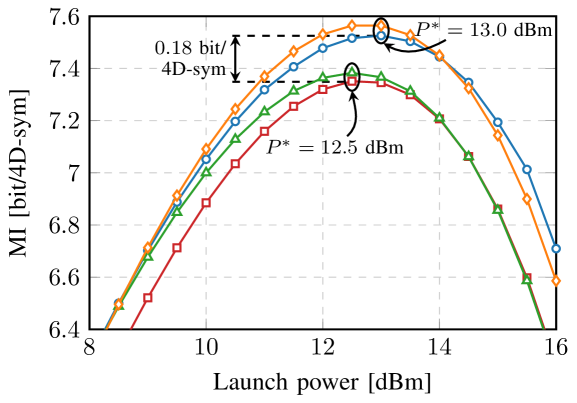
Fig. 8(a) shows MI results for a distance sweep between 120 and 180 km. The inset of Fig. 8(a) shows gains of in distance and in MI for 4D-GSS-4 vs. PM-16QAM and is slightly outperformed by w4-256. Again, Fig. 8(b) shows that 4D-GSS-4 has the largest optimal launch power. Moreover, due to the rapidly-vanishing MI of w4-256, 4D-GSS-4 outperforms w4-256 at very high powers (). However, for lower powers (), w4-256 achieves larger MI than 4D-GSS-4. The observed gap in performance for 4D-GSS-4 when comparing MI to indicates a possible issue where the proposed GSS framework does not provide a structure suitable for a good binary labeling.
Results in Fig. 9 show similar trends to Fig. 6, with the main difference being that the MI optimized 4D-GSS-4 constellations have even lower average PAPR and kurtosis. The difference in PAPR against PM-16QAM increases from to , whilst the difference in kurtosis increases from to . Against w4-256, 4D-GSS-4 shows a reduction in PAPR of and a reduction in kurtosis of , which could contribute to 4D-GSS-4 gaining performance in terms of MI over w4-256 for launch powers larger than dBm.
IV-D Bitwise MI
To investigate possible causes of the binary labeling penalty for 4D-GSS-4, we look at the bit-wise MI . Fig. 10 compares the bit-wise MI of 4D-GSS-4, PM-16QAM and w4-256 at the optimal launch powers. The individual bits are denoted by for . For PM-16QAM, the bits are reordered such that the bits which determine the signs are the first four bits (same as 4D-GSS-4). This does not effect the performance since PM-16QAM is a Cartesian product of four independent pulse amplitude modulation (PAM)-4 constellations. As a result, this also implies symmetry across all four dimensions and thus, PM-16QAM also has orthant symmetry.
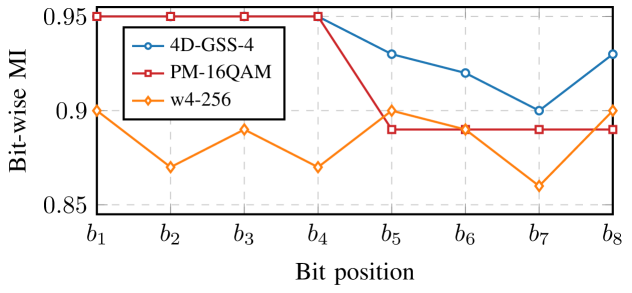
In the binary labels, the bits through determine the orthant for both PM-16QAM and 4D-GSS-4. The bits through determine the amplitude of each of the PAM-4 signals for PM-16QAM. For 4D-GSS-4, the bits and select the shell, bit selects between 2 points on a shell, and bit selects between X-Y symmetric points.
In terms of bit-wise MI, through perform identically for both PM-16QAM and 4D-GSS-4, which is expected due to both constellations employing orthant symmetry. Bits trough have larger bit-wise MI for 4D-GSS-4 compared to PM-16QAM, where bit has the lowest value. This suggests that the proposed structure combined with the chosen constellation cardinality does not allow for a good labeling of . Lastly, as expected, w4-256 has much worse performance in general compared to the other two constellations since the structure of this constellation is not optimized for allowing a good binary labeling at all.
V Conclusion
A novel framework is proposed for generating families of well-structured 4D geometrically-shaped constellations which are more nonlinearity-tolerant than conventional PM-16QAM. Numerical simulations show that the newly proposed 4D-GSS-4 constellations outperform both PM-16QAM and PS-PM-16QAM in a 400ZR-compatible transmission setup when optimized for . It was shown that the imposed constraints lead to negligible performance degradation while considerably reducing the optimization space and resulting in well-structured constellations. It was also found that the chosen constraints combined with the chosen SE do not allow for very good binary labeling, which is indicated by optimizing 4D-GSS-4 for MI, which resulted in a reach increase of .
Investigating better combinations of constellation cardinality ( bits/4D-sym) and GSS (e.g., modifying shell constraints) is left for further investigation. Another area of possible research is to increase the dimensionality across channel time slots or number of wavelength channels (e.g., 8D-GSS).
References
- [1] G. Bocherer, F. Steiner, and P. Schulte, “Bandwidth efficient and rate-matched low-density parity-check coded modulation,” IEEE Trans. on Commun., vol. 63, pp. 4651–4665, Dec. 2015.
- [2] F. Buchali, F. Steiner, G. Böcherer, L. Schmalen, P. Schulte, and W. Idler, “Rate adaptation and reach increase by probabilistically shaped 64-QAM: An experimental demonstration,” J. Lightw. Technol., vol. 34, pp. 1599–1609, Apr. 2016.
- [3] T. Fehenberger, A. Alvarado, G. Bocherer, and N. Hanik, “On probabilistic shaping of quadrature amplitude modulation for the nonlinear fiber channel,” J. Lightw. Technol., vol. 34, pp. 5063–5073, Nov. 2016.
- [4] A. Amari, S. Goossens, Y. C. Gültekin, O. Vassilieva, I. Kim, T. Ikeuchi, C. M. Okonkwo, F. M. Willems, and A. Alvarado, “Introducing enumerative sphere shaping for optical communication systems with short blocklengths,” J. Lightw. Technol., vol. 37, pp. 5926–5936, Dec. 2019.
- [5] S. Goossens, S. V. D. Heide, M. V. D. Hout, A. Amari, Y. C. Gultekin, O. Vassilieva, I. Kim, T. Ikeuchi, F. M. Willems, A. Alvarado, and C. Okonkwo, “First experimental demonstration of probabilistic enumerative sphere shaping in optical fiber communications,” Proc. OptoElectron. Commun. Conf. Int. Conf. Photon. Switch. Comput., Jul. 2019.
- [6] T. Fehenberger, D. S. Millar, T. Koike-Akino, K. Kojima, K. Parsons, and H. Griesser, “Huffman-coded sphere shaping and distribution matching algorithms via lookup tables,” J. Lightw. Technol., vol. 38, pp. 2825–2833, May 2020.
- [7] Z. Qu and I. B. Djordjevic, “Geometrically shaped 16QAM outperforming probabilistically shaped 16QAM,” Proc. Eur. Conf. Opt. Commun., Sep. 2017.
- [8] S. Zhang, F. Yaman, E. Mateo, T. Inoue, K. Nakamura, and Y. Inada, “Design and performance evaluation of a GMI-optimized 32QAM,” Proc. Eur. Conf. Opt. Commun., Sep. 2017.
- [9] B. Chen, C. Okonkwo, D. Lavery, and A. Alvarado, “Geometrically-shaped 64-point constellations via achievable information rates,” Proc. Int. Conf. on Transparent Opt. Netw., Sep. 2018.
- [10] B. Chen, C. Okonkwo, H. Hafermann, and A. Alvarado, “Polarization-ring-switching for nonlinearity-tolerant geometrically shaped four-dimensional formats maximizing generalized mutual information,” J. Lightw. Technol., vol. 37, pp. 3579–3591, Jul. 2019.
- [11] B. Chen, A. Alvarado, S. V. D. Heide, M. V. D. Hout, H. Hafermann, and C. Okonkwo, “Analysis and experimental demonstration of orthant-symmetric four-dimensional 7 bit/4D-sym modulation for optical fiber communication,” J. Lightw. Technol., vol. 39, pp. 2737–2753, May 2021.
- [12] J. X. Cai, H. G. Batshon, M. V. Mazurczyk, O. V. Sinkin, D. Wang, M. Paskov, W. W. Patterson, C. R. Davidson, P. C. Corbett, G. M. Wolter, T. E. Hammon, M. A. Bolshtyansky, D. G. Foursa, and A. N. Pilipetskii, “70.46 Tb/s over 7,600 km and 71.65 Tb/s over 6,970 km transmission in C+L band using coded modulation with hybrid constellation shaping and nonlinearity compensation,” J. Lightw. Technol., vol. 36, pp. 114–121, Jan. 2018.
- [13] J. Ding, B. Sang, Y. Wang, M. Kong, F. Wang, B. Zhu, L. Zhao, W. Zhou, and J. Yu, “High spectral efficiency WDM transmission based on hybrid probabilistically and geometrically shaped 256QAM,” J. Lightw. Technol., vol. 39, pp. 5494–5501, Sep. 2021.
- [14] F. Steiner and G. Böcherer, “Comparison of geometric and probabilistic shaping with application to ATSC 3.0,” Proc. Int. ITG Conf. Syst. Commun. Coding, 2017.
- [15] M. Fuentes, D. Vargas, and D. Gomez-Barquero, “Low-complexity demapping algorithm for two-dimensional non-uniform constellations,” IEEE Trans. Broadcast., vol. 62, pp. 375–383, Jun. 2016.
- [16] T. Yoshida, K. Matsuda, K. Kojima, H. Miura, K. Dohi, M. Pajovic, T. Koike-Akino, D. S. Millar, K. Parsons, and T. Sugihara, “Hardware-efficient precise and flexible soft-demapping for multi-dimensional complementary APSK signals,” Proc. Eur. Conf. Opt. Commun., Sep. 2016.
- [17] T. M. Cover and J. A. Thomas, Elements of Information Theory, 2005.
- [18] Z. Qu and I. B. Djordjevic, “On the probabilistic shaping and geometric shaping in optical communication systems,” IEEE Access, vol. 7, pp. 21 454–21 464, Feb. 2019.
- [19] J. Cho and P. J. Winzer, “Probabilistic constellation shaping for optical fiber communications,” J. Lightw. Technol., vol. 37, pp. 1590–1607, Mar. 2019.
- [20] J. Renner, T. Fehenberger, M. P. Yankov, F. D. Ros, S. Forchhammer, G. Böcherer, and N. Hanik, “Experimental comparison of probabilistic shaping methods for unrepeated fiber transmission,” J. Lightw. Technol., vol. 35, pp. 4871–4879, Nov. 2017.
- [21] B. Chen, G. Liga, Y. Lei, W. Ling, Z. Huan, X. Xue, and A. Alvarado, “Shaped four-dimensional modulation formats for optical fiber communication systems,” Proc. Opt. Fiber Commun. Conf., Mar. 2022.
- [22] K. Kojima, T. Yoshida, T. Koike-Akino, D. S. Millar, K. Parsons, M. Pajovic, and V. Arlunno, “Nonlinearity-tolerant four-dimensional 2A8PSK family for 5-7 bits/symbol spectral efficiency,” J. Lightw. Technol., vol. 35, pp. 1383–1391, Apr. 2017.
- [23] R. Dar, M. Feder, A. Mecozzi, and M. Shtaif, “On shaping gain in the nonlinear fiber-optic channel,” Proc. IEEE Int. Symp. on Inf. Theory, pp. 2794–2798, 2014.
- [24] B. Chen, Y. Lei, G. Liga, Z. Liang, W. Ling, X. Xue, and A. Alvarado, “Geometrically-shaped multi-dimensional modulation formats in coherent optical transmission systems,” J. Lightw. Technol., 2022, (Preprint).
- [25] S. Goossens, Y. C. Gültekin, O. Vassilieva, I. Kim, P. Palacharla, C. Okonkwo, and A. Alvarado, “4D geometric shell shaping with applications to 400ZR,” Proc. Adv. Photon. Congress, Jul. 2022.
- [26] A. Borowiec, A. D. Shiner, D. Charlton, J. Gaudette, K. Roberts, M. O’Sullivan, M. Reimer, P. Mehta, and S. O. Gharan, “Demonstration of an 8-dimensional modulation format with reduced inter-channel nonlinearities in a polarization multiplexed coherent system,” Opt. Express, vol. 22, pp. 20 366–20 374, Aug. 2014.
- [27] B. Chen, C. Okonkwo, H. Hafermann, and A. Alvarado, “Eight-dimensional polarization-ring-switching modulation formats,” IEEE Photon. Technol. Lett., vol. 31, pp. 1717–1720, Nov. 2019.
- [28] K. Kojima, K. Parsons, T. Koike-Akino, and D. S. Millar, “Mapping options of 4D constant modulus format for multi-subcarrier modulation,” Proc. Conf. on Las. and Elect.-Opt, May 2018.
- [29] P. Skvortcov, I. Phillips, W. Forysiak, T. Koike-Akino, K. Kojima, K. Parsons, and D. S. Millar, “Huffman-coded sphere shaping for extended-reach single-span links,” IEEE J. Sel. Topics Quantum Electron., vol. 27, May 2021.
- [30] M. Nakamura, F. Hamaoka, A. Matsushita, H. Yamazaki, M. Nagatani, A. Hirano, and Y. Miyamoto, “Low-complexity iterative soft-demapper for multidimensional modulation based on bitwise log likelihood ratio and its demonstration in high baud-rate transmission,” J. Lightw. Technol., vol. 36, pp. 476–484, Jan. 2018.
- [31] H. Wang, M. Li, and C. Wang, “A universal low-complexity demapping algorithm for non-uniform constellations,” Appl. Sci., vol. 10, p. 8572, Nov. 2020.
- [32] A. Carena, G. Bosco, V. Curri, Y. Jiang, P. Poggiolini, and F. Forghieri, “EGN model of non-linear fiber propagation,” Opt. Express, vol. 22, pp. 16 335–16 362, Jun. 2014.
- [33] G. Liga, B. Chen, and A. Alvarado, “Model-aided geometrical shaping of dual-polarization 4D formats in the nonlinear fiber channel,” Proc. Opt. Fiber Commun. Conf., Mar. 2022.
- [34] E. Sillekens, D. Semrau, D. Lavery, P. Bayvel, and R. I. Killey, “Experimental demonstration of geometrically-shaped constellations tailored to the nonlinear fibre channel,” Proc. Eur. Conf. Opt. Commun., Nov. 2018.
- [35] V. Oliari, B. Karanov, S. Goossens, G. Liga, O. Vassilieva, I. Kim, P. Palacharla, C. Okonkwo, and A. Alvarado, “Hybrid geometric and probabilistic shaping; is it really necessary?” Proc. Adv. Photon. Congress, Jul. 2022.
- [36] Z. Qu, S. Zhang, and I. B. Djordjevic, “Universal hybrid probabilistic-geometric shaping based on two-dimensional distribution matchers,” Proc. Opt. Fiber Commun. Conf., 2018.
- [37] Optical Internetworking Forum, Implementation Agreement 400ZR, Impl. Agrmnt. OIF-400ZR-01.0, Mar. 2020. [Online]. Available: https://www.oiforum.com/wp-content/uploads/OIF-400ZR-01.0_reduced2.pdf
- [38] A. Lapidoth and S. S. Shitz, “On information rates for mismatched decoders,” IEEE Trans. Inf. Theory, vol. 40, pp. 1953–1967, 1994.
- [39] A. Alvarado, T. Fehenberger, B. Chen, and F. M. Willems, “Achievable information rates for fiber optics: Applications and computations,” J. Lightw. Technol., vol. 36, pp. 424–439, Jan. 2018.
- [40] G. Bocherer, “Probabilistic signal shaping for bit-metric decoding,” Proc. IEEE Int. Symp. on Inf. Theory, pp. 431–435, Jun. 2014.
- [41] L. Szczecinski and A. Alvarado, Bit-Interleaved Coded Modulation: Fundamentals, Analysis and Design. Wiley-IEEE Press, Feb. 2015.
- [42] A. G. i Fàbregas and A. Martinez, “Bit-interleaved coded modulation with shaping,” Proc. IEEE Inf. Theory Workshop, Aug. 2010.
- [43] G. Caire, G. Taricco, and E. Biglieri, “Bit-interleaved coded modulation,” IEEE Trans. Inf. Theory, vol. 44, pp. 927–946, 1998.
- [44] P. K. Wai and C. R. Menyuk, “Polarization mode dispersion, decorrelation, and diffusion in optical fibers with randomly varying birefringence,” J. Lightw. Technol., vol. 14, pp. 148–157, Feb. 1996.
- [45] J. Lu, “M-PSK and M-QAM BER computation using signal-space concepts,” IEEE Trans. on Commun., vol. 47, pp. 181–184, 1999.
- [46] OTU4 long-reach interface, Rec. ITU-T G.709.2, Jul. 2018.
- [47] D. Chase, “A class of algorithms for decoding block codes with channel measurement information,” IEEE Trans. Inf. Theory, vol. 18, pp. 170–182, 1972.
- [48] C. Audet and J. E. Dennis, “Analysis of generalized pattern searches,” SIAM J. Optim., vol. 13, pp. 889–903, Jul. 2002.
- [49] G. R. Welti, J. S. Lee, and J. S. Lee, “Digital transmission with coherent four-dimensional modulation,” IEEE Trans. Inf. Theory, vol. 20, pp. 497–502, Jul. 1974.
- [50] B. Chen, “Binary labeling for 2D and 4D constellations,” GitHub.com. Accessed: Nov. 22, 2022. [Online]. Available: https://github.com/TUe-ICTLab/Binary-Labeling-for-2D-and-4D-constellations
- [51] T. Fehenberger, D. S. Millar, T. Koike-Akino, K. Kojima, K. Parsons, and H. Griesser, “Analysis of nonlinear fiber interactions for finite-length constant-composition sequences,” J. Lightw. Technol., vol. 38, pp. 457–465, Jan. 2020.
- [52] W.-R. Peng, A. Li, Q. Guo, Y. Cui, and Y. Bai, “Transmission method of improved fiber nonlinearity tolerance for probabilistic amplitude shaping,” Opt. Express, vol. 28, pp. 29 430–29 441, Sep. 2020.
- [53] A. P. D. Rosiers and P. H. Siegel, “Effect of varying source kurtosis on the multimodulus algorithm,” IEEE International Conference on Communications, vol. 2, pp. 1300–1304, 1999.
- [54] J. Armstrong, “OFDM for optical communications,” J. Lightw. Technol., vol. 27, pp. 189–204, Feb. 2009.