Introduction to the Fifth-rung Density Functional Approximations: Concept, Formulation, and Applications
Abstract
The widespread use of (generalized) Kohn-Sham density functional theory (KS-DFT) lies in the fact that hierarchical sets of approximations of the exchange-correlation (XC) energy functional can be designed, offering versatile choices to satisfy different levels of accuracy needs. The XC functionals standing on the fifth (top) rung of the Jacob’s ladder incorporate the information of unoccupied Kohn-Sham orbitals, and by doing so can describe seamlessly non-local electron correlations that the lower-rung functionals fail to capture. The doubly hybrid approximations (DHAs) and random phase approximation (RPA) based methods are two representative classes of fifth-rung functionals that have been under active development over the past two decades. In this review, we recapitulate the basic concepts of DHAs and RPA, derive their underlying theoretical formulation from the perspective of adiabatic-connection fluctuation-dissipation theory, and describe the implementation algorithms based on the resolution-of-identity technique within an atomic-orbital basis-set framework. Illustrating examples of practical applications of DHAs and RPA are presented, highlighting the usefulness of these functionals in resolving challenging problems in computational materials science. The most recent advances in the realms of these two types of functionals are briefly discussed.
1 Introduction
It is now an undisputed fact that the most widely used method for the first-principles electronic-structure calculations is Kohn-Sham (KS) density functional theory (DFT) [1, 2]. Although the exact exchange-correlation (XC) energy functional within the KS-DFT framework is unknown, there exist many practical approximations – density functional approximations (DFAs). Due to their excellent trade-off between accuracy and efficiency, these DFAs have been applied with great success in chemistry, physics, and materials science. However, in order to meet the increasing demand on the simulation accuracy and efficiency, novel functionals with better accuracy at affordable cost are still under active development.
According to the Jacob’s Ladder of DFT proposed by Perdew and Schmidt, the DFAs can be categorized into five rungs, depending on the complexity of fundamental ingredients used in the functional construction [3]. The first rung of Jacob’s Ladder is the local density approximation (LDA) [2], which depends on the electron density only. On the second rung sit generalized gradient approximations (GGAs), which require the density and density gradient in its functional formula; one of the most widely used DFAs in computational materials science is the non-empirical GGA proposed by Perdew, Burke, and Ernzerhof (PBE) [4]. On the third rung of this hierarchy, the so-called meta-GGAs further incorporate a more complex ingredient, namely the kinetic energy density, which renders the meta-GGA not an explicit functional of density. The importance of kinetic energy density for the density functional development was first recognized by Becke in early 1983 [5]. The most popular meta-GGAs are M06-L [6] and SCAN [7], primarily used in quantum chemistry and computational materials science, respectively. On the fourth-rung of this hierarchy, the “exact exchange” components, or more precisely the ingredients of occupied KS orbitals, are further included, resulting in the so-called hybrid (meta)-GGAs. At present, the most popular DFAs in quantum chemistry are exclusively the fourth-rung functionals, including B3LYP [8], M06 [9] and B97XD [10], to name a few. On the other hand, in computational materials science, the screened hybrid functional HSE [11] is most widely used.
Nevertheless, no matter how intricate they are, DFAs on the first four rungs described above are constructed with information stemming only from occupied orbitals. The explicit use of unoccupied orbitals is considered to be the key feature of the DFAs that stand on the fifth rung – the highest rung of Jacob’s Ladder in DFT. The fifth-rung DFAs hold the promise to approach the simulation accuracy required in the era of precision chemistry. Doubly hybrid approximation (DHA) and random phase approximation (RPA) based functionals are two representative examples of fifth-rung DFAs that have been under active development over the last two decades. In this review, we will focus on the basic concept and the current status of these two types of functionals.
1.1 Doubly Hybrid Approximations
DHAs are now the leading actor in quantum chemistry. The name of “doubly hybrid” was originally used by Truhlar and co-workers for their empirical multi-coefficient methods of MC3BB and MC3MPW [12], where the DFT total energy is linearly mixed with the total energy of the simplest wavefunction-based correlation method, i.e. the second-order Møller-Plesset perturbation theory (MP2). Later, Grimme introduced another kind of doubly hybrid strategy to connect MP2 and meta-GGAs [13]. B2PLYP is the first DHA of this family [13]. Popular B2PLYP-type DHAs include DSD-BLYP [14], B97X-2 [15], and so forth [16].
In fact, DHAs can be derived in the generalized KS-DFT framework and viewed as an empirical extension of the Görling-Levy second-order perturbation theory (GL2) [17] along the adiabatic-connection (AC) approach [18]. It was first proposed by Zhang and co-workers in 2009 [19], which emphasizes on the use of accurate density and orbitals of KS non-interacting systems for evaluating the total energy of DHAs [20, 21]. XYG3 is the first DHA of this family [19]. Popular XYG3-type DHAs includes XYGJ-OS [22], xDH-PBE0 [23], B97M(2) [24], xrevDSD-PBEB86-D4 [25], and so forth.
The rapid growth of computation capacity has been boosting the development of comprehensive databases for main-group chemistry with accurate benchmark reference. Two well-established databases are the MGCDB84 set of the Head-Gordon group with about 5000 test cases [24] and the GMTKN55 set of the Grimme group with 1505 test cases [26], respectively. A serial of recent benchmark works using these databases repeatedly demonstrated that the DHAs present significant and consistent improvement over the conventional DFAs on the first four rungs, and are competent for various kinds of chemical interactions of the main-group chemistry [25, 20]. The XYG3-type DHAs stand out in this round of benchmark according to benchmark results obtained independently by different research groups. The top-class performers all belong to the XYG3 family of DHAs, including the XYG7 of the Xu group, the B97M(2) of the Head-Gordon group, and the xrevSDS-PBEB86-D4 of the Martin group. Their performance on main-group chemistry has been comparable to, or even better than the high-level wavefunction-based methods[20].
At present, the mainstream DHAs aforementioned use the second-order perturbation energy (PT2) to capture the electron correlation effect that involves the unoccupied orbitals. Recently, Santra and co-workers observed further notable improvement by introducing the third-order perturbation energy (PT3) in the context of XYG3-type doubly hybrid framework [27]. However, the computational cost increases significantly. Meanwhile, it is well-documented that the perturbation algorithms at any finite order (PTn) completely fail for describing the strong correlation effect, which is closely related to the so-called static correlation in quantum chemistry. Therefore, the DHAs including the PT2 and/or PT3 correlation contributions cannot be used to study the bond dissociation problem and the complex systems involving transition metals. A number of studies have begun to address this limitation of current DFAs by introducing some kinds of renormalization algorithms to the standard PT2 with little extra computational costs. As will be introduced in the next section, the random-phase approximation (RPA) is another successful fifth-rung DFA in materials science. The RPA-type correlation can be viewed as a renormalization of the direct term of PT2. RPA and its variants have also been taken as the candidate to replace the PT2 in the DHAs [28, 29, 30, 31, 32].
1.2 Random Phase Approximation
RPA is a fundamental concept that plays a central role in many-body physics. The concept was developed by Bohm and Pines [33, 34] in the early 1950’s in an endeavor to describe the cohesive properties of the so-called jellium – interacting electrons moving in a background of uniform positive charge. Using a Hamiltonian formulation of interacting many-electron system, Bohm and Pines were able to decouple the collective motion of electrons – the plasma oscillations – from their individual motions, a procedure named as RPA. It was soon recognized by Hubbard [35] that the original RPA formulation is equivalent to the infinite summation of ring diagrams from the viewpoint of diagrammatic many-body perturbation theory [36]. Since then, the RPA concept has gone beyond the realm of condensed matter physics and significantly influenced all branches of physics.
Although the RPA concept can be applied to any interacting many-particle systems (for its applications in nuclear physics, see e.g., Ref. [37]), the next key step towards applying RPA to real materials was the incorporation of RPA into the KS-DFT framework in the 1970’s [38, 39, 18]. This formulation turned RPA into a first-principles electronic-structure method, suitable for computing the ground-state energy of real materials. Within the KS-DFT framework, RPA can be viewed as a fifth-rung approximation to the exchange-correlation energy functional, according to Jacob’s ladder of DFT [3]. However, the application of RPA to realistic systems was impeded by its high computational cost and the lack of efficient algorithms at the time. The first application of RPA to small molecules only appeared in early 2000’s, carried out by Furche [40] and by Fuchs and Gonze [41]. Since then, RPA has been applied to a variety of systems including atoms [42, 43], molecules [40, 41, 44, 45, 46, 47, 48], solids [49, 50, 51, 52, 53, 54, 55, 56], surfaces [57, 58], interfaces [59, 60], layered materials [61], and defects [62, 63]. The consensus arising from these studies is that RPA is capable of describing the delicate energy differences in complex chemical environments [57, 58, 54, 56, 64, 65, 66], the correct asymptotic behavior of van der Waals (vdW) complexes [67, 68, 69] and layered materials [61, 70], and the correct dissociation limit of closed-shell molecules [40, 41]. Evidences show that RPA can provide unprecedented accuracy compared to lower-rung DFAs at tractable computational cost. As such, RPA is expected to play an increasingly more important role in computational materials science, with the rapid development of more efficient algorithms and the availability of more powerful computing resources.
In a review paper [71] published in 2012, Ren et al. discussed the history of the RPA concept, its formulation as a first-principles method , and its applications in quantum chemistry and computational materials science up to that time. These points were nicely summarized by David Pines in his recent review paper titled as “Emergent behavior in strongly correlated electron systems" [72]. In particular, Pines noted that,
Sixty-plus years later, the RPA continues to play a significant role in nuclear physics [66], bosonic field-theory [67], the quarkgluon plasma [68], many-fermion solvable models [69], and especially in computational chemistry and materials science. A recent review by Ren et al [70], to which the interested reader is referred, describes the impact of the RPA in the theoretical chemistry and materials science community, cites some thirty articles that indicate the renewed and widespread interest in the RPA during the period 2001-2011, discusses how it enables one to derive the interaction between spatially separated closed shell electron systems, and, shows, in some detail, how the RPA enables one to go beyond density functional theory in computing ground state energies.
This paragraph highlights the far-reaching impact of RPA in a variety of fields, in particular in computational chemistry and materials science. It is worthwhile to mention that several other, complementary RPA review papers [73, 74] also appeared around that time, where the theoretical foundation and applications of RPA are discussed from different perspective. More recent account of RPA of review character can be found in Ref. [75].
In this review, we will first give an account of the theoretical foundation of DHAs and RPA, highlighting their unique role in DFT. Computational schemes beyond PT2-based DHAs and RPA will be also briefly discussed in this review. This is followed by a description of the key algorithm of implementing DHAs and RPA using the resolution-of-identity (RI) technique, within an atomic-orbital basis-set framework. We then present some prototypical applications illustrating the usefulness of these fifth-rung functionals particularly in computational materials science. Note that, the general performance of DHAs have been extensively discussed for finite molecules, but only a limited number of their applications on solids were reported, which are introduced in this review. Most recent efforts devoted to further developing the theoretical and computational aspects of DHAs and RPA-based functionals as well as extending their capabilities will be briefly mentioned and commented, before we conclude the review.
2 Theoretical foundation of Fifth-rung DFAs
An interacting -electron system is described by the following Hamiltonian,
| (1) |
where , , and are the Kinetic energy operator, the external potential operator, and the electron-electron Coulomb interaction operators, respectively. The Hartree atomic unit () is used throughout this review. Note that the operators and are universal for any -electron systems, and a system is completely specified by the external potential,
| (2) |
with and being respectively the nuclear charges and positions of the atoms in the system. The Hamiltonian in Eq. 1 cannot be solved, even numerically, for more than a few electrons.
In KS-DFT [1, 2], the ground-state total energy of the interacting -electron system is recast to an (implicit) functional of the electron density and is customarily separated into four terms:
| (3) |
where
| (4) |
is the kinetic energy of the KS independent-particle system,
| (5) |
is the external potential energy due to the nuclei, and
| (6) |
is the classical Hartree energy. The XC energy is often separated into the exchange and correlation parts
| (7) |
Among the four terms in Eq. 3, only and are explicit functionals of . The noninteracting kinetic energy is treated exactly in KS-DFT in terms of the single-particle KS orbitals , which themselves are a functional of . All the many-body complexity is encoded in the unknown, but relatively small term . Moreover, we often define the exact exchange functional as the Hartree-Fock exchange, utilizing again the single-particle KS orbitals
| (8) |
The notation of is equivalent to , representing the two-electron Coulomb integrals,
| (9) |
For completeness, a relevant notation can be defined, which will be used to express the second-order perturbation theory (PT2) in the following section:
| (10) |
Apparently, is also an implicit but not explicit functional of . Here and below, we adopt the convention that refer to occupied KS orbitals, to virtual (unoccupied) orbitals, and to general ones. Furthermore, and are the spin indices. Throughout this review, only the spin collinear case is considered in the presented formulae.
In order to determine the single-particle KS orbitals, , the so-call KS non-interacting system is introduced with the corresponding Hamiltonian written as
| (11) |
where the effective KS potential is defined as
| (12) |
Here the external potential , the Hartree potential
| (13) |
and the XC potential,
| (14) |
if being exact, ensure that the ground-state wave function of this KS non-interacting system, i.e. a Slater determinant composed by the aforementioned occupied single-particle KS orbitals , reproduces the density of the true physical system , with being the interacting ground state. It is worth to note that the ground-state total energy of the KS non-interacting system
| (15) |
is not the same as that of the interacting one (Eq. 3). In Eq. (15), ’s are KS orbital energies and
| (16) |
is the expectation value of the XC potential (Eq. 14).
A central task of the DFT community is to develop accurate and tractable approximations to . The success of KS-DFT lies in the fact that usefully accurate approximations can be found, under which DFT calculations can be done at affordable cost. Widely used approximations to include the aforementioned LDA [2], GGAs [76, 77, 4], meta-GGAs [78, 6, 7, 79], and hybrid functional approximations [8, 11, 6, 80, 81]. As discussed above, these approximations belong to the first four rungs of the Jacob’s ladder [3]. Despite their enormous success, these existing approximate functionals suffer from many-electron self-interaction errors [82], or delocalization errors [83], due to which the localized electronic states tend to delocalize over the system, leading to several severe consequences [83]. Furthermore, the non-local correlation effects between widely separated subsystems are not captured within these approximations by constructions. These intrinsic deficiencies limit the possible accuracy that can be achieved in practical calculations. Quantitative, and sometimes qualitative failures have been documented in a number of situations, among which the most prominent are van der Waals (vdW) bonded systems [84], materials with strong correlations [85], certain surface adsorption problems [86], and chemical reaction barrier heights [87]. To deal with long-range vdW interactions, e.g., lower-rung functionals often have to be complemented by semi-empirical vdW correction terms in various forms [13, 88, 89, 90, 91].
Fifth-rung DFAs, including DHAs and RPA, can be derived within the framework of the so-called adiabatic-connection fluctuation-dissipation theorem (ACFDT) , which offers a powerful mathematical device to construct the exact XC energy functional via the density response functions of a series of fictitious systems with scaled interactions, connecting the KS system and the true physical system. In this formulation, an approximation to the density response function translates into a corresponding approximation to the XC energy functional.
2.1 Adiabatic connection approach to DFT
Within the adiabatic connection (AC) approach to DFT [39, 18], one considers a continuous set of fictitious Hamiltonian’s,
| (17) |
which connects at with (Eq. 12) and at with . The Hamiltonian for describes a collection of particles moving under the auxiliary external potential and interacting with a scaled Coulomb interaction . The auxiliary potential () is chosen such that the density of -scaled systems is kept at the physical density, i.e., , along the AC path. By utilizing the coordinate scaling technique, it can be shown that
| (18) |
Here is the correlation energy with respect to the scaled density (see Ref. [17, 92] for more detailed definition and derivation). when ; while in the high density limit with , . For the fictitious system of with fixed density , the ground-state wavefunction can be denoted as ,
| (19) |
with the normalization condition of . Here is the ground-state energy along the AC path. is nothing but the ground-state energy of non-interacting KS system (Eq. 15) , while is the ground-state energy of the fully interacting system (Eq. 3).
The Hellman-Feynman theorem implies that
| (20) |
Here, we have used the expression for the density operator of the -electron systems
| (21) |
and the condition . By integrating Eq. 20 over the whole adiabatic connection path, the ground-state energy of the interacting system can be obtained as
| (22) |
where we have introduced the fluctuation of the density operator , and used the fact that and the definitions of , , and (Eqs. 6, 15, and 16). Comparing Eq. 3 to Eq. 22 yields the XC energy in terms of the coupling-constant integration
| (23) |
with the XC potential along the AC path defined as
| (24) |
It is easy to see that the XC potential at the starting point with and is nothing but the exact exchange energy (Eq. 8) in the KS framework,
| (25) |
If were known for the whole AC path, we would be able to approach the exact XC functional via the above coupling-constant integration (Eq. 23). From this perspective, better DFAs can be designed by making a better description of the integrands along the AC path.
2.2 Görling-Levy perturbation theory and XYG3-type DHAs
Let us start by reformulating the Hamiltonian (Eq. 17) as
| (26) |
where is the Hamiltonian of the KS non-interacting system (Eq. 11) and the perturbation is therefore
| (27) |
Eq. 27 suggests that the perturbation along the AC path is almost linear, except for the correlation part which evolves nonlinearly with respect to the coupling-constant parameter . As a consequence, the perturbative for is written down as
| (28) |
According to the standard perturbation theory, the ground-state energy of can be expanded perturbatively based on the ground-state energy of the KS non-interacting system (Eq. 15)
| (29) |
where refers to the th-order energy correction to . In particular, the first-order energy correction for is
| (30) |
and the second-order energy correction for is
| (31) |
which is widely recognized as the Görling-Levy (GL) theory of the coupling-constant perturbation expansion to the second order [17]. The first term of is associated with the single excitation (SE) contribution
| (32) |
where is the Hartree-Fock non-local exchange potential, which is the derivative of against the KS orbitals, while is the KS local exchange potential defined in Eq. 14. The second part of counts the contributions from double excitations, namely ,
| (33) |
where is defined in Eq. 10. shares the same formula as the second-order Møller-Plesset perturbation theory (MP2).
As discussed above, the initial integrand along the AC path is given by Eq. 25, which is simply the Hartree-Fock like exact-exchange energy (Eq. 8). Moreover, the second-order derivative against based on Eq. 20 together with Eq. 31 defines the initial slope of
| (34) |
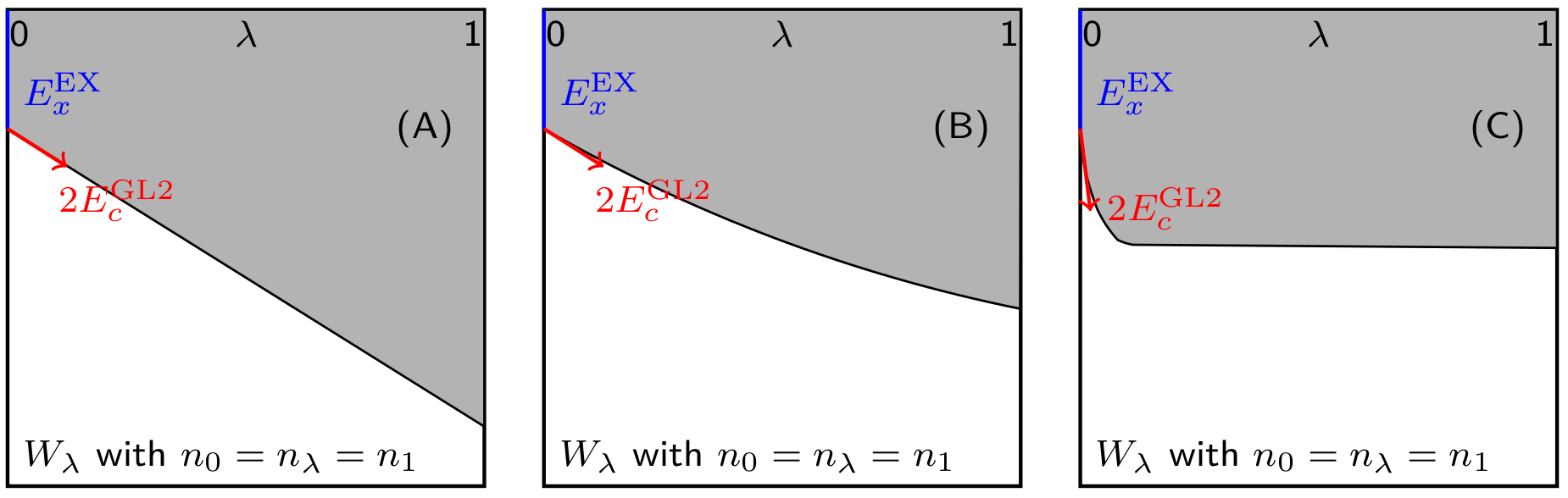
If the XC potential along the AC path is linear (see Figure 1A), it is precisely determined by and
| (35) |
As a result, the corresponding XC functional can be obtained by applying Eq. 23,
| (36) |
Eq. 36 looks similar to the standard MP2 method, which is composed of the HF exchange and the MP2 correlation. However, it has to be emphasized that the MP2 method is the lowest-level correlated wavefunction method for many-electron systems, while Eq. 36 is the exact (very accurate) exchange-correlation functional for any systems with linear (quasi-linear) -dependence. The key difference here is that, the Hartree-Fock orbitals are used for the standard MP2 calculations, while the KS non-interacting orbitals, which deliver the exact density of the interacting system, are employed for the evaluation of HF-like exchange and GL2 correlation in Eq. 36. The linear AC functional in the context of coupling-constant expansion indicates that, for the development of fifth-rung DFAs, the KS unoccupied orbitals can be introduced in the form of second-order perturbation theory. Equally important is the quality of input density and orbitals, which ensures the double of properly represents the initial slope of the XC potential along the AC path.
In this consideration, XYG3-type DHAs were proposed to go beyond the linear model by introducing several empirical parameters to extrapolate the second-order perturbation to infinite order (see Figure 1B). For example, the XYG3-type DHAs utilizing the B3LYP orbitals (xDH@B3LYP)[20] has the form of
| (37) |
where and are the exchange contribution from the Slater-type LDA and the Becke88 GGA. is the local Vosko-Wilk-Nusair correlation, and is the Lee-Yang-Parr correlation approximation. Here, and are the opposite-spin and same-spin part of PT2 (Eq. 33), respectively.
| (38) |
It is easy to find that in xDH@B3LYP, the single-excitation contribution () is not taken into account. It was argued that can be absorbed into the fitting parameters of xDH@B3LYP against the experimental data. Note that, the importance of was revisited by Ren et. al. [47] for improving the RPA method in describing vdW-bonded molecules. This will be discussed in Section 2.4.
Equation 37 suggests that there are at most 7 empirical parameters in the general formula of xDH@B3LYP methods. In fact, any xDH@B3LYP methods can be written down using this formula. The first approximation in this family, i.e., XYG3 proposed in 2009 [19], contains only 3 parameters, indicating that four constraints are imposed during the parameter optimization. Similarly, XYGJ-OS proposed in 2011 contains 4 parameters with 3 constraints [22]. Recently, the accuracy limit of xDH@B3LYP methods was explored by fully optimizing all 7 parameters. The resulting XYG7 functional [20] is among the top-class performers in the comprehensive benchmark for main-group chemistry, which can provide a balanced description of both covalent and noncovalent interactions. Its accuracy is comparable to or even better than the very expensive composite methods in wave function theory.
A key deficiency of PT2-based DHAs is in the description of strong correlation systems, where the degeneration of low-lying states could result in extremely large correlation contributions based on the perturbation treatment at any finite orders. In the context of coupling-constant expansion along the AC path, it means that the initial slope becomes extremely large, such that the initial slope itself is of little relevance to the exact XC energy, which is mainly determined by the XC potential at the fully interacting system (see Figure 1C).
To address this problem, we should go beyond the finite-order perturbation treatment of the correlation effects. Among different kinds of solutions already proposed, RPA is a promising candidate, as will be introduced in the following section. It offers a systematic way to renormalize different contributions in PT2, and thus address the divergence problem of finite-order perturbation theory as well as DHAs for strong-correlation systems.
2.3 RPA derived from the ACFDT framework
Let us return to the coupling-constant integration formula of the XC functional. From the viewpoint of zero-temperature fluctuation-dissipation theorem [93], the density-density correlation (fluctuations) in Eqs. 23 and 24 can be related to the imaginary part of the density response function (dissipation) of the system
| (39) |
Here the density response function describes the variation of the density of the partially interacting system at the spatial point , up to the linear order, due to a change of the local external potential at . From Eqs. 23, 24 and 39, we arrive at the renowned ACFDT expression for the XC energy in DFT,
| (40) |
The fact that the above frequency integration can be performed along the imaginary frequency axis originates from the pole structure of and the fact that it becomes purely real on the imaginary axis. Such a property simplifies the ground-state energy calculation within the ACFDT framework considerably. The ACFDT expression in Eq. 40 translates the problem of computing the XC energy to the computation of the response functions of a continuous set of fictitious systems along the AC path, which in practice have to be approximated as well.
Obviously, the exact density response function is not known either. However, according to linear-response time-dependent DFT (TDDFT), the interacting response function for is linked to the noninteracting response function via the Dyson-like equation
| (41) |
where is the so-called exchange-correlation kernel, which in time domain is given by
| (42) |
Here is the exchange-correlation part of the action functional [94].
Obviously, the kernel is a very complex quantity to deal with, and there are considerable ongoing efforts to find better approximations for it [95]. In this context, the random phase approximation amounts to simply neglecting the kernel, and the resultant interacting response function is termed as the RPA response function,
| (43) |
In physical terms, the RPA here corresponds to linearized time-dependent Hartree approximation, by which the variation of the exchange-correlation potential due to an external perturbation is neglected.
In Eqs. 41 and 43, is the independent-particle response function of the KS reference system () and is known explicitly in terms of the single-particle KS orbitals , orbital energies , and occupation factors ,
| (44) |
Based on Eqs. 40 and 43, the XC energy in RPA can be further decomposed into an exact exchange (EX) term and a RPA correlation term,
| (45) |
where
| (46) |
and
| (47) |
with . Equation 46 defines the exact-exchange energy (Eq. 8) within the ACFDT context, and is extended here to fractional occupation numbers and to be evaluated with KS orbitals. Furthermore, in the second line of Eq. 47, for brevity the following convention
| (48) |
has been adopted.
So far, we have described how the RPA method is defined as an approximate XC energy functional in the KS-DFT context, within the ACFDT framework. As mentioned above, RPA can also be derived from the perspective of the coupled cluster theory and the Green-function based many-body perturbation theory. For instance, to link with the ring coupled cluster doubles (rCCD) theory, the RPA correlation energy can be obtained as,
| (49) |
where is the rCCD amplitude, to be determined by solving the so-called the Riccati equation [96], and . Due to the limited space, here we will not elaborate on the alternative formulations of RPA any further, and interested readers are referred to Ref. [71] and the original references [96, 97] for more details.
Finally, combining Eqs. 3 and 45, one obtains the total ground-state energy of the RPA method,
| (50) |
where the first four terms can be grouped together, yielding an energy expression that corresponds to the Hartree-Fock energy evaluated with KS orbitals. This is simply given by the expectation value of the full interacting Hamiltonian within the KS Slater determinant.
In practice, RPA calculations are usually done perturbatively on top of a preceding calculation based on lower-rung DFAs. That is, the single-particle orbitals and orbital energies employed in Eq. 50 are generated using lower-rung approximations such as LDA, GGAs, or meta-GGAs. Thus, practical RPA calculations are often denoted as “RPA@DFA”, where “DFA” refers to the actual functional used in the preceding reference-state calculation.
2.4 Beyond-RPA computational schemes
Despite its appealing features, RPA does not go without shortcomings. The conventional wisdom is that RPA describes the long-range correlation very well, whereas it is not adequate for short-range correlations. This issue has been well known for homogeneous electron gas. For real materials, RPA was found to underestimate the cohesive energies of both molecules [40, 98] and solids [51]. This stimulated much research interest and several beyond-RPA schemes have been developed to fix this deficiency. Among these, three approaches are particularly noteworthy: 1) Hybridizing RPA with the lower-rung DFAs in the empirical double hybrid framework; 2) improving RPA by restoring the contribution of the kernel within the ACFDT formalism; and 3) improving RPA from the perspective of diagrammatic many-body perturbation theory. The first empirical approach gains increasing attention in quantum chemistry. The proposed RPA-based DHAs includes (a) dRPA75 [99] and PWRB95 [29] where the direct RPA correlation is used to replace the PT2 term in the double hybrid formula; (b) SCS-dRPA75 [100] and scsRPA [101] that utilize different kinds of spin-component scaled RPA; and (c) SCS-dRPA75rs [102] with range-separated RPA. Successful beyond-RPA schemes of the second type include the truncated adiabatic LDA kernel correction [103], and the more systematic construction of the XC kernel with respect to a series expansion of the coupling constant within the ACFDT framework [104, 95].
The diagrammatic many-body expansion approach to correct RPA, on which we shall concentrate here, exploits the fact that RPA, in contrast with other density functional approximations (DFAs), has a clear diagrammatic representation – an infinite summation of the ring diagrams. The question arises if there is a simple and systematic way to incorporate the missing diagrams to arrive at an improved theory. The fermionic nature of electrons requires the many-electron wavefunction to be antisymmetric, and the diagrammatic representation of the correlation energy contains graphs describing both direct processes and exchange processes. For example, in the Møller-Plesset perturbation theory, both types of processes are included at each order, which ensures the theory to be one-electron “self-correlation free” – the correlation energy for an one-electron system being zero. The standard PT2 correlation (Eq. 33) contains one direct term and one exchange term, represented respectively by the leading diagram in the first two rows of Fig. 2. These two terms cancel each other for one-electron systems. RPA is represented by the ring diagrams summed up to infinite order, as represented by the first-row diagrams in Fig. 2, where only “direct” processes are accounted for 333The RPA discussed here is often referred to as direct RPA in quantum chemistry literature. In some literature, RPA in fact corresponds to the time-dependent Hartree-Fock theory, where the exchange terms are also included. Nowadays, RPA with exchange included is usually referred to as RPAX or full RPA. A simple way to include the exchange processes and eliminate the self-correlation error is to antisymmetrize the two-electron Coulomb integrals within the rCCD formulation of RPA [cf. Eq. 49]. By doing so, a second-order screened exchange (SOSEX) term [105, 106, 107] is added, and the resultant RPA+SOSEX correlation energy is given by
| (51) |
with the two terms in Eq. 51 corresponding to RPA and SOSEX correlation energies respectively. The SOSEX contribution can be represented by the diagrams shown in the second row of Fig. 2, where the leading term corresponds to the exchange contribution in PT2. The RPA+SOSEX scheme has the interesting feature that it is one-electron self-correlation free, and improves substantially the total energy [106, 107]. The underbinding problem of RPA for chemically bonded molecules and solids is on average alleviated by the SOSEX correction.
As illustrated in Fig. 2, both RPA and SOSEX correlations can be interpreted as infinite-order summations of selected types of diagrams, with the PT2 terms in the leading order. This perspective is instructive for identifying important contributions that are still missing in the RPA+SOSEX scheme. In fact, at the second order, in addition to the direct and exchange terms, there is yet another type of contribution, arising from the SE, as already discussed above in the context of Görling-Levy perturbation theory (Eqs. 31 and 32). For beyond-RPA corrections, the SE-type correction was initially not derived according to the Görling-Levy perturbation theory in Sec. 2.2, but rather the Rayleigh-Schrödinger perturbation theory (RSPT) [108]. As shown in Ref. [47], within RSPT, the 2nd-order SE contribution is given by
where is the KS mean-field (MF) potential, according to which the reference state is generated, and is the non-local Hartree-Fock potential, evaluated using orbitals which themselves are generated according to the potential . Furthermore, is the single-particle Hartree-Fock Hamiltonian (also known as the Fock matrix in the quantum chemistry literature), and and are the ground-state Slater determinant formed by the lowest-occupied ’s and the singly-excited configuration generated by exciting one electron from an occupied state (with spin and energy ) to a virtual state (with the same spin and energy ), respectively. A detailed derivation of Eq. (2.4) can be found in the supplementary material of Ref. [47]. Obviously, for a Hartree-Fock reference where , Eq. 2.4 becomes zero, a fact known as Brillouin theorem [108]. Therefore, this term is not present in standard MP2 theory based on the Hartree-Fock reference.
One may notice that the SE expression derived within RSPT is different from the GL-SE given by Eq. 32, with the exact-exchange optimized effective potential (OEP) in the GL-SE is replaced in Eq. 2.4 by the mean-field potential, on which the reference state is based. In fact, RSPT can also be interpreted from the ACFDT perspective along a linear adiabatic connection path that linearly interpolates the non-interacting reference Hamiltonian and the full interacting Hamiltonian. However, in this case, the electron density is not (and cannot be) fixed any longer along the adiabatic connection path. Such a linear connection path was considered long ago by Harris and Jones in Ref. [109], and further discussed in Refs. [110, 111, 112]. As pointed by Klimeš et al. in Ref. [112], the SE term given by Eq. 2.4 accounts for the change of the mean-field Hartree and exchange energy as goes from 0 to 1, stemming from the change of both the electron density and density matrix. In contrast, the GL-SE only accounts for the change of exchange energy, since the electron density is fixed, and so does the Hartree energy.
From the practical point of view, Eq. 2.4 is easier to implement, since one can use the readily available LDA- or GGA-type KS potential as , without solving a rather cumbersome OEP equation at the exact change level. Yet, as discussed above, more physical effects missing in the standard RPA are accounted for by Eq. 2.4. Due to these advantages, the SE expression derived within RSPT is de facto the SE correction term for beyond-RPA schemes.
In Ref [47], it was shown that adding the SE term of Eq. 2.4 to RPA significantly improves the accuracy of vdW-bonded molecules, which the standard RPA scheme generally underbinds, and the SOSEX correction does not appreciably improve the situation. Similar to the RPA and SOSEX cases, one can identify a sequence of single-excitation processes up to infinite order, as illustrated in the third row in Fig. (2). Summing these single-excitation diagrams to infinite order represents a renormalization of the 2nd-order SE, and is therefore termed as renormalized single excitations (rSE) [71, 68]. Remarkably, this infinite summation can be translated into a closed expression similar to Eq. (2.4),
| (52) |
where and are the eigenvalues obtained by diagonalizing separately the occupied-occupied and virtual-virtual subblocks of the Fock matrix,
| (53) | ||||
with . Note that matrix is not diagonal since ’s are the reference KS orbitals and not the eigenfunctions of – the single-particle Hartree-Fock Hamiltonian. Now, in the numerator of Eq. (52) are the “transformed" off-diagonal block of the Fock matrix
| (54) |
where the eigenvectors obtained in (53) are used here as the transformation coefficients. The physical origin of the SE corrections is that the commonly used KS references for RPA and beyond-RPA calculations are not the optimal starting point. The SE corrections accounts for the “orbital relaxation" effect, which leads to a lowering of the ground-state total energy. Furthermore, it was found that SE and rSE corrections generally increases the binding energies, in particularly for weakly bonded systems. When the SE contributions are added, the electron density effectively contracts compared to that yielded by local and semilocal DFAs, and this reduces the Pauli repulsion between closed-shell atoms and molecules. Consequently, the underbinding behavior of the standard RPA is corrected for both weakly bonded molecules [47, 68] and solids [112]. Recently, the concept of rSE has been extended to Green’s function by Yang and coworkers [113, 114]. These authors showed that, by utilizing the so-called renormalized singles Green’s function, the starting point dependence in the usual perturbative -type calculations are significantly reduced [113, 114].
Diagrammatically, RPA, SOSEX and rSE are three distinct infinite series of many-body terms, in which the three leading terms correspond to the three terms in second-order many-body perturbation theory. Summing them up, the resultant RPA+SOSEX+rSE scheme can be viewed a renormalization of the second-order many-body perturbation theory. Therefore the RPA+SOSEX+rSE scheme is also termed as “renormalized second-order perturbation theory" or rPT2 . Independent of the rPT2 scheme described above, Bates and Furche developed a beyond-RPA formalism termed as RPA renormalized many-body perturbation theory [115]. The essence of this formalism is to express the correlation energy in terms of an integration over the polarization propagator (closely related to the density response function) along the AC path. The correlation energy can be improved by correcting the polarization propagator based on a series expansion in terms of the RPA polarization propagator multiplied with a four-point kernel. Benchmark calculations [116] show that the approximate exchange kernel (AXK) scheme within this formalism performs better than RPA+SOSEX discussed above. However, the rSE contribution is not included in the AXK scheme.
3 Implementation of the fifth-rung functionals
Now it is clear that the key in the calculations of fifth-rung functionals is to evaluate the exact-exchange energy (Eq. 8) and the corresponding correlation energies that are formed explicitly with unoccupied KS orbitals, like the PT2 correlation used in DHAs (Eq. 33) and the RPA correlation in RPA-based methods (Eq. 47). The algorithms for evaluating the exact-exchange energy in the present context are exactly the same as that of the Hartree-Fock exchange energy, which are routinely done in quantum chemistry calculations [117, 118]. The Hartree-Fock exchange is also the key component of hybrid density functionals, available in increasingly more softwares that can deal with periodic systems [119, 120, 121, 122]. Here, we should not discuss the implementation of the Hartree-Fock exchange, but rather focus on the implementation of the correlation part of DHAs and RPA.
3.1 Implementation of the DHAs
Taking the XYG3-type DHAs using B3LYP orbitals (xDH@B3LYP, Eq. 37) as example, the PT2 correlation is apparently the most time comsuming part. The standard sum-over-state formula of the PT2 correlation was already in Eq. 33. For convenience, here we rewrite the PT2 correlation energy by separating out the direct and exchange terms,
| (55) |
with being two-electron Coulomb repulsion integrals for molecular orbitals . This repulsion integrals can be further expressed in terms of basis functions
| (56) |
where are the two-electron integrals for the atomic orbitals, and are the eign-coefficients for the molecular orbitals.
Here we briefly describe the PT2 implementation in the FHI-aims code [123, 124], which employs real atom-centered numeric orbitals (NAOs) as basis functions,
| (57) |
with being the numerically tabulated radial function and the spherical harmonics. Unlike the gaussian-type orbital (GTO) basis functions, NAOs does not have analytical algorithms to evaluate integrals efficiently. Therefore, the so-called RI technique was employed, which represents the pair products of real atomic basis functions in terms of auxiliary basis functions,
| (58) |
Our auxiliary basis functions are also constructed as a numerically tabulated radial function multiplied by spherical harmonics,
| (59) |
but the radial function has different shapes from . In fact, they are generated in order to best represent the pair products of the one-electron orbitals . Details on how the auxiliary basis functions are constructed can be found in Refs. [124, 125].
Once the auxiliary basis functions are constructed, one can start to determine the triple expansion coefficients . For any finite auxiliary basis set, the expansion in Eq. 58 is an approximation, incurring an error . The accuracy of this approximation will not only depend on the quality and size of the auxiliary basis, but also depend on the expansion coefficients . In the RI approach with Coulomb metric [126], instead of minimizing the norm of the error , one minimizes the self Coulomb repulsion of this error , leading to the following expression for ,
| (60) |
where
| (61) |
and is the inverted Coulomb matrix with elements given by
| (62) |
where is the number of auxiliary basis functions. With such kind of RI expansion, the two-electron integrals can be approximated as
| (63) |
where a new rank-3 tensor is defined as,
| (64) |
By using the RI expansion (Eq. 63), the two-electron Coulomb repulsion integrals (Eq. 56) can be decoupled as follows
| (65) |
with the three-orbital integrals defined as
| (66) |
and defined as
| (67) |
As a result, the RI version of the PT2 correlation energy (RI-PT2) is given by
| (68) |
The RI-PT2 implementation (Eq. 68) scales as with respect to the size of the system. Although it has the same scaling exponent as the standard PT2 formula (Eq. 55), the prefactor in RI-PT2 is one to two orders of magnitude smaller than in the standard PT2 [124, 125]. In recent years, lower-scaling algorithms of PT2 have also been developed, which greatly enhanced the applicability of PT2-based methods, in particular DHAs, to large systems [127, 128, 129].
This conventional (global) RI approach works extremely well for small molecules. For big molecules and periodic systems, one may resort to a localized variant of the RI approach [125]. With enhanced auxiliary basis sets, the localized RI approach has been shown to be sufficiently accurate in practical calculations [125, 121, 130], and is instrumental for periodic systems [120]. The RI version of the PT2 correlation energy (Eq. 68) can be easily generalized from finite molecules to periodic systems. Taking advantage of the localized RI techniques, one can achieve excellent massive-parallel efficiency in periodic PT2 implementation as well. It allows one to perform a comprehensive benchmark on the numerical convergence of the PT2 correlation energies with respect to the basis set and -mesh sizes [131], which is crucial to make the periodic implementation of DHAs practical [132].
3.2 Implementation of the RPA method
As discussed in Sec. 2.3, in most practical RPA calculations, the evaluation of the RPA XC energy as given in Eqs. 45-47 is done perturbatively employing the KS orbitals and orbital energies generated by a preceding KS-DFT calculation with certain lower-rung functionals. The PBE-GGA is often used to serve this purpose, and the RPA calculation based a PBE reference is commonly denoted as “RPA@PBE”. As already indicated in Eq. 50, in standard RPA@PBE calculations, the ground-state total energy is given by
where , are the noninteracting kinetic energy, the external potential energy, the Hartree energy, and the XC energy obtained from the self-consistent PBE calculation, respectively. The RPA@PBE total energy defined in Eq. 3.2 is obtained by subtracting the PBE XC energy from the PBE total energy, and then adding the RPA XC energy, evaluated using PBE orbitals and orbital energies. Eq. 3.2 also suggests that the RPA total energy can be seen as the sum of the Hartree-Fock energy evaluated with respect to the PBE reference and the RPA@PBE correlation energy.
To develop efficient algorithms to evaluate Eq. 47, the key is to realize that both and are non-local operators, depending on two coordinates in space. Their real-space forms and can be seen as basis representations of the corresponding operator and in terms of real-space grid points. Under such a discretization, and become matrices of dimension as large as the number of real space grid points. This is not an efficient representation since the number of grid points is rather large, especially in all-electron implementations. To deal with this problem, an auxiliary basis set , in the form given by Eq. 59, is introduced to represent and , namely,
| (69) |
and the matrix which has been defined in Eq. 62. To find the matrix form , one needs to expand the products of KS orbitals in terms of ; from Eqs. 58 and 66, one has
| (70) |
Inserting Eq. 70 into Eq. 44, and comparing the resultant expression to Eq. 69, one arrives at
| (71) |
Thus, within the auxiliary basis representation, and become matrices. Since is typically much smaller than the number of real-space grid points, or the number of pair products of KS orbitals, the matrix in Eq. 71 and the V matrix in Eq. 62 can be seen as compressed representation of these operators, with the trace of their product unchanged,
| (72) |
Based on this observation, one can conclude that the computed RPA correlation energy is independent of the basis representation of and operators. Thus one may equivalently interpret Eq. 47 as matrix algebra with and represented within the auxiliary basis as given by Eqs. 71 and 62. Using the property ( being the determinant of the matrix ), one obtains the final working expression for evaluating the RPA correlation energy,
| (73) |
In Eq. 73, we have introduced an intermediate quantity and used the property . It is easy to recognize that the matrix can be directly evaluated as
| (74) |
where the coefficients are defined in Eq. 67.
The frequency integration in Eq. 73 can be done relatively easily, since the integrand is rather smooth and peaked at low frequency values. A modified Gauss-Legendre grid, which transforms a standard Gauss-Legendre grid in the range to ,
| (75) |
works rather well for most systems. In Eq. 75, are the abscissas and weights of the grid points generated from the Gauss-Legendre quadrature formula in an integration range , whereas are abscissas and weights of the transformed grid. Usually a few tens of frequency grid points are sufficient to get highly accurate results, except for systems with vanishing gaps, where considerably more grid points have to be used. Alternative frequency grids have been developed for evaluating the RPA correlation energies [133, 63, 134], which have been shown to work well for small gap systems. Especially the minimax grid has proved to be very efficient when used for the Fourier transform between the frequency and time domains, which is essential for the success of the cubic-scaling space-time algorithm for the RPA correlation energy calculations [63, 134].
The implementation scheme described above is known as the RI approach to RPA [133, 124]. From the above discussion, one may see that once the matrix forms of and within the auxiliary basis are determined, the rest of the RPA calculation is rather straightforward. The key steps in RPA calculations are thus: 1) Generate the auxiliary basis functions ; 2) Determine the RI coefficients ; and 3) Construct the matrix using (71), or alternatively the matrix using Eq.74. The choice of auxiliary basis functions depends on the underlying one-electron basis functions used in the KS-DFT calculations. The above-outlined algorithm works rather well for molecular geometries. This algorithm has been extended to periodic systems, utilizing the localized RI approximation. Periodic RPA implementation based on localized RI within the NAO basis set framework has also been available in FHI-aims [123, 124] and used in production calculations [131, 66]. The implementation details, which has not been published yet, follow similar algorithms as for the periodic case, which has been described in Ref. [130].
The key step in RPA correlation energy calculations is to construct the matrix in Eq. 71. Since the number of auxiliary basis functions scales linearly with the number of one-electron basis functions, the computational cost of Eq. 71 scales as with respect to the size of the system, and represent the computational bottleneck of RPA calculations. In recent years, lower-scaling algorithms have also been developed [63, 134, 135], which holds promise for extending the applicability of RPA to large systems.
4 Performance of the fifth-rung functionals and prototypical applications
The increasing interest in DHAs and RPA in recent years comes not only from their appealing concept, but also from their remarkable performance in practical applications. First of all, DHAs and RPA can describe vdW interactions in a seamless way [136], their performance has been demonstrated for varying kinds of weak-interacting systems [49, 47, 137, 138]. For lower-rung DFAs ranging from LDA to hybrid functionals, the long-range vdW interactions are not captured, and ad hoc corrections have to be added in order to describe systems where vdW interactions play an important role. Furthermore, it seems that DHAs and RPA are able to describe the delicate energy differences in complex bonding situations, including molecules adsorbed on surfaces [57, 58, 138], the isostructural phase transition [54] and the relative stability of different polymorphs of crystals [61, 64, 56, 65, 66, 132], the binding and ex-foliation energies of layered compounds [70], and the formation energy of defects [62, 63]. Finally, DHAs and RPA yield accurate chemical reaction barrier heights [71, 19, 21], which is crucial for reliably estimating the rate of chemical reactions.
4.1 vdW interactions
vdW interactions arises from the coupling between spontaneous quantum charge fluctuations separated in space. For two well-separated, spherically symmetric and chargely neutral systems, the interaction energy goes like
| (76) |
where is the dispersion coefficient and is the separation between the two subsystems. Dobson showed that the interaction energy between two subsystems and obtained by RPA exactly follows the asymptotic behavior given by Eq. 76, with the RPA C6 coefficients given by
| (77) |
where is the RPA polarizability of the subsystem , which can be obtained by integrating over the microscopic RPA response function as,
| (78) |
with . In Ref. [69], the RPA coefficients for a set of atoms and molecules were evaluated according to Eqs. 77 and 78. It was shown that, on average, the coefficients were underestimated by 13% by RPA@PBE compared to reference values [69].
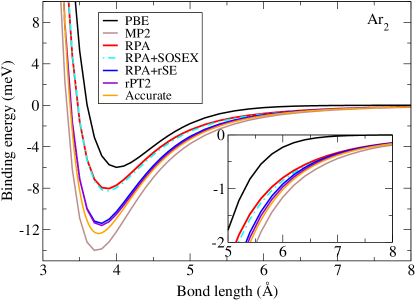
The accuracy of the RPA coefficient only tells about the performance of the method in the asymptotic regime, but not in the entire bonding region. In Fig. 3, the full binding energy curves of Ar2 obtained using PBE and RPA-based methods are presented. In addition, the result of MP2, the simplest post-Hartree-Fock quantum chemistry approach capable of describing vdW interactions, is also included here for comparison. The reference curve is given by the Tang-Toennies potential model, with model parameters determined from experiment. The PBE underestimates the bonding strength of Ar2 considerably, and this is appreciably improved by RPA. More importantly, at large separations, the PBE binding energy decays rapidly (in fact exponentially) to the energy zero, but the RPA curve displays the correct asymptotic behavior. Compared to the reference result, however, the RPA still shows a substantial underbinding, in contrast to the MP2 result which shows too strong binding of Ar2. The underbinding issue of RPA for vdW dimers arises from the too strong Pauli repulsion, which is in turn due to the Hartree-Fock part of the RPA total energy, obtained with the semi-local GGA orbitals. As discussed in Sec. 2.4, this issue can be fixed by the SE correction [47], and in particular its renormalized version [68]. As shown in Fig. (3), the RPA+rSE scheme brings the binding energy curve of Ar2 in close agreement with the reference one. The SOSEX correction, however, does not have a noticeable effect here. Thus the final rPT2 binding energy curve is almost on top of the RPA+rSE one. The performance of RPA-based methods for other rare-gas dimers can be found in Ref. [68].
A widely used benchmark set for weak interactions are the S22 test set designed by Jurečka et al. [141]. This test set collects 22 molecular dimers, among which 7 dimers are of hydrogen binding type, 8 of pure vdW (also called “dispersion") bonding, and another 7 of mixed type. Figure 4(a) shows the structures of water dimer, adenine-thymine dimer, and water-benzene dimer, representing the three bonding types, respectively. Because of its good representability and the availability of accurate reference interaction energies obtained using the the CCSD(T) method [140], S22 has been widely used for benchmarking the performance of or training the parameters for computational schemes that aim at describing weak interactions. The performance of RPA and some of the RPA-related methods has been benchmarked for this test set [45, 48, 47, 142].
In Fig. 4(b) the mean absolute errors (MAE) of PBE, MP2, and RPA-based methods are presented for the three subsets separately and for the entire S22 set. Both PBE and the correlated methods can describe the hydrogen bonding well, since this type of bonding is dominated by the electrostatic interactions, which has already been captured by the semi-local functionals to a large extent. The error of the standard RPA method is still appreciable (MAE > 1 kcal/mol 43 meV) arising from its general underbinding behavior. This can again be corrected by rSE , or by SOSEX terms. However, adding the two types of corrections together, the rPT2 scheme tends to overbind the hydrogen-bonded molecules, and hence the MAE increases again. For dispersion and mixed bondings, RPA performs better, and the MAE can be further decreased by rSE and SOSEX corrections. The MP2 method, on the other hand, yields a relatively large MAE for dispersion-bonded molecules, owing to its well-known overbinding problem for this type of interaction. This benchmark test indicates that the RPA+rSE scheme is a suitable approach which can be recommended for describing weak interactions. The advantage of this scheme is that it does not noticeably increase the computational cost, compared to the standard RPA scheme.
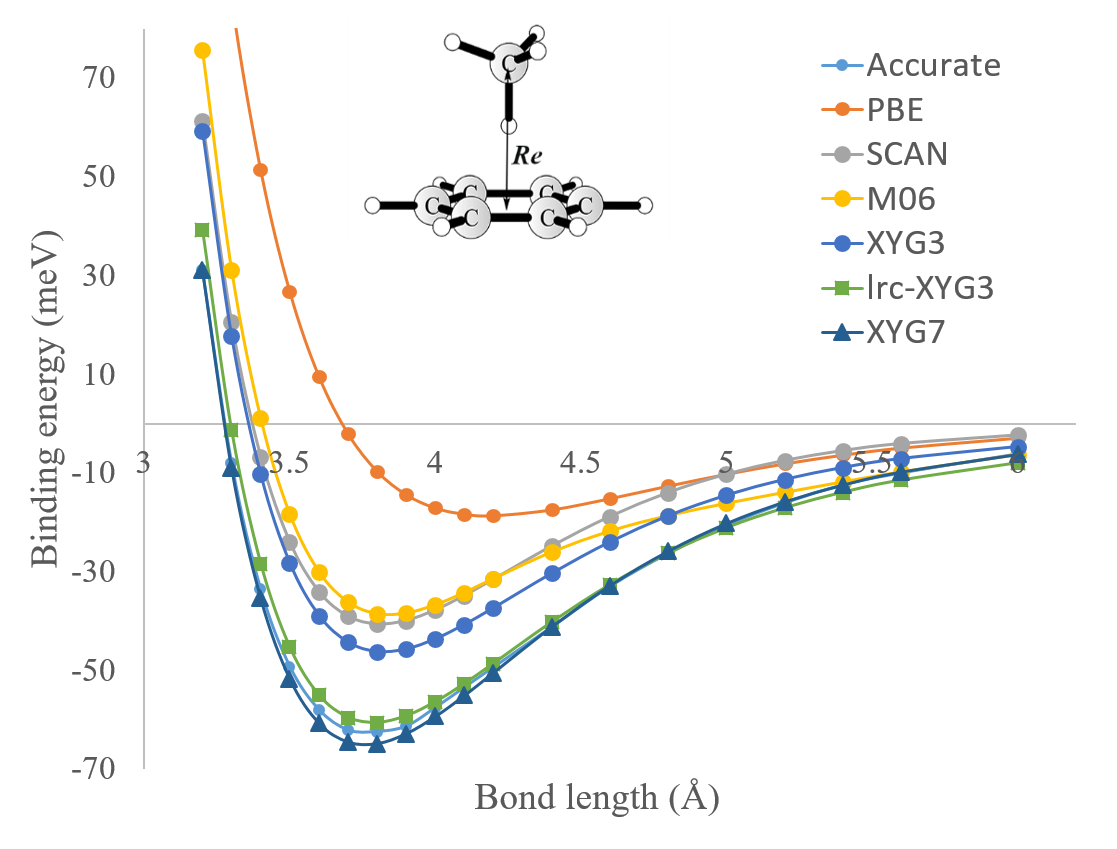
PT2-based DHAs include a portion of advanced PT2 correlation, and thus also exhibit a notable improvement over conventional DFAs for vdW interactions. Taking the binding curve of methane and benzene as example (Fig. 5), we see again that the PBE underestimates the vdW interaction notably, yielding a too shallow potential well and too long bond length. The XYG3 performs much better than the PBE, and is even slightly better than the best meta-GGA SCAN functional [7] and the popular hybrid meta-GGA M06-2X functional [6] in quantum chemistry. However, as shown in Fig. 5, the XYG3 still exhibits an underbinding tendency. In fact, extensive benchmarks suggest that empirical dispersion correction is still needed for most of existing DHAs [26]. By using the long-range part of the PT2 theory as a correction (lrc), the resulting lrc-XYG3 indeed improves over XYG3 notably [143]. Moreover, the good performance of lrc-XYG3 holds for the whole binding curve. A recent work fully relaxed 7 parameters in the xDH@B3LYP model (Eq. 37) and proposed the XYG7 method [20]. Fig. 5 indicates that it is possible to accurately describe vdW interactions in the context of xDH@B3LYP without resorting to the use of the explicit dispersion correction.
It was also found that the aforementioned underestimation of vdW interaction can be largely corrected if the Pople basis set of 6-311+G(3df,2p) is employed [137]. XYG3@6-311+G(3df,2p) and XYGJ-OS@6-311+G(3df,2p) perform well for the S22 set. The overall MAEs are only about 10 meV for both methods [137]. Recently, Chen and Xu extended the applicability of XYG3 to molecular crystals, which was fulfilled with the aid of the eXtended ONIOM method (XO) with periodic boundary conditions (XO-PBC) [144]. The X23 data set consists of 23 molecular crystals dominated by hydrogen bondings, vdW interactions, and those of combined hydrogen bonding-vdW interactions [145]. Chen and Xu computed the lattice energies of these 23 molecular crystals, and reported a MAE of only 30 meV for the XYG3 method [144].
4.2 Surface adsorption
An accurate description of atoms and molecules interacting with surfaces is the key to understand important physical and chemical processes such as heterocatalysis, molecular electronics, and corrosion. Molecules adsorbed on metal surfaces represent a particularly difficult situation, since quantitatively accurate results can only be obtained if the approach is able to describe simultaneously the chemical bonding, vdW interactions, metallic screening, and charge transfer processes. The CO adsorption problem and the water hexamer adsorbed on the Cu(111) surface, to be discussed below, are two prominent examples which require fifth-rung functionals to give a faithful description.
4.2.1 The “CO adsorption puzzle”.
This issue can be well illustrated by the “CO adsorption puzzle", where LDA and several popular GGAs predict the wrong adsorption site for the CO molecule adsorbed on several noble/transition metal surfaces at low coverages [86]. For CO adsorbed on the Cu(111), Pt(111), and Rh(111) surfaces, LDA and popular GGAs erroneously favor the threefold-coordinated hollow site (cf. Fig. 6(a)), whereas experiments clearly show that the singly-coordinated on-top site is the energetically most stable site [147, 148]. This posed a severe challenge to the first-principles modeling of molecular adsorption problems and represents a key test example for the RPA-based methods.
In Ref. [57], the performance of the RPA method for CO adsorbed on Cu(111) was investigated. The computed RPA adsorption energies for both the on-top and fcc (face centered cubic) hollow sites are presented in 6(b), together with the results from LDA, AM05 [149], PBE, and the hybrid PBE0 functional [150]. Figure 6 reveals what happens in the CO adsorption problem when climbing the Jacob’s ladder in DFT [3], when going from the first two rungs (LDA and GGAs) to the fourth (hybrid functionals), and finally to the 5th-rung RPA functional. It can be seen that, along the way, the adsorption energies on both sites are reduced, while the magnitude of the reduction is bigger for the fcc hollow site. The correct energy ordering is already restored at the PBE0 level, but the adsorption energy difference between the two sites is vanishingly small. RPA not only predicts the correct adsorption site, but also produces reasonable adsorption energy difference of 0.22 eV, consistent with experiments. The effect of the starting reference state on the calculated RPA results has also been checked. In Ref. [57], in addition to the commonly used RPA@PBE scheme, RPA calculations were also performed on top of the hybrid functional PBE0. Figure 6 indicates that the small difference between RPA@PBE and RPA@PBE0 results is insignificant for understanding the “CO adsorption puzzle". Schimka et al. extended the RPA benchmark studies of the CO adsorption problem to more surfaces [58], and found that RPA is the only approach that gives both good adsorption energies and surface energies at the same time. GGAs and hybrid functionals at most yield either good surface energies, or adsorption energies, but not both. Following these works, RPA has subsequently been applied to the adsorption of small alkanes in Na-exchanged chabazite [151], benzene on the Si(001) surface [152], graphene on the Ni(111) surface [59, 60] and the Cu(111) and Co(0001) surfaces [60]. In all these studies, RPA was demonstrated to be able to capture the delicate balance between chemical and dispersion interactions, and yields quantitatively reliable results. We expect RPA to become an increasingly more important approach in surface science, with increasing computer power and more efficient implementations.
4.2.2 The water hexamer on Cu(111) surfaces
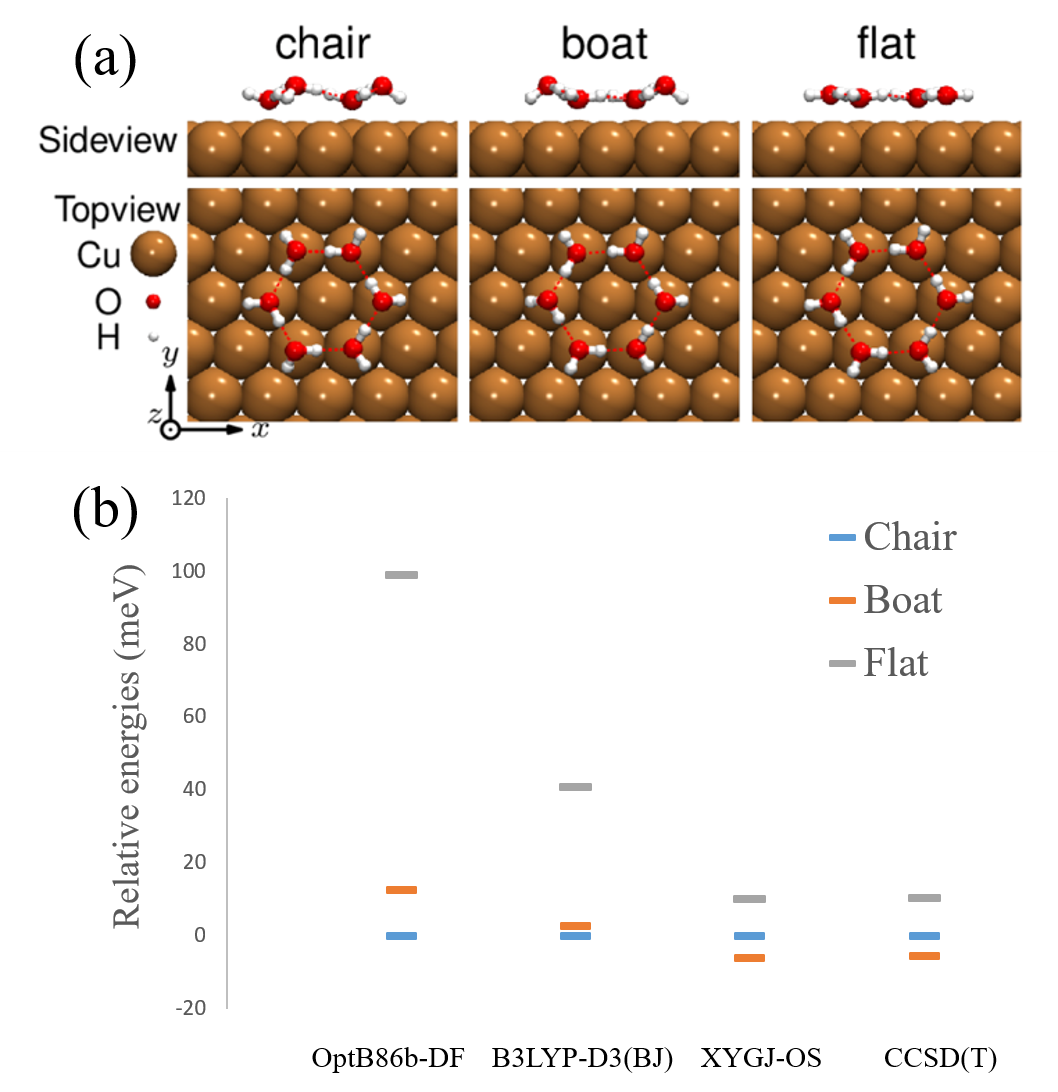
is a more complicated adsorption system, which also imposes a great challenge in computational materials science [153]. As shown in Fig. 7, the conventional DFAs, including OptB86b-DF and B3LYP-D3(BJ), predict the chair configuration to be the most stable adsorption structure of the water hexamer on Cu(111) surfaces. However, the scanning tunneling microscope (STM) image from experiment supported a more symmetric configuration, and led to the assignment of the flat configuration to be the in situ configuration [154]. Recently, Duan et. al. revisited this problem by using the XYG3-type DHA XYGJ-OS and advanced wave-function method CCSD(T) [153]. With a more accurate description of hydrogen bond interaction, XYGJ-OS and CCSD(T) changes the configuration energy ordering. Together with the STM simulation, these authors identified the boat configuration to be the most stable one, solving the aforementioned discrepancy between experiment and simulation.
4.3 Structural phase transition
4.3.1 The - phase transition of Ce.
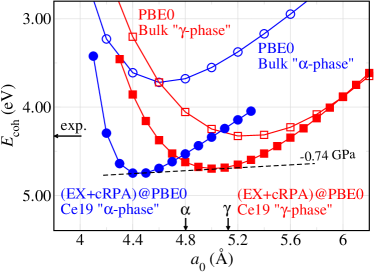
The -electron materials, which contain rare-earth or actinide elements, pose a great challenge to first-principles approaches. A prototypical example of -electron system is the Ce metal, which has an intriguing iso-structural - phase transition, accompanied by a drastic volume collapse (as large as at ambient pressure and zero temperature). The two phases are characterized by distinct spectroscopic and magnetic properties. Various theoretical approaches, including LDA plus dynamical mean-field theory (LDA+DMFT) have been employed to study this system [155, 156]. DFT within its local and semilocal approximations is unable to describe the two phases of Ce. In fact, due to the strong delocalization error in these functionals, the localized nature of the -electrons in the phase cannot be properly described; only the phase is described with some confidence within LDA/GGAs, although not at a quantitative level.
It was shown by Casadei et al. [54, 55] that, remarkably, hybrid functionals like PBE0 and HSE can yield two self-consistent solutions, with distinct lattice constants, cohesive energies, electronic band structures, local magnetic moments, and different degrees of -electron localization. These two solutions can be reasonably associated with the phases of the Ce metal. However, the energetic ordering of the -like and -like phases produced by PBE0 is not consistent with the experimental situation where the phase is energetically more stable at low temperature and ambient pressure. Adding RPA corrections on top of the PBE0 cohesive energies for the two solutions, the energy ordering is reversed, and the -like solution becomes energetically more stable. The transition pressure of the two phases given by the Gibbs construction is consistent with the experimental value.
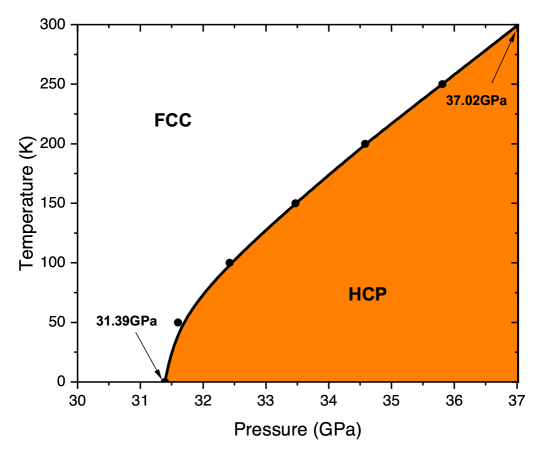
4.3.2 The fcc-hcp phase transition of Ar.
The face-centered cubic (fcc) and hexagonal closed packed (hcp) structures of the rare-gas crystals have very close energies, but at ambient pressures the fcc crystal structure is preferred and there is a phase transition from fcc to hcp at very high pressures. Because of the tiny energy difference between the two phases, it is exceedingly difficult to capture this difference computationally and consequently explain these behaviors. Conventional approximations of DFT do not have the adequate accuracy to describe the system. In the literature, the problem was usually treated by the cluster expansion approach, whereby the two-body, three-body, and four-body potentials are obtained either from empirical models or quantum chemistry coupled cluster calculations [157, 158, 159, 160]. However, this type of approach is difficult to use for non-experts and not suitable for routine calculations.
Thus, it is highly interesting to check how fifth-rung functionals perform for discerning the fcc and hcp structures of the rare-gas crystals. In Ref. [66], focusing on the Ar crystal, the authors found that the correct energy ordering between the fcc and hcp phases at ambient pressure can be obtained if 1) the RPA or RPA+rSE method is employed and 2) the fcc and hcp crystal structures are computationally treated on an equal footing (i.e., invoking the same computational supercell and grid mesh). In contrast with what was previously proposed, it was found that the electronic correlation effect plays a decisive role in determining the relative stability of the two phases, whereas the zero point energy effect is secondary.
Furthermore, by complementing the RPA+rSE electronic ground-state energy with lattice vibrational energies at finite temperatures, one can compute the Helmholtz free energy and derive the pressure-volume (-) curve at a given temperature. The calculated - curve is in excellent agreement with the experimental measurements [66], especially in the high-pressure regime, which has been considered a big challenge for theoretical approaches. Finally, by computing the Gibbs free energies for both phases, it is possible to determine a temperature-pressure (-) phase diagram for the Ar crystal, which signifies the rough temperature and pressure range where the fcc phase can be transformed to the hcp phase. Such a - phase diagram is shown in Fig. 9.
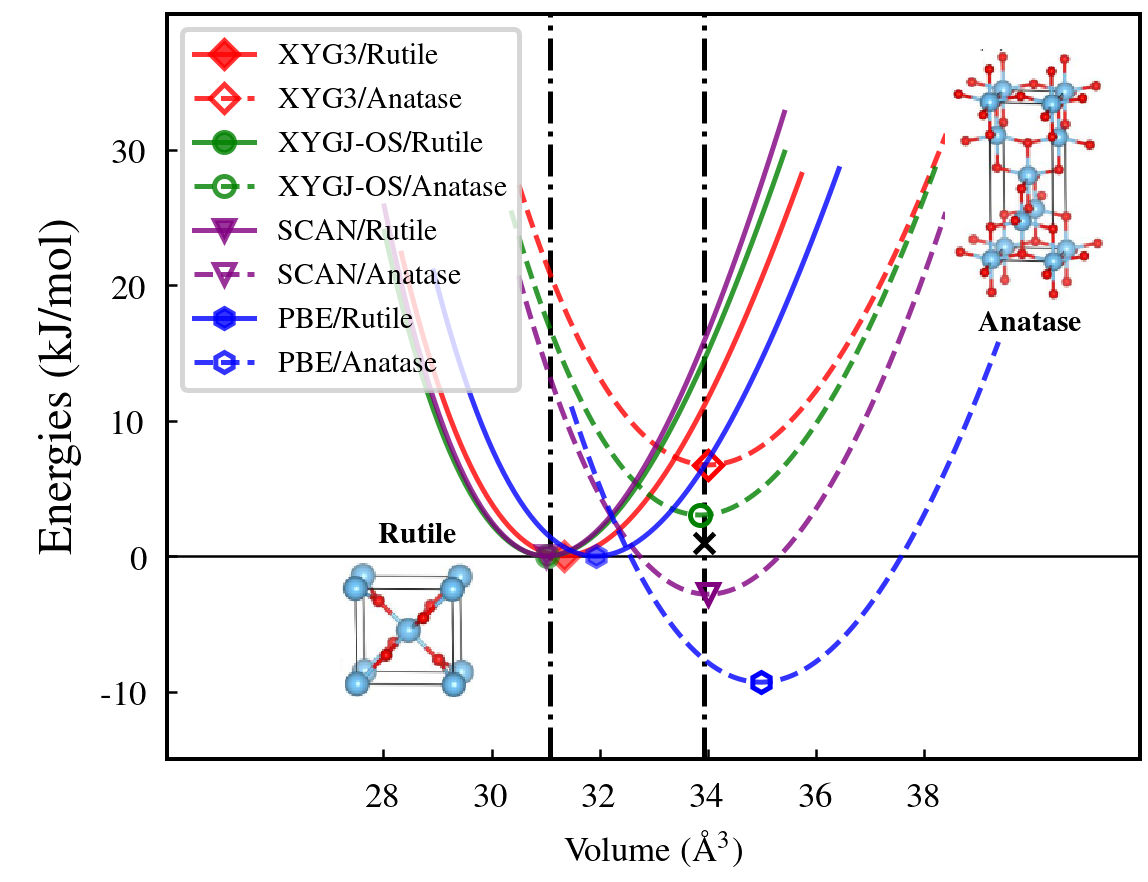
4.3.3 Rutile v.s. Anatase phases for TiO2.
Recently, PT2-based DHAs have been applied to study the relative stability of TiO2, which is also a challenging case in materials science. It was clear from the experiment that the rutile phase is the most stable phase at T=0 K [161]. However, as shown in Fig. 10, most of the popular DFAs, including PBE and SCAN, predict the anatase phase to be more stable than rutile. Zhang et. al. attributed this issue to the self-interaction error in conventional DFAs [161]. They thus suggested to use the empirical DFT+U approach to effectively reduce SIE for PBE and SCAN. However, in order to obtain the correct phase ordering, a very large U is needed (6 eV for PBE and 2 eV for SCAN), which notably deteriorates the description of the structure parameters. On the other hand, Cui et. al. suggested that such kind of error should be attributed to the error in the (semi)local correlation approximations. They found that the correct energy ordering can be obtained by using the RPA method [162]. Fig. 10 shows that the two XYG3-type DHAs, including XYG3 and XYGJ-OS, correctly predict the rutile TiO2 to be the ground phase with a satisfactory description of the optimized equilibrium volume.
In addition to the three systems discussed above, the capability of RPA to capture the delicate energy difference between competing phases or polymorphs has also been demonstrated for Iron disulfide (FeS2), a potentially interesting system for photovoltaic and photoelectrochemical applications. This material turns out to be rather challenging, since popular conventional DFAs fail to produce the relative stability of its two polymorphs: pyrite and marcasite, with the latter artificially stabilized. It was demonstrated by Zhang et al. [56] that RPA, regardless of its reference state, can correctly restore the energy ordering of the two polymorphs of FeS2. These authors further unravel that the fact that RPA tends to stabilize the pyrite polymorph is due to its smaller KS band gap, resulting in a large RPA correlation energy as compared to the the marcasite polymorph. This observation is consistent with the case of the Ce metal [54], where the more metallic -phase is stabilized within the RPA. Another successful application of this kind is that the tiny energy difference between the two allotropes of carbon, graphite and diamond, can be reliably described by RPA, with the correct prediction that graphite is energetically slightly lower than diamond [61]. Similarly, the thermodynamic stability of the most common polymorphs of the bulk BN has been resolved by Cazorla and Gould [65] at the level of RPA. A more systematic benchmark study of the performance of RPA and several beyond-RPA methods for predicting the transition pressure of structural phase transitions of a set of bulk materials have recently been reported in Ref. [163].
Other types of materials science problems to which fifth-rung functionals have been applied include layered compounds [164, 70] and defect systems [62, 63]. We shall not elaborate on these types of applications here due to limited space, and interested readers may look into the original literature for details. In summary, there are ample evidence that fifth-rung DFAs perform well in capturing delicate energy differences in materials, and fix some of the qualitative failures of more conventional approaches. So far, RPA-based method and DHAs are mostly applied by different groups to different materials science problems. A systematic comparison of the performance of these two types of fifth-rung functionals for a well-defined set of benchmark systems still needs to be done in the near future.
5 Recent developments
The field of fifth-rung functional development and applications represents a rapidly evolving branch of computational electronic structure methods. Noteable progress has been achieved in several directions within the last few years, which we would like to briefly recapitulate here.
-
1.
Force calculations of RPA and DHAs. Analytical gradients of the RPA total energy with respect to the atomic positions have been computed within both the atomic orbital basis [165, 166, 167, 135, 168, 169] and plane-wave basis [170] frameworks. Corresponding implementation for DHAs can be found mainly with the atomic orbital basis framework [171]. This allows to compute atomic forces and relax structures at the levels of RPA and DHAs, which is a long-sought goal of the electronic-structure community. Moreover, it is now possible to calculate vibrational frequencies [166] and phonon spectra based on the RPA force constant [170], and even molecular dynamics simulations can be carried out based on the RPA force [170]. These advancements greatly enhanced the capability of these advanced methods in computational chemistry and materials science.
-
2.
Low-scaling implementations for RPA and DHAs. Another noteworthy development is several low-scaling – ranging from linear scaling to cubic scaling – algorithms for RPA [172, 173, 63, 174, 175, 176, 177, 178, 179] and DHAs[129, 180] have been designed and implemented. This paves the way for applying fifth-rung functionals to large-sized and complex materials that are unaccessible in the past.
-
3.
Particle-particle RPA. The above-discussed RPA is represented by ring diagrams and called particle-hole RPA (phRPA) in the literature. In addition to phRPA, another type of RPA, consisting of an infinite summation of ladder diagrams, has also been discussed in the nuclear physics literature [37]. This type of RPA is referred to as particle-particle RPA and has recently been brought into the attention of electronic structure community [181, 182, 183, 184]. Benchmark calculations show that ppPRA carries interesting features that are not present in phRPA. Attempts for combining the two types of RPA in one framework has been made both in a range-separated manner [185] and globally [186]. However, it seems that merging the two RPA channels into one united theory is a highly nontrivial task [186].
-
4.
Self-consistent RPA and DHAs in generalized Kohn-Sham framework. As mentioned before, the majority of practical RPA and DHAs calculations are done in a post-processing fashion, using orbitals and orbital energies generated from a preceding DFA calculation. The importance of the rSE contribution indicates that commonly used semi-local DFAs are not optimal starting points for RPA calculations. Thus running the calculations of RPA and DHAs in a self-consistent way is highly desirable. However, for orbital-dependent functionals like RPA and DHAs, the criterion for “self-consistency" is not uniquely defined. In the RPA case, the optimized effective potential (OEP) scheme [187, 188, 189] is a well-defined self-consistency procedure, but the obtained results for binding energies are not necessarily better than than the perturbative scheme. Similar observation was found for DHAs[190, 24]. Most recently, self-consistent RPA schemes are developed by Jin et al. within generalized OEP framework [191] and by Voora et al. within generalized KS framework [192, 193]. The two schemes differ in details, but the rSE contribution is captured in both schemes. Initial results obtained from these schemes look very promising and there is much to explore along this direction.
-
5.
More beyond-RPA schemes to improve the accuracy. In addition to the beyond-RPA schemes already discussed in Sec. 2.4, one most recent development by Zhang and Xu [101] is to introduce a spin-pair distinctive algorithm in the ACFDT context, whereby the contributions of same-spin and opposite-spin pairs to the correlation energy are separated. By scaling the contributions for two types of spin pairs differently, one can achieve a simultaneous attenuation of both self-interaction errors and static correlation errors. Similar to the power series approximation of Görling and coauthors [104, 95], the spin-pair distinctive formalism of Zhang and Xu [101] is particularly successful in dealing with systems with multi-reference characters.
6 Summary
In this review, we discussed the basic concept, the theoretical formulation, the implementation algorithm, the prototypical applications, as well as the recent developments of PT2-based DHAs and RPA-based methods. We expect that these fifth-rung functionals will have an ever-increasing impact on computational materials science, and become the mainstream methods in the near future. Since this is an actively developing field, and the number of papers is quickly growing, it is well possible some important developments are not covered in our discussion. The purpose of this manuscript is to inform the readers about the overall status of this field, and stimulate more works on the development and applications of fifth-rung functional methodology.
7 Acknowledgements
We are grateful to Matthias Scheffler, Xin Xu, Patrick Rinke and other colleagues for great collaborations and illustrating discussions on the works presented in this review. The authors acknowledge the financial support of National Natural Science Foundation of China (Grant Nos. 12134012, 12188101, 21973015, and 22125301). This work was also supported by the funding of Innovative research team of high-level local universities in Shanghai and a key laboratory program of the Education Commission of Shanghai Municipality (ZDSYS14005). X.R. acknowledges the financial support of the Max Planck Partner Group for Advanced Electronic Structure Methods.
References
- [1] Hohenberg P and Kohn W 1964 Phys. Rev. 136 B864
- [2] Kohn W and Sham L J 1965 Phys. Rev. 140 A1133
- [3] Perdew J P and Schmidt K 2001 Jacob’s ladder of density functional approximations for the exchange-correlation energy Density Functional Theory and its Application to Materials ed Van Doren V, Van Alsenoy C and Geerlings P (Melville, NY: AIP)
- [4] Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett 77 3865
- [5] Becke A D 1983 Int. J. Quantum Chem. 23 1915–1922
- [6] Zhao Y and Truhlar D G 2006 J. Chem. Phys. 125 194101–18
- [7] Sun J, Ruzsinszky A and Perdew J P 2015 Phys. Rev. Lett. 115 036402
- [8] Becke A D 1993 J. Chem. Phys 98 5648
- [9] Zhao Y and Truhlar D G 2006 J. Chem. Phys. 125 194101
- [10] Chai J D and Head-Gordon M 2008 J. Chem. Phys. 128 084106
- [11] Heyd J, Scuseria G E and Ernzerhof M 2003 J. Chem. Phys. 118 8207
- [12] Zhao Y, Lynch B J and Truhlar D G 2005 Phys. Chem. Chem. Phys. 7 43–52
- [13] Grimme S 2006 J. Chem. Phys. 124 034108
- [14] Kozuch S, Gruzman D and Martin J M L 2010 J. Phys. Chem. C 114 20801–20808
- [15] Chai J D and Head-Gordon M 2008 Phys. Chem. Chem. Phys. 10 6615–6620
- [16] Goerigk L and Mehta N 2019 Aust. J. Chem. 72 563–573
- [17] Görling A and Levy M 1993 Phys. Rev. B 47 13105
- [18] Gunnarsson O and Lundqvist B I 1976 Phys. Rev. B 13 4274
- [19] Zhang Y, Xu X and Goddard W A 2009 Proc. Natl. Acad. Sci. USA 106 4963–4968
- [20] Zhang I Y and Xu X 2021 J. Phys. Chem. Lett. 12 2638–2644 publisher: American Chemical Society
- [21] Zhang I Y and Xu X 2014 A New-Generation Density Functional (New York: Springer)
- [22] Zhang I Y, Xu X, Jung Y and Iii W A G 2011 Proc. Natl. Acad. Sci. USA 108 19896–19900 wOS:000298034800020
- [23] Zhang I Y, Su N Q, Brémond E A G, Adamo C and Xu X 2012 J. Chem. Phys. 136 174103–8
- [24] Mardirossian N and Head-Gordon M 2018 J. Chem. Phys. 148 241736
- [25] Santra G, Sylvetsky N and Martin J M L 2019 J. Phys. Chem. A 123 5129–5143 publisher: American Chemical Society
- [26] Goerigk L, Hansen A, Bauer C, Ehrlich S, Najibi A and Grimme S 2017 Phys. Chem. Chem. Phys. 19 32184–32215
- [27] Santra G, Semidalas E and Martin J M L 2021 J. Phys. Chem. Lett. 12 9368–9376 publisher: American Chemical Society
- [28] Mezei P D, Csonka G I, Ruzsinszky A and Kállay M 2015 J. Chem. Theory Comput. 11 4615–4626
- [29] Grimme S and Steinmetz M 2016 Phys. Chem. Chem. Phys. 18 20926–20937 ISSN 1463-9084 URL http://pubs.rsc.org/en/content/articlelanding/2016/cp/c5cp06600j
- [30] Mezei P D, Csonka G I, Ruzsinszky A and Kállay M 2017 Journal of Chemical Theory and Computation 13 796–803
- [31] Zhang I Y and Xu X 2019 J. Phys. Chem. Lett. 10 2617–2623
- [32] Zhang I Y and Xu X 2021 WIREs Computational Molecular Science 11 e1490
- [33] Bohm D and Pines D 1951 Phys. Rev. 82 625–634
- [34] Bohm D and Pines D 1953 Phys. Rev. 92 609
- [35] Hubbard J 1957 Proc. Roy. Soc. (London) A243 336
- [36] Gell-Mann M and Brueckner K A 1957 Phys. Rev. 106 364
- [37] Ring P and Schuck P 1980 The Nuclear Many-Body Problem (New York: Springer)
- [38] Langreth D C and Perdew J P 1975 Solid State Commun. 17 1425
- [39] Langreth D C and Perdew J P 1977 Phys. Rev. B 15 2884
- [40] Furche F 2001 Phys. Rev. B 64 195120
- [41] Fuchs M and Gonze X 2002 Phys. Rev. B 65 235109
- [42] Jiang H and Engel E 2007 J. Chem. Phys 127 184108
- [43] Hellgren M and von Barth U 2007 Phys. Rev. B 76 075107
- [44] Toulouse J, Gerber I C, Jansen G, Savin A and Ángyán J G 2009 Phys. Rev. Lett. 102 096404
- [45] Zhu W, Toulouse J, Savin A and Ángyán J G 2010 J. Chem. Phys. 132 244108
- [46] Heßelmann A and Görling A 2011 Phys. Rev. Lett. 106 093001
- [47] Ren X, Tkatchenko A, Rinke P and Scheffler M 2011 Phys. Rev. Lett. 106 153003
- [48] Eshuis H and Furche F 2011 J. Phys. Chem. Lett. 2 983
- [49] Harl J and Kresse G 2008 Phys. Rev. B 77 045136
- [50] Harl J and Kresse G 2009 Phys. Rev. Lett. 103 056401
- [51] Harl J, Schimka L and Kresse G 2010 Phys. Rev. B 81 115126
- [52] Nguyen H V and de Gironcoli S 2009 Phys. Rev. B 79 205114
- [53] Lu D, Li Y, Rocca D and Galli G 2009 Phys. Rev. Lett. 102 206411
- [54] Casadei M, Ren X, Rinke P, Rubio A and Scheffler M 2012 Phys. Rev. Lett. 109 146402
- [55] Casadei M, Ren X, Rinke P, Rubio A and Scheffler M 2016 Phys. Rev. B 93 075153
- [56] Zhang M Y, Cui Z H and Jiang H 2018 J. Mater. Chem. A 6 6606
- [57] Ren X, Rinke P and Scheffler M 2009 Phys. Rev. B 80 045402
- [58] Schimka L, Harl J, Stroppa A, Grüneis A, Marsman M, Mittendorfer F and Kresse G 2010 Nature Materials 9 741
- [59] Mittendorfer F, Garhofer A, Redinger J, Klimeš J, Harl J and Kresse G 2011 Phys Rev. B 84 201401(R)
- [60] Olsen T, Yan J, Mortensen J J and Thygesen K S 2011 Phys. Rev. Lett. 107
- [61] Lebègue S, Harl J, Gould T, Ángyán J G, Kresse G and Dobson J F 2010 Phys. Rev. Lett. 105 196401
- [62] Bruneval F 2012 Phys. Rev. Lett. 108 256403
- [63] Kaltak M, Klimeš J and Kresse G 2014 J. Chem. Theory Comput. 10 2498
- [64] Sengupta N, Bates J E and Ruzsinszky A 2018 Phys. Rev. B 97(23) 235136 URL https://link.aps.org/doi/10.1103/PhysRevB.97.235136
- [65] Cazorla C and Gould T 2019 Science Advances 5 eaau5832
- [66] Yang S and Ren X 2022 New J. Phys. 24 033049
- [67] Dobson J F, White A and Rubio A 2006 Phys. Rev. Lett 96 073201
- [68] Ren X, Rinke P, Scuseria G E and Scheffler M 2013 Phys. Rev. B 88 035120
- [69] Gao Y, Zhu W and Ren X 2020 Phys. Rev. B 101(3) 035113 URL https://link.aps.org/doi/10.1103/PhysRevB.101.035113
- [70] Björkman T, Gulans A, Krasheninnikov A V and Nieminen R M 2012 Phys. Rev. Lett 108 235502
- [71] Ren X, Rinke P, Joas C and Scheffler M 2012 J. Mater. Sci. 47 7447
- [72] Pines D 2016 Rep. Prog. Phys. 79 092501
- [73] Heßelmann A and Görling A 2011 Mol. Phys. 109 2473
- [74] Eshuis H, Bates J E and Furche F 2012 Theor. Chem. Acc. 131 1084
- [75] Chen G P, Voora V K, Agee M M, Balasubramani S G and Furche F 2017 Annu. Rev. Phys. Chem. 68 421
- [76] Becke A 1988 J. Chem. Phys. 88 2547
- [77] Lee C, Yang W and Parr R G 1988 Phys. Rev. B 37 785–789
- [78] Tao J, Perdew J P, Staroverov V N and Scuseria G E 2003 Phys. Rev. Lett. 91 146401
- [79] Yu H S, He X and Truhlar D G 2016 J. Chem. Theory Comput. 12 1280–1293
- [80] Yu H S, He X, Li S L and Truhlar D G 2016 Chem. Sci. 7 5032–5051
- [81] Mardirossian N and Head-Gordon M 2017 Mol. Phys. 115 2315–2372 wOS:000416508000001
- [82] Perdew J P, Parr R G, Levy M and Balduz, Jr J L 1982 Phys. Rev. Lett. 49 1691
- [83] Cohen A J, Mori-Sanchez P and Yang W 2008 Science 321 792
- [84] Kristyán S and Pulay P 1994 Chem. Phys. Lett. 229 175
- [85] Imada M, Fujimori A and Tokura Y 1998 Rev. Mol. Phys. 70 1039
- [86] Feibelman P J, Hammer B, Nørskov J K, Wagner F, Scheffler M, Stumpf R, Watwe R and Dumestic J 2001 J. Phys. Chem. B 105 4018
- [87] Zhang Y and Yang W 1998 J. Chem. Phys. 109 2604
- [88] Grimme S, Antony J, Ehrlich S and Krieg H 2010 J. Chem. Phys. 132 154104
- [89] Becke A D and Johnson E R 2007 J. Chem. Phys 127 124108
- [90] Tkatchenko A and Scheffler M 2009 Phys. Rev. Lett. 102 073005
- [91] Tkatchenko A, DiStasio Jr R A, Car R and Scheffer M 2012 Phys. Rev. Lett. 108 236402
- [92] Levy M and Perdew J P 1985 Phys. Rev. A 32 2010–2021
- [93] Nozières P and Pines D 1966 The Theory of Quantum Liquids (New York: Benjamin)
- [94] Onida G, Reining L and Rubio A 2002 Rev. Mod. Phys. 74 601
- [95] Görling A 2019 Phys. Rev. B 99 235120
- [96] Scuseria G E, Henderson T M and Sorensen D C 2008 J. Chem. Phys. 129 231101
- [97] Dahlen N E, van Leeuwen R and von Barth U 2006 Phys. Rev. A 73 012511
- [98] Ruzsinszky A, Perdew J P and Csonka G I 2010 J. Chem. Theory Comput. 6 127
- [99] Mezei P D, Csonka G I, Ruzsinszky A and Kállay M 2015 J. Chem. Theory Comput. 11 4615–4626 ISSN 1549-9618
- [100] Mezei P D, Csonka G I, Ruzsinszky A and Kállay M 2017 Journal of Chemical Theory and Computation 13 796–803 ISSN 1549-9618, 1549-9626 URL http://pubs.acs.org/doi/10.1021/acs.jctc.6b01140
- [101] Zhang I Y and Xu X 2019 J. Phys. Chem. Lett. 10 2617
- [102] Mezei P D and Kállay M 2019 J. Chem. Theory Comput. 15 6678–6687 ISSN 1549-9618 publisher: American Chemical Society URL https://doi.org/10.1021/acs.jctc.9b00891
- [103] Olsen T and Thygesen K S 2012 Phys. Rev. B 86 081103(R)
- [104] Erhard J, Bleizier P and Görling A 2016 Phys. Rev. Lett. 117 143002
- [105] Freeman D L 1977 Phys. Rev. B 15 5512
- [106] Grüneis A, Marsman M, Harl J, Schimka L and Kresse G 2009 J. Chem. Phys. 131 154115
- [107] Paier J, Janesko B G, Henderson T M, Scuseria G E, Grüneis A and Kresse G 2010 J. Chem. Phys. 132 094103 erratum: ibid. 133, 179902 (2010).
- [108] Szabo A and Ostlund N S 1989 Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory (New York: McGraw-Hill)
- [109] Harris J and Jones R O 1974 J. Phys. F: Met. Phys. 4 1170
- [110] Toulouse J, Zhu W, Ángyán J G and Savin A 2010 Phys. Rev. A 132 244108
- [111] van Aggelen H, Yang Y and Yang W 2014 J. Chem. Phys. 140 18A511
- [112] Klimeš J, Kaltak M, Maggio E and Kresse G 2015 J. Chem. Phys. 143 102816
- [113] Jin Y, Su N Q and Yang W 2019 The Journal of Physical Chemistry Letters 10 447–452 (Preprint https://doi.org/10.1021/acs.jpclett.8b03337) URL https://doi.org/10.1021/acs.jpclett.8b03337
- [114] Li J and Yang W 2022 The Journal of Physical Chemistry Letters 13 9372–9380 pMID: 36190273 (Preprint https://doi.org/10.1021/acs.jpclett.2c02051) URL https://doi.org/10.1021/acs.jpclett.2c02051
- [115] Bates J E and Furche F 2013 J. Chem. Phys. 139 171103
- [116] Chen G P, Agee M M and Furche F 2018 J. Chem. Theory Comput. 14 5701
- [117] et al M J F Gaussian 09W Revision D.01 gaussian Inc. Wallingford CT 2009
-
[118]
TURBOMOLE V7.3 2018, a development of University of Karlsruhe and
Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007;
available from
http://www.turbomole.com. - [119] Paier J, Marsman M, Hummer K, Kresse G, Gerber I C and Ángyán J G 2006 J. Chem. Phys. 124 154709
- [120] Levchenko S V, Ren X, Wieferink J, Johanni R, Rinke P, Blum V and Scheffler M 2015 Comp. Phys. Comm. 192 60
- [121] Lin P, Ren X and He L 2020 J. Phys. Chem. Lett. 11 3082–3088
- [122] Lin P, Ren X and He L 2021 J. Chem. Theory Comput. 17 222–239 ISSN 1549-9626 (Electronic) 1549-9618 (Linking) URL https://doi.org/10.1021/acs.jctc.0c00960
- [123] Blum V, Hanke F, Gehrke R, Havu P, Havu V, Ren X, Reuter K and Scheffler M 2009 Comp. Phys. Comm. 180 2175
- [124] Ren X, Rinke P, Blum V, Wieferink J, Tkatchenko A, Sanfilippo A, Reuter K and Scheffler M 2012 New J. Phys. 14 053020
- [125] Ihrig A C, Wieferink J, Zhang I Y, Ropo M, Ren X, Rinke P, Scheffler M and Blum V 2015 New J. Phys. 17 093020
- [126] Vahtras O, Almlöf J and Feyereisen M W 1993 Chem. Phys. Lett. 213 514
- [127] Takatsuka A, Ten-no S and Hackbusch W 2008 J. Chem. Phys. 129 044112 publisher: American Institute of Physics
- [128] Lee J, Lin L and Head-Gordon M 2020 J. Chem. Theory Comput. 16 243–263 publisher: American Chemical Society
- [129] Zhen R, Zhang I Y and Xu X 2021 Chemical Journal of Chinese Universities 42 2210–2217
- [130] Ren X, Merz F, Jiang H, Yao Y, Rampp M, Lederer H, Blum V and Scheffler M 2021 Phys. Rev. Materials 5(1) 013807 URL https://link.aps.org/doi/10.1103/PhysRevMaterials.5.013807
- [131] Zhang I Y, Logsdail A J, Ren X, Levchenko S V, Ghiringhelli L and Scheffler M 2019 New J. Phys. 21 013025
- [132] Wang Y, Li Y, Chen J, Zhang I Y and Xu X 2021 JACS Au 1 543–549 publisher: American Chemical Society
- [133] Eshuis H, Yarkony J and Furche F 2010 J. Chem. Phys. 132 234114
- [134] Kaltak M, Klimeš J c v and Kresse G 2014 Phys. Rev. B 90(5) 054115 URL https://link.aps.org/doi/10.1103/PhysRevB.90.054115
- [135] Beuerle M and Ochsenfeld C 2018 J. Chem. Phys. 149 244111
- [136] Dobson J F 1994 Topics in Condensed Matter Physics ed Das M P (New York: Nova)
- [137] Zhang I Y and Xu X 2012 Phys. Chem. Chem. Phys. 14 12554–12570
- [138] Tan S, Wang Y, Zhang I Y and Xu X 2022 cjcp 35 720–726
- [139] Tang K T and Toennies J P 2003 J. Chem. Phys. 118 4976
- [140] Takatani T, Hohenstein E G, Malagoli M, Marshall M S and Sherrill C D 2010 J. Chem. Phys. 132 144104
- [141] Jurečka P, Šponer J, Černý J and Hobza P 2006 Phys. Chem. Chem. Phys. 8 1985
- [142] Eshuis H and Furche F 2012 J. Chem. Phys. 136 084105
- [143] Zhang I Y and Xu X 2013 J. Phys. Chem. Lett. 4 1669–1675
- [144] Chen B and Xu X 2020 J. Chem. Theory Comput. 16 4271–4285
- [145] Reilly A M and Tkatchenko A 2013 J. Chem. Phys. 139 024705
- [146] Paier J, Ren X, Rinke P, Scuseria G E, Grüneis A, Kresse G and Scheffler M 2012 New J. Phys. 14 043002
- [147] Steininger H, Lehwald S and Ibach H 1982 Surf. Sci. 123 264
- [148] Blackman G S, Xu M L, Ogletree D F, Hove M A V and Somorjai G A 1988 Phys. Rev. Lett 61 2352
- [149] Armiento R and Mattsson A E 2005 Phys. Rev. B 72 085108
- [150] Perdew J P, Ernzerhof M and Burke K 1996 J. Chem. Phys. 105 9982
- [151] Göltl F and Hafner J 2011 J. Chem. Phys. 134 064102
- [152] Kim H J, Tkatchenko A, Cho J H and Scheffler M 2012 Phys. Rev. B 85(4) 041403
- [153] Duan S, Zhang I Y, Xie Z and Xu X 2020 J. Am. Chem. Soc. 142 6902–6906 publisher: American Chemical Society
- [154] Michaelides A and Morgenstern K 2007 Nat. Mater. 6 597–601
- [155] Held K, McMahan A and Scalettar R 2001 Phys. Rev. Lett. 87 1–4
- [156] Amadon B, Biermann S, Georges A and Aryasetiawan F 2006 Phys. Rev. Lett. 96 1–4 ISSN 0031-9007
- [157] Lotrich V F and Szalewicz K 1997 Phys. Rev. Lett. 79(7) 1301–1304 URL https://link.aps.org/doi/10.1103/PhysRevLett.79.1301
- [158] Rościszewski K, Paulus B, Fulde P and Stoll H 2000 Phys. Rev. B 62(9) 5482–5488 URL https://link.aps.org/doi/10.1103/PhysRevB.62.5482
- [159] Rościszewski K, Paulus B, Fulde P and Stoll H 1999 Phys. Rev. B 60(11) 7905–7910 URL https://link.aps.org/doi/10.1103/PhysRevB.60.7905
- [160] Schwerdtfeger P, Tonner R, Moyano G E and Pahl E 2016 Angew Chem Int Ed Engl 55 12200–12205 URL https://doi.org/10.1002/anie.201605875
- [161] Zhang Y, Furness J W, Xiao B and Sun J 2019 J. Chem. Phys. 150 014105
- [162] Cui Z H, Wu F and Jiang H 2016 Phys. Chem. Chem. Phys. 18 29914–29922
- [163] Sengupta N, Bates J E and Ruzsinszky A 2018 Phys. Rev. B 97 235136
- [164] Marini A, García-González P and Rubio A 2006 Phys. Rev. Lett 96 136404
- [165] Rekkedal J, Coriani S, Iozzi M F, Teale A M, Helgaker T and Pedersen T B 2013 J. Chem. Phys. 139 081101
- [166] Burow A M, Bates J E, Furche F and Eshuis H 2014 J. Chem. Theory Comput. 10 180
- [167] Mussard B, Szalay P G and Ángyán J G 2014 J. Chem. Theory. Comput. 10 1968
- [168] Chedid J, Jocelyn N and Eshuis H 2021 The Journal of Chemical Physics 155 084303
- [169] Tahir M N, Zhu T, Shang H, Li J, Blum V and Ren X 2022 J. Chem. Theory Comput. 18 5297
- [170] Ramberger B, Schäfer T and Kresse G 2017 Phys. Rev. Lett. 118 106403
- [171] Su N Q, Zhang I Y and Xu X 2013 Journal of Computational Chemistry 1759–1774
- [172] Neuhauser D, Rabani E and Baer R 2013 J. Phys. Chem. Lett. 4 1172
- [173] Moussa J E 2014 J. Chem. Phys. 140 014107
- [174] Kállay M 2015 J. Chem. Phys. 142 204105
- [175] Wilhelm J, Seewald P, Del Ben M and Hutter J 2016 Journal of Chemical Theory and Computation 12 5851–5859 pMID: 27779863 (Preprint https://doi.org/10.1021/acs.jctc.6b00840) URL https://doi.org/10.1021/acs.jctc.6b00840
- [176] Graf D, Beuerle M, Schurkus H F, Luenser A, Savasci G and Ochsenfeld C 2018 J. Chem. Theory Comput. 14 2505
- [177] Luenser A, Schurkus H F and Ochsenfeld C 2017 Journal of Chemical Theory and Computation 13 1647–1655 pMID: 28263577 (Preprint https://doi.org/10.1021/acs.jctc.6b01235) URL https://doi.org/10.1021/acs.jctc.6b01235
- [178] Lu J and Thicke K 2017 Journal of Computational Physics 351 187–202 URL https://doi.org/10.1016/j.jcp.2017.09.012
- [179] Duchemin I and Blase X 2019 The Journal of Chemical Physics 150 174120 (Preprint https://doi.org/10.1063/1.5090605) URL https://doi.org/10.1063/1.5090605
- [180] Martin N M M L 2022 J. Phys. Chem. Lett. 13 9332–9338
- [181] van Aggelen H, Steinmann S N, Peng D and Yang W 2013 Phys. Rev. A 88 030501(R)
- [182] Peng D, Steinmann S N, van Aggelen H and Yang W 2013 J. Chem. Phys. 139 103112
- [183] Yang Y, van Aggelen H, Steinmann S N, Peng D and Yang W 2013 J. Chem. Phys. 139 174110
- [184] Scuseria E, Henderson T M and Bulik I W 2013 J. Chem. Phys. 139 104113
- [185] Shepherd J J, Henderson T M and Scuseria G E 2014 Phys. Rev. Lett. 112 133002
- [186] Tahir M N and Ren X 2019 Phys. Rev. B 99 195149
- [187] Verma P and Bartlett R J 2012 The Journal of Chemical Physics 136 044105 (pages 8)
- [188] Bleiziffer P, Hesselmann A and Görling A 2013 J. Chem. Phys. 139 084113
- [189] Hellgren M, Caruso F, Rohr D R, Ren X, Rubio A, Scheffler M and Rinke P 2015 Phys. Rev. B 91 165110
- [190] Peverati R and Head-Gordon M 2013 The Journal of Chemical Physics 139 024110
- [191] Jin Y, Zhang D, Chen Z, Su N Q and Yang W 2017 J. Phys. Chem. Lett. 8 4746
- [192] Voora V K, Balasubramani S G and Furche F 2019 Phys. Rev. A 99(1) 012518
- [193] Yu J M, Nguyen B D, Tsai J, Hernandez D J and Furche F 2021 The Journal of Chemical Physics 155 040902