Inverse Scattering Method Solves the Problem of Full Statistics of Nonstationary Heat Transfer in the Kipnis-Marchioro-Presutti Model
Abstract
We determine the full statistics of nonstationary heat transfer in the Kipnis-Marchioro-Presutti lattice gas model at long times by uncovering and exploiting complete integrability of the underlying equations of the macroscopic fluctuation theory. These equations are closely related to the derivative nonlinear Schrödinger equation (DNLS), and we solve them by the Zakharov-Shabat inverse scattering method (ISM) adapted by Kaup and Newell (1978) for the DNLS. We obtain explicit results for the exact large deviation function of the transferred heat for an initially localized heat pulse, where we uncover a nontrivial symmetry relation.
Introduction. – Full statistics of currents of matter or energy in macroscopic systems away from thermodynamic equilibrium is a fundamental quantity that has attracted much attention from statistical physicists in the past two decades. Major progress has been achieved in determining this quantity for nonequilibrium steady states in simple models of interacting particles Derrida2007 ; BlytheEvans ; AppertRolland ; Lecomte . Nonstationary fluctuations of current, however, proved to be much harder for analysis DG2009a ; DG2009b ; KrMe ; MS2013 ; MS2014 ; VMS2014 ; ZarfatyM .
A convenient and widely used family of models for studying the full statistics of currents is stochastic lattice gases Spohn ; Liggett ; KL ; Krapivskybook . One important example is the Kipnis-Marchioro-Presutti (KMP) model of heat transfer. The KMP model involves immobile particles occupying a whole lattice and carrying continuous amounts of energy. At each random move the total energy of a randomly chosen pair of nearest neighbors is randomly redistributed among them according to uniform distribution. The KMP model originally attracted much interest as the first model for which Fourier’s law of heat diffusion at a coarse-grained level was proven rigorously KMP . By now it has become a paradigmatic model of nonequilibrium fluctuations of transport Bertini2005 ; BGL ; BodineauDerrida ; DG2009b ; Lecomte ; Tailleur ; HurtadoGarrido ; KrMe ; Pradosetal ; MS2013 ; Peletier ; ZarfatyM ; Spielberg ; Guttierez ; Frassek ; Benichou .
Here we study a full non-stationary heat-transfer statistics in the KMP model on an infinite one-dimensional lattice. Suppose that only one particle has a nonzero energy at . Due to the energy exchange with the neighbors, the energy will start spreading throughout the system. At times much longer than the inverse rate of the energy exchange between the two neighbors (equal to ), and at distances much larger than the lattice constant (equal to ), the mean coarse-grained temperature in the KMP model is governed by the heat diffusion equation KMP ; Spohn ; KL . The initial temperature is a delta-function, , and so the solution is
| (1) |
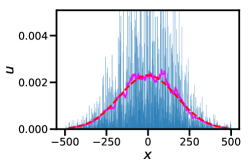
However, in stochastic realizations of the KMP model the coarse-grained temperature will fluctuate around the expected profile , see Fig. 1. To characterize these non-stationary fluctuations, we will consider the total amount of heat , observed on the right half line at time . The expected value of is , and we will study the full time-dependent statistics of the heat excess, . Obviously , the probability distribution of at time , has a compact support .
Similar non-stationary large-deviation settings, but with a step-like initial condition for the particle density or temperature, have been recently studied for a whole family of diffusive lattice gases DG2009b ; KrMe ; MS2013 ; MS2014 ; VMS2014 , of which the KMP model is an important particular case. The main working tool of these studies has been the macroscopic fluctuation theory (MFT) JonaLasinioreview : a weak-noise theory, whose starting point is fluctuational hydrodynamics (FH) Spohn ; KL ; LL . The FH is a coarse-grained description of the lattice gas, which is accurate when the characteristic length scale of the problem (here the diffusion length ) and the observation time are much larger than the lattice constant and the inverse elemental rate of the energy exchange, respectively. For diffusive lattice gases with a single conservation law the FH has the form of a single macroscopic Langevin equation, which accounts for the fluctuational contribution to the heat or mass flux. For the KMP model the Langevin equation reads Spohn ; KL
| (2) |
where is the temperature, and is a delta-correlated Gaussian noise: and .
The MFT JonaLasinioreview relies on a saddle-point evaluation of the path integral for the stochastic process, described by Eq. (2). The small parameter of the saddle-point evaluation is again : long times correspond to a weak noise. The saddle-point evaluation of the path integral boils down to a minimization of the action functional SM , constrained by the specified heat excess at and obeying the specified initial condition . For the statistics of the heat (or mass) excess, the MFT equations and boundary conditions in time were derived in Ref. DG2009b , and we will present them shortly. For completeness, we also present their derivation in SM . The solution of the MFT problem describes the optimal path of the process: the most likely time history of the temperature field which dominates the probability distribution that we are after. The MFT problem, however, has proven to be very hard to solve analytically, especially for quenched (that is, deterministic) initial conditions annealed . In particular, for the KMP model, only small- KrMe and large- MS2013 asymptotes have been obtained until now (but for a step-like initial condition).
This Letter reports a major advance in this area of statistical mechanics. We present an exact solution to the heat excess statistics problem by uncovering and exploiting complete integrability of the underlying MFT equations. We obtain explicit results for an initially localized heat pulse, , for which we uncover a nontrivial time-reversal mirror symmetry. These are the first exact non-steady-state large-deviation results for the statistics of current in a lattice gas of interacting particles for quenched initial conditions.
Formulation of the MFT problem DG2009b ; SM . – Let us rescale , and by , and , respectively. The optimal path we are after is described by two coupled Hamilton’s equations for the rescaled temperature field and the conjugate “momentum density” field which describes the optimal history of the noise , conditioned on the heat excess .
It is convenient to introduce the (minus) gradient field . In the variables and the MFT equations take the form DG2009b ; MS2013 ; SM
| (3) | |||||
| (4) |
The rescaled initial condition is
| (5) |
The condition on the heat excess at becomes
| (6) |
The minimization of the action functional, that enters the constrained path integral, with respect to variations of yields, aside from Eqs. (3) and (4), a second boundary condition in time DG2009b ,
| (7) |
where plays the role of a Lagrange multiplier, to be ultimately fixed by the constraint (6).
Once and are found, one can calculate the rescaled action, which can be written as DG2009b ; KrMe ; MS2013
| (8) |
The action yields the probability density up to a pre-exponent:
| (9) |
Since , Eq. (9) has a clear large-deviation structure, and the action plays the role of a rate function.
A crucial and previously unappreciated observation is that Eqs. (3) and (4) coincides with the derivative nonlinear Schrödinger (DNLS) equation in imaginary time and space DNLSE . The DNLS equation (with real time and space) describes propagation of nonlinear electromagnetic waves in plasmas and other media KN . An initial-value problem for the DNLS equation is completely integrable via the Zakharov-Shabat inverse scattering method (ISM) adapted by Kaup and Newell for the DNLS KN . The MFT formulation presents an difficulty, however, as here one needs to solve a boundary-value problem in time, rather than an initial-value problem. Here we overcome this difficulty by (i) making use of a shortcut that allows one to determine the rate function even without the knowledge of and for all , and (ii) exploiting a previously unknown symmetry relation symmetry , specific to the initial condition (5):
| (10) |
Solution of the MFT problem.– Equations (3) and (4) belong to a class of integrable systems for which a Lax pair exists, i.e., as we explain below, the equations are equivalent to the compatibility condition of a system of two linear differential equations. The latter system defines scattering amplitudes which depend on and . The idea behind the approach that we shall use – the ISM – is to consider the time evolution of these scattering amplitudes, which turns out to be very simple, as shown below. By relating these scattering amplitudes, at and , to the fields and , the method will enable us to find the heat excess which suffices for the calculation of .
Adapting the derivation of Kaup and Newell KN to imaginary time and space, we consider the linear system
| (11) |
where is a column vector of dimension 2,
| (12) |
and is a spectral parameter. As one can check, the compatibility condition , which corresponds to
| (13) |
Let us define the matrix as the -propagator of the system (11), namely, the solution to
| (14) |
with (the identity matrix). At , where the fields and vanish, the matrix becomes very simple,
| (15) |
Therefore, it is natural to define the full-space propagator as follows:
| (18) | ||||
| (19) |
The entries of the matrix are the scattering amplitudes of the system (11). The time evolution of is easy to find. Indeed, the matrix satisfies:
| (20) | |||||
One can check that Eq. (20) is compatible with (14) (i.e. ) due to Eq. (13). The matrix too becomes very simple in the limit ,
| (21) |
Plugging (21) into (20), one finds the time evolution of which in turn, using (18), yields that of
| (22) |
where we have introduced here a notation for the matrix elements of .
Plugging the temporal boundary conditions (5) and (7), we calculate and explicitly by solving Eq. (14), see SM . Comparing the two solutions and using (22) we obtain
| (23) |
where are the Fourier transforms of restricted to and , respectively:
| (24) |
We solve Eq. (23) in SM , with the result
| (25) | ||||
| (26) |
where .
To compute we demand that be regular at the origin, corresponding to a vanishing at infinity. Setting in Eq. (25) and using the Sokhotski–Plemelj formula
| (27) |
we obtain after some algebra
| (28) |
Taking the derivative of Eq. (25) with respect to at , yields SM
| (29) |
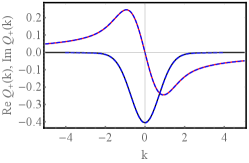
Figure 2 shows and versus at , obtained by plugging Eq. (28) for into Eq. (25). This figure also shows the same quantities computed by solving Eqs. (3) and (4) numerically with a back-and-forth iteration algorithm CS . The analytical and numerical curves are almost indistinguishable.
Using Eqs. (6), (10) and (24) alongside with the conservation law , we determine :
| (30) |
Now we use a shortcut which makes the results we have obtained so far sufficient for obtaining the rate function . The shortcut comes in the form of the relation , which follows from the fact that and are conjugate variables, see e.g. Ref. Vivoetal . It allows one to calculate bypassing Eq. (8) [which would require the knowledge of the whole optimal path ]. We have
| (31) |
Using Eq. (29), we integrate Eq. (31) with respect to to get
| (32) |
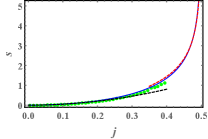
where is the dilogarithm function, is given by Eq. (29), and the integration constant was determined from . Equations (30) and (32) give the complete rate function in a parametric form and represent the main result of this work. The exact optimal history of the temperature profile proved difficult to obtain analytically, but it can be computed numerically SM .
Figure 3 shows alongside with two asymptotes: and , which correspond to and , respectively. Also shown are results of Monte-Carlo simulations. The asymptote can be obtained either from the exact rate function (30) and (32) SM , or from a perturbative expansion applied directly to the MFT equations KrMe . By virtue of the symmetry (10), the latter can be done very easily. Indeed, in the leading order in Eqs. (8), (10) and (1) yield
| (33) |
The shortcut relation can be rewritten as . Combined with Eq. (33) it yields . Then, from Eq. (9), we see that typical fluctuations of are normally distributed with variance . The scaling of the variance should be contrasted with the scaling, obtained for a step-like initial condition DG2009b ; DG2009a ; KrMe . However, the relative magnitude of the fluctuations – the ratio of the standard deviation and the average transferred heat – has the same scaling in both settings, as to be expected from the law of large numbers.
The asymptote of is more subtle SM . The final result, already in terms of , is
| (34) |
where , and is the proper branch of the product log (Lambert ) function LambertW . At , diverges and vanishes, as to be expected. Nested-log large-current asymptotes similar to Eq. (Inverse Scattering Method Solves the Problem of Full Statistics of Nonstationary Heat Transfer in the Kipnis-Marchioro-Presutti Model) appear to be typical for the KMP model and other models of the hyperbolic universality class MS2013 ; MS2014 ; ZarfatyM .
Discussion.– By combining the MFT and the ISM, we calculated exactly the rate function , see Eqs. (30) and (32), which describes the full long-time statistics of nonstationary heat transfer in the KMP model for an initially localized heat pulse. This is the first exact non-steady-state large-deviation result for the statistics of current in a lattice gas of interacting particles for quenched initial conditions. It opens the way to extensions of the ISM to additional fluctuating quantities of the KMP model. Another challenging goal is to apply the ISM to the simple symmetric exclusion process (SSEP) Spohn ; Liggett ; KL ; Krapivskybook – a lattice-gas model with quite different properties MS2014 . Encouragingly, the MFT equations for the SSEP (see e.g. DG2009b ) can be mapped to Eqs. (3) and (4) via a canonical transformation. This transformation, however, complicates the boundary conditions in time.
From a more general perspective, the MFT of lattice gases is a particular case of the weak-noise theory, or optimal fluctuation method (OFM): a highly versatile framework which captures a broad class of large deviations in macroscopic systems. For non-stationary processes the OFM equations – coupled nonlinear partial differential equations for the optimal path – are usually very hard to solve exactly. One class of problems of this type, which has received much recent attention, deals with the complete one-point height statistics of an interface whose dynamics is described by the Kardar-Parisi-Zhang (KPZ) equation KPZ . The OFM captures the complete KPZ height statistics at short times KK ; MKV ; KMS ; JKM ; Lin ; Lamarre . Here too, a previous analytical progress in the solution of the OFM equations was limited to asymptotics of very large or very small interface height. But very recently these OFM equations – which coincide with the Nonlinear Schrödinger equation (NLS) (not the derivative one) JKM – have been solved exactly KLD1 ; KLD2 by the ISM for several “standard” initial conditions. The two integrable systems, the NLS and DNLS, are closely related, so our approach can be compared with that of Refs. KLD1 ; KLD2 . We used only standard techniques of the ISM which do not rely on additional tools, such as Fredholm determinants used in Refs. KLD1 ; KLD2 . Because of its relative simplicity our approach appears to be more readily adaptable to solving additional large-deviation problems BSM2 .
Acknowledgments. – The research of E.B. and B.M. is supported by the Israel Science Foundation (grants No. 1466/15 and 1499/20, respectively). N.R.S. acknowledges support from the Yad Hanadiv fund (Rothschild fellowship).
References
- (1) B. Derrida, J. Stat. Mech. (2007) P07023.
- (2) R. A. Blythe and M. R. Evans, J. Phys. A: Math. Theor. 40, 46 (2007).
- (3) C. Appert-Rolland, B. Derrida, V. Lecomte, and F. van Wijland, Phys. Rev. E 78, 021122 (2008).
- (4) V. Lecomte, A. Imparato, and F. van Wijland, Prog. Theor. Phys. Suppl. 184, 276 (2010).
- (5) B. Derrida and A. Gerschenfeld, J. Stat. Phys. 136, 1 (2009).
- (6) B. Derrida and A. Gerschenfeld, J. Stat. Phys. 137, 978 (2009).
- (7) P. L. Krapivsky and B. Meerson, Phys. Rev. E 86, 031106 (2012).
- (8) B. Meerson and P. V. Sasorov, J. Stat. Mech. (2013) P12011.
- (9) B. Meerson and P. V. Sasorov, Phys. Rev. E 89, 010101(R) (2014).
- (10) A. Vilenkin, B. Meerson and P. V. Sasorov, J. Stat. Mech. (2016) 06007.
- (11) L. Zarfaty and B. Meerson, J. Stat. Mech. (2016) 033304.
- (12) H. Spohn, Large Scale Dynamics of Interacting Particles (Springer, New York, 1991).
- (13) T. M. Liggett, Stochastic Interacting Systems: Contact, Voter, and Exclusion Processes (Springer, New York, 1999).
- (14) C. Kipnis and C. Landim, Scaling Limits of Interacting Particle Systems (Springer, New York, 1999).
- (15) P. L. Krapivsky, S. Redner, and E. Ben-Naim, A Kinetic View of Statistical Physics (Cambridge University Press, Cambridge, UK, 2010).
- (16) C. Kipnis, C. Marchioro and E. Presutti, J. Stat. Phys. 27, 65 (1982).
- (17) L. Bertini, A. De Sole, D. Gabrielli, G. Jona-Lasinio, and C. Landim, Phys. Rev. Lett. 94, 030601 (2005).
- (18) L. Bertini, D. Gabrielli, and J. L. Lebowitz, J. Stat. Phys. 121, 843 (2005).
- (19) T. Bodineau and B. Derrida, Phys. Rev. E 72, 066110 (2005).
- (20) J. Tailleur, J. Kurchan, and V. Lecomte, Phys. Rev. Lett. 99, 150602 (2007); J. Phys. A: Math. Theor. 41 505001 (2008).
- (21) P. I. Hurtado and P. L. Garrido, Phys. Rev. Lett. 107, 180601 (2011).
- (22) A. Prados, A. Lasanta, and P. I. Hurtado, Phys. Rev. E 86, 031134 (2012).
- (23) M. A. Peletier, F. H. J. Redig, and K. Vafayi, J. Math. Phys. 55, 093301 (2014).
- (24) O. Shpielberg, Y. Don, and E. Akkermans, Phys Rev E 95, 032137 (2017).
- (25) C. Gutiérrez-Ariza and P. I. Hurtado, J. Stat. Mech. (2019) 103203.
- (26) R. Frassek, C. Giardinà, and J. Kurchan, SciPost Phys. 9, 054 (2020).
- (27) A. Grabsch, A. Poncet, P. Rizkallah, P. Illien, and O. Bénichou, arXiv:2110.09269.
- (28) L. Bertini, A. De Sole, D. Gabrielli, G. Jona-Lasinio, and C. Landim, Rev. Mod. Phys. 87, 593 (2015).
- (29) L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics. Vol. 5: Statistical Physics (Pergamon Press, Oxford, 1968).
- (30) See Supplemental Material
- (31) For an annealed step-like initial condition (a step-function with equilibrium density distributions with given average densities and at and ), the full heat transfer statistics for the KMP model was found by Derrida and Gerschenfeld DG2009b . They achieved it by uncovering an exact mapping between the KMP model and the simple symmetric exclusion process, where an exact microscopic solution was previously obtained DG2009a .
- (32) A. B. Shabat, V. E. Adler, V. G. Marikhin, and V. V. Sokolov, editors, Encyclopedia of Integrable Systems (L. D. Landau Institute for Theoretical Physics, Moscow, 2010), http://home.itp.ac.ru/~adler/E/e.pdf, p. 312.
- (33) D. J. Kaup and A. C. Newell. J. Math. Phys. 19, 798 (1978).
- (34) Indeed, Eq. (10) leaves Eqs. (3) and (4) and the boundary conditions (5) and (7) invariant.
- (35) A. I. Chernykh and M. G. Stepanov, Phys. Rev. E 64, 026306 (2001).
- (36) F. D. Cunden, P. Facchi, and P. Vivo, J. Phys. A: Math. Theor. 49, 135202 (2016).
- (37) https://mathworld.wolfram.com/LambertW-Function.html.
- (38) M. Kardar, G. Parisi, and Y.-C. Zhang, Phys. Rev. Lett. 56, 889 (1986).
- (39) I. V. Kolokolov and S. E. Korshunov, Phys. Rev. B 75, 140201(R) (2007); Phys. Rev. B 78, 024206 (2008); Phys. Rev. E 80, 031107 (2009).
- (40) B. Meerson, E. Katzav, and A. Vilenkin, Phys. Rev. Lett. 116, 070601 (2016).
- (41) A. Kamenev, B. Meerson, and P. V. Sasorov, Phys. Rev. E 94, 032108 (2016).
- (42) M. Janas, A. Kamenev, and B. Meerson, Phys. Rev. E 94, 032133 (2016).
- (43) Lin and L. C. Tsai, Commun. Math. Phys. 386, 359 (2021).
- (44) P. Y. G. Lamarre, Y. Lin, and L. C. Tsai, arXiv:2106.13313.
- (45) A. Krajenbrink and P. Le Doussal, Phys. Rev. Lett. 127, 064101 (2021).
- (46) A. Krajenbrink and P. Le Doussal, arXiv:2107.13497.
- (47) E. Bettelheim, N. R. Smith, and B. Meerson, in preparation.
Supplementary Material for
“Inverse Scattering Method Solves the Problem of Full Statistics of Nonstationary Heat Transfer in the Kipnis-Marchioro-Presutti Model” by E. Bettelheim et al.
Here we give some technical details of the calculations described in the main text of the Letter.
I Derivation of the MFT equations and boundary conditions
We begin by defining an auxiliary potential
| (S1) |
Integrating Eq. (2) of the main text with respect to and using the boundary condition , we obtain a Langevin equation for :
| (S2) |
Now we use a path-integral approach, by writing the probability density functional of the white Gaussian noise term :
| (S3) |
We now express through via Eq. (S2), enabling us to write the probability density for a given history of the system:
| (S4) |
where is the action functional. The presence of the large parameter enables us to calculate via a saddle-point evaluation of the path integral. Within this framework, is given by minimum of the action functional , constrained on the initial condition and on a given value of heat excess . The heat excess, which we recall is , is conveniently rewritten as (where we used the conservation law ). To take into account the latter constraint on , we add the term to the action, where is a Lagrange multiplier, i.e., we minimize the constrained functional
| (S5) |
The subsequent procedure is pretty standard. Consider a variation . This leads to a variation of , which, to first order in is given by
| (S6) | |||||
where we have defined the momentum density gradient
| (S7) |
Integrating by parts in Eq. (S6), we obtain
| (S8) | |||||
where the first two terms in the single integral are the boundary terms originating from the integration by parts in time. For the quenched (deterministic) initial condition, the variation vanishes.
The second MFT equation, Eq. (4) in the main text is now obtained by requiring the double integral in (S8) to vanish for arbitrary (recalling that and ). The first MFT equation, Eq. (3) in the main text, follows from Eq. (S7) after multiplying by the denominator and then taking a spatial derivative. Note that, under the rescalings of , and described in the text, should be rescaled by . These rescalings leave the MFT equations invariant. Requiring the single integral in Eq. (S8) to vanish for arbitrary , we obtain the boundary condition
| (S9) |
After the rescaling, this becomes Eq. (7) in the main text, where is a rescaled Lagrange multiplier. Finally, using Eq. (S7) in (S4) we find that the action can be rewritten as which, after the rescaling, leads to where the rescaled action is given by Eq. (8) in the main text. The large parameter justifies a posteriori the saddle-point approximation that we used.
II Solving the scattering problem at and
Let us find the matrix at . By solving Eq. (14) of the main text at , using , one gets
| (S10) |
where
| (S11) |
and in the second case in (S10), the sign is to be taken as the sign of Plugging (S10) into Eq. (18) of the main text, we compute :
| (S12) |
in terms of which are defined in Eq. (24) in the main text, with .
It is useful to compare this result to the one obtained at . Here we have . Similarly to the case, one gets
| (S13) |
where in the second case, the sign is to be taken as the opposite of the sign of Now compute :
| (S14) |
where
| (S15) |
Comparing the upper-right elements of from Eq. (S12) and of from Eq. (S14), using Eq. (22) of the main text, leads to Eq. (23) of the main text.
III Solving Eq. (23) of the main text
We can complete the squares in Eq. (23) of the main text by writing
| (S16) |
where . This turns Eq. (23) of the main text into
| (S17) |
which has the solution
| (S18) |
provided the condition
| (S19) |
is satisfied. Eq. (S18) is derived by noting that are analytic in the upper and lower half plane respectively and are well-behaved when is allowed to reach infinity through the respective half-planes. We then use the well-known decomposition of a general function into functions analytic in the upper and lower half-planes, , respectively, given by . This decomposition is applied to the logarithm of Eq. (S17). Plugging Eq. (S18) into Eq. (S16), we obtain the solution given in Eqs. (25) and (26) of the main text.
IV Calculating
Taking the derivative of Eq. (25) with respect to at , yields the equation:
| (S20) |
The imaginary part of the integrand is an odd function of and therefore does not contribute to the integral. Keeping only the real part and simplifying it, we obtain (29) of the main text, where we replaced the principal value integral by a regular integral since the integrand is regular at .
V Asymptotics of small and large
At small Eq. (29) of the main text yields
| (S21) |
therefore . Now, using the asymptotic in the integrand of Eq. (32) of the main text, we obtain after a simple algebra: . This yields the asymptotic behavior given in the main text.
Now we consider the asymptote and start from Eq. (29) of the main text. Due to the symmetry , we consider only . Let us denote the integrand in Eq. (29) (including the factor ) by
We can recast it as
| (S22) |
where
| (S23) |
The integral over the first term of Eq. (S22) yields , and we now focus on the integral of . For , as a function of behaves as follows (see Fig. 4). At , is approximately constant and equal to . This asymptote is obtained when neglecting in the numerator and in the denominator of the fraction inside the logarithm in Eq. (S23). For , behaves as
| (S24) |
This asymptote is obtained when neglecting the second term in the numerator and in the denominator of the fraction inside the logarithm in Eq. (S23). Importantly, the transition from the asymptote to the asymptote (S24) occurs in a narrow boundary layer around , whose width goes to zero as . Furthermore, the region of contributes a term to the integral which, as we shall see a posteriori, is negligible. Therefore, we can divide the integration region into two subregions: and , and use the asymptote in the former subregion, and Eq. (S24) in the latter one. Keeping the leading and two subleading terms in the result and multiplying it by 2 to account for , we obtain
| (S25) |
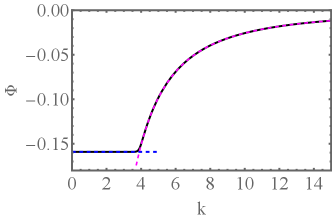
Using the relation (30) of the main text between and , we obtain in the leading order:
| (S26) |
To calculate the large- asymptote of , we plug (S26) into the first equality in (31) in the main text to get
| (S27) |
Integrating this over we obtain
| (S28) |
(Note that, in the limit that we consider here, the integration constant is not important.) Solving Eq. (S26) for , we obtain
| (S29) |
where , and is the proper branch of the product log (Lambert ) function LambertWSM . Plugging Eq. (S29) into Eq. (S28), we obtain the large- asymptote (Inverse Scattering Method Solves the Problem of Full Statistics of Nonstationary Heat Transfer in the Kipnis-Marchioro-Presutti Model) of the main text.
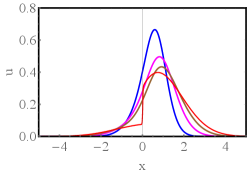
VI Obtaining the optimal path numerically at all times
Our exact solution gives the rate function but it does not give the optimal path at all times. To calculate the latter analytically, one would need to solve Eq. (14) of the main text at arbitrary times , and this is far more challenging than solving it only at and , as we did. The optimal path can, however, be computed numerically, using the back-and-forth iteration algorithm due to Chernykh and Stepanov CSSM . The results of one such calculation are shown in Fig. 5.
VII Monte-Carlo simulations
Here we describe how the numerical data in Fig. 3 of the main text was generated. We performed Monte-Carlo (MC) simulations of the microscopic KMP model. The dynamical object in the simulations is the vector of energies at lattice sites, , where the site represents the origin, . Initially, all of the energy is at the origin, (this corresponds to ). At every Monte-Carlo step, we randomly choose one of the adjacent pairs of lattice sites , and randomly redistribute their total energy between them, i.e., where is sampled from a uniform distribution between and , and . Since (in our convention) the microscopic rate of this elementary process is , the total number of steps in the simulation is randomly sampled from a Poisson distribution with mean . The excess heat was measured at as . Since the distribution is exactly symmetric, , a histogram of the absolute values of the simulated ’s was constructed. For the data plotted on Fig. 3 of the main text, the parameters used were and (we found that increasing beyond this value did not noticeably affect the results displayed in the figure). The symbols in the figure correspond to
| (S30) |
where the probability density function was computed from the histogram of the simulated ’s, and is our prediction for the variance [see the paragraph following Eq. (33) of the main text]. The term in Eq. (S30) comes from the normalization of the central part of the distribution, rather than from a systematic calculation of the pre-exponential factor in which is beyond the leading-order MFT. The normalization approximation of the pre-exponential factor introduces a small systematic error at moderate which is discernible in Fig. 3 of the main text. The relative error, introduced by the pre-exponential factor, must go to zero as goes to infinity.
As to be expected, direct MC simulations become prohibitively long for larger and . Special methods of large deviation sampling should be used for these purposes.
References
- (1) https://mathworld.wolfram.com/LambertW-Function.html.
- (2) A. I. Chernykh and M. G. Stepanov, Phys. Rev. E 64, 026306 (2001).