Ion pseudoheating by low-frequency Alfvén waves Revisited

Plasma heating and acceleration are hot topics in the fields of nuclear fusion, plasma physics and astrophysics for a long time. A great number of heating mechanisms and theories have been proposed. In a collisionless space plasma environment, wave-particle interactions play significant roles of plasma heating and acceleration[2, 1, 3, 4, 5, 6]. Even when collisions are included, plasmas can still be heated by the interplay between waves and particles to a certain degree[7, 8, 9]. Among a suite of electromagnetic waves, Alfvén waves are generally thought to be the major contributor to the ion heating and acceleration since they exist pervasively in the solar wind and interplanetary space[10, 11, 12, 13].

In thermodynamic sense, heating of ions by electromagnetic waves will lead to the dissipation of wave fields, thereby being an irreversible process. Several recent studies however show that ions can be heated by turbulent Alfvén waves in low-beta plasmas even when no dissipation of wave fields occurrs[14, 15, 17, 19, 18, 20, 16, 21]; a process that is called “pseudoheating” or nonresonant wave-particle interaction. Various methods have been used to validate this heating mechanism such as the test-particle approach with analytic solutions[14, 17], and quasi-linear theories[15, 16]. In fact, the name “pseudoheating” may not be the best term to describe this “heating” process due to the kinetic effects of wave spectra[15, 19]. However, we still use this appellation for consistency in this paper. The pseudoheating is caused by the wave forces (or their spectra) that result in a deformation of the distribution function with respect to its initial Maxwellian shape. The mean-square velocity fluctuation due to the wave activity leads to an effective broadening of the distribution function similar to real heating and thus could mimic the genuine heating process[22]. It is important to point out that the heating shown by Ref.[14] contains both pseudoheating and genuine heating, which indicates that even in the particles’ mean-velocity frame, the random kinetic energy of particles still increases via wave-particle interactions. The real heating (or the irreversible dissipation of the wave fields) is caused by the initial pitch-angle scattering of newly created ions[20], indicating that there exists the dissipation of wave fields. In contrast, the first adiabatic invariant (magnetic moment $\mu=w_{\perp}/B$) remains constant during the pseudoheating and thus it is an reversible process. The real heating in Refs.[20, 14] is caused by the violation of the first adiabatic invariant due to the abrupt spatial change of the magnetic field. It is noteworthy that there is a factor of two difference between the temperature expressions in Ref.[14] and Ref.[15], resulting from the fact that quasilinear theory cannot solve the problem of the wave damping appropriately. In addition, Wang et al. pointed out that pitch-angle scattering plays a key role in the pseudoheating process[17].

In this paper, the heating process we focus on is restricted to the pseudoheating and thus the real heating is excluded. We demonstrate that the low-frequency Alfvén wave propagating along the background magnetic field ${\mathbf{B}}_{0}={B}_{0}{\mathbf{i}}_{z}$ can “heat” ions. The pseudoheating can be explained either by $E\times B$ drift (in the electric field of the Alfvén wave and the ambient magnetic field $B_{0}$) proposed in this paper or the pitch-angle scattering previously investigated[17]. Our analytic results, as will be shown below, are identical as those derived from quasilinear theory[15]. As shown in previous work[15, 17]:

$$T_{p\perp}\simeq T_{0}+\frac{W_{B}}{n_{p}}=T_{0}\left(1+\frac{1}{{\beta}_{p}}\frac{B_{W}^{2}}{B_{0}^{2}}\right)$$

(1.1)

where $W_{B}=B_{W}^{2}/2\mu_{0}$ and $n_{p}$ are the wave magnetic field energy density and proton number density, respectively. ${\beta}_{p}$ denotes proton $\beta$ that equals to $\left\langle v\right\rangle^{2}/v_{A}^{2}$ ($\left\langle v\right\rangle$: the thermal speed). $B_{W}^{2}/B_{0}^{2}$ represents the ratio of wave-field energy density to that of the ambient field and $T_{0}=m_{p}\left\langle v\right\rangle^{2}/2k_{B}$ is the initial proton temperature. Here $T_{p}$ represents the “apparent temperature” that should be distinguished from the temperature associated with a real heating process[17].

The structure of the remainder of this paper is as follows: We derive and discuss the analytic results of pseudoheating based on $E\times B$ drift in Section 2. In Section 3, test particle simulation results are presented and discussed based on the comparison of a monochromatic Alfvén wave and a wave spectrum. We also briefly discuss the recent observations of large amplitude magnetic perturbations associated with Alfvén waves and their correlation to the pseudoheating. In the last section, conclusions are summarized.

Without loss of generality, left-hand circular polarized Alfvén waves are considered in this paper. The wave magnetic field vector can thus be expressed as

$$\mathbf{B}_{W}=\sum_{k}{B}_{k}(\cos{\phi}_{k}{\mathbf{i}}_{x}-\sin{\phi}_{k}{\mathbf{i}}_{y}),$$

(2.2)

From the Faraday’s law and the dispersion relation (Ampère’s law) $\omega=kv_{A}$, the electric field vector can be written as

$$\mathbf{E}_{W}=-v_{A}{\mathbf{i}}_{z}\times\mathbf{B}_{W}$$

(2.3)

where ${\mathbf{i}}_{x}$, ${\mathbf{i}}_{y}$ and ${\mathbf{i}}_{z}$ are unit directional vectors, ${\phi}_{k}=k({v}_{A}t-z)+\varphi_{k}$ denotes the wave phase, $\varphi_{k}$ is the random phase for mode $k$ and $v_{A}=B_{0}/\sqrt{\mu_{0}n_{p}m_{p}}$ represents the Alfvén speed. According to the linear approximation, we use Eq.(2.3) and the first order term of the generalized Ohmic law $\mathbf{E}_{W}=-\mathbf{v}_{\perp}\times\mathbf{B}_{0}$ to derive the $E\times B$ drift velocity, $\mathbf{v}_{E}$, that can be expressed as follows:

$$\mathbf{v}_{E}=\mathbf{v}_{\perp}=\frac{\mathbf{E}_{W}\times\mathbf{B}_{0}}{B_{0}^{2}}=\frac{-v_{A}{\mathbf{i}}_{z}\times\mathbf{B}_{W}\times\mathbf{B}_{0}}{B_{0}^{2}}$$

(2.4)

The derivation above is consistent with the traditional procedure to derive the classical Alfvén wave solution[22] in the ideal magnetohydrodynamic (MHD) system. It indicates that the randomized proton motion is actually parasitic to wave fields due to the fact that the drift velocity $\mathbf{v}_{E}$ is expected to disappear if the waves subside. Given the assumption that the characteristic spatial scale of the system is much larger than typical Alfvén wavelength[14], the energy density associated with the wave magnetic field can be written as:

$$W_{B}=\frac{1}{2}n_{p}m_{p}\left\langle\left(\mathbf{v}_{E}-\left\langle\mathbf{v}_{E}\right\rangle\right)^{2}\right\rangle=\frac{1}{2}n_{p}m_{p}v_{A}^{2}\frac{{B}_{W}^{2}}{B_{0}^{2}}=\frac{1}{2}n_{p}m_{p}\frac{B_{0}^{2}}{\mu_{0}n_{p}m_{p}}\frac{{B}_{W}^{2}}{B_{0}^{2}}=\frac{B_{W}^{2}}{2\mu_{0}}$$

(2.5)

where the bracket $\left\langle\cdot\right\rangle$ denotes an average over all particles. Given the large characteristic spatial scale of the system, $l$, as described above, the following approximation is valid:

$$\left\langle\mathbf{v}_{E}\right\rangle=\lim_{l\rightarrow\infty}\frac{1}{l}\int_{0}^{l}\mathbf{v}_{E}dz=0$$

(2.6)

The temperature expression shown below is the same as Eq.(1.1),

$$T_{p\perp}=T_{0}+\frac{1}{2}n_{p}m_{p}\left\langle\left(\mathbf{v}_{E}-\left\langle\mathbf{v}_{E}\right\rangle\right)^{2}\right\rangle=T_{0}+\frac{B_{W}^{2}}{2\mu_{0}}=T_{0}\left(1+\frac{1}{\beta_{p}}\frac{B_{W}^{2}}{B_{0}^{2}}\right)$$

(2.7)

The results shown in Eqs.(2.5)&(2.7) are consistent with the MHD theory due to the fact that the energy density associated with the Alfvén wave magnetic field, $B_{W}^{2}/2\mu_{0}$, equals to the ion (fluid) kinetic energy density, $B_{W}^{2}/2\mu_{0}=B_{0}^{2}u_{1}^{2}/(2\mu_{0}v_{A}^{2})=\rho_{0}u_{1}^{2}/2$, where $u_{1}$ is the perturbed ion (fluid) velocity. The consistency between Eqs.(2.5)&(2.7) and the MHD theory[21] clearly indicates that the analytic theory described here incorporates the local equilibrium velocity distribution of the ions. In the following section, we adopt the test particle approach to simulate pesudoheating and the results will be presented and discussed in detail.

We start with a linearly polarized Alfvén wave with wave magnetic field vector $\mathbf{B}_{W}=\sum_{k}{B}_{k}\cos{\phi}_{k}{\mathbf{i}}_{y}$ in order to show that the drift velocity is in $E\times B$ direction. This is the basis of further understanding. Then we conduct two case studies. In case one, we consider a monochromatic dispersionless Alfvén wave with frequency $\omega$=0.05$\Omega_{p}$. In case two, we test a spectrum of Alfvén waves with random phase $\varphi_{k}$, and the frequencies of the wave modes can be calculated as follows: $\omega_{i}=\omega_{1}+(i-1)\triangle\omega$ ($i$=1,2,…, $N$; $N$=41), where $\triangle\omega=(\omega_{N}-\omega_{1})/(N-1)$; $\omega_{1}$=0.01$\Omega_{p}$ and $\omega_{N}$=0.05$\Omega_{p}$. The amplitude of each wave mode (only one wave mode in case one) is considered to be equal but changes gradually with time such that $B_{W}^{2}=\sum_{k}B_{k}^{2}=\epsilon(t)B_{0}^{2}$, where

$\epsilon(t)=\left\{\begin{array}[]{ccc}\epsilon_{0}e^{-(t-t_{1})^{2}/\tau^{2}},&if&t<t_{1},\\ \epsilon_{0},&if&t_{1}\leq t\leq t_{2},\\ \epsilon_{0}e^{-(t-t_{2})^{2}/\tau^{2}},&if&t>t_{2}.\end{array}\right.$

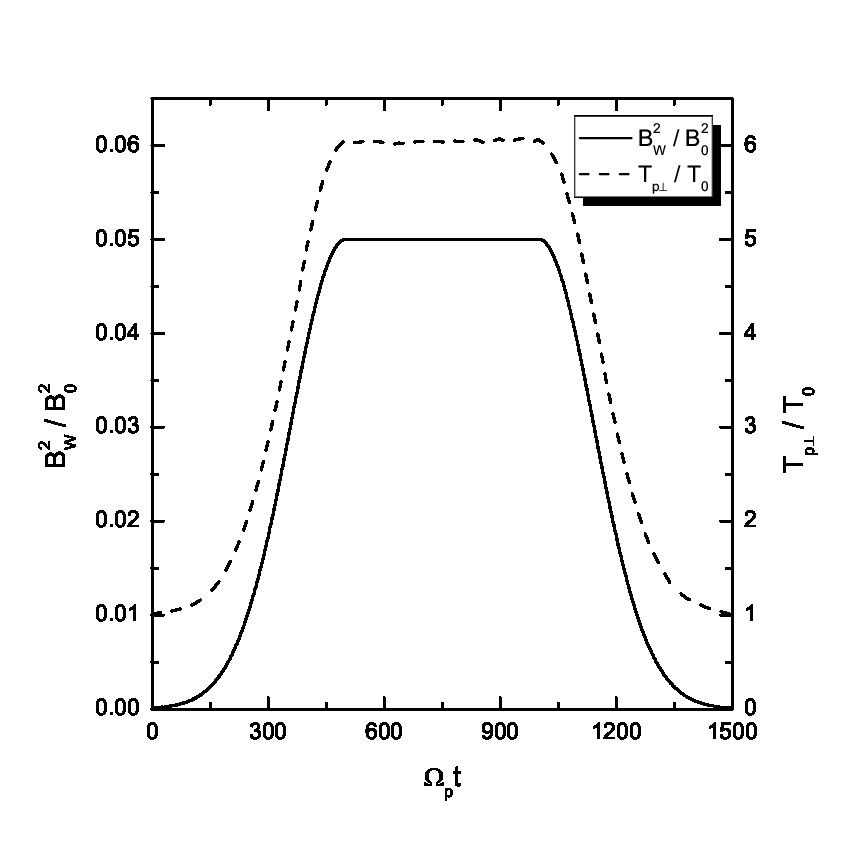
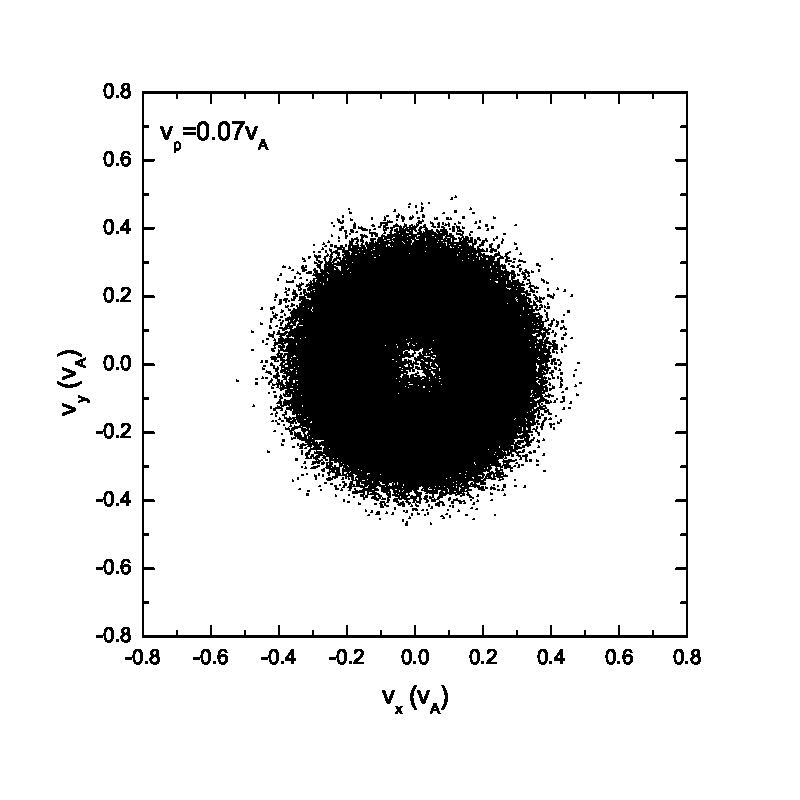
Similar to previous work[17], we set $t_{1}$=500$\Omega_{p}^{-1}$, $t_{2}$=1000$\Omega_{p}^{-1}$, $\tau$=200$\Omega_{p}^{-1}$, and $\epsilon_{0}$=0.05, where $\Omega_{p}$ is the proton gyrofrequency. The initial velocities of test particles are randomly distributed and possess a Maxwellian distribution with thermal speed $v_{p}$=0.07$v_{A}$ (the situations with $v_{p}$=0.01$v_{A}$, 0.03$v_{A}$, and 0.15$v_{A}$ are also discussed later). The numerical scheme is similar to what described in Ref.[14, 7]. It is noteworthy that the ion thermal speed $v_{p}$ in this paper and in Refs.[7, 14, 17, 20] is defined as $v_{p}=\left(k_{B}T/m\right)^{1/2}$[23] while the general thermal speed $\left\langle v\right\rangle=$ $\left(2k_{B}T/m\right)^{1/2}$, causing $v_{p}^{2}=\left\langle v\right\rangle^{2}/2$. Thus it leads to a factor of two difference for proton $\beta_{p}$. The basic reason causing this difference is the different definition of temperature, i.e., $T=m\left\langle v\right\rangle^{2}/2k_{B}$ or $T=mv_{p}^{2}/k_{B}$. The one-dimensional Maxwellian velocity distribution based on $\left\langle v\right\rangle$ and $v_{p}$ can be expressed as follows[23]:

$$f_{v}\left(v_{i=x,y,z}\right)=\frac{n}{\left(\pi\left\langle v_{i}\right\rangle^{2}\right)^{1/2}}\exp\left(-\frac{v_{i}^{2}}{\left\langle v_{i}\right\rangle^{2}}\right)=\frac{n}{\left(2\pi v_{p}^{2}\right)^{1/2}}\exp\left(-\frac{v_{i}^{2}}{2v_{p}^{2}}\right)$$

(3.8)

Different definitions of thermal speed or temperature, however, do not affect the final results since self-consistent definition is maintained throughout the previous studies[7, 14, 17, 20, 15].

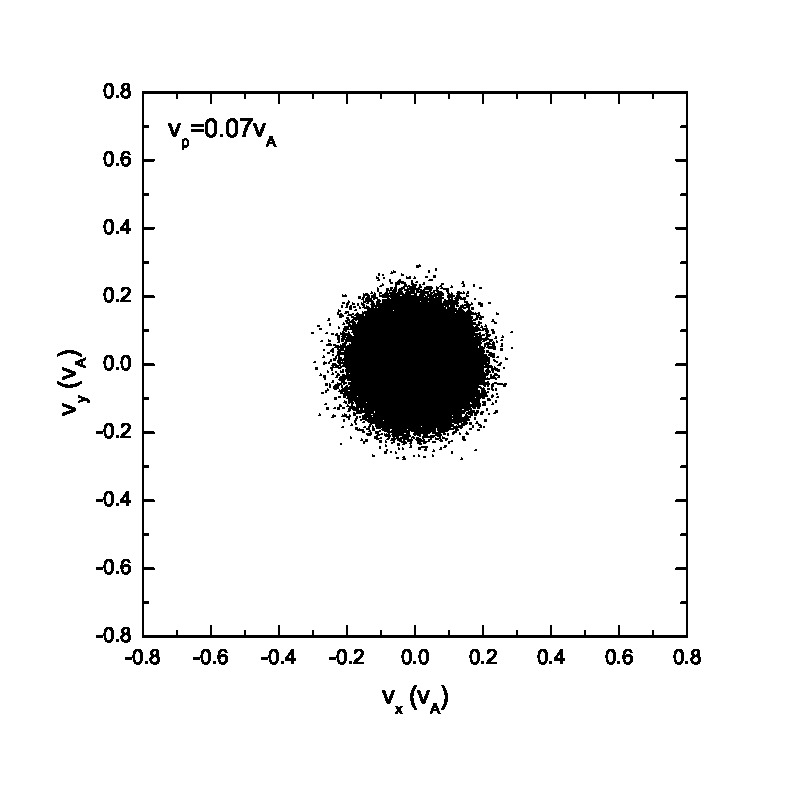
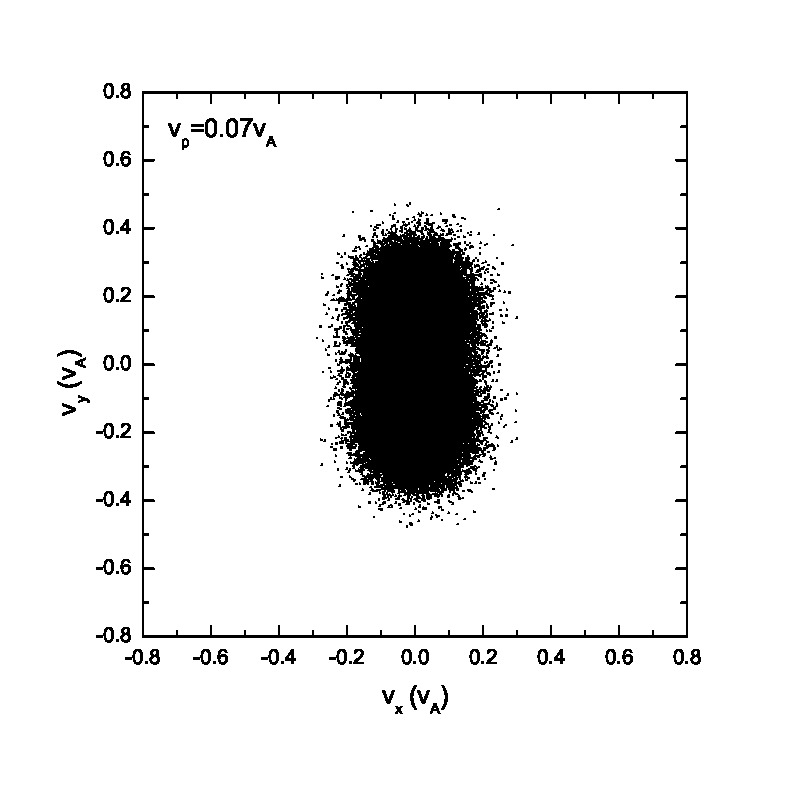
Fig.1 shows the dependence of apparent temperature ($T_{p\perp}$) on time-dependent wave field strength $B_{W}^{2}/B_{0}^{2}$ under a spectrum of Alfvén waves. The result of a monochromatic dispersionless Alfvén wave is almost the same as that under a spectrum of Alfvén waves, which is in consistency with the analytic result shown above; the temperature expression Eq.(2.7) is independent of the number of wave modes, $N$. In Fig.1, apparent temperature versus time step shows the same tendency as the wave field strength, indicating that the proton temperature returns to its original value when the waves subside, in accordance with the work of Wang et al.[17, 20]. It implies once again that the pseudoheating process is parasitic to the waves, as indicated by the aforementioned $E\times B$ drift. It is very important that the consistency between Eqs.(2.5)&(2.7) and the numerical solution shown in Fig.1 indirectly ensures the self-consistency of the test particle simulation debated in the Refs.[25, 24]. Furthermore, this process is analogous to the ion motion in a magnetic mirror, where the magnetic moment is invariant. This physical picture helps us to better understand the reversibility in pseudoheating.

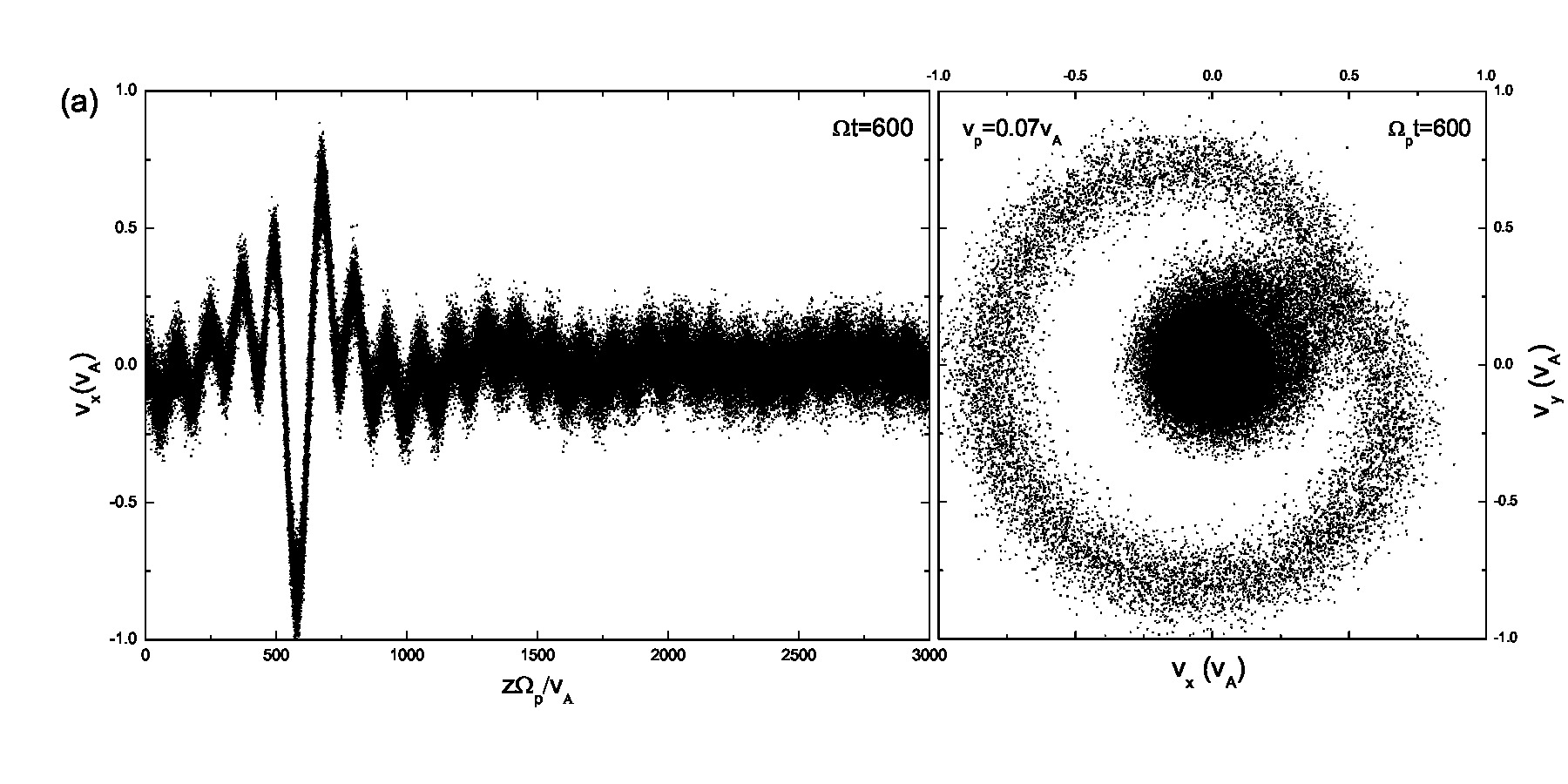
In order to show that the pesudoheating is caused by $E\times B$ drift, we first illustrate the velocity scatter plots of test particles in the $v_{x}-v_{y}$ space for a linearly polarized Alfvén wave. According to Eq.(2.3), if $\mathbf{B}_{W}$ is in the $y$ direction, $\mathbf{E}_{W}$ is in the $x$ direction; therefore, $\mathbf{E}_{W}\times\mathbf{B}_{0}$ is in the $y$ direction (ignore the negative sign here). As indicated in Fig.2, the drift velocity is in the $y$ direction, in agreement with the analytic results. To be consistent with the previous work[14, 15, 17, 19, 18, 20, 16, 21], we will focus on the circularly polarized condition in the following paragraphs. The further discussions are based on the comparison of a monochromatic Alfvén wave and a wave spectrum.

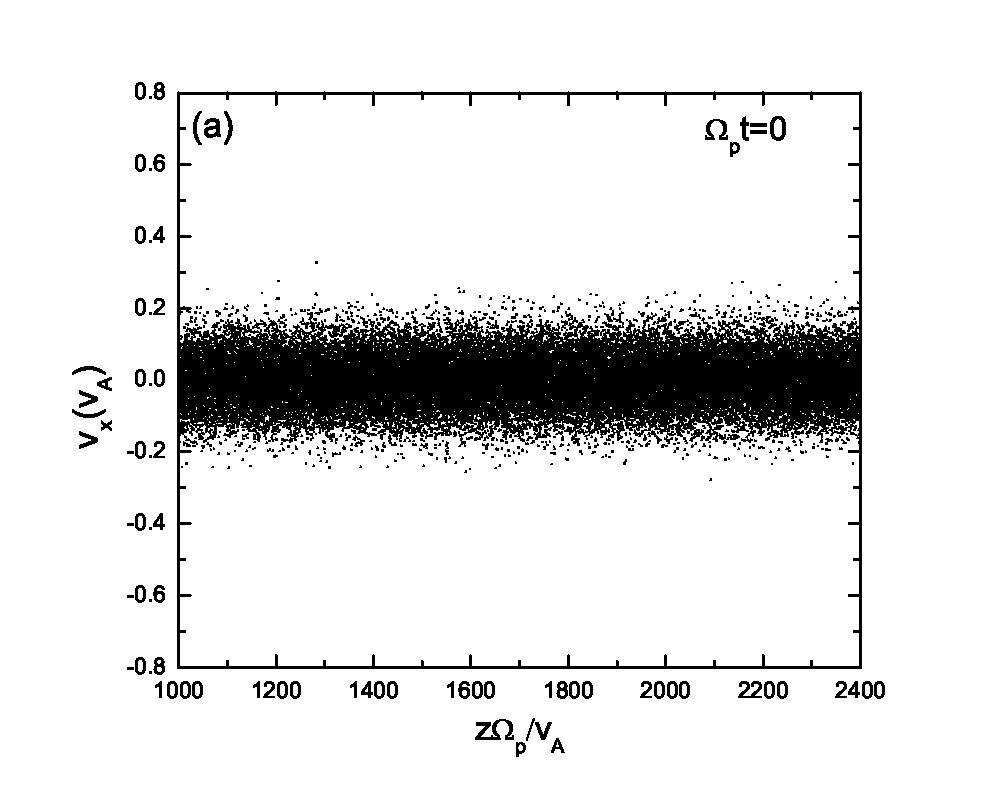
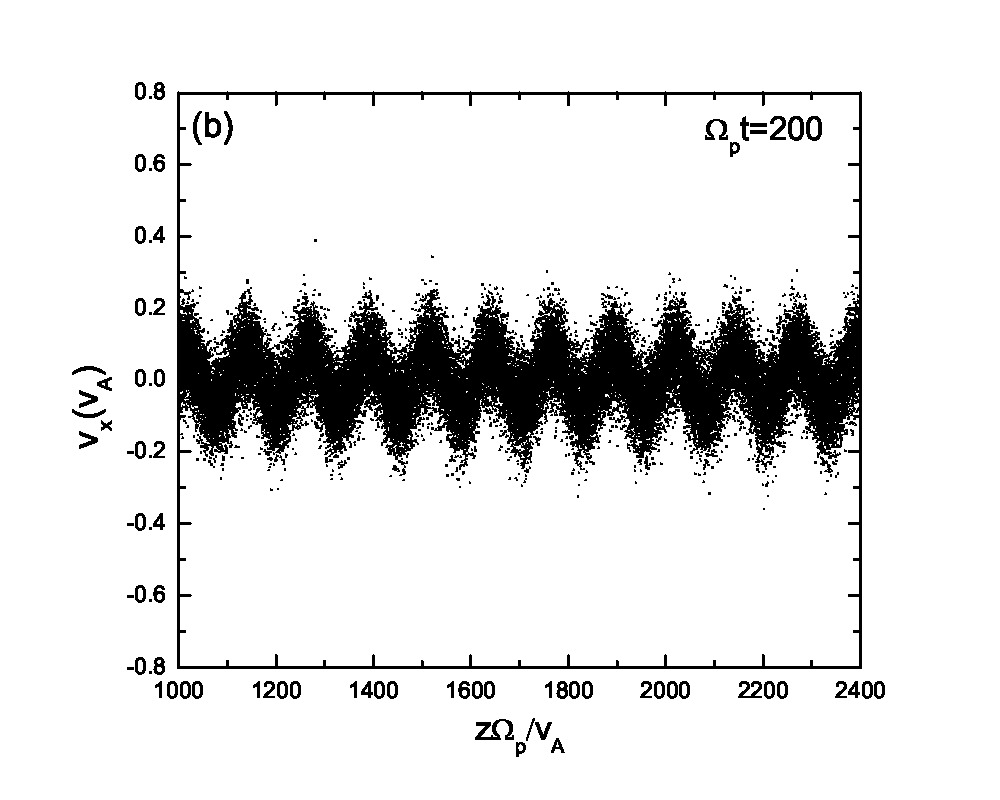
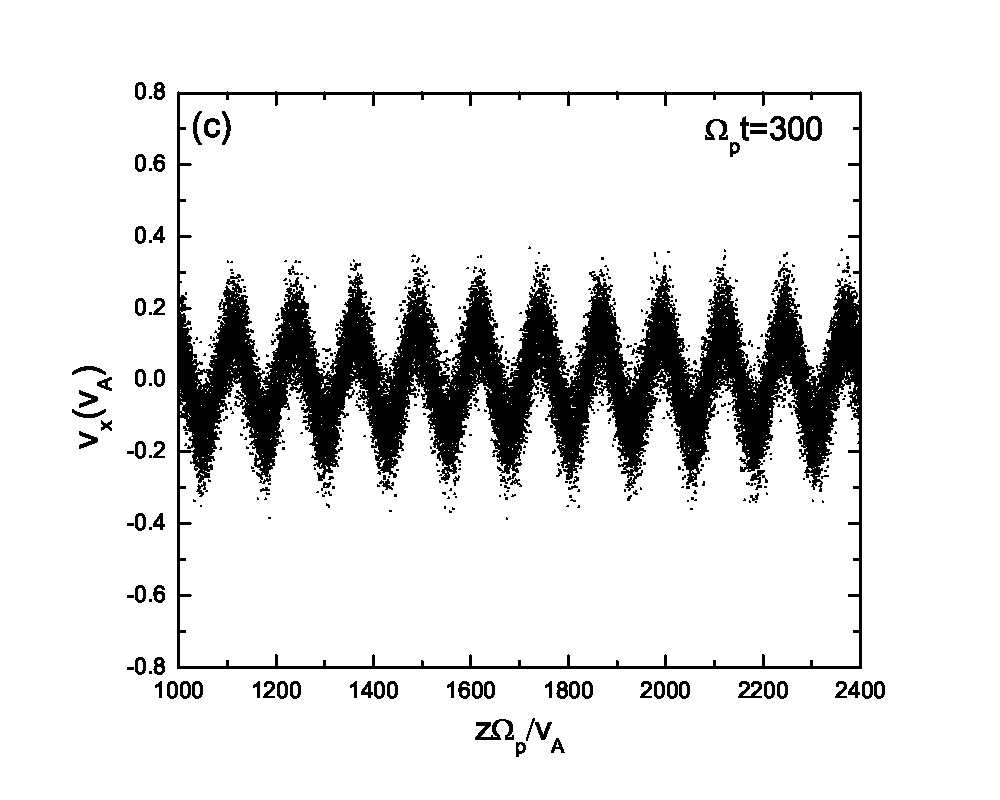
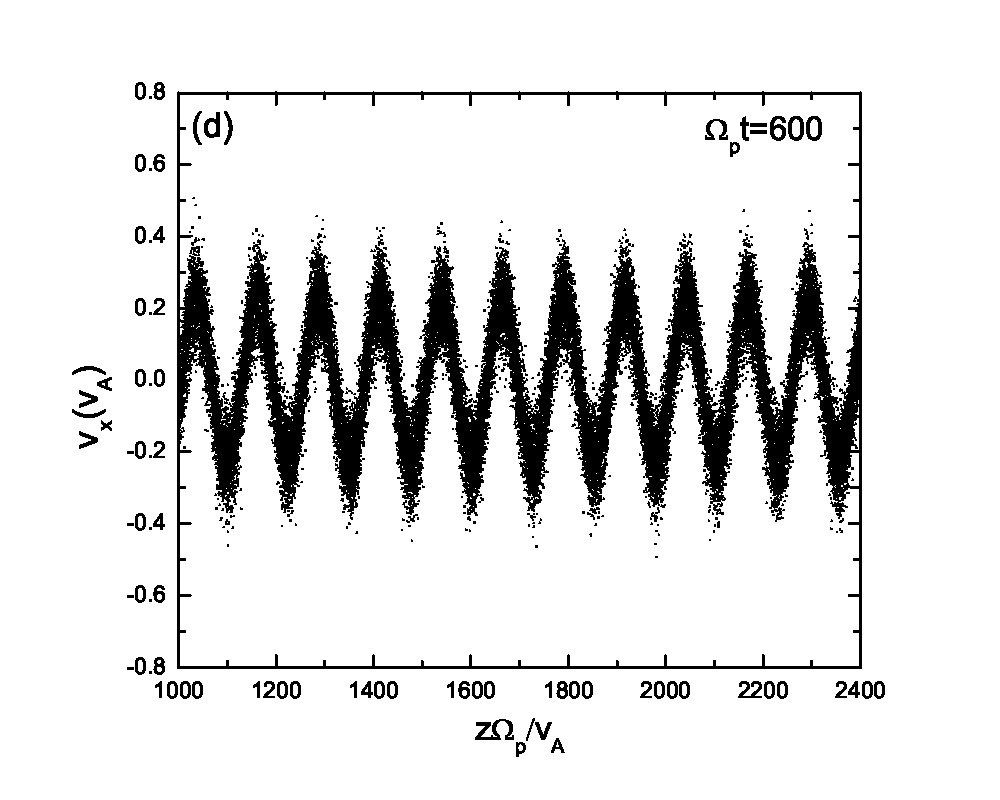
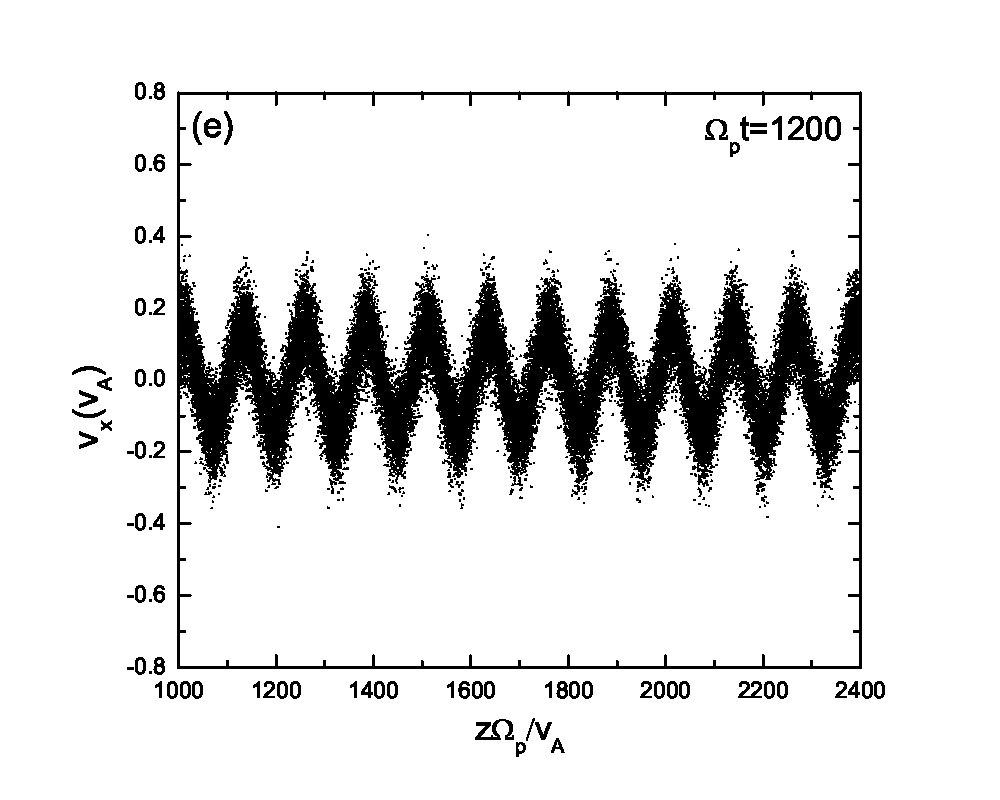
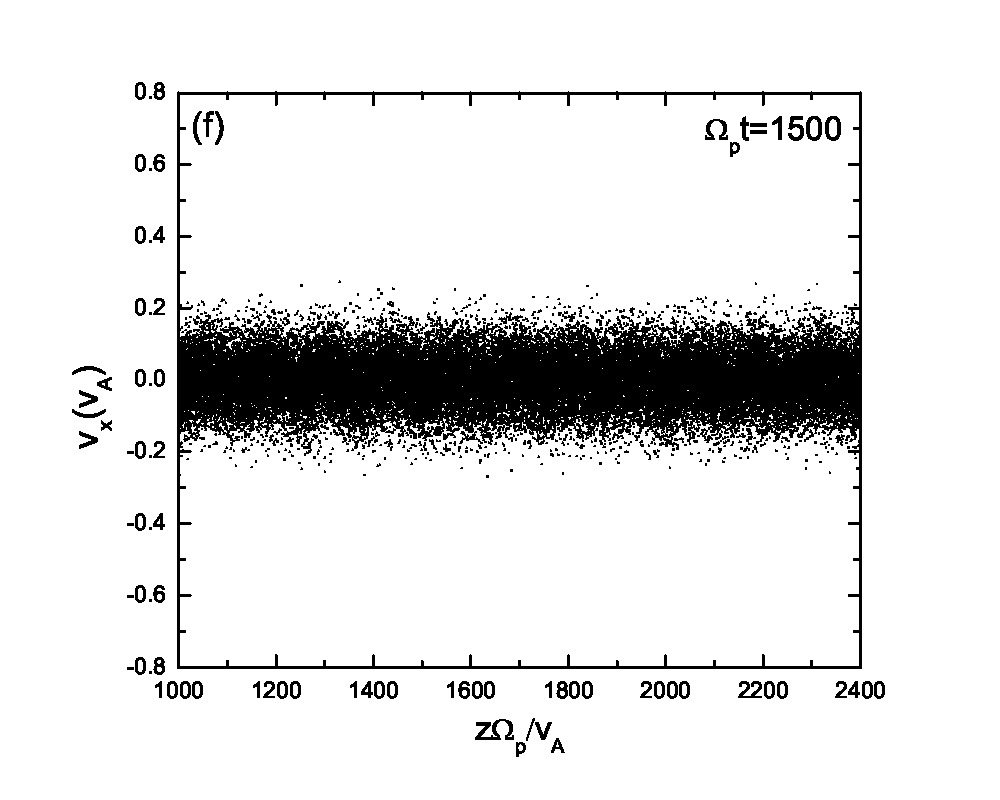
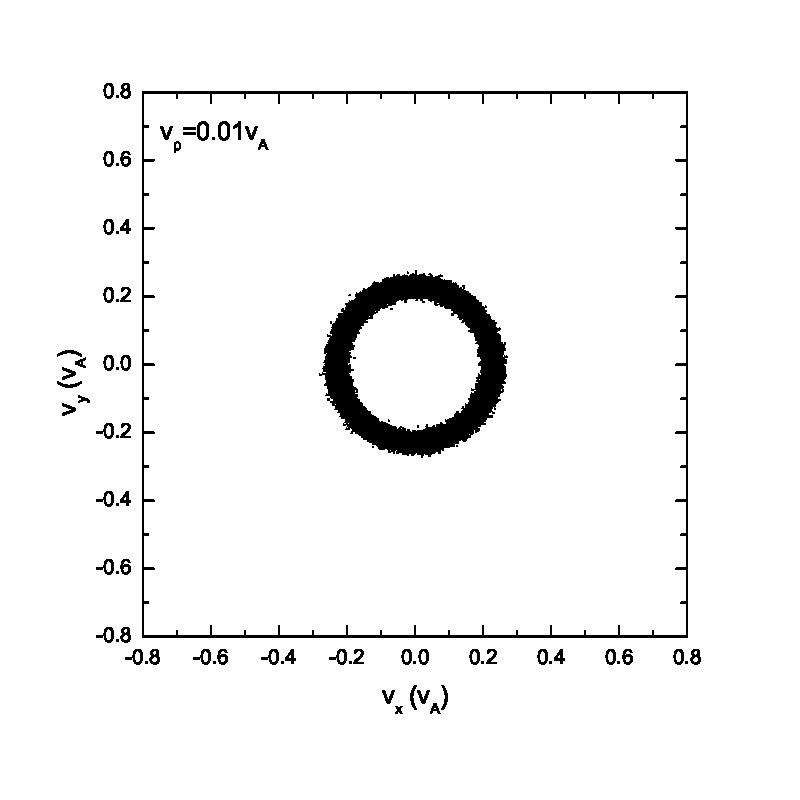
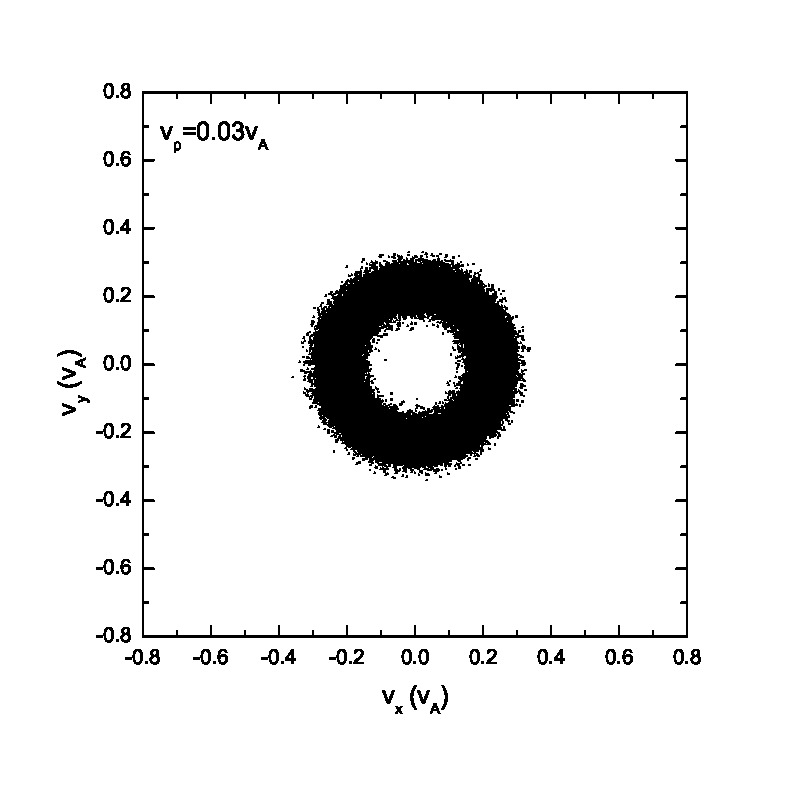
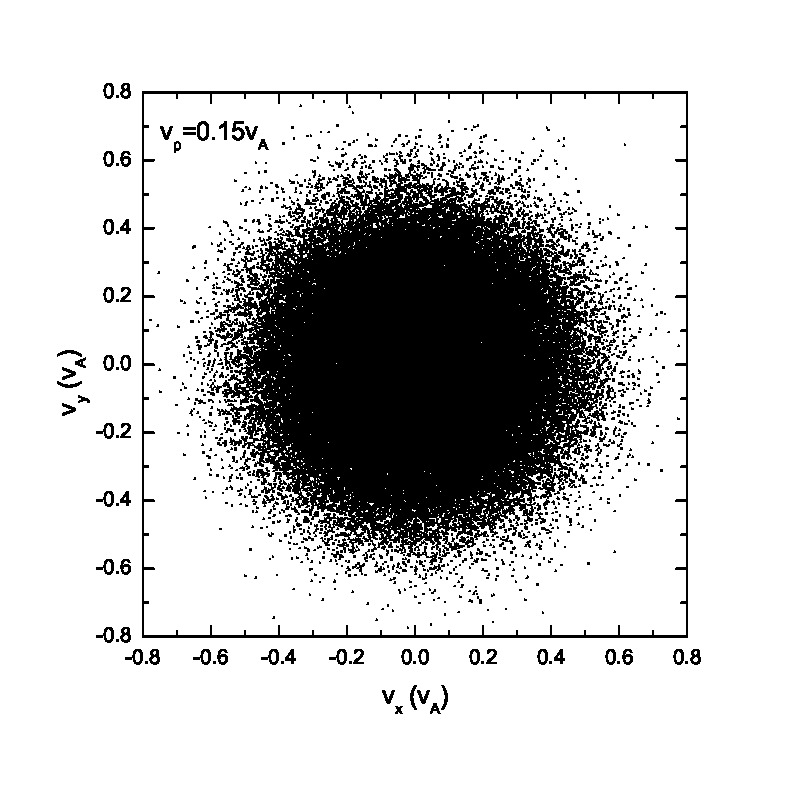
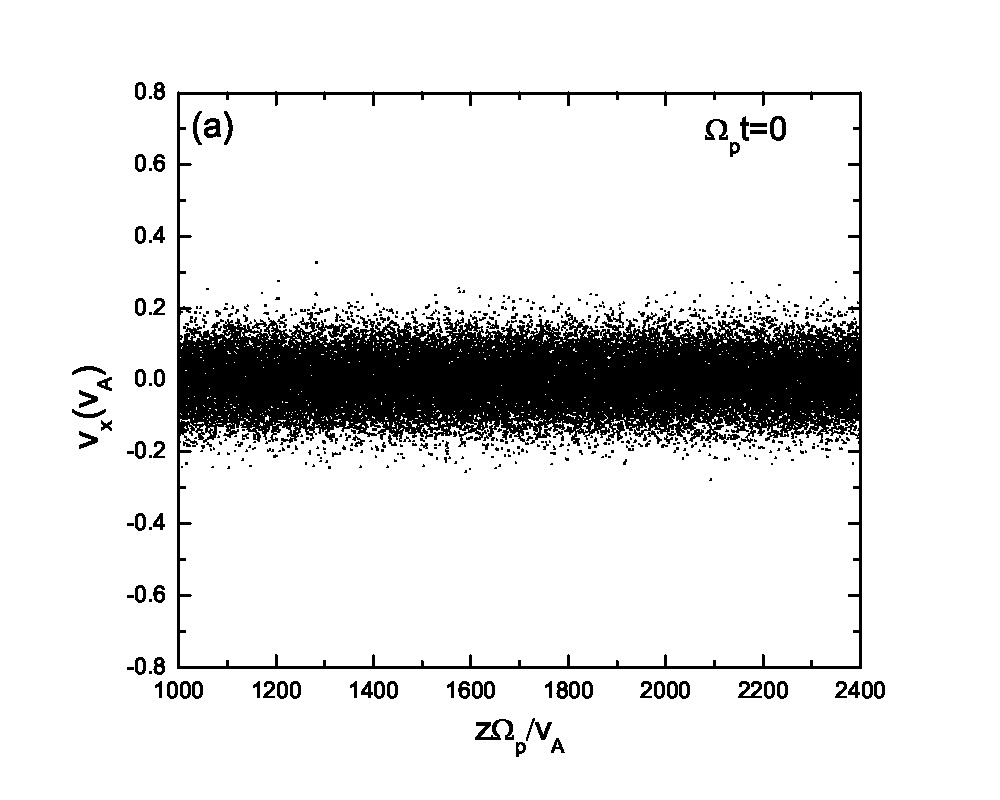
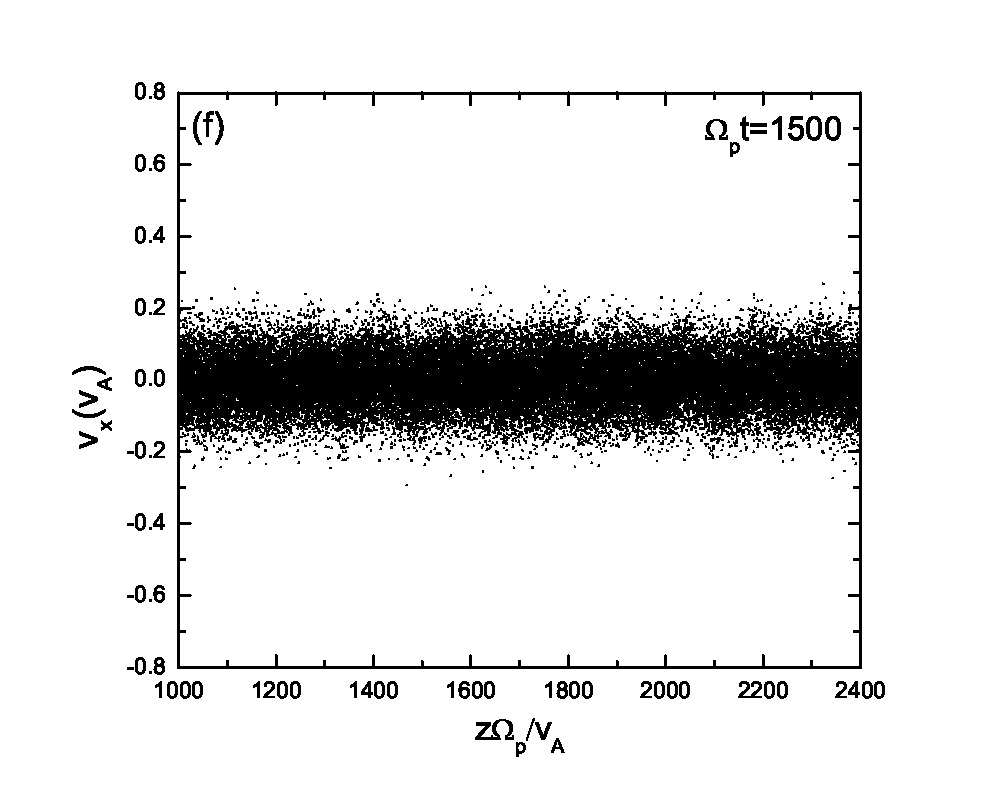
Fig.3 presents the velocity scatter plots of ions for a circularly polarized Alfvén wave with different initial thermal speeds: $v_{p}$=0.01$v_{A}$, 0.03$v_{A}$, 0.07$v_{A}$ and 0.15$v_{A}$. Inspection of Fig.3 reveals that when the thermal speed is quite small with respect to the Alfvén speed $v_{A}$ (i.e., $v_{p}$=0.01$v_{A}$ and 0.03$v_{A}$), test particles form a ring distribution in the $v_{x}-v_{y}$ velocity space. Although the ring distribution eventually can be filled with test particles with different velocities when $v_{p}$ becomes large, the heating efficiency becomes relatively low [refer to Eq.(2.7)]. Besides the velocity scatter plot, particle distribution in the phase space is also essential for our understanding of the pesudoheating. Fig.4 shows the scatter plots of protons between 1000 and 2400$v_{A}\Omega_{p}^{-1}$ at different times $\Omega_{p}$t=0, 200, 300, 600, 1200 and 1500 for a monochromatic dispersionless Alfvén wave. The results agree with that shown in Fig.1; the stronger the wave fields are, the more obvious the velocity fluctuations are. A common feature that stands out in Fig.4 is that the particle motion is periodic under a monochromatic Alfvén wave. It indicates that the kinetic behavior of test particles under a monochromatic dispersionless wave versus a wave spectrum, as will be shown below, is fairly different.

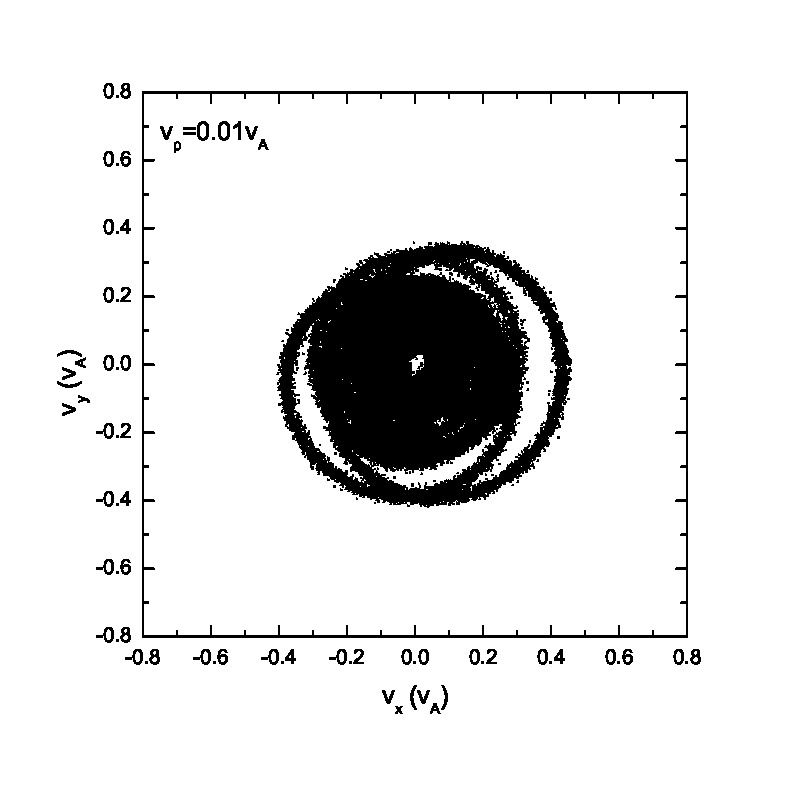
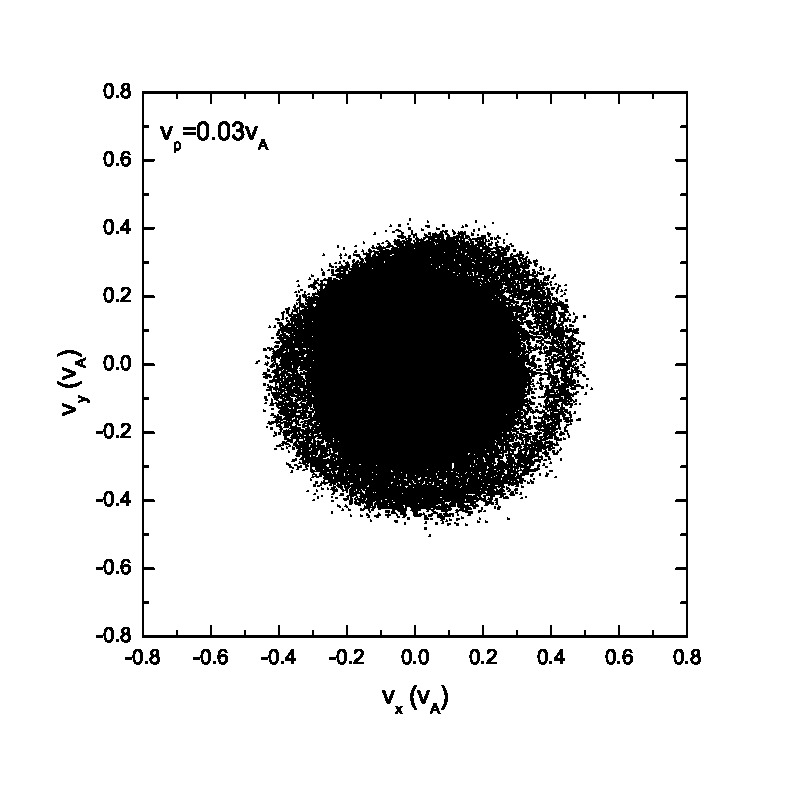
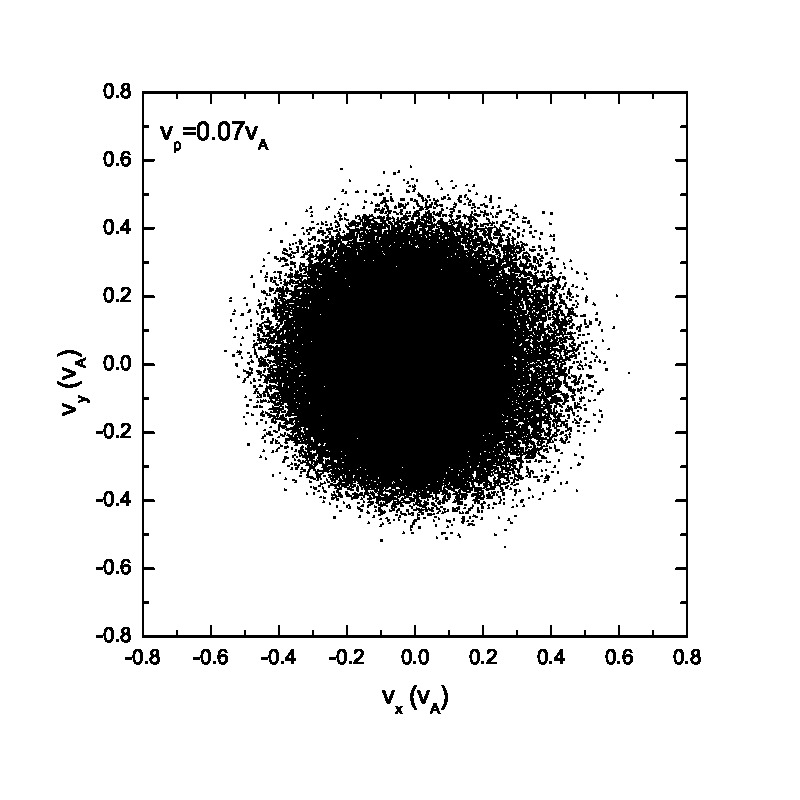
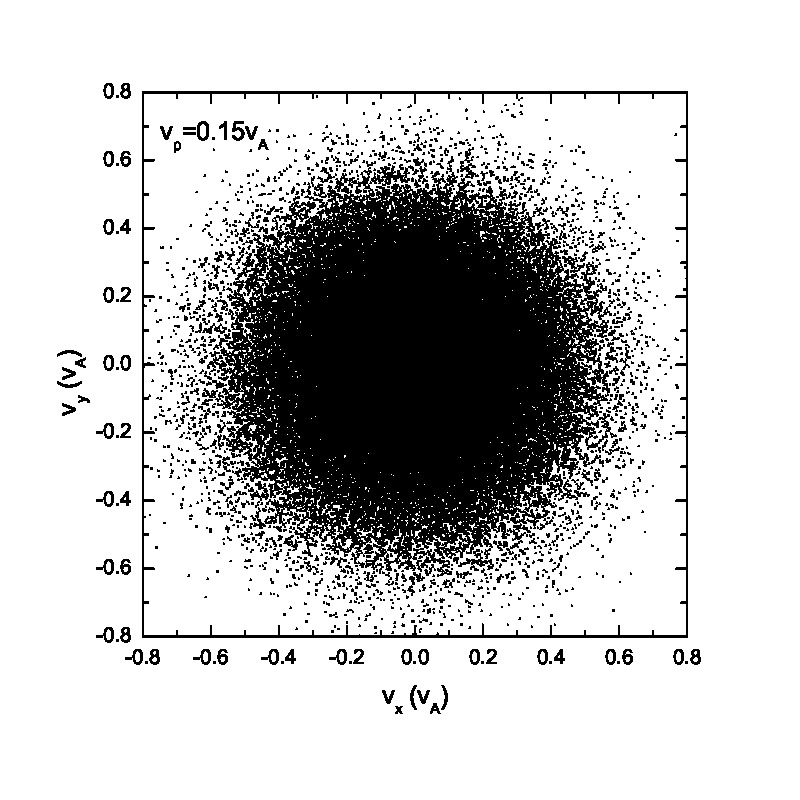
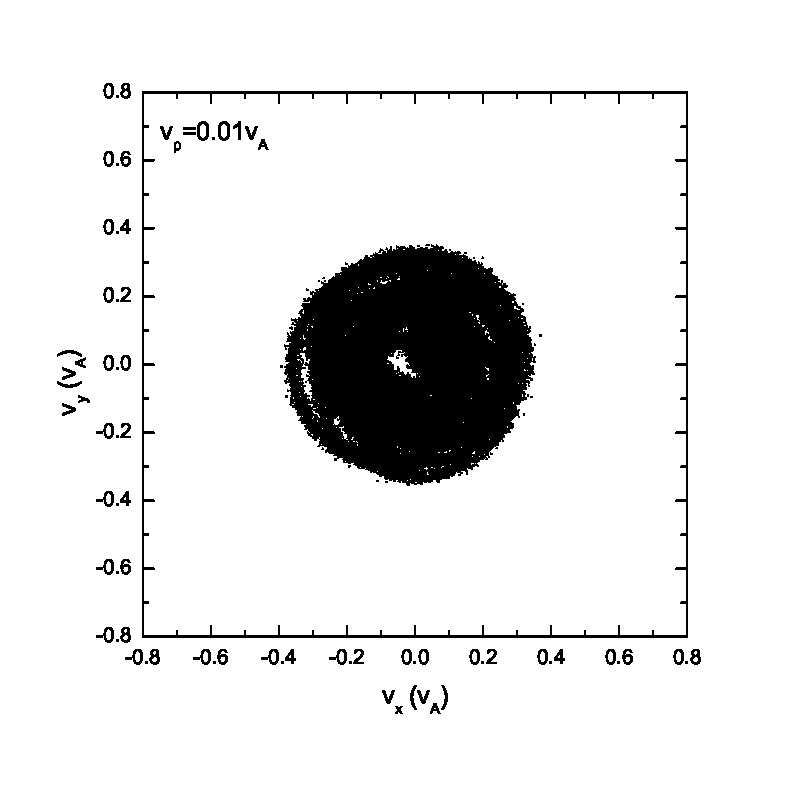
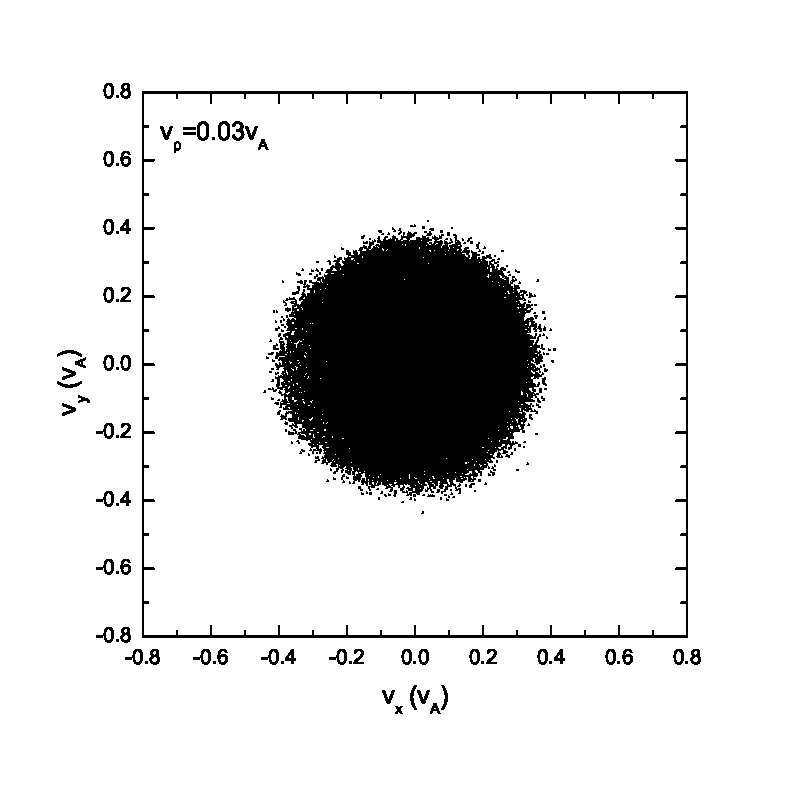
Compared with the ion behavior under a monochromatic wave, the ion motion tends to become random under a wave spectrum as indicated in Figs.5 & 6. Fig.5 presents the velocity scatter plots of test particles in the $v_{x}-v_{y}$ space for a spectrum of circularly polarized Alfvén waves with random phases $\varphi_{k}$. When the thermal speed is two orders of magnitudes smaller than the Alfvén speed $v_{A}$ (i.e., $v_{p}$=0.01$v_{A}$ and 0.03$v_{A}$), test particles cannot fully fill the circle in the $v_{x}-v_{y}$ velocity space. However, with the increase of the initial thermal speed $v_{p}$, the circle in the velocity space is fully filled with test particles with different velocities. Figs.5(e)&(f) show the velocity scatter plots when adopting 1001 wave modes. Compared with Figs.5(a)&(b), Figs.5(e)&(f) show that protons tend to fully fill the circle in the velocity space, indicating that the ion velocity distribution tends to be a full-filled circle in the velocity space when the number of wave modes, $N$, is large enough, regardless of the relatively small thermal speed. It can be observed based on the comparison between Fig.3 and Fig.5 as well. The phase space proton scatter diagrams by adopting a wave spectrum with wave modes $N$=41 are shown in Fig.6 . The results, however, reveal significantly different particle distributions in the phase space compared with those shown in Fig.4. The main conclusion drawn from Fig.6 is that the velocity fluctuations caused by wave activity is quasirandom, and thereby could mimic the real heating (also refer to Fig.8). However, as indicated in both Fig.2 and Fig.6, the pseudoheating caused by these wave activities is reversible, indicating no dissipation of wave fields, and therefore does not represent real heating in thermodynamic sense. It is also interesting to investigate the ion behavior under a spectrum of circularly polarized Alfvén waves with same initial phases $\varphi_{k}$. It is noteworthy that the wavelength and wave frequency among different wave modes are still different. Fig.7 illustrates the scatter plots of the test particles in the $v_{x}-z$ and $v_{x}-v_{y}$ space. There is a pulse-like structure in the protons’ phase space distribution due to the coherence of wave modes. The proton distribution in the $v_{x}-v_{y}$ space is primarily consist of two parts: the broadening core Maxwellian distribution and the outer ring structure. The broadening is caused by the wave forces (or their spectra) while the accelerated particles in the outer ring result from the Alfvénic turbulence with phase coherent wave modes as indicated in Ref.[26], where the acceleration of charged particles by large amplitude MHD waves was studied. In contrast, if Alfvénic turbulence without any envelope modulation[27] is given, the “acceleration” may not be observed. These high energy particles in the outer ring may escape from the region of interaction with the Alfvén waves and can contribute to the fast particle population in astrophysical and space plasmas.

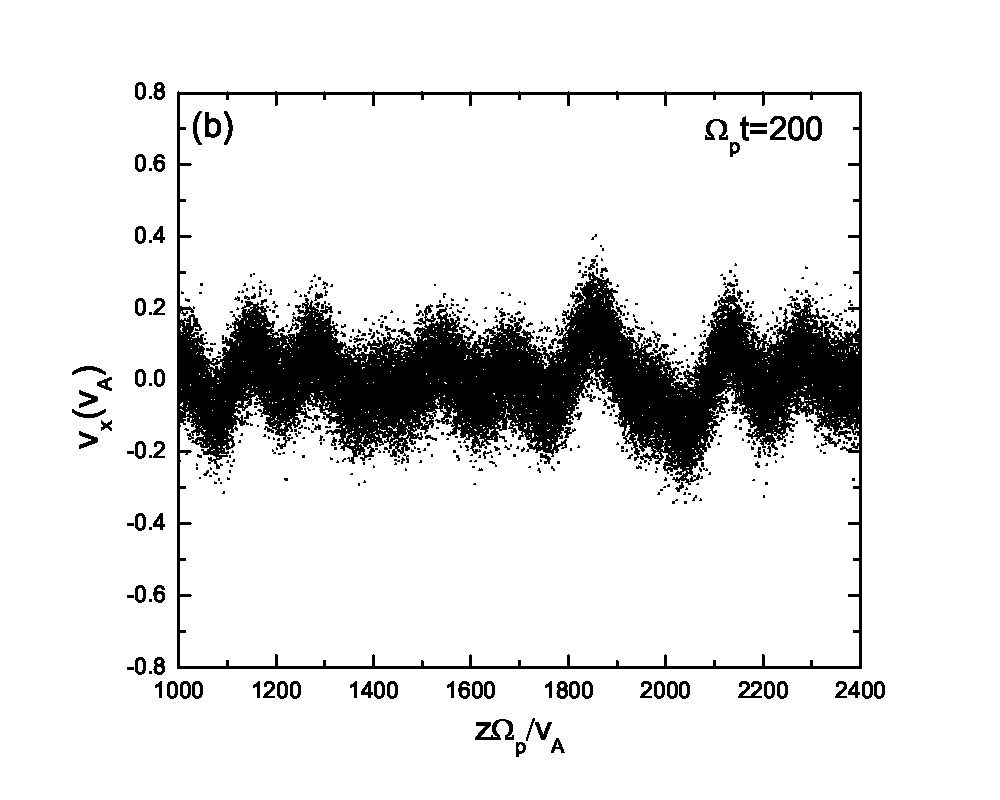
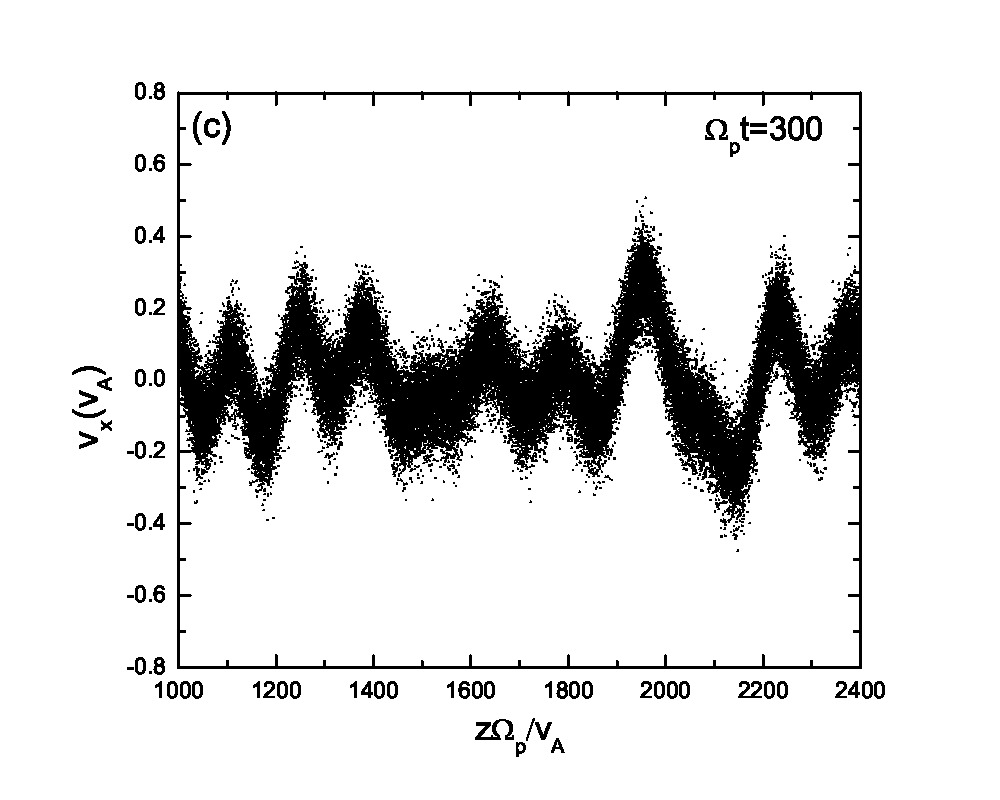
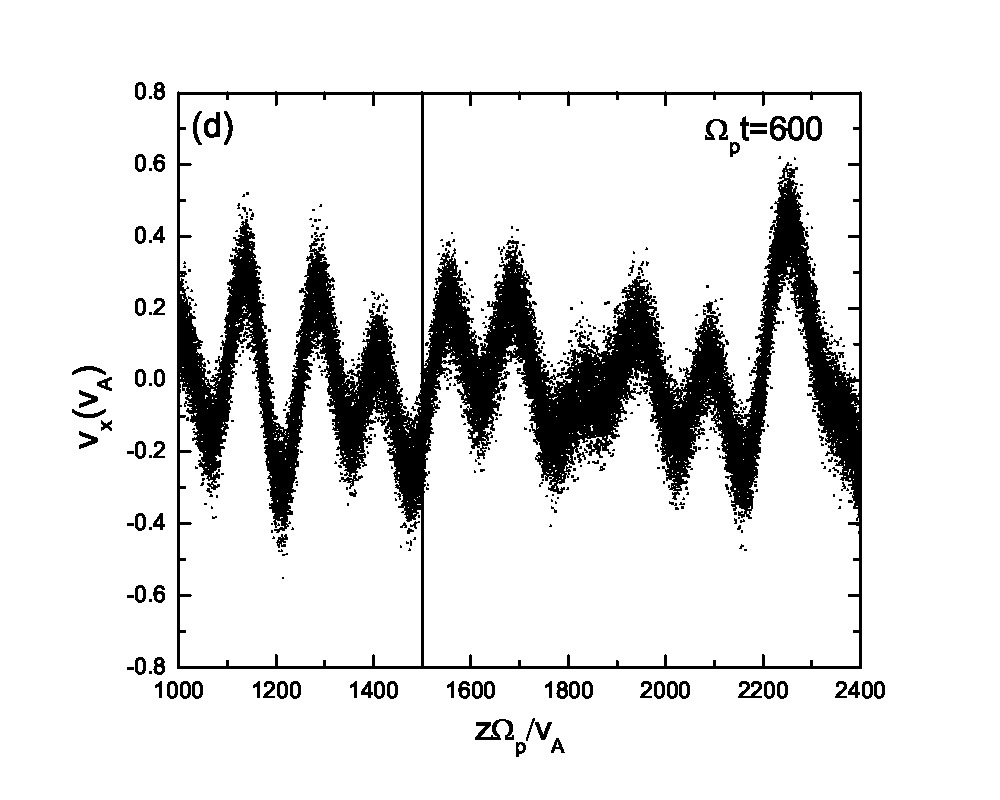
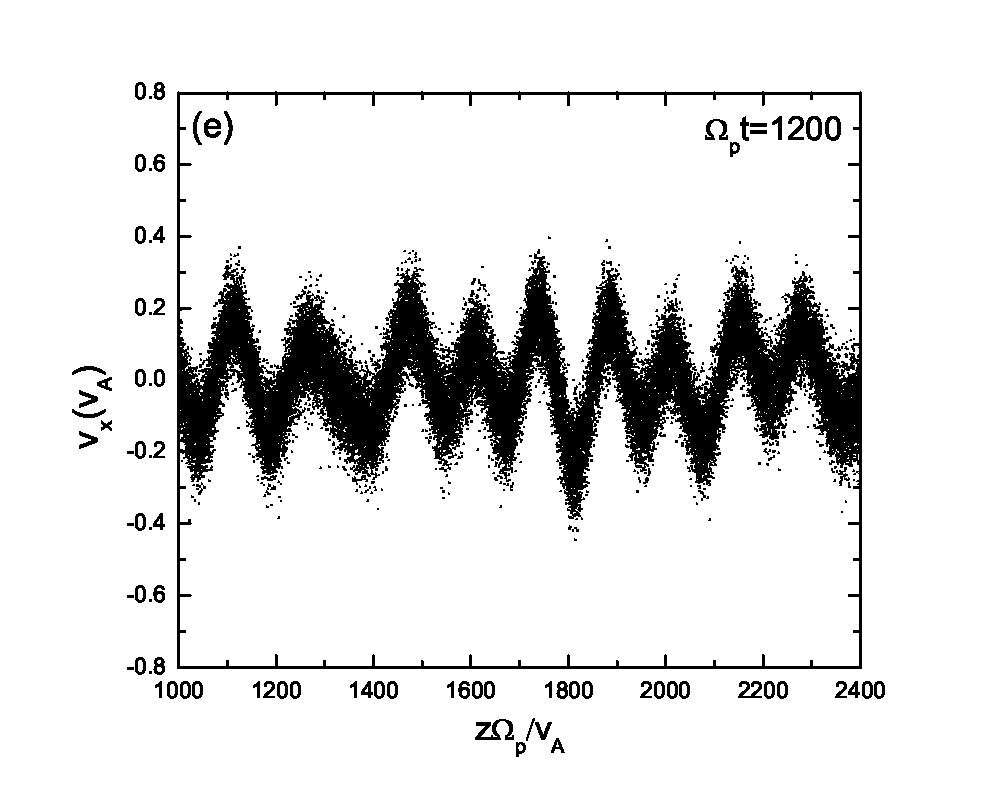
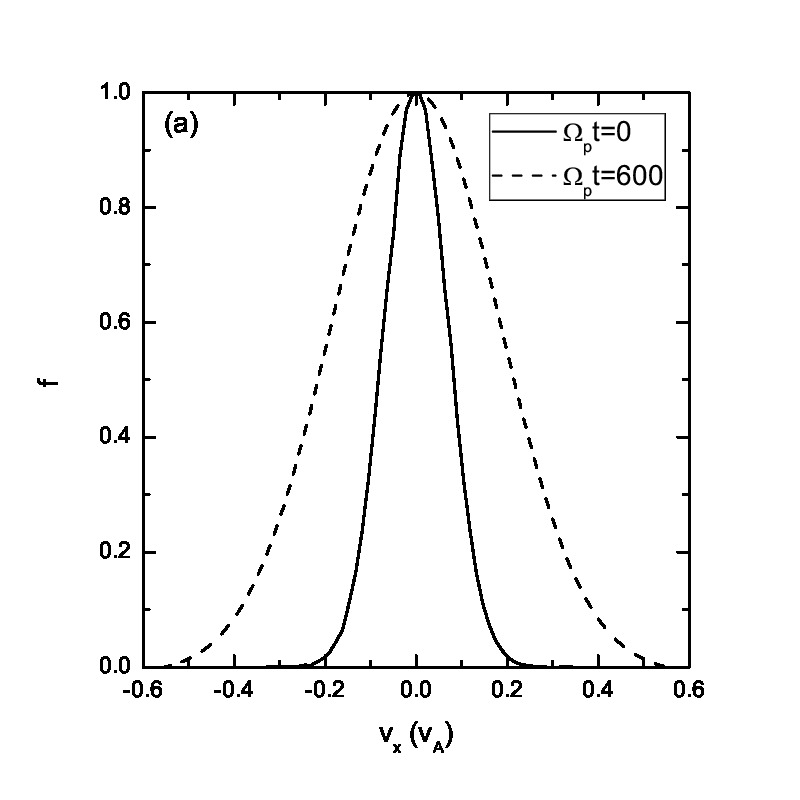
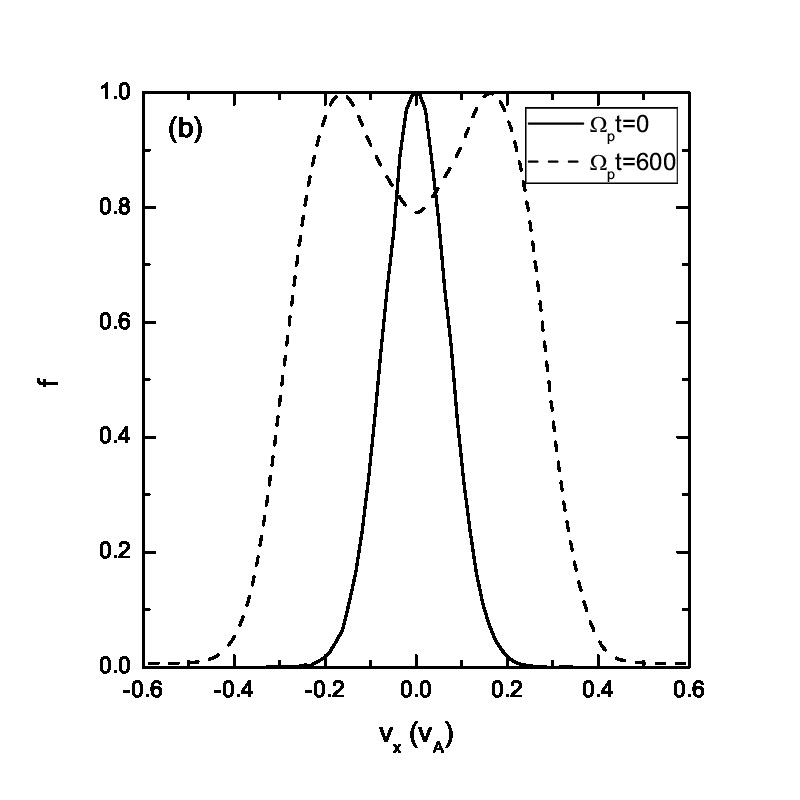
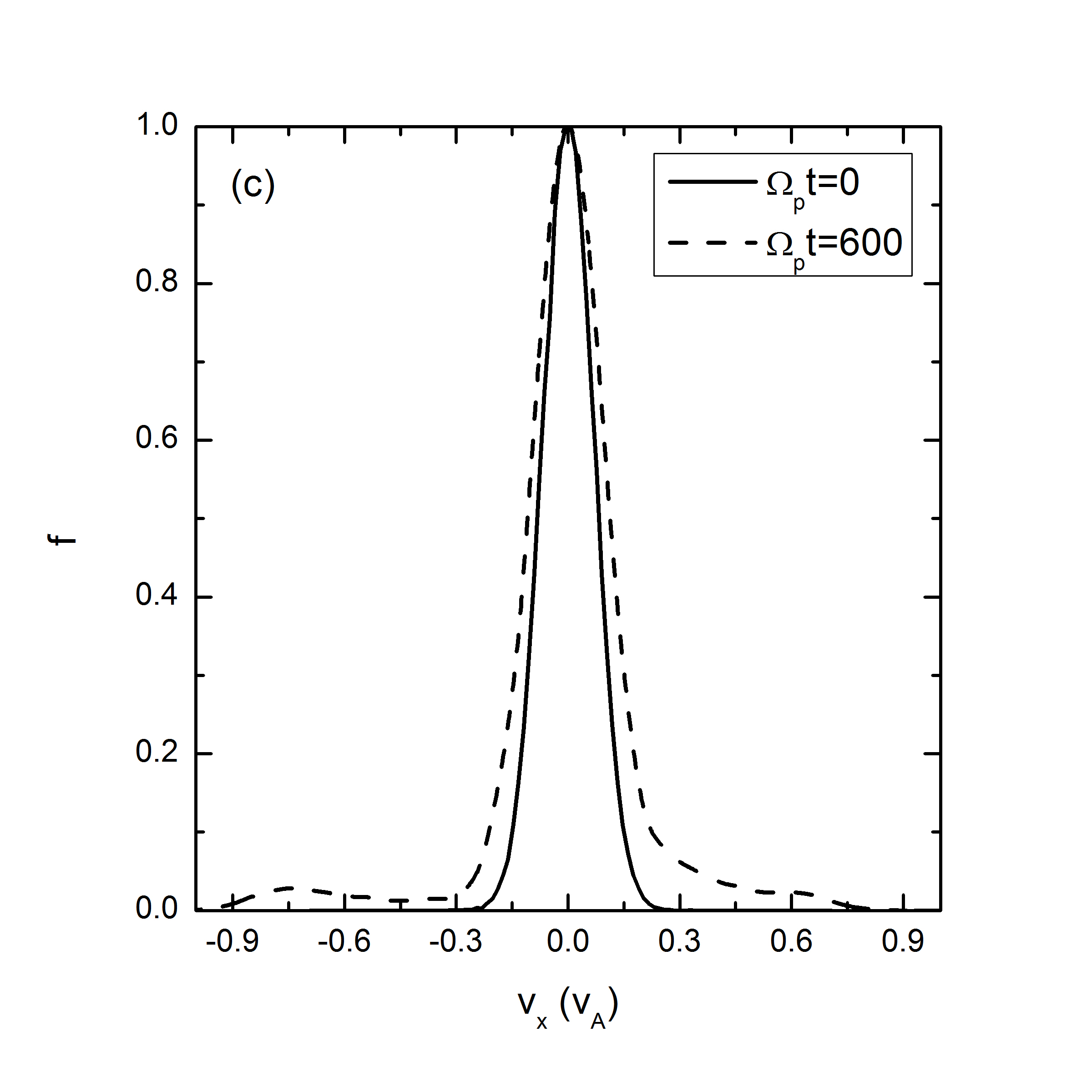
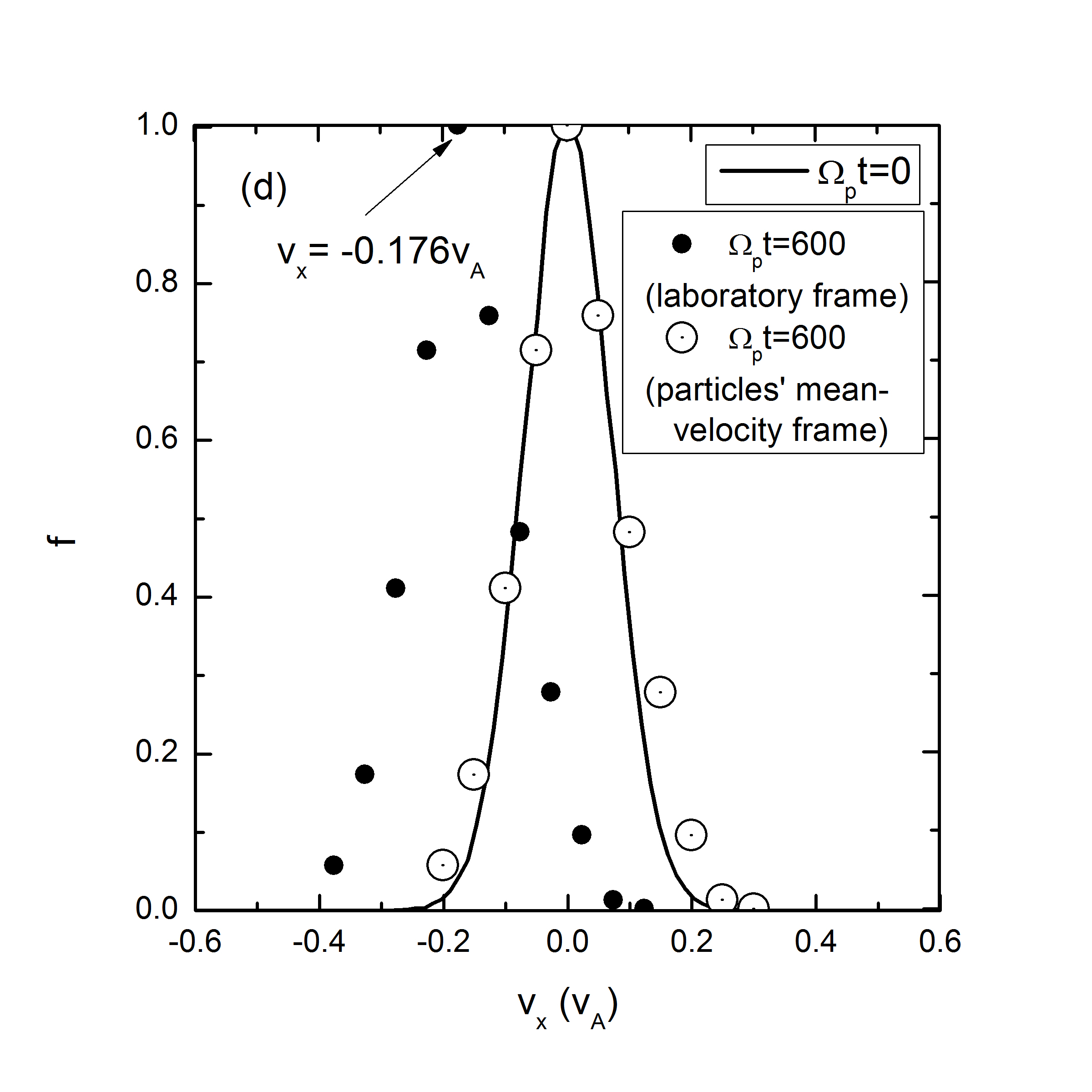
In Fig.8, we present the normalized velocity distribution function at different time $\Omega_{p}$t=0 (solid line) and 600 (dashed line). The broadening of the distribution functions shown in Figs.8(a)-(c) are based on the statistics of all the particles with different spatial coordinates $z$ while Fig.8(d) is based on the local statistics of protons in the spatial range $1490<z\Omega_{p}/v_{A}<1510$, thus being a local normalized velocity distribution function around $z\Omega_{p}/v_{A}=1500$ as indicated by the line in Fig.6(d). The velocity spreading in Figs.8(a)-(c) is caused by averaging over the wave effects. Inspection of Figs.8(a)-(b) reveals that the Maxwellian distribution is more likely to maintain under a wave spectrum compared with a monochromatic Alfvén wave due to the fact that the ion motion under a wave spectrum is quasirandom, which is in good agreement with the analytic derivation by Wu and Yoon using the quasi-linear theory[15]. It also points towards different kinetic behaviors of particles under a wave spectrum and a monochromatic Alfvén wave. It is well known that enhanced Alfvénic turbulences exist pervasively in the solar wind and interplanetary space, while in astrophysical observation measurements of temperature are based on spectroscopic data collected from the source region of interest. Therefore it is very difficult to distinguish the real heating from the pseudoheating due to the restriction of spatial resolution of the instruments and the presence of wave forces (or their spectra). The suprathermal tail and small bump shown in Fig.8(c), where the $v_{x}$ axis scale is different from Figs.8(a)-(b), corresponds to the accelerated (suprathermal) ions due to the wave modes coherence. The bump-on-tail structure may excite plasma instabilities, however, the detailed discussion of these instabilities is beyond the scope of this paper. It also needs to point out that here we only consider the pseudoheating and investigate the normalized velocity distribution function corresponding to this process while the real heating via nonresonant interaction with Alfvén waves always coexists[14, 25]. The velocity distribution function, therefore, is supposed to be broader than that shown in Fig.8 and it is possible that the broadening effects smooth the velocity distribution function and eliminate the bump on the tail. In Fig.8(d), we investigate the local normalized velocity distribution function based on the statistics of protons in the spatial range $1490<z\Omega_{p}/v_{A}<1510$. If the spatial range is too small, there will be insufficient particles to be counted for statistics. The local statistical mean velocity equals to $v_{x}$=-0.176$v_{A}$ which agrees well with the result shown in Fig.6(d). The local normalized velocity distribution function in the particles’ mean-velocity frame at $\Omega_{p}t=600$ (as indicated by the white dots) is in good agreement with the initial Maxwellian distribution based on Eq.(3.8). The slight difference between these two distribution functions results from the fact that the local statistics are based on a small spatial range ($1490<z\Omega_{p}/v_{A}<1510$) and therefore it can be potentially affected by the effects of wave spectra. This leads to a slightly broader local velocity distribution. The result shown in Fig.8(d) indicates that the analytic theory in Sec.2 is on the basis of the local equilibrium velocity distribution of the ions.

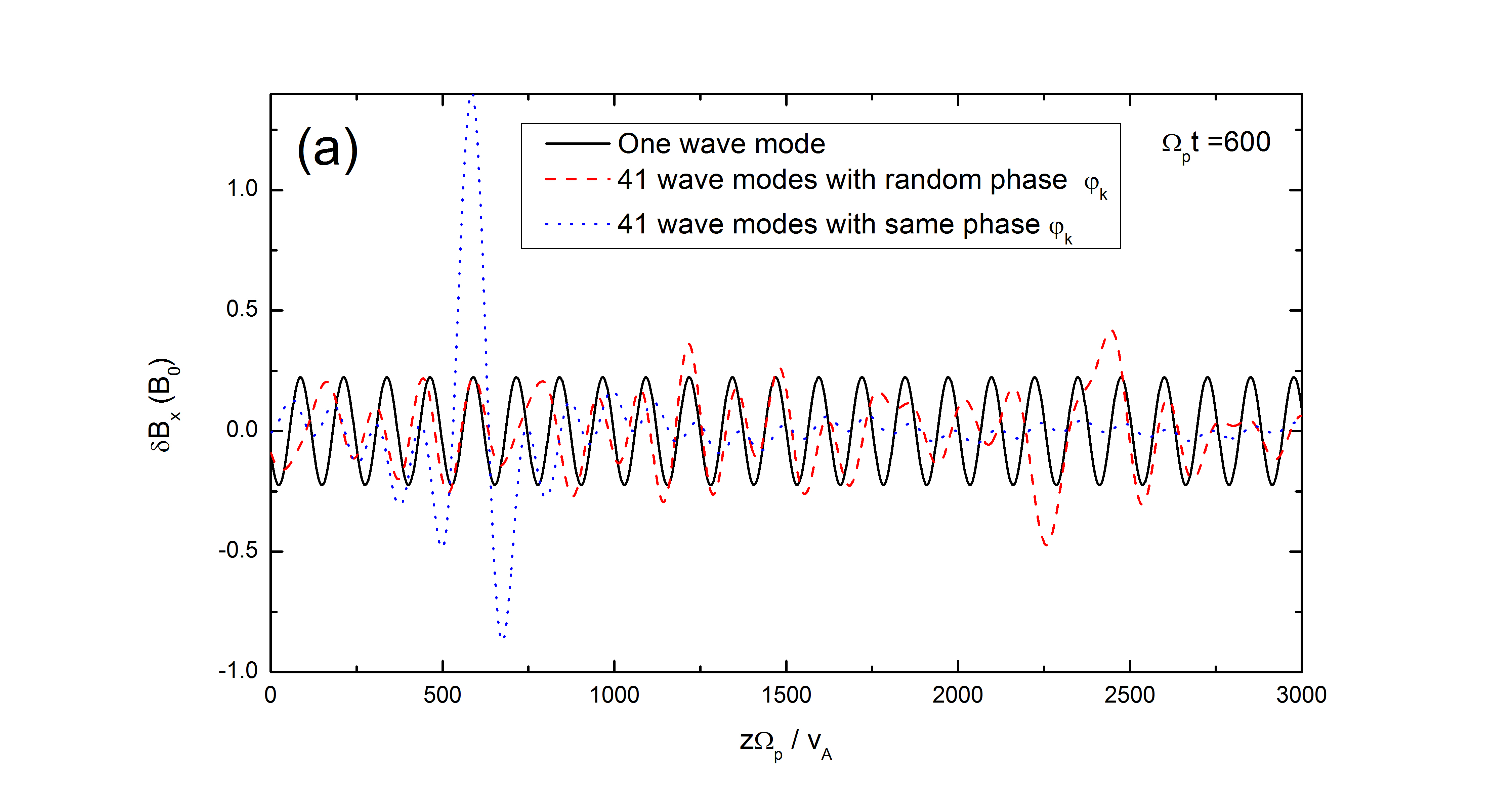
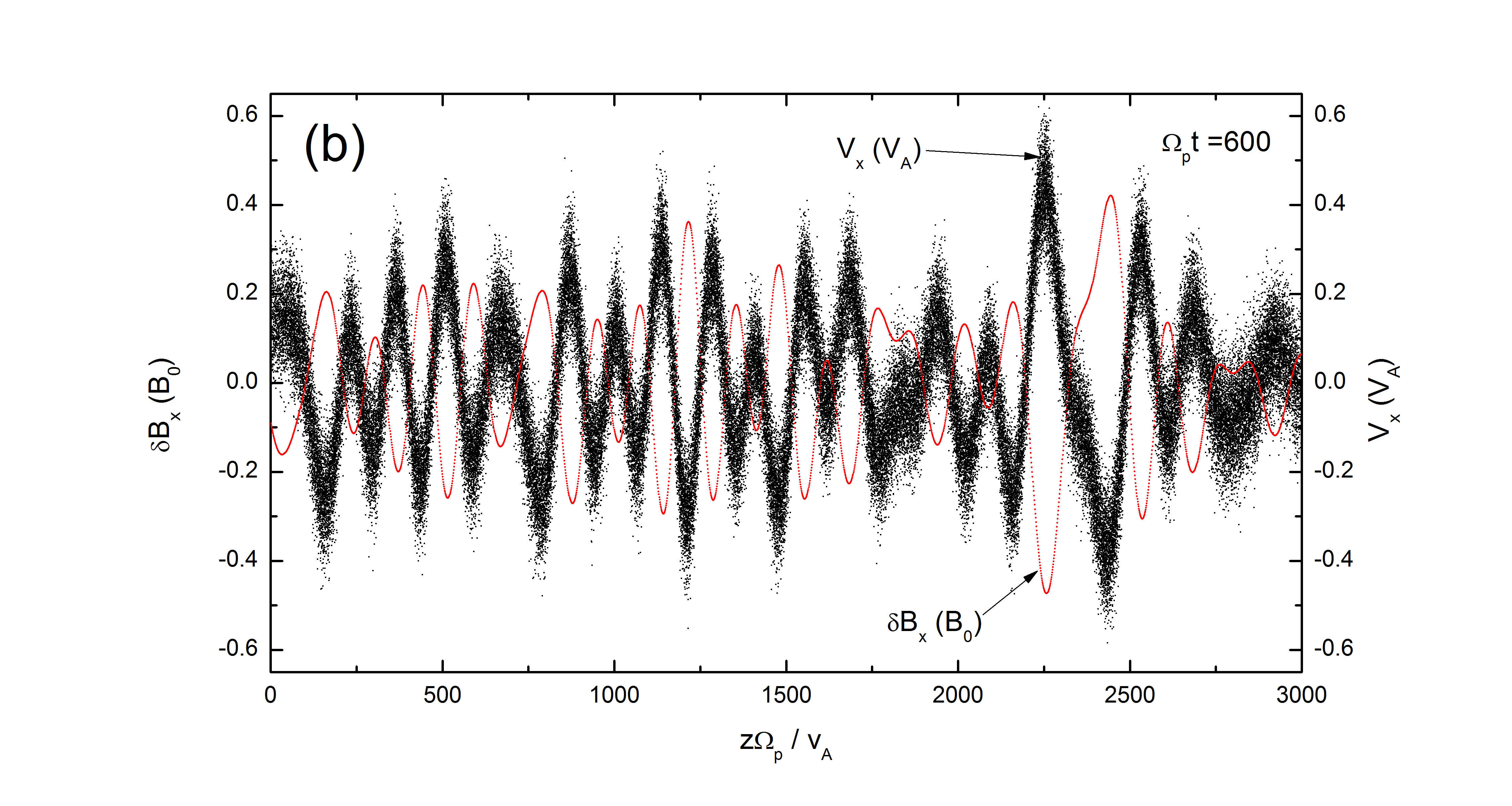
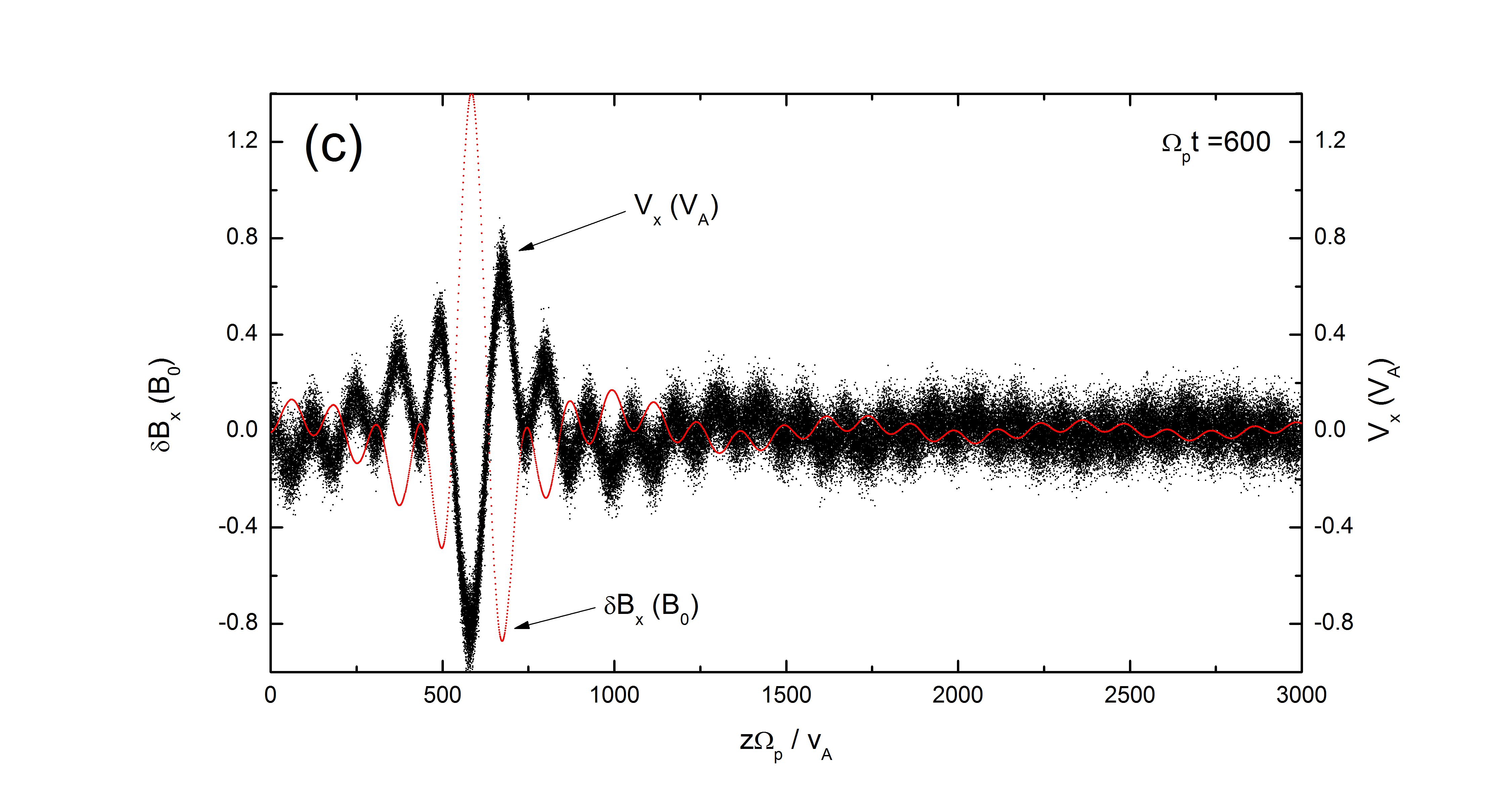
The pseudoheating becomes important when the magnetic perturbation ($\delta B$) is relatively large compared with the background magnetic field ($B_{0}$). Fig.9 illustrates the spatial distribution of the Alfvén wave magnetic fields with different wave modes, $N$, and the corresponding scatter plot in the $v_{x}-z$ phase space. The solid curve for the magnetic field of a monochromatic Alfvén wave is simply a sinusoidal wave. The dashed and dotted curves represent a spectrum of Alfvén waves with 41 wave modes that has random and same phase $\varphi_{k}$, respectively. They can mimic the Alfvénic turbulence due to the quasirandom fluctuations of the wave fields. The amplitude of the magnetic perturbation can be quite large locally, thus may produce some energetic particles that can escape from the constraint of the Alfvén waves and contribute to fast particle population in astrophysical and space plasmas. As indicated in Fig.9, the larger the magnetic perturbations are, the more effective the distribution functions are broadened. Refs.[33, 32] suggest that small scale reconnection events occur during the solar flares, which can provide large magnitude spike-like magnetic field fluctuations. Additionally, the cluster observation of surface waves in the ion jets from magnetotail reconnection also shows that $\delta B/|B|$ can be as high as 0.5 and occasionally even higher[34]. Furthermore, the amplitude of the magnetic perturbation associated with Alfvén waves can be even larger than the ambient magnetic field in certain cases observed by the Wind satellite[35]. Figs.9(b)&(c) also show that the distribution of test particles in the $v_{x}$-$z$ phase space and the wave field perturbations are in antiphase ($\pi$ phase difference) due to the fact that the proton motion is parasitic to Alfvén waves, indicating an exchange of energy between the particles’ kinetic energy and the magnetic energy. Therefore Fig.9(b) indicates that the psuedoheating is a consequence of equilibrium MHD system.

It is noteworthy that the parallel electric field and wave damping are not included in the test particle simulations of our current work. In the self-consistent simulations such as hybrid simulations (i.e., kinetic description of ions, fluid electrons), the phase-correlation among the Fourier modes could affect, for instance, that the ponderomotive force resulting from the envelope-modulated Alfvén waves heat ions through the nonlinear Landau damping[28] and the parallel heating of ions due to the nonlinear Landau damping[29]. In Ref.[28], the ponderomotive force and beat interaction are identified as the most important nonlinear effects in proton heating by nonlinear field-aligned Alfvén waves in the solar coronal holes. Interestingly, they found that the nonlinearity is particularly strong when the wave spectrum consists of counterpropagating modes of equal intensity, even if the intensity is relatively low. Moreover, from the hybrid approach, dissipation processes of the Alfvénic turbulence with the broadband wave number spectrum can be different from those of monochromatic Alfvén waves, since the former is associated with the density fluctuations, $|\delta n/n|$, and the resultant spatial modulation of $|B|^{2}$ due to compressive effects of ponderomotive forces[30, 31]: right-hand polarized Alfvénic turbulence with such an envelope modulation can be dissipated due to the nonlinear Landau damping, while left-hand polarized Alfvénic turbulence with the broadband spectrum is preferentially dissipated by the modulational instability. On the other hand, low-frequency, monochromatic Alfvén waves are relatively stable to the linear collisionless dissipations such as Landau damping and cyclotron damping, nonlinear wave-wave interactions parametric instabilities are important for the dissipation of these waves. The decay instability is dominant for dissipation of the right-hand polarized finite-amplitude monochromatic Alfvén waves in low $\beta$ plasmas, while the left-hand polarized waves can also be dissipated via the modulational instability[29]. These wave damping mechanisms are closely related to the present work; therefore, in order to study the characteristics of the “acceleration” and “heating” process in more detail, comprehensive and self-consistent studies are necessary in the future.

Ion pseudoheating by low-frequency Alfvén waves is investigated based on the comparison between a monochromatic Alfvén wave and a wave spectrum. Both analytic and simulation results show that $E\times B$ drift plays a principal role in this process and the proton motion is parasitic to Alfvén waves. It indicates the psuedoheating is a consequence of the equilibrium in the MHD system. Our results are in good agreement with the previous studies based on pitch-angle scattering. More importantly, it provides a simple understanding of the reversible property of this process from $E\times B$ drift point of view; if wave magnetic and electric fields disappear, there will be no drift velocity $v_{E}$ and therefore no pseudoheating. We showed that the wave spectra contribute to the broadening of the Maxwellian distribution during the pseudoheating, and it is therefore difficult to exclude the apparent temperature $T_{p}$ from observations due to the low spatial resolution of the instruments. It is of particular interests to note that the Maxwellian shape is more likely to maintain during the pseudoheating under a wave spectrum compared with a monochromatic Alfvén wave. We, therefore can conclude that the kinetic behavior of ions under a monochromatic wave and a wave spectrum is totally different. Moreover, we illustrated that $E\times B$ drift can produce energetic particles under a spectrum of Alfvén waves, which may contribute to fast particle population in astrophysical and space plasmas.