Ionization potentials in the limit of large atomic number
Abstract
By extrapolating the energies of non-relativistic atoms and their ions with up to 3000 electrons within Kohn-Sham density functional theory, we find that the ionization potential remains finite and increases across a row, even as . The local density approximation becomes chemically accurate (and possibly exact) in some cases. Extended Thomas-Fermi theory matches the shell-average of both the ionization potential and density change. Exact results are given in the limit of weak electron-electron repulsion.
pacs:
71.10.Ca,71.15.Mb,71.45.GmA central problem of electronic structure is the calculation of the ground-state energy of the electrons of any atom, molecule, or solid, within the non-relativistic Born-Oppenheimer limit. Density functional theory (DFT) is a popular choice, balancing computational efficiency with useful accuracy. The original DFT was that of Thomas Thomas and Fermi Fermi , TF theory, in which a local density approximation is made for the the kinetic energy and the electron-electron repulsion is approximated by the simple Coulomb energy of the charge density. In the 1970’s, Lieb and co-workers Lieb1 showed that the TF energy becomes relatively exact for neutral matter as in a specific way. The energy, , grows in magnitude as , where is the total charge. For atoms and their ions, the leading corrections in powers of were found by Scott S52 , Dirac Dir , Schwinger and others Sa80 ; ESa84 , as summarized by Englert En88 . These corrections are given exactly by extended Thomas-Fermi (ETF) theory, which includes both the gradient correction for the kinetic energy (one-ninth the von Weisacker functional vW ), and the local density approximation for exchange (LSDX KS ).
However, TF theory and its extensions are insufficiently accurate to predict chemical propertiesTeller . Modern DFT uses the Kohn-Sham (KS) scheme, in which only a very small fraction of the total energy, the exchange-correlation (XC), needs be approximated. But the idea of asymptotic correctness was recently extended to KS, relating the success of exchange GGA’s such as PBE PBE for total energies to their recovery of the term in the expansion of the exchange energy PCSB ; EB09 . The relation between semiclassical and local density approximations ELCB contributed to the creation of PBEsol PRCVSCZB , a PBE-like functional that is nearly optimum for solids near equilibrium but not for atoms and molecules, and to revTPSS PRCCS , a nearly optimal semi-local functional for all three kinds of systems.
But total electronic energies are irrelevant to chemistry. Only differences matter, such as the ionization potential of an atom ( is the energy difference between the positive ion and the neutral) or the dissociation energy of a chemical bond. How relevant are asymptotic expansions for these quantities? The asymptotic expansion for is in powers of , so if remains finite as , the neutral and ion energies must agree for the first seven powers in such an expansion, a truly remarkable balancing act between quantum effects, the Pauli principle, and the Coulomb forces of nuclear attraction and inter-electron repulsion. In this letter, we demonstrate by both calculation and analysis that (i) has no limit as , but remains column-dependent (ii) that each column has a finite limit; (iii) the local (spin) density approximation (LSD KS ) of KS theory becomes very accurate (if not exact) for for certain cases; (iv) ETF theory becomes very accurate (if not exact) for the average of over an entire shell; (v) the shell-averaged difference in density between the neutral and its ion approches that of TF. We demonstrate these statements in the limit of weak interelectron repulsion.
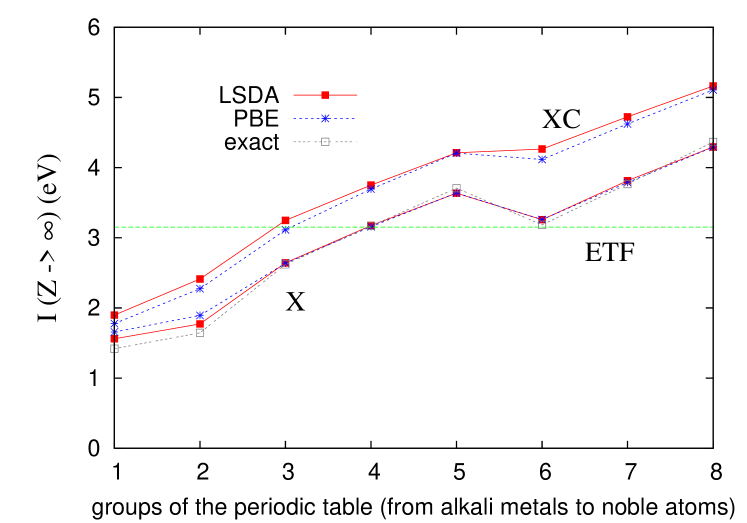
Our most important results are shown in Fig. 1. We plot from various calculations, extrapolated to infinite row number, versus the column number for main-group elements ( and valence shells). We calculate exchange exactly KLI ; TS , using the optimized effective potential (OEP, which here should be indistinguishable from Hartree-Fock primer ), extrapolating all values to . At the exchange level, LSD and PBE are almost exact for -valence elements, and are highly accurate but inexact for the -valence cases. Furthermore, ETF yields En88 a single number (3.15 eV), very close to the - and -average (3.02 eV). When correlation is included, gradient effects are slight, and it is in the regime of large electron number that approximate density functionals work best, sometimes exactly PCSB ; ELCB ; x . We speculate that LSDX on accurate densities becomes almost exact in this limit for -shell cases, that ETF is exact for some shell-average, and that our XC results are extremely accurate and practically impossible to calculate with any other method.
To understand why local functionals become accurate in this limit, begin with total energies of neutral atoms, whose large- expansion is
| (1) |
where is the energy of an atom with atomic number and charge , and the are coefficients depending on the degree of ionization, . We use atomic units throughout. The neutral coefficients were derived via semiclassical analysis by Schwinger and Englert Sa80 ; ESa84 . The TF energy is exactly . The second term S52 comes from the -orbitals at the nucleus and must be treated quantum mechanically. The third term is derivable in ETF theory Sa80 , of which 2/11 arises from the gradient correction to the kinetic energy, and 9/11 from LSDX. When treated in terms of the potential, the divergence at the nucleus is avoided En88 .
The extension of these ideas to has proven more difficult. Terms of higher order than those shown in Eq. (1) oscillate ESa84 with , as a precursor to the periodic variation of chemical properties that is missed by ETF, but well-described in KS DFT. The oscillations in dominate over trends with . While numerous studies exist in the literature CGDPFF for fixed electron number with , we are interested in as . Within TF theory, Lieb proved Lieb2 that does not grow with , and by considering as , Englert showed eV, where is a known constant En88 , and . Even this simple result requires explanation, because , the chemical potential, is zero for the neutral atom in TF theory, suggesting should be too. But the TF energy is the smooth envelope of as a function of , whereas the true energy consists of line segments between integer values PPLB . Thus for the exact system, but the TF energy behaves as for small . So , but the better value of is the energy difference En88 with .
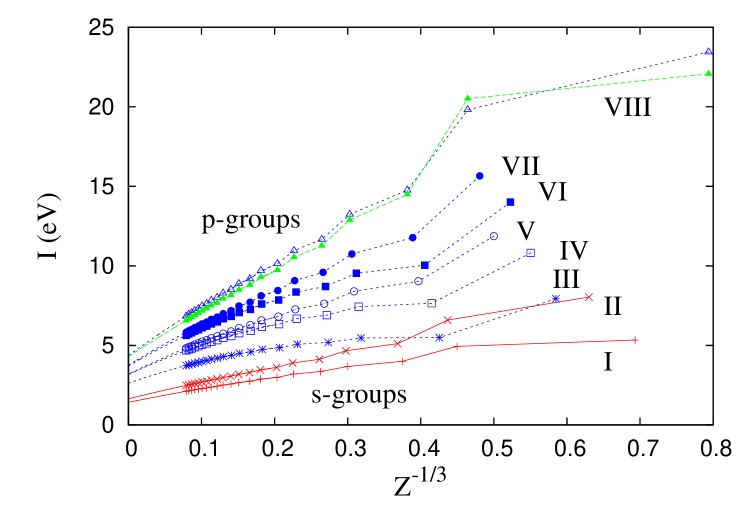
Next we discuss KS DFT, in which the (non-interacting) kinetic energy is not approximated, but is found exactly from the KS orbitals. We perform KS self-consistent calculations for atoms and ions up to 2938 electrons using LSD and PBE XC functional approximations, as well as the exact OEP exchange. These were done using the Engel code primer , but with tightened convergence criteria and maximum numbers of orbitals, and a logarithmic radial grid with 800 points. In Fig. 2 we show versus for each main-group column of the periodic table. In all cases, the behavior is almost linear as a function of for all , so we extrapolated these curves using a parabolic fit in and found the ionization energy for as shown in Fig. 1. The spherical approximations of the density (LSD, PBE) and of the potential (OEP), used in the Engel code (see Ref. TS ), give errors less that 0.1 eV for . We use electronic configurations based on the aufbau principle and Madelung rule Made . For the noble gases, , where is the row number and for even and 1 for odd rows.
| group | LSD | PBE | OEP | LSD | PBE | A | |
| I | 1.56 | 1.66 | 1.42 | 1.90 | 1.77 | -0.15 | 14.13 |
| II | 1.77 | 1.89 | 1.65 | 2.41 | 2.27 | - | 13.56 |
| - m.a.d. | 0.13 | 0.24 | 0 | 0.13 | 0 | ||
| - avg | 1.67 | 1.78 | 1.54 | 2.16 | 2.02 | -0.15 | 13.85 |
| III | 2.64 | 2.64 | 2.62 | 3.25 | 3.11 | 0.43 | 10.16 |
| IV | 3.17 | 3.16 | 3.17 | 3.75 | 3.69 | 0.92 | 9.82 |
| V | 3.64 | 3.64 | 3.71 | 4.21 | 4.21 | 1.34 | 9.49 |
| VI | 3.26 | 3.26 | 3.18 | 4.26 | 4.12 | 1.21 | 9.35 |
| VII | 3.81 | 3.79 | 3.76 | 4.72 | 4.62 | 1.62 | 9.07 |
| VIII | 4.29 | 4.29 | 4.37 | 5.16 | 5.11 | - | 8.82 |
| - m.a.d. | 0.05 | 0.05 | 0 | 0.08 | 0 | ||
| - avg | 3.47 | 3.46 | 3.47 | 4.23 | 4.14 | 1.10 | 9.45 |
To understand in detail the results shown in Fig. 1, which are also tabulated in Table I, we begin at the exchange level. Both PBE and LSD exchange are almost identical to the OEP values for the -group elements, with a maximum difference between them of 0.02 eV, and of either from OEP of 0.08 eV. This is not so for the alkalis and alkali earths, presumably because they have only one or two electrons outside a closed shell, with accompanying self-interaction error of approximate functionals. The ionization of -elements involves removing electrons from a full (or almost full) shell with electrons, where is the row number for even , and rows and have the same structure.
In fact, Englert also showed that the TF result is not correct as . The terms of in Eq. (1) also yield a finite contribution, which is included in ETF, yielding an of 3.15 eV, very close to the average over both and -shell values (3.02 eV).
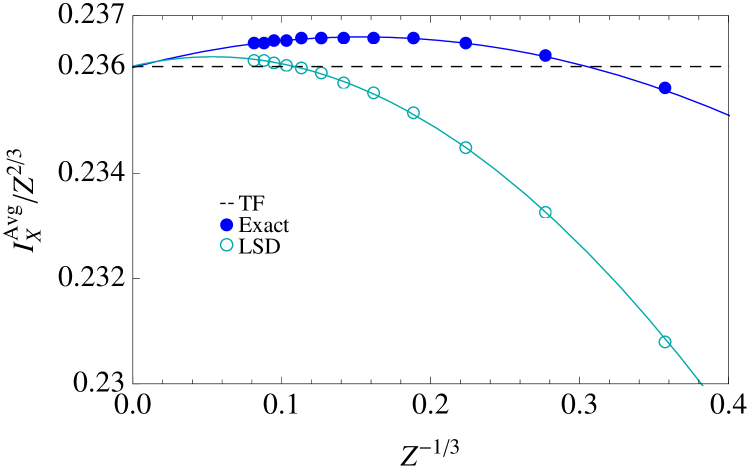
To check this is no accident, consider the simpler system of atoms with an infinitesimal electron-electron repulsion, , sometimes called Bohr atoms. The orbitals are hydrogenic, requiring no self-consistency and simplifying the integrals HL . One finds that is exact for large at . In Fig. 3, we show the exchange correction (divided by ) to for LSDX applied to the TF density (yielding ), to the exact densities (each averaged over entire shells), and exactly. All three match as , but a small error remains if, e.g., just the -shell is used. Thus we speculate that, for real atoms, LSDX (in a KS calculation) matches the average over the entire shell as .
Next, we discuss the DFT calculations with correlation, which remains finite as and varies across a row. The differences between PBE and LSD are relatively small, giving greater confidence in both. The maximum deviation between them for -elements is 0.14 eV, comparable to the deviations of these functionals at the exchange-only level from OEP for the alkali and alkali earths. Thus the gradient corrections are not vanishing, suggesting that while both calculations are accurate, neither is exact. The PBE average, 3.61 eV, is our best estimate of a universal ionization potential, defined as the limit of averaged over the -th shell, as .
The other major descriptor of chemistry is the electron affinity . Within LSD or PBE, the first negative atomic ion of energy has no stable solution, but can still be estimated P88 via a charged conductor model, in which , and is the centroid of the added charge. Define the radial ionization density as
| (2) |
which integrates to . Then choose . Table I shows PBE limits for , , and . Averaging over and , our best estimate for a universal value of is 0.78 eV.
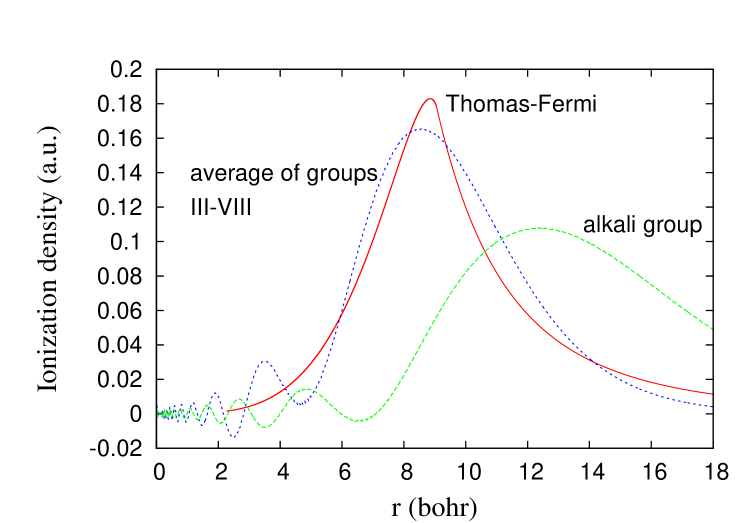
We next extrapolate the ionization density via
| (3) |
which correctly integrates over to . Here , , and , with fit parameters , and . Finally, we also averaged over the 6 -shell curves, to find the results shown in Fig. 4. The TF solution for the infinitesimally charged ion has a finite sizeEn88 ; Lieb2 , i.e.,
| (4) |
Beyond this radius, is just the radial density of the neutral, which has reached its asymptotic form, decaying as . The maximum of this curve is about 0.1830 at . The agreement between the extrapolated -shell densities and the TF theory is remarkably good, but not exact, while the extrapolated alkali ionization density is very different. We speculate that averaging over an entire shell would yield perfect agreement, as we find numerically for the Bohr atom.
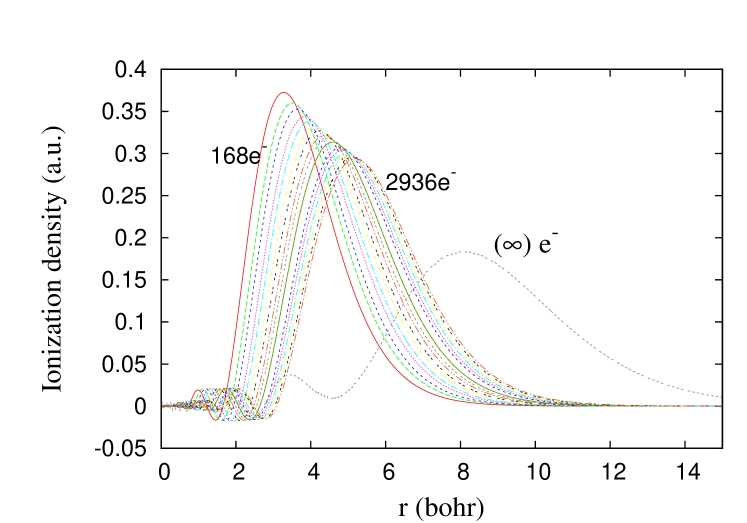
Finally, we justify why such large atomic numbers (larger by a factor of 10 than those of Ref. CMA ) are needed to get these results. Because of the scaling with , even only makes , while brings below 0.1, making the extrapolation much more reliable. In Fig. 5, we show accurate ionization densities for the 8-th column of the extended table at finite . The scaling of the TF ionization density is quite different from that of the exact solutions: Before extrapolation, even at , the TF ionization density agrees much better with that of the alkalis, not the -shell average. For the same reasons, having HF energies for only , Englert erroneously concluded that was the limit of the alkalis, not the shell-average (see Fig. 4-8 and its discussion of Ref. En88 ).
Thomas-Fermi theory produces the first term of Eq. (1) and extended TF yields an average limit for the ionization energy, but no periodic variation of chemical properties and no binding Teller of atoms to form molecules or solids. Within non-relativistic KS theory, any reasonable approximation to the XC energy with the correct uniform-density limit for exchange will produce the total-energy expansion of Eq. (1) and a finite column-dependent limit for the ionization energy. It appears that LSD is extremely accurate and possibly exact in certain cases for . We have shown this for shell-averages in the limit of weak inter-electron repulsion. But in that case, the last shell is spread throughout the entire atom, and average gradients contributing to ionization vanish as , which is not true for real atoms.
Thus we have established that, in the large- limit, the periodic table becomes perfectly periodic. Moreover, local approximations appear to become exact, even for energy differences that are relatively vanishingly small in this limit. These are new, numerically relevant, exact conditions that approximate functionals should satisfy.
All conclusions are based upon numerical calculations and extrapolation. Proving them rigorously is a challenge to mathematical physics. This work was supported by DOE grant DE-FG02-08ER46496 at Irvine, and NSF (Grants DMR-0501588 and DMR-0854769) at Tulane.
References
- (1) L.H. Thomas, Proc. Camb. Phil. Soc. , 542 (1926).
- (2) E. Fermi, Rend. Accad. Naz. Lizei , 602 (1927).
- (3) E.H. Lieb, Rev. Mod. Phys. , 553 (1976).
- (4) J.M.C. Scott, Philos. Mag. , 859 (1952).
- (5) P.A.M. Dirac, Proc. Camb. Phil. Soc. , 376 (1930).
- (6) J. Schwinger, Phys. Rev. A , 1827 (1980); ibid. , 2353 (1981).
- (7) B.-G. Englert and J. Schwinger, Phys. Rev. A ,2339 (1984); ibid. , 26 (1985).
- (8) B.-G. Englert, Semiclassical Theory of Atoms, (Lecture Notes in Physics, Springer-Verlag, Berlin, 1988).
- (9) C.F. von Weizsäcker, Z. Phys. , 431 (1935).
- (10) W. Kohn and L.J. Sham, Phys. Rev. , A1133 (1965).
- (11) E. Teller, Rev. Mod. Phys. , 627 (1962).
- (12) J.P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. , 3865 (1996); ibid. , 1396 (1997) (E).
- (13) J.P. Perdew et al., Phys. Rev. Lett. , 223002 (2006).
- (14) P. Elliott and K. Burke, Can. J. Chem. , 1485 (2009).
- (15) P. Elliott et al., Phys. Rev. Lett. , 256406 (2008).
- (16) J.P. Perdew et al., Phys. Rev. Lett. , 136406 (2008); ibid. , 039902 (2009) (E).
- (17) J.P. Perdew et al., Phys. Rev. Lett. , 026403 (2009).
- (18) J.B. Krieger, Y. Li and G.J. Iafrate, Phys. Rev. A , 101 (1992).
- (19) J.D. Talman and W.F. Shadwick, Phys. Rev. A , 36 (1976).
- (20) E. Engel, in A Primer in Density Functional Theory, eds. C. Fiolhais, F. Nogueira, and M. Marques, Springer (2003).
- (21) A. Cangi et al., Phys. Rev. B, to appear.
- (22) E.R. Davidson et al., Phys. Rev. A , 7071 (1991).
- (23) E.H. Lieb, Rev. Mod. Phys. , 603 (1981).
- (24) J.P. Perdew et al., Phys. Rev. Lett. , 1691 (1982).
- (25) E. Madelung, in Die Matematischen Hilfsmittel des Physikers, third ed., Springer, Berlin, 1936 (p. 359).
- (26) O.J. Heilmann and E.H. Lieb, Phys. Rev. A , 3628 (1995).
- (27) J.P. Perdew, Phys. Rev. B , 6175 (1988).
- (28) N. Cordero, N.H. March, and J.A. Alonso, Phys. Rev. A , 012505 (2007), and references therein.