ipie: A Python-based Auxiliary-Field Quantum Monte Carlo Program with Flexibility and Efficiency on CPUs and GPUs

Fionn D. Malone Google Research, Venice, CA 90291, United States Ankit Mahajan Department of Chemistry, University of Colorado, Boulder, CO 80302, USA James S. Spencer DeepMind, 6 Pancras Square, London N1C 4AG Joonho Lee linusjoonho@gmail.com Department of Chemistry, Columbia University, New York, NY, USA Google Research, Venice, CA 90291, United States

Abstract

We report the development of a python-based auxiliary-field quantum Monte Carlo (AFQMC) program, ipie, with preliminary timing benchmarks and new AFQMC results on the isomerization of \ce[Cu2O2]^2+. We demonstrate how implementations for both central and graphical processing units (CPUs and GPUs) are achieved in ipie. We show an interface of ipie with PySCF as well as a straightforward template for adding new estimators to ipie. Our timing benchmarks against other C++ codes, QMCPACK and Dice, suggest that ipie is faster or similarly performing for all chemical systems considered on both CPUs and GPUs. Our results on \ce[Cu2O2]^2+ using selected configuration interaction trials show that it is possible to converge the ph-AFQMC isomerization energy between bis( $\mu$ -oxo) and $\mu$ - $\eta^{2}$ : $\eta^{2}$ peroxo configurations to the exact known results for small basis sets with $10^{5}$ to $10^{6}$ determinants. We also report the isomerization energy with a quadruple-zeta basis set with an estimated error less than a kcal/mol, which involved 52 electrons and 290 orbitals with $10^{6}$ determinants in the trial wavefunction. These results highlight the utility of ph-AFQMC and ipie for systems with modest strong correlation and large-scale dynamic correlation.

I Introduction

The development of new electronic structure methods can often be accelerated by programs written in high-level, interpreted languages such as Python and Julia. Prominent recent examples are Psi4Numpy,Smith et al. (2018), PySCF,Sun et al. (2020) PyQMC,pyq (2022a) PyQuante,pyq (2022b, c) JuliaChem.jl,Poole et al. (2020, 2022) Fermi.jl,Aroeira et al. (2022) and iTensors.jl.Fishman et al. (2020) If programs written in such high-level languages reach similar performance compared to other production-level programs written in Fortran or C++, much more scientific development can be achieved at a faster pace. Motivated by this, in this work, we report our progress on developing a Python-based auxiliary-field quantum Monte Carlo (AFQMC) code that is both performant and flexible for new feature developments.

AFQMC has proven to be one of the more promising approaches to many-electron correlation problems.Koonin et al. (2013); Simons Collaboration on the Many-Electron Problem et al. (2015); Motta and Zhang (2018); Simons Collaboration on the Many-Electron Problem et al. (2020a); Shi and Zhang (2021); Lee et al. (2022a) Historically, the method has been mostly applied to lattice models within the constrained path approximationZhang et al. (1995) but there has been an increasing interest in applying this method within the phaseless approximationZhang and Krakauer (2003) to ab initio systems.Motta and Zhang (2018); Simons Collaboration on the Many-Electron Problem et al. (2020b); Shi and Zhang (2021); Lee et al. (2022a) Despite its success, the open-source code development has seen rather slow progress until recently although a proof-of-concept implementation in MATLABNguyen et al. (2014) was available for the Hubbard model in 2014. For ab initio systems, it was only within the last 10 years when the first production-level, open-source implementation developed by Morales and co-workers in QMCPACK appeared.Kim et al. (2018); Kent et al. (2020) Since then, another proof-of-concept program, PAUXY,pau (2022) written in Python by Malone and Lee, was made available. Finally, Sharma and co-workers released their free-projection (fp-) and phaseless (ph-) AFQMC implementation as a part of their open-source software project, Dice.dic (2022)

Our new code,ipi (2022) distributed under the Apache 2.0 license, intelligent python-based imaginary-time evolution (ipie), was largely motivated by the utility of PAUXY recognized by two of us after having used it for several research articles.Lee et al. (2019); Lee and Reichman (2020); Lee et al. (2021a, b, c) Nonetheless, the full potential of PAUXY was limited due to its computational inefficiency as well as its lack of graphics processing unit (GPU) support. AFQMC has two computational hotspots: propagation and local energy evaluation. The cost of these steps are dominated by dense linear algebra where the overhead of performing these in Python could be small. Propagation is mainly matrix-matrix multiplication that can be performed on Python efficiently using dot operations in NumPyHarris et al. (2020) and CuPy.Nishino and Loomis (2017) Similarly, the local energy evaluation can be performed efficiently utilizing just-in-time (jit) compilation in Numba.Lam et al. (2015) Furthermore, other computationally light-weight parts such as walker orthogonalization and population control of AFQMC do not cause much overhead in Python. These observations led us to develop ipie, an AFQMC code written in Python. The key goal of this open-source project is to aim for both flexibility for development and efficiency for production-level calculations.

At the same time, the recent development of quantum-classical hybrid ph-AFQMC algorithmHuggins et al. (2022); Lee et al. (2022b) started to involve a new scientific community in AFQMC, namely the quantum information science (QIS) community. As many code developments in QIS have been dominated by Python,quantumlib (2022a); Qiskit (2022); quantumlib (2022b); Rubin et al. (2021); Stair and Evangelista (2022) the development of a production-level python-based AFQMC code has become even more relevant. ipie has been mostly written by few core developers, but we hope that our progress report here will attract many scientists to this open-source software project.

Our paper is organized as follows. First, we will briefly review the theory behind the core features of ipie. Next, we will present some timing comparisons on both central processing units (CPUs) and GPUs against QMCPACK and Dice to showcase the performance of ipie. As an example of developing new features, we show how one can add a new mixed estimator to AFQMC without modifying internal codes in ipie. Finally, we report the AFQMC study of \ce[Cu2O2]^2+ with a heat-bath configuration interaction (HCI) trial wavefunction, compare with unbiased results,Mahajan et al. (2022) and present highly accurate complete basis set limit results.

II Theory

II.1 Notation

Notation	Description
MPI	Message Passing Interface
( $n$ e, $m$ o)	$n$ electrons in $m$ spatial orbitals
$M$ , nbasis	the number of orbitals
$N$ , nocc	the number of electrons
$N_{\text{aux}}$ , naux	the number of auxiliary vectors
$N_{\text{walkers}}$ , nwalkers	the number of walkers
$N_{\text{dets}}$	the number of determinants
$p,q,r,s$ , etc.	indices for orbitals
$i,j,k,l$ , etc.	indices for occupied orbitals
$\alpha,\beta,\gamma$ , etc.	indices for auxiliary vectors
$a,b,c,d$ , etc.	indices for determinants
$x,y,z$ , etc.	indices for walkers

Table 1: Notation used in this work.

In Table 1, we summarize the notation used in the later sections. We assume that we work in spin-orbital basis unless spins are labeled explicitly although our implementations write out spin degrees of freedom explicitly.

II.2 Review of AFQMC

In this paper, we hope to focus more on the computational and implementational aspects of ph-AFQMC as relevant to ipie. We will only summarize the essence of AFQMC, so interested readers are referred to recent ph-AFQMC reviewsKoonin et al. (2013); Motta and Zhang (2018); Shi and Zhang (2021); Lee et al. (2022a) for more theoretical details on ph-AFQMC.

Projector QMC algorithms approximate the exact ground state, $|\Psi_{0}\rangle$ , via imaginary time evolution:

|\Psi_{0}\rangle=\lim_{\tau\to\infty}e^{-\tau\hat{H}}|\Phi_{0}\rangle,

(1)

where $\tau$ is the imaginary time, $\hat{H}$ is the Hamiltonian, and $|\Phi_{0}\rangle$ is an initial wave function with non-zero overlap with $|\Psi_{0}\rangle$ . Different QMC algorithms differ in how one implements the imaginary time propagation in Eq. 1, how the Hamiltonian and initial wavefunction is represented and how the method controls the fermionic sign (or phase) problem.

In ipie, we implemented a specific flavor of QMC, namely, AFQMC. In AFQMC, we work with a second quantized representation of the Hamiltonian

\hat{H}=\sum_{pq}h_{pq}a_{p}^{\dagger}a_{q}+\frac{1}{2}\sum_{pqrs}(pr|qs)a_{p}^{\dagger}a_{q}^{\dagger}a_{s}a_{r},

(2)

and assume that the two-electron integral tensor is factorized by the Cholesky or density-fitting factorization

(pr|qs)=\sum_{\alpha=1}^{N_{\text{aux}}}L_{pr}^{\alpha}L_{qs}^{\alpha},

(3)

with $L_{pr}^{\alpha}$ being auxiliary vectors. In AFQMC, one further discretizes $\tau$ and applies the Trotter decomposition Trotter (1959) followed by the Hubbard-Stratonovich (HS) Hubbard (1959) transformation to the propagator $e^{-\Delta\tau\hat{H}}$ . This then leads to the integral representation of the imaginary-time propagator for a small time step, $\Delta\tau$ ,

e^{-\Delta\tau\hat{H}}=\int\mathrm{d}^{N_{\text{aux}}}\textbf{x}p(\textbf{x})\hat{B}(\textbf{x})+\mathcal{O}(\Delta\tau^{2}),

(4)

where $p(\textbf{x})$ is the normal distribution and $\hat{B}(\textbf{x})$ is a one-body propagator coupled to a vector of $N_{\text{aux}}$ auxiliary fields x.

From here the AFQMC algorithm could proceed by evolving a set of walkers by sampling the application of the propagator in Eq. 4 and updating the walker weights accordingly. This free-projection algorithm (fp-AFQMC) is however plagued by the fermion phase problem(Koonin et al., 2013). Although using an accurate initial state and trial wavefunction can delay the onset of the phase problem, ultimately it limits the applicability of fp-AFQMC to relatively short projection times (typically 1-2 a.u.), a situation which only gets worse with system size.

To overcome this, Zhang et al. introduced the phaseless approximation Zhang and Krakauer (2003) (ph-AFQMC hereafter) utilizing importance sampling based on an a priori chosen trial wavefunction, $|\Psi_{T}\rangle$ in addition to a fixing of the walker’s phase which is approximately enforced through the trial wavefunction. With importance sampling, the global wave function at time $\tau$ is written as a weighted statistical sum over $N_{\text{walkers}}$ walkers,

|\Psi(\tau)\rangle=\sum_{z=1}^{N_{\text{walkers}}}w_{z}(\tau)\frac{|\phi_{z}(\tau)\rangle}{\langle\Psi_{T}|\phi_{z}(\tau)\rangle}.

(5)

where $\{\phi_{z}(\tau)\}$ consists of single Slater determinants in arbitrary single-particle basis. ph-AFQMC ensures the positivity of walker weights $\{w_{z}(\tau)\}$ at all time $\tau$ and is thereby statistically efficient (i.e., the variance only grows linearly with system size), albeit at the expense of introducing a systematically improvable bias. We note that systematically improving the bias is generally thought to be exponentially expensive, similar to other constrained projector Monte Carlo approaches.

This importance sampling transformation yields the ‘hybrid method’ for propagating walkers:

	$\displaystyle w_{z}(\tau+\Delta\tau)\|\phi_{z}(\tau+\Delta\tau)\rangle=$
	$\displaystyle\left[I(\mathbf{x}_{z},\mathbf{\bar{x}}_{z},\tau,\Delta\tau)\hat{B}(\Delta\tau,\mathbf{x}_{z}-\mathbf{\bar{x}}_{z})\right]w_{z}(\tau)\|\phi_{z}(\tau)\rangle,$		(6)

where the importance function is defined as

I(\mathbf{x}_{z},\mathbf{\bar{x}}_{z},\tau,\Delta\tau)=O_{z}(\tau,\Delta\tau)e^{\mathbf{x}_{z}\cdot\mathbf{\bar{x}}_{z}-\mathbf{\bar{x}}_{z}\cdot\mathbf{\bar{x}}_{z}/2},

(7)

$O_{z}$ is the overlap ratio

O_{z}(\tau,\Delta\tau)=\frac{\langle\Psi_{T}|\hat{B}(\Delta\tau,\mathbf{x}_{z}-\mathbf{\bar{x}}_{z})|\phi_{z}(\tau)\rangle}{\langle\Psi_{T}|\phi_{z}(\tau)\rangle},

(8)

and $\mathbf{\bar{x}}_{z}$ is the optimal force bias, given as

\mathbf{\bar{x}}_{z}(\Delta\tau,\tau)=-\sqrt{\Delta\tau}\frac{\langle\Psi_{T}|\hat{\mathbf{v}}^{\prime}|\phi_{z}(\tau)\rangle}{\langle\Psi_{T}|\phi_{z}(\tau)\rangle}.

(9)

The phaseless approximation (ph) is then defined as a modification to this importance function

I_{ph}(\mathbf{x}_{z},\mathbf{\bar{x}}_{z},\tau,\Delta\tau)=|I(\mathbf{x}_{z},\mathbf{\bar{x}}_{z},\tau,\Delta\tau)|\times\text{max}(0,\cos(\theta_{z}(\tau)))

(10)

where the phase $\theta_{z}(\tau)$ is given by

\theta_{z}(\tau)=\text{arg}\left(O_{z}(\tau,\Delta\tau)\right).

(11)

The walker weights and Slater determinants are then updated as

	$\displaystyle w_{z}(\tau+\Delta\tau)$	$\displaystyle=I_{ph}(\mathbf{x}_{z},\mathbf{\bar{x}}_{z},\tau,\Delta\tau)\times w_{z}(\tau)$		(12)
	$\displaystyle\|\phi_{z}(\tau+\Delta\tau)\rangle$	$\displaystyle=\hat{B}(\Delta\tau,\mathbf{x}_{z}-\mathbf{\bar{x}}_{z})\|\phi_{z}(\tau)\rangle.$		(13)

III Implementational details

In this section, we focus on three computational kernels that are at the core of ph-AFQMC and discuss how they are implemented. The general strategy that we take is to avoid looping over walkers as much as we can because loops often involve additional overheads in Python.

We currently support two types of trial wavefunctions, $|\Psi_{T}\rangle$ : single- and multi-Slater determinant (SD and MSD) wavefunctions,

|\Psi_{T}\rangle=\sum_{a=0}^{N_{\text{det}}-1}c_{a}|\psi_{a}\rangle=\sum_{a=0}^{N_{\text{det}}-1}c_{a}\hat{t}_{a}|\psi_{0}\rangle

(14)

where $c_{a}$ is the expansion coefficient (sorted in descending order) for the $a$ -th determinant, and $\hat{t}_{a}$ is the $a$ -th excitation operator that generates $|\psi_{a}\rangle$ from $|\psi_{0}\rangle$ (a reference determinant). While our implementation for SD is relatively straightforward, the implementation for $N_{\text{det}}>1$ (i.e., MSD) is more involved following the generalized Wick’s theorem.Mahajan and Sharma (2021); Mahajan et al. (2022) We assume that the determinants, $|\psi_{a}\rangle$ , are mutually orthonormal and the corresponding coefficient matrices for each determinant are represented over orthogonal basis sets. ipie currently supports SD trials for both CPU and GPU and MSD trials for only CPU.

III.1 Overlap

In ph-AFQMC, one needs to compute the overlap between trial and walker wavefunctions:

\langle\Psi_{T}|\phi_{z}\rangle=\sum_{a=0}^{N_{\text{det}}-1}c_{a}\langle\psi_{a}|\phi_{z}\rangle

(15)

For SD trials ( $N_{\text{det}}=1$ ), this involves straightforward linear algebra function calls:

\langle\psi_{0}|\phi_{z}\rangle=\det\left(\mathbf{C}^{\dagger}_{\psi_{0}}\mathbf{C}_{\phi_{z}}\right)=\det\left(\mathbf{C}_{\phi_{z}}^{T}\mathbf{C}^{*}_{\psi_{0}}\right)

(16)

where $\mathbf{C}_{\psi_{0}}$ and $\mathbf{C}_{\phi_{i}}$ are coefficient matrices for $|\psi_{0}\rangle$ and $|\phi_{i}\rangle$ , respectively. We implement this operation for both CPU and GPU by using an einsum call followed by a determinant evaluation:

⬇

1S = einsum("zpi,pj->zij", phi, psi.conj())

2overlap = linalg.det(S)

Listing 1: Code snippet for constructing overlap on CPU and GPU.

where einsum and linalg.det are using NumPy and CuPy implementations for CPU and GPU, respectively. We note that walker coefficient matrices are stored as a three-dimensional array with size of $N_{\text{walkers}}\times M\times N$ . This then allows for a single einsum call for computing the dot product between two wavefunctions. The cost of this operation scales as $\mathcal{O}(N_{\text{walkers}}MN^{2})$ in general cases although the cost reduction to $\mathcal{O}(N_{\text{walkers}}MN)$ is possible in the molecular orbital basis (which is typical for MSD trials). The subsequent determinant evaluation costs $\mathcal{O}(N_{\text{walkers}}N^{3})$ .

For MSD trials, the code is much more involved. We compute the overlap by

\langle\Psi_{T}|\phi_{z}\rangle=\langle\psi_{0}|\phi_{z}\rangle+\langle\psi_{0}|\phi_{z}\rangle\left(\sum_{a=1}^{N_{\text{det}}-1}c_{a}\frac{\langle\psi_{0}|\hat{t}_{a}^{\dagger}|\phi_{z}\rangle}{\langle\psi_{0}|\phi_{z}\rangle}\right).

(17)

The summation over determinants in the second term is performed via the generalized Wick’s theoremMahajan and Sharma (2021) that uses the following quantity as an intermediate:

G_{pq}^{0,z}=\frac{\langle\psi_{0}|\hat{a}_{p}^{\dagger}\hat{a}_{q}|\phi_{z}\rangle}{\langle\psi_{0}|\phi_{z}\rangle}

(18)

where the upper index 0 refers to the first determinant index. The implementation to compute this intermediate will be discussed below. Implementation details on this algorithm for GPU will be reported in the future work.

III.2 One-body Green’s function and force bias

The most common propagation algorithm for ph-AFQMC is called the hybrid algorithm.Zhang and Krakauer (2003); Purwanto and Zhang (2004) A key component this algorithm involves computing the so-called optimal “force bias” potential defined as

	$\displaystyle\bar{x}_{\alpha}^{z}$	$\displaystyle=\frac{\langle\Psi_{T}\|a_{p}^{\dagger}a_{q}\|\phi_{z}\rangle}{\langle\Psi_{T}\|\phi_{z}\rangle}L_{pq}^{\alpha}$
		$\displaystyle=\sum_{pq}G_{pq}^{z}L_{pq}^{\alpha},$		(19)

where the one-body Green’s function reads

G_{pq}^{z}=\frac{\langle\Psi_{T}|\hat{a}_{p}^{\dagger}\hat{a}_{q}|\phi_{z}\rangle}{\langle\Psi_{T}|\phi_{z}\rangle}.

(20)

The force bias evaluation is a simple dot product so Eq. 19 can be naively performed at the cost of $\mathcal{O}(N_{\text{walkers}}N_{\text{aux}}M^{2})$ .

It is helpful for computational efficiency when constructing the force bias and also evaluating the local energy to construct the following intermediate tensor by transforming one-index of auxiliary vectors:

L_{ir}^{\alpha}=\sum_{p}(\mathbf{C}_{\psi_{0}}^{\dagger})_{ip}L_{pr}^{\alpha}.

(21)

This is stored in shared memory as a $N_{\text{aux}}\times NM$ matrix in our code and only needs to be constructed once in the beginning of the simulation (per computational node).

For SD trials this allows us to exploit a rank-revealing, factorized form for the Green’s function,

G_{pq}^{z}=(\mathbf{C}_{\psi_{z}}(\mathbf{C}_{\psi_{0}}^{\dagger}\mathbf{C}_{\psi_{z}})^{-1}\mathbf{C}_{\psi_{0}}^{\dagger})_{qp}=\sum_{j=1}^{N}\theta^{z}_{jp}(\mathbf{C}_{\psi_{0}}^{\dagger})_{jq},

(22)

where the walker-dependent part of the Green’s function is

\theta^{z}_{jp}=(\mathbf{C}_{\psi_{z}}(\mathbf{C}_{\psi_{0}}^{\dagger}\mathbf{C}_{\psi_{z}})^{-1})_{pj},

(23)

so, for example, we can write Eq. 19 as

\bar{x}_{\alpha}^{z}=\sum_{pj}\theta_{jp}^{z}L_{pj}^{\alpha}.

(24)

The cost of building the force bias in this form is $\mathcal{O}(N_{\text{walkers}}N_{\text{aux}}MN)$ . In our GPU implementation, we build $\theta_{jp}^{z}$ by

⬇

1import cupy as cp # For GPU implementation

2S = cp.einsum("zpi,pj->zij", phi, psi.conj())

3Sinv = cp.inv(S)

4theta = cp.einsum("zji,zpi->zjp", Sinv, phi)

Listing 2: Code snippet for constructing

\theta_{jp}^{z}

on GPU.

For CPU, we found that it is faster to loop over the walker index and perform dot and inv operations than using einsum and batched inv. Using $\theta_{jp}^{z}$ , the force bias can be built as a matrix-matrix multiplication for all walkers in a given MPI task at once:

⬇

1theta = theta.reshape((nwalkers, nocc*nbasis))

2force_bias_real = rchol.dot(theta.T.real)

3force_bias_imag = rchol.dot(theta.T.imag)

4force_bias = empty((nwalkers, naux),

5 dtype=theta.dtype)

6force_bias.real = force_bias_real.T.copy()

7force_bias.imag = force_bias_imag.T.copy()

Listing 3: Code snippet for constructing force bias on CPU and GPU.

where rchol denotes $L_{pj}^{\alpha}$ with a shape of ( $N_{\text{aux}}$ , $NM$ ). We use the same code for both CPU and GPU where empty is from NumPy for CPU and from CuPy for GPU. We found it more efficient to compute real and imaginary parts of the force bias separately. Naïve dot operations between a real-valued array rchol and a complex-valued array theta create a complex-valued copy for rchol, which consumes additional memory and slows down the overall operation. Therefore, we avoid this by creating copies.

For MSD trials, we compute the denominator of Eq. 20 using Eq. 17 and the numerator via the generalized Wick’s theorem:Mahajan and Sharma (2021)

\langle\Psi_{T}|\hat{a}_{p}^{\dagger}\hat{a}_{q}|\phi_{z}\rangle=\langle\psi_{0}|\phi_{z}\rangle\left(\sum_{a=0}^{N_{\text{det}}-1}c_{a}\frac{\langle\psi_{0}|\hat{t}_{a}^{\dagger}\hat{a}^{\dagger}_{p}\hat{a}_{q}|\phi_{z}\rangle}{\langle\psi_{0}|\phi_{z}\rangle}\right).

(25)

The necessary intermediate in Eq. 18 can be computed by Eq. 22. We largely followed the CPU implementation described in Ref. 40 with some necessary changes to avoid excessive looping due to Python overheads. We will report more detailed descriptions about it in our forthcoming GPU implementation paper.

III.3 Local energy

The local energy is one of the most important mixed estimators to compute in QMC methods. It is defined as

E^{z}_{L}=\frac{\langle\Psi_{T}|\hat{H}|\phi_{z}\rangle}{\langle\Psi_{T}|\phi_{z}\rangle},

(26)

and the global energy (i.e. walker averaged) estimate can then be computed by

E=\frac{\sum_{z}w_{z}E_{L}^{z}}{\sum_{z}w_{z}}

(27)

There are many algorithms developed for the local energy evaluationMotta et al. (2019); Malone et al. (2019); Lee and Reichman (2020); Weber et al. (2022) and we implemented some of the more commonly used algorithms.

For brevity, we focus on the exact exchange-like energy contribution as it is more computationally demanding (i.e., quartic-scaling) than that of Coulomb-like one (i.e., cubic-scaling.) For SD trials, this contribution reads

E^{z}_{L,\text{K}}=-\frac{1}{2}\sum_{ij}\sum_{pq}\sum_{\alpha}L_{ip}^{\alpha}L_{jq}^{\alpha}\theta_{iq}\theta_{jp}.

(28)

Looping over $\alpha$ and contracting over other indices to accumulate the energy contribution will scale as $\mathcal{O}(N_{\text{walkers}}N_{\text{aux}}N^{2}M)$ . The computational bottleneck in this step is to form

T_{ij}^{z,\alpha}=\sum_{p}L_{ip}^{\alpha}\theta_{jp}^{z}.

(29)

To avoid storing this object in memory, we use a direct algorithm where $T_{ij}^{z,\alpha}$ for each of $z$ and $\alpha$ is formed and consumed immediately. Looping over both walker and auxiliary indices creates additional overheads in Python so we resort to Numba and its jit compilation to remove such overheads:

⬇

1import numba.jit as jit

2import numpy as np

3@jit(nopython=True, fastmath=True)

4def compute_exchange(rchol, theta):

5 naux = rchol.shape[0]

6 nwalkers = theta.shape[0]

7 nocc = theta.shape[1]

8 nbasis = theta.shape[2]

9 T = np.zeros((nocc, nocc),dtype=np.complex128)

10 exx = np.zeros((nwalkers),dtype=np.complex128)

11 rchol = rchol.reshape((naux, nocc, nbasis))

12 for iw in range(nwalkers):

13 theta_r = theta[iw].T.real.copy()

14 theta_i = theta[iw].T.imag.copy()

15 for jx in range(naux):

16 T = (

17 rchol[jx].dot(theta_r)

18 +

19 1.0j * rchol[jx].dot(theta_i)

20 )

21 exx[iw] += np.dot(T.ravel(),

22 T.T.ravel())

23 exx *= 0.5

24 return exx

Listing 4: Code snippet for computing exchange-like contribution to the local energy. It is written for Numba’s jit capability.

In the above code, we split real and imaginary parts of $\theta_{jp}^{z}$ by creating appropriate copies (line 13-14). This was found to be helpful in performing subsequent dot operations as these copies store real and imaginary elements of $\theta_{jp}^{z}$ contiguously in memory. Furthermore, it avoids creating a complex-valued copy of rchol as explained before for LABEL:list:fb. For our GPU implementation, we found that utilizing only existing CuPy functions leads to either inefficient or very memory-demanding local energy evaluations. It was therefore necessary to write our own GPU kernel with Numba’s cuda.jit based on the same local energy algorithm implemented in QMCPACK.(Kent et al., 2020)

For MSD trials, we utilize the generalized Wick’s theorem similarly to how overlap and Green’s functions were evaluated. For one-body energies, we can easily compute the contribution by using the one-body Green’s function in Eq. 20. Additional complications arise for the two-body local energy contribution where we evaluate the numerator as

	$\displaystyle\langle\Psi_{T}\|\phi_{z}\rangle E_{L,2}^{z}=$	$\displaystyle-\frac{1}{2}\langle\psi_{0}\|\phi_{z}\rangle\sum_{prqs}\sum_{\alpha=1}^{N_{\text{aux}}}\sum_{a=0}^{N_{\text{det}}-1}$
		$\displaystyle\bigg{(}c_{a}\frac{\langle\psi_{0}\|\hat{t}_{a}^{\dagger}\hat{a}^{\dagger}_{p}\hat{a}_{r}\hat{a}_{q}^{\dagger}\hat{a}_{s}\|\phi_{z}\rangle}{\langle\psi_{0}\|\phi_{z}\rangle}L_{pr}^{\alpha}L_{qs}^{\alpha}\bigg{)}.$		(30)

We extensively used Numba’s jit capability and exploit BLAS for implementing the necessary loops and contractions for the generalized Wick’s theorem over determinants, walkers, and excitations. More detailed description about this implementation and its GPU extension will be reported in our forthcoming paper.

III.4 Code Structure and Development Process

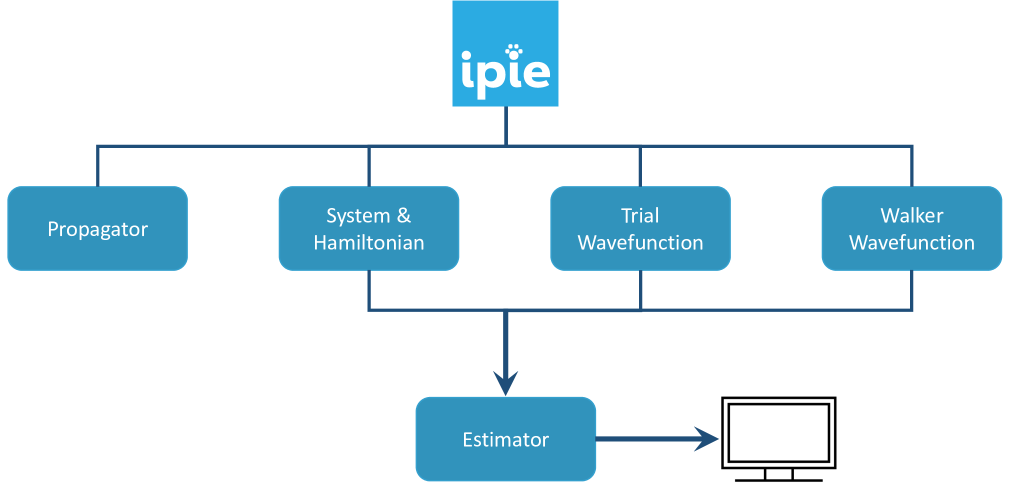
Refer to caption — Figure 1: Diagram on how different classes are organized in ipie.

In Fig. 1, we present an overview of the internal structure of ipie. We have seven distinct classes in ipie for propagator, system, Hamiltonian, trial wavefunction, walker wavefunction, and estimator. The propagator class interacts with all other classes except estimator to evolve the walker wavefunction. The system class specifies the number of electrons, symmetry of the system, and other information pertinent to the problem. The Hamiltonian class stores necessary one-body matrix elements and auxiliary vectors. The trial wavefunction class contains information about $|\Psi_{T}\rangle$ along with necessary integral intermediates that depend on $|\Psi_{T}\rangle$ . The walker wavefunction class stores weights and $|\phi_{z}\rangle$ . The estimator class takes in system, Hamiltonian, trial wavefunction, and walker wavefunction to produce the global observables at a given imaginary time. We designed the program in a modular way to maximize the flexibility of adding new features in the future.

When adding new features to the code we try to follow a test driven development process, with new features initially prototyped as unit tests before being fully incorporated into the code. In addition to unit tests we have a set of deterministic serial and parallel integration tests designed to test the full AFQMC application. The test suite is run through continuous integration upon a pull request being opened on GitHub with one approving code review required before any new feature or fix is merged into the development branch.

IV Applications and Discussion

In this section, we hope to demonstrate the ease of running our program when interfaced with PySCFSun et al. (2020) and adding a new estimator $\langle\hat{S}^{2}\rangle$ as well as a new application of ph-AFQMC to the computation of isomerization energy of \ce[Cu2O2]^2+.

IV.1 Interface with PySCF

ipie is a Python program, and thus the most natural quantum chemistry package to be paired with for obtaining integrals is currently PySCF. While our interface is generic enough to be coupled with any quantum chemistry software such as Q-ChemEpifanovsky et al. (2021) as long as users provide integrals in an expected format, we expect that our biggest user base at the point of writing will be familiar with PySCF.

An AFQMC calculation on one-dimensional \ceH10 (bond distance of 1.6 Bohr) in the STO-6G basis with a Hartree-Fock trial wavefunction can be performed by running a script like the following:

⬇

1from pyscf import gto, scf

2from mpi4py import MPI

3from ipie.utils.from_pyscf import (

4 gen_ipie_input_from_pyscf_chk

5 )

7comm = MPI.COMM_WORLD

8mol = gto.M(

9 atom=[("H", 1.6 * i, 0, 0)\

10 for i in range(0, 10)],

11 basis="sto-6g",

12 verbose=4,

13 unit="Bohr",

14 )

15nelec = mol.nelec

16if comm.rank == 0:

17 mf = scf.UHF(mol)

18 mf.chkfile = "scf.chk"

19 mf.kernel()

20 gen_ipie_input_from_pyscf_chk(mf.chkfile,

21 verbose=0)

22comm.barrier()

24from ipie.qmc.calc import build_afqmc_driver

25afqmc = build_afqmc_driver(comm, nelec=nelec,

26 nwalkers_per_task=1000)

28afqmc.qmc.nblocks = 200

29afqmc.run(comm=comm)

31if comm.rank == 0:

32 from ipie.analysis.extraction import (

33 extract_observable

34 )

35 fname = afqmc.estimators.filename

36 qmc_data = extract_observable(fname,

37 "energy")

38 y = qmc_data["ETotal"]

39 y = y[50:] # discard first 50 blocks

41 from ipie.analysis.autocorr import (

42 reblock_by_autocorr

43 )

44 df = reblock_by_autocorr(y)

45 print(df.to_csv(index=False))

Listing 5: Script that runs a Hartree-Fock calculation using PySCF, generates relevant ipie inputs, runs a ph-AFQMC calculation via ipie, and analyzing the output of ipie for the final ph-AFQMC energy and its error bar.

This script uses 1000 walkers per MPI process to sample 200 AFQMC blocks, where a block consists of a number of steps where the propagator is applied (typically 25) and one energy evaluation. Projector Monte Carlo methods generally produce serially correlated data and thus it is necessary to account for the autocorrelation time through approximately estimating it or using a reblocking analysis.(Flyvbjerg and Petersen, 1989) Thus, we next discard 50 blocks for equilibration and reblock the remaining 150 blocks to produce an estimate of the energy and its error bar. The resulting energy is -5.3825(7) which is comparable to the energy of CCSD(T), -5.3841.

Note, the above example is for demonstration purposes only. For large scale production calculations it is not advised to run the initial SCF step in the same script as the subsequent AFQMC calculation, as often one needs to use hundreds or thousands of MPI processes and thus it is not a good use of computational resources, and we advise users to run the QMC workflow in distinct steps.

IV.2 Customized mixed estimators

Often, the total energy is not all that one wants to compute from ph-AFQMC simulations. Ideally, adding arbitrary mixed estimators or even back-propagated estimatorsMotta and Zhang (2017) should be possible without much effort. As an example of how this is accomplished in ipie, we show an implementation of $\langle\hat{S}^{2}\rangle$ . Since $[\hat{S}^{2},\hat{H}]=0$ , a mixed estimator for $\hat{S}^{2}$ is unbiased. For an SD trial ( $|\Psi_{T}\rangle=|\psi_{0}\rangle$ ), it can be computed by

	$\displaystyle\frac{\langle\psi_{0}\|\hat{S}^{2}\|\phi_{z}\rangle}{\langle\psi_{0}\|\phi_{z}\rangle}$	$\displaystyle=N_{\downarrow}+M_{S}(M_{S}+1)$
		$\displaystyle-\sum_{pq}G^{z}_{p_{\downarrow}q_{\downarrow}}G^{z}_{p_{\uparrow}q_{\uparrow}}$		(31)

where $N_{\downarrow}$ is the number of spin- $\downarrow$ electrons and $M_{S}$ is the $\hat{S}_{z}$ quantum number of the state. $G^{z}_{p_{\downarrow}q_{\downarrow}}$ and $G^{z}_{p_{\uparrow}q_{\uparrow}}$ are one-body Green’s functions (Eq. 22) for each spin section.

To add this new estimator to ipie, one can define a pertinent estimator class and add it to the driver class to run ph-AFQMC as the following:

⬇

1import numpy as np

2from ipie.estimators.estimator_base import (

3 EstimatorBase

4 )

5from ipie.estimators.greens_function_batch import (

6 greens_function

7 )

9class S2Mixed(EstimatorBase):

10 def __init__(self, ham):

11 self._data = {

12 "S2Numer": np.zeros((1),

13 dtype=np.complex128),

14 "S2Denom": np.zeros((1),

15 dtype=np.complex128),

16 }

17 # shape of the estimator

18 self._shape = (1,)

20 # optional variables

21 # whether to print into text output

22 self.print_to_stdout = True

23 # new filename if needed

24 self.ascii_filename = None

25 # whether to store it as scalar

26 self.scalar_estimator = False

28 def compute_estimator(self, sys, walkers,

29 hamiltonian, trial):

30 greens_function(walkers, trial,

31 build_full=True)

33 ndown = sys.ndown

34 nup = sys.nup

35 Ms = (nup-ndown)/2.0

37 two_body = -np.einsum("zij,zji->z",

38 walkers.Ga,walkers.Gb)

39 two_body = two_body * walkers.weight

41 denom = np.sum(walkers.weight)

42 numer = np.sum(two_body)\

43 + denom*(Ms*(Ms+1)+ndown)

45 self["S2Numer"] = numer

46 self["S2Denom"] = denom

49# ... Build afqmc inputs and driver class

50# afqmc is the driver class

51ham = afqmc.hamiltonian

52afqmc.estimators["S2"] = S2Mixed(ham=ham)

53afqmc.run(comm=comm)

Listing 6: Code snippet for implementing a new mixed estimator,

\langle\hat{S}^{2}\rangle

and running ipie with it.

The design uses inheritance with the custom estimator class deriving from the base EstimatorBase class which defines generic functionality common to all estimators. In this way complications such as MPI are abstracted away from the developer and only core functionality needs to be implemented. As this code demonstrates, adding new mixed estimators to ipie does not require modifying any code inside ipie lowering the barrier for prototyping research related to estimators. In the future, we hope to support other ways to compute estimators such as backpropagationMotta and Zhang (2017) or automatic differentiation.Sorella and Capriotti (2010)

IV.3 Timing benchmarks

One of the common concerns about writing a Python code for many-body methods is that it may be difficult for a Python-based code to perform as well as those written in C++ or Fortran. Therefore, in this section, we report some preliminary timing benchmarks comparing ipie against two production-level C++ codes, QMCPACKKent et al. (2020) and Dice.dic (2022)

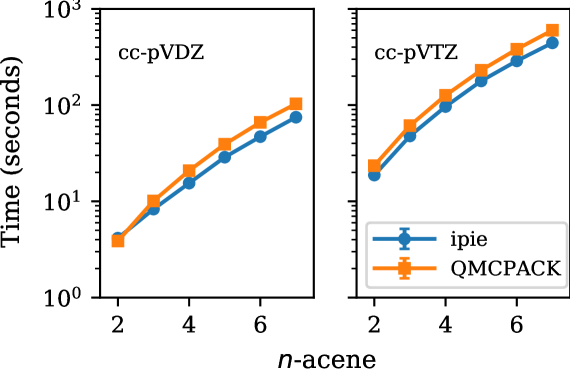
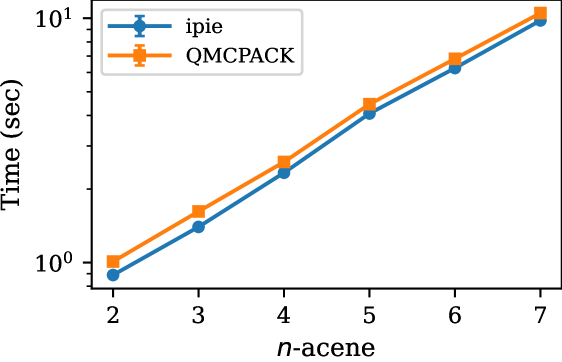
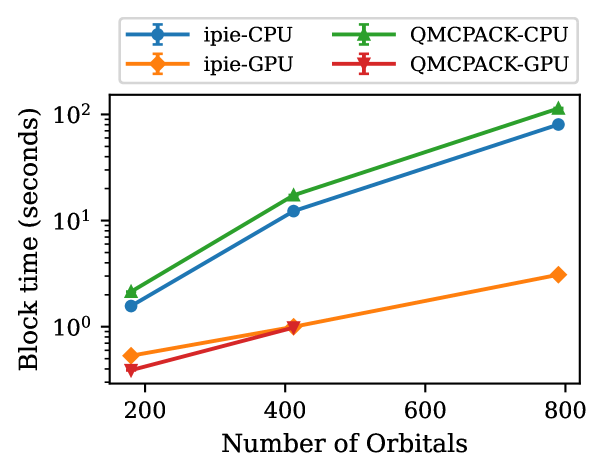
In Fig. 2, we compare the CPU performance of ipie with SD trials for studying acene series from naphthalene to heptacene with cc-pVDZ and cc-pVTZ bases against QMCPACK. For both bases, we see that ipie outperforms QMCPACK for all system sizes except naphthalene in cc-pVDZ. Similarly in Fig. 3, we compare the GPU performance of ipie with SD trials for studying acene series with cc-pVDZ basis against QMCPACK. ipie is faster than QMCPACK for all acenes. Finally, in Fig. 4 we compare timings as a function of basis sets size on a single CPU node (30 MPI processes) and a single V100, both with 30 walkers total. Again we find ipie performs favorably relative to QMCPACK and we see a roughly order of magnitude gain in speed on the GPUs. We find that the ipie is typically slower than QMCPACK on GPUs when an insufficient number of walkers are used for small system sizes (indicating the the GPU is not being saturated), which is clear when comparing the cc-pVDZ naphthalene times in Fig. 3 and Fig. 4. These timing benchmarks emphasize the utility of ipie beyond prototyping and shows its potential for production-level AFQMC calculations.

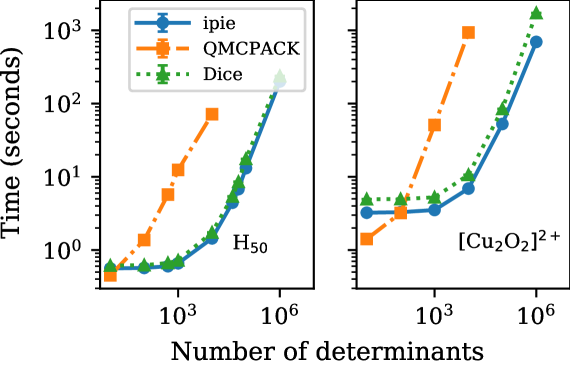
We also benchmarked our CPU implementation of the generalized Wick’s theorem as shown in Fig. 5. QMCPACK employs a different algorithm based on the Sherman-Morrison formula, which inevitably becomes too slow to run for large determinant counts.Shee et al. (2018); Mahajan et al. (2022) However, both Dice and ipie implement the same generalized Wick’s theorem algorithm and therefore they both can handle many more determinants in the trial wavefunction. We test our implementation on \ceH50 and \ce[Cu2O2]^2+ using the heat-bath configuration interaction (HCI) wavefunctionsHolmes et al. (2016); Smith et al. (2017) made available in ref. 43 as our trial. Note that a converter is provided with ipie to allow HCI wavefunctions generated with Dice to be used. We found our code to be slightly faster than Dice. The implementation in QMCPACK is already 10 times slower for a modest determinant count ( $10^{3}$ ). We expect that our implementation will be well suited for studying systems with modest strong correlation and large-scale dynamic correlation.

For GPU, it is often the case that one cannot store the auxiliary vectors on one GPU due to the limited memory available on GPU. In that case, we split auxiliary vectors into multiple blocks and distribute each block over multiple GPUs. To minimize the size of communications during the run, we communicate walker wavefunctions instead of auxiliary vectors as well as the result of computation such as local energy and force bias. This multi-GPU implementation will become important when studying large systems. We hope to report applications that utilize this feature in the future.

IV.4 Isomerization energy of \ce[Cu2O2]^2+

\ce

[Cu2O2]^2+ is one of the widely studied model problems and has been commonly referred to as the torture track.Cramer et al. (2006) Both strong and weak correlation play an important role in its electronic structure, and hence this system poses a great challenge to many of the existing electronic structure methods. The computation of isomerization energies between bis( $\mu$ -oxo) and $\mu$ - $\eta^{2}$ : $\eta^{2}$ peroxo configurations is often of interest in this problem. These are motifs that can be found in enzymes such as tyrosinase.Solomon et al. (1992) These two structures are often characterized by $f=0$ and $f=1$ , respectively, where $f$ is a structural parameter that allows one to interpolate between the two conformations by choosing $f\in[0,1]$ . In this work, we focus on computing the isomerization energy between these two structures. The geometries used here have been taken from Ref. 43. We use 640 walkers and $\Delta t$ of 0.005 a.u. for all calculations.

IV.4.1 (32e,108o) correlation space

Due to the difficulty of this problem, it is necessary to employ ph-AFQMC with an MSD trial based on HCI with self-consistent field (HCISCF) calculations. A recent unbiased QMC (i.e., fp-AFQMC)Mahajan and Sharma (2021) study reported statistically exact energies for this problem in double and triple-zeta bases. For the smallest problem studied by fp-AFQMC (the double-zeta ANO basis denoted BS1 in Ref. 43), we first assess the accuracy of ph-AFQMC as a function of the number of determinants in our trial. Following Ref.43 we freeze 10 core orbitals so that the trial wavefunction correlates 32 electrons and 108 orbitals.

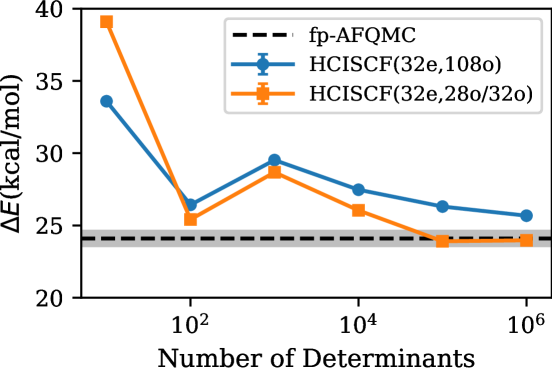
In Fig. 6, we have two sets of ph-AFQMC results. They are using different HCISCF wavefunctions as trial wavefunctions. One is using the HCISCF wavefunction generated for 32 electrons and 108 spatial orbitals, but the other one is using a trial generated for 32 electrons and 28 spatial orbitals ( $f=0$ ) or 32 spatial orbitals ( $f=1$ ). For (32e,108o) HCISCF, we followed the procedure from Ref. 43 and used $\epsilon_{1}=10^{-3}$ (a relatively loose thresholdHolmes et al. (2016); Smith et al. (2017) for orbital optimization, followed by a single-shot HCI calculation with $\epsilon_{1}=10^{-4}$ . This HCISCF trial with a larger active space shows a quite long tail in its convergence and even with $10^{6}$ determinants the isomerization energy is off by a kcal/mol or more. This points towards the poor quality of this HCI trial wavefunction.

To remedy this situation, we took a different strategy where we generate a reduced active space based on natural occupation numbers obtained from the HCI trial with a larger active space (in this case (32e,108o)). For the purpose of obtaining a smaller active space, we found that the HCI wavefunction for (32e,108o) active space with $\epsilon_{1}=10^{-4}$ is accurate enough. We included orbitals with occupation $n$ that satisfies $0.01\leq n\leq 1.99$ in the subsequent, more precise HCISCF calculations. These active spaces are 28-orbital and 32-orbital, respectively, for $f=0$ and $f=1$ . Using these new active spaces, we perform more accurate HCISCF calculations with $\epsilon_{1}=5\times 10^{-5}$ . For these smaller active spaces, the variational HCISCF calculation is nearly converged in that the perturbative contribution within the active space is only 3-4 m $E_{h}$ . These new more compact HCISCF trials show quick convergence in the isomerization energy where our ph-AFQMC relative energies are within the error bar of the exact fp-AFQMC energies with $N_{\text{det}}=10^{5}$ or more.

IV.4.2 Larger correlation space

Given the success of natural orbital active spaces in the previous section, it is useful to extend this approach to larger correlation space. For a larger number of electrons and orbitals, even qualitatively correct HCISCF calculations become computationally infeasible. Therefore, we chose to project the converged HCISCF orbitals in a smaller basis on to a larger basis. For BS1 (52e,108o), such a projection is not necessary as one can use the same trial wavefunction as the one used for (32e,108o).

For larger ANO-RCC basesFdez. Galván et al. (2019) (ANO-RCC-VTZP; called BS2 in Ref. 43), we performed HCISCF calculations ( $\varepsilon_{1}=2.5\times 10^{-5}$ ) with ANO-RCC-VDZP to obtain a compact active space based on natural orbital occupation numbers for both configurations. For the larger basis sets we tightened the natural orbital threshold to $0.02\leq n\leq 1.98$ . These active spaces are (32e,31o) and (32e,32o), respectively, for $f=0$ and $f=1$ , similar to those in BS1. The projection onto a larger basis set can be performed via

\mathbf{C}_{\text{large}}=\mathbf{S}_{\text{large}}^{-1}\bar{\mathbf{S}}_{\text{large,small}}\mathbf{C}_{\text{small}}

(32)

where $\mathbf{C}_{\text{small}}$ is the molecular orbital (MO) coefficient in the smaller basis set, $\mathbf{C}_{\text{large}}$ is the MO coefficient in the larger basis set, $\mathbf{S}_{\text{large}}^{-1}$ is the inverse of the overlap matrix between atomic orbitals (AOs) in the larger basis set, and $\bar{\mathbf{S}}_{\text{large,small}}$ is the overlap between AOs in large and small basis sets.Montgomery et al. (2000) After symmetrically orthogonalizing these projected MOs, we perform HCISCF calculations to relax orbitals further.

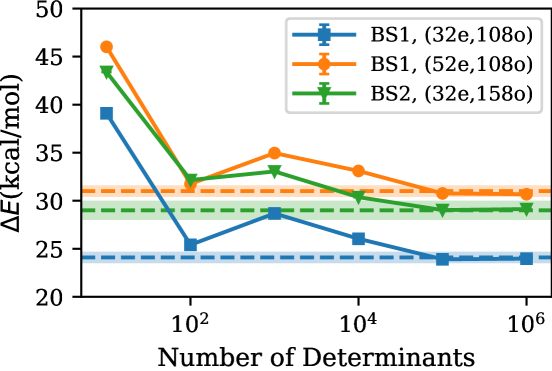
Using the strategy described above, we performed larger correlation space calculations as shown in Fig. 7. In both BS1 (52e,108o) and BS2 (32e,158o), we reach exact isomerization energies at a determinant count of $10^{5}$ . We note that ph-AFQMC absolute energies for both $f=0$ and $f=1$ are converged better than 1 m $E_{h}$ with $N_{\text{det}}=10^{6}$ from available fp-AFQMC total energies. However, for $N_{\text{det}}=10^{5}$ , we are benefiting from cancellation of error.

IV.4.3 Towards the basis set limit

$N_{\text{det}}$	TZ	QZ	CBS
$10^{4}$	30.4(2)	27.0(2)	28.1(3)
$10^{5}$	29.0(4)	25.4(3)	26.3(5)
$10^{6}$	29.1(6)	25.2(4)	26.0(7)
fp-AFQMCMahajan and Sharma (2021)	29(1)	N/A	N/A

Table 2: ph-AFQMC \ce[Cu2O2]^2+ isomerization energies (kcal/mol) for ANO-RCC-VTZP (BS2), ANO-RCC-VQZP, and the complete basis set (CBS) limit for different determinant counts (

N_{\text{det}}

). 32 electrons were correlated in these calculations and the X2C HamiltonianLiu (2010) was used for relativistic effects. N/A means “not available.”

$N_{\text{det}}$	TZ	QZ	CBS
$10^{4}$	31.6(4)	29.6(3)	31.8(5)
$10^{5}$	29.1(5)	27.2(4)	29.5(6)
$10^{6}$	29.0(7)	27.1(9)	29(1)

Table 3: Same as Table 2 except that 52 electrons are correlated.

Method	Basis	Correlation Space	$\Delta E$
fp-AFQMC	TZ	(32e, 158o)	29(1)
ph-AFQMC		(32e, 158o)	29.1(6)
CCSD(T)		(32e, 158o)	34.8
ph-AFQMC	TZ	(52e, 166o)	29.0(7)
CCSD(T)		(52e, 166o)	33.6
ph-AFQMC	QZ	(52e, 290o)	27.1(9)
CCSD(T)		(52e, 290o)	33.0

Table 4: Comparison between ph-AFQMC(

N_{\mathrm{det}}=10^{6})

fp-AFQMC and CCSD(T) for different basis set and correlation space sizes. CCSD(T) and fp-AFQMC results are from Ref. 43. Note that the fp-AFMQC result for BS3 are actually the (32e, 158o) results from BS2 with a basis set correction from CCSD(T) added(Mahajan and Sharma, 2021), whereas the fp-AFQMC results were run in the full correlation space. For comparison purposes, the HSCISCF trial wavefunction isomerization energies are 59.2 and 55.7 kcal/mol for BS2 and BS3 respectively.

We further apply our ph-AFQMC implementation to computing the isomerization energy towards the complete basis set (CBS) limit. ANO-RCC-VQZP involves correlation space of (32e,280o) and (52e,290o). We computed the correlation energy of TZ and QZ using the mean-field energy computed by the dominiant determinant. These correlation energies were extrapolated to the CBS limit using $1/Z^{3}$ where $Z$ is the cardinality of basis sets.(Helgaker et al., 1997; Halkier et al., 1998) We then combine the CBS limit correlation energy with the QZ mean-field energy to compute the final CBS total energy.

As shown in Table 2, for ANO-RCC-VQZP, the ph-AFQMC isomerization energy changes less than 1 kcal/mol going from $10^{5}$ to $10^{6}$ determinants similarly to ANO-RCC-VTZP. Similarly, our CBS estimates also show a small change between $10^{5}$ and $10^{6}$ determinants. In the CBS limit, our best estimate for the isomerization energy with 32 electrons correlated is 26.0(7) kcal/mol. Given the comparison against fp-AFQMC for small bases and the energy change smaller than 1 m $E_{h}$ between $10^{5}$ and $10^{6}$ determinants, we think our ph-AFQMC CBS correlation energy for both $f=0$ and $f=1$ is converged better than 1 m $E_{h}$ . In Table 3, we present a similar result where 52 electrons are correlated. While we observe quantitative differences between Table 2 and Table 3, the qualitative behavior as a function of $N_{\text{det}}$ is similar. Our best theoretical estimate for the isomerization with 52-electron correlation space is 29(1) kcal/mol. We expect our estimate of the isomerization energy for 32- and 52-electron correlation space in the CBS limit to be nearly within its statistical error bar from the exact theoretical answer. We emphasize that such reliable high-level calculations have never been possible with other single- and multi-reference methods such as density matrix renormalization group Yanai et al. (2010); Phung et al. (2016) or high-order coupled-cluster theory in such large correlation spaces.Cramer et al. (2006); Malmqvist et al. (2008); Zou et al. (2022) Finally, Table 4 provides some comparison between ph-AFQMC, ph-AFQMC and CCSD(T) in these larger correlation spaces.

V Conclusions

In this paper, we report a Python implementation of ph-AFQMC, ipie, that can efficiently run on both CPU and GPU. ipie offers flexible development environment utilizing Python infrastructure as well as sufficient performance for production use. In ipie, we make an extensive use of NumPy for CPU and CuPy for GPU and sometimes rely on Numba’s jit capability for certain computational kernels. Our preliminary implementation achieves similar or better CPU and GPU performance compared to other C++ codes such as QMPACK and Dice. For CPU, our code significantly accelerates prototyping new theoretical developments pertinent to ph-AFQMC due to the flexibility provided by Python. For GPU, we only had to write a few customized CUDA kernels. For instance, for SD trials, we only needed one customized CUDA kernel written with Numba’s cuda.jit for the local energy evaluation. This is in contrast to Refs. 52; 66, which were written in C++. These C++ implementations relied on many customized CUDA kernels which we could avoid largely due to CuPy handling complex tensor operations.

Using ipie, we also reported new ph-AFQMC results using HCISCF trials on \ce[Cu2O2]^2+ where ph-AFQMC isomerization energies could be converged to exact answers whenever these are available from unbiased fp-AFQMC.Mahajan and Sharma (2021) Furthermore, we report isomerization energies with QZ and in the basis set limit. The largest correlation calculation involves $10^{6}$ determinants in trial, 52 electrons, and 290 orbitals. We expect our isomerization energies are better than 1 kcal/mol from the exact answer given the relatively small changes observed when increasing the number of determinants in our trial. Since \ce[Cu2O2]^2+ is an example where ph-AFQMC with other trial wavefunctions is significantly inaccurateLandinez Borda et al. (2019) and other multi-reference perturbation theory methods fail, our results highlight the utility of ph-AFQMC with HCISCF trials.

We plan to expand our code’s capability to finite-temperature ph-AFQMC,Lee et al. (2021a) electron-phonon problems,Lee et al. (2021b) lattice Hamiltonians, and other QMC methods in the future. We hope that our open-source package, ipie (https://github.com/linusjoonho/ipie), will gain larger user and developer bases and will ultimately serve as a community code for prototyping and applying ph-AFQMC in quantum chemistry.

VI Acknowledgements

We thank Hung Pham and Nick Rubin for initial involvement. J.L. thanks David Reichman and Ryan Babbush for encouragement and support. We thank Soojin Lee for the ipie logo design and illustration. The work of J.L. was supported in part by a Google research award.

VII Data Availability

The data that support the findings of this study are openly available in our Zenodo repository at https://doi.org/10.5281/zenodo.7061987.

References

Smith et al. (2018) Daniel G. A. Smith, Lori A. Burns, Dominic A. Sirianni, Daniel R. Nascimento, Ashutosh Kumar, Andrew M. James, Jeffrey B. Schriber, Tianyuan Zhang, Boyi Zhang, Adam S. Abbott, Eric J. Berquist, Marvin H. Lechner, Leonardo A. Cunha, Alexander G. Heide, Jonathan M. Waldrop, Tyler Y. Takeshita, Asem Alenaizan, Daniel Neuhauser, Rollin A. King, Andrew C. Simmonett, Justin M. Turney, Henry F. Schaefer, Francesco A. Evangelista, A. Eugene DePrince, T. Daniel Crawford, Konrad Patkowski, and C. David Sherrill, “Psi4NumPy: An Interactive Quantum Chemistry Programming Environment for Reference Implementations and Rapid Development,” J. Chem. Theory Comput. 14, 3504–3511 (2018).
Sun et al. (2020) Qiming Sun, Xing Zhang, Samragni Banerjee, Peng Bao, Marc Barbry, Nick S. Blunt, Nikolay A. Bogdanov, George H. Booth, Jia Chen, Zhi-Hao Cui, Janus J. Eriksen, Yang Gao, Sheng Guo, Jan Hermann, Matthew R. Hermes, Kevin Koh, Peter Koval, Susi Lehtola, Zhendong Li, Junzi Liu, Narbe Mardirossian, James D. McClain, Mario Motta, Bastien Mussard, Hung Q. Pham, Artem Pulkin, Wirawan Purwanto, Paul J. Robinson, Enrico Ronca, Elvira R. Sayfutyarova, Maximilian Scheurer, Henry F. Schurkus, James E. T. Smith, Chong Sun, Shi-Ning Sun, Shiv Upadhyay, Lucas K. Wagner, Xiao Wang, Alec White, James Daniel Whitfield, Mark J. Williamson, Sebastian Wouters, Jun Yang, Jason M. Yu, Tianyu Zhu, Timothy C. Berkelbach, Sandeep Sharma, Alexander Yu. Sokolov, and Garnet Kin-Lic Chan, “Recent developments in the PySCF program package,” J. Chem. Phys. 153, 024109 (2020).
pyq (2022a) See https://github.com/WagnerGroup/pyqmc for details on how to obtain the source code. (2022a), [Online; accessed 31. Aug. 2022].
pyq (2022b) See https://github.com/gabrielelanaro/pyquante for details on how to obtain the source code. (2022b), [Online; accessed 31. Aug. 2022].
pyq (2022c) See https://github.com/rpmuller/pyquante2 for details on how to obtain the source code. (2022c), [Online; accessed 31. Aug. 2022].
Poole et al. (2020) David Poole, Jorge L. Galvez Vallejo, and Mark S. Gordon, “A New Kid on the Block: Application of Julia to Hartree–Fock Calculations,” J. Chem. Theory Comput. 16, 5006–5013 (2020).
Poole et al. (2022) David Poole, Jorge L. Galvez Vallejo, and Mark S. Gordon, “A Task-Based Approach to Parallel Restricted Hartree–Fock Calculations,” J. Chem. Theory Comput. 18, 2144–2161 (2022).
Aroeira et al. (2022) Gustavo J. R. Aroeira, Matthew M. Davis, Justin M. Turney, and Henry F. Schaefer, “Fermi.jl: A Modern Design for Quantum Chemistry,” J. Chem. Theory Comput. 18, 677–686 (2022).
Fishman et al. (2020) Matthew Fishman, Steven R. White, and E. Miles Stoudenmire, “The ITensor software library for tensor network calculations,” (2020), arXiv:2007.14822 .
Koonin et al. (2013) S. E. Koonin, G. Sugiyama, H. Friedrichl, and W. K. Kellogg, “Auxiliary-Field Quantum Monte Carlo for Correlated Electron Systems,” in Emergent Phenomena in Correlated Matter: Autumn School organized by the Forschungszentrum Jülich and the German Research School for Simulation Jülich 23 – 27 September 2013 (Forschungszentrum Jülich, 2013) p. 15.1.
Simons Collaboration on the Many-Electron Problem et al. (2015) Simons Collaboration on the Many-Electron Problem, J. P. F. LeBlanc, Andrey E. Antipov, Federico Becca, Ireneusz W. Bulik, Garnet Kin-Lic Chan, Chia-Min Chung, Youjin Deng, Michel Ferrero, Thomas M. Henderson, Carlos A. Jiménez-Hoyos, E. Kozik, Xuan-Wen Liu, Andrew J. Millis, N. V. Prokof’ev, Mingpu Qin, Gustavo E. Scuseria, Hao Shi, B. V. Svistunov, Luca F. Tocchio, I. S. Tupitsyn, Steven R. White, Shiwei Zhang, Bo-Xiao Zheng, Zhenyue Zhu, and Emanuel Gull, “Solutions of the Two-Dimensional Hubbard Model: Benchmarks and Results from a Wide Range of Numerical Algorithms,” Phys. Rev. X 5, 041041 (2015).
Motta and Zhang (2018) Mario Motta and Shiwei Zhang, “Ab initio computations of molecular systems by the auxiliary-field quantum Monte Carlo method,” WIREs Comput. Mol. Sci. 8, e1364 (2018).
Simons Collaboration on the Many-Electron Problem et al. (2020a) Simons Collaboration on the Many-Electron Problem, Mingpu Qin, Chia-Min Chung, Hao Shi, Ettore Vitali, Claudius Hubig, Ulrich Schollwöck, Steven R. White, and Shiwei Zhang, “Absence of Superconductivity in the Pure Two-Dimensional Hubbard Model,” Phys. Rev. X 10, 031016 (2020a).
Shi and Zhang (2021) Hao Shi and Shiwei Zhang, “Some recent developments in auxiliary-field quantum Monte Carlo for real materials,” J. Chem. Phys. 154, 024107 (2021).
Lee et al. (2022a) Joonho Lee, Hung Q Pham, and David R Reichman, “Twenty years of auxiliary-field quantum monte carlo in quantum chemistry: An overview and assessment on main group chemistry and bond-breaking,” arXiv preprint arXiv:2208.01280 (2022a).
Zhang et al. (1995) Shiwei Zhang, J. Carlson, and J. E. Gubernatis, “Constrained Path Quantum Monte Carlo Method for Fermion Ground States,” Phys. Rev. Lett. 74, 3652–3655 (1995).
Zhang and Krakauer (2003) Shiwei Zhang and Henry Krakauer, “Quantum Monte Carlo Method using Phase-Free Random Walks with Slater Determinants,” Phys. Rev. Lett. 90, 136401 (2003).
Simons Collaboration on the Many-Electron Problem et al. (2020b) Simons Collaboration on the Many-Electron Problem, Kiel T. Williams, Yuan Yao, Jia Li, Li Chen, Hao Shi, Mario Motta, Chunyao Niu, Ushnish Ray, Sheng Guo, Robert J. Anderson, Junhao Li, Lan Nguyen Tran, Chia-Nan Yeh, Bastien Mussard, Sandeep Sharma, Fabien Bruneval, Mark van Schilfgaarde, George H. Booth, Garnet Kin-Lic Chan, Shiwei Zhang, Emanuel Gull, Dominika Zgid, Andrew Millis, Cyrus J. Umrigar, and Lucas K. Wagner, “Direct Comparison of Many-Body Methods for Realistic Electronic Hamiltonians,” Phys. Rev. X 10, 011041 (2020b).
Nguyen et al. (2014) Huy Nguyen, Hao Shi, Jie Xu, and Shiwei Zhang, “CPMC-Lab: A Matlab package for Constrained Path Monte Carlo calculations,” Comput. Phys. Commun. 185, 3344–3357 (2014).
Kim et al. (2018) Jeongnim Kim, Andrew D Baczewski, Todd D Beaudet, Anouar Benali, M Chandler Bennett, Mark A Berrill, Nick S Blunt, Edgar Josué Landinez Borda, Michele Casula, David M Ceperley, et al., “Qmcpack: an open source ab initio quantum monte carlo package for the electronic structure of atoms, molecules and solids,” J. Phys. Cond. Mat. 30, 195901 (2018).
Kent et al. (2020) P. R. C. Kent, Abdulgani Annaberdiyev, Anouar Benali, M. Chandler Bennett, Edgar Josué Landinez Borda, Peter Doak, Hongxia Hao, Kenneth D. Jordan, Jaron T. Krogel, Ilkka Kylänpää, Joonho Lee, Ye Luo, Fionn D. Malone, Cody A. Melton, Lubos Mitas, Miguel A. Morales, Eric Neuscamman, Fernando A. Reboredo, Brenda Rubenstein, Kayahan Saritas, Shiv Upadhyay, Guangming Wang, Shuai Zhang, and Luning Zhao, “QMCPACK: Advances in the development, efficiency, and application of auxiliary field and real-space variational and diffusion quantum Monte Carlo,” J. Chem. Phys. 152, 174105 (2020).
pau (2022) See https://github.com/pauxy-qmc/pauxy for details on how to obtain the source code. (2022), [Online; accessed 31. Aug. 2022].
dic (2022) See https://github.com/sanshar/Dice for details on how to obtain the source code. (2022), [Online; accessed 31. Aug. 2022].
ipi (2022) See https://github.com/linusjoonho/ipie for details on how to obtain the source code. (2022), [Online; accessed 31. Aug. 2022].
Lee et al. (2019) Joonho Lee, Fionn D. Malone, and Miguel A. Morales, “An auxiliary-Field quantum Monte Carlo perspective on the ground state of the dense uniform electron gas: An investigation with Hartree-Fock trial wavefunctions,” J. Chem. Phys. 151, 064122 (2019).
Lee and Reichman (2020) Joonho Lee and David R. Reichman, “Stochastic resolution-of-the-identity auxiliary-field quantum Monte Carlo: Scaling reduction without overhead,” J. Chem. Phys. 153, 044131 (2020).
Lee et al. (2021a) Joonho Lee, Miguel A. Morales, and Fionn D. Malone, “A phaseless auxiliary-field quantum Monte Carlo perspective on the uniform electron gas at finite temperatures: Issues, observations, and benchmark study,” J. Chem. Phys. 154, 064109 (2021a).
Lee et al. (2021b) Joonho Lee, Shiwei Zhang, and David R. Reichman, “Constrained-path auxiliary-field quantum Monte Carlo for coupled electrons and phonons,” Phys. Rev. B 103, 115123 (2021b).
Lee et al. (2021c) Joonho Lee, Fionn D. Malone, Miguel A. Morales, and David R. Reichman, “Spectral Functions from Auxiliary-Field Quantum Monte Carlo without Analytic Continuation: The Extended Koopmans’ Theorem Approach,” J. Chem. Theory Comput. 17, 3372–3387 (2021c).
Harris et al. (2020) Charles R. Harris, K. Jarrod Millman, Stéfan J. van der Walt, Ralf Gommers, Pauli Virtanen, David Cournapeau, Eric Wieser, Julian Taylor, Sebastian Berg, Nathaniel J. Smith, Robert Kern, Matti Picus, Stephan Hoyer, Marten H. van Kerkwijk, Matthew Brett, Allan Haldane, Jaime Fernández del Río, Mark Wiebe, Pearu Peterson, Pierre Gérard-Marchant, Kevin Sheppard, Tyler Reddy, Warren Weckesser, Hameer Abbasi, Christoph Gohlke, and Travis E. Oliphant, “Array programming with NumPy,” Nature 585, 357–362 (2020).
Nishino and Loomis (2017) ROYUD Nishino and Shohei Hido Crissman Loomis, “Cupy: A numpy-compatible library for nvidia gpu calculations,” 31st confernce on neural information processing systems 151 (2017).
Lam et al. (2015) Siu Kwan Lam, Antoine Pitrou, and Stanley Seibert, “Numba: A llvm-based python jit compiler,” in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC (2015) pp. 1–6.
Huggins et al. (2022) William J. Huggins, Bryan A. O’Gorman, Nicholas C. Rubin, David R. Reichman, Ryan Babbush, and Joonho Lee, “Unbiasing fermionic quantum Monte Carlo with a quantum computer,” Nature 603, 416–420 (2022).
Lee et al. (2022b) Joonho Lee, David R. Reichman, Ryan Babbush, Nicholas C. Rubin, Fionn D. Malone, Bryan O’Gorman, and William J. Huggins, “Response to ”Exponential challenges in unbiasing quantum Monte Carlo algorithms with quantum computers”,” ArXiv (2022b), 10.48550/arXiv.2207.13776, 2207.13776 .
quantumlib (2022a) quantumlib, “Cirq,” (2022a), [Online; accessed 31. Aug. 2022].
Qiskit (2022) Qiskit, “qiskit-terra,” (2022), [Online; accessed 31. Aug. 2022].
quantumlib (2022b) quantumlib, “qsim,” (2022b), [Online; accessed 31. Aug. 2022].
Rubin et al. (2021) Nicholas C. Rubin, Klaas Gunst, Alec White, Leon Freitag, Kyle Throssell, Garnet Kin-Lic Chan, Ryan Babbush, and Toru Shiozaki, “The Fermionic Quantum Emulator,” Quantum 5, 568 (2021), 2104.13944v2 .
Stair and Evangelista (2022) Nicholas H. Stair and Francesco A. Evangelista, “QForte: An Efficient State-Vector Emulator and Quantum Algorithms Library for Molecular Electronic Structure,” J. Chem. Theory Comput. 18, 1555–1568 (2022).
Mahajan et al. (2022) Ankit Mahajan, Joonho Lee, and Sandeep Sharma, “Selected configuration interaction wave functions in phaseless auxiliary field quantum Monte Carlo,” J. Chem. Phys. 156, 174111 (2022).
Trotter (1959) H. F. Trotter, “On the Product of Semi-Groups of Operators,” Proc. Amer. Math. Soc. 10, 545–551 (1959).
Hubbard (1959) J. Hubbard, “Calculation of partition functions,” Phys. Rev. Lett. 3, 77 (1959).
Mahajan and Sharma (2021) Ankit Mahajan and Sandeep Sharma, “Taming the Sign Problem in Auxiliary-Field Quantum Monte Carlo Using Accurate Wave Functions,” J. Chem. Theory Comput. 17, 4786–4798 (2021).
Purwanto and Zhang (2004) Wirawan Purwanto and Shiwei Zhang, “Quantum Monte Carlo method for the ground state of many-boson systems,” Phys. Rev. E 70, 056702 (2004).
Motta et al. (2019) Mario Motta, James Shee, Shiwei Zhang, and Garnet Kin-Lic Chan, “Efficient Ab Initio Auxiliary-Field Quantum Monte Carlo Calculations in Gaussian Bases via Low-Rank Tensor Decomposition,” J. Chem. Theory Comput. 15, 3510–3521 (2019).
Malone et al. (2019) Fionn D. Malone, Shuai Zhang, and Miguel A. Morales, “Overcoming the Memory Bottleneck in Auxiliary Field Quantum Monte Carlo Simulations with Interpolative Separable Density Fitting,” J. Chem. Theory Comput. 15, 256–264 (2019).
Weber et al. (2022) John L. Weber, Hung Vuong, Pierre A. Devlaminck, James Shee, Joonho Lee, David R. Reichman, and Richard A. Friesner, “A Localized-Orbital Energy Evaluation for Auxiliary-Field Quantum Monte Carlo,” J. Chem. Theory Comput. 18, 3447–3459 (2022).
Epifanovsky et al. (2021) Evgeny Epifanovsky, Andrew T. B. Gilbert, Xintian Feng, Joonho Lee, Yuezhi Mao, Narbe Mardirossian, Pavel Pokhilko, Alec F. White, Marc P. Coons, Adrian L. Dempwolff, Zhengting Gan, Diptarka Hait, Paul R. Horn, Leif D. Jacobson, Ilya Kaliman, Jörg Kussmann, Adrian W. Lange, Ka Un Lao, Daniel S. Levine, Jie Liu, Simon C. McKenzie, Adrian F. Morrison, Kaushik D. Nanda, Felix Plasser, Dirk R. Rehn, Marta L. Vidal, Zhi-Qiang You, Ying Zhu, Bushra Alam, Benjamin J. Albrecht, Abdulrahman Aldossary, Ethan Alguire, Josefine H. Andersen, Vishikh Athavale, Dennis Barton, Khadiza Begam, Andrew Behn, Nicole Bellonzi, Yves A. Bernard, Eric J. Berquist, Hugh G. A. Burton, Abel Carreras, Kevin Carter-Fenk, Romit Chakraborty, Alan D. Chien, Kristina D. Closser, Vale Cofer-Shabica, Saswata Dasgupta, Marc de Wergifosse, Jia Deng, Michael Diedenhofen, Hainam Do, Sebastian Ehlert, Po-Tung Fang, Shervin Fatehi, Qingguo Feng, Triet Friedhoff, James Gayvert, Qinghui Ge, Gergely Gidofalvi, Matthew Goldey, Joe Gomes, Cristina E. González-Espinoza, Sahil Gulania, Anastasia O. Gunina, Magnus W. D. Hanson-Heine, Phillip H. P. Harbach, Andreas Hauser, Michael F. Herbst, Mario Hernández Vera, Manuel Hodecker, Zachary C. Holden, Shannon Houck, Xunkun Huang, Kerwin Hui, Bang C. Huynh, Maxim Ivanov, Ádám Jász, Hyunjun Ji, Hanjie Jiang, Benjamin Kaduk, Sven Kähler, Kirill Khistyaev, Jaehoon Kim, Gergely Kis, Phil Klunzinger, Zsuzsanna Koczor-Benda, Joong Hoon Koh, Dimitri Kosenkov, Laura Koulias, Tim Kowalczyk, Caroline M. Krauter, Karl Kue, Alexander Kunitsa, Thomas Kus, István Ladjánszki, Arie Landau, Keith V. Lawler, Daniel Lefrancois, Susi Lehtola, Run R. Li, Yi-Pei Li, Jiashu Liang, Marcus Liebenthal, Hung-Hsuan Lin, You-Sheng Lin, Fenglai Liu, Kuan-Yu Liu, Matthias Loipersberger, Arne Luenser, Aaditya Manjanath, Prashant Manohar, Erum Mansoor, Sam F. Manzer, Shan-Ping Mao, Aleksandr V. Marenich, Thomas Markovich, Stephen Mason, Simon A. Maurer, Peter F. McLaughlin, Maximilian F. S. J. Menger, Jan-Michael Mewes, Stefanie A. Mewes, Pierpaolo Morgante, J. Wayne Mullinax, Katherine J. Oosterbaan, Garrette Paran, Alexander C. Paul, Suranjan K. Paul, Fabijan Pavošević, Zheng Pei, Stefan Prager, Emil I. Proynov, Ádám Rák, Eloy Ramos-Cordoba, Bhaskar Rana, Alan E. Rask, Adam Rettig, Ryan M. Richard, Fazle Rob, Elliot Rossomme, Tarek Scheele, Maximilian Scheurer, Matthias Schneider, Nickolai Sergueev, Shaama M. Sharada, Wojciech Skomorowski, David W. Small, Christopher J. Stein, Yu-Chuan Su, Eric J. Sundstrom, Zhen Tao, Jonathan Thirman, Gábor J. Tornai, Takashi Tsuchimochi, Norm M. Tubman, Srimukh Prasad Veccham, Oleg Vydrov, Jan Wenzel, Jon Witte, Atsushi Yamada, Kun Yao, Sina Yeganeh, Shane R. Yost, Alexander Zech, Igor Ying Zhang, Xing Zhang, Yu Zhang, Dmitry Zuev, Alán Aspuru-Guzik, Alexis T. Bell, Nicholas A. Besley, Ksenia B. Bravaya, Bernard R. Brooks, David Casanova, Jeng-Da Chai, Sonia Coriani, Christopher J. Cramer, György Cserey, A. Eugene DePrince, Robert A. DiStasio, Andreas Dreuw, Barry D. Dunietz, Thomas R. Furlani, William A. Goddard, Sharon Hammes-Schiffer, Teresa Head-Gordon, Warren J. Hehre, Chao-Ping Hsu, Thomas-C. Jagau, Yousung Jung, Andreas Klamt, Jing Kong, Daniel S. Lambrecht, WanZhen Liang, Nicholas J. Mayhall, C. William McCurdy, Jeffrey B. Neaton, Christian Ochsenfeld, John A. Parkhill, Roberto Peverati, Vitaly A. Rassolov, Yihan Shao, Lyudmila V. Slipchenko, Tim Stauch, Ryan P. Steele, Joseph E. Subotnik, Alex J. W. Thom, Alexandre Tkatchenko, Donald G. Truhlar, Troy Van Voorhis, Tomasz A. Wesolowski, K. Birgitta Whaley, H. Lee Woodcock, Paul M. Zimmerman, Shirin Faraji, Peter M. W. Gill, Martin Head-Gordon, John M. Herbert, and Anna I. Krylov, “Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package,” J. Chem. Phys. 155, 084801 (2021).
Flyvbjerg and Petersen (1989) Henrik Flyvbjerg and Henrik Gordon Petersen, “Error estimates on averages of correlated data,” J. Chem. Phys. 91, 461–466 (1989).
Motta and Zhang (2017) Mario Motta and Shiwei Zhang, “Computation of Ground-State Properties in Molecular Systems: Back-Propagation with Auxiliary-Field Quantum Monte Carlo,” J. Chem. Theory Comput. 13, 5367–5378 (2017).
Sorella and Capriotti (2010) Sandro Sorella and Luca Capriotti, “Algorithmic differentiation and the calculation of forces by quantum Monte Carlo,” J. Chem. Phys. 133, 234111 (2010).
Shee et al. (2018) James Shee, Evan J. Arthur, Shiwei Zhang, David R. Reichman, and Richard A. Friesner, “Phaseless Auxiliary-Field Quantum Monte Carlo on Graphical Processing Units,” J. Chem. Theory Comput. 14, 4109–4121 (2018).
Holmes et al. (2016) Adam A. Holmes, Norm M. Tubman, and C. J. Umrigar, “Heat-Bath Configuration Interaction: An Efficient Selected Configuration Interaction Algorithm Inspired by Heat-Bath Sampling,” J. Chem. Theory Comput. 12, 3674–3680 (2016).
Smith et al. (2017) James E. T. Smith, Bastien Mussard, Adam A. Holmes, and Sandeep Sharma, “Cheap and Near Exact CASSCF with Large Active Spaces,” J. Chem. Theory Comput. 13, 5468–5478 (2017).
Cramer et al. (2006) Christopher J. Cramer, Marta Włoch, Piotr Piecuch, Cristina Puzzarini, and Laura Gagliardi, “Theoretical Models on the Cu2O2 Torture Track: Mechanistic Implications for Oxytyrosinase and Small-Molecule Analogues,” J. Phys. Chem. A 110, 1991–2004 (2006).
Solomon et al. (1992) Edward I. Solomon, Michael J. Baldwin, and Michael D. Lowery, “Electronic structures of active sites in copper proteins: contributions to reactivity,” Chem. Rev. 92, 521–542 (1992).
Fdez. Galván et al. (2019) Ignacio Fdez. Galván, Morgane Vacher, Ali Alavi, Celestino Angeli, Francesco Aquilante, Jochen Autschbach, Jie J. Bao, Sergey I. Bokarev, Nikolay A. Bogdanov, Rebecca K. Carlson, Liviu F. Chibotaru, Joel Creutzberg, Nike Dattani, Mickaël G. Delcey, Sijia S. Dong, Andreas Dreuw, Leon Freitag, Luis Manuel Frutos, Laura Gagliardi, Frédéric Gendron, Angelo Giussani, Leticia González, Gilbert Grell, Meiyuan Guo, Chad E. Hoyer, Marcus Johansson, Sebastian Keller, Stefan Knecht, Goran Kovačević, Erik Källman, Giovanni Li Manni, Marcus Lundberg, Yingjin Ma, Sebastian Mai, João Pedro Malhado, Per Åke Malmqvist, Philipp Marquetand, Stefanie A. Mewes, Jesper Norell, Massimo Olivucci, Markus Oppel, Quan Manh Phung, Kristine Pierloot, Felix Plasser, Markus Reiher, Andrew M. Sand, Igor Schapiro, Prachi Sharma, Christopher J. Stein, Lasse Kragh Sørensen, Donald G. Truhlar, Mihkel Ugandi, Liviu Ungur, Alessio Valentini, Steven Vancoillie, Valera Veryazov, Oskar Weser, Tomasz A. Wesołowski, Per-Olof Widmark, Sebastian Wouters, Alexander Zech, J. Patrick Zobel, and Roland Lindh, “OpenMolcas: From Source Code to Insight,” J. Chem. Theory Comput. 15, 5925–5964 (2019).
Montgomery et al. (2000) J. A. Montgomery, M. J. Frisch, J. W. Ochterski, and G. A. Petersson, “A complete basis set model chemistry. VII. Use of the minimum population localization method,” J. Chem. Phys. 112, 6532–6542 (2000).
Liu (2010) Wenjian Liu, “Ideas of relativistic quantum chemistry,” Mol. Phys. 108, 1679–1706 (2010).
Helgaker et al. (1997) Trygve Helgaker, Wim Klopper, Henrik Koch, and Jozef Noga, “Basis-set convergence of correlated calculations on water,” The Journal of chemical physics 106, 9639–9646 (1997).
Halkier et al. (1998) Asger Halkier, Trygve Helgaker, Poul Jørgensen, Wim Klopper, Henrik Koch, Jeppe Olsen, and Angela K Wilson, “Basis-set convergence in correlated calculations on ne, n2, and h2o,” Chemical Physics Letters 286, 243–252 (1998).
Yanai et al. (2010) Takeshi Yanai, Yuki Kurashige, Eric Neuscamman, and Garnet Kin-Lic Chan, “Multireference quantum chemistry through a joint density matrix renormalization group and canonical transformation theory,” J. Chem. Phys. 132, 024105 (2010).
Phung et al. (2016) Quan Manh Phung, Sebastian Wouters, and Kristine Pierloot, “Cumulant approximated second-order perturbation theory based on the density matrix renormalization group for transition metal complexes: A benchmark study,” J. Chem. Theory Comput. 12, 4352–4361 (2016).
Malmqvist et al. (2008) Per Åke Malmqvist, Kristine Pierloot, Abdul Rehaman Moughal Shahi, Christopher J. Cramer, and Laura Gagliardi, “The restricted active space followed by second-order perturbation theory method: Theory and application to the study of CuO2 and Cu2O2 systems,” J. Chem. Phys. 128, 204109 (2008).
Zou et al. (2022) Jingxiang Zou, Qingchun Wang, Xiaochuan Ren, Yuqi Wang, Haodong Zhang, and Shuhua Li, “Efficient implementation of block-correlated coupled cluster theory based on the generalized valence bond reference for strongly correlated systems,” J. Chem. Theory Comput. 18, 5276–5285 (2022).
Malone et al. (2020) Fionn D. Malone, Shuai Zhang, and Miguel A. Morales, “Accelerating Auxiliary-Field Quantum Monte Carlo Simulations of Solids with Graphical Processing Units,” J. Chem. Theory Comput. 16, 4286–4297 (2020).
Landinez Borda et al. (2019) Edgar Josué Landinez Borda, John Gomez, and Miguel A. Morales, “Non-orthogonal multi-Slater determinant expansions in auxiliary field quantum Monte Carlo,” J. Chem. Phys. 150, 074105 (2019).

	$\displaystyle\langle\Psi_{T}\|\phi_{z}\rangle E_{L,2}^{z}=$	$\displaystyle-\frac{1}{2}\langle\psi_{0}\|\phi_{z}\rangle\sum_{prqs}\sum_{\alpha=1}^{N_{\text{aux}}}\sum_{a=0}^{N_{\text{det}}-1}$
		$\displaystyle\bigg{(}c_{a}\frac{\langle\psi_{0}\|\hat{t}_{a}^{\dagger}\hat{a}^{\dagger}_{p}\hat{a}_{r}\hat{a}_{q}^{\dagger}\hat{a}_{s}\|\phi_{z}\rangle}{\langle\psi_{0}\|\phi_{z}\rangle}L_{pr}^{\alpha}L_{qs}^{\alpha}\bigg{)}.$		(30)